Algorytmy wyznaczania

dyskretnej transformaty

Fouriera

2

Metoda bezpośrednia i jej

złożoność obliczeniowa

 

 

1

,...,

2

,

1

,

0

,

1

1

0















N

k

W

n

x

N

k

X

N

n

kn

N

N

j

N

e

W



2



 

 

 





 

 

 

 





































































































































n

x

x

x

x

W

W

W

W

W

W

W

W

W

N

N

X

X

X

X

N

N

N

N

N

N

N

N

N

N

N

N

N

N

N























2

1

0

1

1

1

1

1

1

1

1

1

2

1

0

)

1

)(

1

(

)

1

(

2

)

1

(

)

1

(

2

4

2

)

1

(

2

1

• Dyskretna transformacja Fouriera (DFT) dla

sygnału spróbkowanego x(n) ma postać:

, (1)

gdzie:

Równanie (1) można zapisać w postaci
macierzowej i ma ono postać :

(2)

3

Metoda bezpośrednia i jej

złożoność obliczeniowa

• Na podstawie N- próbek sygnału x(n) wyznaczamy N wartości

widma Fouriera X(k), a wyznaczenie dyskretnej transformaty

Fouriera X(k) sygnału x(n) metodą bezpośrednią sprowadza

się do realizacji numerycznej równania (1) zapisanego w

postaci macierzowej (2).

• Złożoność obliczeniowa DFT metodą bezpośrednią

rozwiązania równania (2) jest proporcjonalna do N2 i wynosi :

- N2 mnożeń liczb zespolonych oraz N(N-1) sumowań liczb

zespolonych,
czyli:
4N2 mnożeń liczb rzeczywistych i N(4N-2) sumowań liczb

rzeczywistych.

• Przykładowo dla ciągu próbek N = 256 mamy 65 536 mnożeń

i 65 280 sumowań, a dla N = 1024 otrzymamy 1 048 676

mnożeń i 1 047 552 sumowań.

4

• Liczba działań arytmetycznych bardzo

szybko rośnie wraz ze wzrostem próbek

sygnału dlatego ta metoda nie jest

stosowana w praktyce ze względu na

czasochłonne wykonywanie działań nawet

dla procesorów o wysokiej wydajności

• W analizie częstotliwościowej sygnałów

wykorzystuje się szybką transformatę

Fouriera (FFT), która daje identyczne

wyniki w znacznie krótszym czasie.

Metoda bezpośrednia i jej

złożoność obliczeniowa

5

Algorytmy FFT – ich podział

i ogólna idea

• Algorytm FFT (ang. Fast Fourier Transform) został

opracowany w roku 1965 roku przez dwóch

amerykańskich matematyków J. W. Cooleya i J.W.

Tukeya. Ich praca była wynikiem poszukiwań

szybszego wyznaczania DFT sygnału na

podstawie próbek z powodu mało efektywnej

metody bezpośredniej. To wydarzenie przyczyniło

się w bardzo dużym stopniu do rozwoju cyfrowego

przetwarzanie sygnału, ponieważ algorytm ten

pozwolił na radykalne zmniejszenie wymagań

sprzętowych do obliczenia DFT, a w konsekwencji

umożliwił szersze wykorzystanie.

6

Algorytmy FFT – ich podział

i ogólna idea

• Owoc pracy uczonych J. W. Cooleya i J.W. Tukeya

stał się podstawą całej grupy algorytmów FFT,

których wspólną cechą jest zastępowanie obliczeń

DFT o długości ciągu danych wejściowych N

odpowiednio krótszym ciągiem.

• Algorytmy FFT dzielą się na dwie grupy. Pierwsza

określana jest mianem algorytmów z podziałem

czasowym, w której ciąg x(n) dzielony jest na

coraz krótsze podciągi, w drugiej grupie – z

podziałem częstotliwościowym – dokonuje się

identycznego podziały pośród współczynników

X(n).

7

Algorytmy FFT – ich podział

i ogólna idea

• Aby wykorzystać ten algorytm do efektywnego

obliczenia DFT, trzeba spełnić kilka warunków, a

mianowicie:

- ciąg danych wejściowych x(n) musi mieć długość

równą potędze 2,
- kolejność próbek sygnału muszą być zmienione

zgodnie z odwrotną propagacją bitu przeniesienia

(reverse carry propagation), współczesne

procesory sygnałowe mają zaimplementowane

sprzętowo tą funkcję,
- obliczenia numeryczne można rozpocząć w

momencie zebrania wszystkich próbek sygnału.

8

Algorytmy FFT typu radix-2

(“dwie części”)

• Podział w dziedzinie czasu DIT (ang. Decimation In Time) –

w tym algorytmie próbki transformowanego sygnału dzieli

się na próbki o indeksach parzystych i nieparzystych i

dokonuje się wyznaczenia DFT dla obu tych zbiorów.

Odtworzenie widma sygnału otrzymuje się na podstawie

dwóch cząstkowych.

• W algorytmie radix 2 DIT (decymacja w czasie, czyli próbek

sygnału) wymagane jest by spróbkowany sygnał składał się

z N = 2p, następnie dysponując ciągiem próbek sygnału

x(n) :

– dokonuje się zmiany kolejności próbek, dzieląc je rekurencyjnie

na próbki o indeksach parzystych i nieparzystych, aż do

uzyskania zbiorów dwuelementowych,

– wykonuje się serię N/2 dwupunktowych DTF,

– następnie składa się widma dwukrążkowe w czteroprążkowe,

czteroprążkowe w ośmiokrążkowe itd., aż do uzyskania widma

N- prążkowego – pełnego widma sygnału.

9

Algorytmy FFT typu radix-2

(“dwie części”)

• Dla danego wektora danych wejściowych N mamy

etapów obliczeń, np. dla N = 8, mamy etapy:

(etap 1) – wykonanie serie czterech

dwupunktowych transformacji DFT, (etap 2) –

następnie 4 widma dwupunktowe złożyć w 2

czteropunktowe, (etap 3 ) – 2 widma

czteropunktowe złożyć w jedno widmo

ośmiopunktowe co dam nam pełne widmo

sygnału.

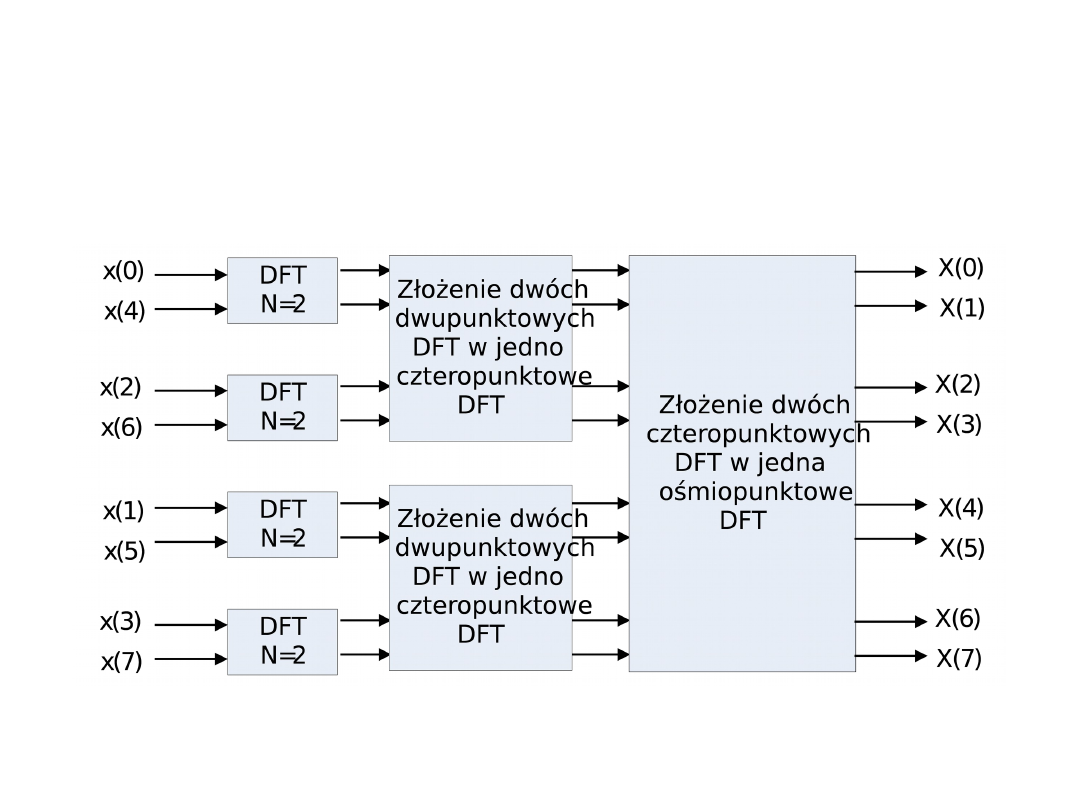
Na rysunku 1 przedstawiono uproszczony

schemat blokowy działania algorytmu.

10

Algorytmy FFT typu radix-2

(“dwie części”)

Rys.1.Uproszczony schemat blokowy algorytmu DIT FFT radix-2 dla N = 8

11

Wyprowadzenie algorytmu

radix – 2

 

 

1

,...,

2

,

1

,

0

,

1

0















N

k

W

n

x

k

X

N

n

kn

N

N

j

N

e

W



2



 

 





1

,...,

2

,

1

,

0

,

1

2

2

1

2

0

)

1

2

(

1

2

0

)

2

(





























N

k

W

n

x

W

n

x

k

X

N

n

n

k

N

N

n

n

k

N

• Przy wyprowadzeniu algebraicznym algorytmu

przyjęto założenie, że dzielenie przez N jakie

występuje w DFT wykonanie zostanie na końcu

obliczeń, obecnie zwracając uwagę na samo

równanie:

, (3)

• Dzielimy zgodnie z algorytmem próbki sygnału na

parzyste i nieparzyste:

(4)

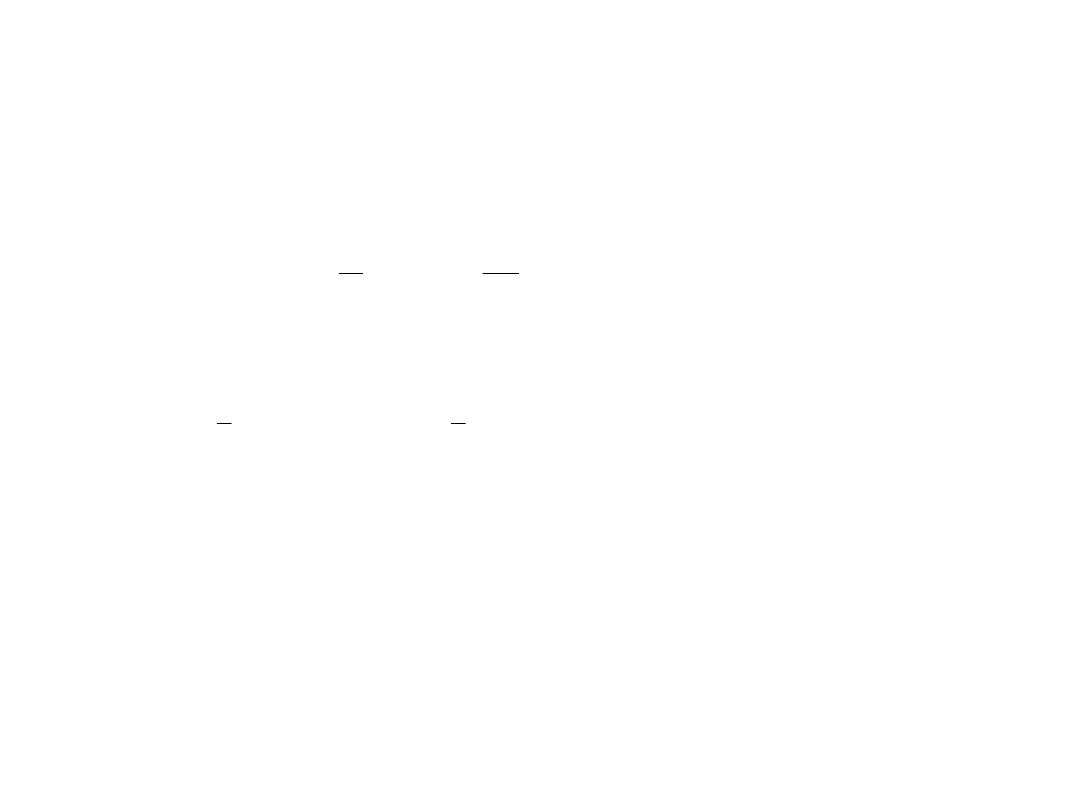
12

Wyprowadzenie algorytmu

radix – 2

kn

N

kn

N

kn

N

n

k

N

W

e

e

W







































2

/

)

(

2

/

2

)

2

(

2

2





 

 





1

,...,

2

,

1

,

0

,

1

2

2

1

2

0

2

/

1

2

0

2

/





































































N

k

W

n

x

W

W

n

x

k

X

N

n

kn

N

k

N

N

n

kn

N

• Korzystając z faktu :

,

stąd:

(5)

• W sumach znajdujących się w nawiasach kwadratowych

występuje N/2 punktowe równania DFT próbek parzystych i

nieparzystych. Istnieją jednak pewne różnice: w N/2

punktowym DFT indeks k zmienia się a w równaniu (5) od 0

do N-1. Dodatkowo brak jest dzielenia sum przez N/2. W

algorytmach DFT operacja ta jest wykonywana poza tokiem

obliczeniowym i dzieli się tylko otrzymany wynik.

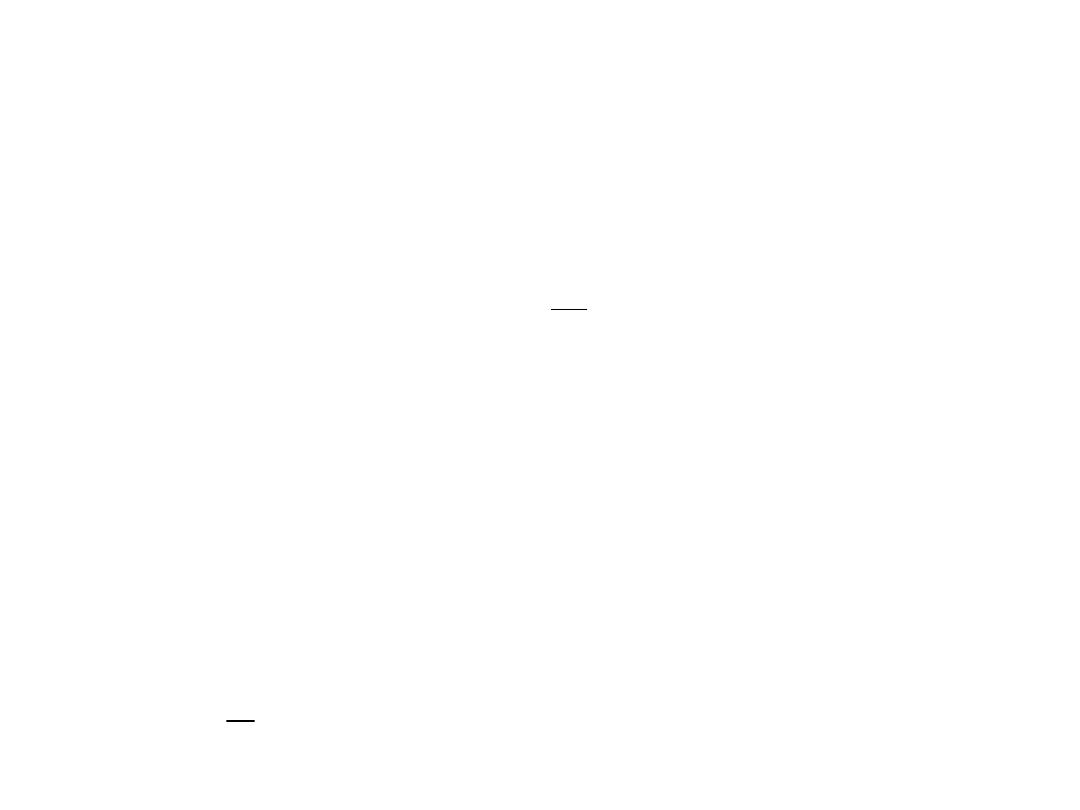
13

Wyprowadzenie algorytmu

radix – 2

kn

N

W



2

/





kn

N

n

kn

N

n

N

N

kn

N

n

N

N

kn

N

n

N

k

N

W

e

W

e

W

W

W

W

















 



















2

/

2

2

/

)

2

/

(

2

/

2

2

/

)

2

/

(

2

/

2

/

)

2

/

(

2

/





 

1

,...,

2

,

1

,

0

),

(

)

(

1

2

2













N

k

k

X

W

k

X

k

X

n

k

N

n

1

,...,

2

,

1

,

0

),

(

)

(

2

1

2

)

2

/

(

2



















 







N

k

k

X

W

k

X

N

k

X

n

N

k

N

n

• Przy zmniejszeniu indeksu k do N/2 -1 wykorzystuje się fakt iż

współczynnik ma okres N/2 ze względu na k:

dla k = 0,1,2,.., N/2 – 1 równanie (5) wygląda następująco:

(6)

X2n(k) i X2n+1(k) oznaczają N/2 punktowe nienormowane

(brak dzielenia przez N/2) transformaty DFT próbek

parzystych i nieparzystych.

Widmo X(k) dla k = N/2,…,N-1 wyznaczane jest z zależności:

(7)

14

Wyprowadzenie algorytmu

radix – 2

• Ponieważ :

Zatem równanie (7) można ostatecznie zapisać w
postaci:

• Wzory (6) i (7) można łącznie zapisać w postaci

macierzowej :

(8)

k

N

j

k

N

N

N

k

N

N

k

N

W

e

W

W

W

W

























2

/

)

2

/

(

1

,...,

2

,

1

,

0

),

(

)

(

2

1

2

2



















 





N

k

k

X

W

k

X

N

k

X

n

k

N

n

1

,...,

2

,

1

,

0

,

)

(

)

(

1

1

)

2

(

)

(

1

2

2























































N

k

k

X

k

X

W

W

N

k

X

k

X

n

n

k

N

k

N

15

Wyprowadzenie algorytmu

radix – 2

• Otrzymany wzór 8 jest prawdziwy dla na

wszystkich etapach dekompozycji. Na każdym
kolejnym etapie stosuje się podstawienie N= N/2,
czyli połowę N z etapu poprzedniego, aż uzyska się
N = 2. Jeżeli prążki widmowe X2n(k) i X2n+1(k)
złożymy razem jeden po drugim i wynikowy wektor
nazwiemy X(k) to wzór ten przyjmuję formę
rekurencyjną:

(9)

1

,...,

2

,

1

,

0

,

)

2

(

)

(

1

1

)

2

(

)

(

























































N

k

N

k

X

k

X

W

W

N

k

X

k

X

k

N

k

N

16

Wyprowadzenie algorytmu

radix – 2

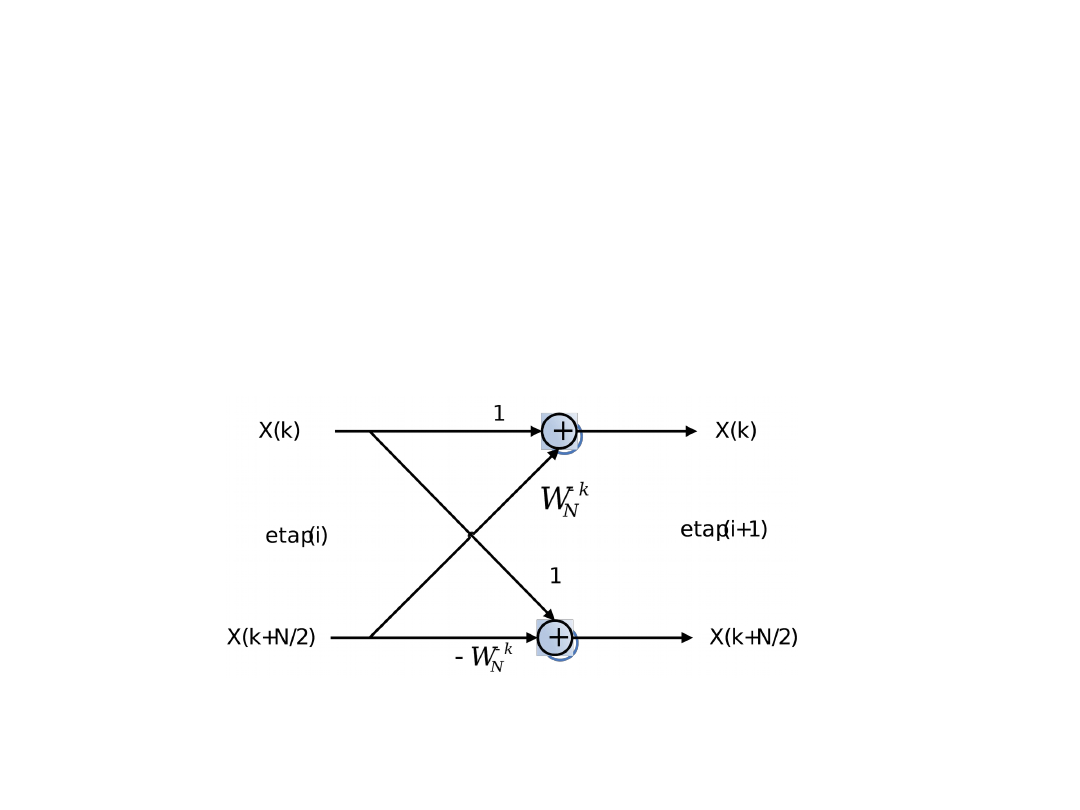
• Graficzna ilustracja tego równania została

przedstawiona poniżej.

Rys.2. Struktura obliczeniowa podstawowego bloku algorytmu DIT FFT radix-2, tzw. Motylek

17

Wyprowadzenie algorytmu

radix – 2

• Strukturę ta można uprościć wykorzystując

właściwości współczynnika :

Wzór (9) ma wówczas postać :

(10)

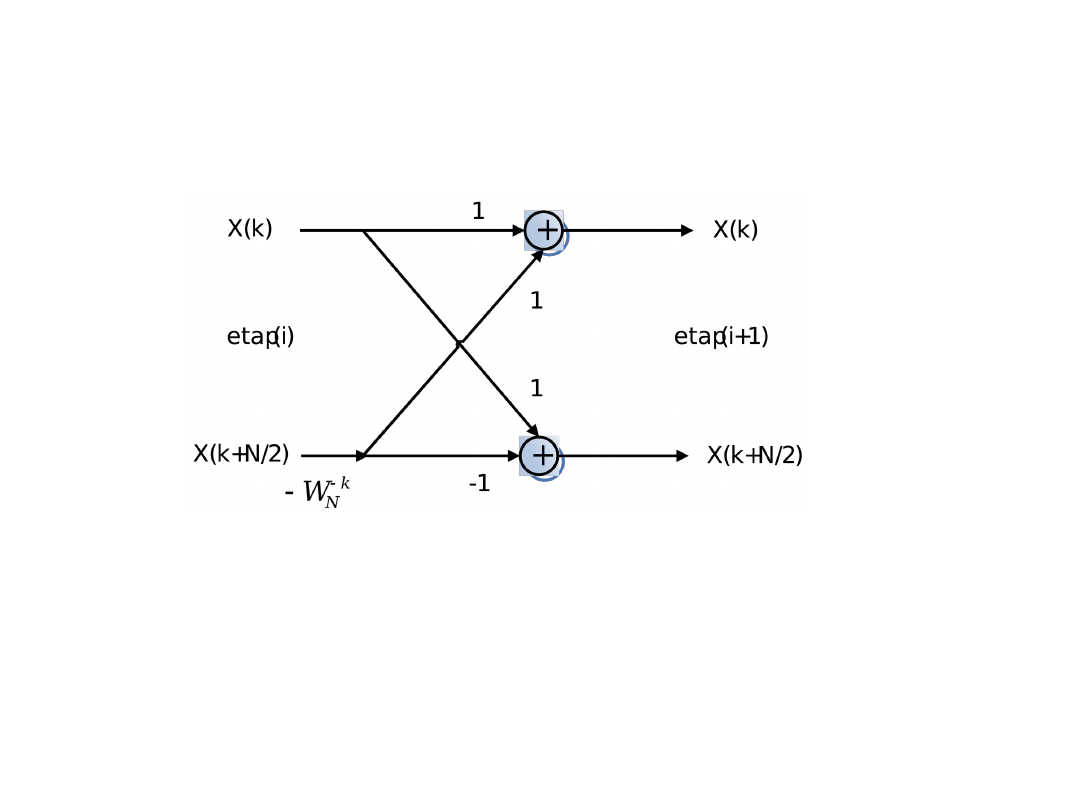
• Na podstawie wzoru (10 ) otrzymamy graf

przedstawiony na rys.3.

)

2

/

(

N

k

N

k

N

W

W











1

,...,

2

,

1

,

0

,

)

2

(

)

(

1

1

1

1

)

2

(

)

(

























































N

k

N

k

X

W

k

X

N

k

X

k

X

k

N

18

Wyprowadzenie algorytmu

radix – 2

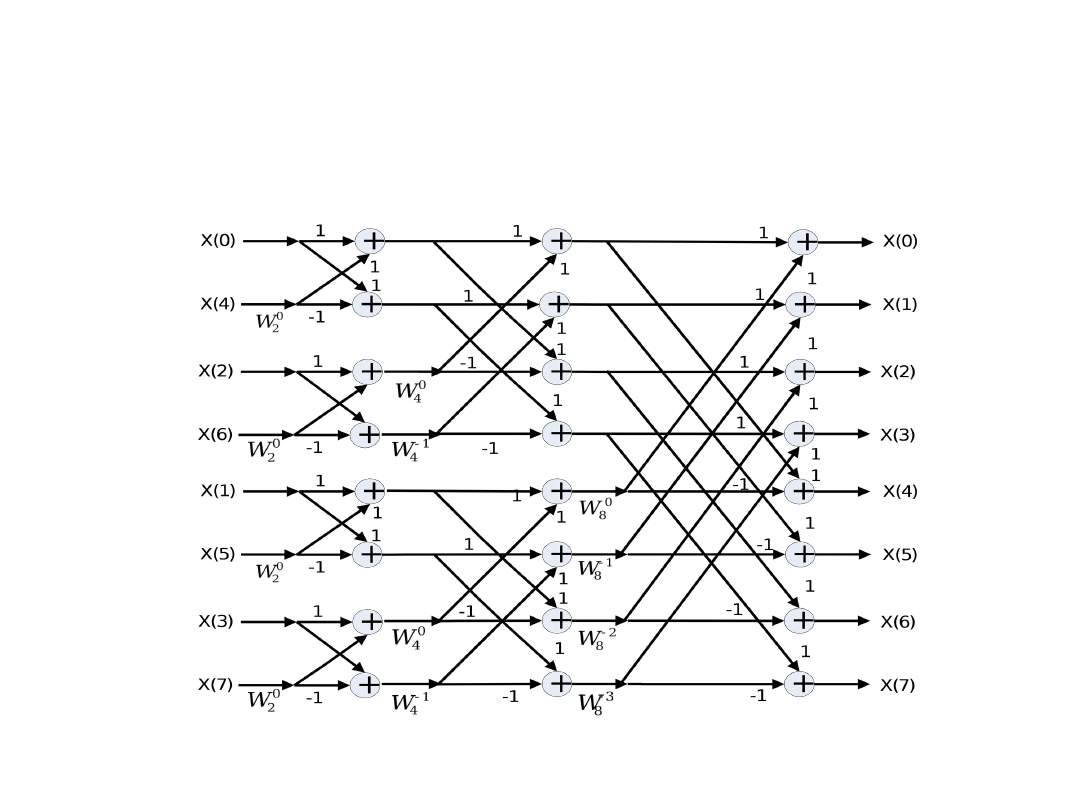
• Znając podstawową strukturę motylkową można pokusić się o

rozrysowanie pełnego algorytmu dla określonej liczby próbek.
Dla przykładu zostało to zrobione na rys. 4 wykorzystano strukturę

„uproszczony motylek” przy długości wektora danych N = 8.

Rys.3. Struktura obliczeniowa podstawowego bloku algorytmu DIT FFT radix-2, „uproszczony motylek”

19

Wyprowadzenie algorytmu

radix – 2

Rys.4. Pełny schemat blokowy algorytmu DIT FFT radix-2

20

Wyprowadzenie algorytmu

radix – 2

• Nietrudno zauważyć, że podstawowe obliczenia w algorytmie

radix-2 związane są ze struktura pojedynczego „motylka”,

zmiennie się tylko jego położenie i szerokość na poszczególnych

etapach.

• Ponadto aby uniknąć wielokrotnego wyznaczania wartości tych

samych próbek baz Fouriera w kolejnych etapach obliczeń, np.

z etapu pierwszego, z etapu drugiego itd., współczynniki te

są identyczne, więc można je wyznaczyć tylko raz na początku i

pobierać odpowiedni współczynnik dana z tego wektor.

• Złożoność obliczeniowa w algorytmie DIT FFT radix-2 wynosi:

• W przypadku zastosowania uproszczonego motylka

odpowiadającemu równaniu (10) liczba mnożeń zespolonych

maleje
z do .

1

4



W

2

8



W

N

N

2

log

N

N

2

log

N

N

2

log

)

2

/

(

21

Wyprowadzenie algorytmu

radix – 2

• Podział w dziedzinie częstotliwości DIF(ang.

Decimation In Frequency) – zasada dokonywania

obliczeń tym algorytmie jest analogiczna jak w w

poprzednio przedstawionym algorytmie DIT z ta

różnicą, że w tym przypadku nie dokonuje się

decymacji próbek sygnału x(n) lecz prążków widma

X(k).

• Wyznaczenie k-tego prążka X(k) widma Fouriera

wyznacza się na podstawie wzoru:

,

(11)

• Następnie oblicza się osobno prążki widma o

indeksach parzystych i nieparzystych:

 

 

1

,...,

2

,

1

,

0

,

1

0















N

k

W

n

x

k

X

N

n

kn

N

N

j

N

e

W



2



 

 





 

1

,...,

2

,

1

,

0

,

1

2

1

,...,

2

,

1

,

0

,

2

1

0

)

1

2

(

1

0

)

2

(

































N

k

W

n

x

k

X

N

k

W

n

x

k

X

N

n

k

n

N

N

n

k

n

N

22

Wyprowadzenie algorytmu

radix – 2

• Otrzymane wzory można zredukować dla wartości

k = 0,1,2,…,N/2-1, wtedy otrzymamy:

• Po dalszej redukcji zmiennych w zapisie sum

otrzymamy dla k= 0,1,2,…,N/2-1:

 

 

 





 

 















































1

2

/

)

1

2

(

1

2

/

0

)

1

2

(

1

2

/

)

2

(

1

2

/

0

)

2

(

1

2

2

N

N

n

k

n

N

N

n

k

n

N

N

N

n

k

n

N

N

n

k

n

N

W

n

x

W

n

x

k

X

W

n

x

W

n

x

k

X

 

 









 



























































1

2

/

0

)

1

2

)(

2

/

(

1

2

/

0

)

1

2

(

1

2

/

0

2

)

2

/

(

1

2

/

0

)

2

(

2

/

1

2

2

/

2

N

n

k

N

n

N

N

n

k

n

N

N

n

k

N

n

N

N

n

k

n

N

W

N

n

x

W

n

x

k

X

W

N

n

x

W

n

x

k

X

23

Wyprowadzenie algorytmu

radix – 2

• Wykorzystując własności współczynnika WN :

• Wzór na parzyste i nieparzyste prążki widma X(k)

przyjmuje postać dla k= 0,1,2,…,N/2-1:

kn

N

kn

N

kN

N

kn

N

N

n

k

N

W

W

W

W

W





















2

/

2

2

)

2

/

(

2

 

  







 





















































1

2

/

0

)

1

2

(

)

1

2

(

)

2

/

(

1

2

/

0

)

1

2

(

2

/

1

2

/

0

2

/

1

2

]

2

/

[

2

N

n

k

n

N

k

N

N

N

n

k

n

N

kn

N

N

n

W

N

n

x

W

W

n

x

k

X

W

N

n

x

n

x

k

X

24

Wyprowadzenie algorytmu

radix – 2

• Wykorzystując fakt, ze :

• Po prostych przekształceniach otrzymuję się

końcowy wzór na prążki widma o indeksach
nieparzystych dla k= 0,1,2,…,N/2-, który ma
postać:

1

)

1

)(

1

(

2

/

)

2

/

)(

1

2

(





















N

N

kN

N

N

k

N

W

W

W





  



  



  



kn

N

n

N

N

n

n

N

kn

N

N

n

n

k

N

N

n

W

W

N

n

x

n

x

W

W

N

n

x

n

x

W

N

n

x

n

x

k

X





















































2

/

1

2

/

0

2

1

2

/

0

)

1

2

(

1

2

/

0

}

]

2

/

{[

]

2

/

[

]

2

/

[

1

2

25

Wyprowadzenie algorytmu

radix – 2

• Zgodnie z otrzymanymi wzorami parzyste i nieparzyste

prążki widma Fouriera X(2k) i X(2k+1) można otrzymać w

wyniku transformacji DFT, która jest dokonywana dla

połowy próbek (N/2) sygnału wejściowego x(n).
Operacja ta nie jest jednak wykonywana na sygnale

oryginalnym lecz na sztucznie zmodyfikowanym zgodnie z

poniższymi zależnościami:

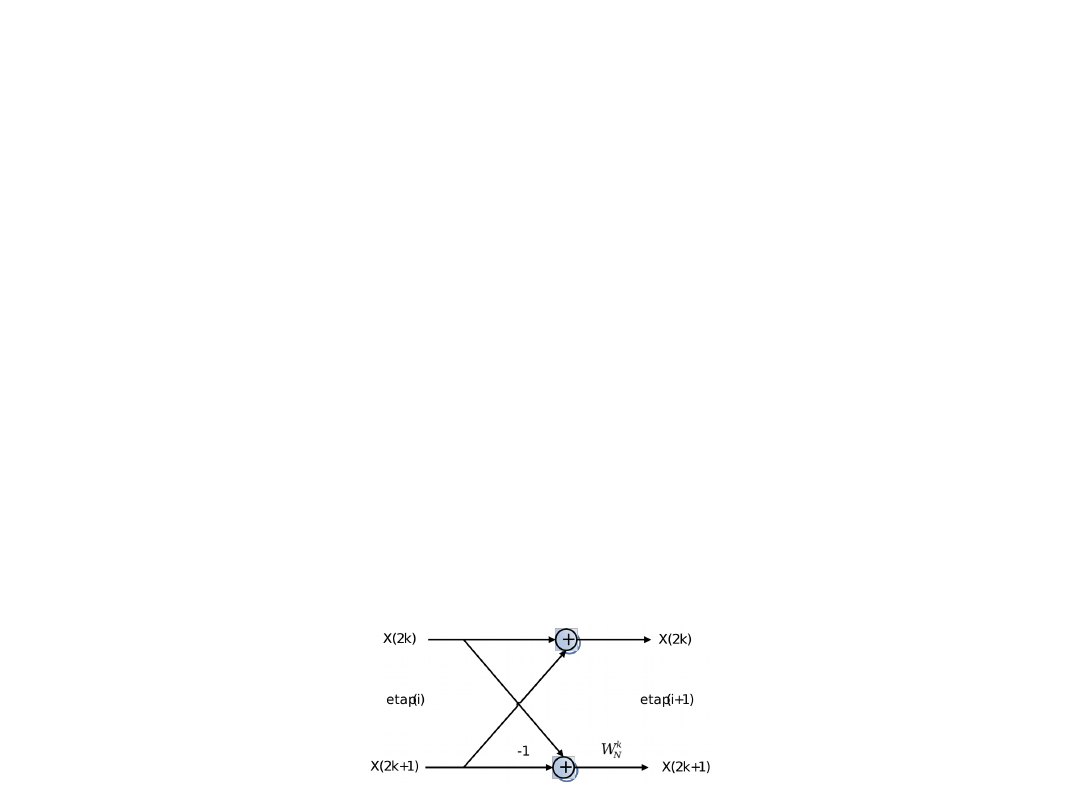
• Z zapisu macierzowego równań na prążki parzyste i

nieparzyste otrzymuje się następujący graf zwany

„motylkiem”:

1

2

/

,...,

2

,

1

,

0

,

)]

2

/

(

)

(

[

)

(

1

2

/

,...,

2

,

1

,

0

),

2

/

(

)

(

)

(

2

1























N

n

W

N

n

x

n

x

n

x

N

n

N

n

x

n

x

n

x

n

N

26

Wyprowadzenie algorytmu

radix – 2

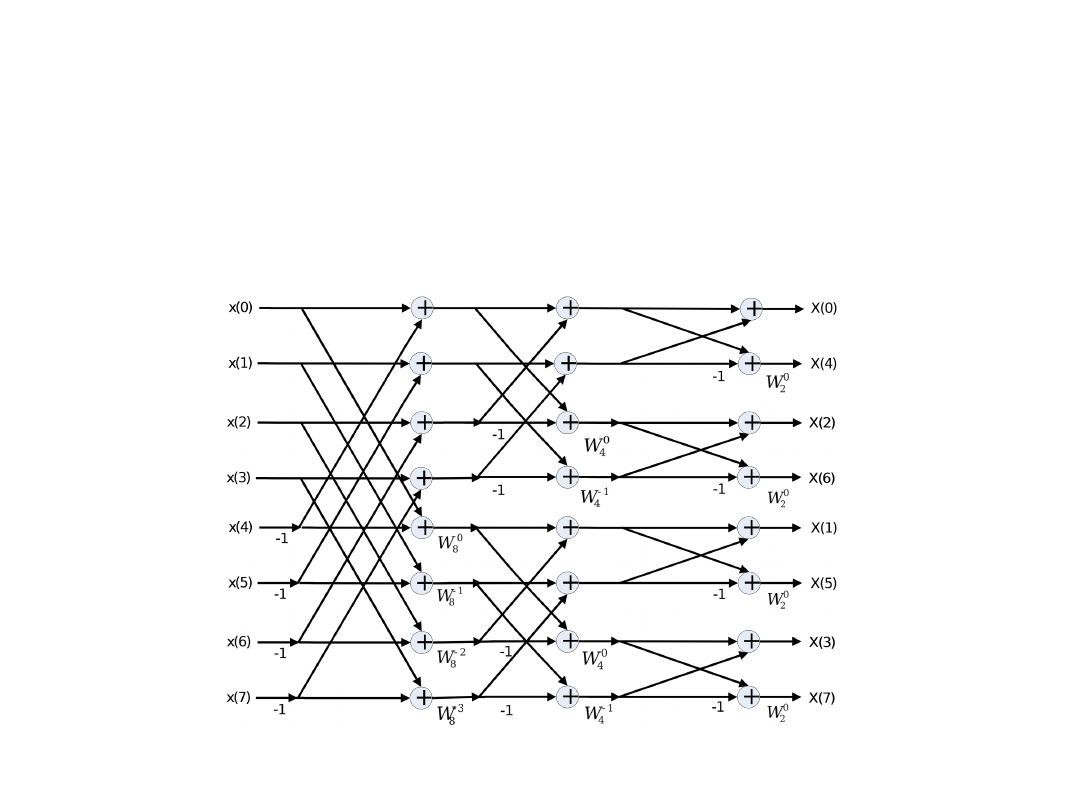
• Na rysunku 5 przedstawiono schemat blokowy

działania algorytmu dla N= 8:

Rys.5. Pełny schemat blokowy algorytmu DFT FFT radix-2

27

Wyprowadzenie algorytmu

radix – 2

• Algorytm FFT z podziałem częstotliwościowym (DFT) ma taką

samą złożoność obliczeniowa jak algorytm FFT z podziałem

czasowym (DIT) i jest proporcjonalna do . W

przeciwieństwie do DIT, alg. Z podziałem częstotliwościowym

wymaga zamiany próbek na wyjściu.
Aby zmienić kolejność próbek stosuje się metodą z odwrotną

propagacją bitu przeniesienia.

• Wyjaśnić jeszcze należy proces zmiany kolejności próbek w

wektorze wejściowym przy zastosowaniu algorytmu DIT FFT

radix-2. Jak już wspomniano wcześniej dokonuje się to metodą z

odwrotną propagacją bitu przeniesienia (reverse carry

propagation).

• W celu pełnego zrozumienia działania tej metody zostanie ona

przedstawiona na przykładzie dla długości wektora wejściowego

N = 8.

N

N

2

log

28

Wyprowadzenie algorytmu

radix – 2

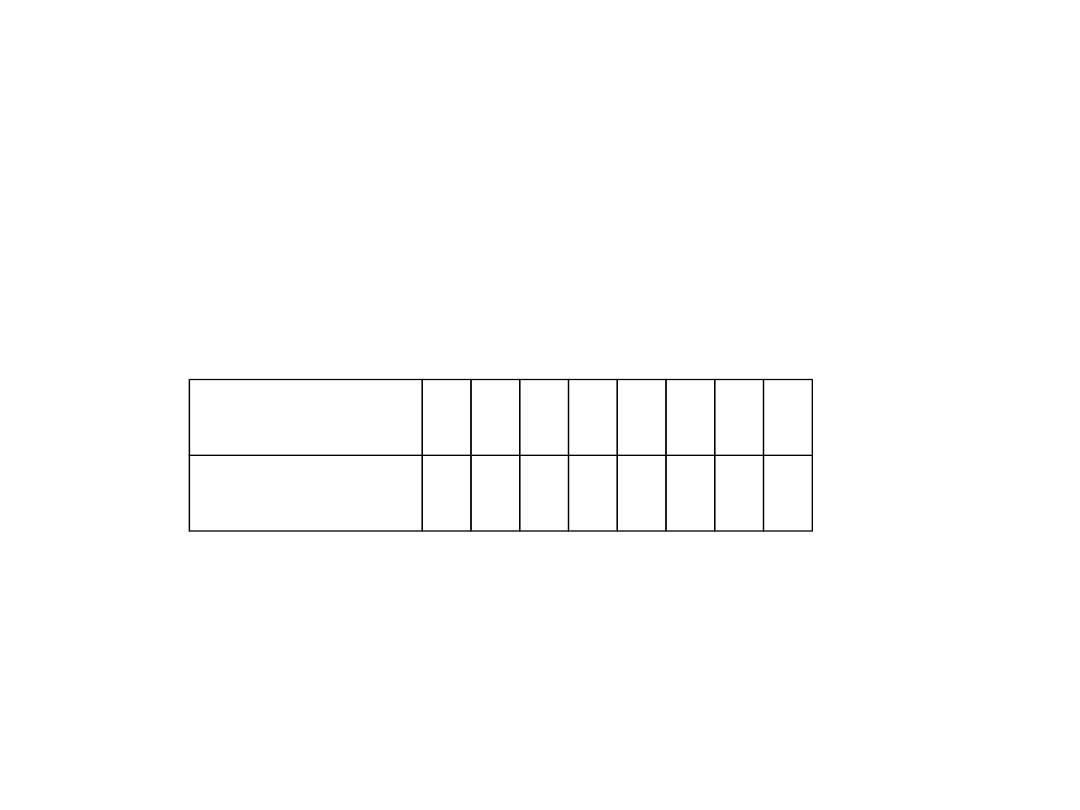
• W pierwszym kroku należy zmienić indeksy poszczególnych

próbek z wartości dziesiętnej na binarną:

• Dysponując wartościami binarnymi indeksów próbek w

kolejnym etapie należy dokonać sumowań binarnych

zgodnie z sposobem pokazanym poniżej:

gdzie: +rc – oznacza dodawanie z odwrotna propagacją bitu

przeniesienia,
i0…7 – indeksy próbek po zmianie kolejności.

Indeks

dziesięt

ny

0

1

2

3

4

5

6

7

Indeks

binarny

00

0

00

1

01

0

01

1

10

0

10

1

11

0

11

1

29

Wyprowadzenie algorytmu

radix – 2

• Wynikiem działania jest zmieniona kolejność

próbek wymagana przy zastosowaniu algorytmu.

• Taką operację możemy przeprowadzać do

dowolnej długości wektora danych wejściowych.

Indeks pierwotny

próbek

00

0

(0)

00

1

(1)

01

0

(2)

01

1

(3)

10

0

(4)

10

1

(5)

11

0

(6)

11

1

(7)

Indeks po zmianie

kolejności

00

0

(0)

10

0

(4)

01

0

(2)

11

0

(6)

00

1

(1)

10

1

(5)

01

1

(3)

11

1

(7)

30

Właściwości algorytmu

FFT

• ciąg danych wejściowych x(n) musi mieć długość równą potędze

2 co ma znaczący wpływ na efektywności działania algorytmu,

przy liczbie danych wejściowych różnej od wspomnianej liczby

wydajność algorytmu znacznie spada,

• względem metody bezpośredniej obliczania DFT algorytm ten

przyspiesza obliczenia krotnie,

• istnieje możliwość obliczania współczynników przed

pomiarem, ponieważ nie ma to nic wspólnego z procesem

próbkowania sygnału, do wyznaczenia wszystkich

współczynników potrzebna jest tylko długość wektora danych,

taka realizacja obliczania DTF wpływa na poprawę szybkości

działania algorytmu,

• istnieje możliwość policzenia transformaty odwrotnej (IFFT)

dzięki własności:

N

N

2

log

N

W

)

)}

(

{

(

)

)

(

(

1

)

(

1

))

(

(

)

(

*

*

1

0

*

/

2

*

1

0

/

2

k

X

FFT

e

k

X

N

e

k

X

N

k

X

IFFT

n

x

N

n

N

kn

j

N

n

N

kn

j



























31

Właściwości algorytmu

FFT

• zastosowanie algorytmu FFT wymaga w przeciwieństwie do

algorytmów rekurencyjnych wyznaczania DTF rozpoczęcia

obliczeń po zebraniu wszystkich próbek co stanowi problem

w przypadku obliczania DTF „on-line”

• z zależności od zastosowanego algorytmu czy to będzie DIT

czy DFT następuje konieczność zamiany próbek na wejściu

lub wyjściu procesy przetwarzania sygnału, obecnie aby

unikną przestawiania próbek sygnału bądź prążków widma

stosuję się oba algorytmy równocześnie. Przykład: