Analiza Zmienności

- struktura i miary

Jan M. Myszewski

Techniki wspomagające zarządzanie jakością

Wyższa Szkoła Przedsiębiorczości

i Zarządzania im. L. Koźmińskiego

Warszawa, Kwiecień

2005

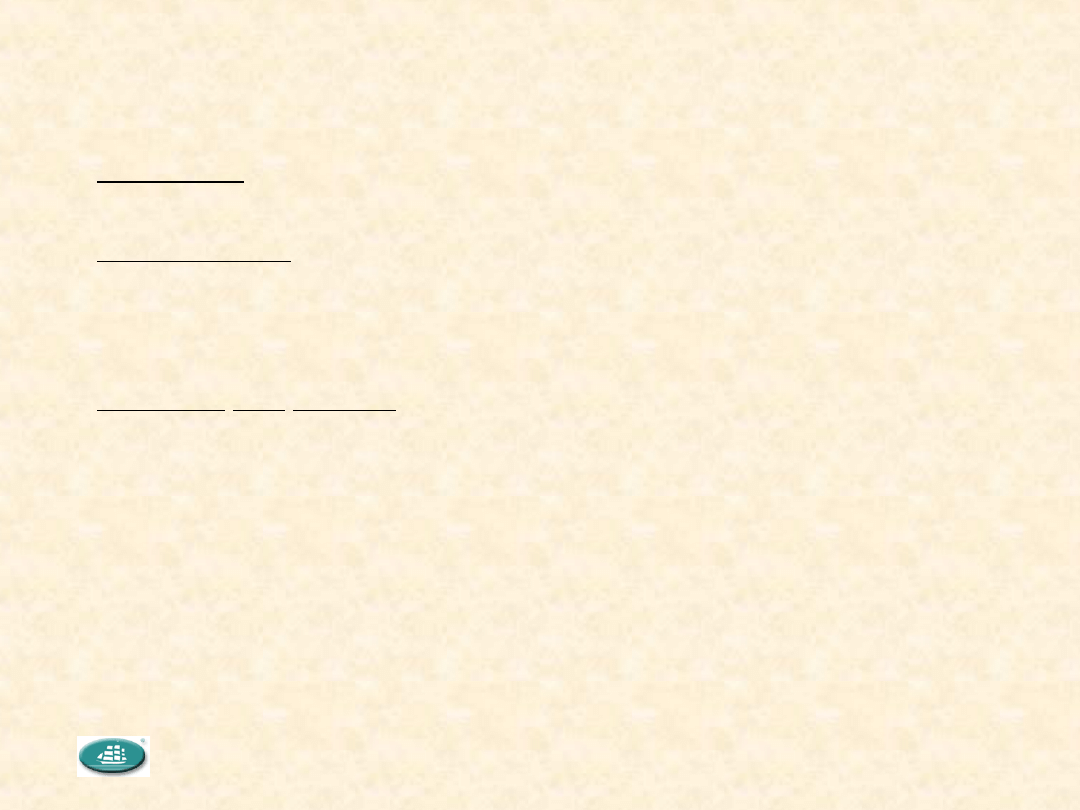
Analiza Zmienności Jan M. Myszewski

2

Istota losowości

Zmienność = zróżnicowanie wyników obserwacji, którego
przyczyny nie są znane obserwatorowi
Różnorodność= zróżnicowanie wyników obserwacji, którego
przyczyny są znane obserwatorowi

Zjawisko jest losowe= obserwacje zjawiska powtarzane w
identycznych warunkach wykazują zmienność.

Analiza Zmienności Jan M. Myszewski

3

Przyczyny zmienności

Zmienność

Człowiek

cechy X

Metody

Zarządzanie

Maszyna

Materiał Otoczenie

Analiza Zmienności Jan M. Myszewski

4

Struktura zmienności

Zmienność losowa = zmienność wywołana przez układ
czynników, o nieograniczonej liczności, każdy o
zaniedbywalnym indywidualnym oddziaływaniu, nazywana
przyczyną pospolitą.

Zmienność systematyczna = zmienność wywołana przez
skończony układ czynników, o znaczących
indywidualnych oddziaływaniach, nazywana przyczyną
specjalną.

Zmienność ma dwie składowe

Analiza Zmienności Jan M. Myszewski

5

Struktura zmienności

całkowita

zmienność

zmienność

systematyczna

zmienność

losowa

Analiza Zmienności Jan M. Myszewski

6

Zmienność systematyczna

Czynniki powodujące zmienność systematyczną są
stosunkowo łatwe do zidentyfikowania i wyeliminowania

Częstymi źródłami zmienności systematycznej są np.
Niejednakowe nastawy maszyn, różnice właściwości
materiałów i surowców z różnych dostaw, zużywanie się
narzędzi, zatykanie filtrów itp.

Ich usuwanie to przykład Kaizen.

Analiza Zmienności Jan M. Myszewski

7

Zmienność losowa

Ograniczanie zmienności losowej wymaga identyfikacji i
eliminacji bardzo drobnych czynników: “wybieranie łyżeczką
wody z jeziora”

Zazwyczaj wymaga wymiany fragmentu procesu (technologii,
maszyn, operatorów, dostawców itp.).

Przykładem ograniczania zmienności losowej jest reinżynieria.

Miary zmienności losowej wyznaczają granice:
•

ekonomicznej możliwości ograniczania zmienności w
danym systemie

• tolerancji dla zróżnicowania jednostek
• celowości podejmowania działań korekcyjnych

Analiza Zmienności Jan M. Myszewski

8

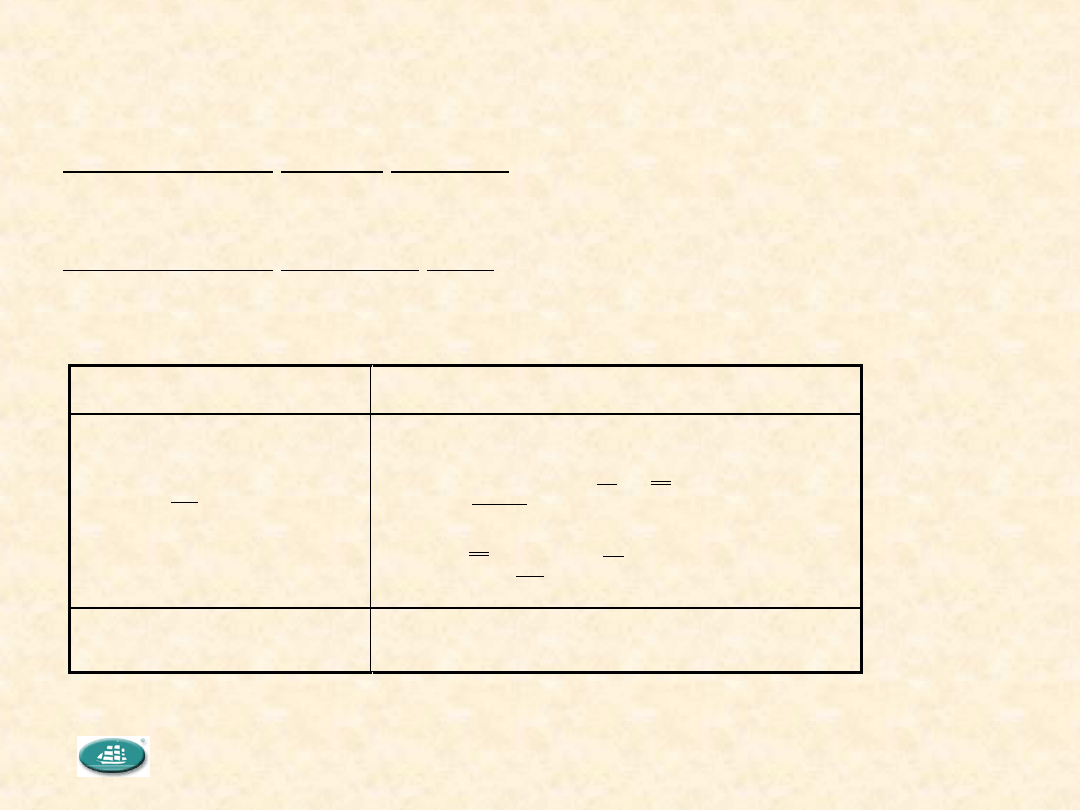
Zróżnicowanie między i wewnątrz grup

Miary zmienności

wewnątrz grup

między grupami

Średnia wariancja

M0 1m

Si

i 1

m

2

=

=

∑

Wariancja średnich w grupach

 







m

1

i

2

)

X

i

X

(

1

m

1

2

0

S

gdzie

 



m

1

i

i

X

m

1

X

.

M1 nS0

2

=

Zróżnicowanie między grupami = rozrzut wartości średnich otrzy­
manych w poszczególnych grupach.

Zróżnicowanie wewnątrz grup= średni rozrzut w grupach.

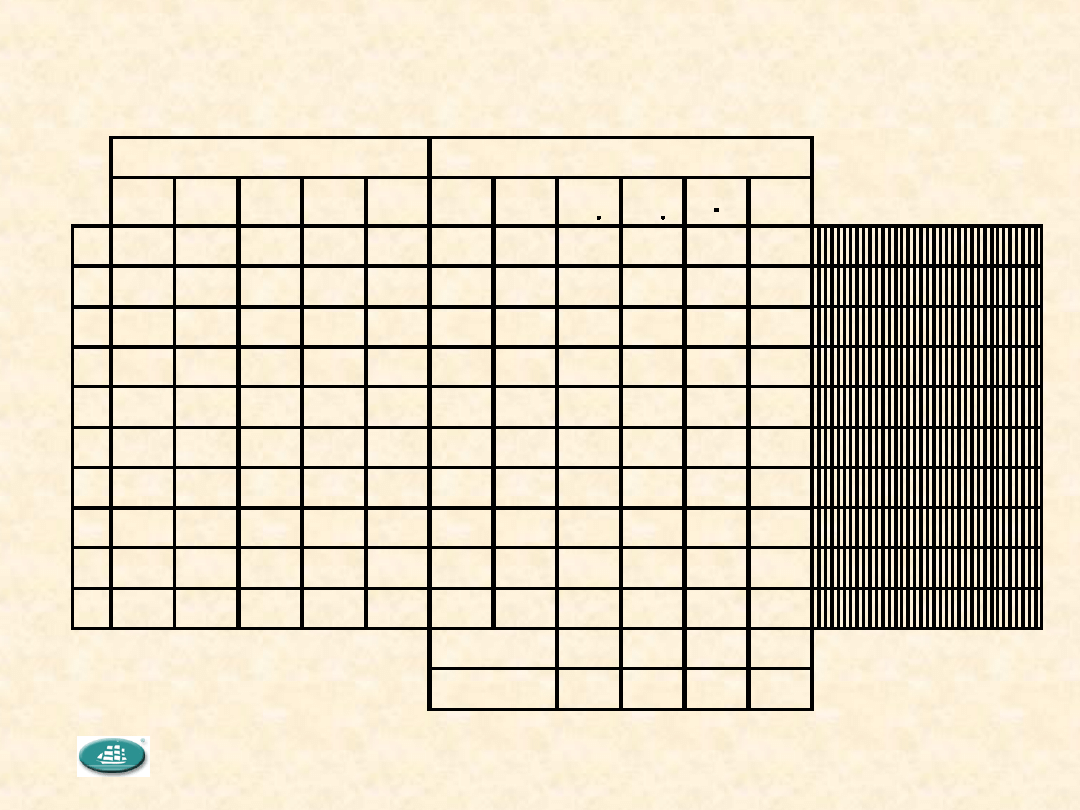
Analiza Zmienności Jan M. Myszewski

9

Zróżnicowanie między i wewnątrz grup

Roz-

step

Odch

.stand.

Wari-

ancja

Sred

nia.

Max

Analiza zmienności

Min

Średnia

Wariancja

5

4

3

2

Grupy danych

1

1

2

3

4

5

6

7

8

9

10

Analiza Zmienności Jan M. Myszewski

10

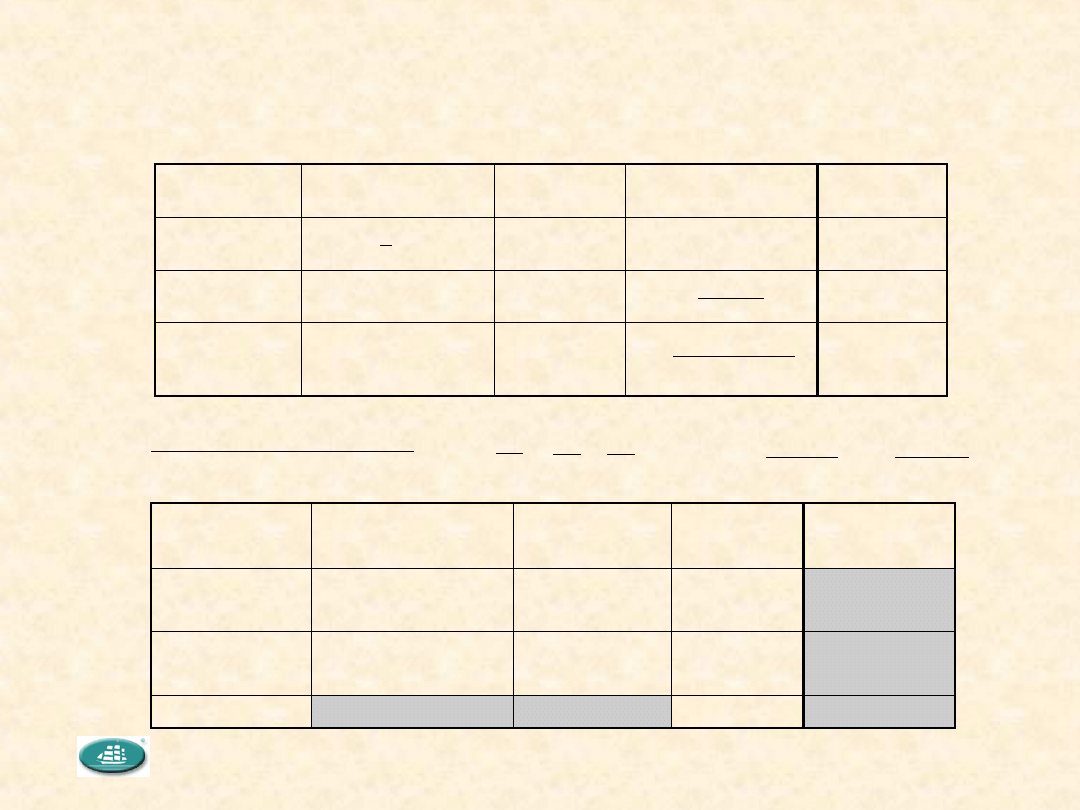
Zróżnicowanie między i wewnątrz grup

(*)

 













f

m(m 1) M

n 1 M

m

M

m 1 n 1 M

c

1

0

2

1

2

0

2

(

(

)

)

(

)(

)

,

V

c

M

0

=

M

0

M

1

+n - 1

n

SS

1

mn

1

V

1

mn

1

n

V

m

c











Zróżnicowanie Miara średnio-

kwadratowa (1)

Stopnie
swobody (2)

Wariancja
(3)

Stopnie
swobody (4)

wewnątrz grup
(w)
między grupami
(m)
Całkowita (c)

Zróżnicowanie Miara średnio-

kwadratowa (1)

Stopnie
swobody (2)

Wariancja
(3)

Stopnie
swobody (4)

wewnątrz grup

(w)

fw = m(n-1)

f'w = m(n-1)

między

grupami (m)

M : nS

1

0

2

=

fm = m-1

f'm  m-1

Całkowita (c)

SS

m 1 M

m n 1 M

1

0









(

)

(

)

fc = mn-1

f'c (*)

M

0

=

1
n

∑

i

=1

m

S

i

2

V

w

=M

0

V

m

=

M

1

−M

0

n

V

c

=

M

1

n−1M

0

n

Analiza Zmienności Jan M. Myszewski

11

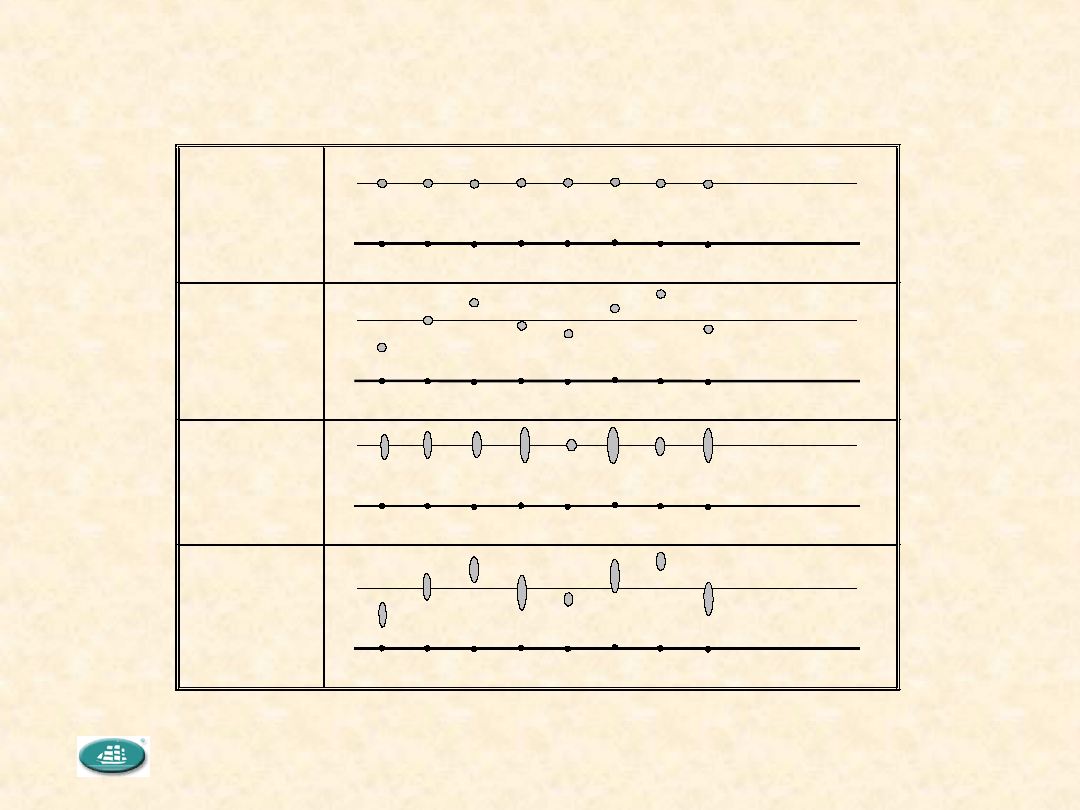
Interpretacja zróżnicowania między i wewnątrz grup

1. sm=0,

sw=0

1

2

3

4

5

6

7

8

Nr grupy

2. sm>0, sw=0

1

2

3

4

5

6

7

8

Nr grupy

3. sm=0, sw>0

1

2

3

4

5

6

7

8

Nr grupy

4. sm>0, sw>0

1

2

3

4

5

6

7

8

Nr grupy

Analiza Zmienności Jan M. Myszewski

12

Weryfikacja zróżnicowania między grupami

Przyjmujemy:
Xi = badana właściwość w i-tej warstwie (i=1,2,...,m)

Założenie:
X

i

≈ N(

m

i

,

s) dla i=1,2,...,m (odchylenia standardowe we

wszystkich warstwach są jednakowe)

Stawiamy formalne hipotezy statystyczne:
H0: m

1

=

m

2

= ... =

m

n

.

H1: tak nie jest

Xi N( i, )

≈ µ σ

Analiza Zmienności Jan M. Myszewski

13

Weryfikacja zróżnicowania między grupami

Jako statystykę testującą przyjmuje się funkcję

F

M1

M0

=

gdzie M1 i M0 obliczone na podstawie grup danych pobranych w
warstwach.

Jeżeli H0 jest prawdziwa, to F ma rozkład F-Snedecora z m-1 i m(n-
1) stopniami swobody.

Obszar krytyczny = zbiór wartości statystyki F, które będą pod­
stawą do odrzucenia hipotezy H0 = przedział

)

,

(F





gdzie wartość F

a

jest odczytana z tablic rozkładu

F-Snedecora z m-1 i m(n-1) stopniami swobody
dla poziomu istotności

.

a

F

odrzucić -

przyjąć -

hipotezę: "grupy danych różnią się między sobą"

Analiza Zmienności Jan M. Myszewski

14

a. Zaplanuj i przeprowadź obserwacje niezbędne do przeprowadzenia
analizy zmienności

b. Narysuj wykres wartości minimalnych, maksymalnych i średnich w
poszczególnych grupach. Sformułuj hipotezy dotyczące przyczyn
specjalnych zmienności

c. Przeprowadź wnioskowanie statystyczne wykorzystując test F-
Snedecora. Jakie wnioski można stąd wyciągnąć odnośnie struktury
przyczyn zmienności obserwowanego procesu?

d. Oszacuj miary zmienności poszczególnych składowych. Porównaj
miary zmienności losowej i całkowitej z wymaganiami

Ćwiczenia