1

11. DYNAMIKA RUCHU

SWOBODNEGO PUNKTU MATERIALNEGO

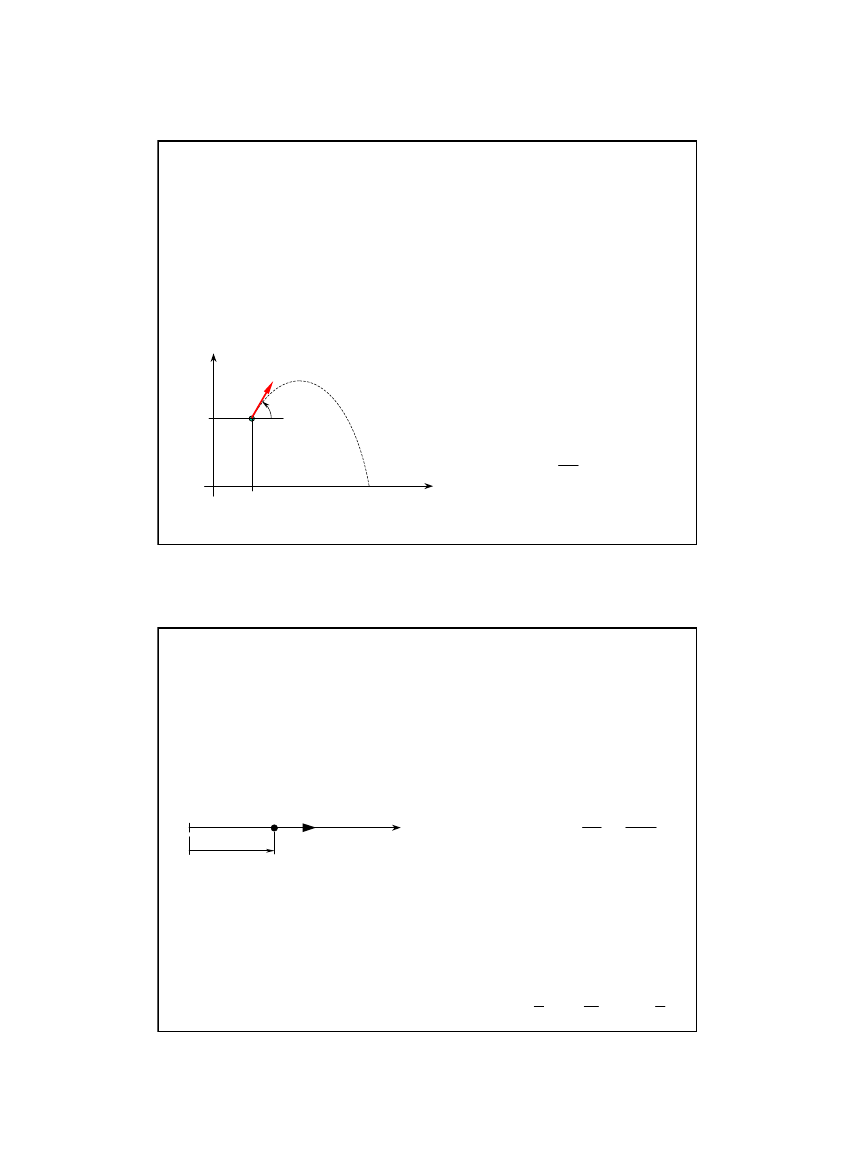
Zadanie 1/11

W polu przyciąganie ziemskiego z punktu o współrzędnych x

0

, y

0

wyrzucono punkt materialny o masie m z prędkością początkową
υ

0

pod kątem α do poziomu.

Znaleźć równania ruchu punktu. Przeprowadzić dyskusję.

x

y

α

υ

0

x

0

y

0

α

υ

υ

α

υ

υ

υ

υ

sin

cos

2

0

0

0

0

0

0

2

0

0

=

=

+

+

−

=

+

=

y

x

y

x

y

t

gt

y

x

t

x

Odp.:

Zadanie 2/11

Punkt materialny o masie m znajduje się w jednorodnym zmiennym polu
magnetycznym. Znaleźć równanie ruchu punktu x(t), jeżeli pole magne-
tyczne działa na punkt siłą F=F

0

sinωt (F

0

, ω − stałe). Położenie oraz

prędkość początkowa punktu równe są 0.

x

(t)

0

m

F

(t)

x













−

=

ω

ω

ω

t

t

m

F

x

sin

0

Odp.:

Zadanie 3/11

Ciało o masie m spada pionowo bez prędkości początkowej w ośrodku,
który stawia opór R=km

υ

proporcjonalny do prędkości

υ

(k − stała).

Obliczyć do jakiej maksymalnej prędkości

υ

max

rozpędzi się ciało oraz

podać równanie ruchu x(t).

(

)

t

k

g

e

k

g

x

k

g

kt

+

−

=

=

−

1

2

max

υ

Odp.:

2

Zadanie 4/11

Ciało o masie m porusza się po prostej poziomej pod wpływem siły

(k − stała)

Znaleźć prędkość

υ

ciała jako funkcję czasu, jeśli w chwili początkowej

jego prędkość równa była

υ

0

.

t

k

F

2

υ

=

3

3

0

2

2

3

υ

υ

+

=

t

m

k

Odp.:

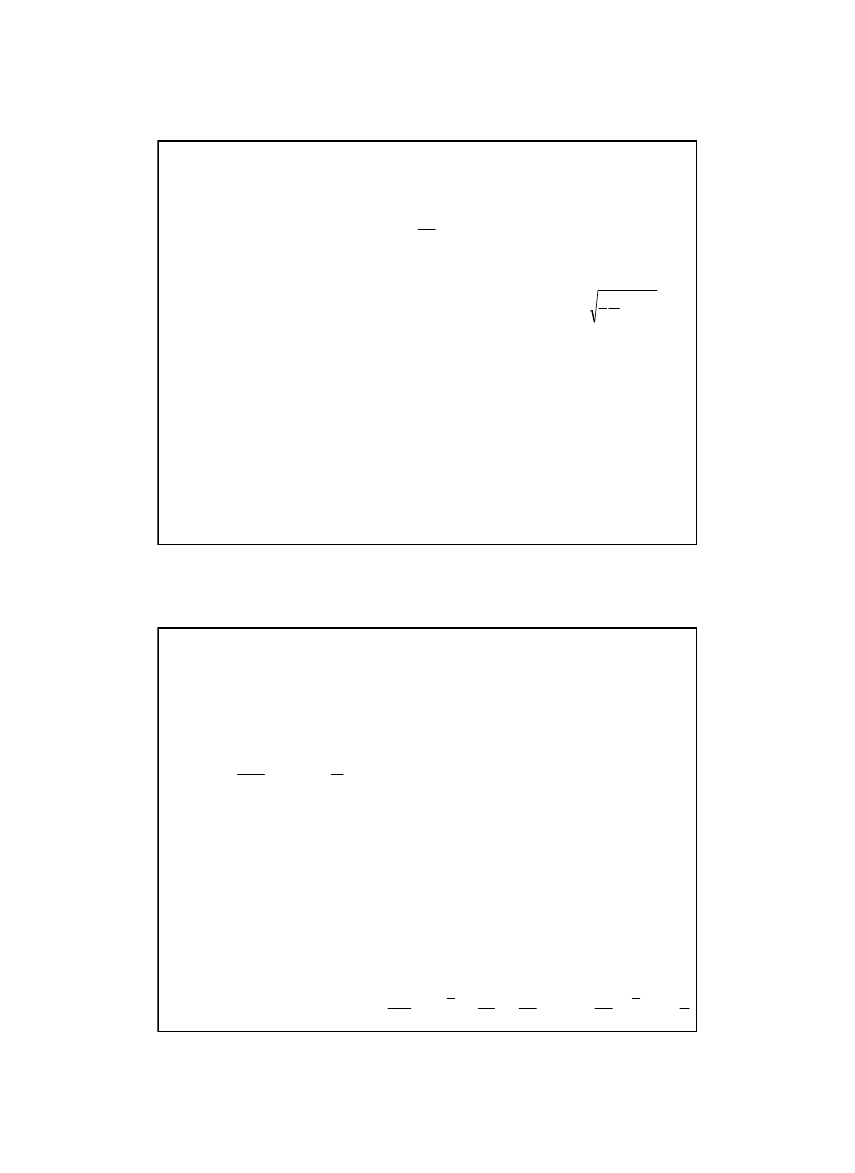
Zadanie 5/11

Z jaką prędkością υ

0

należy wystrzelić pocisk z powierzchni Ziemi w

kierunku Księżyca, aby doleciał on do punktu, w którym siły przyciąga-
nia Ziemi i Księżyca równoważą się i aby zatrzymał się w tym punkcie?
Ruch Ziemi i Księżyca oraz opór atmosfery pominąć.

Przyjąć: R=6370km g=9.81m/s

2

gdzie: M

Z

- masa Ziemi, M

K

– masa Księżyca, d – odległość między

ś

rodkami Ziemi i Księżyca, R – promień Ziemi.

Odp.: υ

0

≈

11.065km/s

Odp.:

60

80

=

=

=

=

b

R

d

a

M

M

K

Z

Zadanie 6/11

Na punkt materialny o masie m działa siła proporcjonalna do czasu F

1

=kt

oraz siła oporu proporcjonalna do prędkości F

2

=αυ. Znaleźć prędkość

punktu υ(t) oraz położenie x(t) w zależności od czasu. Warunki
początkowe: dla t=0 x=0,

υ

=0.

( )

( )

t

k

e

mk

t

t

mk

t

k

e

k

m

t

x

t

m

t

m

α

α

υ

α

α

α

α

α

+

















−

=

−

+

















−

=

−

−

1

2

1

2

2

2

3

2

3

Zadanie 7/11

Kulę o masie m wyrzucono pod kątem α

0

do poziomu z prędkością początkową υ

0

.

Opór powietrza R=kυ jest proporcjonalny
do prędkości. Znaleźć równanie y(x) toru
ruchu kuli.

Odp.:

Odp.:

y

x

υ

0

α

0

m

y

(x)

0

0

2

2

0

0

0

cos

1

ln

cos

α

υ

α

υ

α

m

kx

k

m

g

k

mg

tg

x

y

−

+













+

=

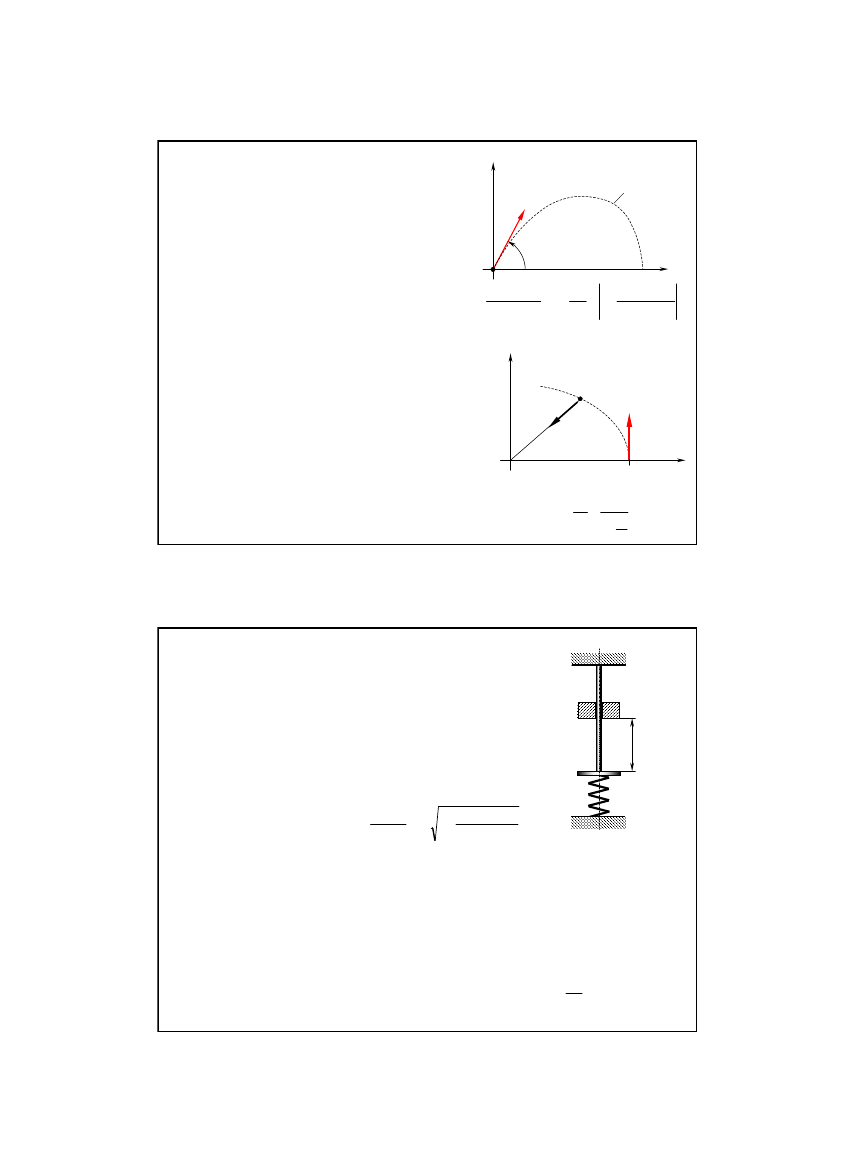
Zadanie 8/11

Punkt o masie m porusza się w płaszczyźnie
Oxy

, pod działaniem siły centralnej skiero-

wanej do początku układu współrzędnych.
Siła ta jest wprost proporcjonalna do odle-
głości punktu od początku układu. W chwili
początkowej punkt zajmował położenie x=b,
y

=0 i posiadał prędkość υ

x

=0, υ

y

= υ

0

.

Znaleźć równanie toru ruchu punktu.

1

2

0

2

2

2

=

+

k

m

y

b

x

υ

elipsa

x

y

υ

0

m

b

O

l

P

=kl

Zadanie 9/11

Ciężar o masie m może ślizgać się po pionowym
pręcie AB, którego sztywność na rozciąganie równa
jest k

1

.Koniec B pręta opiera się o śrubową sprężynę

o sztywności k

2

. Obliczyć największe wydłużenie

pręta h przy spadku ciężaru z wysokości H bez
prędkości początkowej. Masę pręta i sprężyny
pominąć.

Odp.:

Odp.:

(

)















+

+

+

+

=

mg

k

k

H

k

k

mg

h

2

1

2

1

2

1

1

A

B

m

H

k

1

k

2

Zadanie 10/11

Na końcu nie odkształconej nici o sztywności c, która może przenieść
maksymalną siłę Q, zaczepiono ciężar o masie m i puszczono bez
prędkości początkowej. Jaka jest minimalna wartość m, przy której nić
zerwie się i jaka będzie prędkość ciężaru w chwili zerwania nici?

0

2

=

=

υ

g

Q

m