14 Zagadnienia wybrane

155

ZAGADNIENIA WYBRANE

Wyboczenie sprężyste konstrukcji

Utrata przez konstrukcję zdolności do przenoszenia obciążeń może

nastąpić w różny sposób. W poprzednich rozdziałach kryterium oceny tej
zdolności sformułowano w postaci warunku wytrzymałościowego lub wa-
runku sztywnościowego. Przekroczenie naprężeń lub przemieszczeń
dopuszczalnych dyskwalifikowało konstrukcję pod względem użytkowym,
nie powodując jednak jej fizycznego zniszczenia. W projektowaniu pew-
nego typu konstrukcji, charakteryzujących się smukłością lub cienko-
ściennością, pod uwagę musi być brane jeszcze inne kryterium oceny, a
mianowicie ich

podatność na wyboczenie. Przykładami takich kon-

strukcji są osiowo ściskane pręty, kolumny, cienkościenne płyty i powło-
ki, ramy i kratownice. Wyboczenie tych konstrukcji, utrata przez nie tzw.
stateczności, prowadzi do ich nieuniknionego fizycznego zniszczenia.
Wyboczenie jednego elementu pociąga za sobą zazwyczaj lawinowe
zniszczenie powiązanych elementów. Utrata stateczności była przyczyną
wielu głośnych katastrof budowlanych, takich jak zawalenia się budyn-
ków, mostów czy masztów radiowych. Przy projektowaniu konstrukcji
prętowych, płyt, powłok itp. kryterium stateczności konstrukcji jest głów-
nym kryterium wytrzymałościowym, spychającym na dalsze miejsce kry-
teri

um naprężeniowe i sztywnościowe.

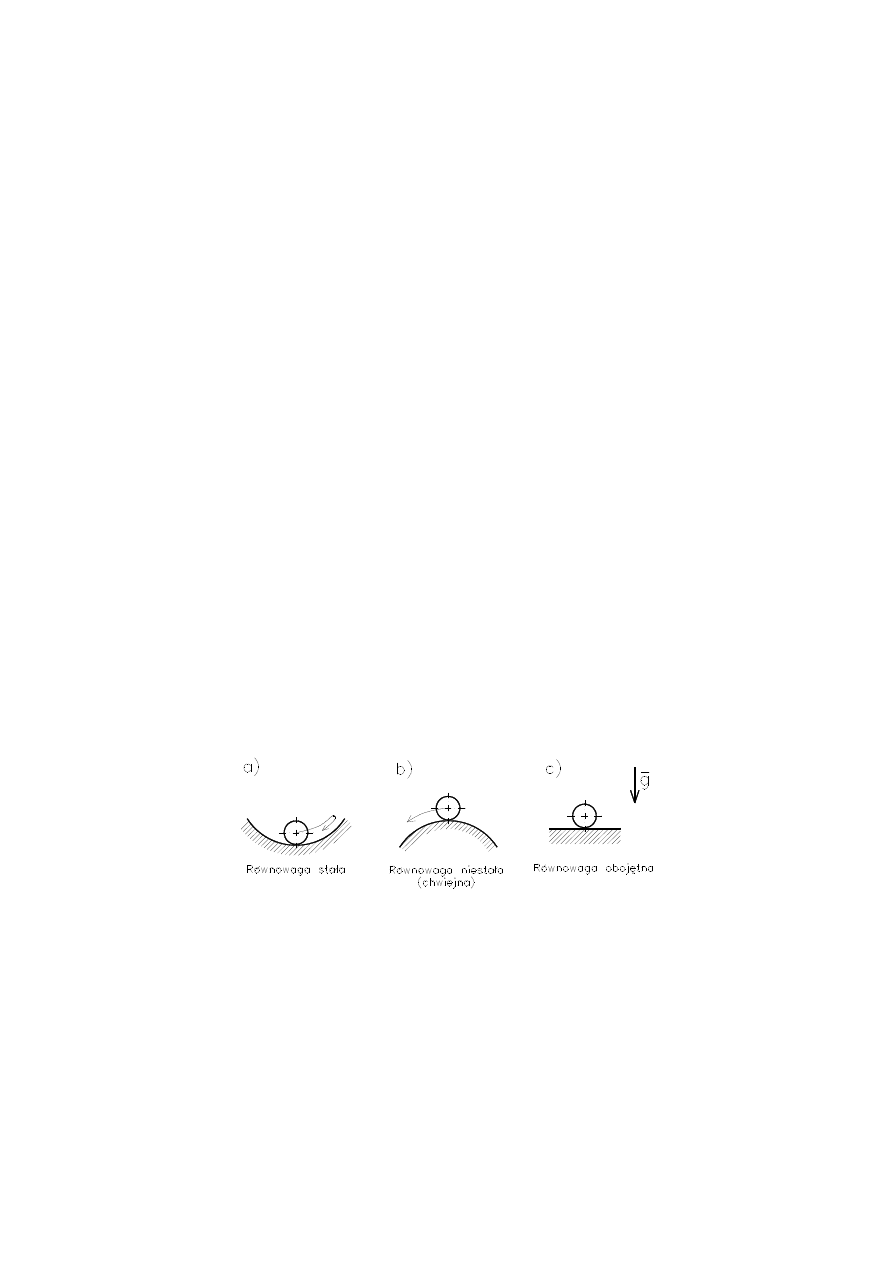
Badanie stateczności konstrukcji porównuje się z sytuacją kulki znaj-

du

jącej się w polu grawitacyjnym (polu przyciągania ziemskiego.

Dowolnie małe wychylenie kulki (zakłócenie) znajdującej się w najniż-

sz

ym punkcie wklęsłej powierzchni spowoduje zmianę jej położenia i

powrót do położenia początkowego – stan kulki można określić jako
równowagę stałą (rys. a).

Kulka znajdująca się w najwyższym punkcie powierzchni wypukłej

(rys. b) teoretycznie znajduje się w równowadze, lecz jest to równowaga
niestała (chwiejna), praktycznie nie do zrealizowania.

Kulka znajdująca się na powierzchni płaskiej (rys. c) znajduje się w

stanie określanym jako równowaga obojętna, gdyż jej stan jest taki sam
w każdym miejscu na płaszczyźnie.

14 Zagadnienia wybrane

156

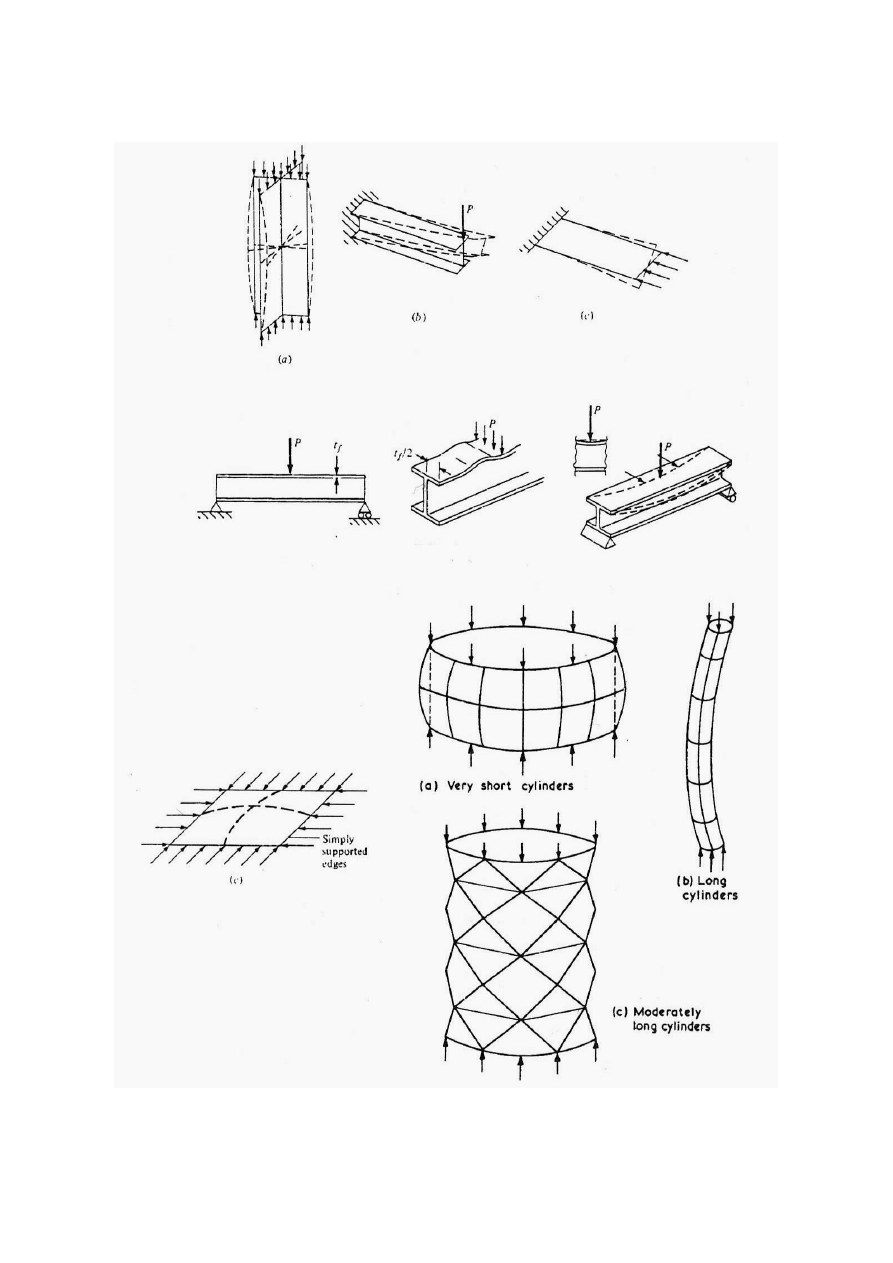
Przykłady wyboczenia ściskanych konstrukcji cienkościennych

14 Zagadnienia wybrane

157

Zmęczenie materiału

Zmęczenie materiału jest związane ze zmniejszeniem wytrzymałości

elemen

tów konstrukcyjnych poddanych działaniu okresowo zmiennych

obciążeń. Zjawisko zmęczenia materiałów jest bardzo niebezpieczne,
ponieważ zniszczenie elementu konstrukcyjnego lub części maszyny na-
stępuje nieoczekiwanie przy naprężeniach znacznie mniejszych od wy-
trzymałości doraźnej, wyznaczonej ze statycznej próby rozciągania.
Zniszczenie następuje bez żadnych dostrzegalnych wcześniej odkształ-
ceń plastycznych.

Zmęczenie materiałów ma olbrzymie znaczenie praktyczne, ponieważ

większość współczesnych konstrukcji inżynierskich jest poddana działa-
niu zmiennych obciążeń (pojazdy, samoloty, maszyny z ruchomymi czę-
ściami).

Przyczyną zmęczeniowego zniszczenia materiału jest zmienny stan

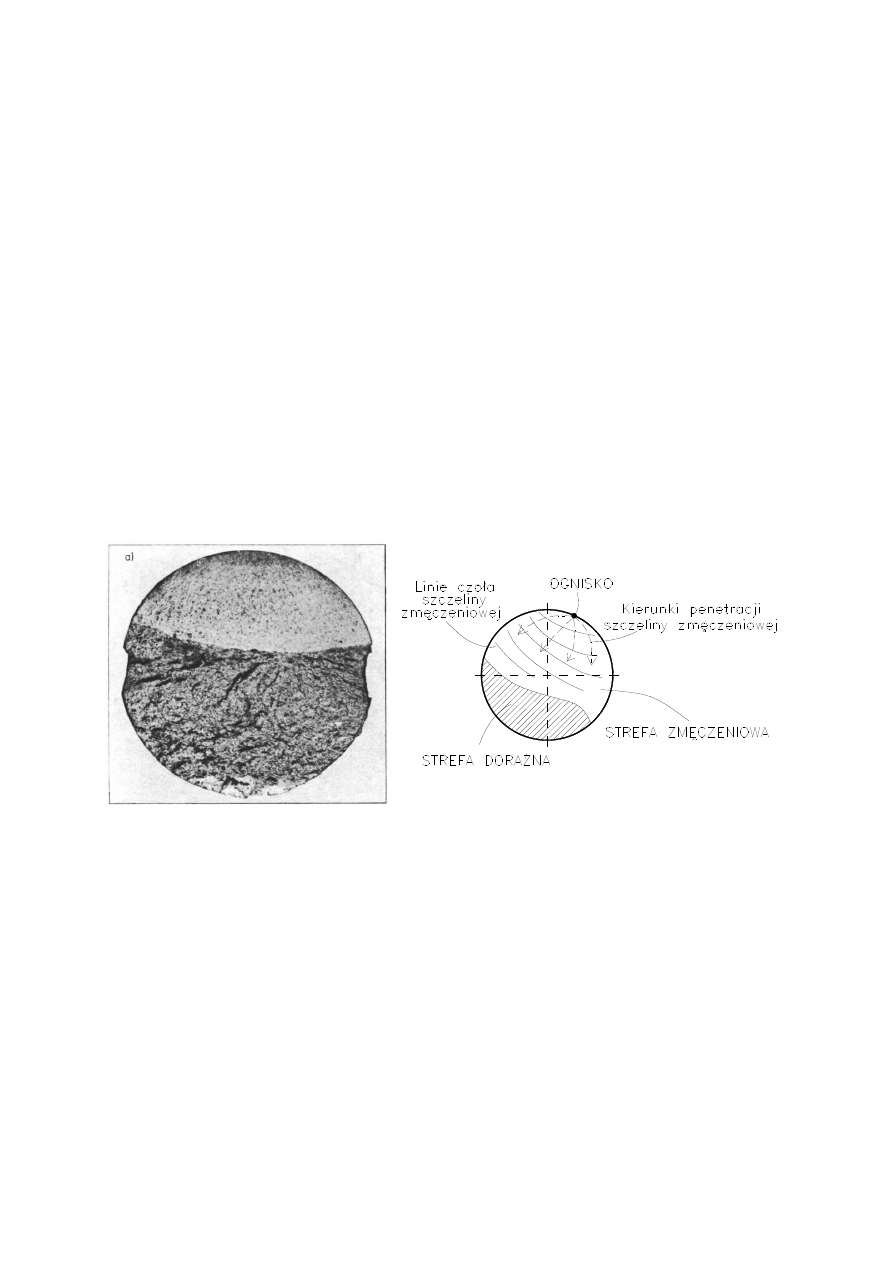
naprężenia. Przebieg zniszczenia można prześledzić na przykładzie
przełomu okrągłej próbki (np. osi wagonu kolejowego) przedstawionej na
rysunku.

Początek zniszczenia wału nastąpił w tzw. ognisku. Przyczyną zapo-

czątkowania procesu zmęczeniowego jest spiętrzenie naprężeń wywoła-
ne np. pęknięciem, rysą, wadą materiałową, karbem. Szczelina zmęcze-
niowa rozszerza się, penetruje w głąb przekroju – następuje tzw. propa-
gacja pęknięcia. Wał ulega zniszczeniu, gdy niezniszczona część wału
nie jest w stanie przenieść obciążenia. W przełomie zmęczeniowym roz-
różnia się dwie strefy. Strefa zniszczenia zmęczeniowego ma wygładzo-
ną, błyszczącą powierzchnię z charakterystycznymi liniami, w których
propagacja pęknięcia została np. na skutek zmniejszenia obciążenia za-
hamowana. Wygładzenie tej strefy wynika z tarcia powierzchni w czasie
pracy. Druga strefa nosi nazwę strefy doraźnej (resztkowej) i ma wygląd
gruboziarnisty, matowy. Istnieje wiele teorii na temat powstawania ogni-
ska i propagacji szczelin zmęczeniowych. Większość z teorii przyjmuje
dyslokacje i inne wady sieci krystalicznej za przy

czynę tych zjawisk.

14 Zagadnienia wybrane

158

Metody energetyczne

„Tradycyjna” wytrzymałość materiałów opiera się na ciągłym, jednorodnym modelu

ciała sprężystego. Aby otrzymać rozwiązania problemów inżynierskich trzeba stoso-
wać różne uproszczenia, pomijać pewne czynniki, stosować przybliżone metody roz-
wiązywania równań.

Obliczenia wytrzymałościowe oparte na „klasycznych” metodach prowadzą w wie-

lu

przypadkach do bardzo skomplikowanych zależności. Trudno jest też sobie wy-

obrazić ich stosowanie np. do prętów o zakrzywionej osi (łuków) – w tym przypadku
metody klasyczne są nieprzydatne. Wprowadzenie do wytrzymałości pojęcia energii
po

tencjalnej pozwala na sformułowanie stosunkowo prostych metod umożliwiających

określanie przemieszczeń konstrukcji czy rozwiązywanie zadań statycznie niewyzna-
czalnych. Dodatkową korzyścią jest zastosowanie prostych metod rachunkowych,
wyk

orzystujących powszechnie znane metody analizy matematycznej (różniczki, cał-

ki). Metody wykorzystujące energię stanowią jedyne narzędzie pozwalające obliczać
wytrzymałościowo ramy, łuki i zadania o wysokim stopniu statycznej niewyznaczal-
ności. Metody oparte na energii wewnętrznych sił sprężystości, zwane metodami
energetycznymi

, stanowią powszechnie stosowane w praktyce narzędzie do obli-

czeń wytrzymałościowych zarówno elementów konstrukcyjnych, jak i całych kon-
strukcji. Znaczenie metod energetycznych wzrast

a z rozwojem możliwości oblicze-

niowych

współczesnej techniki komputerowej.

Należy jednak pamiętać, że do prawidłowego stosowania metod energetycz-

nych niezbędna jest odpowiednia znajomość wspomnianych „klasycznych”
metod obliczeniowych.

Pojęcie energii potencjalnej wewnętrznych sił sprężystości (krótko – energii sprę-

żystej) nawiązuje do zagadnień znanych z dynamiki. W podejściu tym wykorzystuje
się analogię do definicji pracy ciał sztywnych – praca jest iloczynem siły na przesu-
nięciu (drodze) i wyraża się za pomocą Nm (kNm – niutonometrów (dżuli J), kiloniu-
tonometrów

1

). Podejście wykorzystujące energię sił sprężystości wymaga przyjęcia

pewnego modelu, określanego jako układ Clapeyrona (sprężystość liniowa, możli-
wość stosowania zasady superpozycji, równowaga układu). Dla układu Clapeyrona
można wprowadzić dodatkowe pojęcia, upraszczające dalszą analizę. Pojęciami tymi
są:



Pręt uogólniony (pręt jednocześnie obciążony siłami osiowymi, siłami po-
przecznymi, momentem skręcającym i momentem zginającym).



Siła uogólniona (rozciąganie, ścinanie, skręcanie, zginanie).



Przemieszczenie uogólnione (wydłużenia, ugięcia i obroty).

Uogólnienie powyższych pojęć pozwala na wyprowadzenie ogólnych zależności

i przystosowanie ich do konkretnych praktycznych sytuacji.

Metody energet

yczne są efektywnym narzędziem rozwiązywania złożonych pro-

blemów obliczeń wytrzymałościowych, polegających na wyznaczaniu przemieszczeń
oraz rozwiązywaniu zadań wielokrotnie statycznie niewyznaczalnych. W oparciu o
metody energetyczne można stosunkowo łatwo napisać programy komputerowe.
Metody energetyczne są także podstawą metod elementów skończonych, współ-
czesnego narzędzia szeroko obecnie stosowanego w projektowaniu konstrukcji inży-
nierskich wszelkiego typu.

1

Dla odróżnienia – dla momentu stosuje się zapis N



m (kN



m): niuton razy metr, kiloniuton razy metr.

14 Zagadnienia wybrane

159

W poniższej tabeli przedstawiono w uproszczonej formie zależności pozwalające

na zrozumienie energii sprężystej dla podstawowych modeli stosowanych w „kla-
sycznej” wytrzymałości materiałów.

Model

Energia sprężysta

EA

dx

du

N

ROZCIĄGANIE (ŚCISKANIE) PRĘTA

Praca wykonana na wydłużeniu (skróceniu) liniowym pręta o
długości dx siłą normalną N wynosi

.

EA

dx

N

du



Energia sprężysta:

,

EA

2

dx

N

du

N

2

1

dV

2







gdzie: EA

– sztywność pręta na rozciąganie.

dx

GJ

S



d

M

S

SKRĘCANIE WAŁU OKRĄGŁEGO

Moment skręcający M

S

wał o długości dx wykonuje pracę

.

GJ

dx

M

d

S

2
S





Energia sprężysta:

,

GJ

2

dx

M

d

M

2

1

dV

S

2
S

S









gdzie: GJ

S

– sztywność wału na skręcanie.

dx

ds



d



d



EJ

M

zg

ZGINANIE PROSTE BELKI

Moment zginający M

zg

belkę o długości dx wykonuje prace na

kącie obrotu przekroju d



. Na podstawie hipotezy płaskich

przekrojów w zginaniu wyprowadzona jest zależność

.

EJ

dx

M

d

EJ

M

1

dx

d

zg

zg



















Energia sprężysta:

,

EJ

2

dx

M

d

M

2

1

dV

2
zg

zg









gdzie: EJ

– sztywność belki na zginanie.

dx

T

dy

GA

ŚCINANIE BELKI (PRĘTA)

Siła poprzeczna T ścinająca belkę o długości dx wykonuje
pracę na przemieszczeniu środka ciężkości przekroju dy.
Działanie siły poprzeczne T wymaga przyjęcia szeregu
uproszczeń opisanych w literaturze i wprowadzenia bezwy-
miar

owego współczynnika kształtu przekroju. W rezultacie

otrzymuje się wzór na energię sprężystą ścinanego pręta:

,

GA

dx

T

dy

T

2

1

dV

2









gdzie:



– współczynnik kształtu przekroju, GA – sztywność

belki na ścinanie. Uwaga – związek między dy i dx jest
szcze

gółowo opisany w literaturze.

14 Zagadnienia wybrane

160

Energia

sprężysta pręta uogólnionego pod działaniem sił rozciągających (ściska-

jących), momentu skręcającego, momentu zginającego i sił ścinających wynosi:



















L

0

L

0

2

2
g

L

0

0

2
S

L

0

2

dx

GA

2

T

dx

EJ

2

M

dx

GJ

2

M

dx

EA

2

N

V

,

gdzie: A

– pole powierzchni przekroju [cm

2

], L

– długość pręta L [m],

E

– moduł Younga [MPa], G – moduł Kirchoffa [MPa].

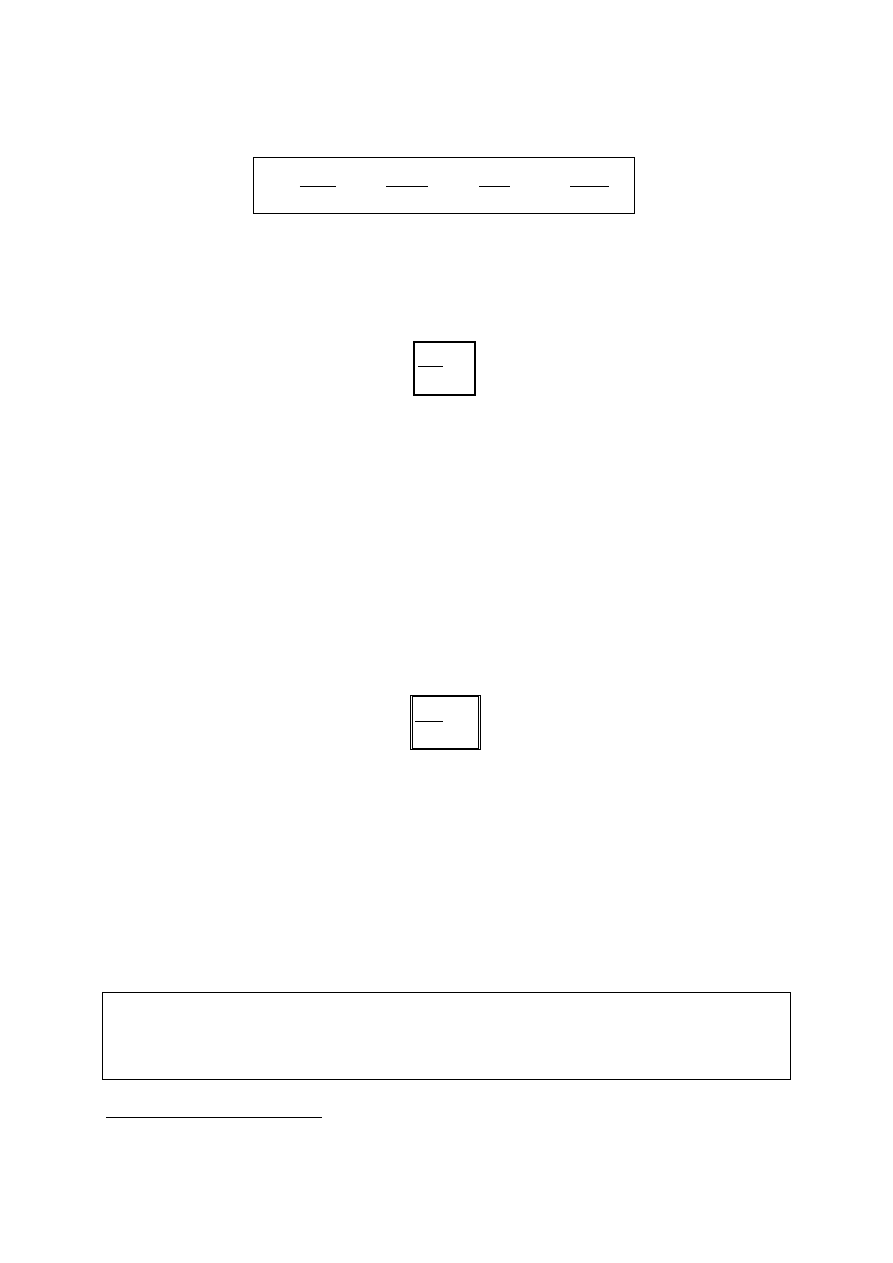
Dzięki wprowadzeniu uogólnionych pojęć sił i przemieszczeń można sformułować

zależności szeroko stosowane w obliczeniach wytrzymałościowych. Podstawowym
twierdzeniem w metodach energetycznych jest twierdzenie Castigliano (1873):

i

i

f

P

V







,

które mówi, że

pochodna cząstkowa energii sprężystej układu względem siły uogól-

nionej jest równa przemieszczeniu uogólnionemu odpowiadającemu tej sile.

Twierdzenie Castigliano jest stosowane do wyznaczania przemieszczeń

układów statycznie wyznaczalnych. Nie przysparza ono żadnych trudności w za-
daniach, w których poszukiwane przemieszczenie odpowiada rzeczywiście działają-
cej sile. W zadaniach mających na celu poszukiwanie przemieszczeń w przekrojach,
w których nie ma rzeczywistej siły, można dodać fikcyjne obciążenie odpowiadające
szukanemu przemieszczeniu. Po zróżniczkowaniu energii to fikcyjne obciążenie na-
leży przyrównać do zera.

Obciążenie układu siłami zewnętrznymi czynnymi powoduje powstanie w podpar-

ciach (więzach) sił zewnętrznych biernych (reakcji). Dla podparcia sztywnego oraz
bez tarcia przemieszczenie odpowiadające reakcji podporowej R

i

jest równe zeru.

Wykorzystując twierdzenie Castigliano, powyższe stwierdzenie można przedstawić w
postaci zależności

.

0

R

V

i







W układzie sprężystym wszystkie siły czynne i wszystkie siły bierne są związane

ogólnymi warunkami równowagi, wyrażonymi przez równania statyki. Powyższa za-
leżność będzie prawdziwa tylko dla reakcji przyjętych za statycznie niewyznaczalne
(nadliczbowe

). Mówi o tym twierdzenie Menabre’a (1857): w układzie liniowo-sprę-

żystym sztywno podpartym pochodna cząstkowa energii sprężystej całego układu
względem reakcji podporowej statycznie niewyznaczalnej jest równa zeru.

Twierdzenie Menabre’a pozwala na rozwiązywanie układów statycznie nie-

wyznaczalnych.

W układach z większą liczbą wielkości statycznie niewyznaczal-

nych należy zastosować twierdzenie Menabre’a tyle razy, ile jest wielkości statycznie
niewyznaczalnych. T

wierdzenie Menabre’a jest też zwane zasadą minimum energii

lub

zasadą najmniejszej pracy Menabre’a.

Za pomocą twierdzenia Castigliano można wyznaczać przemieszczenia w układach
statycznie wyznaczalnych.

Twierdzenie Menabre’a pozwala na rozwiązywanie zadań

statycznie niewyznaczal

nych. Oba twierdzenia pozwalają na rozwiązywanie płaskich

i przestrzennych konstrukcji typu ramy

i łuki.

2

2

Patrz:

Ostwald M.: Podstawy wytrzymałości materiałów. Wydawnictwo Politechniki Poznańskiej 2007.

Ostwald M.: Wytrzymałość materiałow. Zbiór zadań. Wydawnictwo Politechniki Poznańskiej 2008.

14 Zagadnienia wybrane

161

Metoda elementów skończonych

Metoda elementów skończonych (MES) w ostatnich latach stała się powszechnie

stosowanym narzędziem w praktyce inżynierskiej. Jej błyskawiczny rozwój oraz dal-
sze perspek

tywy są związane bezpośrednio z rozwojem informatyki (w zakresie

hardware i software, sprzętu i oprogramowania). Niewiele jest dziedzin techniki, w
których rozwój informatyki miałby tak znaczący wpływ na metody obliczeń, jak w
przypadku obliczeń wytrzymałościowych.

„Tradycyjna” wytrzymałość materiałów opiera się na ciągłym, jednorodnym modelu

ciała sprężystego. Dla spotykanych w praktyce inżynierskiej zagadnień, polegających
na wyznaczaniu naprężeń, przemieszczeń i innych wielkości (np. rozkładów tempera-
tur), tylko w przypadku stosunkowo prostych modeli geometrycznych można otrzy-
mać za pomocą metod analizy matematycznej (rachunek różniczkowy i całkowy)
rozwiązania ścisłe, dokładne. Chodzi tu o takie rozwiązania, za pomocą których w
dowolnych punktach konstrukcji można wyznaczyć interesujące konstruktora takie
wielkości, jak naprężenia czy przemieszczenia. Aby otrzymać rozwiązania ilościowe
trzeba stosować różne uproszczenia, pomijać pewne czynniki, stosować przybliżone
metody rozwiązywania równań. Charakterystyczną cechą tych wszystkich uprosz-
czeń i przybliżeń jest to, że dla ciągłego modelu geometrycznego otrzymuje się roz-
wiązania dla określonej liczby punktów.

Metoda elementów skończonych polega na odejściu od ciągłego modelu kon-

strukcji na rzecz jej podziału na skończoną liczbę ściśle zdefiniowanych elementów –
elementów skończonych. Podział konstrukcji na elementy nazywa się dyskretyza-
cją konstrukcji, która ciągły model obliczeniowy zastępuje pewną skończoną liczbą
elementów. W konstrukcjach dużych, złożonych można wydzielić pewne powtarzalne
grupy elementów, które definiuje się jako tzw. superelementy, złożone z kolei z pew-
nej liczby elementów.

Praktyczne stos

owanie MES wymaga przede wszystkim dogłębnej znajomo-

ści wytrzymałości materiałów, jak również podstaw metod numerycznych i zna-
jomości technik komputerowych. Jedną z najważniejszych czynności mających
wpływ na końcowy wynik jest właściwy podział konstrukcji na odpowiednio dobrane
elementy. Wymaga to umiejętności analizowania rozkładów naprężeń i przemiesz-
czeń w konstrukcji oraz formułowania warunków brzegowych. Analiza otrzymanych
wyników oraz wyciąganie właściwych wniosków również wymagają znajomości wy-
trzy

małości materiałów. Niemożliwe jest traktowanie MES jako jednego z wielu

narzędzi informatycznych, wymagającego jedynie znajomości posługiwania się
komputerem.

Rozwój MES, a także rozszerzanie zakresu jej zastosowań są nierozłącznie zwią-

zane z rozwojem i

możliwościami techniki komputerowej. Współczesne konstrukcje

inżynierskie dzieli się na dziesiątki tysięcy elementów. Rozwiązanie takiego układu
równań wymaga komputerów o odpowiedniej mocy obliczeniowej. Różnorodność
spotykanych problemów technicznych powoduje, że współczesne sytemy kompute-
rowe zawierają w swoich bibliotekach setki gotowych elementów z opcją umożliwia-
jącą tworzenie własnych elementów. Wprowadzanie danych wejściowych, a także
analiza wyników jest oparta przede wszystkim na wysoko wyspecjalizowanych pro-
cesorach graficznych.

14 Zagadnienia wybrane

162

Współczesne zadania inżynierskie są rozwiązywane przez odpowiednio przygoto-

wane systemy komputerowe

. Każdy system komputerowy składa się z trzech za-

sadniczych cz

ęści:

– preprocesora, umożliwiającego graficzne wprowadzanie danych wejściowych,

dyskretyzację konstrukcji (automatyczną), dysponującego biblioteką elementów
skończonych, umożliwiającego kontrolę poprawności dyskretyzacji,

– procesora, rozwiązującego z wymaganą dokładnością olbrzymie układy równań

algebraicznych, oblic

zającego poszukiwane wielkości we wszystkich węzłach,

– postprocesora, przedstawiającego w zwartej postaci otrzymane wyniki, wykorzy-

stującego możliwości graficzne współczesnych komputerów, tworzącego trwałe
kopie otrzymanych wyników w postaci rysunków, wykresów, rozkładów poszuki-
wanych wielkości na płaszczyźnie i w przestrzeni.
Do rozwiązywania dużych, skomplikowanych zadań inżynierskich wykorzystuje się

wyspecjalizowane komputery, tzw. stacje robocze

, dysponujące odpowiednio szyb-

kimi procesorami (systemy wie

loprocesorowe), dużą pamięcią operacyjną, monito-

rami o dużym ekranie i odpowiedniej rozdzielczości.

Najbardziej obecnie znane systemy komputerowe MES to ALGOR, COSMOS

i

ABAQUS, umożliwiające rozwiązywanie szerokiej gamy zadań statycznych, dyna-

micznych, sta

tecznościowych, dysponujące olbrzymimi bibliotekami gotowych ele-

mentów. Prawidłowe korzystanie z tych systemów wymaga przede wszystkim do-
głębnej znajomości mechaniki i wytrzymałości materiałów, opanowania liczących
często setki stron instrukcji użytkownika, jak również nabycia odpowiedniej praktyki
obliczeniowej. Wymagania stawiane konstruktorom chcącym twórczo rozwiązywać
za pomocą MES skomplikowane zagadnienia techniczne są olbrzymie, jednakże
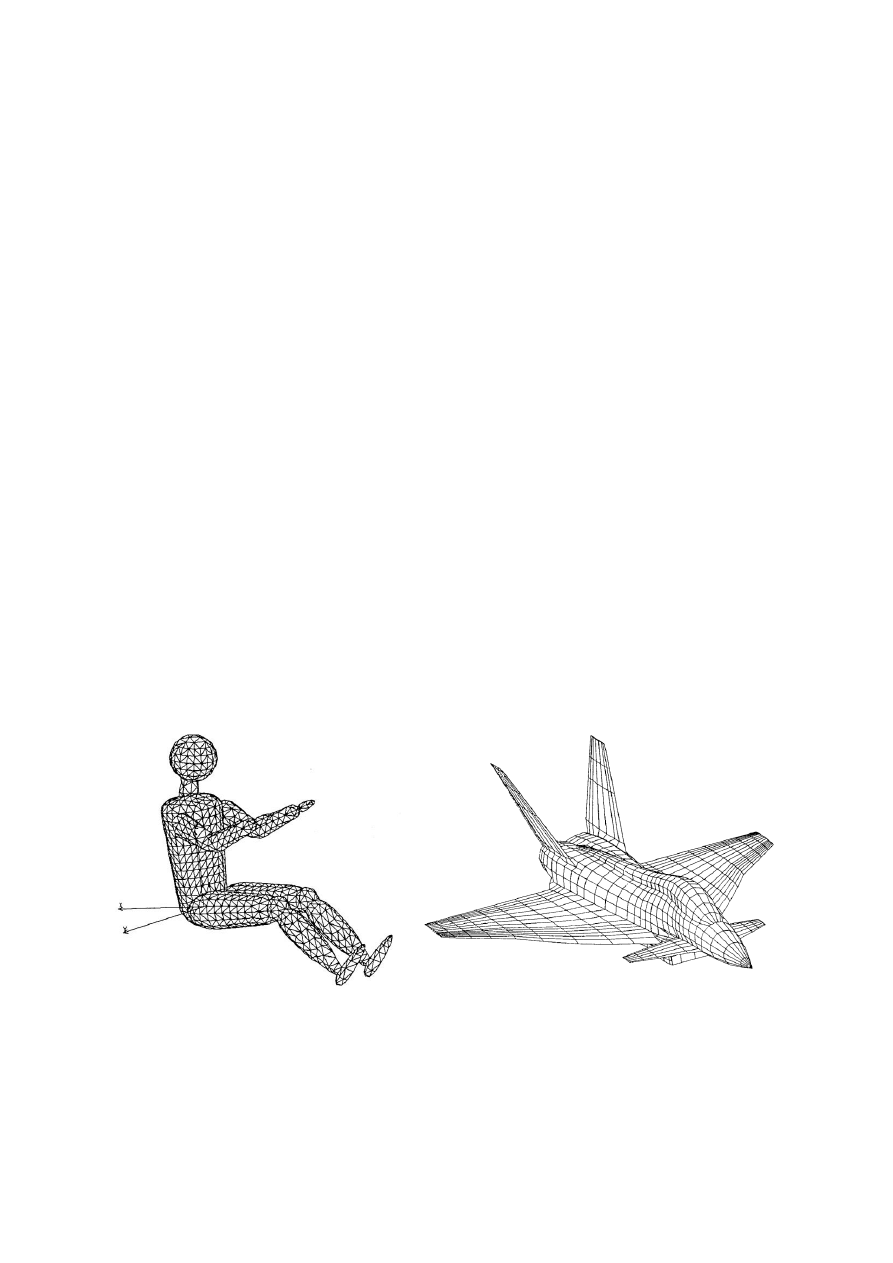
otrzymywanie zadowalających rezultatów innymi sposobami jest niemożliwe. Rysu-
nek

poniżej przedstawia przykłady zastosowania MES w różnych dziedzinach obli-

czeń wytrzymałościowych.

Przykłady zastosowania metody elementów skończonych

14 Zagadnienia wybrane

163

Współczesne materiały konstrukcyjne

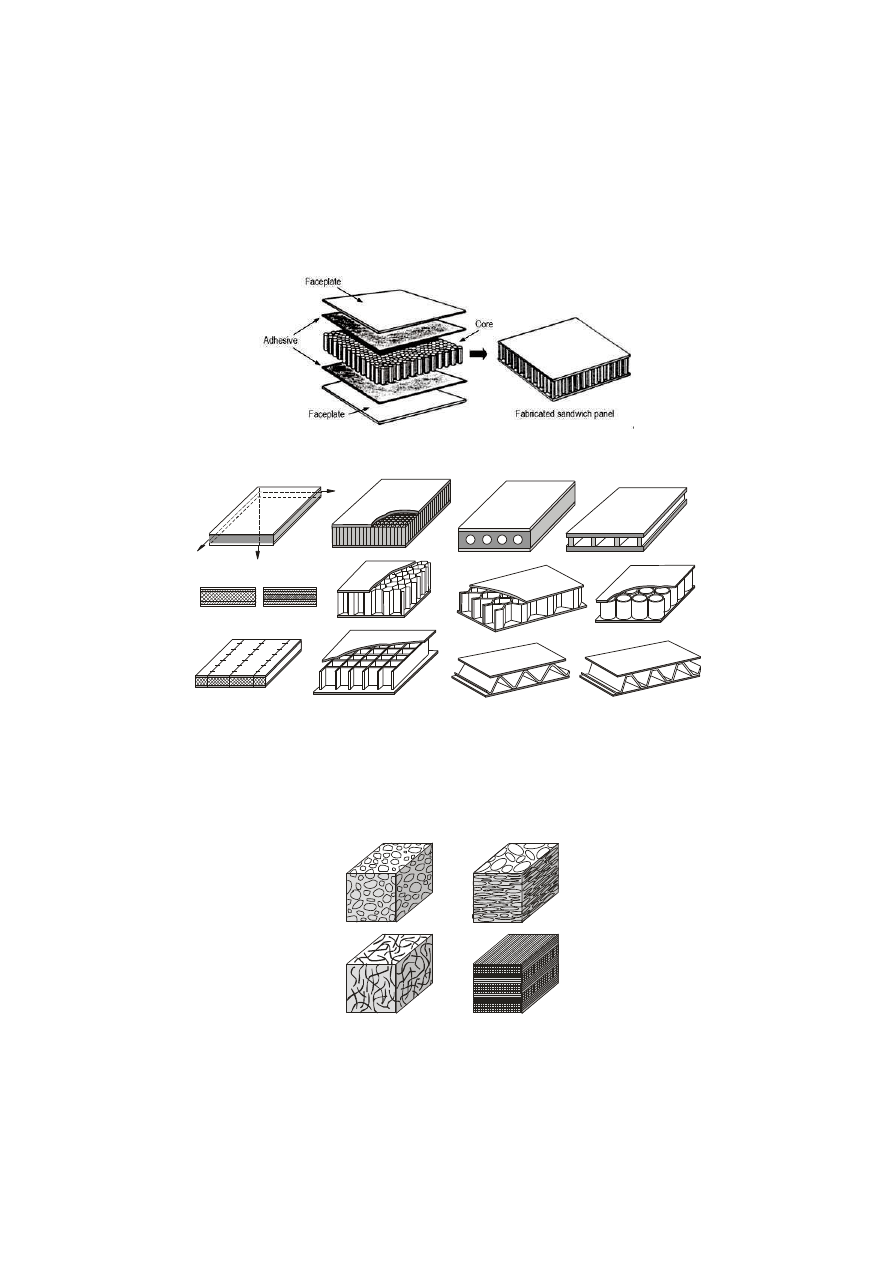
Współczesne konstrukcje inżynierskie coraz częściej stosują wielowarstwowe ma-

teriały kompozytowe (laminaty), których budowa nie spełnia przedstawionych powy-
żej warunków jednorodności i izotropowości. Wzorem dla materiałów kompozytowych
są konstrukcje spotykane w naturze (pnie drzew, łodygi zbóż itp.).

Przykład trójwarstwowej płyty

x

y

z

Przykłady zastosowania konstrukcji trójwarstwowych.

Konstrukcje wielowarstwowe

, oprócz spełnienia warunków wytrzymałościowych,

są lekkie, sztywne i pozwalają na wykorzystanie warstwy wypełniającej do zwiększe-
nia ich właściwości użytkowych (np. izolacje termiczne, miejsce na różne instalacje
itp.)

a)

d)

c)

b)

Przykłady niejednorodnych konstrukcji kompozytowych

Projektowanie i obliczenia wytrzymałościowe konstrukcji kompozytowych wymaga-

ją stosowania skomplikowanych modeli matematycznych i metod ich rozwiązywania,
opartych w głównej mierzy o metody numeryczne.

14 Zagadnienia wybrane

164

POZNANIE MODELI, UPROSZCZEŃ I METOD KLASYCZNEJ WY-

TRZYMAŁOŚCI MATERIAŁÓW STANOWI NIEZBĘDNY WARUNEK
PRAKTYCZNEGO ZASTOSOWANIA TYCH MATERIA

ŁÓW

.

Współczesne konstrukcje inżynierskie wymagające zastosowania odpo-

wiednich metod projektowania i obliczania

wytrzymałościowego (metody

komputerowego wspomagania obliczeń CAx).

Zastosowanie różnych materiałów w przekroju historycznym

14 Zagadnienia wybrane

165

Współczesne konstrukcje lotnicze, a w ślad za nimi inne konstrukcje

cechuje coraz szersze zastosowanie materiałów kompozytowych (mate-
riały niejednorodne, anizotropowe, o nieliniowej charakterystyce)

3

.

3

Porównaj model ciała w klasycznej wytrzymałości materiałow – rozdział 7.