1.Postulaty statyki

1)Zasada równoległoboku R=P

1

+P

2

2)Dwie siły przyłożone do ciała sztywnego równoważą się tylko wtedy, gdy
działają wzdłuż tej samej prostej, są przeciwnie skierowane i mają te same

wartości liczbowe 3)Działanie układu sił przyłożonych do ciał sztyw. nie
ulegnie zmianie, gdy do układu dodamy lub odejm. dowolny układ

równoważących się sił tzw. układ zerowy 4)Zasada zesztywnienia – równowaga
sił działających na ciało odkształcalne nie zostanie naruszona przez

zesztywnienie tego ciała 5)Każdemu działaniu towarzyszy równe co do
wartości i przeciwnie skierowane wzdłuż tej samej prostej przeciwdziałanie

6)Każde ciało nieswobodne można myślowo oswobodzić od więzów, zastępując
przy tym ich działanie odpowiednimi reakcjami.

2. Tw. o trzech siłach:

Trzy nierównoległe do siebie działające w jednej płaszczyźnie pozostają w
równowadze wtedy i tylko w tedy gdy tworzą układ zbieżny a ich kierunki

tworzą trójkąt zamknięty. P

1

=P

2

+P

3

3. Tw. Varignona:
Suma momentów sił układu zbieżnego względem dowolnego punktu jest równa

momentowi wypadkowej tego układu względem punktu ∑

n

i=1

r∙∑P

i

=r∙W

4. Para sił:
Układ dwóch sił równoległych P’ = −P, P’ = P nie leżących na jednej

prostej nazywamy parą sił. Odległość między siłami nazywamy ramieniem pary
sił.

Aby pary sił działające w jednej płaszczyźnie na ciało sztywne znajdowały
się w równowadze, suma momentów tych par musi

się równać zeru.

5. Moment sił względem punktu: Mo=r∙F
Moment sił względem osi: M=r∙P , moment ten jest wektorem swobodnym do

płaszczyzny π czuli ma kierunek prostej l

6. Kratownica – jest to układ złożony z prętów połączonych przegubowo,
mający niezmienną postać geometryczną. Warunek sztywności p=2w-3

7. Redukcja płaskiego układu sił

P’=P

a’=-a

8. Redukcja przestrzennego ukł. Sił – dowolny układ sił przyłożonych do
jednego punktu zastąpić możemy jedną siłą wypadkową przyłożoną w tym

punkcie i równą sumie geometrycznej sił.

10. Kinematyczne równania ruchu:
x=x(t). y=y(t). z=z(t)

lub

⃗r=⃗r (t )

11. Prędkość

v=lim Δr/Δt = dr/dt = r’ prędkość zawsze jest styczna do toru i zawsze
jest wektorem v=x’i+y’j+z’k v=√(x’)

2

+(y’)

2

+(z’)

2

12. Przyspieszenie

a=lim Δv/Δt = dv/dt = r’’ przyspieszenie nigdy nie jest styczne do toru
chyba że jest linią prostą v=x’’i+y’’j+z’’k v=√(x’’)

2

+(y’’)

2

+(z’’)

2

13. Przyspieszenie styczne i normalne:

a

s

=dv/dt – przyspieszenie styczne

a

n

=v

2

/ρ – przyspieszenie normalne

14. Droga:

s=

∫

t

1

t

2

Vdt

18. Rodzaje ruchów bryły sztywnej:
l. ruch postępowy - to taki ruch w którym dowolna prosta sztywno związana z

tą bryłą zajmuje położenie wzajemnie równoległe (3 stopnie swobody).
2. ruch obrotowy - to taki ruch bryły w którym dowolne dwa punkty bryły są

nieruchome, prosta przechodząca przez dwa punkty to oś obrotu (1 stopień
swobody).

3.ruch płaski - to taki ruch bryły w którym dowolny przekrój tej bryły
płaszczyzną zajmuje położenie równoległe i jest równoległy do pewnej stałej

płaszczyzny zwanej kierującą (3 stopnie swobody).
4. ruch kulisty - to taki ruch bryły w którym bryła porusza się dookoła

nieruchomego punktu bryły (3 stopnie swobody).
5. ruch ogólny -jest to złożenie ruch postępowego i kulistego.

19 . Ruch postępowy bryły sztywnej:

v=dr

o

/dt=v

o

a=d

2

r

o

/dt

2

=dv

o

/dt=a

o

- wszystkie punkty bryły sztywnej w ruchu postępowym mają te same prędkości

v

o

i przyśpieszenia a

o

w tej samej chwili czasu.

- tory wszystkich punktów bryły mają ten sam kształt.

- dla opisu ruchu postępowego bryły wystarczy podać równanie ruchu jednego
punktu bryły, np. początku ruchomego układu współrzędnych O’.

20 . Ruch obrotowy bryły:

ω =

d ϕ /dt

ε =

d ω /dt=d

2

ϕ /

dt

2

v=ω ×r '

a=ε ×r ' +ω ×(ω ×r ' )

a=ε×r '+ω(ω∗r ')−ω

2

r '

21. Prędkość kątowa:
Prędkość kątowa jest równa kątowi zakreślonemu podczas ruchu podzielonemu

przez czas.

ω

=

Δ α

Δ

t

22. Przyspieszenie kątowe, ε, wielkość pseudowektorowa charakteryzująca
zmiany prędkości kątowej ω bryły sztywnej lub punktu materialnego.

Przyspieszenie kątowe określone jest równaniem:

ε =

d ω

dt

=

d

2

dt

2

23. Prędkość liniowa punktu, a prędkość kątowa bryły.

v=

dx

dt

⃗

ω =

d ϕ

dt

24. Prędkość i przyspieszenie bryły w ruchu płaskim.

v=v

o

+

ω×r '

a=a

o

+

ε×r ' +ω(ω∗r ')−ω

2

r '

25. Twierdzenie o rzutach prędkości dwóch punktów bryły poruszającej się
ruchem płaskim.

Tw. o trzech rzutach – jeśli bryła znajduje się w ruchu płaskim to rzuty

prędkości 2 dowolnych punktów A i B na łączące je proste są równe.
Taki punkt należący do bryły lub leżący poza nią który w pewnej chwili ma

prędkość 0 nazywa się chwilowym środkiem obrotu (punkt C). Przy pomocy
chwilowego środka obrotu możemy znaleźć prędkość punktów posługując się
wzorem

v=ω×CA

. Wektor prędkości kątowej jest zawsze taki sam i jest

jeden dla wszystkich punktów bryły.

26. Chwilowy środek obrotu.
Patrz 25.

33. Ruch złożony punktu.

Ruch punktu względem układu nieruchomego nazywamy ruchem bezwzględnym, a
względem układu ruchomego ruchem względnym. Ruch układu ruchomego względem

układu nieruchomego nazywamy ruchem unoszenia

34. Prędkość bezwzględna

⃗

v

b

= ⃗

v

u

+ ⃗

v

w

Prędkość w ruchu obrotowym unoszenia
Prędkość w ruchu względnym (prostoliniowym)

35 Przyspieszenie bezwz.

Jest sumą wektorową przyspieszenia unoszenia, względnego i przyspieszenia
Coriolisa:

⃗

a

b

= ⃗

a

u

+ ⃗

a

w

+ ⃗

a

c

⃗

a

c

=

2 ⃗

ω × ⃗

υ

n

36. Przyspieszenie Coriolisa.

Przyspieszenie Coriolisa równe jest podwojonemu iloczynowi wektorowemu
prędkości kątowej układu ruchomego i prędkości względem punktu A. p

c

=2ω×v

r.

Przyspieszenie Coliolisa nie występuje gdy ruchem unoszenia są ruchy:
prostoliniowy, harmoniczny prosty i postępowy (w= zero),gdy wektor

prędkości kątowej jest równoległy do wektora prędkości względnej oraz gdy
prędkość względna jest równa zeru.

37. Zasady Newtona.

I prawo bezwładności: punkt materialny, na który nie działa żadna siła lub
działające siły się równoważą, pozostaje w spoczynku lub porusza się ruchem

jednostajnym po linii prostej.
II prawo: przyśpieszenie punktu materialnego jest proporcjonalne do siły

działającej na ten punkt i ma kierunek taki jak ta siła. F=ma.
III prawo akcji i reakcji: siły wzajemnego oddziaływania dwóch punktów

materialnych mają jednakowe wartości, leżą na prostej łączącej te punkty i
są przeciwnie skierowane.

IV prawo zasady superpozycji: jeżeli na punkt materialny działa
jednocześnie kilka sił, to każda z nich działa niezależnie od pozostałych,

a wszystkie razem działają jak jedna siła równa wektorowej sumie danych
sił.

V prawo powszechnego ciążenia: Każde dwa punkty materialne o masach m

1

i m

2

przyciągają się z siłą wprost
proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu

odległości r między nimi. Kierunek siły leży na prostej łączącej te punkty.
F=k m

1

m

2

/r

2

38. Zasada d’Alemberta.

Suma sił rzeczywistych i siły bezwładności działających na punkt materialny
jest w każdej chwili równa zeru.

F+(-ma)=0

39. Zasada zachowania pędu; 40. Zasada pędu i popędu.
Pędem punktu materialnego o masie m i prędkości v nazywamy iloczyn masy

punktu i jego prędkości: p=mv
Zasada pędu: Pochodna względem czasu pędu układu punktów materialnych jest

równa wektorowi głównemu sił zewnętrznych działających na ten układ. ma=F ;
a=dv/dt → m dv/dt=F ; m=const. d/dt (mv)=F → dp/dt=F.

Zasada pędu i popędu (lub inaczej, prawo zmienności pędu) Przyrost pędu
układu materialnego w skończonym przedziale czasu jest równy popędowi

wektora głównego sił zewnętrznych działających na ten układ. p(t)-
p(0)=∫

t

0

Fdt

Zasada zachowania pędu: jeżeli wektor główny układu sił zewnętrznych
działających na ten układ materialny jest równy zeru, to pęd tego układu

materialnego jest stały: dp/dt=F; F=0; dp/dt=0; p=const.

41. Zasada zachowania krętu: jeżeli moment główny sił zewnętrznych względem
nieruchomego punktu redukcji O jest równy zeru, to kręt układu materialnego

(bryły) względem tego punktu jest wielkością stałą. Jeżeli M

o

=0 to k

0

=const.

42. Zasada krętu: pochodna względem czasu krętu układu punktów materialnych
względem dowolnego nieruchomego punktu jest równa momentowi głównemu

wszystkich sił zewnętrznych względem tego samego punktu. dk

o

/dt=M

o

43. Dynamiczne równania ruchu punktu materialnego.

a=dv/dt e

s

+v

2

/ρ e

n

e

s

=m dv/dt

e

n

=m v

2

/ρ

e

b

=e

s

x e

n

44.Definicja pracy.
Praca jest to mechaniczny sposób przekazu energii. Jednostką pracy jest

Jul.

45.Moc mechaniczna.
Mocą siły nazywamy pracą wykonaną w jednostce czasu. Jeśli praca siły

zmienia się z czasem to wówczas moc jest pochodna pracy względem czasu:

M =

dL

dt

[

W ]

46.Zasada równoważności pracy i energii kinetycznej.
Jeżeli na poruszający się punkt materialny o masie m działa siła czynna P

to przyrost en. kinetycznej tego punktu jest równy pracy wykonanej przez
siłę działającą na ten punkt: L=1/2mV2k - 1/2mV2p

57. Drgania swobodne.

Drgania swobodne mx’’=-kx ; ω

2

=k/m → x’’+ ω

2

x=0

x=Asinω

o

t gdzie. x-wychylenie ciała z położenia równowagi w chwili czasu t,

A – amplituda drgań, ω – częstość kołowa drgań. Brak tłumienia i brak
wymuszenia.

48.Potencjalne (zachowawcze) pole sił.

POLE JEST POTENCJALNYM POLEM SIL, GDY PRACA PRZY PRZESOWANIU PUNKTU NIE
ZALEZY OD DROGI (TZN PRACA PO DRODZE ZAMKNIETEJ = 0)

CENTRALNE POLE SIL:
POLE SIL O TEJ WLASNOSCI ZE LINIE DZIALANIA SIL TEGO POLA ZAWSZE PRZECHODZA

PRZEZ JEDEN PUNKT
Zdolność do wykonania pracy ciała znajdującego się w spoczynku nazywamy en.

potencjalną E

p

: E

p

=mgh.

49.Twierdzenie o ruchu środka masy układu punktów materialnych.

∑

mr ''=

∑

F +

∑

W

,

gdzie

∑

F −R

,

∑

W =0

0

2

2

2

2

Mr

dt

d

mr

dt

d

∑

=

;

Mr

0

' ' =R

Ruch układów punktów materialnych odbywa się tak jakby cała masa układu

skupiona była w jego środku masy i na który to punkt działają wszystkie
siły zewnętrzne.

⃗

M ⃗

ρ =

R

50.Pęd układu punktów materialnych.

R

MV

dt

d

=

0

;

Q=MV

0

=

∑

mV

- pęd ukł. punktów_materialnych;

R

dt

dQ

=

- zasada pędu

Na pęd ma tylko wpływ siła zew, a nie wew.

R=0 >> Q=const
Jeżeli jedno ciało zyskuje pęd to drugie też go zyskuje lecz z przeciwnym

znakiem.
PED DOTYCZY TYLKO RUCHU POSTEPOWEGO, NIE OBROTOWEGO, BO NIE MA MASY

BEZWLADNOSCI PREDKOSCI KATOWEJ
ZASADA ZACHOWANIA PEDU: JEŻELI NA UKLAD NIE DZIALAJA SILY LUB DZIALAJACE

SILY SIĘ ZNOSZA TO PED JEST STALY CZYLI ZACHOWANY R=0 TO Q=const.
OKRESLA SIĘ GO TYLKO PRZY RUCHU POSTEPOWYM, PRZY RUCHU OBROTOWYM NIE

ISTNIEJE.

51.Kręt układu punktów materialnych.

K

S

=

∑

ρ

i

∗

mV

i

-kręt

c

c

M

dt

dK

=

Zmiana krętu ukł. punktów mat. W czasie wywołana jest przez moment główny

działający na układ brany względem nieruchomego punktu lub środka masy.
M

c

=0 >> K

c

=const

52.Energia kinetyczna układu punktów materialnych.

Energia kinetyczna układu punktów materialnych jest równa sumie energii
kinetycznej w ruch postępowym i energii kinetycznej w ruchu względnym
dookoła środka masy C układu.

E=½V

c

p +½ωK

c

;

p=mVc

;

K

c

=

I

c

ω

53.Twierdzenie Koeniga.

Energia kinetyczna układu punktów materialnych równa jest sumie energii
kinetycznej, jaką miałby pkt materialny o masie całego układu, poruszający

się z prędkością środka masy oraz energii kinetycznej tegoż układu względem
środka masy.

T =

1
2

mυ

C

2

+

1
2

I

L

ω

2

54. Zasada zachowania energii mechanicznej - w układzie izolowanym suma

składników wszystkich rodzajów energii całości (suma energii wszystkich
jego części) układu jest stała (nie zmienia się w czasie).

57. Drgania swobodne

Aby wystąpiły drgania, punkt musi poruszać się ruchem prostoliniowym pod
wpływem siły F przyciągającej ten punkt do stałego punktu O zwanego

środkiem drgań.
Siła sprężystości jest proporcjonalna do wychylenia punktu

F = -kx, k-stała sprężystości.
Równanie będzie miało postać

mx” = F
mx” = -kx lub

x ' '

k

m

x=0

k

m

=

ω

Otrzymujemy równanie różniczkowe drgań swobodnych

x ' '=ω

2

x=0

ω - częstość ruchu.
Otrzymane równanie jest równaniem liniowym, jednorodnym drugiego rzędu.

Rozwiązanie:

x=a sin( ωt+ϕ)

a-amplituda

ϕ

- faza początkowa ruchu drgań

)

(

ϕ

ω

+

t

-faza drgań

Ruch określony powyższym wzorem jest okresowy o okresie

T =2π/ω , ω=

√

k /m

T =2π

√

m/k

58. Drgania tłumione
Drgania tłumione występują w ośrodku stawiającym opór. Siły oporu są

proporcjonalne do prędkości

R

¿

=−

βν

x

=−

βx '

-siła tłumiąca.

Równania ruchu:

mx ' '=−kx− βx '

x ' ' +2 nx ' +ω

2

x=0

ω=

√

k /m,2 n= β /m

Ponieważ równanie charakterystyczne

0

2

2

2

=

+

+

ω

α

α

n

jest kwadratowe, to mogą zajść 3 przypadki(delta większa, mniejsza, równa
0)
1.Małe tłumienie

ω>n ⇒ Δ<0

Rozwiązanie:

x=ae

−

nt

sin(

√

ω

2

−

n

2

t+ϕ)

Jeżeli

0

,

→

∞

→

tox

t

- drgania zanikają. Okres:

2

2

2

2

,

2

n

n

T

t

−

=

−

=

ω

ω

ω

ω

2.Duże tłumienie.

0

>

∆

⇒

<

n

ω

Mamy rozw. rzeczywiste nie będzie drgań.

Rozwiązanie

x=ae

−

nt

sinh(

√

ω

2

−

n

2

t+ϕ)

Jeżeli

0

,

→

∞

→

tox

t

- drgania zanikają. Okres:

2

2

2

2

,

2

n

n

T

t

−

=

−

=

ω

ω

ω

ω

2.Duże tłumienie.

0

>

∆

⇒

<

n

ω

Mamy rozw. rzeczywiste nie będzie drgań.

Rozwiązanie

x=ae

−

nt

sinh(

√

ω

2

−

n

2

t+ϕ)

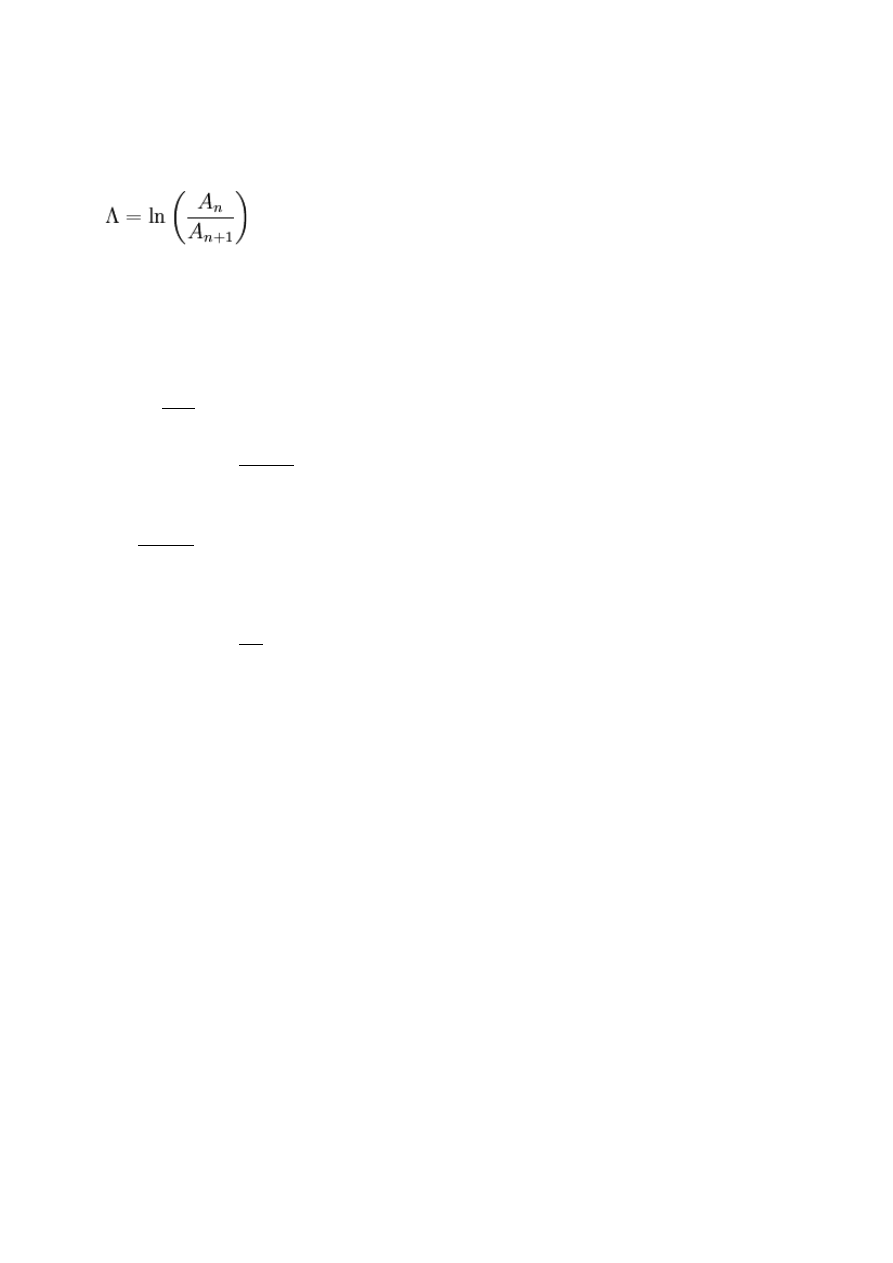
59. Logarytmiczny dekrement tłumienia.
wielkość charakteryzująca tłumienie drgań, zdefiniowana jako logarytm

naturalny stosunku amplitud dwóch kolejnych wychyleń w tę samą stronę
drgającej cząsteczki.

60. Drgania wymuszone

Jeżeli na punkt dodatkowo działa siła wymuszająca okresowa to występują
drgania wymuszone.

Siła wymuszająca S=H sin(pt),
p-czestość siły wymuszającej.

Równanie ruchu tych drgań

mx ' '=−kx −H sin( pt )

x ' ' +2 nx '=h sin ( pt )

ω=

√

k /m , h=H /m

Rozwiązanie ostateczne tych drgań

x=a sin(ωt +ϕ)+

h

ω

2

−

p

2

sin ( pt )

Jest to złożenie dwóch drgań: własnych i wymuszonych. Widzimy, że amplituda

drgań wymuszonych

2

2

p

h

B

−

=

ω

zależy od częstości drgań wymuszonych.
Jeżeli

∞

→

→

toB

p

,

ω

i występuje rezonans. W przypadku rezonansu rozwiązanie

drgań będzie miało postać.

x=a sin(ωt +ϕ)+

h

2ω

t cos(ωt )

61. Rezonans.
zjawisko fizyczne zachodzące dla drgań wymuszonych, objawiające się

pochłanianiem energii poprzez wykonywanie drgań o dużej amplitudzie przez
układ drgający dla określonych częstotliwości drgań.

62. Amplituda.

największa wartość A

0

osiągana przez wielkość fizyczną A, zmieniającą się w

czasie t w sposób harmoniczny, tj. proporcjonalnie do sin (ωt+ϕ

0

), gdzie ω –

częstotliwość kątowa, ϕ

0

– początkowa faza drgań.

63. Okres drgań.
dla ruchu periodycznego czas, po jakim układ drgający znajduje się ponownie

w takiej samej fazie.

64. Częstotliwość drgań.
Częstotliwość drgań to liczba cykli wykonywanych przez drgające środowisko

w ciągu jednej sekundy. Częstotliwość określa się w hercach (Hz)

65. Częstość (Częstotliwość) drgań własnych.
Ciała mogą mieć wiele częstotliwości drgań własnych - Często wielokrotność

drgań najmniejszych. Częstotliwość drgań własnych zależy od sposobu
wzbudzania i ilości dostarczonej energii. Uderzając w przedmiot w różnych

miejscach z różną siłą Drgania te będą różniły się składem widmowym, czyli
będą wzbudzane drgania własne o różnych częstotliwościach i natężeniach.

66. Faza drgań. Dla drgań harmonicznych opisanych równaniem:

x (t)=A∗sin (ω∗t +ϕ )

fazą drgań określa się argument funkcji sinus, czyli:

ω∗

t +ϕ

lub resztę z dzielenia tego kąta przez miarę kąta pełnego

(

ω ∗

t+ω )mod (2 π )

Faza jest wyrażana w jednostkach kąta, zwykle w układzie SI w radianach.

Kąt φ nazywa się fazą początkową drgań, czyli fazą w chwili początkowej t =
0.

67. Faza początkowa drgań patrz 66.

78. Środek masy bryły

x

S

=

1

M

∫

V

ϱ

x d V

y

s

=

1

M

∫

V

ϱ

y d V

z

s

=

1

M

∫

V

ϱ

z d V

77. Środek masy układu punktów materialnych.
Wektor środka masy wyznaczany jest następująco:

⃗

r

CM

=

∑

i=1

N

m

i

⃗

r

i

∑

i=1

N

m

i

, gdzie:

M =

∑

i=1

N

m

i

78. Definicja momentu bezwładności
Momentem bezwładności punktu materialnego względem płaszczyzny,

osi lub bieguna nazywamy iloczyn masy tego punktu przez kwadrat odległości
tego punktu od płaszczyzny, osi lub bieguna.

I = mr

2

81. Tw. Steinera

Moment bezwładności względem dowolnej osi jest równy momentowi względem osi
równoległej przechodzącej przez środek masy powiększonemu o iloczyn masy

całkowitej
układu przez kwadrat odległości obu osi.

I

z

=

I

xx

+

I

yy

=

I

z

+

md r

2

I

l

=

I

1

=

md

2

82. Moment bezwładności względem dowolnie skierowanej osi
Moment bezwładności względem osi:

I =

∫

v

Vr

2

dm

dm, zatem:

I =I

x

cos2α+I

y

cos2β+ I

z

cos2γ −

2Dxy cos αcos β − 2Dyz cos β cosγ −

2Dzx cosγ cosα

84. Osie centralne - osie współrzędne przecinające się w środku mas.

83. Główna oś bezwładności
Można przyjąć układ współrzędnych taki, ze

Dαβ= I

1

x

2

+

I

2

y

2

+

I

3

z

2

=

k

2

gdzie I

1

,

2

,

3

-główne momenty bezwładności

Takimi osiami są: każda oś symetrii, każda prosta prostopadła do

płaszczyzny symetrii, każda prosta, na której leżą środki mas warstw
elementarnych, otrzymanych przez podział ciała płaszczyznami prostopadłymi

do tej prostej.

85. Główna centralna oś bezwładności
Są to osie główne przechodzące przez środek masy

86. Macierz bezwładności

Macierz bezwładności jest macierzą symetryczną. Elementy na przekątnej –
momenty bezwładności. Elementy poza przekątną – momenty dewiacyjne bądź

iloczyny bezwładności.

I =

[

I

11

I

12

I

13

I

21

I

22

I

23

I

31

I

32

I

33

]