Maria Kotełko

Mechanika

i Wytrzymało

ść

Materiałów

————————————————————————————————————————

Zadanie nr 32 - Dostosowanie kierunku Automatyka i Robotyka

do prowadzenia studiów niestacjonarnych

2

Mechanika i …

Cz

ęść

I - Mechanika

Wykład 4.

1. Tarcie i prawa tarcia
2. Sto

ż

ek tarcia

3. Tarcie ci

ę

gien – wzór Eulera

4. Tarcie przy toczeniu si

ę

ciał

3

Mechanika i …

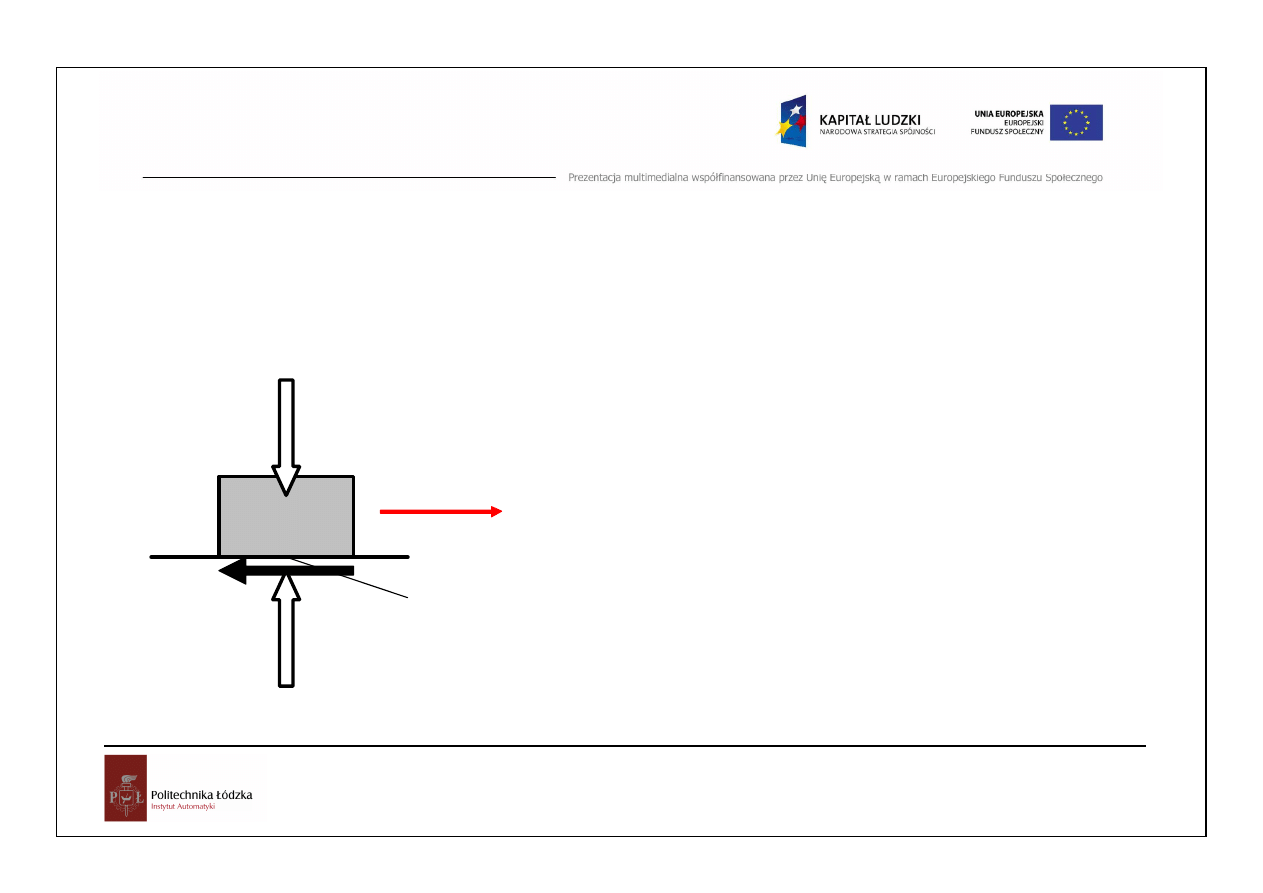
Zjawisko

tarcia

Jeżeli będziemy powoli zwiększać siłę S, dojdziemy do stanu,

w którym równowaga nie będzie już możliwa. Zatem widzimy,

że wielkość siły tarcia jest ograniczona i nie może przekroczyć

pewnej maksymalnej wartości.

S

Q

S = T

N = Q

T=

µµµµ

N

µµµµ

Potencjalny
kierunek ruchu

4

Mechanika i …

Prawa tarcia (Coulomb i Moren)

1. Siła tarcia jest niezale

ż

na od wielko

ś

ci stykaj

ą

cych si

ę

ze sob

ą

powierzchni i zale

ż

y jedynie od ich rodzaju.

2. Wielko

ść

siły tarcia dla ciała znajduj

ą

cego si

ę

w spoczynku mo

ż

e zmienia

ć

si

ę

od zera do warto

ś

ci

maksymalnej proporcjonalnej do nacisku normalnego N.

µ

- współczynnik tarcia statycznego ( spoczynkowego).

Gdy siła tarcia osi

ą

ga warto

ść

maksymaln

ą

, tzn. tarcie jest całkowicie rozwini

ę

te, mamy:

3. W przypadku, gdy ciało

ś

lizga si

ę

po powierzchni, siła tarcia skierowana jest zawsze przeciwnie do kierunku

ruchu. Wielko

ść

jej za

ś

nie zale

ż

y ( w przybli

ż

eniu) od pr

ę

dko

ś

ci po

ś

lizgu.

µ

’- współczynnik tarcia kinetycznego

T

k

<T - w tym przypadku siła tarcia jest mniejsza od warto

ś

ci maksymalnej, jak

ą

mo

ż

e ona osi

ą

gn

ąć

, gdy ciało

jest w spoczynku. T

N

T

⋅

≤

µ

N

T

⋅

=

µ

N

T

⋅′

=

µ

S

5

Mechanika i …

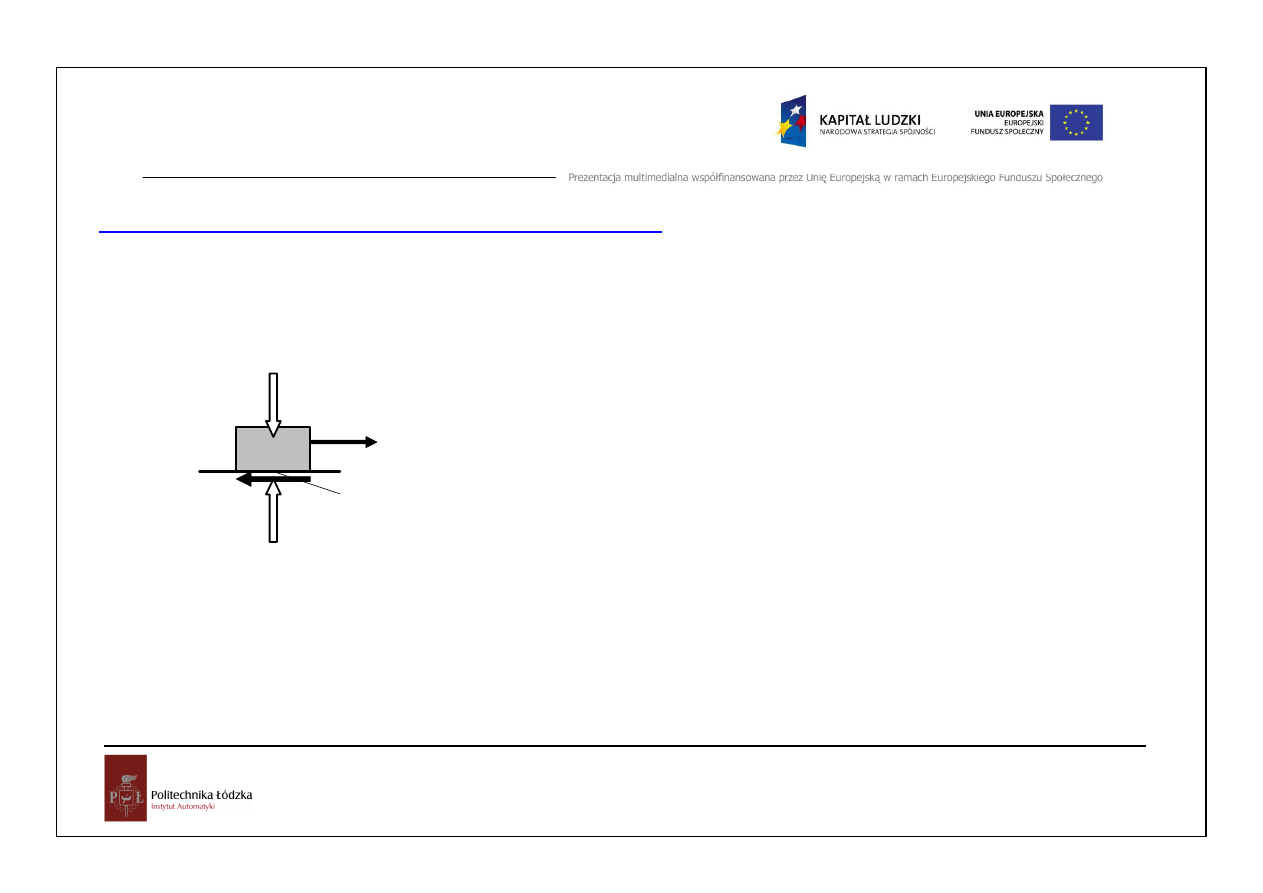
Układ równa

ń

równowagi w zagadnieniach tarcia

W przypadku ciała, którego wymiary s

ą

pomijalnie małe i sprowadza si

ę

je do punktu materialnego siły działaj

ą

ce

na ciało mo

ż

na w przybli

ż

eniu potraktowa

ć

jako układ sił zbie

ż

nych.

Q

N

P

n

i

iy

=

→

=

∑

=

1

0

N

T

⋅

=

µ

S

T

P

n

i

ix

=

→

=

∑

=

1

0

Q

S = T

N = Q

T=

µµµµ

N

µµµµ

6

Mechanika i …

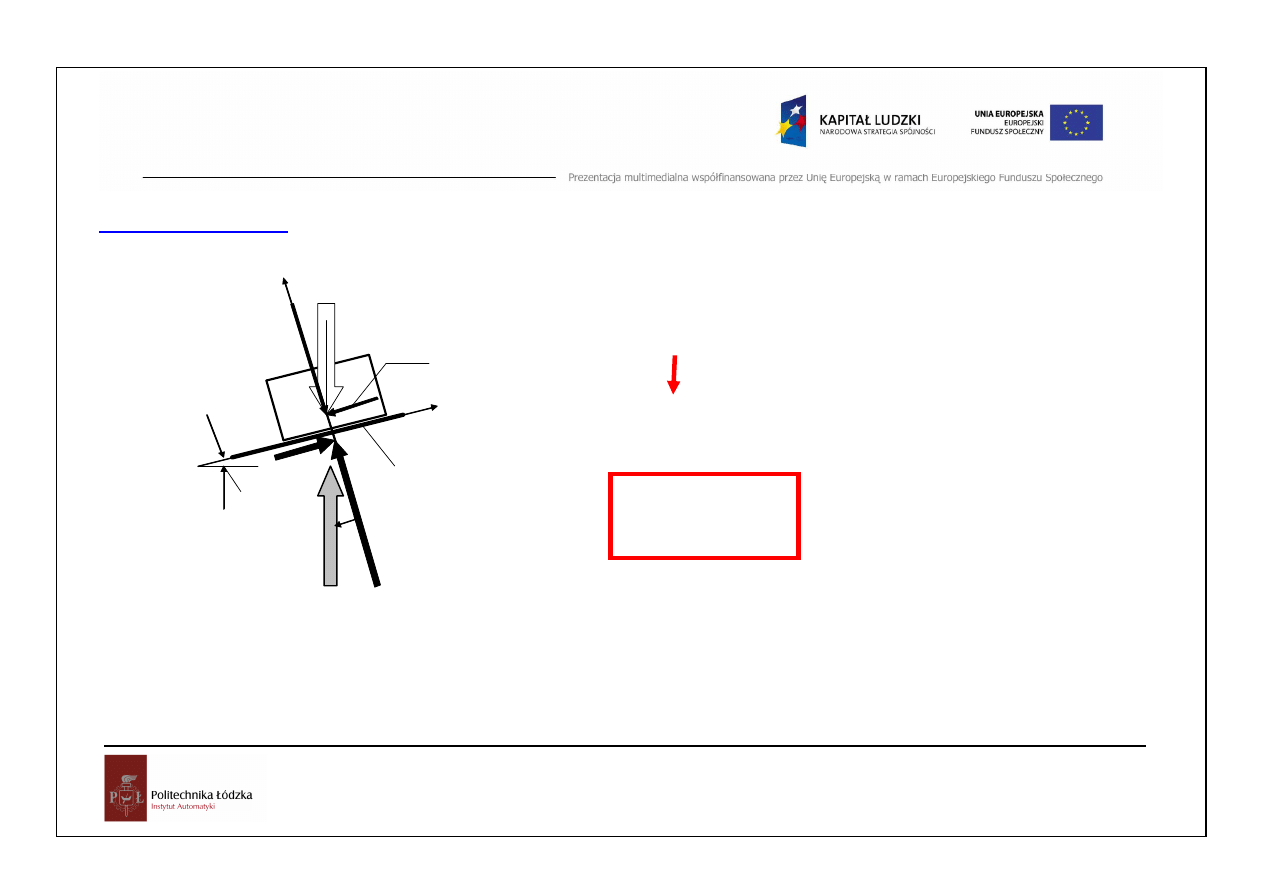
Równia pochyła

Je

ż

eli k

ą

t

α

jest zmienny i równia jest nachylona pod takim k

ą

tem

α

, przy którym ciało zaczyna si

ę

zsuwa

ć

,

wówczas k

ą

t ten nazywamy granicznym, a tangens

α

jest równy współczynnikowi tarcia

µ

. Schemat ten wyja

ś

nia

sens fizyczny współczynnika tarcia oraz poj

ę

cia k

ą

ta tarcia.

α

sin

0

1

⋅

=

→

=

∑

=

Q

T

P

n

i

ix

Q

Q sin

αααα

R = Q

T=

µµµµ

N

µµµµ

Q cos

αααα

N

αααα

αααα

x

y

α

cos

0

1

⋅

=

→

=

∑

=

Q

N

P

n

i

iy

α

µ

tg

=

α

µ

α

µ

cos

sin

⋅

⋅

=

⋅

→

⋅

=

Q

Q

N

T

7

Mechanika i …

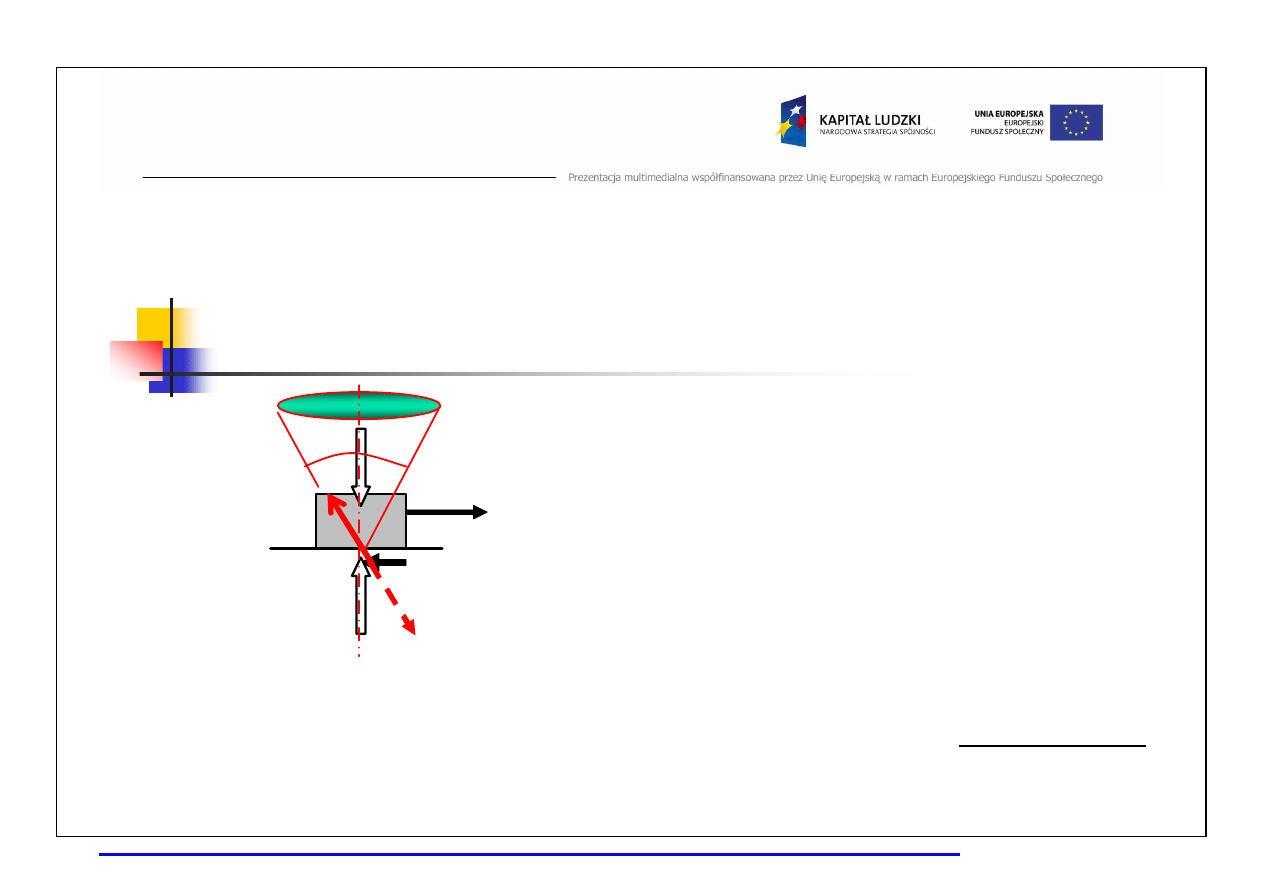
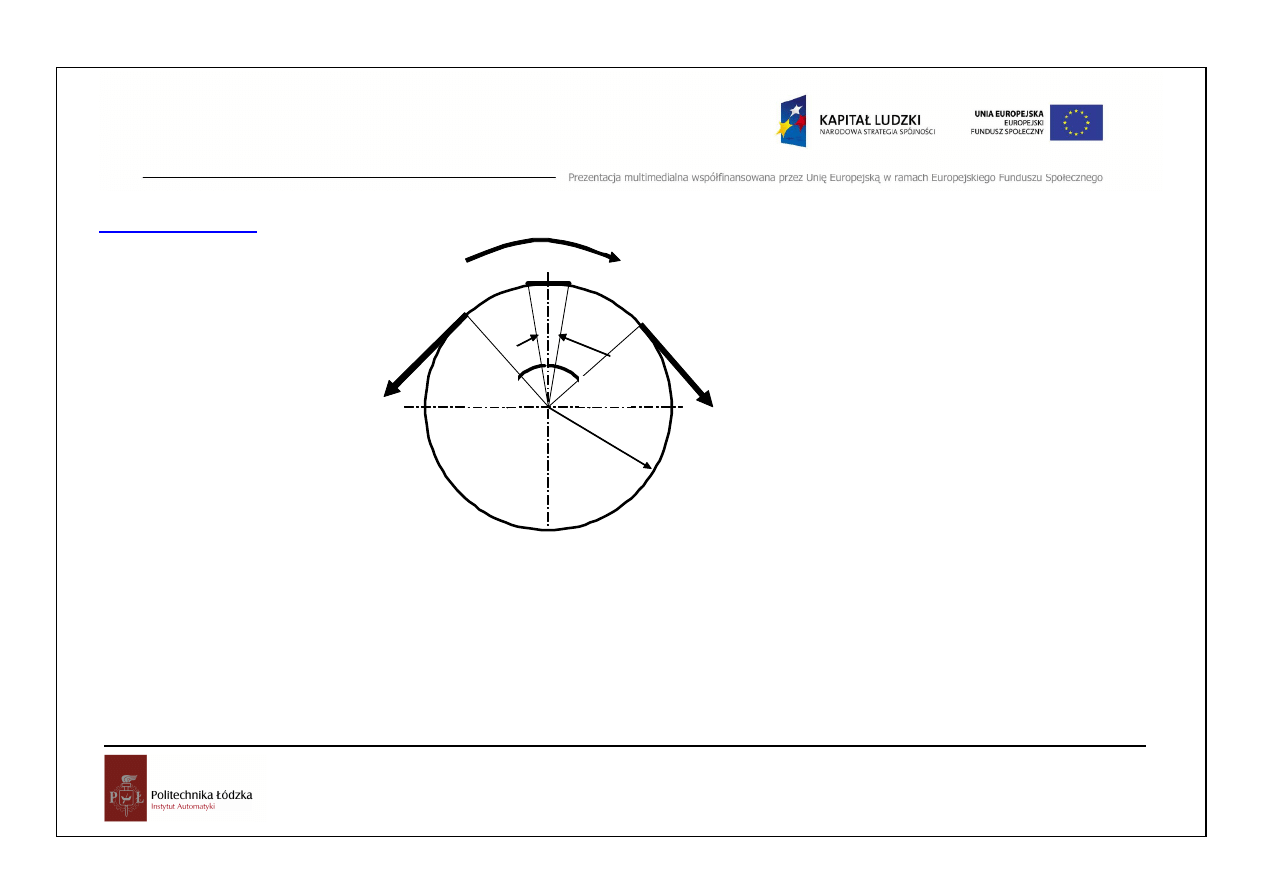
Kąt tarcia i stożek tarcia

Q

S = T

N

T

Maks ymalny k

ą

t mi

ę

dz y reakcj

ą

R a ki erunkiem

normalnej do powierzchni st yku naz ywamy

k

ą

tem

tarcia.

φ

µ

=

arctg

Miejsce geometryczne mo

ż

liw ych kierunków reakcji R, a w i

ę

c i wypadkow ej W

nazyw amy

sto

ż

kiem tarcia

. Aby cia

ł

o sztyw ne pozostaw a

ł

o w rów now adze

reakcja R musi le

żęć

w ewn

ą

trz lub na pow ierzchni sto

ż

ka tarcia.

R

W

2φ

8

Mechanika i …

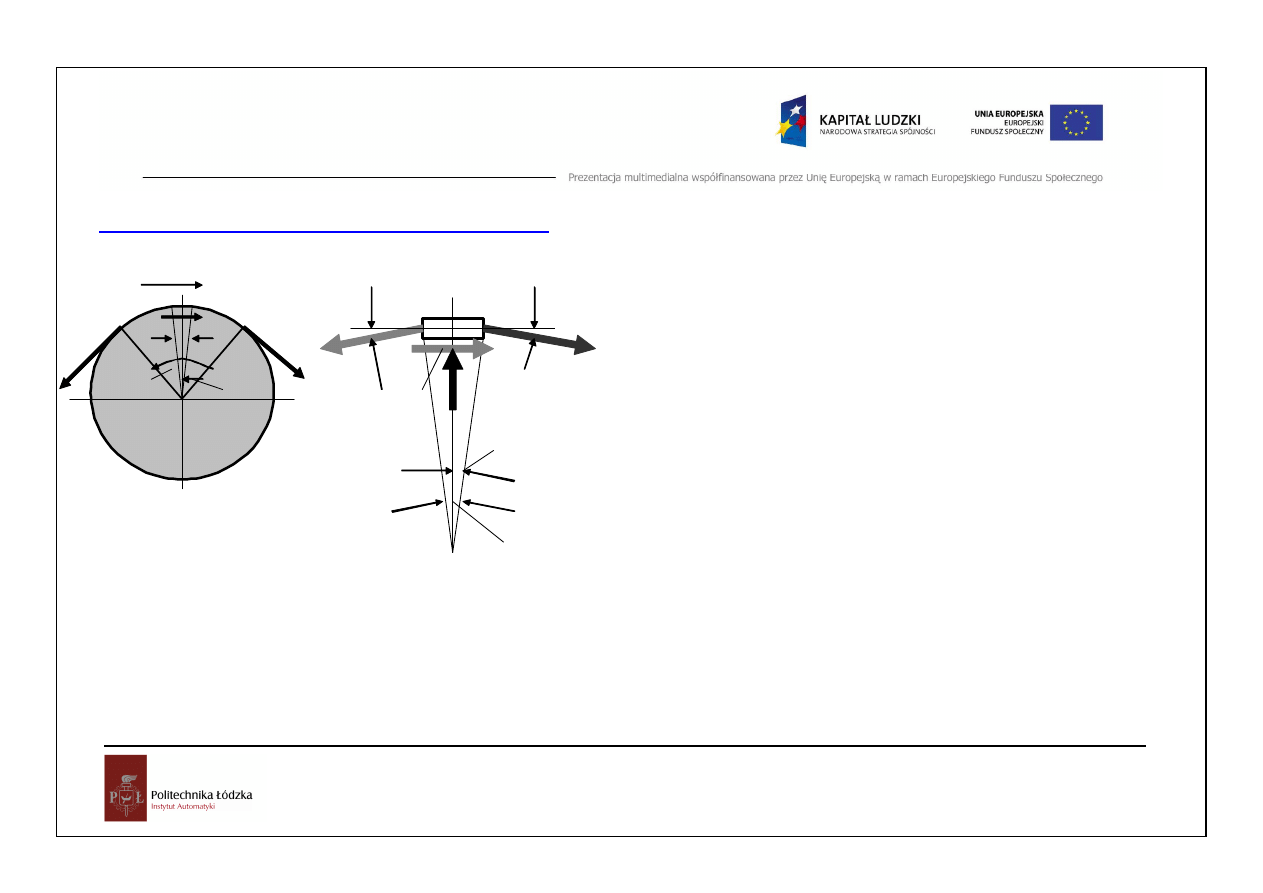
Tarcie ci

ę

gien

Rozpatrzmy przypadek tarcia ci

ę

gna (np. liny) o b

ę

ben (koło). Ci

ę

gno znajduje si

ę

w płaszczy

ź

nie prostopadłej do

osi b

ę

bna. Poniewa

ż

mi

ę

dzy powierzchni

ą

b

ę

bna a powierzchni

ą

ci

ę

gna wyst

ę

puje tarcie, to S

1

jest ró

ż

ne od S

2

.

Zakładamy S

2

> S

1

oraz

ż

e siła S osi

ą

gn

ę

ła maksimum, przy którym mo

ż

liwa jest jeszcze równowaga.

αααα

ϕϕϕϕ

d

ϕϕϕϕ

r

ds = rd

ϕϕϕϕ

S

2

S

1

T

9

Mechanika i …

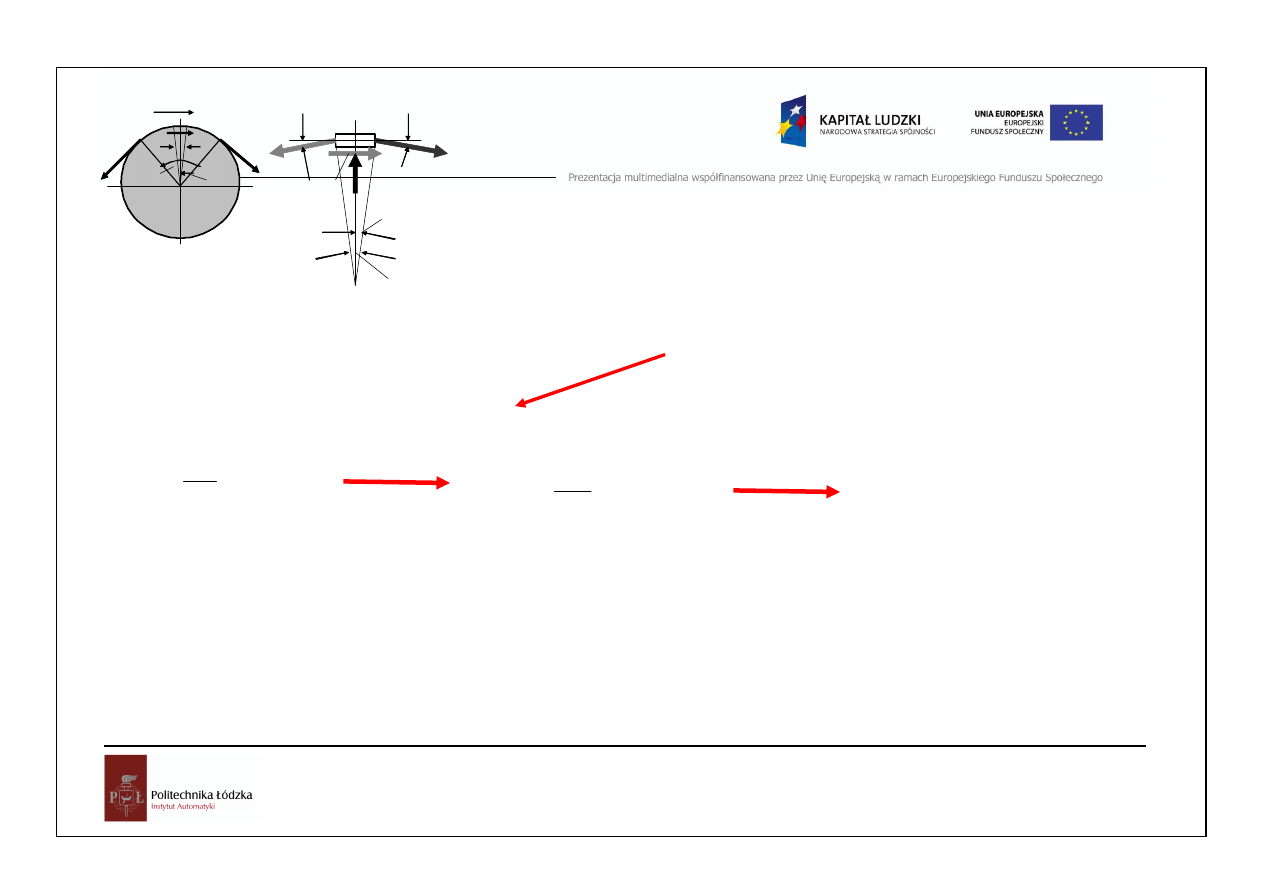
Tarcie ci

ę

gien – wzór Eulera dla ci

ę

gien

Równania równowagi wzgl

ę

dem osi t i n:

Po uwzgl

ę

dnieniu,

ż

e dla elementarnych k

ą

tów

d

ϕ

→

0

⇒

cos (d

ϕ

/2)

≅

1 i sin(d

ϕ

/2)

→

0

otrzymujemy zale

ż

no

ś

ci mi

ę

dzy elementarn

ą

sił

ą

tarcia dT oraz przyrostem siły dS:

S

2

>>>>

S

1

S

2

S

S

1

S+dS

dN

dT

dT=

µ

dN

d

ϕ

d

ϕ

/2

d

ϕ

/2

d

ϕ

/2

α

d

ϕ

ϕ

ϕ

(

) (

) (

)

(

) (

) (

)

0

2

/

sin

2

/

sin

0

2

/

cos

2

/

cos

=

+

−

⋅

−

=

+

+

−

⋅

ϕ

ϕ

ϕ

ϕ

d

dS

S

d

S

dN

dT

d

dS

S

d

S

ϕ

µ

Sd

dN

dN

dT

dS

dT

=

⋅

=

=

10

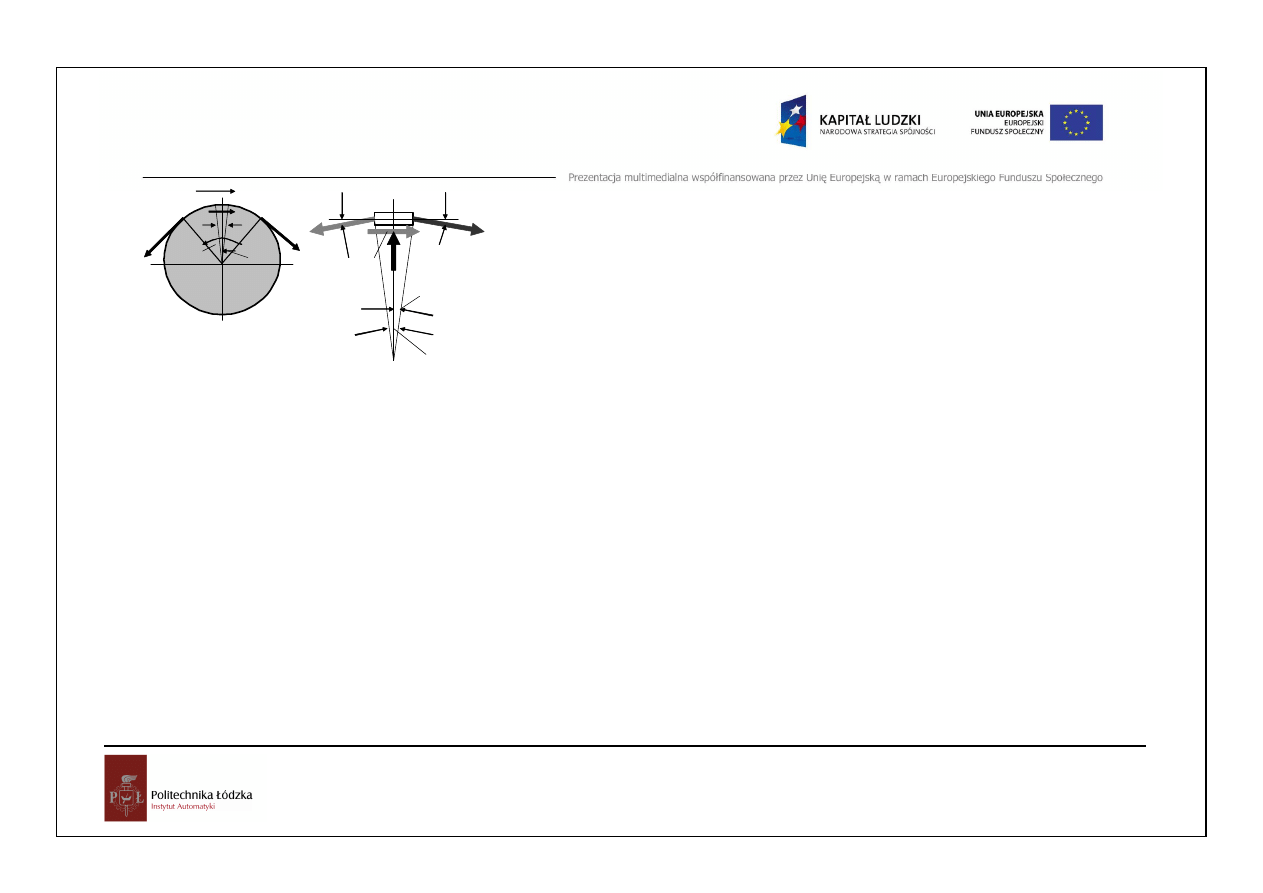
Mechanika i …

ϕ

µ

Sd

dN

dN

dT

dS

dT

=

⋅

=

=

µϕ

e

C

S

⋅

=

1

ln

C

S

+

⋅

=

ϕ

µ

ϕ

µ

d

S

dS

⋅

=

∫

∫

S

2

>>>>

S

1

S

2

S

S

1

S+dS

dN

dT

dT=

µ

dN

d

ϕ

d

ϕ

/2

d

ϕ

/2

d

ϕ

/2

α

d

ϕ

ϕ

ϕ

ϕ

µ

ϕ

µ

µ

d

S

dS

Sd

dN

dT

dS

⋅

=

⋅

=

⋅

=

=

11

Mechanika i …

Stał

ą

całkowania C wyznaczamy z warunku: dla

ϕ

= 0 siła S = S1 sk

ą

d C = S1 oraz dla

ϕ

=

α

S = S2 otrzymujemy warto

ść

siły S2 dla k

ą

ta opasania walca

α

oraz współczynnika tarcia

µ

:

Wzór Eulera dla ci

ę

gien

µα

e

S

S

⋅

=

1

2

S

2

>>>>

S

1

S

2

S

S

1

S+dS

dN

dT

dT=

µ

dN

d

ϕ

d

ϕ

/2

d

ϕ

/2

d

ϕ

/2

α

d

ϕ

ϕ

ϕ

µϕ

e

C

S

⋅

=

12

Mechanika i …

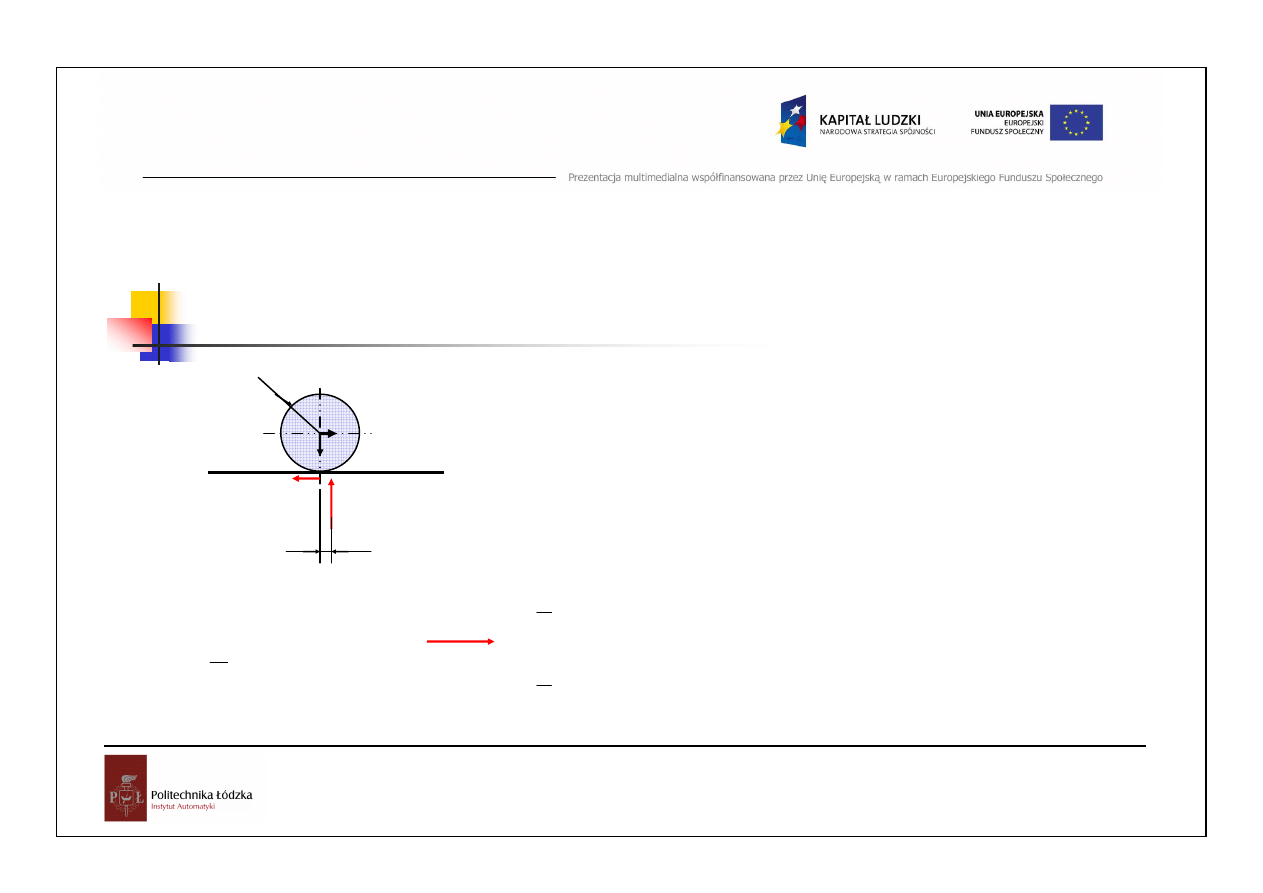
Opór przy toczeniu się ciał

f

-

współczynnik oporu przy toczeniu [mm]

A

Warunek równowagi momentów względem p. A:

P

G

T

N

Nf

=

Pr

P ozostałe warunki równowagi:

G

N

G

P

=

=

µ

r

f

G

P

G

P

≤

≤

µ

-

warunek, aby nie było poślizgu

- warunek, aby koło nie potoczyło się

µ

<

r

f

µ

>

r

f

-Koło zacznie się toczyć
(bez poślizgu)

-

Najpierw nastąpi poślizg

r