POLITECHNIKA BIAŁOSTOCKA - Studia stacjonarne - Inżynieria i Ochrona Środowiska 

Rysunek techniczny, Geometria wykreślna i grafika inżynierska - 

 ćwiczenie nr 04

, sem zimowy 

 

1

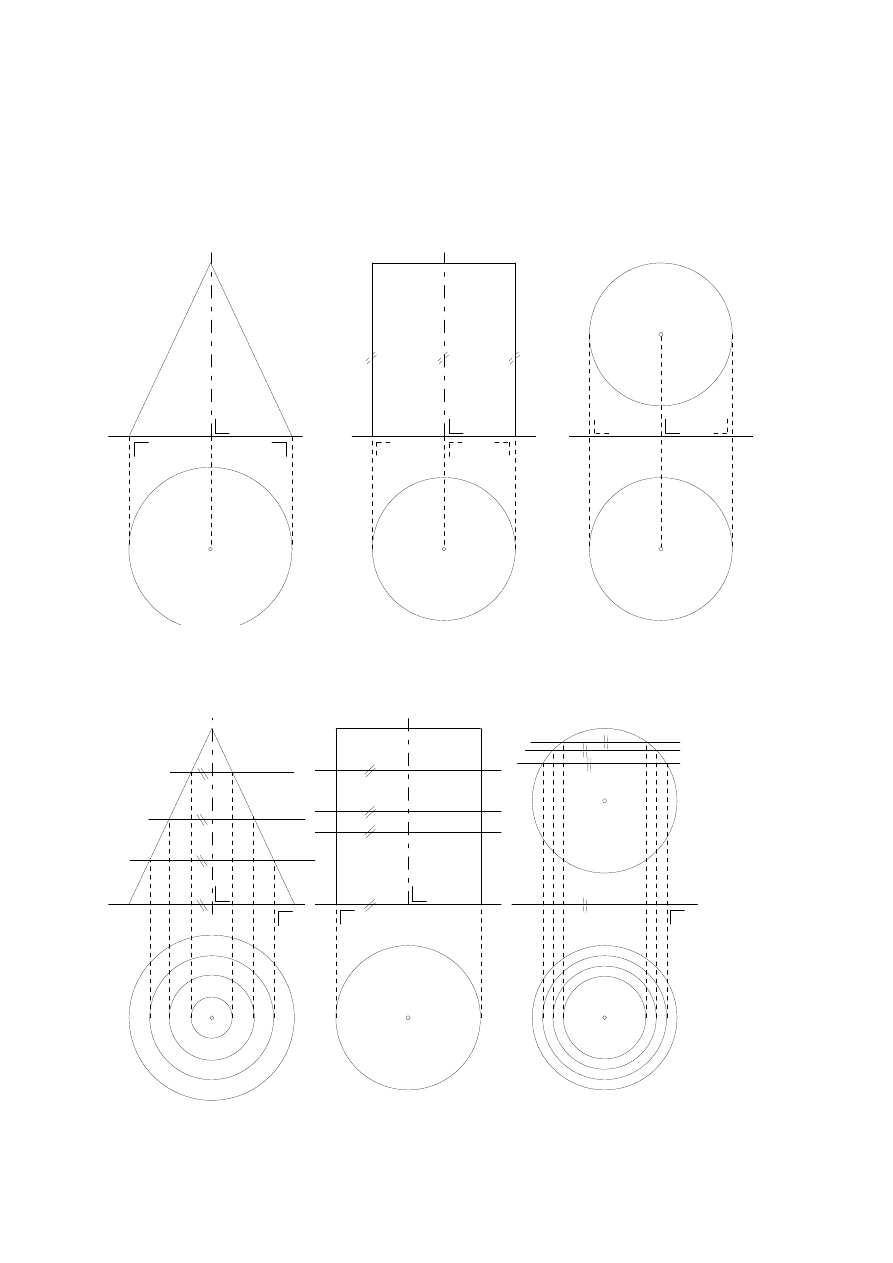
Zad.01. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. 
 

Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, 

ż

e rzutem powierzchni jest brzeg rzutu tej powierzchni (figury rozumianej jako zbiór rzutów wszystkich punktów 

powierzchni).  Rzutem  każdej  z  omawianych  tu  powierzchni  jest  trójkąt,  prostokąt,  koło  (w  reprezentacji 
konturowej - okrąg). Rysunek 4.1  przedstawia rzuty Monge'a: (a) - powierzchni stożka,  (b) - powierzchni walca, 
(c) - sfery. Znależć rzuty (poziome i pionowe) punktów leżących na powierzchni stożka, walca i sfery. Dane są 
rzuty  punktów  A”,  B”, C”, należy znaleźć rzuty poziome tych punktów (A’, B’,C’oraz rzuty poziome punktów 
D’, E’, F’ należy znaleźć rzuty pionowe tych punktów D”, E”, F”.  

O"

O'

l"

l"

l'

l'

(a)

(b)

(c)

 

Rys.4.1 

Każda z powierzchni stożka, walca i sfery ma oś symetrii. Przekrój płaszczyzną prostopadłą do osi symetrii w 
każdym przypadku jest okręgiem, zaś przekrój płaszczyzną przechodzącą przez oś symetrii jest w przypadku: 
stożka  -  parą  prostych  (tworzących  stożka)  przecinających  się,  walca  -  parą  prostych  (tworzących  walca) 
równoległych, sfery - okręgiem (równoleżnikiem sfery) (Rys.4.2).  

o1"

o2"

o3"

o1'

o2'

o3'

o1"

o2"

o3"

o1'=o2'=o3'

o1"
o2"

o3"

o1'

o2'

o3'

O"

O'

l"

l"

l'

l'

(a)

(b)

(c)

"=

"=

"=

"=

"=

"=

"=

"=

"=

γ3

γ1

γ2

γ1

γ2

γ2

γ2

γ2

γ2

 

Rys.4.2. 

Przynależność  punktu  do  powierzchni  (figury)  oprzemy  na  zasadzi:  Punkt  należy  do  figury  jeżeli  leży  na 
pewnej  krzywej  (prostej,  okręgu)  zawartej  w  tej  figurze.  Przynależność  prostej  do  płaszczyzny  -  na  znanym 
fakcie: Prosta leży na płaszczyźnie jeżeli należą do niej dwa punkty leżące na tej płaszczyźnie. 

POLITECHNIKA BIAŁOSTOCKA - Studia stacjonarne - Inżynieria i Ochrona Środowiska 

Rysunek techniczny, Geometria wykreślna i grafika inżynierska - 

 ćwiczenie nr 04

, sem zimowy 

 

2

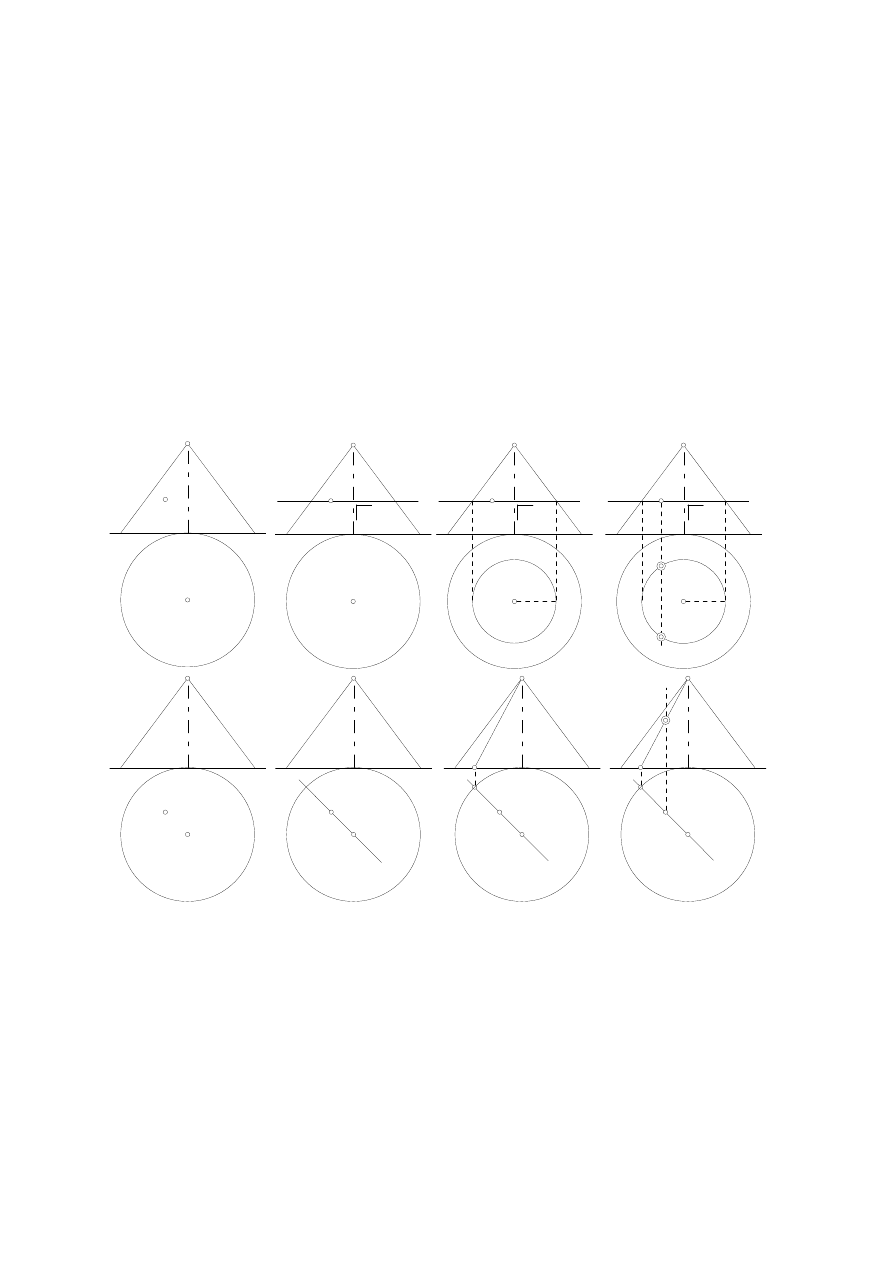
Rysunek Rys.4.3(a,a1,a2,a3) pokazuje rozwiązanie zadania w odniesieniu do powierzchni stożkowej.  
Zadanie  1.  Mamy  daną  powierzchnię  stożkową 

Γ

  oraz  rzut  pionowy  A"  punktu  A.  Należy  wyznaczyć  rzut 

poziomy punktu A tak, by punkt ten leżał na powierzchni 

Γ

 (Rys.4.3a). Rozwiązanie: Prowadzimy przez szukany 

punkt A płaszczyznę poziomą p, t.zn. przez punkt A" prowadzimy prostą p" (Rys.4.3a1). Płaszczyzna p przecina 
powierzchnię stożkową w okregu o (Rys.4.3a2). Później przekonamy się, że w przeciwieństwie  do rozwiązania 
zadania  1  płaszczyzna  p  musi  być  pozioma  lub  (por.  zadanie  3)  poziomorzutująca  i  przechodząca  przez 
wierzchołek  powierzchni.  Rzutem  pionowym  okręgu  jest  odcinek  o"  prostej  p"  zawarty  w  konturze  pionowym 
powierzchni  stożkowej,  czyli  w  trójkącie.  Rzut  poziomy  o'  jest  okręgiem  o  środku  W'  i  promieniu  równym 
połowie długości odcinka o". Istnieją dwa punkty A

1

, A

2

 których rzutem pionowym jest punkt A". Aby znaleźć 

ich  rzuty  poziome  A'

1

,  A'

2

  prowadzimy    odnoszącą  z  punktu  A"  do  przecięcia  z  okręgiem  o  (Rys.4.3a3). 

Zadanie  3.  Mamy  daną  powierzchnię  stozkową 

Γ

  oraz  rzut  poziomy  B'  punktu  B.  Należy  wyznaczyć  rzut 

pionowy  punktu  B  tak,  by  punkt  ten  leżał  na  powierzchni 

Γ

  (Rys.4.3b)).  Rozwiązanie:  Prowadzimy  przez 

szukany punkt B i przez wierzchołek W stożka płaszczyznę poziomorzutującą v, t.zn. przez punkt B' prowadzimy 
prostą  v'  (Rys.4.3b1).  Płaszczyzna  v  przecina  powierzchnię  stożkową  w  prostych  a,  b,  z  których  interesuje nas 
tylko jedna, mianowicie prosta a, do której należy punkt B (Rys.4.3b2). Rzut poziomy a' prostej a pokrywa się z 
prostą  v'.  Prosta  v  ma  ślad  poziomy  H

a

w  punkcie  przecięcia  z  okręgiem  podstawy  stożka.  Rzut  pionowy  a" 

przechodzi przez H"

a

 i przez W". Punkt B" znajdujemy na prostej a" i na odnoszącej poprowadzonej z punktu 

B' (Rys.4.3b3). 

A"

W'

W'

A"

A"

W'

A"

W'

A'

A'

2

1

W'

B'

B'

W'

W'

B'

B'

W'

B"

(a)

(a1)

(a2)

(a3)

(b)

(b1)

(b2)

(b3)

'

o'

o'

' =a'

=a'

'

a"

a"

a

H

H"a

a

H

H"a

W"

W"

W"

W"

W"

W"

W"

W"

"

γ

o"

o"

Rys.II21.

"

γ

γ

"

"

γ

γ

γ

 

Rys.4.3 

Powierzchnie stożka, walca, sfery, znane ze szkoły, w przekroju płaszczyzną dają prostą (odcinek lub łamaną) 
lub okrąg a więc dwie figury, które potrafimy wykreślić linijką i cyrklem, czyli t.zw. klasycznymi (platońskimi) 
ś

rodkami kreślenia.  

 
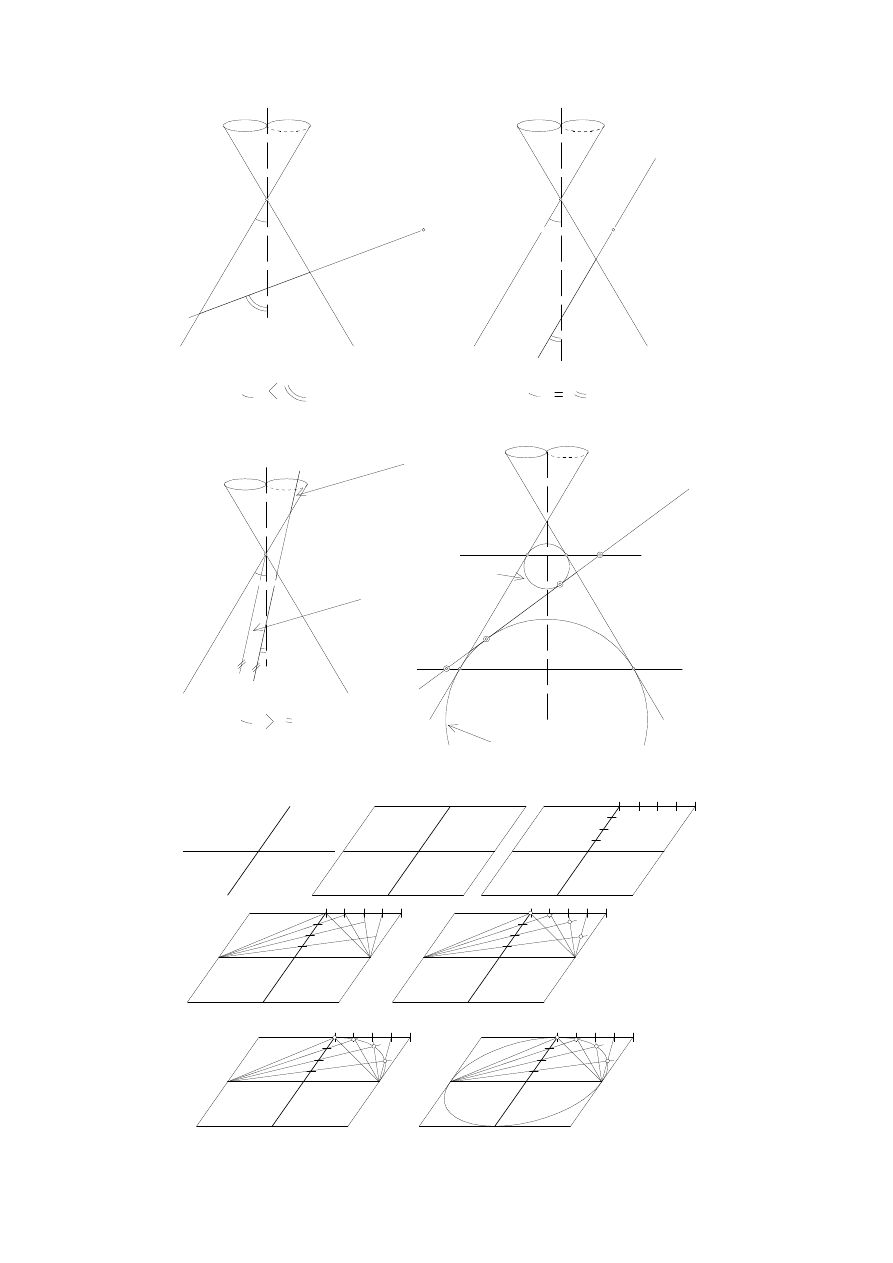
Przekrojem  sfery,  stożka,  walca  jest  zawsze  stożkowa.  Przekrojem,  pomijając  przypadki  zdegenerowane,    w 
przypadku  sfery  jest  okrąg,  w  przypadku  walca  elipsa  (okrąg),  w  przypadku  stożka  elipsa  (okrąg),  parabola 
lub hiperbola w zależności od kąta nachylenia płaszczyzny przekroju do osi stożka (Rys.4.4a,b,) (Rys.4.5a). 
Rzutem  prostokątnym  okręgu  i  elipsy  jest  elipsa  lub  odcinek,  paraboli  -  parabola  lub  półprosta  lub  prosta, 
hiperboli - hiperbola, prosta lub dwie półproste zawarte w jednej prostej. 

POLITECHNIKA BIAŁOSTOCKA - Studia stacjonarne - Inżynieria i Ochrona Środowiska 

Rysunek techniczny, Geometria wykreślna i grafika inżynierska - 

 ćwiczenie nr 04

, sem zimowy 

 

3

elipsa

elipsa

parabola

parabola

Rys.10A1.

(a)

(b)

 

Rys.4.4 

hiperbola

F

k

elipsa

2

1

1

F

k

(kierownica)

(ognisko)

(kierownica)

(ognisko)

sfera

sfera

e

1

(płasz. przekroju)

πσ

(a)

(B)

Rys.10A2.

πσ

π

2

2

hiperbola

kierunki asymptot

 

Rys.4.5 

 

Rys.10A3.

(f)

(a)

(b, c)

(d)

(e)

(g)

1

1

2

2

3

3

3

3

2

2

1

1

1

1

2

2

3

3

 

Rys.4.6 

 
 

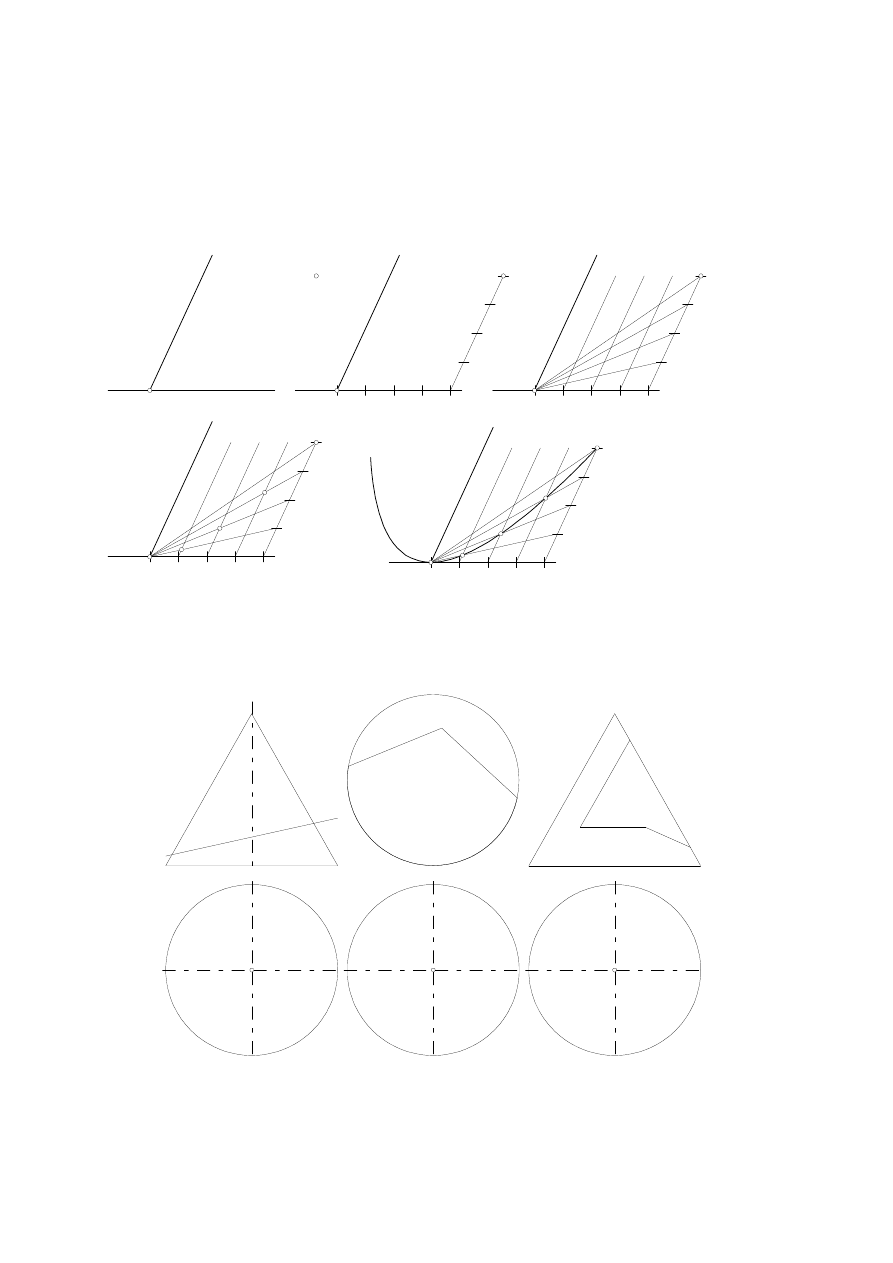
POLITECHNIKA BIAŁOSTOCKA - Studia stacjonarne - Inżynieria i Ochrona Środowiska 

Rysunek techniczny, Geometria wykreślna i grafika inżynierska - 

 ćwiczenie nr 04

, sem zimowy 

 

4

 

Elipsa jest jednoznacznie wyznaczona na przykład przez swoje średnice sprzężone.  Średnice sprzężone 

są to dwie połowiące się cięciwy elipsy, przechodzące przez jej środek, o tej własności, że każda z tych średnic 

połowi odcinki równoległe do drugiej średnicy. Średnice elipsy, jako połowiące się odcinki, możemy wybrać 

dowolnie (Rys.4.6a ). Konstrukcję elipsy na podstawie średnic sprzężonych przedstawiają rysunki (Rys.4.6b-g).  

Uzupełnienie pozostałych ćwiartek elipsy zrealizujemy w podobny sposób (Rys.4.6g). 
 

Parabola jest jednoznacznie określona przez prostą styczną, punkt styczności, kierunek osi i inny punkt 

(Rys.4.7a). Konstrukcję (siatkową) paraboli przedstawiają rysunki (Rys.4.7b-e) 

(a)

(b)

(c)

(e)

(d)

Rys.10A4.

1

1

3

2

3

2

4

4

1

1

2

2

3

4

3

4

1

2

2

1

3

3

4

4

1

1

2

2

3

3

4

4

 

Rys.4.7 

 

Zad.02. Wykreślić rzuty przekroju stożka płaszczyzną (Rys.4.8a), wkreślić rzuty bryły będącej częścią kuli po 

wycięciu  płaszczyznami (Rys.4.8b),  wkreślić rzuty bryły będącej częścią stożka po wycięciu płaszczyznami 

(Rys.4.8c). W ostatnim przypadku jedna z płaszczyzn tnących jest równoległa do tworzącej stożka, druga jest 

równoległa do podstawy.  

(a)

(b)

(c)

 

 

Rys.4.8 

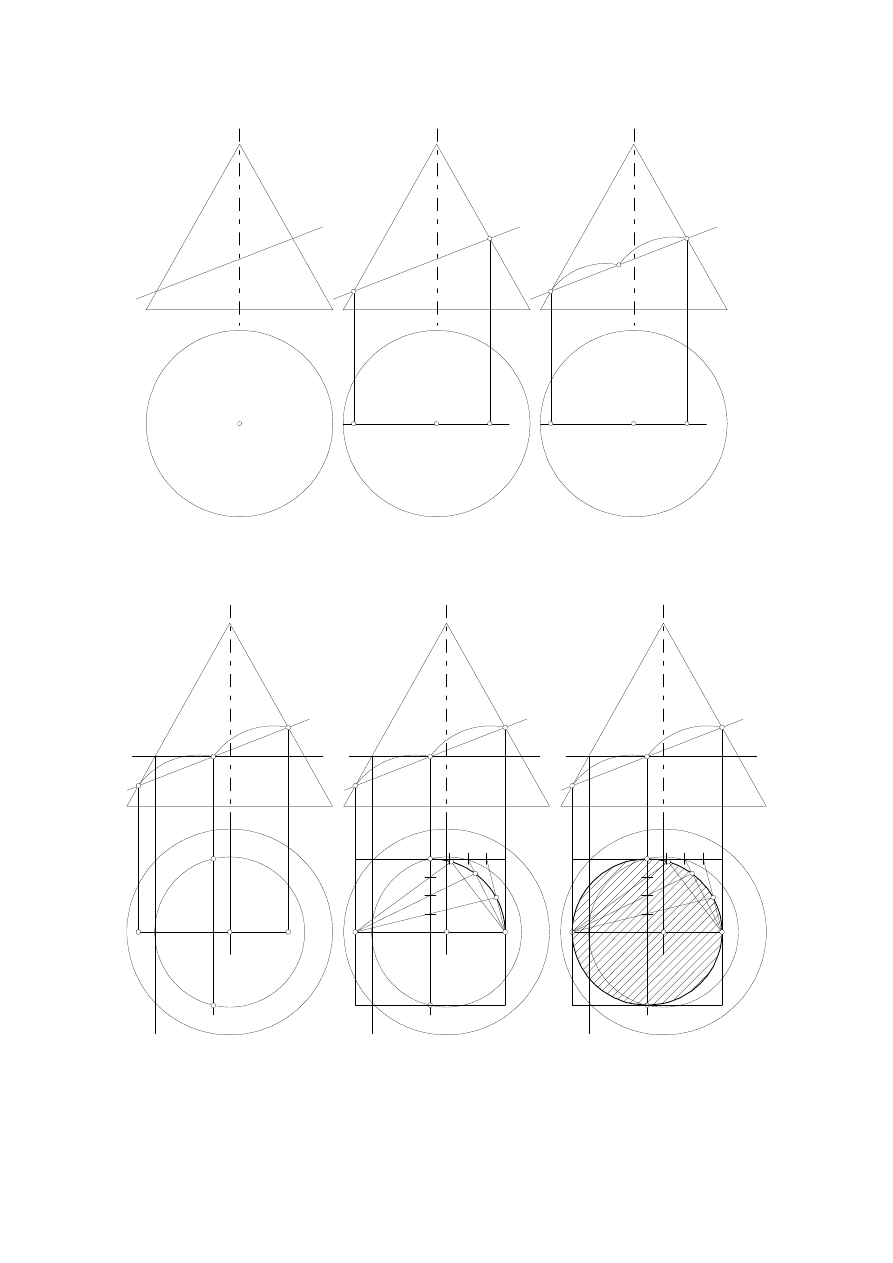
Na rysunkach Rys.4.9  zilustrowano konstrukcję przekroju stożka płaszczyną wraz z konstrukcją siatkową elipsy. 

POLITECHNIKA BIAŁOSTOCKA - Studia stacjonarne - Inżynieria i Ochrona Środowiska 

Rysunek techniczny, Geometria wykreślna i grafika inżynierska - 

 ćwiczenie nr 04

, sem zimowy 

 

5

Rys.10A6.

A"

A'

B'

B"

C"=D"

B"

A"

A'

B'

 

Rys.4.9 

Elispę  przekroju  wyznaczamy  poprzez  rzuty  jej  osi  (średnic  sprzężonych  prostopadłych  AB  (A'B',A"B"), 
CD(C'D',C"D") (Rys.4.9).  Średnice te są podstawą konstrukcji siatkowej elipsy  (Rys.4.10). 

A'

B'

B'

B'

A'

A'

C'

D'

D'

C'

C'

D'

C"=D"

A"

B"

B"

B"

A"

A"

C"=D"

C"=D"

 

Rys.4.10 

 
 
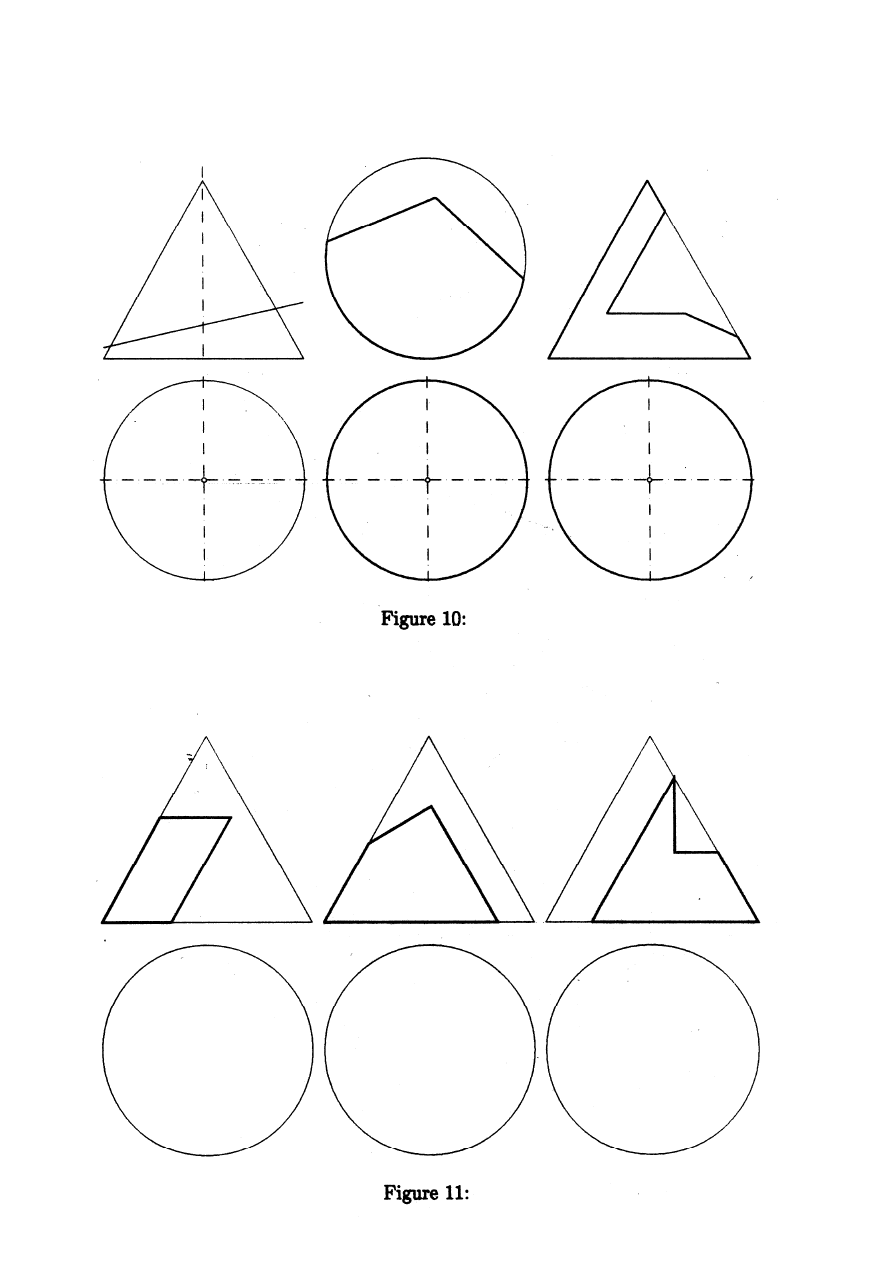
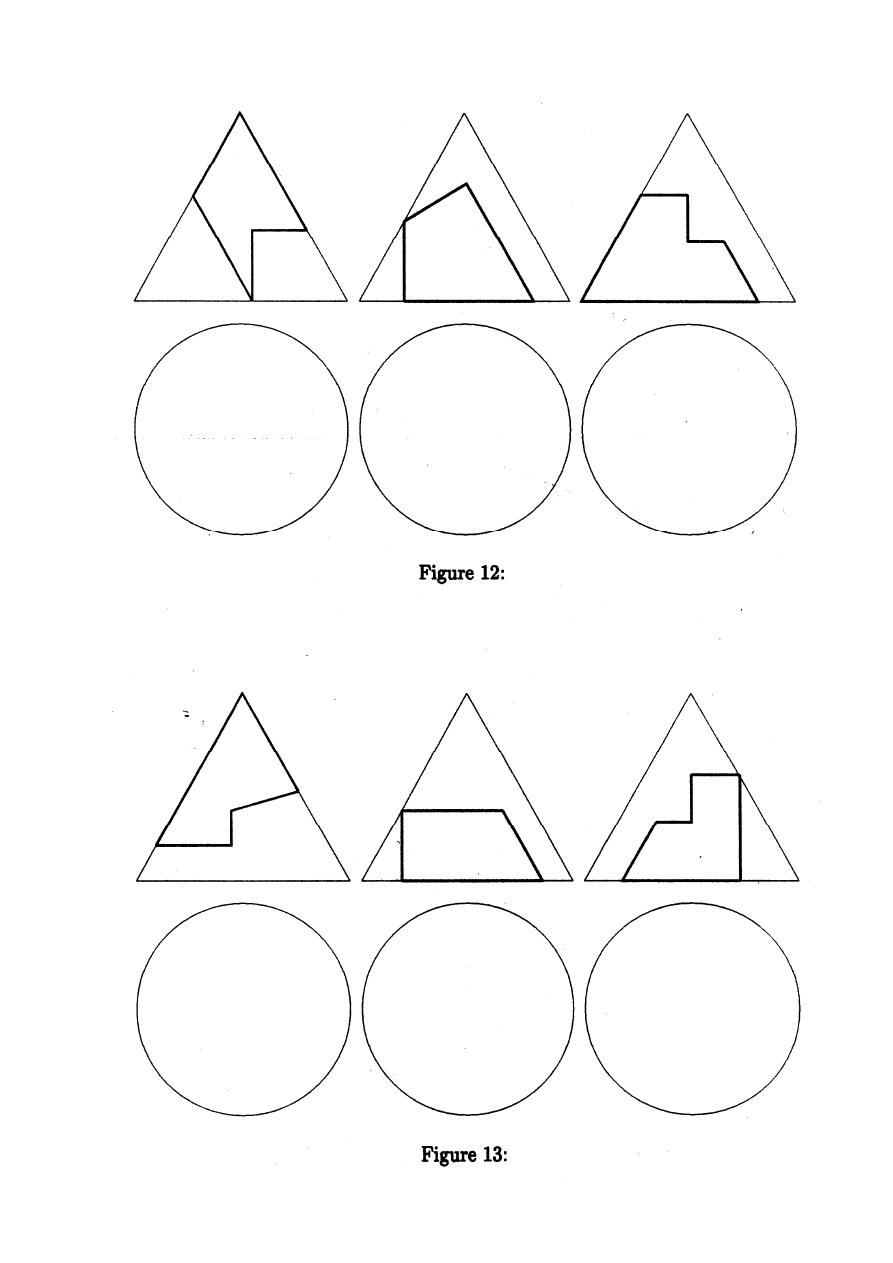
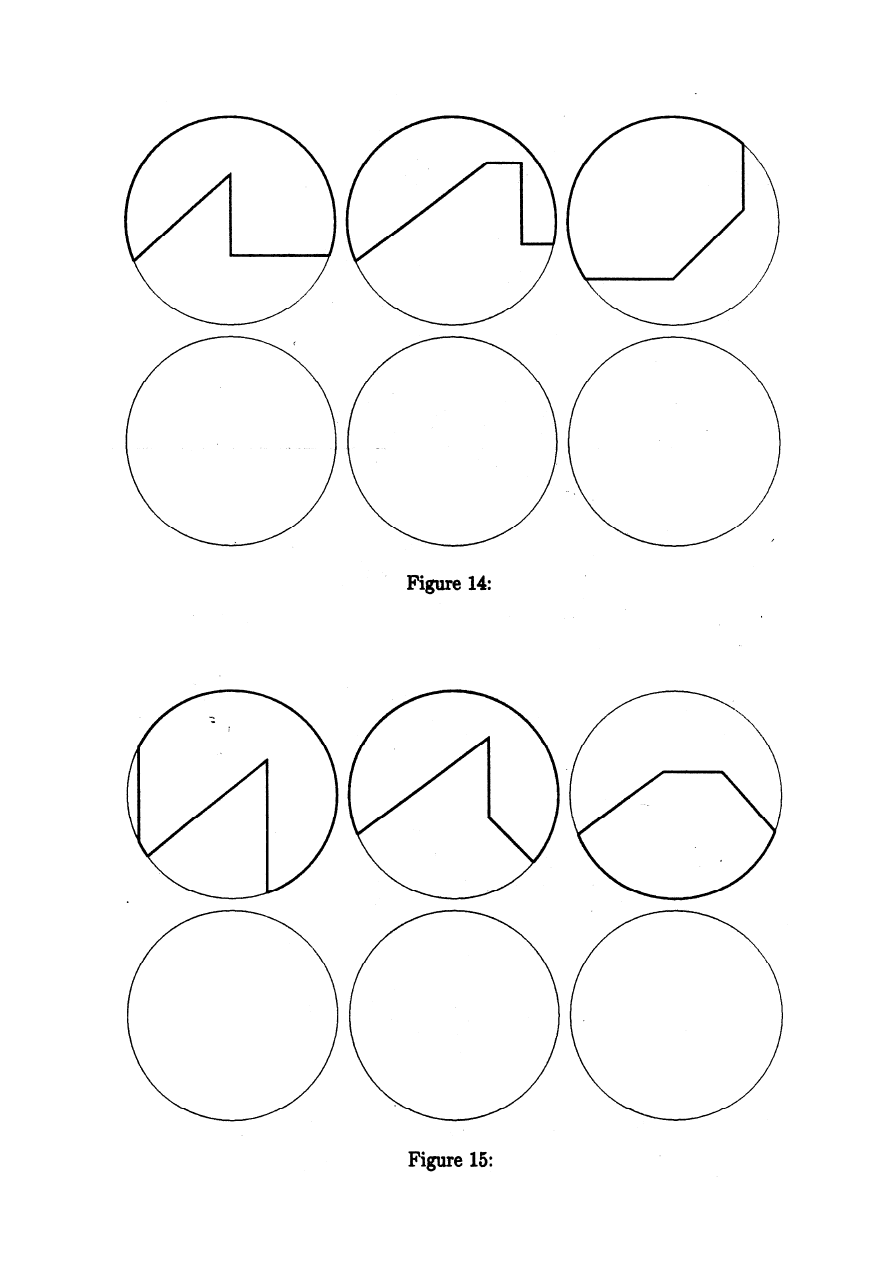
Zad.03. 
Wykreślić rzuty bryły będącej częścią stożków  oraz sfer  po wycięciu  płaszczyznami z rys.Fig 11,12,13,14,15 
(zgodnie z karta przydziału tematu).  
 
 

POLITECHNIKA BIAŁOSTOCKA - Studia stacjonarne - Inżynieria i Ochrona Środowiska 

Rysunek techniczny, Geometria wykreślna i grafika inżynierska - 

 ćwiczenie nr 04

, sem zimowy 

 

6

 

POLITECHNIKA BIAŁOSTOCKA - Studia stacjonarne - Inżynieria i Ochrona Środowiska 

Rysunek techniczny, Geometria wykreślna i grafika inżynierska - 

 ćwiczenie nr 04

, sem zimowy 

 

7

 

POLITECHNIKA BIAŁOSTOCKA - Studia stacjonarne - Inżynieria i Ochrona Środowiska 

Rysunek techniczny, Geometria wykreślna i grafika inżynierska - 

 ćwiczenie nr 04

, sem zimowy 

 

8

 

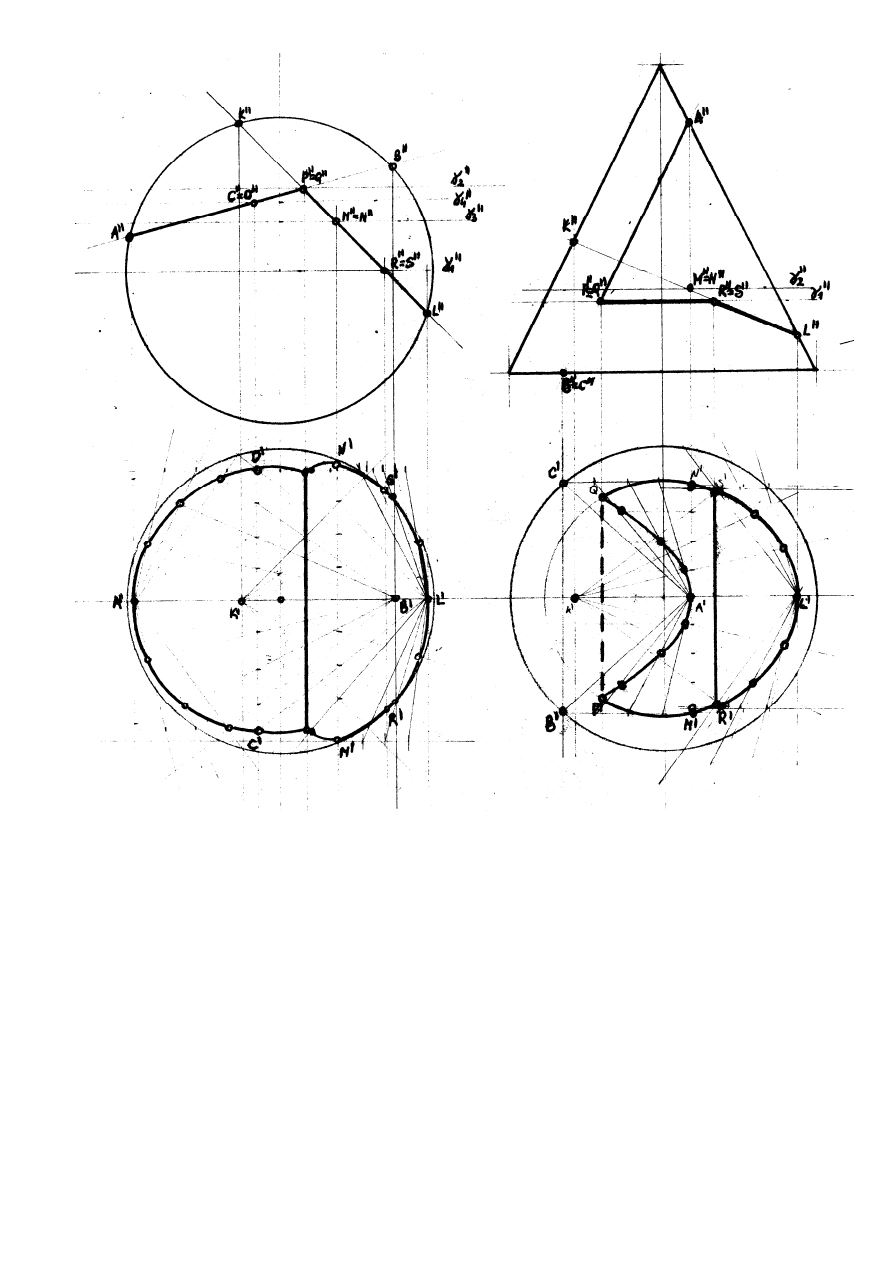
POLITECHNIKA BIAŁOSTOCKA - Studia stacjonarne - Inżynieria i Ochrona Środowiska 

Rysunek techniczny, Geometria wykreślna i grafika inżynierska - 

 ćwiczenie nr 04

, sem zimowy 

 

9