AKADEMIA GÓRNICZO – HUTNICZA

im. Stanisława Staszica w Krakowie

Systemy Wizyjne

Sprawozdanie z laboratorium nr 4 MatLab

Michał Grudziński

Maciej Bajor

Mechatronika (IMiR)

grupa 26, rok III

Zadanie 1



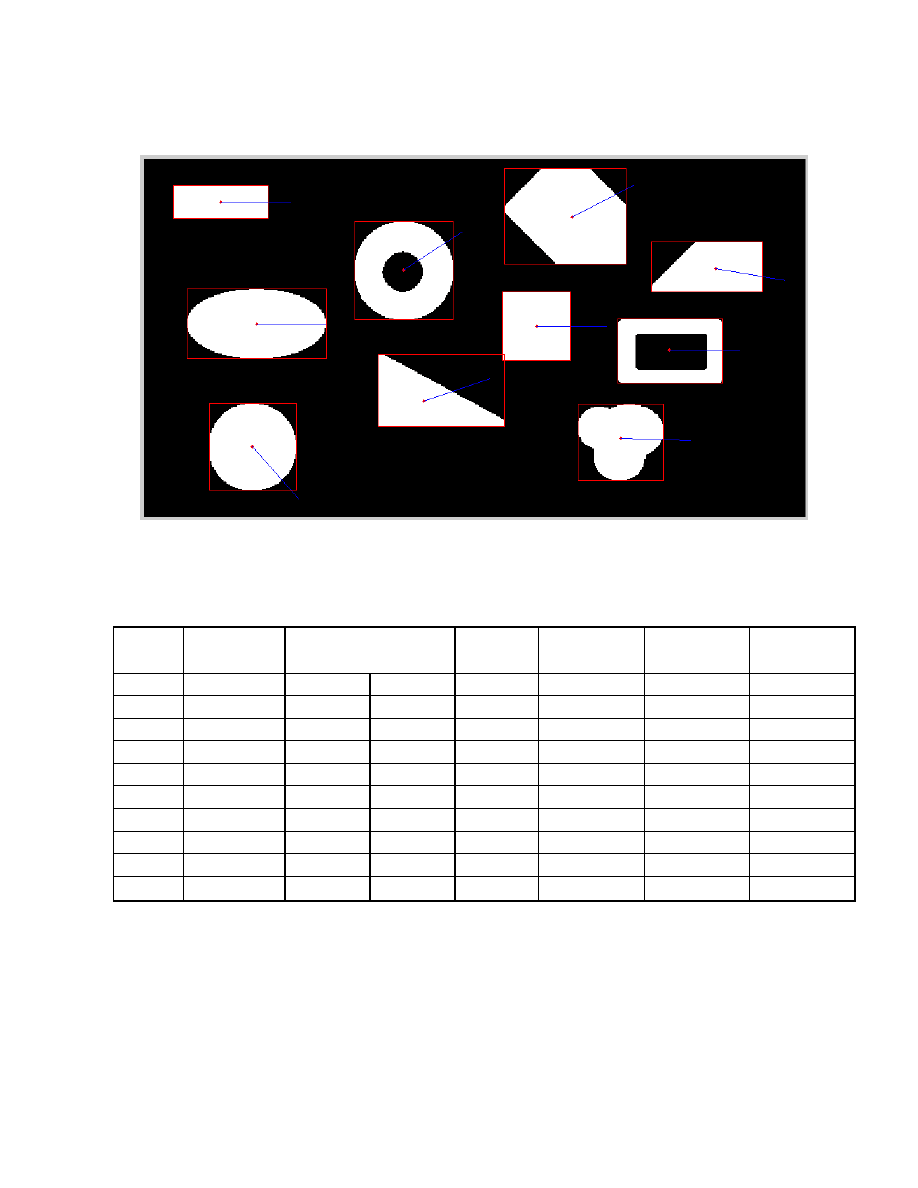
Obraz poddany analizie



Obraz z zaznaczonymi środkami ciężkości, orientacjami oraz prostokątami
opisanymi na obiektach



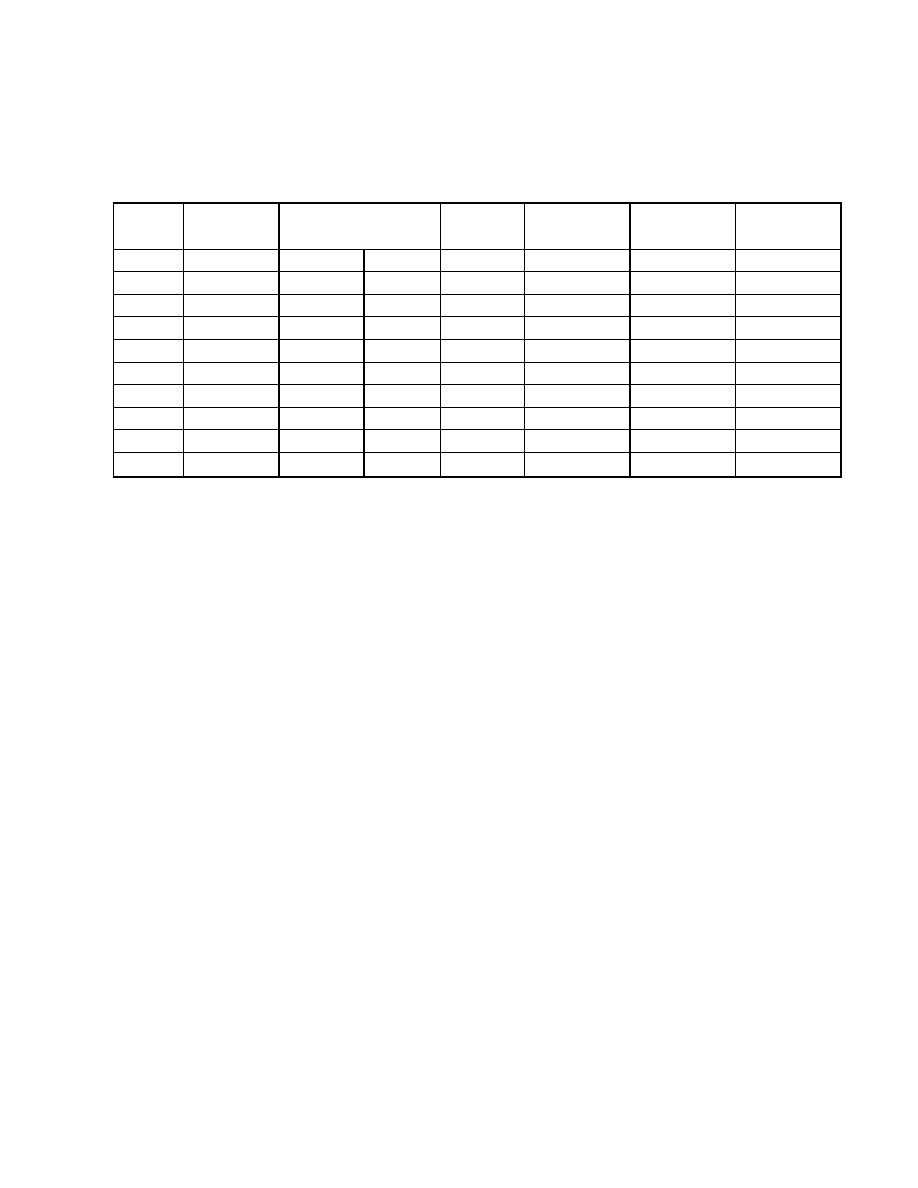
Tabela z wynikami policzonych współczynników Malinowskiej, Fereta i
Haralicka

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

8424.0000

139.5000

78.5000

0.0000

0.3032

3.1154

0.9300

2

22702.0000

204.5000

300.0043

0.0000

0.1500

2.0504

0.9324

3

17891.0000

197.0302

524.0332

73.1233

0.0480

1.0000

0.9936

4

17950.0000

471.9364

202.8036

-29.6612

0.1947

1.0000

0.9909

5

14539.0000

504.8058

440.7033

-18.6189

0.4553

1.8211

0.9185

6

13689.0000

713.0000

305.0000

0.0000

0.1187

1.0000

0.9967

7

26617.0000

777.7446

106.9645

-29.1862

0.0768

1.2695

0.9982

8

13533.0000

865.4423

508.1669

2.7378

0.1541

1.1298

0.9959

9

10113.0000

953.5085

348.9995

0.0876

0.6030

1.6396

0.9981

10

13345.0000

1038.1128

200.8029

9.1389

0.2576

2.2941

0.9988



Współczynnik Malinowskiej, nazywany współczynnikiem krągłości pozwala
na rozpoznanie koła, przyjmując dla tej figury wartość bliską zeru. Niską
wartość współczynnik przyjmuje również dla elipsy, w odróżnieniu do
prostokąta, dla którego wartość równa się 0.30.



Współczynnik Fereta określa stosunek największych średnic obiektów w
poziomie i pionie, służy więc do określania figur niesmukłych.
Współczynnik nie jest samowystarczalny, ponieważ przyjmuje takie same
wartości dla chociażby koła i kwadratu.



Współczynnik Haralicka jest bardzo dokładnym współczynnikiem lecz na
jego obliczenie potrzebny jest dłuższy czas niż na pozostałe.

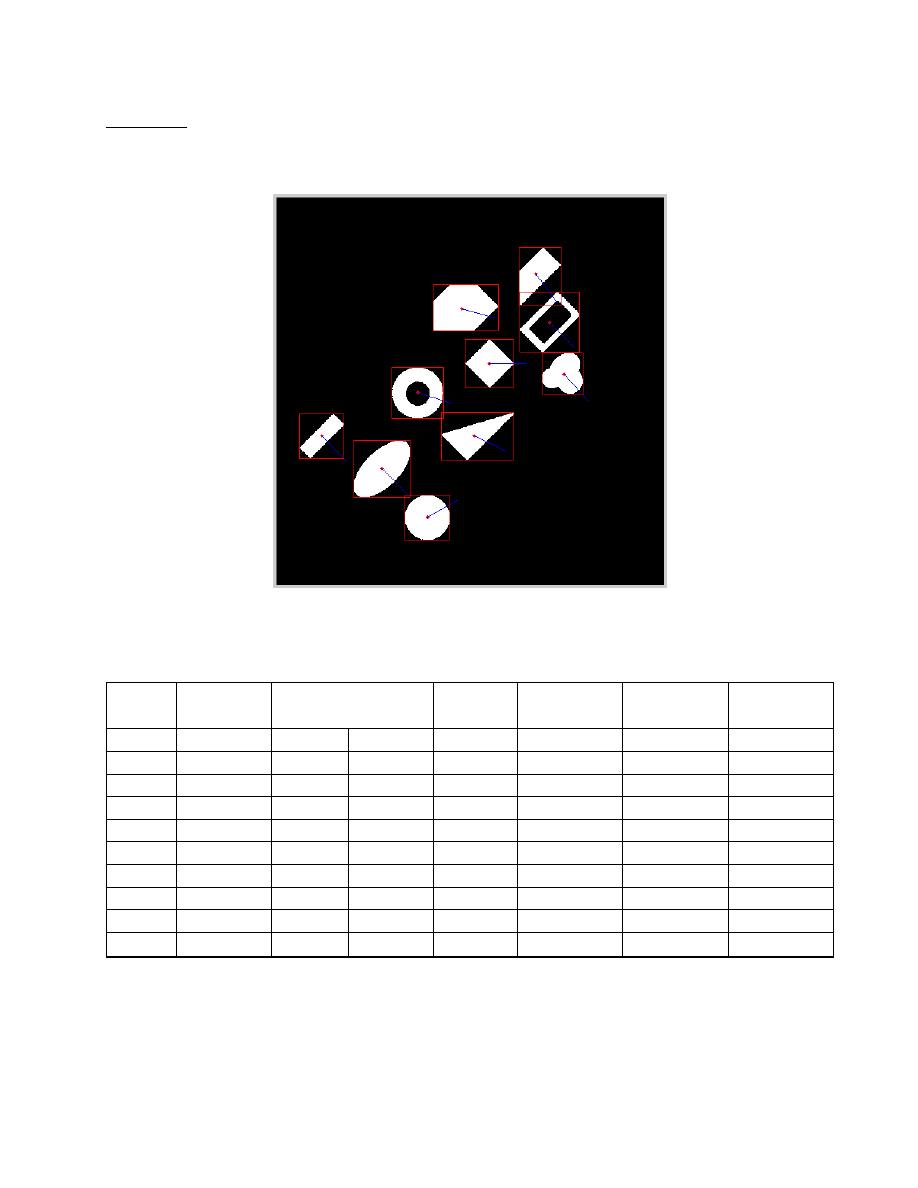
Zadanie 2



Obrót obrazu o 45°



Tabela wyników

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

8473.0000

154.2489

806.2489

45.0000

0.3020

1.0000

0.9981

2

22708.0000

356.9919

917.0078

44.9973

0.1771

1.0000

0.9949

3

17899.0000

510.0984

1080.6946

-29.9389

0.1078

1.0000

0.9979

4

17946.0000

477.3054

659.1677

17.8505

0.2729

1.0000

0.9812

5

14602.0000

669.1398

804.1069

26.3759

0.4984

1.5123

0.9280

6

13613.0000

720.0000

561.0000

0.0000

0.1215

1.0000

0.9800

7

26613.0000

625.6400

375.1839

15.9172

0.1315

1.4167

0.9799

8

13533.0000

971.5335

596.8214

47.6861

0.2141

1.0000

0.9959

9

10114.0000

921.4896

422.4566

45.0534

0.6111

1.0000

0.9962

10

13324.0000

876.3338

257.5311

54.1064

0.2645

0.7208

0.9972



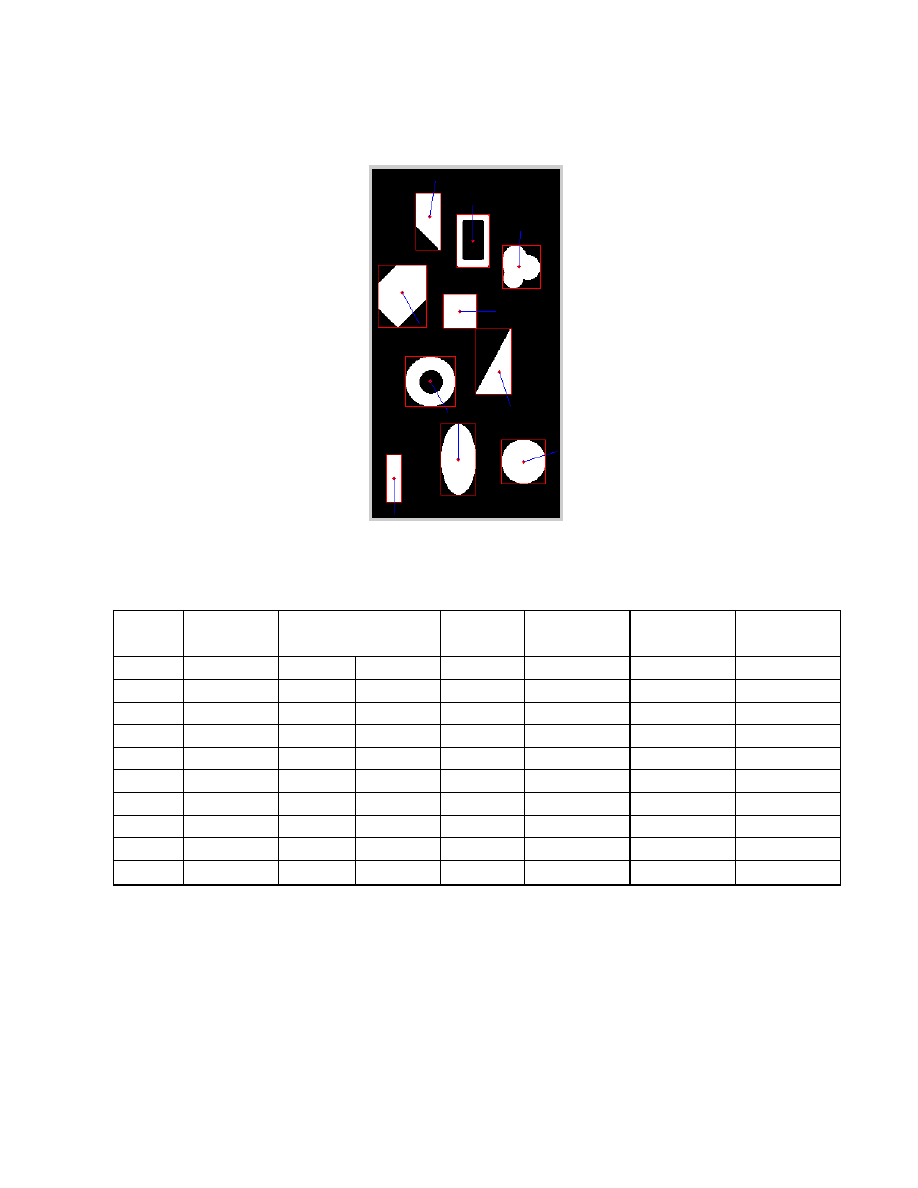
Obrót obrazu o 90°



Tabela wyników

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

8424.0000

78.5000

1061.5000

90.0000

0.3032

0.3210

0.9995

2

22702.0000

300.0043

996.5000

-90.0000

0.1500

0.4877

0.9980

3

17891.0000

524.0332

1003.9698

-16.8767

0.0480

1.0000

0.9970

4

17950.0000

202.8036

729.0636

60.3388

0.1947

1.0000

0.9976

5

14539.0000

440.7033

696.1942

71.3811

0.4553

0.5491

0.9815

6

13689.0000

305.0000

488.0000

0.0000

0.1187

1.0000

0.9842

7

26617.0000

106.9645

423.2554

60.8138

0.0768

0.7877

0.9860

8

13533.0000

508.1669

335.5577

-87.2622

0.1541

0.8851

0.9826

9

10113.0000

348.9995

247.4915

-89.9124

0.6030

0.6099

0.9495

10

13345.0000

200.8029

162.8872

-80.8611

0.2576

0.4359

0.9222



Po analizie wyników można stwierdzić, że współczynnik Malinowskiej i
Haralicka są odporne na zmianę orientacji obiektu.



Współczynnik Fereta jest bardzo wrażliwy na zmianę orientacji, wyjątkiem
są figury foremne jak koło czy kwadrat.

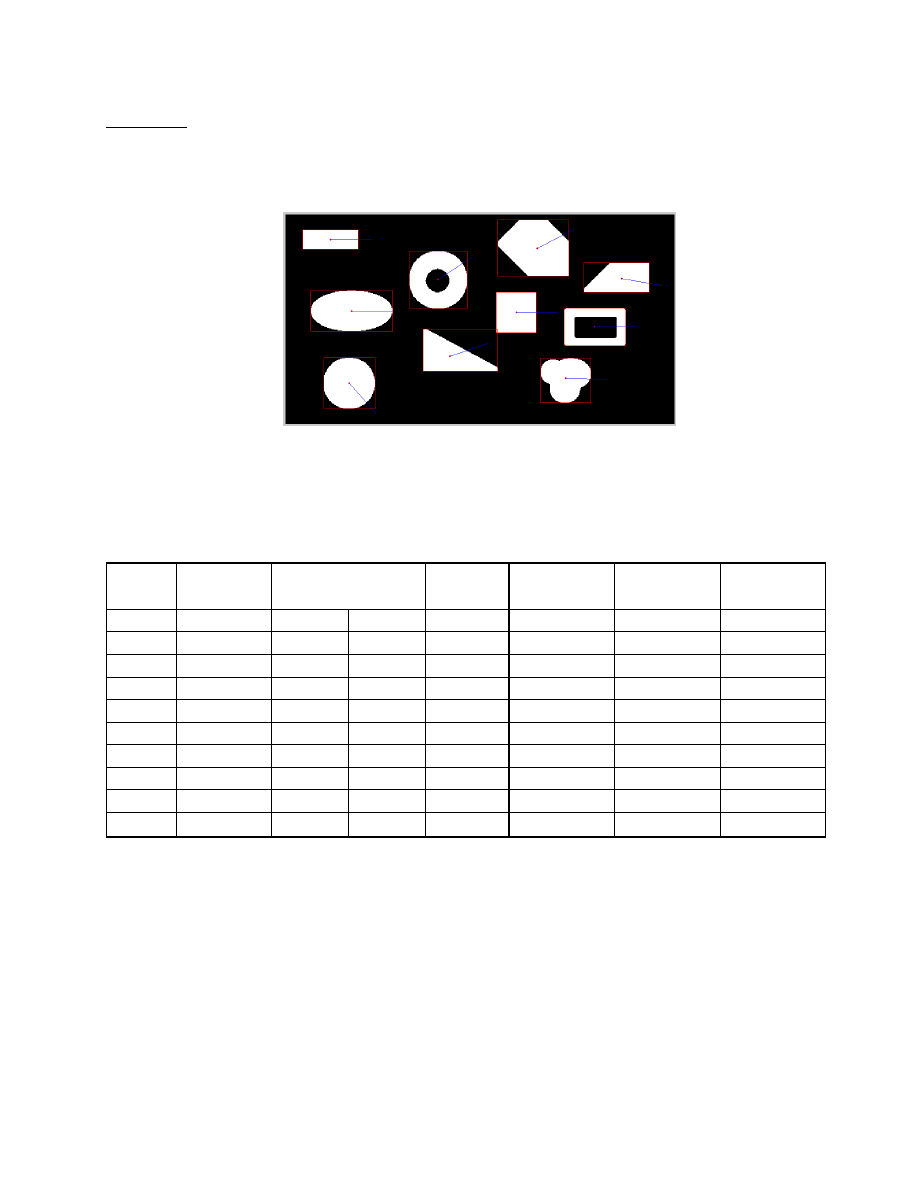
Zadanie 3



Dwukrotne pomniejszenie (0.5x)



Tabela wyników

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

2550.0000

70.0000

39.5000

0.0000

0.2625

2.8333

0.9247

2

6328.0000

102.5000

150.2276

0.0000

0.2352

2.0000

0.9284

3

5013.0000

98.7796

262.2340

48.5276

0.0400

1.0000

0.9929

4

5372.0000

236.1385

101.7759

-33.3846

0.1883

1.0000

0.9899

5

4264.0000

254.0886

220.6986

-18.6276

0.4486

1.7692

0.9171

6

3844.0000

356.5000

152.5000

0.0000

0.1102

1.0000

0.9963

7

7353.0000

388.6812

53.5683

-27.7011

0.1072

1.2644

0.9980

8

3895.0000

432.9271

254.3859

2.0194

0.1160

1.1159

0.9954

9

3448.0000

477.3802

174.4313

0.0939

0.4323

1.6102

0.9980

10

3826.0000

518.9300

100.5361

9.3064

0.2157

2.1957

0.9987



Dwukrotne powiększenie (2x)



Tabela wyników

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

36300.0000

278.5000

156.5000

0.0000

0.2970

3.0000

0.9273

2

95200.0000

408.5000

599.5080

0.0000

0.2473

2.0246

0.9291

3

75224.0000

393.5588

1047.5651

72.7201

0.1570

1.0000

0.9932

4

77872.0000

943.2320

405.3390

-29.5331

0.2934

1.0000

0.9904

5

62356.0000

1011.2811

880.7567

-18.6179

0.5138

1.8016

0.9234

6

57600.0000

1425.5000

609.5000

0.0000

0.1237

1.0000

0.9965

7

111052.0000

1554.4096

213.3134

-28.6645

0.1892

1.2647

0.9980

8

57608.0000

1730.2920

1015.9370

2.1458

0.2572

1.1269

0.9956

9

46500.0000

1907.2494

697.8653

0.0635

0.5456

1.6228

0.9981

10

56776.0000

2074.3611

401.3336

9.1864

0.3011

2.2500

0.9988



Po

przeanalizowaniu

danych

można

stwierdzić,

że

wszystkie

ze

współczynników są niepodatne na zmianę wielkości obiektów obrazu.

Wnioski



Przeprowadzone analizy wyników jednoznacznie wskazują na odporność na obrót i
zmianę rozmiarów obiektów obrazu przy wyliczaniu wartości współczynników
Malinowskiej i Haralicka. Oznacza to, iż mogą one być skutecznie wykorzystane w
procesie wykrywania i rozpoznawania obiektów.



Współczynnik Fereta nie może być stosowany samoistnie do rozpoznawania obiektów,
ponieważ jego wartość ulega zmianie wraz ze zmianą orientacji obiektów obrazu. Za
przykład może posłużyć prostokąt, dla którego po zmianie orientacji o kąt 45°
współczynnik Fereta osiągnął wartość 1 co wskazuje na rozpoznanie koła lub kwadratu.
Oznacza to, że bez użycia dodatkowych filtrów rozpoznanie jest niejednoznaczne a
wyniki mogą być zafałszowane w stosunku do obrazu rzeczywistego.