S

S

z

z

u

u

m

m

y

y

w

w

ł

ł

a

a

s

s

n

n

e

e

e

e

l

l

e

e

m

m

e

e

n

n

t

t

ó

ó

w

w

i

i

u

u

k

k

ł

ł

a

a

d

d

ó

ó

w

w

e

e

l

l

e

e

k

k

t

t

r

r

o

o

n

n

i

i

c

c

z

z

n

n

y

y

c

c

h

h

Źródła i rodzaje szumów

Mechanizm generacji – szumy cieplne, śrutowe, generacyjno-rekombinacyne,
rozpływu, 1/f (

strukturalne, małoczęstotliwościowe, prądowe, nadmiarowe

), upływu,

lawinowe, wybuchowe, Barkhausena (

w materiałach magnetycznych

), kwantowe,

fotonowe, pochodzące od gorących nośników czy też emisji spontanicznej.

Szumy cieplne

Każdy rezystor (dwójnik stratny o części rzeczywistej impedancji R )

w równowadze termodynamicznej jest źródłem szumów o rozporządzalnej
gęstości widmowej mocy

( )

( )

f

kTp

f

G

nT

=

, (1)

gdzie:

K

s

W

.

k

⋅

⋅

=

−23

10

38

1

-

stała Boltzmanna

T

- temperatura

bezwzględna

f

- częstotliwość

( )

















+









−













=

−

2

1

1

1

kT

hf

exp

kT

hf

f

p

(2)

2

34

10

62

6

s

W

.

h

⋅

⋅

=

−

- stała Plancka.

W zakresie częstotliwości, gdzie nie występują jeszcze zjawiska kwantowe (do
~

10

12

Hz

),

( )

1

≅

f

p

i gęstość widmowa

( )

f

nT

G

jest stała.

Wartość skuteczną równoważnej siły elektromotorycznej szumu cieplnego
(szumu Johnsona) w paśmie f

∆ określa wzór Nyquista:

f

kTR

E

NT

∆

= 4

. (3a)

Na schematach zastępczych szum cieplny reprezentuje źródło napięciowe,
o wydajności określonej zależnością (3a), połączone szeregowo z rezystorem
bezszumowym, lub równoważne źródło prądowe o wydajności

f

kTG

I

NT

∆

= 4

, (3b)

1

gdzie

R

G

1

= , połączone równolegle z rezystorem. Dla temperatury pokojowej

(

K

~ 300

) podstawiając do zależności (3) rezystancję

[ ]

Ω

k

R

uzyskuje się









≅

Hz

nV

R

E

nT

4

, (3a’)









≅

Hz

pA

R

I

nT

4

. (3b’)

Przykład.

Dla

Ω

= k

R 9

,









≈









≅

Hz

nV

Hz

nV

E

nT

12

9

4

,

natomiast









Hz

pA

.3

≈









≅

Hz

pA

I

nT

1

9

4

. W paśmie

kHz

10

wartość skuteczna (rms)

rms

NT

V

Hz

nV

E





≅

10

12

4

.

µ

=





2

1

, zaś

rms

nT

pA

Hz

pA

I

130

=









≅ . 10

3

1

4

.

Szumy śrutowe

Są związane z przepływem prądu przez barierę potencjału. Wartość skuteczną
fluktuacji prądu (o wartości średniej I w paśmie

f

∆ określa wzór

Schottky’ego:

f

qI

I

NS

∆

= 2

, (4)

gdzie

jest ładunkiem elementarnym. Zależność ta (stałość

gęstości widmowej mocy prądu szumu śrutowego) jest słuszna w zakresie

częstotliwości do

C

.

q

19

10

6

1

−

⋅

=

τ

1

, gdzie jest czasem przejścia nośnika przez barierę. Po

podstawieniu stałej q i wartości prądu

τ

[ ]

A

I

µ









≅

Hz

pA

I

.

I

nS

57

0

. (4’)

Przykład.

Dla

A

I

µ

=100

,









=









≅

Hz

pA

.

Hz

pA

.

I

nS

7

5

100

57

0

. W paśmie

kHz

10

wartość skuteczna (rms)

.

rms

nA

.

Hz

pA

.

I

NS

57

0

10

57

0

4

=









≅

2

Szumy rezystorów

Szumy: cieplne i prądowe

Szumy prąd

owe – zależne od technologii wykonania rezystora.

Wartość skuteczna równoważnego źródła napięciowego szumów prądowych
rezystora o rezystancji , przez który przepływa prąd stały , w paśmie

R

I

f

∆

2

1

2

2













∆

⋅

⋅

⋅

=

α

f

f

R

I

K

E

Nf

, (5)

gdzie

K

jest stałą zależną od struktury materiału rezystywnego i technologii

jego wytwarzania. Zwykle

α

.

1

≅

Wskaźnik szumów prądowych

U

E

W

Nf

f

=

, (6)

gdzie

jest wartością skuteczną napięcia szumów (wyrażoną

w

Nf

E

mikrowoltach w dekadzie częstotliwości

), zaś

U

spadkiem napięcia stałego

na rezystorze (w woltach). W skali logarytmicznej

[ ]







µ

=

V

V

W

log

dB

W

f

f

20

. (7)

Przykład.

Rezystor węglowy, kompozycyjny o rezystancji

Ω

k

10

i wskaźniku

szumów prądowych

czyli

dB

0

V

V

µ

1

. Zastosowano go w układzie o paśmie

przenoszenia

kHz

Hz 10

÷

10

, przy czym spadek napięcia na rezystorze wynosi

.

V

10

1

2

2

2

2

f

f

ln

U

K

E

Nf

=

. (8)

W każdej dekadzie czy oktawie częstotliwości moc szumów prądowych jest

stała.

3

U

U

p

p

r

r

o

o

s

s

z

z

c

c

z

z

o

o

n

n

y

y

m

m

o

o

d

d

e

e

l

l

s

s

z

z

u

u

m

m

o

o

w

w

y

y

w

w

z

z

m

m

a

a

c

c

n

n

i

i

a

a

c

c

z

z

a

a

(

(

c

c

z

z

w

w

ó

ó

r

r

n

n

i

i

k

k

a

a

l

l

i

i

n

n

i

i

o

o

w

w

e

e

g

g

o

o

)

)

Każdy element elektroniczny jest potencjalnym źródłem szumów, zatem

analiza szumowa wzmacniacza składającego się z wielu elementów jest złożona.
Uproszczony model szumowy wzmacniacza

n

n

I

E

−

zawiera tylko dwa

parametry szumowe, stosunkowo łatwe do zmierzenia.

Czwórnik przyjmuje się jako bezszumowy, natomiast wewnętrzne źródła

szumów czwórnika są reprezentowane przez dwie pary źródeł szumowych
usytuowane na wejściu lub na wyjściu (bądź na wejściu i wyjściu) czwórnika.
Najczęściej przyjmuje się model ze źródłami na wejściu. Szumy wzmacniacza
(może to być czwórnik pasywny, tranzystor, wzmacniacz scalony) są w nim
reprezentowane przez źródło napięciowe, źródło prądowe oraz zespolony
współczynnik korelacji, co daje w sumie cztery parametry szumowe. Pomijając
korelację między źródłami model upraszcza się do dwóch parametrów jak na
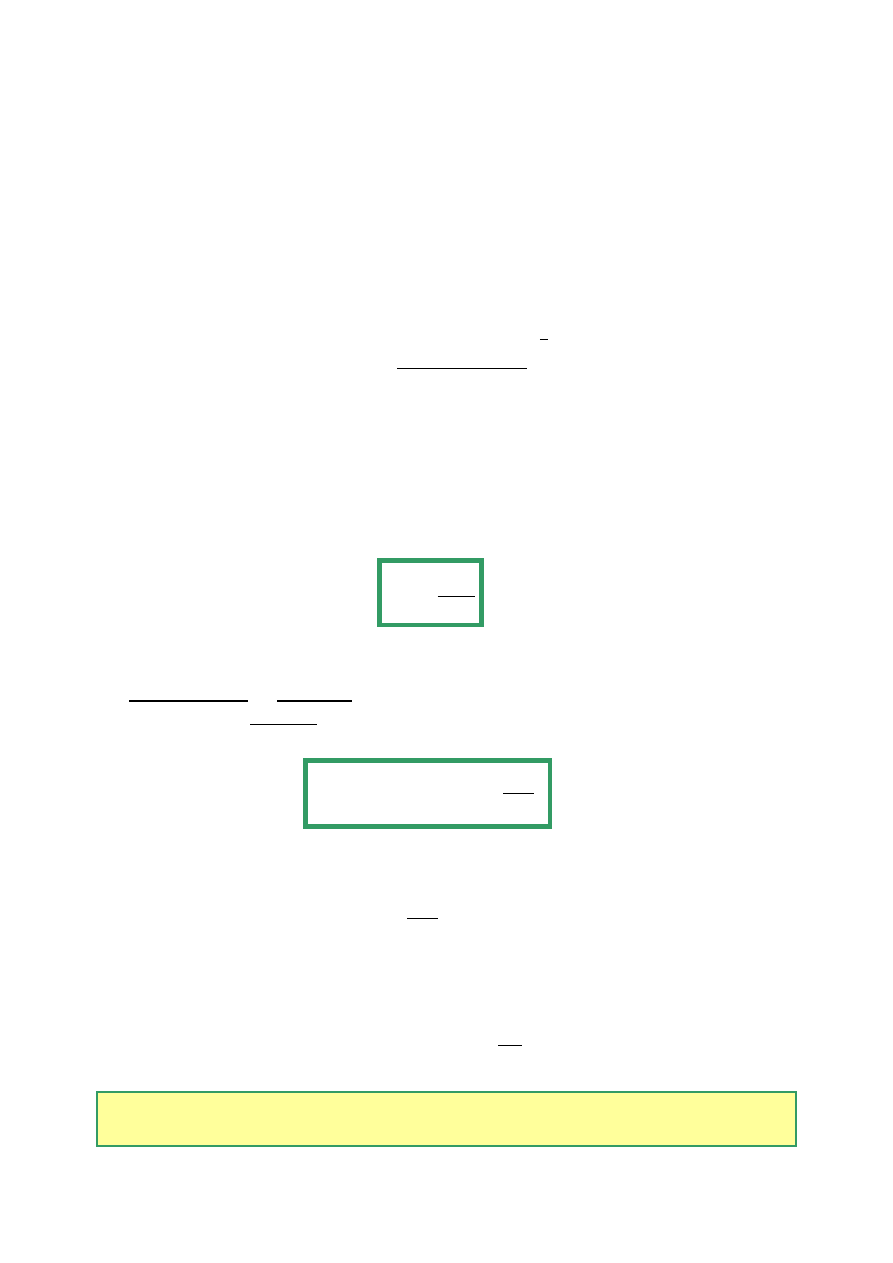
rys. 1. Zawiera on również źródło sygnału V oraz szumiącą rezystancję źródła
sygnału

.

in

s

R

Rys. 1. Uproszczony model szumowy wzmacniacza ze źródłem sygnału

Szumy wzmacniacza są w pełni reprezentowane przez źródło napięciowe
– równoważne wejściowe napięcie szumów

(o zerowej impedancji)

połączone szeregowo z wejściem, źródło prądowe - równoważny wejściowy
prąd szumów (o nieskończonej impedancji) połączone równolegle

z wejściem oraz zespolony współczynnik korelacji c (nie uwzględniony na
rysunku). Każdy z tych czterech parametrów szumowych czwórnika jest funkcją

n

E

n

I

4

częstotliwości. Źródło

reprezentuje szumy cieplne impedancji źródła

sygnału.

t

E

A

V

n

I

2

t

E

Trzy źródła szumów z rys. 1 można zastąpić jednym – całkowitym

napięciem szumów odniesionym do wejścia

. Odnosi ono wszystkie źródła

szumów do zacisków źródła sygnału co pozwala na proste wyznaczenie

stosunku mocy sygnału do mocy szumów

ni

E

N

S

.

Napięcie sygnału i napięcie szumów na zaciskach

jest mnożone przez

wzmocnienie napięciowe

. Zatem wzmocnienie sygnału (transfer function,

system gain)

in

Z

v

in

so

t

V

V

K

=

. (10)

Jest ono różne od wzmocnienia napięciowego wzmacniacza

. Jest ono

zależne zarówno od impedancji wejściowej wzmacniacza, jak i od rezystancji
źródła sygnału i jest funkcją częstotliwości. Wartość skuteczna napięcia sygnału
na wyjściu czwórnika wynosi

v

A

v

in

s

in

in

so

A

Z

R

Z

V

+

=

. (11)

Podstawiając (11) do (10) można wyrazić

za pomocą jedynie parametrów

czwórnika (wzmacniacza)

t

K

in

s

in

v

t

Z

R

Z

A

K

+

=

. (12)

Dla oszacowania poziomu szumów należy brać pod uwagę wartości
średniokwadratowe (kwadraty wartości skutecznych), zatem całkowity poziom
szumów na wyjściu czwórnika

2

2

2

i

v

no

E

A

E

=

. (13)

Poziom szumów na wejściu wzmacniacza wynosi (jeśli źródła szumów
wzmacniacza:

oraz są nieskorelowane)

n

E

(

)

2

2

2

2

2

s

in

n

s

in

in

n

i

R

Z

I

R

Z

Z

E

E

+

+

+

=

, (14)

5

zatem na wyjściu

(

)

2

2

2

2

2

2

2

2

s

in

v

n

s

in

in

v

n

t

no

R

Z

A

I

R

Z

Z

A

E

E

E

+

+

+

=

. (15)

Dzieląc go przez kwadrat modułu wzmocnienia systemu wyrażonego przez (12)
uzyskuje się ważne wyrażenie na całkowite równoważne szumy odniesione do
wejścia

2

ni

E

2

2

2

2

2

s

n

n

t

ni

R

I

E

E

E

+

+

=

(16)

Mówi ono, że pojedyncze źródło szumów o wydajności

(

2

ni

E

niezależnej od

wzmocnienia wzmacniacza i jego impedancji wejściowej co umożliwia
porównanie charakterystyk szumowych różnych wzmacniaczy) umieszczone
szeregowo ze źródłem sygnału

wytworzy poziom całkowitych szumów na

wyjściu

wyrażony przez (16). Impedancja wejściowa wzmacniacza musi

jednakże być brana pod uwagę przy określaniu

oraz

.

in

V

2

no

E

t

K

no

E

W przypadku korelacji (

c - współczynnik korelacji) między źródłami

szumów wzmacniacza wyrażenie (16) modyfikuje się do postaci

s

n

n

s

n

n

t

ni

R

I

cE

R

I

E

E

E

2

2

2

2

2

2

+

+

+

=

. (17)

Człon korelacyjny może być uwzględniony jako dodatkowe źródło napięciowe
szumów o wartości skutecznej napięcia

s

n

n

R

I

cE

2

połączone szeregowo z

lub jako dodatkowe źródło prądowe szumów o wartości skutecznej prądu

n

E

s

n

n

R

I

cE

2

połączone równolegle z .

n

I

Pomiar parametrów

oraz

n

E

n

I

Model

jest tak powszechnie akceptowany z uwagi na łatwość

pomiaru tych parametrów szumowych.

n

n

I

E

−

Pierwsza składowa

- szumy cieplne rezystancji źródła

ni

E

t

E

mogą być

łatwo wyznaczone ze wzoru Nyquista

f

kTR

E

s

t

∆

= 4

.

Biorąc pod uwagę równanie (16) łatwo zauważyć, że jeśli przyjmie się

0

=

s

R

, to dwie składowe po prawej stronie się zerują i całkowite napięcie

szumów odniesione do wejścia jest równe równoważnemu wejściowemu

6

napięciu szumów wzmacniacza

. Mierząc zatem całkowite szumy na wyjściu

przy warunku

n

E

0

=

s

R

otrzymuje się w rezultacie wielkość

i dzieląc ją

przez

uzyskuje się

.

n

v

E

A

v

A

n

E

n

I

s

R

s

R

~

s

n

K

n

n

I

I

s

R

Trzecia składowa (

s

R

) może być najprościej wyznaczona przy bardzo

dużych wartościach

. Szumy cieplne są bowiem

, natomiast

wyrażenie

n

R

I

zależy liniowo od

s

R

, dominuje zatem dla odpowiednio dużych

wartości rezystancji źródła sygnału. Aby zatem wyznaczyć

należy zmierzyć

całkowitą moc szumów na wyjściu wzmacniacza

przy dużej wartości

I

2

no

E

~

s

R

i podzielić uzyskany wynik przez

2

t

uzyskując

, na co składa się głównie

2

ni

E

2

2

s

n

R

I

2

ni

E

. Jeśli składowa szumów cieplnych nie jest pomijalna, można odjąć ją od

.

Wartości

oraz

zależą od częstotliwości, punktu pracy (np. polaryzacji

tranzystora) czy też rodzaju elementu aktywnego na wejściu wzmacniacza.

E

Przykłady

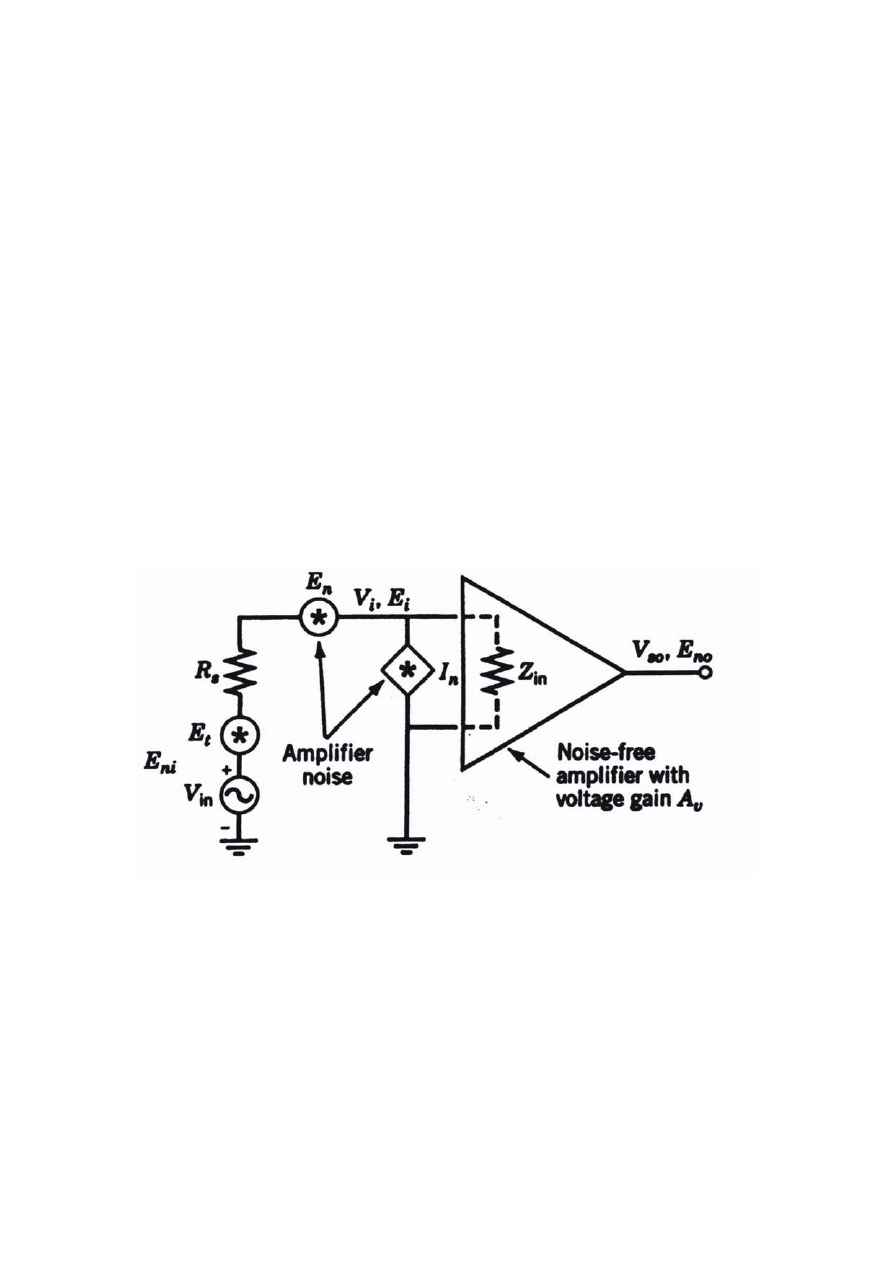
Krzywa reprezentująca całkowite szumy odniesione do wejścia

jest

ograniczona przez trzy różne proste odpowiadające poszczególnym składowym
w równaniu (16). Dla małych wartości

ni

E

s

R

decyduje

. Ze wzrostem

n

E

s

R

szumy cieplne zaczynają być znaczące. Dla odpowiednio dużych wartości

s

R

na wartość

składa się głównie człon

ni

E

s

n

R

I

.

Na rys. 2a składowe

oraz

dominują nad szumami cieplnymi prawie

dla całego zakresu wartości

n

E

n

. Na rys. 2b równoważny wejściowy prąd

szumów

wzmacniacza operacyjnego AD743 (technologia BiFET) jest rząd

wielkości mniejszy. Całkowite szumy odniesione do wejścia są zatem
zdeterminowane przez szumy cieplne dla stosunkowo szerokiego zakresu

n

I

s

R

.

7

Rys. 2. Zależność

od rezystancji

ni

E

s

R

Zmniejszając wartości

oraz

poszerza się obszar dominacji

n

E

n

I

s

R

.

W idealnym przypadku szumy własne czujnika pomiarowego są limitowane
szumami cieplnymi jego rezystancji wewnętrznej.
Krzywe pokazane na rys. 2 mogą być stosowane dla dowolnych elementów
aktywnych, jednak poziomy będą się różniły. I tak, np. dla wzmacniaczy opera-

8

cyjnych bipolarnych lub CMOS, wartości

będą typowo jak dla

częstotliwości powyżej częstotliwości narożnej szumów 1/f. Dla przyrządów
FET i wzmacniaczy operacyjnych z pierwszym stopniem zawierającym
tranzystory FET,

może przyjmować wartości równe typowo jedynie 1/100

wartości przedstawionych na rysunku.

n

E

n

I

Szumy tranzystorów bipolarnych

Celem będzie wyznaczenie parametrów szumowych

,

oraz

dla

BJT korzystając z modelu szumowego tranzystora, zawierającego źródła
szumów cieplnych, śrutowych i typu 1/f. Parametry te są zależne od punktu
pracy tranzystora, zatem należy tak go dobrać, aby zminimalizować poziom
szumów.

ni

E

n

E

n

I

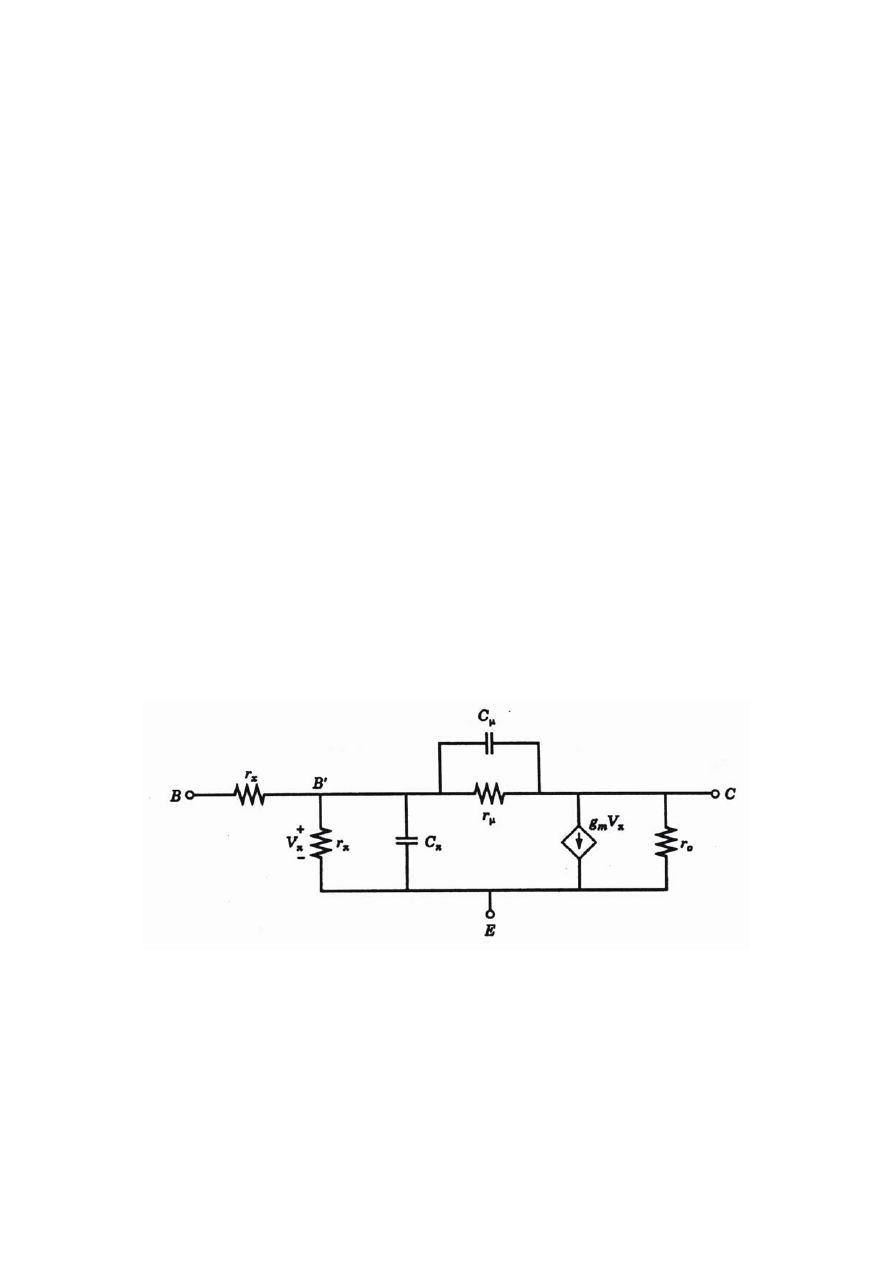
Małosygnałowy model mieszane-

π

Parametry modelu są ogólnie niezależne od częstotliwości. Na rys. 3

pokazano model dla konfiguracji CE zawierający 7 elementów niezależnie od
rodzaju tranzystora (

npn lub pnp). Elementy oraz

C

(powstałe wskutek

efektu modulacji szerokości obszaru bazy oraz jako pojemność warstwy
zubożonej) reprezentują przeważającą część impedancji wejściowej tranzystora.

π

r

π

Rys. 3. Małosygnałowy model typu mieszane-

π tranzystora bipolarnego

Właściwości wzmacniające tranzystora reprezentuje zależne źródło prądowe

, gdzie

V

odpowiada napięciu sygnału między zaciskami

π

V

g

m

π

E

'

B

. Element

przedstawia dynamiczną rezystancję wyjściową tranzystora.

o

r

9

Ważniejsze parametry modelu mieszane-

π mogą być wyrażone za pomocą

łatwo mierzalnych wielkości.

Zwarciowe wzmocnienie prądowe

lub

β

nie

jest parametrem modelu mieszane-

π. Jeżeli jednak dokona się zwarcia pomiędzy

i

fe

h

0

C E

i ograniczy się do zakresu m.cz. (pojemności można wówczas pominąć),

to dla dużych wartości

π

r

π

π

π

π

=

=

β

r

g

r

V

V

g

m

m

0

. (18)

Parametr

, wiążący małosygnałowy parametr dla prądu zmiennego ze stałym

prądem kolektora, może być wyprowadzony z r-nia diody (relacji między

m

g

C

I

i

BE

V

):

kT

qI

g

C

m

=

. (19)

W temperaturze pokojowej

V

kT

q

40

=

.

Innym parametrem użytecznym w analizie szumowej jest tzw. rezystancja

emitera Shockleya , będąca odwrotnością

. W temperaturze pokojowej jest

ona równa

e

r

m

g

[

Ω

≅

=

C

m

e

I

.

g

r

025

0

1

]

. (20)

Rezystancja baza-emiter może być też wyrażona przez zależność od prądu

C

I

. Podstawiając (20) do (18) uzyskuje się

e

m

r

g

r

0

1

β

=

=

π

. (21)

Iloczyn wzmocnienia i pasma

T

f

jest częstotliwością przy której współczynnik

zwarciowego wzmocnienia prądowego maleje do jedności. Wyrażając go za
pomocą parametrów modelu mieszane-

π

µ

π

−

π

=

C

f

g

C

T

m

2

. (22)

Częstotliwość odcięcia

lub

jest częstotliwością, przy której

hfe

f

β

f

β

maleje do

wartości równej 0.707 jej wartości dla m.cz.

0

β

. Można wykazać, że

10

0

β

≅

=

β

T

hfe

f

f

f

. (23)

Typowy zbiór wartości parametrów modelu mieszane-

π (tranzystor pnp 2N4250

małej mocy, w.cz., w punkcie pracy:

mA

.

I

C

1

0

=

,

V

V

CE

5

−

=

):

Ω

=

π

k

r

97

Ω

=

M

.

r

o

6

1

Ω

= 278

x

r

Ω

=

µ

M

r

15

S

.

g

m

0036

0

=

pF

C

4

=

µ

350

0

=

β

pF

C

25

=

π

M

M

o

o

d

d

e

e

l

l

s

s

z

z

u

u

m

m

o

o

w

w

y

y

t

t

r

r

a

a

n

n

z

z

y

y

s

s

t

t

o

o

r

r

a

a

b

b

i

i

p

p

o

o

l

l

a

a

r

r

n

n

e

e

g

g

o

o

(schemat zastępczy)

Rzeczywiste rezystancje generują szumy cieplne, prądy złącz są źródłem

powstawania szumów śrutowych, zaś przepływ prądu generuje szumy typu 1/f.

Rezystancja rozproszona bazy

x

r

generuje szum cieplny, prądy

oraz

B

I

C

I

generują szum śrutowy przepływając przez odpowiednie złącza, natomiast
przepływ prądu bazy przez obszar zubożony złącza baza-emiter powoduje
powstanie szumów 1/f (rys.4).

Rys.4. Szumowy schemat zastępczy tranzystora bipolarnego według modelu

mieszane-

π

11

Elementy sprzężenia zwrotnego

C

oraz

zostały pominięte dla uproszczenia

analizy, co ogranicza zastosowanie tego modelu do zakresu częstotliwości

mniejszych od

µ

µ

r

0

β

T

f

. Dla częstotliwości większych od

mechanizmy

generacji szumów są częściowo skorelowane i całkowity poziom szumów jest
nieco wyższy od oszacowanego za pomocą tego modelu. Źródła szumów na
schemacie mają następujące wydajności:

β

f

x

x

kTr

E

4

2

=

, (24)

B

nb

qI

I

2

2

=

, (25)

C

nc

qI

I

2

2

=

, (26)

s

s

kTR

E

4

2

=

, (27)

α

γ

=

f

KI

I

B

f

2

. (28)

Parametr

γ

w zależności (28) przyjmuje się zwykle jako równy 1, chociaż

często dochodzi do wartości 2, natomiast stała

K

przyjmuje wartości

z przedziału

1

. Stałą

12

15

10

2

2

10

2

−

−

×

÷

×

.

.

K

można zastąpić przez wyrażenie

, gdzie jest ładunkiem elementarnym równym

1

, a

stałą,

reprezentującą częstotliwość narożną szumów 1/f (skorelowaną z nią),
przyjmującą wartości z przedziału

L

qf

2

q

C

19

10

−

×

.6

L

f

MHz

kHz

.

3

7

7

÷

. Wykładnik przyjmuje

zwykle wartość bliską 1. Wyrażenie (28) można zatem zapisać jako

α

f

I

qf

I

B

L

f

γ

=

2

2

. (29)

Źródło napięciowe szumów 1/f jest iloczynem prądu szumów określonego
zależnością (29) i rezystancją obwodu "zwierającego"

. Ponieważ udział

2

f

I

x

r

w szumach 1/f jest mniejszy niż wynikałoby to z teorii dla tranzystorów
planarnych, należy przyjąć wartość

'

x

r

, mniejszą od

x

r

, bardziej odpowiadającą

wynikom pomiarów. Przyjmuje się zwykle

2

x

'

x

r

r

≈

, zatem źródło napięciowe

szumów 1/f przyjmuje wartość

f

r

I

qf

E

x

B

L

f

2

2

2

γ

≅

. (30)

12

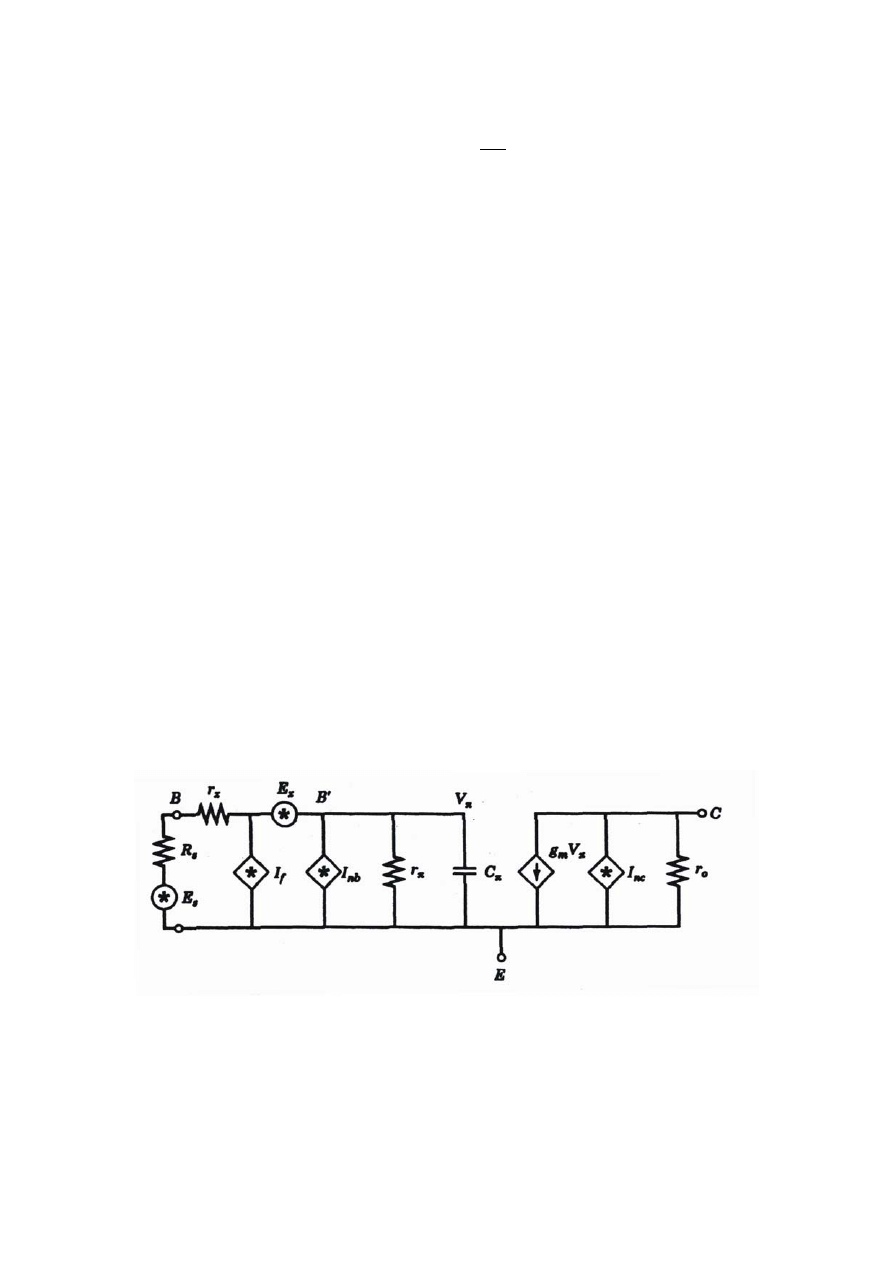
Całkowite równoważne wejściowe napięcie szumów

tranzystora bipolarnego

Należy wyznaczyć całkowity poziom szumów na wyjściu tranzystora,

wzmocnienie od źródła sygnału do wyjścia i odnieść poziom szumów
całkowitych do wejścia.

Zwierając wyjście na szumowym schemacie zastępczym tranzystora (rys. 4)

można poziom całkowitego prądu szumów na wyjściu określić jako

(

)

(

)

(

)

(

)

(

)

(

)















+

+

+

+

+

+

+

+

+

=

=

+

=

π

π

π

π

π

2

2

2

2

2

2

2

2

2

2

2

2

2

2

Z

R

r

R

r

Z

I

I

Z

R

r

Z

E

E

g

I

V

g

I

I

s

x

s

x

f

nb

s

x

s

x

m

nc

m

nc

no

. (32)

Napięcie sygnału na wyjściu tranzystora wynosi

π

π

π

+

+

=

=

Z

R

r

Z

V

g

V

g

I

s

x

s

m

m

o

(33)

Wzmocnienie układu jest równe

π

π

+

+

=

=

Z

R

r

Z

g

V

I

K

s

x

m

s

o

t

. (34)

Całkowite równoważne wejściowe napięcie szumów

2

2

2

t

no

ni

K

I

E

=

(35)

należy teraz wyrazić za pomocą impedancji i źródeł szumowych:

(

)

(

)

(

)

2

2

2

2

2

2

2

2

2

2

π

π

+

+

+

+

+

+

+

=

Z

g

Z

R

r

I

R

r

I

I

E

E

E

m

s

x

nc

s

x

f

nb

s

x

ni

(36)

podstawiając wartości gęstości widmowych odpowiednich źródeł

13

(

)

(

)

(

)

(

)

2

2

2

2

2

2

2

2

2

4

π

π

γ

+

+

+

+

+

+

+

+

+

=

Z

g

Z

R

r

qI

f

R

r

I

qf

R

r

qI

R

r

kT

E

m

s

x

C

s

'

x

B

L

s

x

B

s

x

ni

. (37)

Dla m.cz ostatni składnik (zależny od częstotliwości) upraszcza się do postaci:

(

)

2

0

2

2

β

+

+

π

r

R

r

qI

s

x

C

. (38)

Dla w.cz. (aż do częstotliwości

0

β

≈

T

f

) składnik ten z kolei przyjmuje

następującą postać

(

)

2

2

2

2

2

2

2

1

2













+

≅

ω













ω

+

+

π

π

T

s

x

C

m

s

x

C

f

f

R

r

qI

C

g

C

R

r

qI

. (39)

Ostatecznie, całkowite równoważne odniesione do wejścia napięcie szumów
tranzystora bipolarnego wyrażone przy pomocy parametrów modelu
zastępczego tranzystora, temperatury, prądów polaryzacji, częstotliwości oraz
rezystancji źródła ma postać

(

)

(

)

(

)

(

)

(

)

2

2

2

2

0

2

2

2

2

2

2

2

4













+

+

+

+

+

β

+

+

+

+

+

+

=

γ

π

T

s

x

C

s

'

x

B

L

s

x

C

s

x

B

s

x

ni

f

f

R

r

qI

f

R

r

I

qf

r

R

r

qI

R

r

qI

R

r

kT

E

. (40)

Jest to tylko przybliżenie, choć praktycznie bardzo przydatne. W modelu z rys. 4
pominięto pojemność sprzężenia zwrotnego

co powoduje, że dla zakresu

w.cz. rzeczywisty poziom szumów może być wyższy niż określony przez (40).
Pierwsze trzy człony nie zależą od częstotliwości, zatem wyznaczają one
graniczny poziom szumów tranzystora. Pierwszy człon

µ

C

x

kTr

4

reprezentuje

szum cieplny rezystancji rozproszonej bazy. Człon

( )

2

2

x

B

qI r

jest napięciem

związanym z szumem śrutowym prądu bazy i zwykle może być pominięte, gdyż

14

rezystancja źródła jest zwykle większa od rezystancji bazy i

s

E

dominuje.

Człon

( )

2

0

2

2

β

π

r

qI

C

odpowiada szumom śrutowym prądu kolektora i może być

również zapisany jako

2

2

e

C

r

qI

lub

. Należy przypomnieć, że

jest

rezystancją dynamiczną i nie wytwarza szumów cieplnych.

e

kTr

2

e

r

2

2

+

π

r

2

+

x

B

r

qI







T

f

f

x

r

2







2

+

L

qf

2

+

x

qI

kTr

n

I

B

qI

4

2

s

R

→

s

2

0

2

β

+

B

qI

2

γ

B

L

f

I

qf

2

=

B

qI

+

γ

B

L

f

I

Równoważne wejściowe napięcie i prąd szumów tranzystora bipolarnego

Równoważne wejściowe napięcie szumów

można uzyskać z (40) przy

n

E

0

=

s

R

2

2

2

2

0

2

2

2

2

4







+

β

+

=

γ

x

C

'

x

B

L

C

x

n

r

qI

f

r

I

qf

qI

kTr

E

. (41)

Ponieważ

oraz ponieważ zwykle

e

r

r

0

β

=

π

2

0

2

e

r

β

<<

, zatem

2

2

2

2

2

4







+

=

γ

T

x

C

'

x

B

e

C

n

f

f

r

qI

f

r

I

r

E

. (42)

Równoważny wejściowy prąd szumów

wyznacza się również z równania

(40) przyjmując tym razem dużą wartość

s

R

, mianowicie

s

kTR

>

2

,

dzieląc obie strony (40) przez

i wyznaczając wartość graniczną dla

∞

R

2

2

2

2













+

+

=

T

C

C

n

f

f

qI

qI

I

. (43)

Ponieważ

B

C

I

I <<

β

2

0

, drugi człon w (43) można pominąć i ostatecznie

2

2

2

2













+

T

C

n

f

f

qI

qf

I

. (44)

15

Przykład

Wyznaczyć średni kwadrat całkowitego równoważnego odniesionego do

wejścia napięcia szumów

dla tranzystora 2N4250 pracującego przy prądzie

kolektora

i rezystancji źródła sygnału

2

ni

E

mA

1

Ω

=

k

R

s

10

w paśmie

częstotliwości

Hz

f

10

=

∆

wokół częstotliwości

kHz

1

korzystając z danych

katalogowych.

I sposób

Łatwiejszy. Odczytuje się wartości

oraz

przy

n

E

n

I

kHz

f

1

=

z katalogu:

Hz

nV

E

n

2

=

,

Hz

pA

I

n

1

=

, a następnie oblicza się

z równania:

2

ni

E

(

)

f

R

I

E

E

E

s

n

n

t

ni

∆

+

+

=

2

2

2

2

2

(

) ( ) ( )

( )

10

10

10

10

2

10

6

1

2

4

2

12

2

9

16

2









+

×

+

×

=

−

−

−

.

E

ni

(

)

( )

10

10

10

4

10

6

1

16

18

16

2

−

−

−

+

×

+

×

= .

E

ni

2

15

2

10

64

2

V

.

E

ni

−

×

=

nV

.

E

ni

4

51

=

Dominujący wpływ mają szumy cieplne rezystancji źródła sygnału oraz człon

2

2

s

n

R

I

; człon

jest do pominięcia.

2

n

E

II sposób

Wykorzystując dane liczbowe parametrów tranzystora wyznacza się

oraz

bezpośrednio z zależności (42) i (44), co umożliwia oszacowanie, który

mechanizm generacji szumów stanowi dominujące źródło szumów. Dla

2

n

E

2

n

I

I

mA

C

1

=

,

. Z równania (42) uzyskuje się

Ω

= 25

e

r

Hz

V

.

f

E

n

2

2

10

63

2

×

=

∆

18

−

Ω

.

Pierwszy człon w tym równaniu, pochodzący od rezystancji bazy

150

, jest

dominujący. Z równania (44) otrzymuje się

Hz

A

.

f

I

n

24

2

10

18

1

−

×

=

∆

2

n

I

2

. Szum

śrutowy prądu bazy jest najistotniejszym składnikiem

; szum 1/f wnosi

16

również istotny wkład. Można teraz wyznaczyć wartość

w paśmie

uzyskując

2

ni

E

Hz

10

2

15

2

10

79

2

V

.

E

ni

−

×

=

nV

.

E

ni

8

52

=

Uzyskany wynik potwierdza poprawność obliczeń nawet przy małej dokładności
odczytu danych z krzywych katalogowych.

17