CPA
POLITECHNIKA KRAKOWSKA
Dr inż. Krzysztof Krupa
tel. +12 628 3224
krupa@mech.pk.edu.pl
Critical Path Analysis
CPA
POLITECHNIKA KRAKOWSKA
Dr inż. Krzysztof Krupa
tel. +12 628 3224
krupa@mech.pk.edu.pl
Critical Path Analysis
Pojęcia podstawowe
W każdym przedsięwzięciu można
wyodrębnić wspólne elementy:
Czynności,
Zdarzenia,
Zależności czasowe.
CPA
Pojęcia podstawowe
Czynność
– dowolnie wyodrębniona część przedsięwzięcia, której realizacja
związana jest z upływem czasu oraz ze zużyciem zasobów,
CPA
Zależność czasowa
– fikcyjna czynność, służąca do przekazywania
zależności między zdarzeniami.
Zdarzenie
– moment czasowy, w którym zaczyna się lub kończy
przynajmniej jedna czynność,
Zasady tworzenia sieci czynności
Początkiem każdej czynności jest zdarzenie (zdarzenie poprzedzające
i
)
CPA
i
Końcem każdej czynności jest zdarzenie (zdarzenie następujące
j
)
j
Zdarzeniem zrealizowanym nazywa się każde zdarzenie, jeżeli
czynności, dla których jest ono zdarzeniem następującym, zostały
zrealizowane.
Czynność lub czynności mogą się rozpocząć tylko od zdarzenia
zrealizowanego.
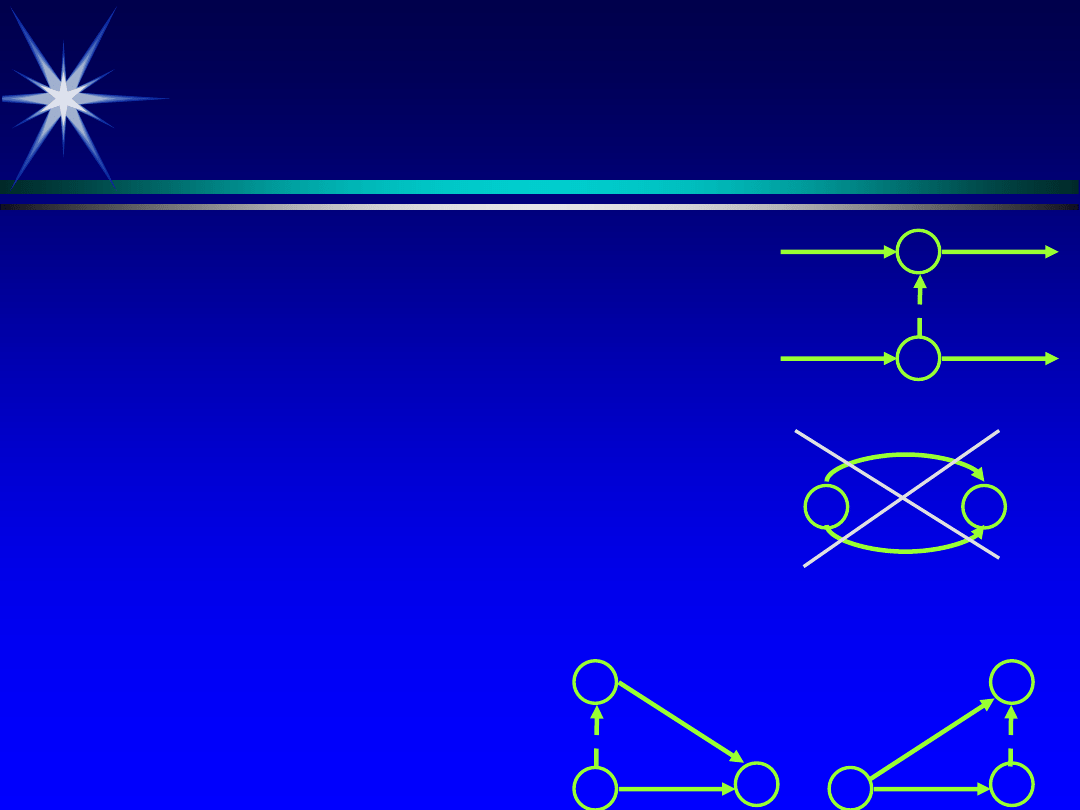
Zasady tworzenia sieci czynności
Żądany warunek równoczesności zdarzeń lub
czynności przedstawiony jest w sieci za pomocą
zależności czasowej.
CPA
Dwa zdarzenia nie mogą być bezpośrednio połączone
przez dwie lub więcej czynności czy zależności czasowe.
W takim przypadku należy rozdzielić początki lub końce
na dwa zdarzenia, wykorzystując zależność czasową.
j
i
i
j
i
j
Zasady tworzenia sieci czynności
Każde zdarzenie ma przyporządkowany numer.
Przyporządkowanie jest dowolne, ale unikatowe.
CPA
i
Każda czynność i zależność czasowa identyfikowana jest
za pomocą dwóch numerów: numeru zdarzenia poprzedzającego
i
oraz numeru zdarzenia następującego
j
.
i
j
Zasady tworzenia sieci czynności
CPA
Kolejność czynności przy tworzeniu sieci:
1.
Ustalenie stopnia szczegółowości podziału procesu realizacji przedsięwzięcia na
poszczególne czynności,
2.
Zestawienie wszystkich czynności obejmujących proces wykonania
przedsięwzięcia z wyznaczeniem momentu jego rozpoczęcia i zakończenia,
3.
Określenie logicznych związków zachodzących między poszczególnymi
czynnościami:
• Kolejność czynności,
• Następstwa czynności,
• Równoległość czynności.
Przykład
CPA
Dane jest przedsięwzięcie, wymagające realizacji dziewięciu
czynności:
a, b, c, d, e, f, g, h, i
.
e, f > b; d > a, e; g > b, c; h > d; i > f, g
Zdefiniowane są relacje między czynnościami:
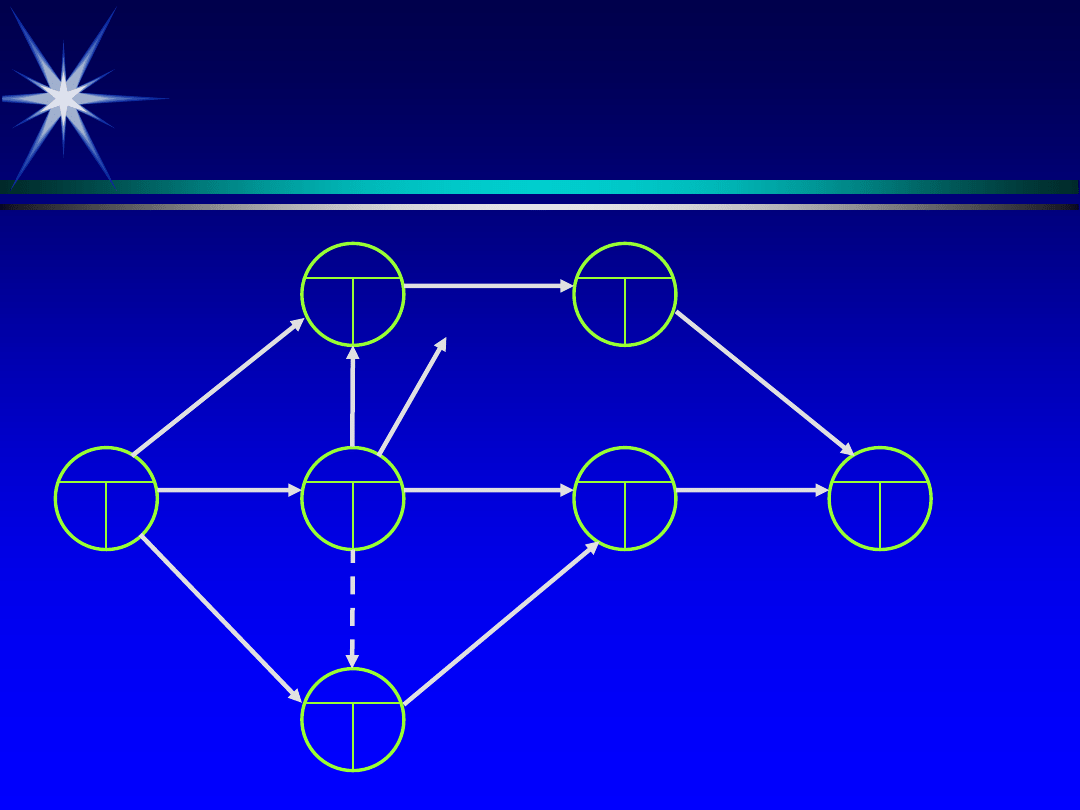
Zasady tworzenia sieci czynności
CPA
1
a
b
c
d
f
e
g
i
h
2
3
4
5
6
7
e, f > b
d > a, e
g > b, c
h > d
i > f, g
e
Zasady tworzenia sieci czynności
CPA
1
5
8
Najwcześniejszy termin
zdarzenia
Numer zdarzenia
Najpóźniejszy termin
zdarzenia
Przykład
CPA
Dla zdefiniowanych czynności podano czasy ich trwania:
f = 3
g = 4
h = 4
i = 5
a = 6
b = 2
c = 5
d = 5
e = 2
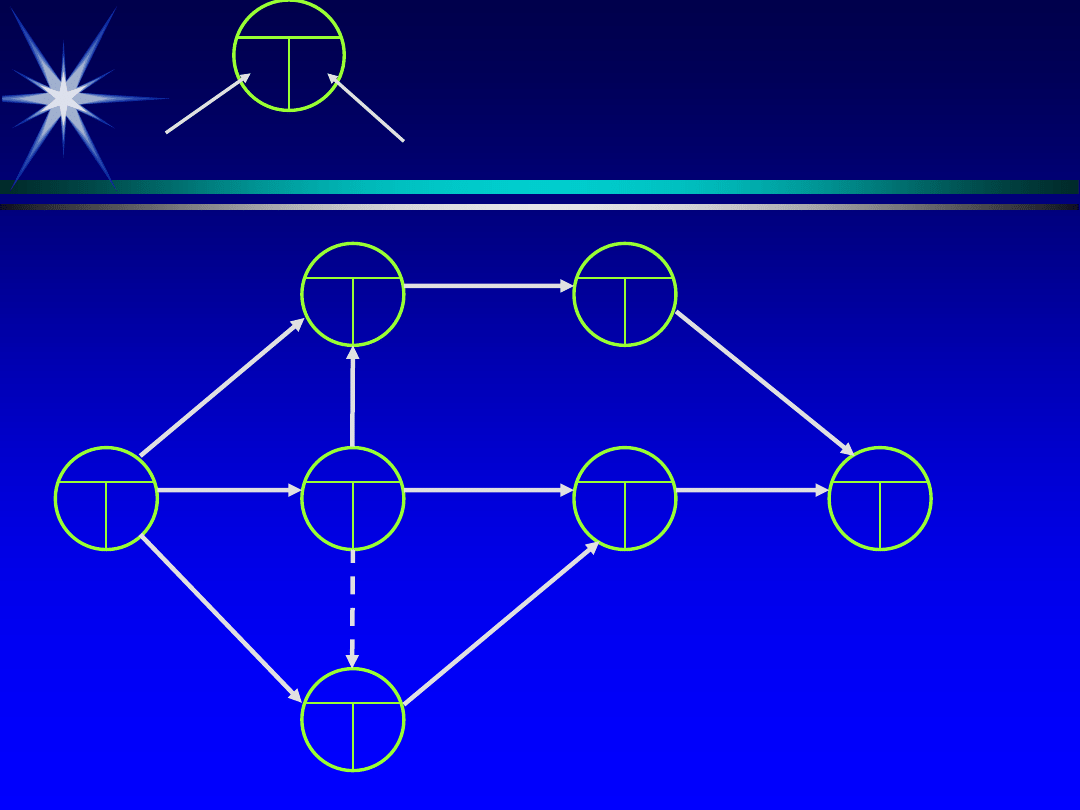
CPA
1
2
3
4
5
6
7
e, f > b
d > a, e
g > b, c
h > d
i > f, g
a = 6
b = 2
c = 5
e = 2
d = 5
f = 3
g = 4
h = 4
i = 5
a = 6
b = 2
c = 5
d = 5
e = 2
f = 3
g = 4
h = 4
i = 5
0
2
6
5
9
11
15
i
5
8
Najwcześniejszy termin zdarzenia
t
wi
Najpóźniejszy termin zdarzenia
t
pi
15
11
10
6
6
4
0
t
pi
= min(t
pj
-T
ij
)
t
wj
= max(t
wi
+T
ij
)
T
ij
-
czas trwania czynności rozpoczynającej się zdarzeniem i,
a kończącej się zdarzeniem j
Drogi sieci czynności
CPA
Każdy ciąg czynności prowadzący od zdarzenia
początkowego do zdarzenia końcowego nazywa
się
drogą sieci
.
Ciąg czynności, których suma czasów jest największa,
czyli najdłuższa droga w sieci, nazywana jest
drogą krytyczną
.
Drogi sieci czynności
CPA
Czynności leżące na drodze krytycznej nazywane są
czynnościami krytycznymi
.
Czas trwania drogi krytycznej jest najkrótszym
możliwym czasem realizacji całego przedsięwzięcia.
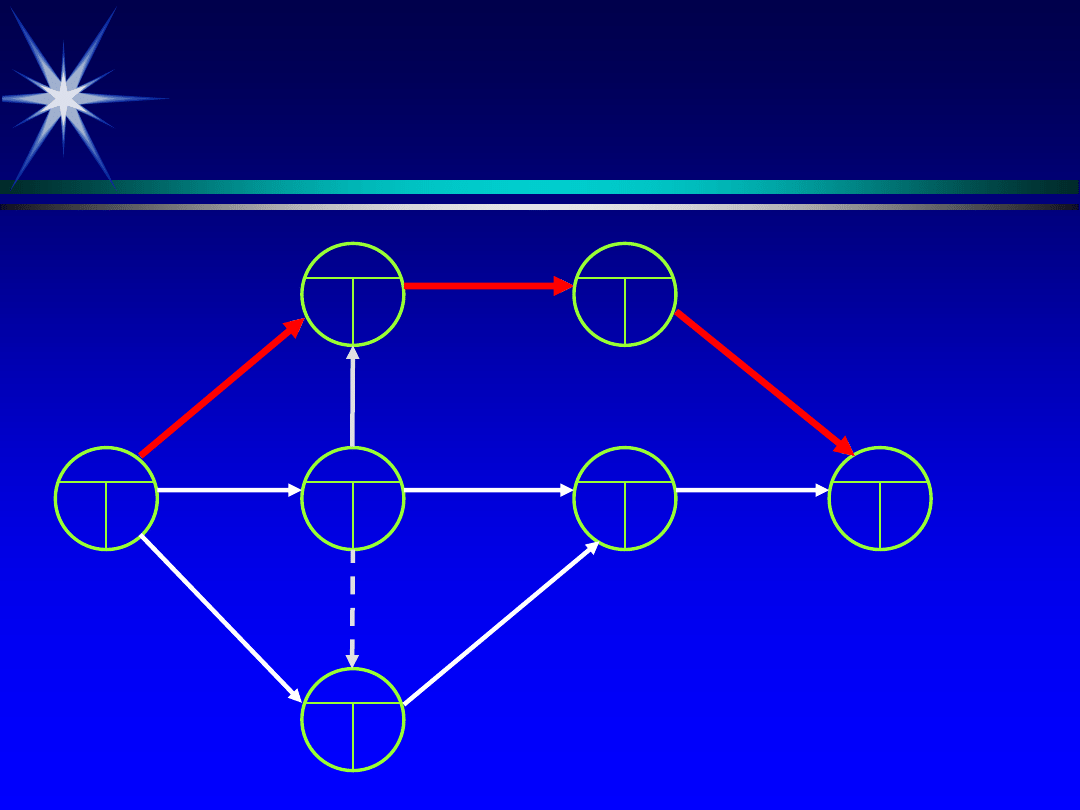
CPA
1
a = 6
2
3
4
5
6
7
e, f > b
d > a, e
g > b, c
h > d
i > f, g
b = 2
c = 5
e = 2
d = 5
f = 3
g = 4
h = 4
i = 5
a = 6
b = 2
c = 5
d = 5
e = 2
f = 3
g = 4
h = 4
i = 5
0
2
6
5
9
11
15
15
11
10
6
6
4
0
Droga krytyczna
Droga krytyczna
CPA
Znajomość najwcześniejszych i najpóźniejszych terminów zdarzeń, pozwala obliczyć
najwcześniejsze i najpóźniejsze terminy rozpoczęcia i zakończenia czynności.
Wprowadzono następujące oznaczenia:
t
wj
- najwcześniejszy termin zdarzenia
j
t
pi
- najpóźniejszy termin zdarzenia
i
t
pi
= min(t
pj
-T
ij
)
t
wj
= max(t
wi
+T
ij
)
Droga krytyczna
CPA
T
ij
-
czas trwania czynności rozpoczynającej się zdarzeniem
i
, a kończącej się zdarzeniem
j
t
wp
(ij)
- najwcześniejszy termin rozpoczęcia czynności
ij
t
wk
(ij)
- najwcześniejszy termin zakończenia czynności
ij
t
pp
(ij)
- najpóźniejszy termin rozpoczęcia czynności
ij
t
pk
(ij)
- najpóźniejszy termin zakończenia czynności
ij
t
wp
(ij) = t
wi
t
wk
(ij) = t
wp
(ij)+T
ij
=t
wi
+T
ij
t
pp
(ij) = t
pk
(ij)-T
ij
=t
pj
-T
ij
t
pk
(ij) = t
pj
Droga krytyczna
CPA
Czynności nie leżące na drodze krytycznej nie wpływają
na termin wykonania całego przedsięwzięcia
i w stosunku do nich dopuszczalne są przesunięcia
terminów rozpoczęcia i zakończenia.
Droga krytyczna
CPA
Czynności nie leżące na drodze krytycznej mają zapas czasu.
Wyróżnia się cztery rodzaje zapasów czasu:
Zapas całkowity z
c
(ij) = t
pp
(ij)-t
wp
(ij) = t
pj
– T
ij
- t
wi
Zapas swobodny z
s
(ij) = t
wp
(jk)-t
wk
(ij) = t
wj
- t
wi
– T
ij
Zapas warunkowy z
w
(ij) = z
c
(ij)-z
s
(ij) = t
pj
- t
wj
Zapas niezależny z
n
(ij) = max(0, t
wj
- t
pi
– T
ij
)
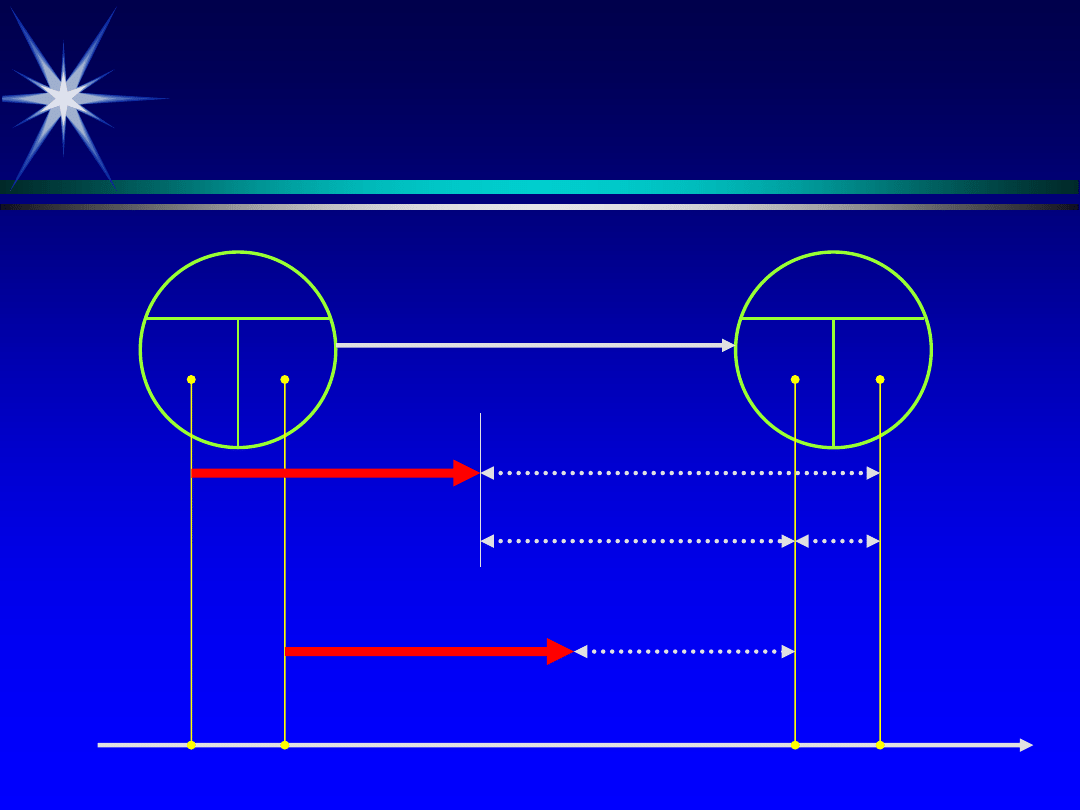
CPA
j
15
18
i
0
2
Zapasy czasów
ij
Z
n
(ij)
Z
c
(ij)
Z
s
(ij)
Z
w
(ij)
T(ij)
T(ij)
t
wi
t
pi
t
wj
t
pj