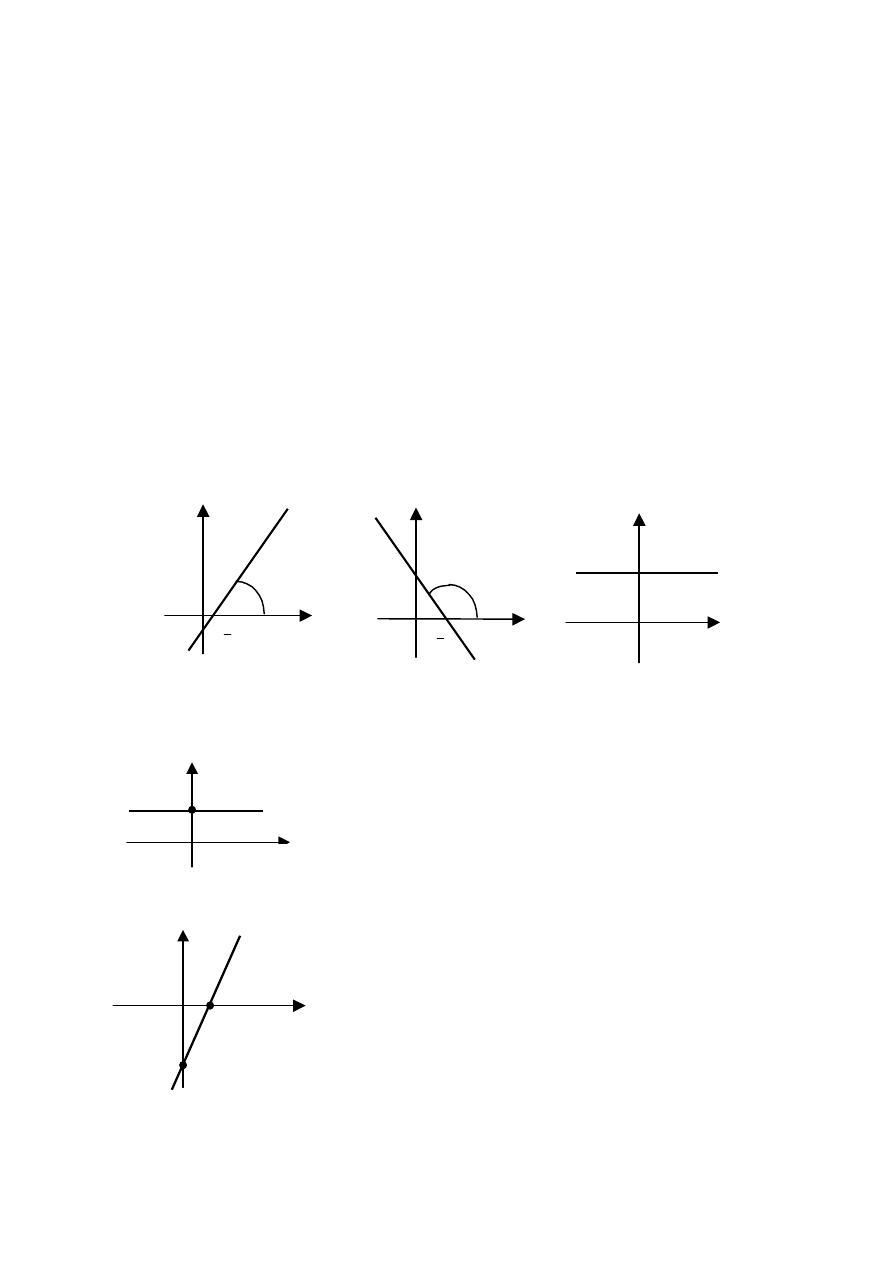
Tomasz Kowalski
Wykłady z matematyki dla studentów kierunków ekonomicznych
Wykład 8
PRZEGLĄD FUNKCJI ELEMENTARNYCH
1. Funkcje liniowe
Funkcją liniową nazywamy funkcję postaci
b
ax
x
f
y
)
(
,
gdzie a, b - są danymi liczbami zwanymi odpowiednio: a - współczynnik kierunkowy, b - wyraz wolny.
Dziedziną funkcji jest zbiór R, wykresem - linia prosta równoległa do osi OX, gdy
,
0
a
albo przecinająca oś OX , gdy
.
0
a
Współczynnik kierunkowy a prostej jest równy tangensowi kąta
- kąta nachylenia prostej do osi OX.
Wyraz wolny b jest rzędną punktu przecięcia się wykresu z osią OY (rys.1)
y
ax b
a
(
)
0
Y
X
b
b
a
y
ax b
a
(
)
0
Y
X
b
b
a
Y
X
b
y b
Przykład 1.
Naszkicować wykres funkcji: a)
2
y
, b)
4
2
x
y
.
Rozwiązanie.
O
2
y
X
Y
a) Wykresem jest prosta równoległa do osi OX i przecinająca oś OY
w punkcie o rzędnej 2 przedstawiona na rys.2.
Rys. 1.
Rys. 2.
4
2
x
y
X
O
)
0
,
2
(
Q
)
4
,
0
(
P
Y
Rys. 3.
b) Przyjmując 0
x
otrzymujemy rzędną punktu przecięcia się
prostej z osią OY równą
4
y
. Przyjmując otrzymujemy
równanie:
0
y
0
4
2
x
(
P
, z którego wynika, że odciętą punktu
przecięcia się prostej z osią OX jest
. Prosta przechodzi
więc przez punkty
)
2
x
0
,
2
(
,
0
i
)
4
Q
(patrz rys.3.).
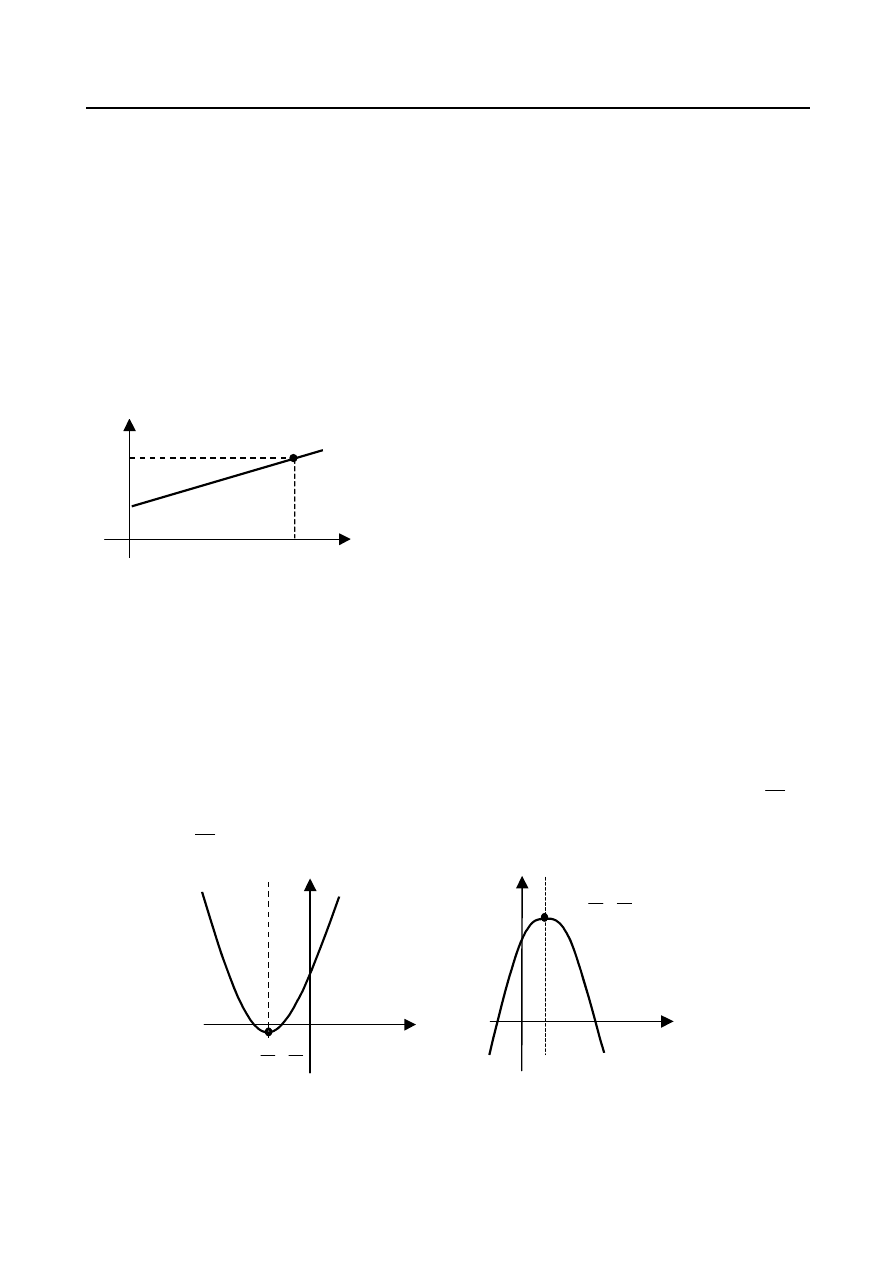
Wykład 8. Przegląd funkcji elementarnych
2
Inne własności funkcji liniowej
1. Funkcja liniowa jest monotoniczna w całej swojej dziedzinie: rosnąca gdy
, malejąca gdy
a
0
a
0
i stała gdy
.
0
a
2. Funkcja liniowa niestała przyjmuje każdą wartość rzeczywistą.
3. Funkcja liniowa niestała rozpatrywana w przedziale domkniętym osiąga wartość najmniejszą na jednym,
a wartość największą na drugim końcu przedziału.
4. Jeżeli funkcja jest liniowa, to przyrost wartości funkcji jest proporcjonalny do przyrostu jej argumentu.
Także na odwrót: Jeżeli dziedziną funkcji jest R i przyrost wartości funkcji jest proporcjonalny do
przyrostu jej argumentu, to funkcja jest liniowa. Współczynnik proporcjonalności wynosi wtedy a.
Funkcja liniowa znajduje wszechstronne zastosowanie w opisie zjawisk ekonomicznych. Opisuje ona np.
zależność wartości towaru od jego ceny, wielkość kosztów produkcji w zależności od liczby jednostek
wyprodukowanego towaru.
x
y
10
120
Y
Przykład 2. Aby uruchomić produkcję pewnego towaru
należy zainwestować 120zł (koszty stałe). Produkcja każdej
kolejnej jednostki tego wyrobu pochłania dodatkowo 10 zł
(koszty zmienne). Zależność między kosztami produkcji y, a
ilością wyprodukowanego towaru x wyraża się wzorem
x
y
10
120
. Wykres tej funkcji dla
przedstawiony jest
na rys.4.
0
x
120
X
240
12
Rys. 4.
2. Funkcje kwadratowe
Funkcją kwadratową (trójmianem kwadratowym) nazywamy funkcję określoną wzorem
c
bx
ax
x
f
y
2
)
(
,
gdzie
a
są danymi liczbami.
b
0, , c
Dziedziną funkcji jest zbiór R. Wykresem trójmianu kwadratowego jest parabola, której ramiona
(gałęzie) skierowane są w dół, jeżeli
a
, oraz skierowane w górę, jeżeli
. Osią symetrii paraboli
jest prosta równoległa do osi OY i przechodząca przez wierzchołek W , który ma współrzędne
0
a
0
a
b
x
w
2
,
a
x
f
y
w
w
4
)
(
. gdzie
oznacza wyróżnik trójmianu . Parabola przecina oś OY
w punkcie o rzędnej c (rys.5).
ac
4
b
2
Y
X
c
y
ax
bx c
a
2
0
W
b
a
a
(
,
)
2
4
y
ax
bx c
a
2
0
Y
X
c
W
b
a
a
(
,
)
2
4
Rys. 5.
Położenie paraboli względem osi OX , związane jest z liczbą rozwiązań równania
i zależy od wyróżnika :
0
2
c
bx
ax
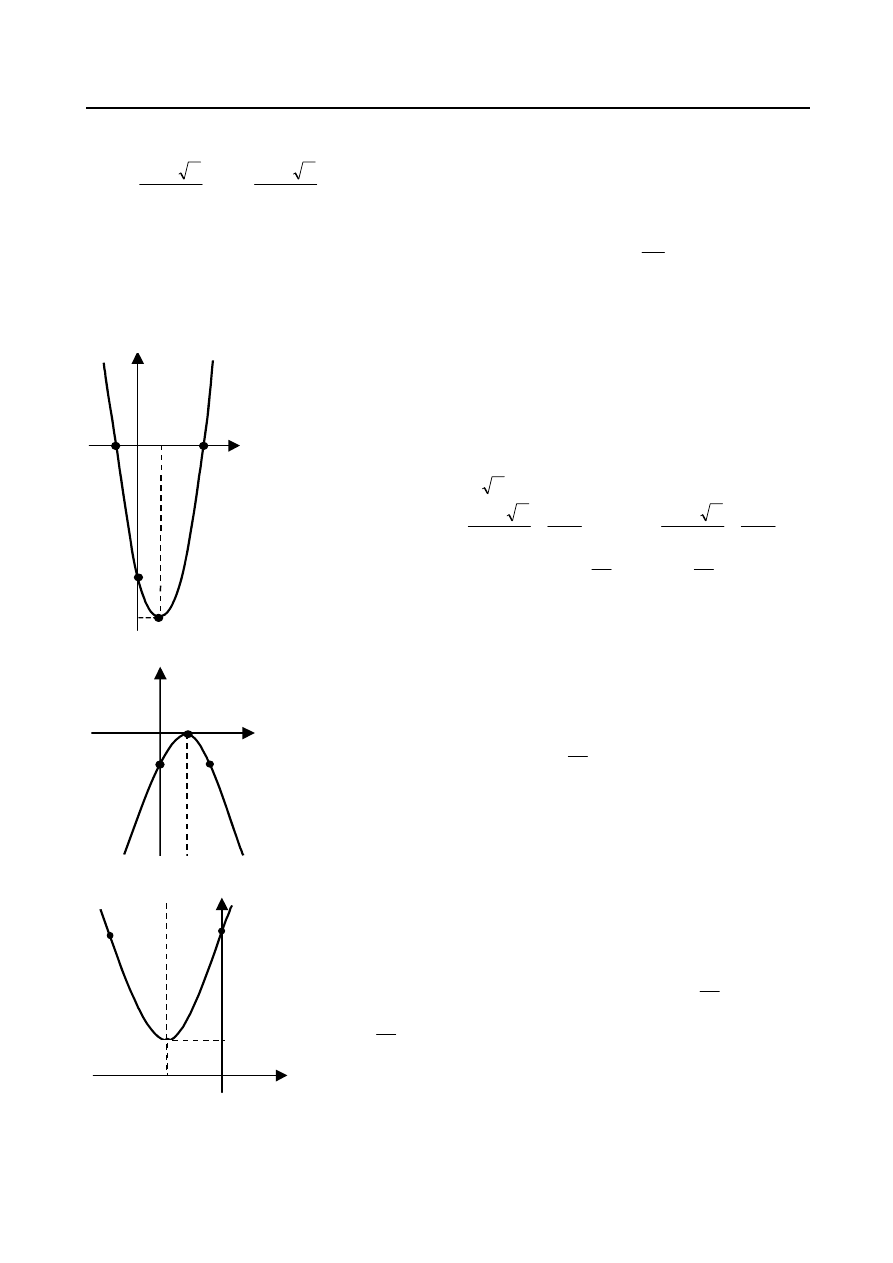
Wykład 8. Przegląd funkcji elementarnych
3
1. Gdy
parabola przecina oś w punktach o odciętych stanowiących pierwiastki tego równania:
0
a
b
x
2
1
,
a
b
x
2
2
. T
rójmian kwadratowy można wtedy przedstawić w tzw. postaci
iloczynowej
: .
)
)(
(
2
1
x
x
x
x
a
y
2. Gdy
parabola dotyka swoim wierzchołkiem oś w punkcie o odciętej
0
a
b
x
2
0
, stanowiącej tzw.
pierwiastek podwójny równania. Postacią iloczynową trójmianu jest wtedy:
.
y
a x x
(
)
0
2
3. Gdy
parabola nie przecina osi, a równanie nie ma pierwiastków.
0
X
Y
)
8
,
1
(
W
–1
3
1
–6
Przykład 3.
Naszkicować wykresy funkcji:
a) , b)
, c)
.
6
4
2
2
x
x
y
1
2
2
x
x
y
5
4
2
x
x
y
Rozwiązanie:
a) Dla
otrzymujemy 6
0
x
y
. Oznacza to, że parabola przecina oś OY
w punkcie
)
6
,
0
(
P
48
16
ac
. W przypadku równania
mamy
0
6
4
2
2
x
x
,
64
4
2
b
8
. Zatem odciętymi punktów przecięcia się
wykresu z osią OX są
1
4
8
4
2
a
b
1
x
,
3
4
8
4
2
2
a
b
x
.
Wierzchołek paraboli ma współrzędne:
1
2
a
b
x
w
,
8
4
a
y
w
.
Wykres funkcji przedstawiony jest na rys. 6.
Rys. 6.
b) Dla
otrzymujemy 1
0
x
y
0
. Parabola przecina oś OY w punkcie
. W przypadku równania
mamy
. Oznacza to, że parabola dotyka osi OX swoim
wierzchołkiem. Mamy przy tym
)
1
,
0
4
2
b
(
1
P
0
1
2
2
x
x
4
4
ac
0
,
1
2
w
w
y
a
b
x
. Dodatkowo
znajdujemy punkt
)
1
,
2
(
2
P
1
(wykorzystując symetrię paraboli względem
prostej
).Wykres funkcji przedstawiony jest na rys.7.
x
Rys. 7.
Y
)
0
,
1
(
W
X
-1 P
1
P
2
x=1
c) Dla
0
x
otrzymujemy 5
y
4
. Parabola przecina oś OY w punkcie
. W przypadku równania
mamy
. Oznacza to, że parabola nie przecina
)
5
,
0
4
2
b
(
1
P
0
5
4
2
x
x
20
16
ac
X
Y
)
1
,
2
(
W
P
1
P
2
5
1
–2
osi OX . Wierzchołek paraboli ma współrzędne:
2
2
a
b
x
w
,
1
4
a
y
w
. Wykorzystując symetrię paraboli względem prostej
znajdujemy punkt
)
2
x
5
,
4
(
2
P
.
Wykres funkcji przedstawia rys.8.
Rys. 8.
Wykład 8. Przegląd funkcji elementarnych
4
Przykład 4.
Podać postać iloczynową trójmianów: a)
, b)
.
Przykład 4.
Podać postać iloczynową trójmianów: a)
, b)
.
6
8
2
2
x
x
y
6
8
2
2
x
x
y
3
6
3
2
x
x
y
3
6
3
2
x
x
y
Rozwiązanie.
Rozwiązanie.
a) Mamy tutaj
. Zatem
,
a) Mamy tutaj
. Zatem
,
6
,
8
,
2
c
b
a
6
,
8
,
2
c
b
a
16
48
64
4
2
ac
b
16
48
64
4
2
ac
b
4
. Trójmian ma dwa
pierwiastki:
3
4
4
8
2
1
a
b
x
,
1
4
4
8
2
2
a
b
x
. Postacią iloczynową w tym
przypadku jest więc
, czyli
)
)(
(
2
1
x
x
x
x
a
y
)
1
)(
3
(
2
x
x
y
.
b) Ponieważ
3
,
6
,
3
c
b
a
, to
. Trójmian ma jeden pierwiastek podwójny
0
36
36
4
2
ac
b
1
6
6
2
0
a
b
x
. Postacią iloczynową w tym przypadku jest
czyli
.
2
0
)
(
x
x
a
y
2
)
1
(
3
x
y
(Podobny wynik można było uzyskać wyłączając 3 przed nawias i stosując odpowiedni wzór skróconego
mnożenia).
Uwaga.
W wielu przypadkach w prosty sposób można uzyskać postać iloczynową trójmianu i na tej
podstawie określić pierwiastki.
Przykład 5.
Wyznaczyć pierwiastki równania bez obliczania wyróżnika: a)
,
0
4
2
x
x
b) .
0
9
2
x
Rozwiązanie.
a) Wyłączając przed nawias czynnik:
x
otrzymujemy
0
)
4
(
x
x
. Pierwiastkami równania są więc
4
,
0
2
.
1
x
x
b) Stosując wzór skróconego mnożenia otrzymujemy
0
)
3
)(
3
(
x
x
. Pierwiastkami są
3
,
3
2
1
x
x
.
Przykład 6.
Rozwiązać nierówność: a)
, b)
, c)
.
0
3
2
2
x
x
0
4
2
x
0
1
2
2
x
x
Rozwiązanie. W każdym przypadku naszkicujemy wykres trójmianu uwzględniając jedynie położenie
względem osi OX.
a) Ponieważ
16
12
,
4
4
2
ac
b
4
, to trójmian ma dwa
pierwiastki:
3 ,
2
4
2
2
1
a
b
x
1
2
4
2
2
2
a
b
x
.
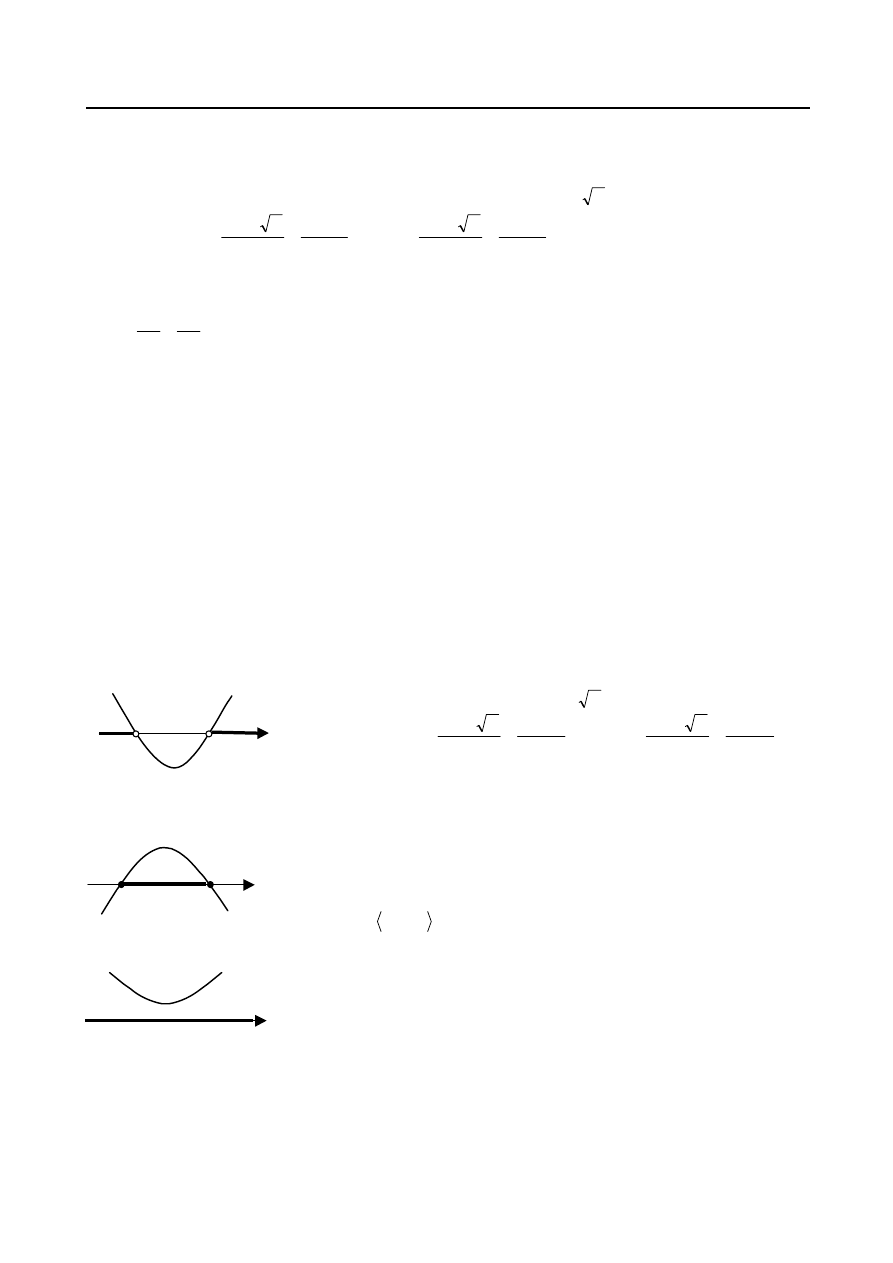
Ramiona paraboli skierowane są do góry. Z wykresu (rys.9.)
odczytujemy, że zbiorem rozwiązań nierówności jest suma przedziałów:
)
;
1
(
)
3
;
(
.
3
1
X
Rys. 9.
b) Mamy tutaj
) . Pierwiastkami trójmianu są
2
)(
2
(
4
2
x
x
x
2
,
2
2
1
x
x
. Gałęzie paraboli skierowane są do dołu. Na podstawie
wykresu (rys.10.) stwierdzamy, że zbiorem rozwiązań nierówności jest
przedział
2
;
2
.
X
2
2
Rys. 10.
c) Ponieważ
, to trójmian nie ma pierwiastków.
7
8
1
4
2
ac
b
R
x
X
Ramiona paraboli skierowane są ku górze. Wykres trójmianu
przedstawiony jest na rys.11. Nierówność spełniona jest dla wszystkich
.
Rys. 11.
. 11.
Funkcję
wykorzystuje się m.in. do opisu zależności między popytem na nowe dobro
(w fazie rozpowszechniania) a czasem t, jaki upłynął od momentu wprowadzenia tego dobra na rynek.
c
bt
at
y
2
Funkcja kwadratowa jest też dla
typową funkcją kosztów całkowitych.
0
,
0
,
0
c
b
a

Wykład 8. Przegląd funkcji elementarnych
5
m.
acji wynika, że wys
ę wzorem
. Przy jakim x całkowity zysk ze sprzedaży puszek będzie
zanie. P
ówny
Przykład 7.
Supermarket zakupuje puszki z szynką po 5 zł, a następnie sprzedaje je z pewnym zyskie
Z przeprowadzonych obserw
okość sprzedaży n w zależności od ceny detalicznej x
(
5
x
) wyraża si
2200
200
)
(
x
x
n
maksymalny?
Rozwią
rzy cenie detalicznej
x zysk
jednostkowy jest r
5
x
c
h puszek jest równa wtedy
P
yc
, to
zysk całkowity wynosi
kwadratowy
osiąga wartość największą, gdy
onieważ liczba
sprzedan
2200
200
x
n
00
11
3200
200
)
2200
200
)(
5
(
2
x
x
x
x
cn
z
Otrzymana funkcja jest trójmianem
m, który
0 .
8
2
a
b
x
. Największą
artością (maksymalnym zyskiem) jest wtedy
w
700
11
)
8
(
z
[zł]. Wykres funkcji zysku przedstawia rys.12.
. Wielomiany
Wielomianem stopnia n
nazywamy funkcję określoną wzorem
rem
a
3
0
)
(
a
x
W
y
,
gdzie n - jest daną liczbą naturalną lub ze
1
1
1
...
x
a
x
a
x
a
n
n
n
n
,
a
a
a
n
n
0
1
1
,
, ... , ,
0
- są danymi liczbami rzeczywistymi
wanymi współczynnikami wielomianu.
z
Dziedziną tej funkcji jest zbiór
R. Każdą liczbę a, dla której
0
)
(
a
W
nazywamy pierwiastkiem
ielomianu
. Wielomian stopnia
n może posiadać co najwyżej n pierwiastków.
etody wyznaczania pierwiastków wielomianu
(pierwiastków równania
):
1.
adratowych o
w
M
W x
( )
0
)
(
x
W
Metoda sprowadzająca wielomian do postaci iloczynu czynników liniowych lub kw
0
.
Wykorzystuje się w niej tzw. grupowanie wyrazów i wzory skróconego mnożenia.
2. Metoda polegająca na "odgadywaniu" pierwiastków. Powołujemy się w niej na następujące twierdzen
Pierwiastkami całkowity
ie:
mi wielomianu o współczynnikach całkowitych mogą być jedynie dzielniki
yrazu wolnego.
3.
Jeżeli liczba a jest
tkiem
wić w postaci
przez
w
Metoda "kombinowana" łącząca obie powyższe i opierająca się na twierdzeniu Bezouta:
pierwias
wielomianu
W x
( ) , to wielomian można przedsta
)
(
)
(
)
(
x
P
a
x
x
W
, gdzie
)
(
x
P
jest wielomianem otrzymanym przez podzielenie
x)
W(
a
x
.
Pozostałymi pierwiastkami wielomianu
s wówczas pierwiastki wielomianu
Rozwiązanie. Przyjmując lewą stronę równania przez
mamy kolejno:
tąd pierwiastkami równania są
W x
( ) ą
)
(
x
P
.
Przykład 8. Rozwiązać równanie
2
2
2
3
x
x
x
0
.
)
(
x
W
)
1
)(
1
)(
2
(
)
1
2
(
)
2
(
)
2
2
x
x
x
x
x
.
)(
(
)
(
2
x
x
x
x
W
S
: 1
,
1
,
2
3
2
1
x
x
x
.
Przykład 9. Rozwiązać równanie:
0
6
7
3
x
x
.
Rozwiązanie. Pierwiastków wielomianu poszukujemy wśró
Obliczamy teraz war
i wielomianu dla pod
O
5 8 11
000
11
3200
200
)
(
2
x
x
x
z
X
Y
11 700
Rys. 12.
d podzielników liczby 6:
.
6
,
3
,
2
,
1
tośc
anych liczb:

Wykład 8. Przegląd funkcji elementarnych
6
0
6
7
1
)
1
(
W
,
0
6
7
1
)
1
(
W
zatem pierwiastkiem wielomianu jest
1
1
x
,
0
6
14
8
)
2
(
W
,
6
14
8
)
2
(
0
W
zatem
2
2
x
,
0
6
21
27
)
3
(
W
zatem
3
3
x
.
Ob
ły trzy pierwiastki wielomianu (w tym przypadku nie
o
Przykład 10. Zna
Rozwiązanie. Pierwiastkiem całko
y tutaj
. Ponieważ l
ę bez
liczenia możemy zakończyć, gdyż znalezione zosta
m że ich być więcej).
leźć pierwiastki wielomianu
4
3
)
(
2
3
x
x
x
W
.
witym tego wielomianu może być tylko podzielnik liczby 4. Mam
iczba 1
jest pierwiastkiem wielomianu, to wielomian ten dzieli si
0
)
1
(
,
0
)
1
(
W
W
4
4
4
4
0
4
4
0
3
(
4
4
2
2
3
2
x
x
x
x
x
x
x
x
x
x
x
x
1
x
reszty przez
. Dzielenie to przedstawione jest obok. Mamy
.
i wielomianu są
)
1
(
:
) x
zatem
2
3
2
2
)
2
)(
1
(
)
4
4
)(
1
(
)
(
x
x
x
x
x
x
W
2
2
,
1
x
Pierwiastkam
(pierwiastek podwójny)
2
i 1
3
x
.
4
4x
Uwaga. Jeżeli w rozkładzie wielomianu na czynniki liniowe lub kwadratowe o
0
czynnik
a
x
występuje dokładnie k razy, to liczbę a nazywamy pierwiastkiem k-krotnym.
wielomianu niezbędnego do znal
Uwaga.
Kolejne kroki przy szkicowaniu wykresu
ezienia rozwiązań
przypadku
jest parzystej krotności.
- leżała w przedziale
)
powyżej osi OX , gdy współczynnik
jest dodatni (
oznacza
m przypadku.
11.
Rozwiązać nierówność
Rozwiązanie: Pr
ijmy oznaczenie
. Wielomian można przedstawić
powyższej
Odp: Rozwiązania nierówności stanowią zbiór:
nierówności wielomianowych (algebraicznych):
1. Nanosimy na oś OX wszystkie pierwiastki wielomianu (zaznaczając ich krotność).
ty prowad
2. Przez naniesione punk
zimy linię tak, aby
- przecinała ona oś w
pierwiastka nieparzystej krotności,
- „dotykała” osi lecz jej nie przecinała w przypadku, gdy pierwiastek
(
,
x
a
n
x
max
max
największy z pierwiastków) i poniżej w przeciwny
Przykład
: 0
12
20
7
2
2
3
4
x
x
x
x
.
zyjm
12
20
7
2
)
(
2
3
4
x
x
x
x
x
W
w postaci:
2
( ) (
2) (
1)(
3)
W x
x
x
x
. P
3
,
1
4
3
x
x
.
ierwiastkami tego wielomianu są więc:
,
2
2
1
x
x
Wykres wielomianu sporządzony z uwzględnieniem
uwagi przedstawiony jest na rys.13.
}
2
{
1
;
3
.
Wielomian stopnia 3 postaci
dla
służy w wielu
iększenia produkcji o jedną tonę od wartości x do wartości
jest równy
X
1
2
-3
Rys. 13.
d
cx
bx
ax
y
2
3
ac
b
c
b
a
3
,
0
,
0
,
0
2
przypadkach do opisu kosztów całkowitych.
Przykład 12. Koszt produkcji x ton materiału wybuchowego wynosi
186
2
)
(
x
x
x
x
K
Dla jakiej wartości x koszt zwiększenia produkcji tego materiału o jedną tonę będzie najmniejszy?
100
33
2
3
.
1
x
Rozwiązanie. Koszt zw

Wykład 8. Przegląd funkcji elementarnych
7
)
100
186
33
2
(
100
)
1
(
33
)
1
(
2
)
(
)
1
(
)
(
2
3
3
x
x
x
x
x
x
K
x
K
x
f
.
Po przekształceniach 155
60
6
)
(
2
x
x
x
f
.
Jest to funkcja kwadratowa osiągająca minimum dla
)
1
(
186
x
5
2
0
a
b
x
. Oznacza to, że koszt zwiększenia
produkcji materiału wybuchowego o jedną tonę będzie najmniejszy przy przejściu od 5 do 6 ton. Wykresy
obu funkcji przedstawione zostały na rys.14. i rys.15.
O 5
100
186
33
2
)
(
2
3
x
x
x
x
K
455
100
Y
X
Rys. 14. Ry
O 5
155
60
6
)
(
2
x
x
x
f
155
5
Y
X
s. 15.
y funkcję postaci
4. Funkcje wymierne
)
(
)
(x
P
Funkcją wymierną
nazywam
x
Q
y
, gdzie
ą wielomianami.
Dziedziną funkcji jest zbiór
, gdzie
ą wszystkimi różnymi między
b
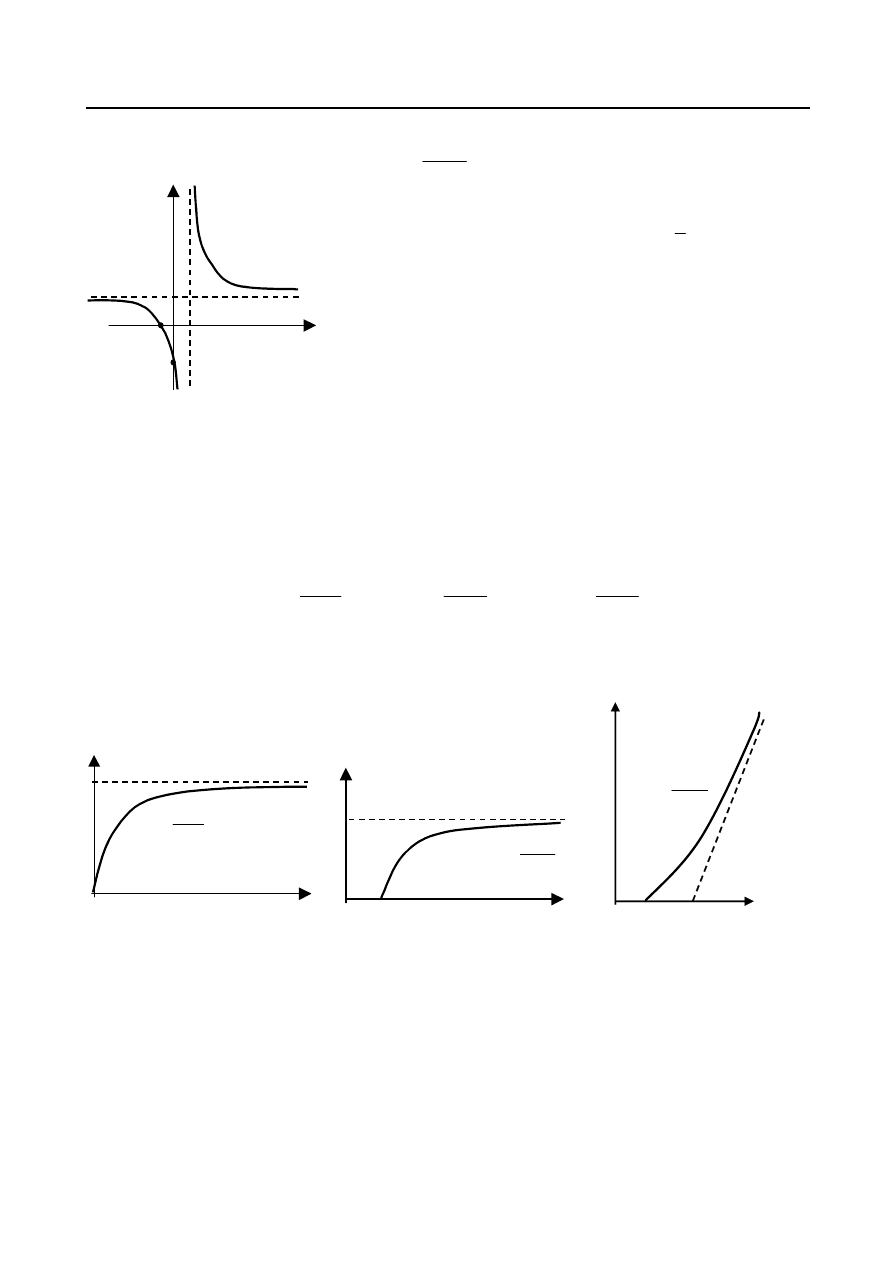
Szczególnym przypadkiem funkcji wymiernej jest funkcja zwana funkcją homograficzną. Jest to funkcja
P x
Q x
( )
( )
i
s
R x x
x
k
\ { , , ...,
}
1
2
x x
x
k
1
2
, , ...,
s
so ą pierwiastkami wielomianu
Q x
( )
.
postaci
d
cx
b
ax
y
, gdzie a, b, c
nymi liczbami spełniającymi warunki:
c
ad bc
0
0
,
.
Dziedziną funkcji jest zbi
, d są da
ór
}
{
\
d
, wykresem - krzywa zwana hiperbolą, której asymptotami są:
asymptotą poziomą - prosta
c
R
c
a
y
(równanie to powstaje przez podzielenie współczynników stojących przy
miennej x), asymptotą pionową - prosta
c
d
z
x
(równanie to otrzymujemy przyrównując mianownik do
zera). Hiperbola jest symetryczna względem punktu przecięcia się asymptot (rys.16.).
c
d
x
c
a
y
X
Y
ad bc
0
c
d
x
c
a
y
X
Y
0
bc
ad
Rys. 16
Wykład 8. Przegląd funkcji elementarnych
8
Przykład 13.
Naszkicować wykres funkcji
1
2
2
x
x
y
.
1
x
2
y
X
Y
Q
P
Rozwiązanie: Dana funkcja jest funkcją homograficzną.
2
1
2
y
Asymptotą poziomą tej funkcji jest prosta
.
Przyjmując
0
1
x
uzyskujemy równanie asymptoty
pionowej
1
x
0
. Gdy
x
2
, to
y
0
y
1
, gdy
, to
x
2
,
0
(
.
Oznacza to, że hiperbola przecina osie w punktach
P
),
Q
)
0
,
1
(
. Na tej podstawie kreślimy gałąź
leżącą w III ćwiartce. Gałąź leżąca w I ćw. jest symetryczna
względem punktu przecięcia się asymptot. Wykres funkcji
przedstawiony jest na rys.17.
Rys. 17
Dobra nabywane przez konsumentów można podzielić na 3 grupy:
1. dobra pierwszej potrzeby nabywane nawet przy bardzo niskich dochodach (chleb, sól),
2. dobra wyższego rzędu (meble, słodycze, owoce),
3. dobra luksusowe (samochód, willa).
Badając zależność popytu na te dobra od dochodów ludności szwedzki ekonomista Törnquist postawił
hipotezę, że zależności te opisują następujące funkcje:
1
1
1
)
(
b
x
x
a
x
T
,
2
2
2
2
)
(
b
x
c
x
a
x
T
,
3
3
3
3
)
(
b
x
c
x
x
a
x
T
,
gdzie
są pewnymi stałymi dodatnimi charakteryzującymi dane dobro.
3
3
3
2
2
2
1
1
,
,
,
,
,
,
,
c
b
a
c
b
a
b
a
Wykresy funkcji Törnquista, z których dwie pierwsze są funkcjami homograficznymi, przedstawione
zostały na rys.18.
Y
X
1
1
b
x
x
a
y
1
a
2
c
2
2
2
b
x
c
x
a
y
X
Y
2
a
X
Y
3
3
3
b
x
c
x
x
a
y
3
3
3
c
b
c
Rys. 18.
Kształt krzywych będących wykresami funkcji Törnquista odzwierciedla ogólne tendencje zachowania
się konsumentów w zależności od wysokości dochodów. Przy niskim poziomie dochodu większość
wydatków przeznacza się na dobra pierwszej potrzeby. Wzrastają one w miarę zwiększania się dochodów
dążąc do poziomu nasycenia . Przy wyższych dochodach równych
c zaczynają pojawiać się wydatki na
dobra wyższego rzędu, które rosną osiągając poziom nasycenia
a . Wreszcie po osiągnięciu poziomu
dochodu pojawiają się wydatki na dobra luksusowe, które w przeciwieństwie do poprzednich wzrastają
nieograniczenie.
1
a
2
2
3
c
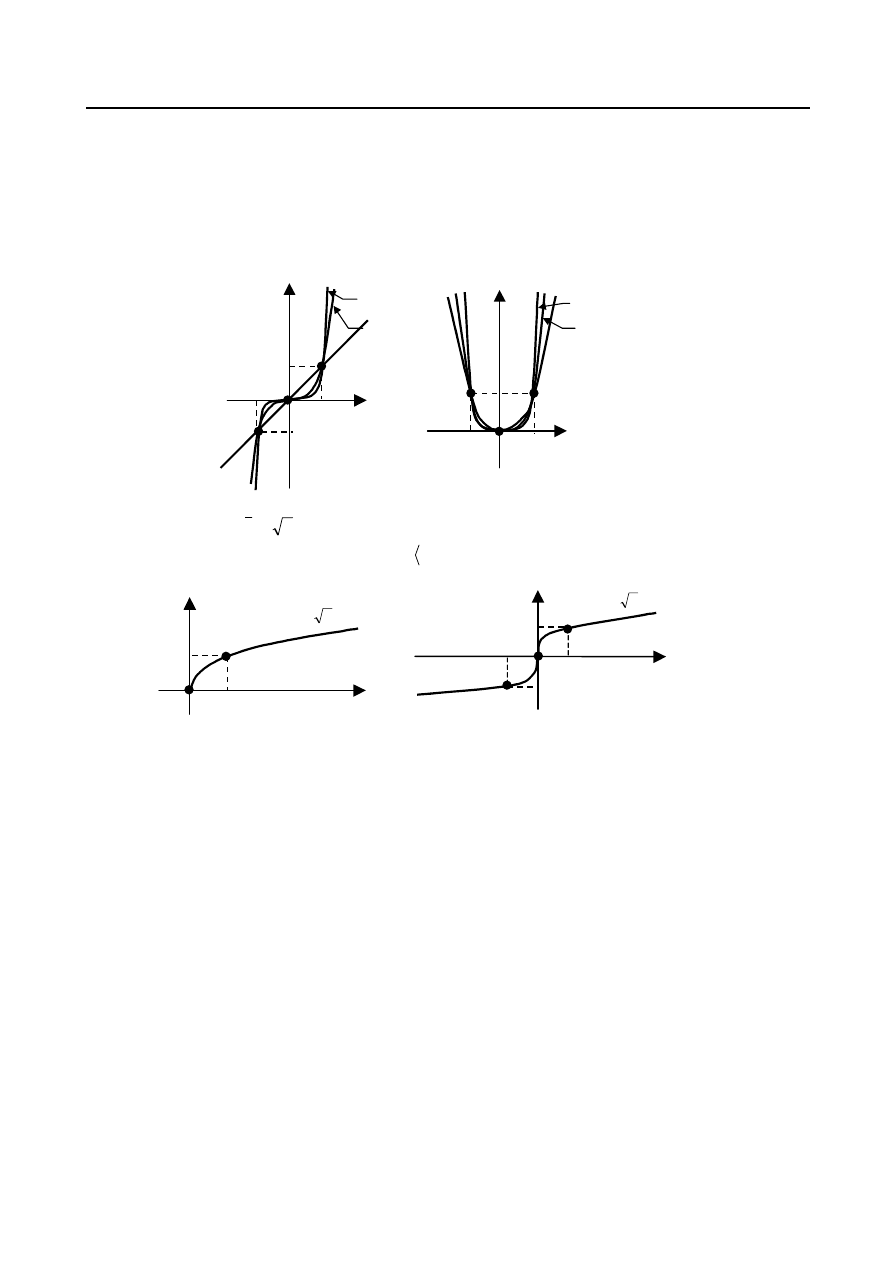
Wykład 8. Przegląd funkcji elementarnych
9
5. Funkcje potęgowe
Funkcję postaci
, gdzie
x
y
0
jest daną liczba rzeczywistą , nazywamy funkcją potęgową.
Dziedzina tej funkcji i jej własności zależą od wykładnika
. Jeżeli jest on liczbą naturalną (
n
), to
dziedziną funkcji jest zbiór
R, przy tym dla n parzystych jest to funkcja parzysta, dla nieparzystych -
nieparzysta. Wykresy niektórych funkcji o wykładnikach naturalnych przedstawione zostały na rys.19.
Y
y
x
5
y
x
6
y
x
4
y
x
2
Y
X
y
x
3
y
x
X
1
1
1
–1
1
–1
–1
Rys. 19.
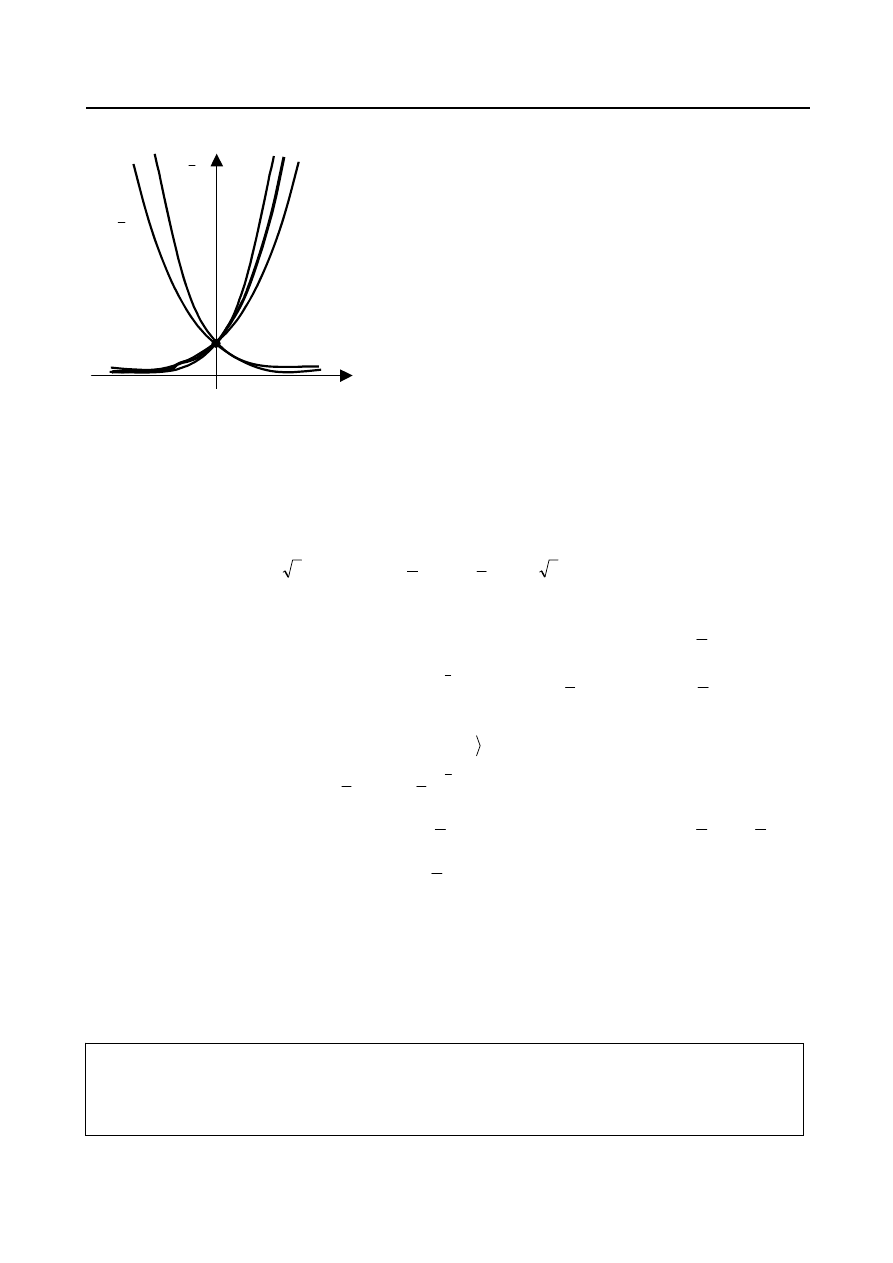
Funkcja postaci
n
n
x
x
y
1
, gdzie
jest liczba naturalną, jest dla nieparzystych n określona
w zbiorze R, dla parzystych - tylko w przedziale
2
n
)
;
0
. Na rys.20. przedstawione zostały dwa wykresy
funkcji tego typu.
Y
X
y
x
1
1
Y
X
y
x
3
1
–1
1
–1
Rys. 20
Funkcja
postaci
przy
znajduje zastosowanie w analizie rynku przy badaniu popytu
na nowowprowadzone dobro. Przy
b
ax
y
1
,
0
b
a
,
0
0
b
a
służy do opisu zależności między wydajnością pracy
robotników a czasem dojazdu do pracy.
6. Funkcje wykładnicze
Funkcją wykładniczą nazywamy funkcję postaci
, gdzie a jest daną liczbą rzeczywistą
spełniającą warunek
x
a
y
1
0
a
.
Wykresy niektórych funkcji wykładniczych przedstawione zostały na rys.21.
Dziedziną każdej funkcji wykładniczej jest zbiór R , przeciwdziedziną - przedział
( ;
. Funkcja jest
monotoniczna: rosnąca gdy
, malejąca gdy
a
)
0
a
1
1
(jest więc funkcją różnowartościową).
Szczególnie ważną rolę w analizie matematycznej odgrywa funkcja
x
e
y
Wykład 8. Przegląd funkcji elementarnych
10
Y
X
x
e
y
x
y 3
x
y
)
(
2
1
x
y 2
x
y
)
(
3
1
1
Rys. 21.
Uwaga.
Konsekwencją monotoniczności funkcji
wykładniczych są następujące równoważności, które
wykorzystujemy przy rozwiązywaniu równań i nierówności
wykładniczych:
2
1
2
1
x
x
a
a
x
x
,
,
1
dla
,
1
dla
2
1
2
1
2
1
a
x
x
a
x
x
a
a
x
x
Równania lub nierówności, w których niewiadoma występuje tylko w wykładniku potęgi nazywamy
wykładniczymi.
Aby rozwiązać takie równanie albo nierówność należy (wystarczy):
1. Przedstawić wyrażenia po obu stronach równania lub nierówności jako potęgi o tej samej podstawie.
2. Uwolnić się od podstaw (zmieniając znak nierówności w przypadku podstawy z przedziału )
1
;
0
(
).
3. Rozwiązać otrzymane równanie lub nierówność.
Przykład 14.
Rozwiązać równania lub nierówności:
a)
, b)
81
3
2
1
x
3
1
3
e
e
x
, c)
2
1
2
4
x
,
d)
3
3
1
2
4
)
(
x
.
Rozwiązanie.
a) Prawą stronę równania zapiszemy w postaci potęgi liczby 3. Mamy zatem:
. Tym
samym po uwolnieniu się od podstawy
4
2
1
3
3
x
4
2
1
x
. Rozwiązaniem równania jest więc
2
3
x
.
b) Równanie to jest równoważne równaniu:
3
1
1
3
e
e
x
. Zatem
3
1
1
3
x
i ostatecznie
9
4
x
.
c) Nierówność tę można zapisać w postaci:
1
4
2
2
x
, z której wnioskujemy, że 1
4
. Tym samym
zbiorem rozwiązań nierówności jest przedział
x
5
;
(
.
d) Zapisując nierówność w postaci
2
1
2
4
)
(
)
(
3
1
3
1
x
po opuszczeniu podstawy z uwzględnieniem, że jest
ona liczbą z przedziału )
1
;
0
(
, mamy
2
1
2
4
x
. Stąd kolejno otrzymujemy
2
9
2
x
,
4
9
x
.
Zbiorem rozwiązań nierówności jest przedział
)
;
4
9
(
.
Funkcjami
wykładniczymi postaci
przy
, posługujemy się w badaniach dynamiki
dochodu narodowego, a także przy badaniu popytu na nowe dobra.
bx
ae
x
f
)
(
,
0
a
7. Funkcje logarytmiczne
Logarytmem liczby dodatniej b przy podstawie a
, gdzie
0
a 1
, nazywamy wykładnik potęgi, do
której należy podnieść a, aby otrzymać b. Zatem przy powyższych założeniach
b
a
t
b
t
a
log
.
Wykład 8. Przegląd funkcji elementarnych
11
Przykład 15.
Obliczyć wartości logarytmów: a)
, b)
32
log
2
2
log
2
, c)
9
1
log
3
, d)
2
2
log
2
1
.
Rozwiązanie.
Bezpośrednio z definicji wynika, że
a) , ponieważ
,
b)
5
32
log
2
32
2
5
2
1
2
log
2
, ponieważ
2
2
2
1
,
c)
2
9
1
log
3
, ponieważ
9
1
3
2
, d)
2
3
, poniew
2
2
log
2
1
aż
2
2
)
2
1
(
2
3
.
Przykład 16.
Obliczyć wartości logarytmów: a)
, b)
e
ln
e
ln
,
c)
3
1
ln
e
.
Logarytm liczby dodatniej b przy podstawie e nazywamy logarytmem naturalnym i oznaczamy
.
b
ln
b
e
t
b
t
ln
.
Rozwiązanie.
Na podstawie definicji logarytmu naturalnego mamy
a) , ponieważ
, b)
1
ln
e
e
e
1
2
1
ln
e
, ponieważ
e
e
2
1
, c)
3
1
ln
, ponieważ
3
e
3
3
1
e
e
.
Własności logarytmów
1. Każdą liczbę t można zamienić na logarytm o danej podstawie a , ( 0
1
a
) korzystając z zależności:
t
a
a
t
log
.
2. Każdą liczbę dodatnią m można przedstawić w postaci potęgi o danej podstawie a , (
):
1
0
a
m
a
a
m
log
3. Dla dowolnych liczb dodatnich x, y i dowolnego n przy danej podstawie a ,
, zachodzą
wzory:
1
0
a
a) log
,
b)
y
x
y
x
a
a
a
log
log
)
(
y
x
y
x
a
a
a
log
log
log
, c)
.
x
n
x
a
n
a
log
log
Funkcją logarytmiczną nazywamy funkcję postaci
x
y
a
log
, gdzie a jest daną liczbą zwaną podstawą,
spełniającą warunek
1
0
a
.
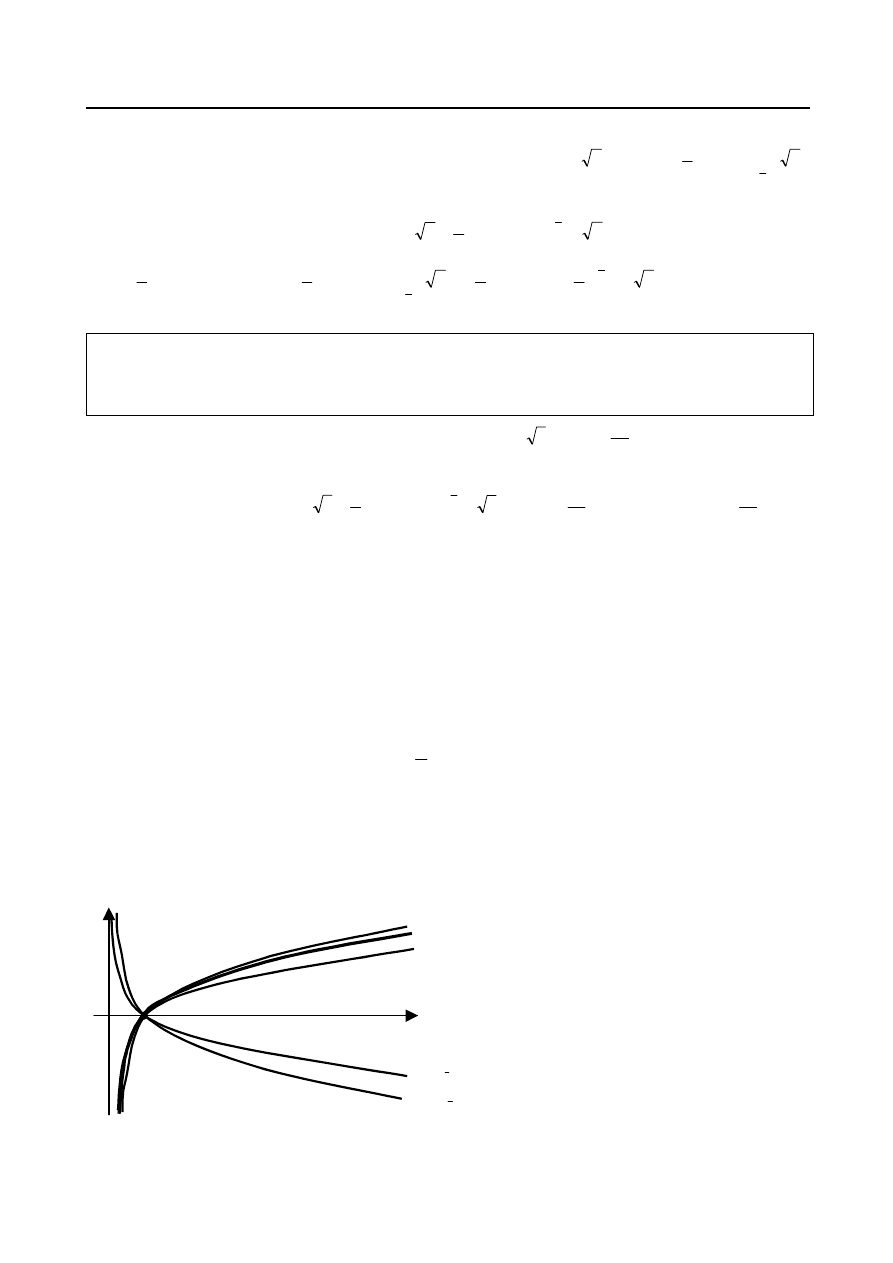
Wykresy niektórych funkcji logarytmicznych przedstawione zostały na rys.22.
Y
X
y
x
log
2
x
y
ln
y
x
log
3
y
x
log
1
3
y
x
log
1
2
Dziedziną każdej funkcji logarytmicznej
jest przedział
)
;
0
(
, zbiorem wartości
zbiór R. Funkcja jest monotoniczna:
rosnąca gdy
, malejąca gdy
(w obu przypadkach jest więc
różnowartościowa).
1
a
1
a
1
Rys. 22.
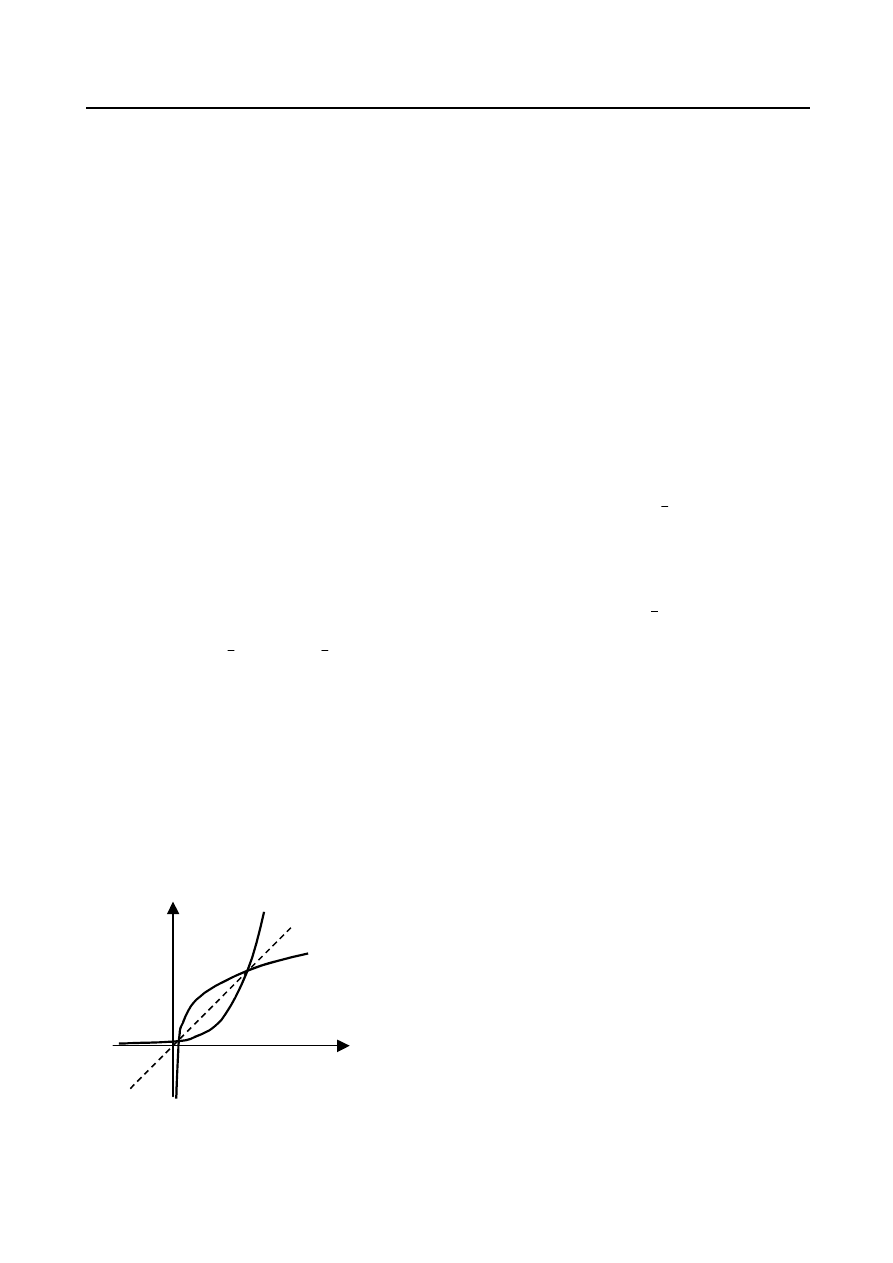
Wykład 8. Przegląd funkcji elementarnych
12
Uwaga.
Konsekwencją monotoniczności funkcji logarytmicznej są następujące równoważności ,
zachodzące dla dodatnich argumentów, wykorzystywane przy rozwiązywaniu równań i nierówności
logarytmicznych:
2
1
2
1
log
log
x
x
x
x
a
a
.
log
log
,
.
a
a
x
x
x
x
a
x
x
a
1
2
1
2
1
2
1
0
1
dla
dla
3
Równania lub nierówności, w których niewiadoma występuje tylko w wyrażeniach logarytmowanych
nazywamy logarytmicznymi. Aby rozwiązać takie równanie lub nierówność należy (wystarczy):
1. Wyznaczyć dziedzinę równania lub nierówności zakładając, że wszystkie wyrażenia logarytmowane
zawierające niewiadomą są dodatnie.
2. Obie strony zapisać w postaci logarytmów o identycznych podstawach (wykorzystując własność 1.).
3. Uwolnić się od logarytmów zmieniając ewentualnie znak w przypadku nierówności i podstawy
z przedziału )
1
;
0
(
.
4. Rozwiązać otrzymane równanie lub nierówność, a następnie odrzucić rozwiązania nie należące do
dziedziny.
Przykład 17. Rozwiązać równania lub nierówności: a)
log (
)
2
2
x
, b) log (
)
1
2
2
2
x
Rozwiązanie.
a) Dziedziną równania jest D
x R x
{
:
) ( ;
2 0
2
2
8
)
8
. Zapisując liczbę 3 w postaci
mamy
. Stąd po uwolnieniu się od logarytmu otrzymujemy
3
2
log
log (
) log
2
2
x
x
2 8 . Zatem
rozwiązaniem jest x
10 .
D
x R
x
b) Dziedziną nierówności jest
{
:
) (
; )
2
0
2 . Ponieważ
2
1
2
log 4 , to nierówność
przyjmuje postać log (
)
1
2
x
log
1
2
2
4
. Opuszczając logarytm, przy uwzględnieniu, że jego podstawa jest
liczbą z przedziału mamy
)
1
;
0
(
2
4
x
. Stąd x
2 . Ponieważ rozwiązania nierówności muszą należeć
do zbioru D, to ostatecznie rozwiązaniem danej nierówności jest przedział (
; )
2 2 .
Funkcją logarytmiczną postaci
0
,
0
,
0
),
ln(
c
b
a
c
x
b
a
y
posługujemy się do opisu kosztów całkowitych oraz do opisu zależności indywidualnej wydajności pracy od
stażu pracy w danym zawodzie.
Przykład 18.
Wyznaczyć w postaci
funkcję odwrotną do
)
(
1
x
f
y
)
(x
f
y
. Naszkicować wykresy
obu funkcji: a)
b)
2
3
)
(
x
x
f
)
2
ln(
)
(
x
f
x
. Rozwiązanie.
2
log
)
(
3
1
x
x
f
2
3
)
(
x
x
f
a) Dokonując we wzorze danej funkcji
zamiany
zmiennych otrzymujemy równanie
, które
można zapisać w postaci
. Stąd
2
3
x
y
2
3
y
x
2
y
log
3
3
3
x
x
y
3
log
2
i ostatecznie funkcją odwrotną jest
2 . Wykresy obu funkcji
przedstawia rys.23.
)
(
1
x
f
y
log
3
x
Rys. 23.
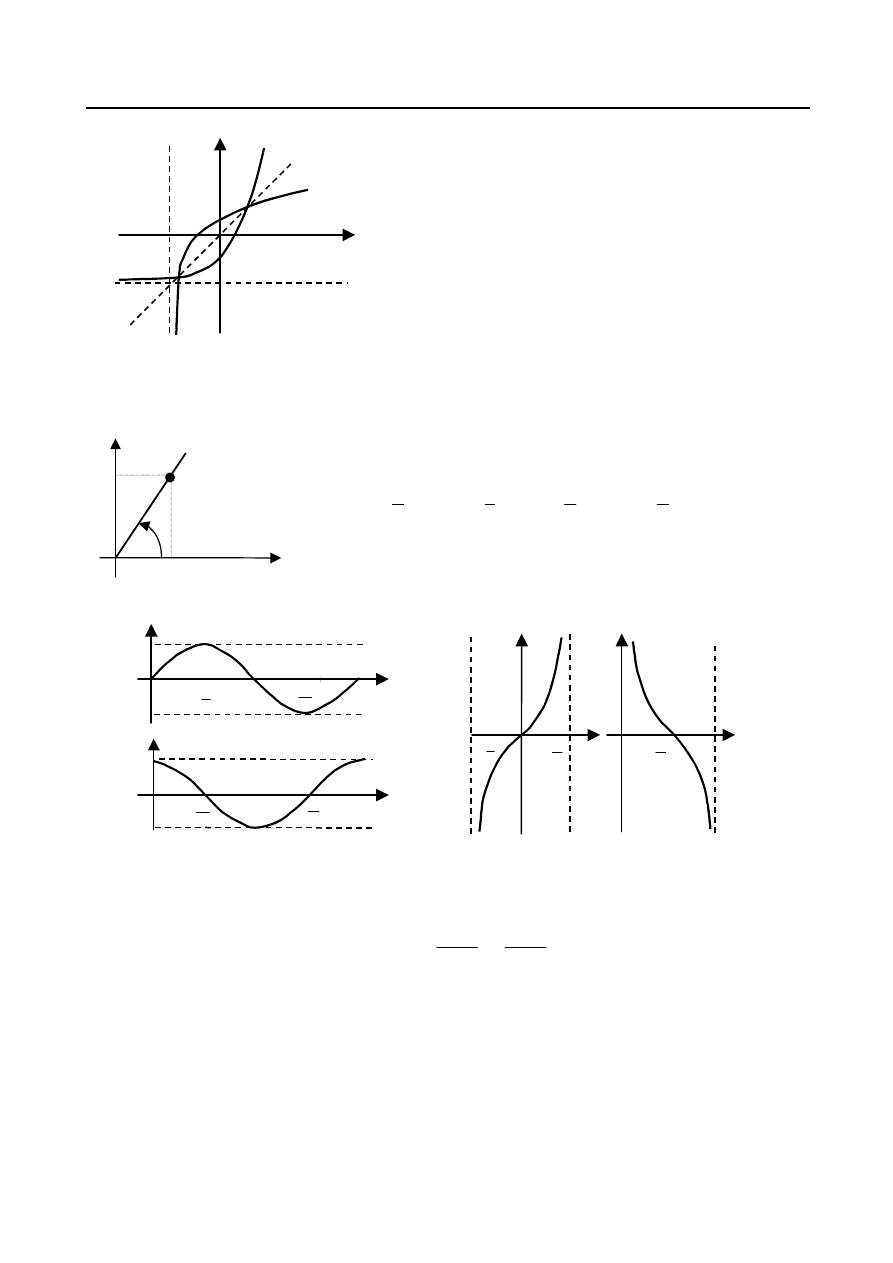
Wykład 8. Przegląd funkcji elementarnych
13
2
)
(
1
x
e
x
f
)
2
ln(
)
(
x
x
f
–
2
–
1
–
2
–
1
X
Y
)
2
ln(
x
y
b) Daną funkcję można zapisać w postaci
.
Po zamianie zmiennych otrzymujemy równanie
)
2
ln(
y
x
x
e
y
. Powołując się na definicję logarytmu
otrzymujemy
. Stąd funkcja odwrotna ma
postać: . Wykresy obu funkcji przedstawia
rys.24.
x
e
y
2
2
Rys. 24.
8. Funkcje trygonometryczne i cyklometryczne
Niech
x
oznacza miarę kąta skierowanego
TOM
na płaszczyźnie TOY (rys.25).
M t y
( , )
Y
T
O
t
y
x
r
Funkcje trygonometryczne określamy wtedy następująco:
r
y
x
sin
r
t
x
cos
t
y
x
tg
y
t
x
ctg
,
,
,
.
Wykresy funkcji trygonometrycznych przedstawione zostały
na rys.26.
Rys. 25.
Y
X
y
x
sin
y
x
cos
Y
1
0
1
X
2
2
2
3
2
3
2
2
-1
0
-1
Y
X
y
x
tg
Y
y
x
ctg
2
2
2
0
X
Rys. 26.
Dziedziną funkcji sinus i cosinus jest zbiór R. Funkcje te są ograniczone, bowiem dla każdego
R
x
mamy: oraz
1
sin
1
x
1
cos
1
x
.
Funkcja
tangens
określona jest na przedziałach
)
(
2
1
2
;
2
1
2
k
k
, funkcja cotangens - na
przedziałach )
)
1
(
;
(
k
k
, gdzie k jest dowolną liczbą całkowitą.
Funkcje trygonometryczne są okresowe. Okresem podstawowym funkcji sinus i cosinus jest liczba
2 ,
co oznacza, że dla każdego
zachodzą warunki:
R
x
x
x
sin
)
2
sin(
,
x
x
cos
)
2
cos(
.
Okresem podstawowym funkcji tangens i cotangens jest liczba
. Oznacza to, że dla x pochodzących z
odpowiedniego zbioru mamy:
x
x
tg
)
(
tg
,
x
ctg
x
)
(
ctg
.
Funkcja cosinus jest parzysta, tzn.
x
x
cos
)
cos(
dla każdego
R
x
. Pozostałe funkcje
trygonometryczne są nieparzyste, tzn. dla odpowiednich x zachodzą wzory:
x
x
sin
)
sin(
,
x
x
tg
)
(
tg
,
.
x
x
ctg
)
(
ctg
Wykład 8. Przegląd funkcji elementarnych
14
Funkcje
trygonometryczne
x
y
x
y
x
y
x
y
ctg
,
tg
,
cos
,
sin
nie są funkcjami różnowartościowymi w swoich naturalnych dziedzinach. Są jednak różnowartościowe
odpowiednio na zbiorach:
)
;
0
(
,
2
;
2
,
;
0
,
2
;
2
)
(
a ich przeciwdziedzinami są odpowiednio:
R
R
,
,
1
;
1
,
1
;
1
.
Dla tak zawężonych funkcji trygonometrycznych istnieją więc funkcje odwrotne. Funkcje te nazywamy
funkcjami cyklometrycznymi
odpowiednio: arcus sinus, arcus cosinus, arcus tangens, arcus cotangens.
Mamy zatem
y
x
x
y
sin
arcsin
,
y
x
x
y
cos
arccos
,
y
x
x
y
tg
arctg
,
y
x
x
y
ctg
arcctg
.
Przykład 19.
Obliczyć: a)
2
3
arcsin
,
b)
)
1
(
arcsin
, c)
2
1
arccos ,
d)
3
arctg
.
Rozwiązanie. Na podstawie definicji funkcji cyklometrycznych otrzymujemy
a)
3
2
3
arcsin
, ponieważ
2
3
3
sin
i
2
;
2
3
,
b)
2
)
1
(
arcsin
, ponieważ
1
)
2
sin(
i
2
;
2
2
,
c)
3
2
1
arccos
, ponieważ
2
1
3
cos
i
;
0
3
,
d)
3
3
arctg
, ponieważ
3
3
tg
i
)
2
;
2
(
3
.
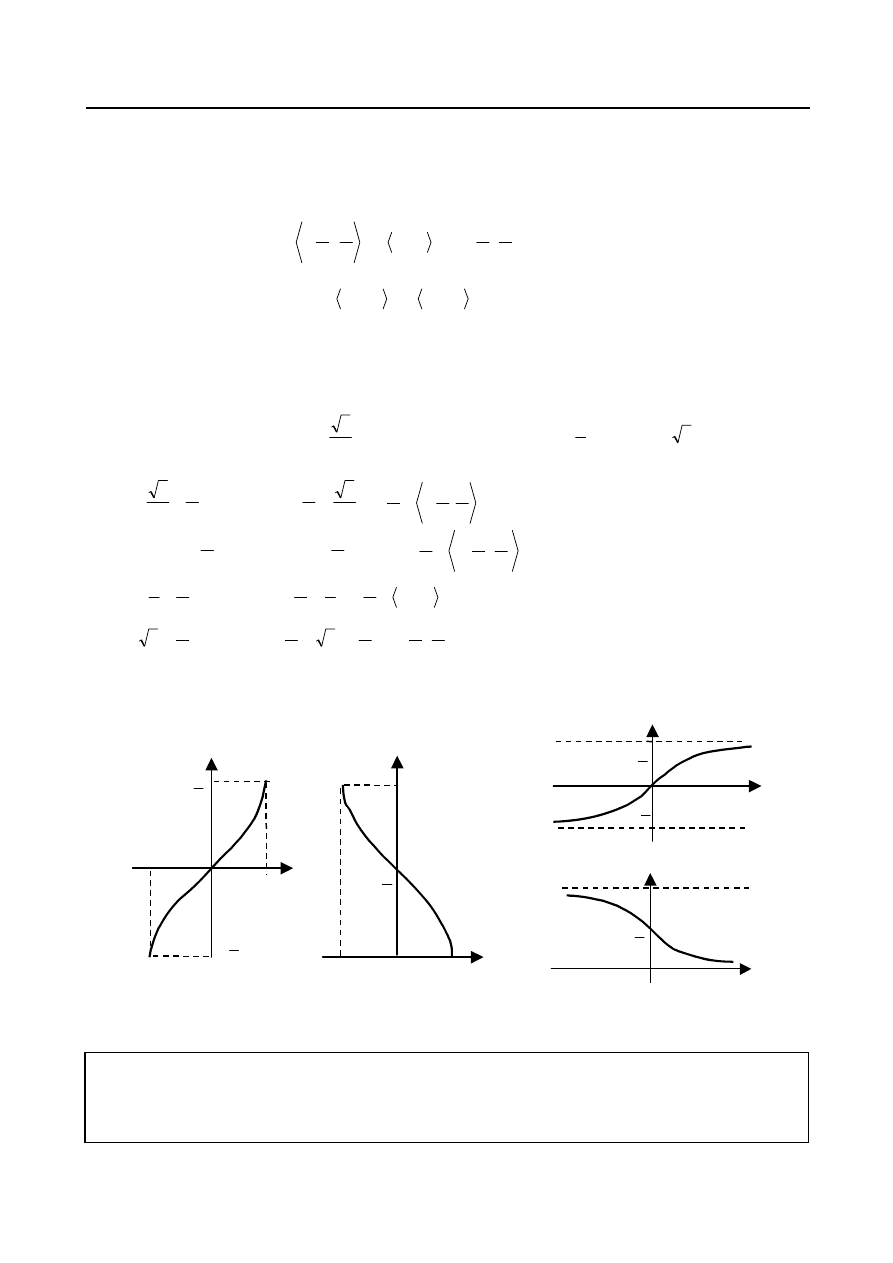
Wykresy funkcji cyklometrycznych przedstawione zostały na rys.27.
X
y
x
arcsin
Y
X
y
x
arccos
2
2
2
1
1
1
Y
1
Y
X
y
x
arctg
Y
X
y
x
arcctg
2
2
2
Rys. 27.
Uwaga.
Funkcje, które można otrzymać z funkcji stałych, wielomianów, funkcji potęgowych,
wykładniczych, logarytmicznych , trygonometrycznych i cyklometrycznych wykonując skończoną liczbę
działań typu: dodawanie, odejmowanie, mnożenie, dzielenie i składnie funkcji nazywamy funkcjami
elementarnymi
(w szerszym sensie).
Document Outline
Wyszukiwarka
Podobne podstrony:
FiR matma w2N
FiR Matma w7 2011
FiR matma 11
FiR matma L6
FiR matma 6
FiR matma L4
FiR matma 07
FiR matma L7 8
FiR matma L13 id 172577 Nieznany
FiR matma w10 2011
FiR matma 5 id 172575 Nieznany
FiR matma 14
FiR matma w11N
FiR matma L3
FiR matma 4 id 172574 Nieznany
FiR matma L14
FiR matma 13
FiR matma L2
więcej podobnych podstron