Wyrównanie obserwacji bezpośrednich. Podstawowe definicje i oznaczenia

Zdefiniujemy pewne pojęcia, którymi często będziemy się posługiwali.

Błędem prawdziwym
, i-tej obserwacji
nazywamy różnicę między wartością prawdziwą L mierzonej wielkości, a wartością zaobserwowaną:

Błędem pozornym
albo poprawką i-tej obserwacji nazwiemy różnicę między wartością najbardziej prawdopodobną
mierzonej wielkości, a wartością zaobserwowaną

Z powyższych określeń wynika, że błędami prawdziwymi można operować w tych przypadkach, gdy znana jest wartość prawdziwa mierzonej wielkości. Błędami pozornymi posługujemy się wtedy, gdy wartość prawdziwa nie jest znana, lecz potrafimy obliczyć wartość bliską prawdziwej, którą nazywa się powszechnie wartością najprawdopodobniejszą. W przypadku, gdy dokonujemy wielokrotnych pomiarów tego samego elementu geometrycznego, np. kąta, długości za wartość najprawdopodobniejszą uważamy średnią arytmetyczną uzyskanych wyników.

Przykład. Wykonano trzykrotny pomiar trzech kątów trójkąta otrzymując następujące wyniki:

1	70°02'	50°18'	59°36'
2	70°01'	50°20'	59°37'
3	70°04'	50°19	59°58'

Obliczyć błąd prawdziwy sumy kątów trójkąta dla każdej z trzech serii.

Ponieważ wartość prawdziwa sumy kątów w trójkącie wynosi L = 180°, natomiast z obserwacji otrzymaliśmy odpowiednio
;
,
, więc otrzymamy następujące wartości dla błędów prawdziwych:

;
,

Przykład. Pomiar kąta, którego wartości prawdziwej nie znamy, dał następujące wyniki: 37°05', 37^o05'; 37°01'. Obliczyć błędy pozorne obserwacji.

Jako wartość ostateczną mierzonego kąta przyjmiemy średnią arytmetyczną z uzyskanych wyników. Wynosi ona
skąd, mamy:

,
,

Jak widać każdy z obliczonych błędów prawdziwych, czy pozornych, dotyczy odpowiedniej i tylko jednej obserwacji. W pierwszym przykładzie obserwacją jest każda z trzech zmierzonych sum kątów trójkąta; w przykładzie drugim za obserwację uważamy każdy z trzech uzyskanych wyników.

Przykład wprowadzający. Załóżmy, że oddając do tarczy serię 100 strzałów, każdy z dwóch strzelców uzyskuje przeciętnie następujące wyniki:

	I strzelec			II strzelec
Liczba uzyskanych punktów	5	2	1	3	2	1
Liczba trafień	70	15	15	60	40	0

Postawmy sobie zadanie wyznaczenia kryterium liczbowego, które pozwoliłoby dać odpowiedź na pytanie, który z nich jest lepszy? Za liczbę charakteryzującą jakość każdego ze strzelców przyjmiemy średnią ilość punktów przypadającą na jeden strzał każdego z nich. Łatwo, bowiem można policzyć liczbę punktów uzyskiwanych średnio w 100 strzałach. Wynosi ona:

dla I strzelca P_I = 5 • 70 + 2 • 15 + 1 • 15 = 255;

dla II strzelca P_II =3 • 60 + 2 • 40 + 0 • l = 260.

Stąd już widać, że pierwszy strzelec jednym strzałem uzyskuje przeciętnie 2,55 punktu, zaś drugi 2,60 punktu. Uznamy, więc, że drugi jest lepszy.

Rozpatrzmy teraz zadanie formalnie podobne do powyższego, lecz dotyczące teorii błędów. Załóżmy, że pewien kąt pomierzono w dwóch seriach wykonu­jąc po 100 obserwacji w każdej z nich, a następnie obliczono błędy prawdziwe uzyskanych wyników i zestawiono je w dwóch tabelach, oddzielnie dla każdej serii, otrzymując:

I seria	-1"	0"	+1"		II seria	-10"	0	+10"
Ilość wystąpień	25	50	25			Ilość wystąpień	25	50	25

Jak na tej podstawie ocenić, który z tych dwóch zespołów obserwacji jest lepszy? Gdybyśmy chcieli rozumować analogicznie jak w zadaniu poprzednim to należałoby obliczyć średnią wartość błędu prawdziwego dla każdej serii i dwie otrzymane liczby porównać. Tą serię, której średnia wartość błędu prawdziwego byłaby większa uznalibyśmy za gorszą. Zauważmy, że kryterium to nie nadaje się jednak do charakterystyki jakości tych dwóch zespołów obserwacji. Średnia wartość błędu prawdziwego v; obu przypadkach jest równa zeru, chociaż widać wyraźnie, że drugi pomiar dał wyniki gorsze. Przypadek ten jest charakterystyczny dla błędów pomiarów geodezyjnych. Zestawiając szeregi błędów prawdziwych wielkości zmierzonej n-krotnie, widzimy, że przy dużych wartościach n = 500; 400; 500 obserwacji wystąpi, w przybliżeniu, ta sama liczba błędów dodatnich i ujemnych mających tę samą wartość bezwzględną. Zmusza nas to do wybrania innego kryterium liczbowego charakteryzującego jakość zespołu obserwacji. Musimy je zdefiniować w ten sposób by zlikwidować wpływ różnych znaków na ostateczny wynik. Obliczmy np. wartość średnią bezwzględnej wartości błędu prawdziwego dla każdej serii. Otrzymamy:

Liczby d_I i d_II nazwiemy błędami przeciętnymi. Jak widać można je przyjąć za liczbowe kryterium jakości obserwacji, choć w geodezji jest ono rzadko stosowane, z następującego powodu.

Często zachodzi konieczność scharakteryzowania jakości pewnej funkcji obserwacji

gdy błędy obserwacji są znane. Zwykle mówi się wtedy, że chcemy obliczyć dokładność funkcji y, znając dokładność argumentów
. Gdybyśmy za miernik dokładności przyjęli błąd przeciętny, okazałoby się, że obliczenie błędu przeciętnego funkcji y na podstawie błędów przeciętnych obserwacji byłoby uciążliwe. Rezygnujemy, więc z błędu przeciętnego i wprowadzimy inaczej zdefiniowaną liczbę jako miernik dokładności zespołu obserwacji. Jest nią wartość średnia kwadratu błędu prawdziwego, którą nazywamy kwadratem błędu średniego i oznaczamy symbolem
, Dla naszego przykładu możemy, więc obliczyć:

skąd otrzymujemy następujące błędy średnie poszczególnych serii:

Możemy teraz powiedzieć, że druga seria jest mniej dokładna, gdyż jej błąd średni jest większy. Okazuje się, że znając błędy średnie obserwacji można obliczyć błąd średni funkcji obserwacji, bowiem, jak to dalej zobaczymy, błąd średni łatwo przenosi się na sumę.

Możemy stwierdzić, że w geodezji, jako kryterium dokładności obserwacji przyjmuje się błąd średni. W przypadku, gdy mamy duży szereg błędów prawdziwych tej samej wielkości, jej błąd średni wyznaczamy z wzoru

.

gdzie n jest liczbą wszystkich błędów prawdziwych rozważanego szeregu.

Nie zawsze istnieje możliwość obliczenia błędów prawdziwych; na ogół nie są nam znane wartości prawdziwe mierzonej wielkości. W tych przypadkach wielokrotny pomiar tego samego elementu geometrycznego pozwala obliczyć błędy pozorne v oraz wyznaczyć błąd średni ze wzoru

.

W niektórych przypadkach, na obliczenie błędu średniego istnieją wzory empiryczne, np.

na wyznaczenie błędu średniego długości.

Prawo przenoszenia się błędów średnich

Wyznaczymy błąd średni funkcji obserwacji

zakładając, że błędy średnie obserwacji są dane i wynoszą odpowiednio
.

Dla funkcji

gdzie a jest stałą, zaś m dane np. obliczone na podstawie szeregu błędów prawdziwych dla konkretnych wartości
funkcja y przybierze wartości
z błędami prawdziwymi równymi odpowiednio
. Błąd średni funkcji y można obliczyć ze wzoru
. Mamy, więc

.

Natomiast błąd średni
funkcji

przy założeniu znajomości błędów średnich
i
obserwacji
i
określony jest wzorem:
.

Wykorzystując powyższe zależności błąd średni funkcji liniowej obserwacji
wyznacza się z zależności:

.

Natomiast błąd średni dowolnej funkcji
wyznaczamy przy założeniu, że jest ona rozwijalna w szereg Taylora. Przyjmując bowiem przybliżone wartości
obserwacji x, y ,..., t , można przedstawić każdą wielkość zaobserwowaną
, jako sumę odpowiadającej jej wartości przybliżonej
i niewielkiego przyrostu df uzależnionego od przyrostów obserwacji
tj.:
. Z wzorów tych wynika, że błąd średni
obserwacji x jest równy błędowi średniemu przyrostu dx, bowiem błąd średni stałej
jest, oczywiście, równy zeru. Stąd, gdy rozwiniemy funkcję f w szereg Taylora w sąsiedztwie punktu
zachowując tylko wyrazy pierwszego rzędu, otrzymamy:

.

(Zauważmy, że wartości pochodnych cząstkowych wyznaczono w punkcie
.)

Jest to przybliżenie liniowe funkcji f o zmiennych
. Ponieważ błędy średnie
tych zmiennych są znane, a błąd średni stałej
jest równy zeru, to można zastosować wzór na błąd średni funkcji liniowej. Otrzymujemy, więc związek

.

Przykład. Obliczyć błąd średni różnicy wysokości w ciągu niwelacyjnym złożonym z
stanowisk, jeśli błąd średni odczytu łaty

Ponieważ przewyższenie na i-tym stanowisku obliczamy jako różnicę:
odczytów wstecz i w przód, dlatego dla n stanowisk będzie:
.

Stosując tu wzór na błąd funkcji liniowej mamy:
.

Przykład. Obliczyć błąd średni boku L = 180 m zmierzonego taśmą 20 m, gdy błąd średni jednego przyłożenia taśmy wynosi m = 1 cm.

Ponieważ uzyskany wynik jest rezultatem dziewięciokrotnego odłożenia taśmy, więc możemy napisać
, gdzie
- i-te przyłożenie taśmy, a
.

Stąd mamy
.

Przykład. Obliczyć błąd średni powierzchni prostokąta o bokach
,
, wiedząc, że
,

Ponieważ
mamy:

Wyrównanie obserwacji bezpośrednich jednakowo dokładnych

Załóżmy, że z tą samą dokładnością pomierzyliśmy n razy pewien element geometryczny otrzymując wyniki:
i chcemy wyznaczyć jeden ostateczny rezultat L tej wielokrotnie zaobserwowanej wielkości. Żądamy przy tym, aby był on w pewnym sensie najlepszy, najbardziej zbliżony do prawdziwego. Należy zwrócić uwagę, że wyrażenie "wynik najlepszy" jest pozbawione ścisłego znaczenia dopóki nie ustali się kryterium tej "najlepszości". Oznaczmy przez v różnicę między nieznaną na razie, wartością najwłaściwszą liczby L, a wartością i - tej obserwacji, czyli

.

Przyjmiemy, że znane jest przybliżenie
wielkości wyznaczanej L, różne od niej o niewielką wartość x. Będzie wtedy

.

Jeżeli oznaczyć
to otrzymamy n równań

,

z których nie da się jednoznacznie wyznaczyć
niewiadomych
bez poczynienia dodatkowych założeń. Wprowadźmy warunek, który pozwoli rozwiązać zadanie jednoznacznie, precyzując tym samym pojęcie najlepszego wyniku L. Wyznaczymy taką wartość
, aby błąd średni pojedynczego spostrzeżenia obliczony ze wzoru

(m1)

przyjął wartość najmniejszą. Wtedy, oczywiście, musi być
minimum, ponieważ n - 1 jest stałe przy ustalonej liczbie obserwacji n. Sprowadziliśmy, więc zadanie do znalezienia minimum funkcji:

,

gdzie:
tj.

.

Skąd, wyznaczając pochodną i przyrównując ją do zera otrzymamy

czyli
, a więc ostatecznie

i

.

Za szukaną wartość L wyznaczaną w oparciu o szereg obserwacji jednakowo dokładnych przyjmiemy, więc średnią arytmetyczną uzyskanych wyników. Uważamy ją za najlepszą w tym sensie, że suma kwadratów różnic
jest najmniejsza.

Różnice te nazwaliśmy błędami pozornymi. Łatwo jest uzasadnić, że suma błędów pozornych jest równa zeru, czyli

.

Ponieważ

skąd po zsumowaniu otrzymamy

.

Błąd średni M średniej arytmetycznej L oblicza się ze następującego wzoru (Dlaczego ? Dowiesz się w dalszej części wykładu.)

.

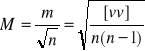
Należy nadmienić, że przy niewielkiej liczbie obserwacji n, wartość m obliczona z wzoru (m1) ma cechę dużej przypadkowości. Lepiej jest wyznaczyć m ze znanego wzoru empirycznego, co w geodezji jest bardzo często możliwe.

Przykład. Zmierzono bok sześciokrotnie otrzymując wyniki zestawione w tabeli. Obliczyć średnią arytmetyczną, jej średni błąd oraz błąd średni pojedynczego spostrzeżenia.

Nr obs.	[m]	[cm]	[cm]
1	214,27	+ 5	- 2,5	6,25
2	,22	0	+ 2,5	6,25
5	,22	0	+ 2,5	6,25
4	,28	+ 6	- 5,5	12,25
5	,25	+ 5	- 0,5	0,25
6	,25	+ 1	+ 1,5	2,25
[t] = 15 [v]= 0,0 [vv] = 35,50

(Aby operować mniejszymi liczbami od wszystkich wyników można odjąć, ten którego wartość jest najmniejsza. W naszym przypadku będzie to
)

;

;

;

.

Wyrównanie obserwacji bezpośrednich o różnej dokładności

Niech będzie dany szereg obserwacji tej samej wielkości
o błędach średnich równych
. Obliczymy najwłaściwszą wartość mierzonej wielkości, jej średni błąd oraz błąd średni tzw. "typowego spostrzeżenia" (tj. spostrzeżenia o wadze p = 1).

Powyższe zadanie można sprowadzić do znanego nam przypadku obserwacji jednakowo dokładnych. Zauważmy, że każdą wartość
można traktować jako średnią arytmetyczną z liczby
jednakowo dokładnych obserwacji o błędzie średnim spostrzeżenia równym
. Będzie, więc

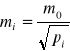
, a stąd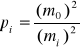

Obserwację
traktujemy, więc jako średnią arytmetyczną z
fikcyjnych, jednakowo dokładnych obserwacji,
będzie średnią arytmetyczną z
fikcyjnych obserwacji o tym samym błędzie średnim
itd. Wynika stąd, że wartość
można wyznaczyć ze wzoru

gdzie
, jest nieznaną nam sumą wartości fikcyjnych, jednakowo dokładnych obserwacji, potrzebnych do wyznaczenia średniej. Poszukiwaną wartość średnią obliczymy, więc jako średnią arytmetyczną ze wzoru:

,

gdzie w liczniku występuje suma wartości wszystkich fikcyjnych obserwacji, natomiast w mianownika liczba tych obserwacji. Otrzymany wynik można też napisać w postaci:

Liczbę L nazywamy ogólną średnią arytmetyczną a
wagą i-tej obserwacji.

W zastosowaniach praktycznych stosuje się inną postać powyższego wzoru. Ponieważ wartości
niewiele odbiegają od, siebie, przeto każdą z nich można przedstawić jako sumę pewnej stałej L oraz niewielkiego przyrostu
, czyli:
. Podstawiając prawą stronę powyższego związku do wzoru otrzymamy:

.

Zwykle za
obiera się najmniejszy z zaobserwowanych wyników.

Z uzyskanych wzorowych wynika, że użycie w rachunku k - krotnych wartości wag nie zmienia wartości ogólnej średniej arytmetycznej. Ponieważ błąd średni typowego spostrzeżenia liczymy ze wzoru:
, gdzie
więc błąd średni M ogólnej (ważonej) średniej arytmetycznej L przedstawia następujący związek:

.

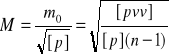
Wynika to z tego, że ogólną średnią arytmetyczną traktujemy jako zwykłą średnią z
jednakowo dokładnych obserwacji. Ze wzoru wynika, że użycie w rachunku k - krotnych wartości wag nie zmienia błędu średniego ogólnej średniej arytmetycznej. Analogicznie jak w przypadku obserwacji jednakowo dokładnych można udowodnić, że [pv] = 0, oraz że błędy pozorne obliczone na podstawie ogólnej średniej arytmetycznej spełniają warunek
.

Przykład. Pomierzono bok poligonowy otrzymując wyniki, które wraz z błędami średnimi zamieszczono w poniższej tabeli. Obliczyć L, m, M.

Nr obs.		m [cm]		[cm]			pv	[cm^2]
1	128,36	4	1	3	3	- 2,1	- 2,1	4,41
2	,34	1	16	1	16	- 0.1	- 1,6	0,16
3	,33	2	4.	0	0	+ 0,9	+ 3,6	3,24
L0 = 128			[p] = 21		[pt] = 19		[pv] = -0,1	[pvv]=7.81

,
,

,

.

Przykład. Pomierzono kąt otrzymując następujące wyniki;

68°32' jako średnia z 2 obserwacji,

68° 34' jako średnia z 4 obserwacji;

68°35' jako średnia z 6 obserwacji.

Obliczyć wartość kąta, błąd średni pojedynczego pomiaru i błąd średni średniej arytmetycznej. Przyjmujemy, że wagi poszczególnych wyników są równe liczbie obserwacji.

Nr obs.						pv	[cm^2]
1	68,32	2	0	0	+2,2	+4,4	9.68
2	,34	4	2	8	+0,2	+0,8	0,16
5	,35	6	3	18	-0,8	-4,8	3.84

,
,
,
.

Metoda spostrzeżeń pośredniczących. Uwagi ogólne.

Załóżmy, że chcemy wyznaczyć wysokości punktów A i B (rys. m2) w odniesieniu do pewnego poziomu, przy czym znane są wysokości punktów R₁ i R₂ w odniesieniu do tego poziomu (tj. w tym samym układzie odniesienia).

Rys. m2.

Ponieważ bezpośredni pomiar wysokości punktów A i B na ogół nie jest możliwy, to wyznacza się je na drodze pomiaru pośredniego na przykład mierząc różnice wzniesień między którymkolwiek z punktów R₁, R₂ a punktami A i B. Pomiar dwóch ciągów (np. R₁A i AB) pozwala pośrednio obliczyć wysokości punktów A i B, a tym samym rozwiązać postawione zadanie.

W geodezji rzadko stosuje się konstrukcje dające matematycznie jednoznaczne rozwiązanie. Jest niemal regułą, że materiał polowy zawiera obserwacje nadliczbowe, a to z następujących powodów;

1) można wtedy stwierdzić, czy wyniki pomiarów nie są obarczone błędami grubymi,

2) możliwe jest obliczenie dokładności wyznaczanych wielkości,

5) dokładność takich konstrukcji jest większa.

Te względy powodują, że oprócz obserwacji koniecznych do jednoznacznego wyznaczenia wysokości punktów, dokonuje się zwykle szeregiem dodatkowych obserwacji pozwalających obliczyć te wysokości na innej drodze. Gdybyśmy w rozważanym przykładzie oprócz ciągów R₁A i AB rozważyli jeszcze ciąg BR₂ mielibyśmy trzy wartości pomierzonych przewyższeń. Mając dane wysokości punktów R₁, R₂ i wybierając z tego zespołu po dwie dowolne obserwacje, zawsze jesteśmy w stanie obliczyć poszukiwane wysokości. Wartość wysokości każdego punktu będzie na ogół zależna od tego, jakie obserwacje uwzględniono w rachunku. Różnice wyników tych obserwacji pozwalają zwykle upewnić się, że w pomiarze nie ma omyłek, a ponadto obliczyć dokładność wyznaczanej wysokości.

W rozważanej przez nas sieci niwelacyjnej, mierząc wszystkie trzy ciągi R₁A, AB, BR₂, mamy o jedną obserwację więcej niż to jest potrzebne do jednoznacznego określenia wysokości punktów A i B. Będziemy, więc mieli jedną obserwację nadliczbową. Obserwacjami nadliczbowymi będziemy dalej nazywali te obserwacje, których wykonanie nie jest konieczne do jednoznacznego rozwiązania danej konstrukcji geodezyjnej. Aby ustalić ich ilość należy przede wszystkim ustalić ilość obserwacji koniecznych. Różnica między wszystkimi wykonanymi obserwacjami, a ilością obserwacji koniecznych, daje ilość obserwacji nadliczbowych. Można to ująć wzorem:
, gdzie n_n - ilość obserwacji nadliczbowych, n_w - ilość wszystkich obserwacji, n_k - ilość obserwacji koniecznych.

Rachunek wyrównawczy zajmuje się matematyczno rachunkowym opracowaniem wyłącznie takich konstrukcji geodezyjnych, w których występują obserwacje nadliczbowe. Jako cel stawia sobie obliczenie najbardziej prawdopodobnych wartości wielkości poszukiwanych oraz wyznaczenie ich średnich błędów. To matematyczne opracowanie nosi nazwę wyrównania, które można przeprowadzić na różnych formalnie drogach. Sposoby, jakimi się tego dokonuje, noszą nazwę metod. Jedną z nich jest omawiana metoda pośrednicząca. Celem wniknięcia w jej istotę posłużymy się prostym przykładem rachunkowym. Trzeba zaznaczyć, że ten sposób rozwiązania nie jest stosowany w praktyce, gdzie podobne zadania opracowuje się w na innej drodze.

Weźmy pod uwagę sieć niwelacyjną przedstawioną na rysunku m2. Opierając się na dwóch punktach stałych (reperach) oznaczonych na szkicu literami R₁ i R₂, chcemy wyznaczyć wysokości punktów A i B mając zaobserwowane przewyższenia h₁, h₂, h₃ (różnice wysokości między punktami R₁ i A itd. Strzałki oznaczają kierunki wzniesień ( mogą też oznaczać spadki), a długości ciągów są w przybliżeniu równe.

Niech wysokość punktu R₁, H₁ = 0,000 m, natomiast punktu R₂, H₂ = 6,000 m, a zaobserwowane różnice wzniesień między punktami sieci wynoszą:

dla ciągu R₁A: h₁= 0,996 ,

dla ciągu AB: h₂ = 1,999 ,

dla ciągu BR₂: h₃ = 2,999 .

Widać, że posiadamy tu obserwacje nadliczbowe (jedną!), trzeba więc będzie przeprowadzić wyrównanie tej sieci. Aby pokazać, że jest to konieczne, obliczymy wysokość jednego tych punktów, np. punktu A, opierając się na wielkościach pomierzonych:

,
.

Zauważmy, że w zależności od tego, jaką kombinację zaobserwowanych przewyższeń uwzględnimy w rachunku, otrzymamy różne wartości dla wysokości punktu A. Dla punktu B rzecz przedstawia się podobnie. Aby każdej wysokości zapewnić jednoznaczną wartość, niezależną od wyboru ciągów, jakimi się posłużymy do jej wyznaczenia można zniekształcić nasze (trzy) obserwacje przyporządkowując im poprawki. Poprawione wyniki pomiaru przyjmą, więc wartości:

,
,
.

Oznaczając poszukiwane wysokości punktów A i B odpowiednio przez X₁, X₂, możemy ułożyć następujące trzy równania wiążące nieznane poprawki
i wartości X₁, X₂

(w1)

.

Aby uprościć dalszy rachunek dokonujemy pewnych przekształceń. Wynikają one stąd, że zwykle znamy przybliżone wartości X₁₀, X₂₀ poszukiwanych rzędnych X₁, X₂ różniące się od nich odpowiednio o
. Będzie, więc:

,
.

(Takie postępowanie pozwala operować, co jest korzystne z obliczeniowego punktu widzenia, liczbami o małych wartościach)

Równania (w1) można, więc zapisać następująco:

;

;

.

czyli

;

;

.

Składniki ujęte w nawiasy są to przewyższenia odpowiednich ciągów obliczone z wysokości przybliżonych. Nazywamy je przewyższeniami przybliżonymi i oznaczamy przez
. Związki można zapisać, więc w postaci:

;

;

.

Przyjmując, że w naszym zadaniu:
,
i podstawiając te oraz pozostałe

( H₁ = 0,000 m, H₂ = 6,000 m) wartości liczbowe do powyższej zależności otrzymamy równania:

;

; (w2)

.

w których wyrazy wolne wyrażone są w milimetrach.

Po dokonaniu powyższych przekształceń zadanie nasze polega na wyznaczeniu przyrostów
, które dodane do rzędnych przybliżonych X₁₀, X₂₀, dadzą rzędne poszukiwane X₁, X_2. Łatwo zauważyć, że otrzymany układ nie może dać jednoznacznego rozwiązania bez postawienia dodatkowych założeń. Zawiera on, bowiem trzy równania i pięć niewiadomych
; niewiadomych jest więcej niż równań. Dodatkowego warunku, pozwalającego rozwiązać to zagadnienie, dostarcza nam teoria błędów, według, której należy przyporządkować obserwacjom takie poprawki, aby suma ich kwadratów przyjęła wartość minimalną. Stwierdziliśmy już, że układ nie ma rozwiązania jednoznacznego. Posiada on, jednakże, rozwiązania wieloznaczne, które łatwo otrzymać z przytoczonych związków. Wystarczy w tym celu do równań podstawić dowolne liczby dla x₁ oraz x₂ i wyznaczyć odpowiednie wartości
. I tak, jeśli np.
,
to mamy:
. Natomiast przy
,
otrzymujemy:
itd.

Stawiając warunek, aby suma kwadratów poprawek była najmniejsza, co zapisujemy w postaci

żądamy, aby ze wszystkich możliwych trójek wartości
wybrać tą trójkę, dla której suma
jest najmniejsza.

Zadanie to można, więc sformułować następująco: znaleźć minimum funkcji

(f1)

gdy zmienne v, spełniają zależności:

;

; (w3)

.

Jak wiemy funkcja f przyjmuje wartość najmniejszą w punkcie, dla którego jej pochodne cząstkowe względem zmiennych niezależnych są równe zeru. Obliczając te pochodne należy pamiętając, że poprawki v są funkcjami zmiennych x₁ i x₂ i wobec tego sama funkcja f jest też funkcją tych zmiennych. Wykonując różniczkowanie względem x₁ i x₂ otrzymamy:

,

Podstawiając tu pochodne cząstkowe obliczone ze wzorów (f1) dla funkcji f i (w3) dla poprawek otrzymamy dodatkowe związki:

.

W rezultacie otrzymujemy do rozwiązania układ pięciu równań z pięcioma niewiadomymi,

;

,

który posiada już rozwiązanie jednoznaczne.

Obliczenie niewiadomych znacznie upraszcza, gdy wielkości v wzięte z pierwszych trzech równań podstawimy do dwóch równań ostatnich. W ten sposób mamy:

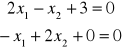
Rozwiązując ten układ równań z dwiema niewiadomymi uzyskujemy wartości niewiadomych:
,
, które podstawione do pierwszych trzech równań układu pozwalają obliczyć wartości poprawek:
.

Suma kwadratów tych poprawek jest najmniejszą ze wszystkich możliwych. Wynosi ona w naszym przypadku [vv] =12. Dla przyjętych powyżej wartości zmiennych niezależnych
oraz
stwierdzimy, że
, a więc

.

Mając wartości poprawek możemy łatwo obliczyć poprawione wartości obserwacji (obserwacje wyrównane) pamiętając, że rozwiązania otrzymaliśmy w milimetrach mamy:

.

2

15

---