Ruch drgający

Wykład 5

1

Przypominam

Zasady zaliczania w semestrze I

• Przedmiot w tym semestrze jest zaliczany na ostatnich

zajęciach

• Zaliczanie w formie pracy pisemnej polega na

odpowiedzi na 6 pytań definicyjnych i jedno opisowe.
(

Obowiązuje materiał z kursu i wykładów)

• Podstawą do wpisania do indeksu zaliczenia

przedmiotu jest wcześniejsze zaliczenie ćwiczeń
rachunkowych i kursu.

• Osoby które nie zaliczą przedmiotu na ostatnich

zajęciach przed kolejnym zaliczeniem muszą uzyskać
pozytywny wpis z ćwiczeń i zaliczyć kurs

6.1. Ruch drgający

Ruch

w

przyrodzie

jest

zjawiskiem

powszechnym. Wszystkie obserwowane w przyrodzie
ruchy dzielimy na dwie klasy:

-         oscylacje (tzw. drgania) – gdy poruszający się
obiekt pozostaje w pobliżu ustalonego miejsca –
punktu równowagi. Przykłady takich drgań to:
ciężarek na sprężynie, wahadło matematyczne, ruch
elektronów w atomach, ruch fotonów między
zwierciadłami lasera;

-         fale – gdy obserwowane zjawisko (poruszający
się obiekt) przemieszcza się w przestrzeni: np. fale
morskie, ruch elektronów w lampie kineskopowej,
ruch odkształcenia biegnącego wzdłuż napiętej liny.

3

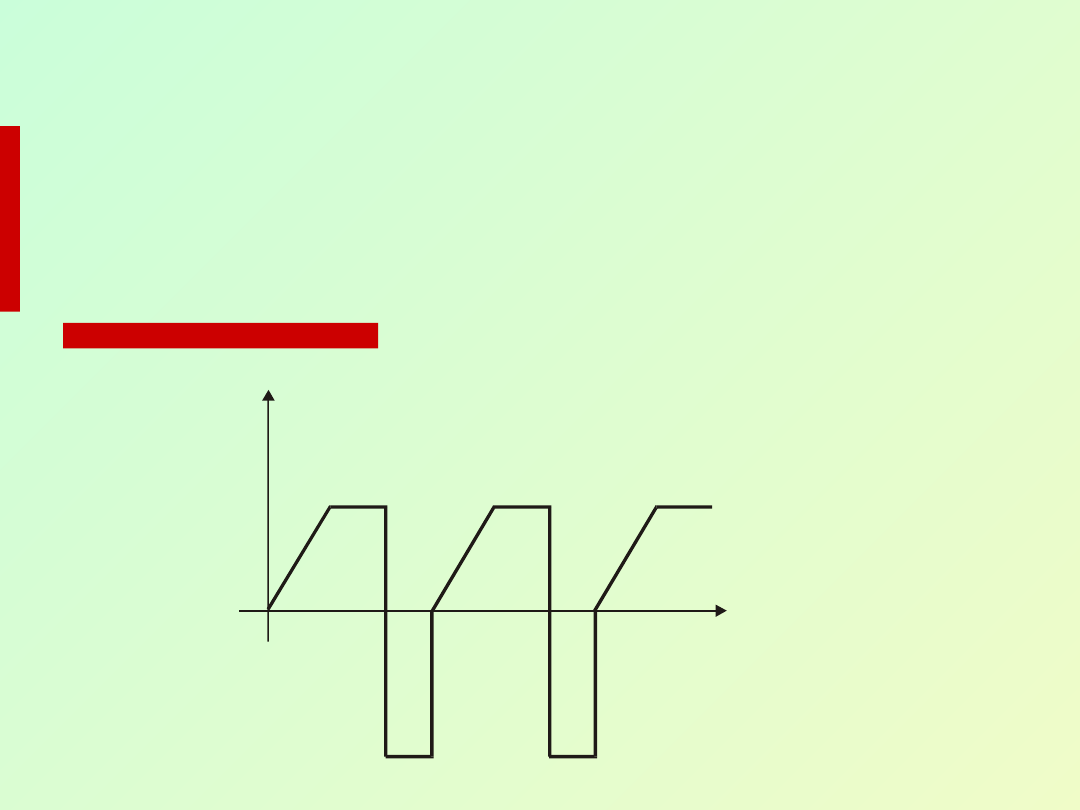
A ( t )

t

Ruchem drgającym, lub wprost drganiami
nazywamy dowolne zjawisko fizyczne (każdy
ruch lub zmianę stanu) charakteryzujące się
powtarzalnością w czasie wielkości fizycznej
A(t) opisującej ten proces.

4

Ze względu na opisujący „drgający” parametr A(t)
drgania możemy podzielić na:

-        

mechaniczne

: zmieniają się współrzędne

opisujące położenie ciała;

-        

elektryczn

e: zmienia się np. napięcie U(t) lub

ładunek Q(t) na kondensatorze obwodu RLC;

-        

elektromagnetyczne

: drgają pola elektryczne i

magnetyczne. Zmieniają się wektory opisujące te pola.

Wśród szerokiej klasy drgań możemy wyróżnić

drgania harmoni-czne

.

Drgania harmoniczne to takie drgania, w których
wielkość charakteryzująca dany układ zmienia się
z czasem sinusoidalnie lub kosinusoidalnie.

5

Wśród szerokiej klasy drgań możemy wyróżnić drgania
harmoniczne.

Drgania harmoniczne to takie drgania, w których
wielkość charakteryzująca dany układ zmienia się z
czasem sinusoidalnie lub cosinusoidalnie.

 





o

o

t

cos

A

t

A









T

T

A

o

A

o

A

o

t

A ( t )

A c o s

o

o



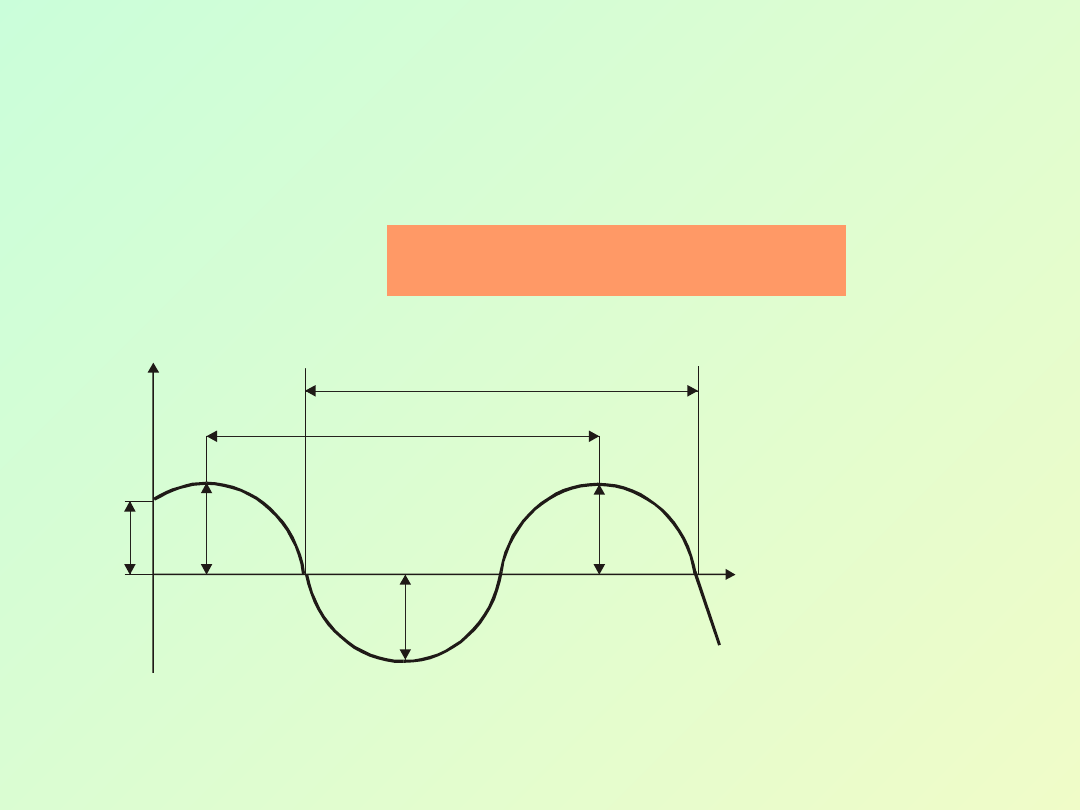
Wykres
przedstawia
drgania
harmoniczne z
fazą początkową


o

różną od zera,

amplitudą A

o

i

okresem T.

6

Drgania harmoniczne charakteryzuje:

1.     > okresowość; tzn. istnieje taki odstęp czasu T, że
dla dowolnego czasu t zachodzi:

T – nazywamy okresem drgań;

2.     > stałość maksymalnego „wychylenia” A

o

zwanego amplitudą drgań;

3.     > Stałość okresu T.

Skoro T=const, to wielkość określa liczbę drgań
w ciągu jednostki czasu.

Wielkość  nosi nazwę częstości drgań

 





T

t

A

t

A





T

1





7

Wielkość  nosi nazwę częstości drgań i spełnia

związki

(6.2)

gdzie:

to częstość kątowa lub pulsacja

drgań.

Częstość  mierzymy w hercach .

Argument funkcji cosinus (lub sinus)

(6.3)

w wyrażeniu (6.1) nazywamy fazą drgań, a wielkość 

o

= const fazą początkową.











2

T

1

T

2





1

s

1

Hz

1





 

o

t

t











8

Jeżeli chcemy opisać matematycznie drgania to
musimy podać:

-       >> postać funkcji A(t) albo

-      >>równanie matematyczna – zwane
równaniem ruchu, z którego funkcja A(t) może
być obliczona

.

9

6.2.

Prędkość

i

przyspieszenie

punktu

drgającego

Pamiętamy, że prędkość ruchu ciała 

wyrażamy jako pochodną

Zaś przyspieszenie ruchu ciała a ma postać:

zatem dla dowolnej wielkości A(t) prędkość

punktu drgającego otrzymujemy, różniczkując
funkcję (6.1) względem czasu

Różniczkując ponownie tę zależność względem
czasu, znajdujemy przyspieszenie

dt

ds

t

S

lim

0

t















2

2

0

t

dt

s

d

dt

d

t

lim

a























o

o

t

sin

A

dt

dA





















o

2

o

t

cos

A

dt

d

a

















10

Porównując

ww.

wzory

widzimy,

że

przyspieszenie jest proporcjonalne do wychylenia

(6.6)

Jak widać wzór (6.6) pozwala zdefiniować

ruch

harmoniczny jako taki ruch, w którym siła F(t)
działająca na układ drgający jest wprost
proporcjonalna do wychylenia i przeciwnie do
tego wychylenia skierowana

 

t

A

a

2







 

 

t

A

m

a

m

t

F

2











Drgania harmoniczne opisane równaniem

(6.1) można także wyrazić w postaci

przy czym .

 





1

t

sin

A

t

A









2

0

1











11

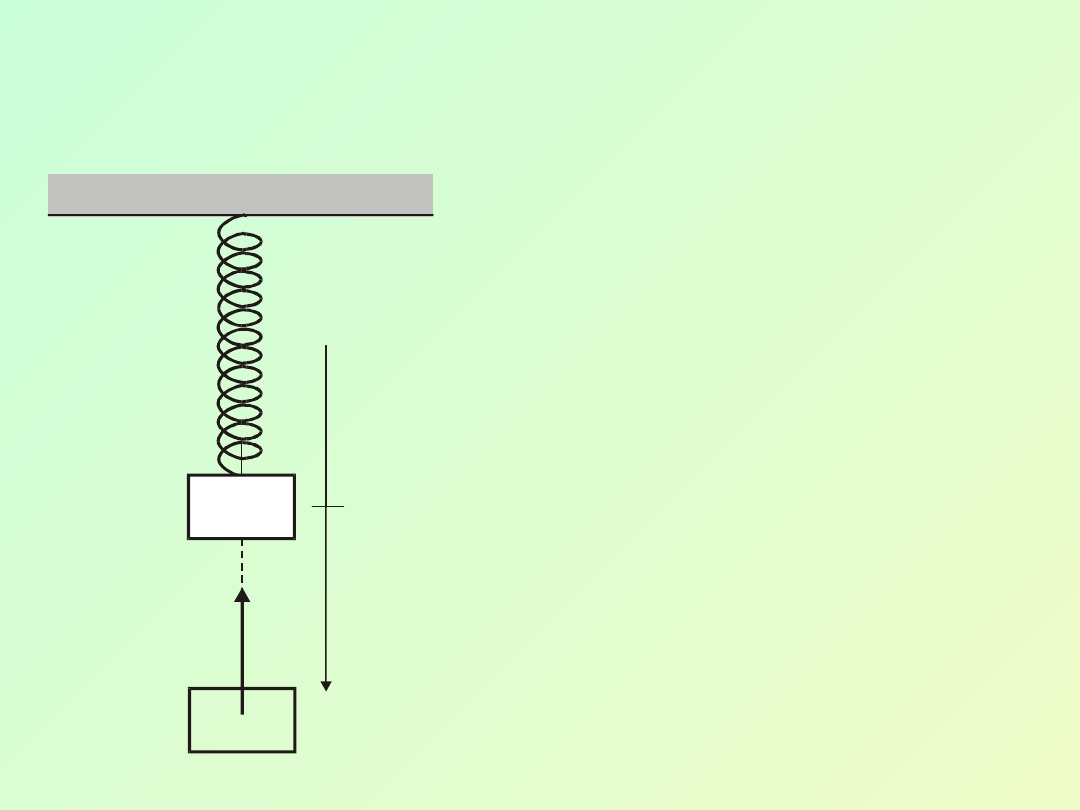
6.3. Drgania swobodne

Niech na sprężynie będzie zaczepiona masa m,

tak jak na rys.

m

F

s

0

x

 F = F

s

Mechaniczny oscylator
harmoniczny

Gdy wychylamy ciało o masie m z
położenia równowagi x = 0 o x to
zgodnie z definicją siły sprężystej
na układ działa siła F

s

:

(6.7)

Siła

sprężystości

F

s

jest

proporcjonalna do wychylenia x i
przeciwnie do niego skierowana.

Współczynnik proporcjonalności
k

nazywany

jest

zwykle

współczynnikiem

sprężystości

lub stałą siłową sprężyny.

Współczynnik sprężystości mówi
nam jaka siła jest potrzebna do
wydłużenia sprężyny o jednostkę
długości i ma wymiar [N/m].

kx

F

s





12

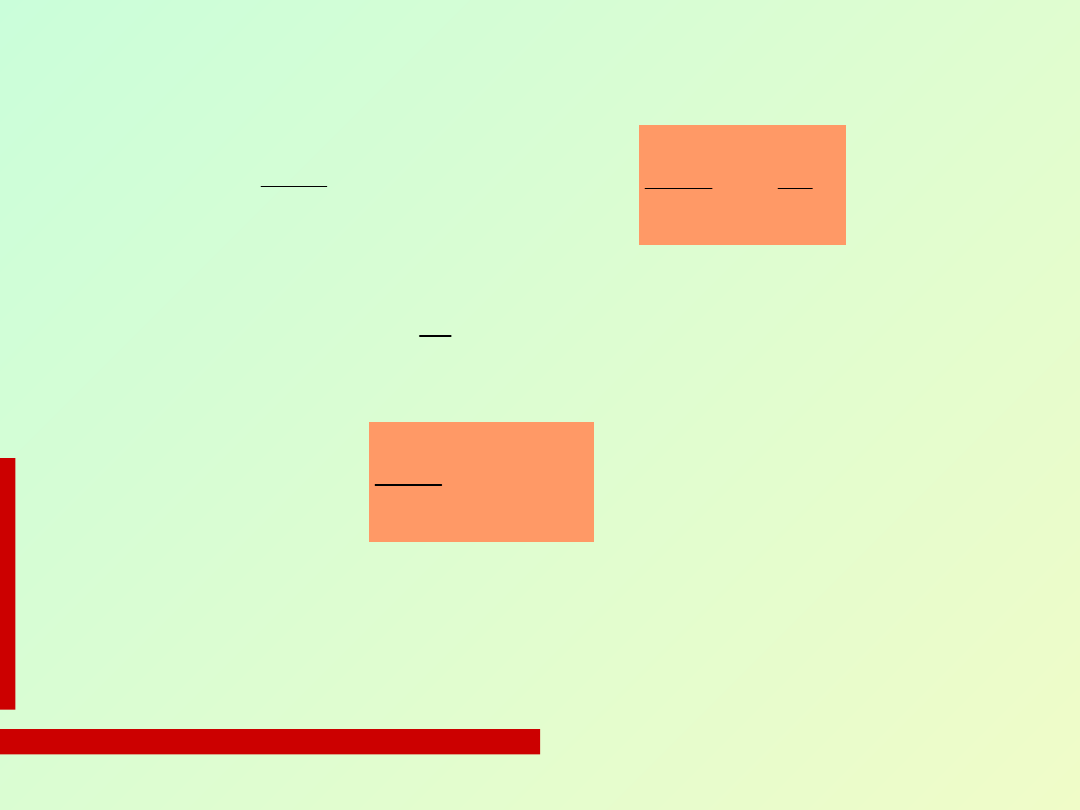
Zgodnie z II zasadą dynamiki Newtona:

dla oscylatora harmonicznego możemy zapisać:

czyli

(6.8)

Oznaczając formalnie

(6.9)

(6.8) przyjmie postać:

(6.10)

Równanie (6.10) nosi nazwę równania ruchu drgań
swobodnych punktu materialnego

. Jest to

równanie różniczkowe rzędu drugiego

jednorodne.

ma

F



2

2

dt

x

d

m

kx







x

m

k

dt

x

d

2

2





2

o

m

k





x

dt

x

d

2

o

2

2







13

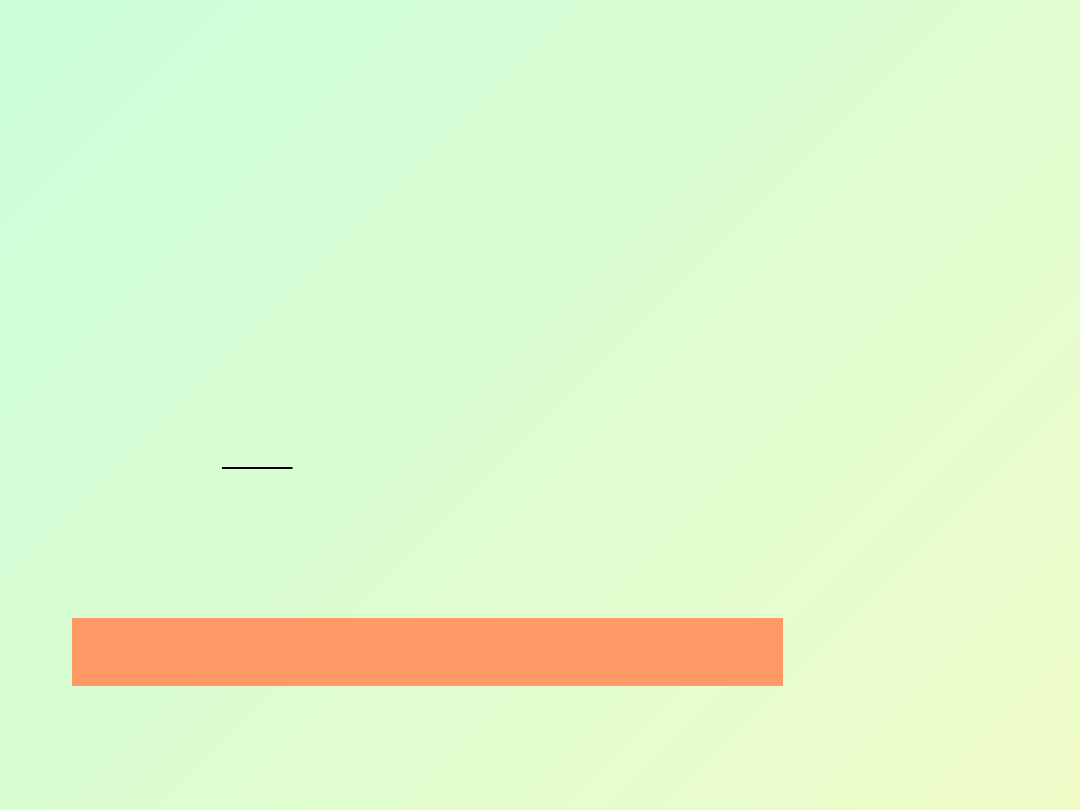
Aby znaleźć funkcję x(t) opisującą drgania

oscylatora swobodnego należy rozwiązać równanie
(6.10).

Na podstawie naszej wiedzy z matematyki i

wcześniejszych rozważań postulujemy, że funkcja
typu

(6.11)

winna być rozwiązaniem równania ruchu (6.10).

Podstawiając (6.11) i wyrażenie (6.12)

(6.12)

obliczone z (6.11) do równania (6.10) otrzymujemy:

(6.13)

 





o

o

t

cos

A

t

x













o

o

2

2

2

t

cos

A

dt

x

d





















o

o

2

o

o

o

2

t

cos

A

t

cos

A























14

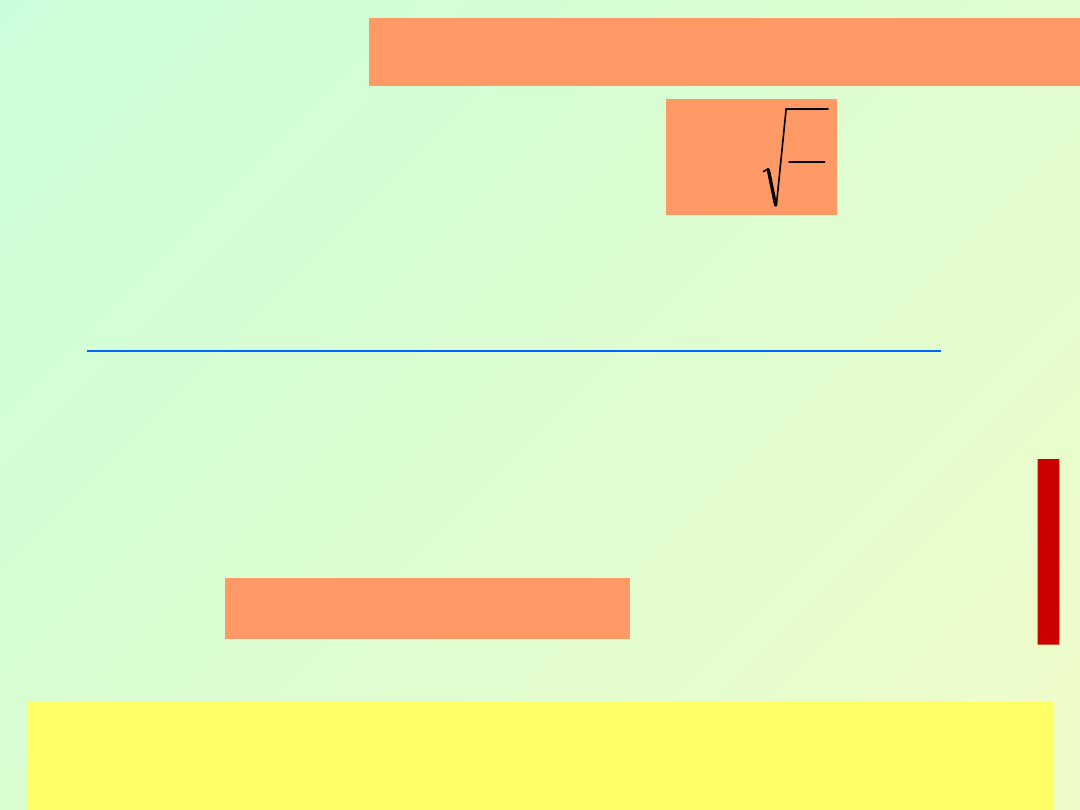
Widzimy, że równość

zachodzi jeżeli

gdzie

(6.14)

jest

częstotliwością kołową drgań własnych układu

.

Jeżeli znamy stałą siłową k sprężyny i masę m

ciała zawieszonego na tej sprężynie, to możemy
obliczyć 

o

(okres T) drgań własnych układu. Drgania

swobodne (własne) są zatem drganiami harmonicznymi
opisanymi funkcją

(6.15)









o

o

2

o

o

o

2

t

cos

A

t

cos

A























o







m

k

o





 





o

o

o

t

cos

A

t

x









Punkt materialny wykonujący drgania
harmoniczne opisane (6.15) nosi nazwę
oscylatora harmonicznego nietłumionego.

15

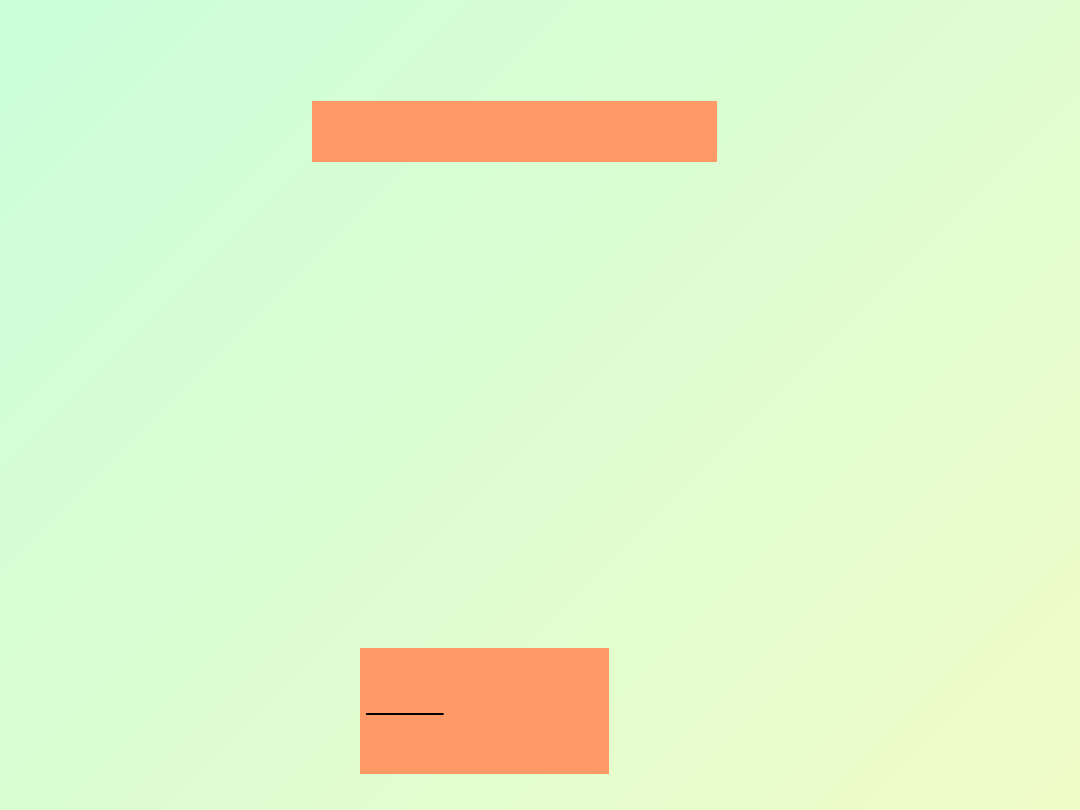
Punkt materialny wykonujący drgania harmoniczne
opisane (6.15) nosi nazwę oscylatora harmonicznego
nietłumionego.

Amplituda A

o

i faza początkowa 

o

drgań

swobodnych (własnych) zależą od sposobu pobudzania
układu drgań.

Drgania

swobodne

wykonują

też

wahadła

matematyczne i fizyczne.

Drgania

swobodne

nie

muszą

być

wyłącznie

mechaniczne, np. w obwodzie elektrycznym złożonym z
indukcyjności L i pojemności C występują drgania
(swobodne) elektryczne.

Jeżeli w równaniu (6.10) zastąpimy x(t) przez A(t)

to uzyskamy uogólnione równanie ruchu drgań
swobodnych w postaci:

(6.16)

A

dt

A

d

2

o

2

2







 





o

o

o

t

cos

A

t

x









16

Obliczmy teraz całkowitą energię mechaniczną E
drgającego harmonicznie punktu materialnego.

Energia kinetyczna E

k

wyrazi się wzorem:

, gdzie

(6.17)

Energia kinetyczna zmienia się od zera dla największego
wychylenia x i osiąga wartość maksymalną

dla wychylenia x = 0.

2

2

k

dt

dx

m

2

1

2

m

E























o

o

o

t

cos

A

x













o

o

2

2

o

2

o

k

t

sin

A

m

2

1

E











2

o

2

o

max

k

A

m

2

1

E





17

Energię potencjalną E

p

drgającego punktu obliczamy,

wyznaczając

energię

potencjalną

rozciągniętej

sprężyny. Energia potencjalna zgromadzona w
rozciągniętej sprężynie równa się pracy W włożonej
przy rozciąganiu tej sprężyny.

Czyli ,

gdzie











 









x

0

2

x

0

x

0

s

kx

2

1

kxdx

dx

kx

dx

F

W

2

p

kx

2

1

W

E









o

o

o

t

cos

A

x













o

o

2

2

o

p

t

cos

kA

2

1

E









Ale

pamiętamy

(patrz

(6.14)), że

m

k

o





2

o

m

k





wtedy





o

o

2

2

o

2

o

p

t

cos

A

m

2

1

E











18

Całkowita energia mechaniczna E jest
równa













o

o

2

o

2

2

o

2

o

p

k

t

cos

t

sin

A

m

2

1

E

E

E























2

o

2

o

A

m

2

1

E





Widzimy zatem, że w ruchu harmonicznym energia
potencjalna i kinetyczna punktu wykonującego
drganie zmieniają się w taki sposób, że ich suma
pozostaje stała. Jest to zgodne z zasadą zachowania
energii mechanicznej, gdyż w przypadku drgań
swobodnych straty energii mechanicznej nie
występują.

19

T / 2 T 3 T / 2 t

T / 2 T 3 T / 2 t

T / 2 T 3 T / 2 t

T / 2 T 3 T / 2 t

x

a

E

E = E + E

c

k

p

E

E

k

p



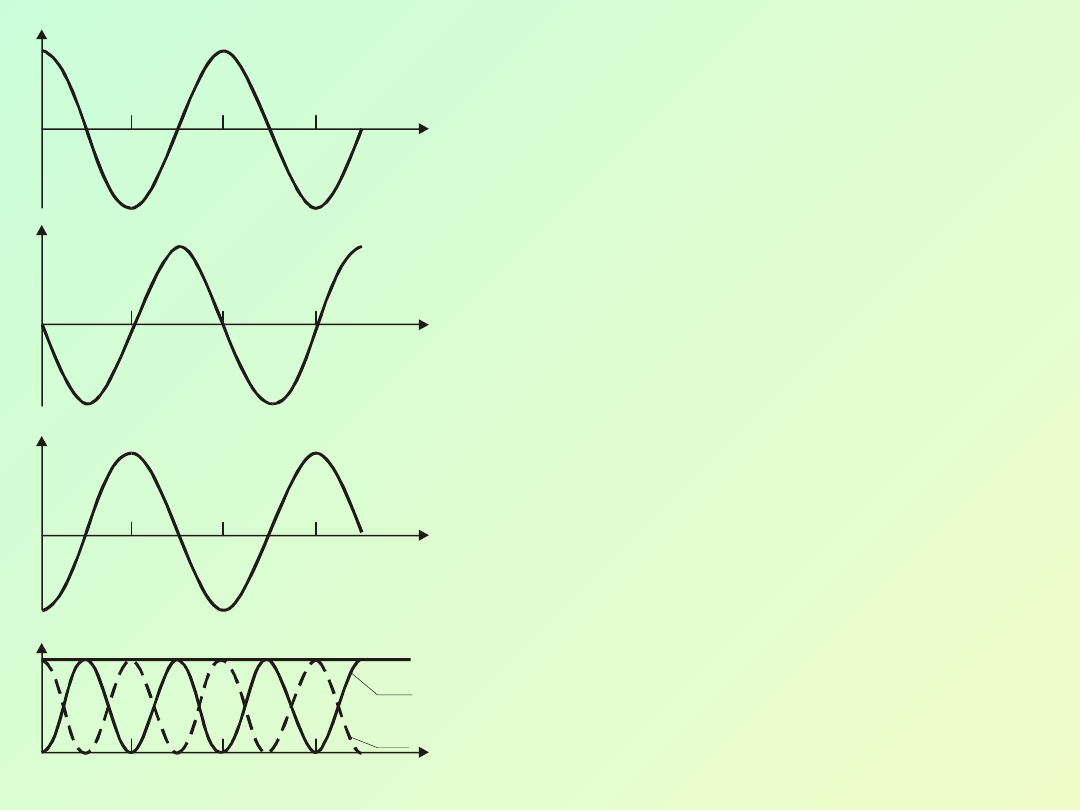
Na

rysunku

pokazano

zależność x(t), (t), a(t), E

k

(t)

i E

p

(t) drgań swobodnych.

Zwróćmy uwagę, że

wykres

(t) jest przesunięty w

stosunku do wykresu x(t) o
/4

;

to samo dotyczy wykresu

a(t) w stosunku do wykresu
(t).

Mówimy, że między

prędkością a wychyleniem
oraz

między

przyspieszeniem

a

prędkością

występuje

przesunięcie

fazowe

równe /4.

20

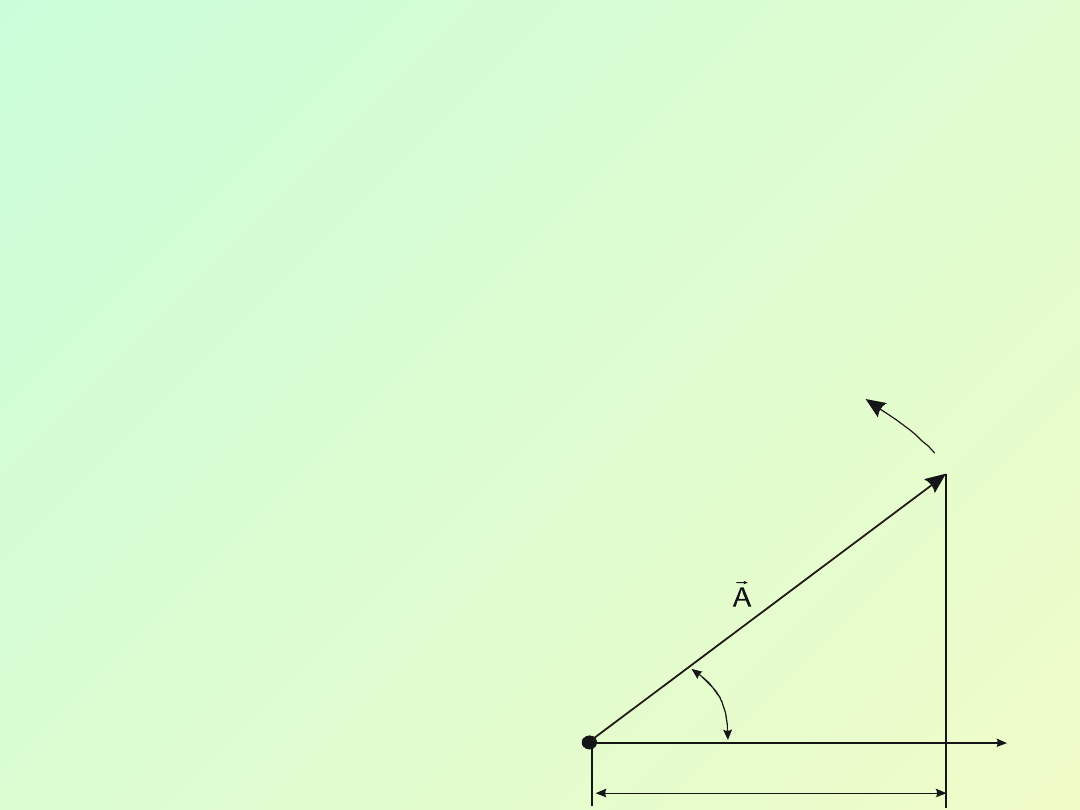
Drgania harmoniczne można również

przedstawić graficznie za pomocą obracającego
się wektora amplitudy

.

Jest to metoda wektorowa. W tym celu z

dowolnego punktu 0 osi x pod kątem równym fazie
początkowej drgań wykreślamy wektor , którego
moduł jest równy amplitudzie A rozważanego drgania
(rys. 8.2). Jeżeli wektor wprawimy w obrót z
prędkością kątową , to rzut końca wektora będzie się
przemieszczać wzdłuż osi x i przyjmować wartości od
+A do –A, a drgająca wielkość będzie zmieniać się w
czasie według wzoru .





o

0

s

x

A

zatem

obracający

się

wektor

ampli-tudy

w

zupełności

charakteryzuje

drganie harmoniczne.

21

Dodawanie drgań harmonicznych równoległych o tej

samej częstotliwości

Rozważmy teraz przypadek, gdy punkt materialny

wykonuje jednocześnie dwa (lub więcej drgania
harmoniczne równoległe o tej samej częstotliwości
kołowej, czyli o tej samej pulsacji, lecz różniące się fazą.
Drgania nazywamy równoległymi, gdy zachodzą wzdłuż
tej samej prostej. Załóżmy, że rozważane przez nas
drgania zachodzą wzdłuż osi x. Możemy je wtedy wyrazić
równaniami





1

1

1

t

cos

A

x













2

2

2

t

cos

A

x









przy czym występująca między drganiami różnica faz

, nosi nazwę przesunięcia fazowego.

1

2













Drganie wypadkowe rozważanego punktu jest
superpozycją jego drgań składowych, a wychylenie
wypadkowe jest sumą jego wychyleń składowych

22

Drganie wypadkowe rozważanego punktu jest

superpozycją jego drgań składowych, a wychylenie
wypadkowe jest sumą jego wychyleń składowych, zatem

Stosując

odpowiednie

wzory

trygonometryczne,

wyrażenie powyższe można sprowadzić do postaci









2

2

1

1

2

1

t

cos

A

t

cos

A

x

x

x

































t

cos

A

x

1





1

2

2

1

2

2

2

1

cos

A

A

2

A

A

A













2

2

1

1

2

2

1

1

cos

A

cos

A

sin

A

sin

A

tg

















gdzie

Widzimy, że złożenie dwóch drgań harmonicznych o jednakowych
pulsacjach różniących się fazą daje w wyniku drganie o tej samej
pulsacji. Jasne jest, że to samo dotyczy złożenia większej liczby
drgań.

Konkludując

możemy

stwierdzić,

że

dodawanie

drgań

harmonicznych

równoległych,

o

jednakowych

pulsacjach

różniących się fazą, daje w wyniku drganie harmoniczne o tej
samej pulsacji.

23

Składanie drgań harmonicznych równoległych o

jednakowej częstości. Dudnienie

Ciało drgające może brać udział w kilku

procesach drgających, a wówczas należy określić
wypadkowy ruch drgający ciała. Dokonamy złożenia
drgań harmonicznych o jednakowych częstotliwościach

x

x

1

x

2

x

1

A

2

A

A

O



1

 

1

2

-



2







1

1

1









t

cos

A

x

o





2

2

2









t

cos

A

x

o

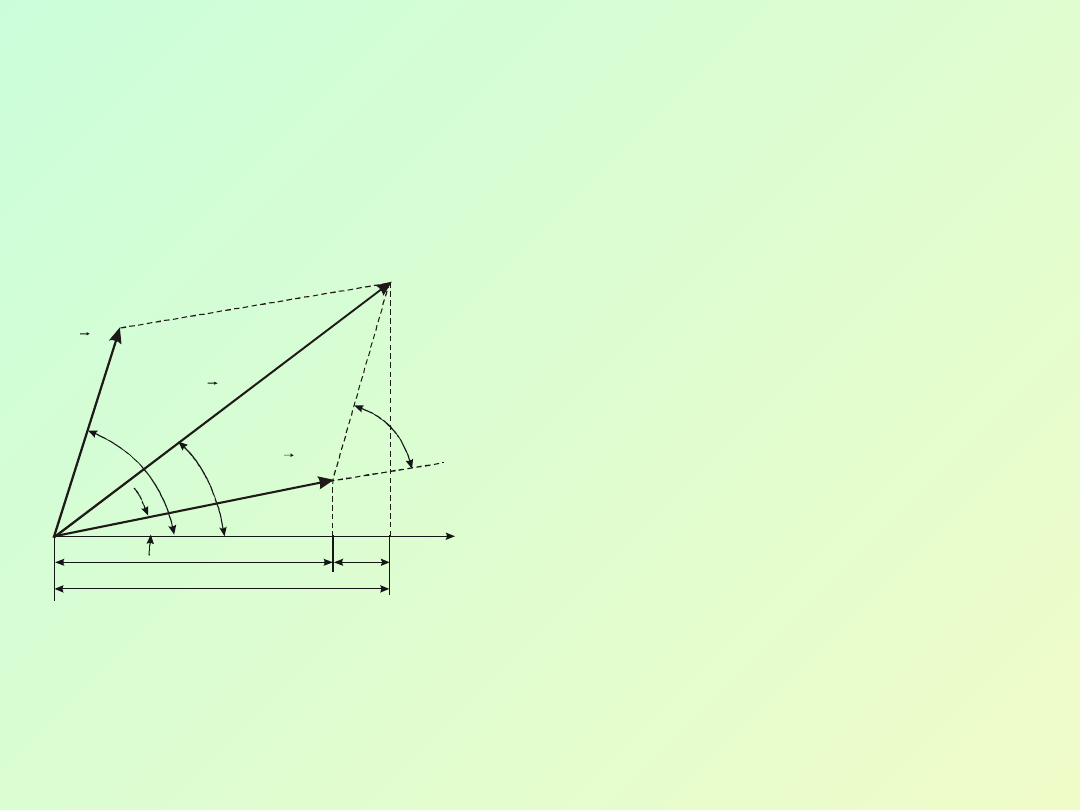
Wektory

i

obracają

się z jednakową częstością
kątową

, a różnica faz

pomiędzy nimi pozostaje
stała. Wówczas równanie
drgania wypadkowego ma
postać

A

1



A

1



o



1

2























t

cos

A

x

x

x

o

2

1

24

















t

cos

A

x

x

x

o

2

1

gdzie amplituda A i faza φ są określone wyrażeniami





1

2

2

1

2

2

2

1

2

2













cos

A

A

A

A

A

2

2

1

1

2

2

1

1











cos

A

cos

A

sin

A

sin

A

tg







Wobec tego ciało biorące udział w dwóch drganiach

harmonicznych o jednakowych kierunkach wykonuje
także drgania harmoniczne w tym kierunku i o tej samej
częstotliwości co drgania składowe. Amplituda drgania
wypadkowego zależy od różnicy faz

drgań

składowych:

1

2







       gdy

, wówczas ,

       gdy

,wówczas .





,...

,

,

m

m

2

1

0

2

1

2

















 



,...

,

,

m

m

2

1

0

1

2

1

2

















2

1

A

A

A





2

1

A

A

A





25

Interesujący

jest

przypadek,

gdy

dwa

dodawane drgania równoległe nieznacznie różnią
się częstotliwościami drgań

. W wyniku dodania tych

drgań otrzymujemy drgania o okresowej zmianie
amplitudy zwane dudnieniem.

Niech amplitudy składanych drgań będą równe A, a ich
częstości kołowe ω i ω+Δω przy czym Δω << ω .
Przyjmijmy, że fazy początkowe drgań są zerowe,
wówczas

t

cos

A

x





1





t

A

x









 cos

2

Dodając te wyrażenia i uwzględniając że

,

znajdujemy

ω

/

ω

Δ



2

t

cos

t

cos

A

x





















2

2

26

t

cos

t

cos

A

x





















2

2

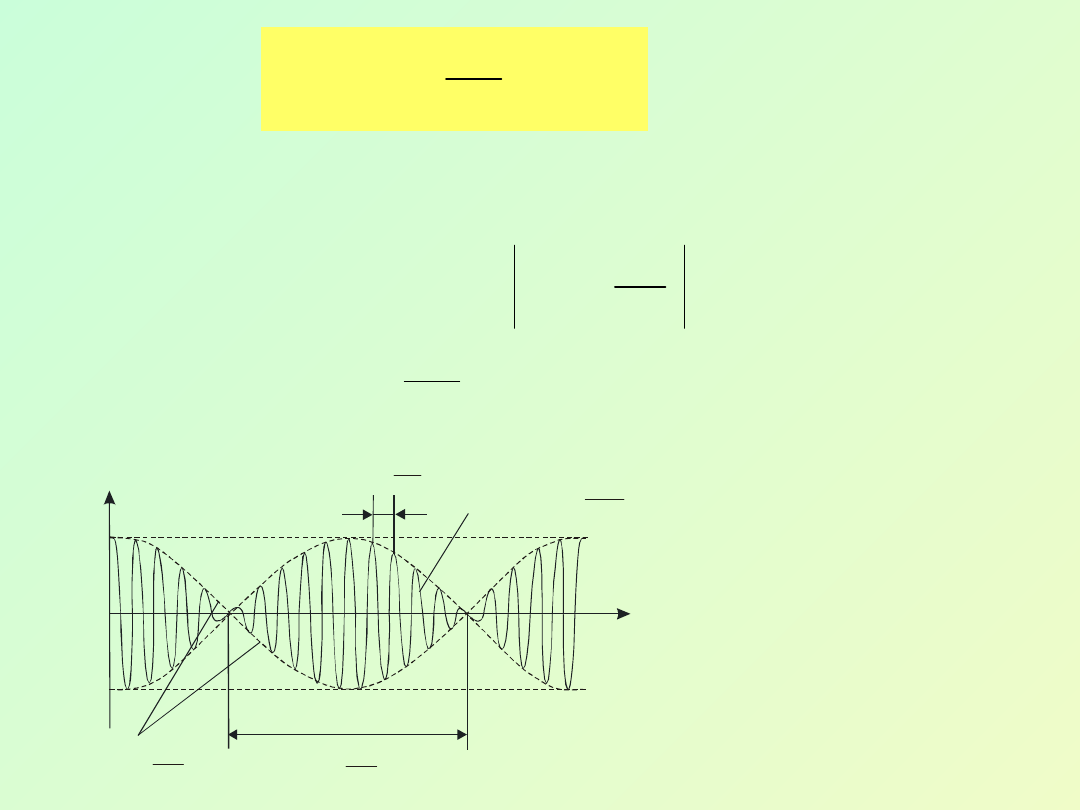
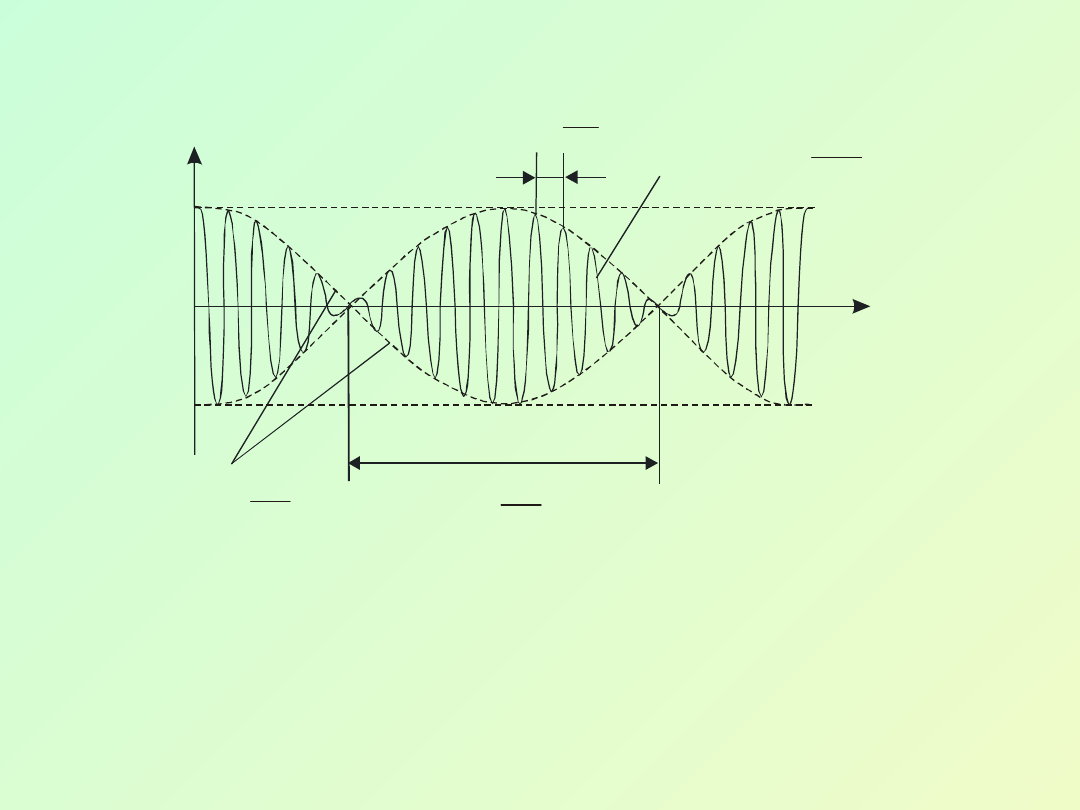
Otrzymane

wyrażenie

jest

iloczynem

czynnika

stanowiącego modulowaną amplitudę

(8.25)

o okresie dudnień

t

cos

A

A

~

2

2













2



o

T

i szybko zmieniającego
się członu cos



t.







2

T

o









2

T

t

c o s

2

t

c o s

A

2

x





















t

2

c o s

A

2

A

~







t

2 A

- 2 A

~

A

,

x

27







2

T

o









2

T

t

c o s

2

t

c o s

A

2

x





















t

2

c o s

A

2

A

~







t

2 A

- 2 A

~

A

,

x

28

Składanie drgań wzajemnie prostopadłych

 

Rozważmy

przypadek

złożenia

dwóch

drgań

harmonicznych o jednakowej częstości ω, zachodzących
w kierunkach wzajemnie prostopadłych wzdłuż osi x i y.
Dla prostoty przyjmiemy, że faza początkowa pierwszego
drgania jest zerowa:

















t

cos

B

y

t

cos

A

x

Równanie

trajektorii

drgania

wypadkowego

znajdujemy poprzez wyłączenie z ww. wyrażeń
parametru t. Zapisując drganie składowe w postaci











sin

t

sin

cos

t

cos

B

y

;

t

cos

A

x







i zmieniając w drugim wyrażeniu cos ωt na x/A i

sin ωt na

, otrzymujemy po prostych

przekształceniach równanie elipsy





2

1

A

/

x



29



2

2

2

2

2

2

sin

B

y

AB

xy

A

x







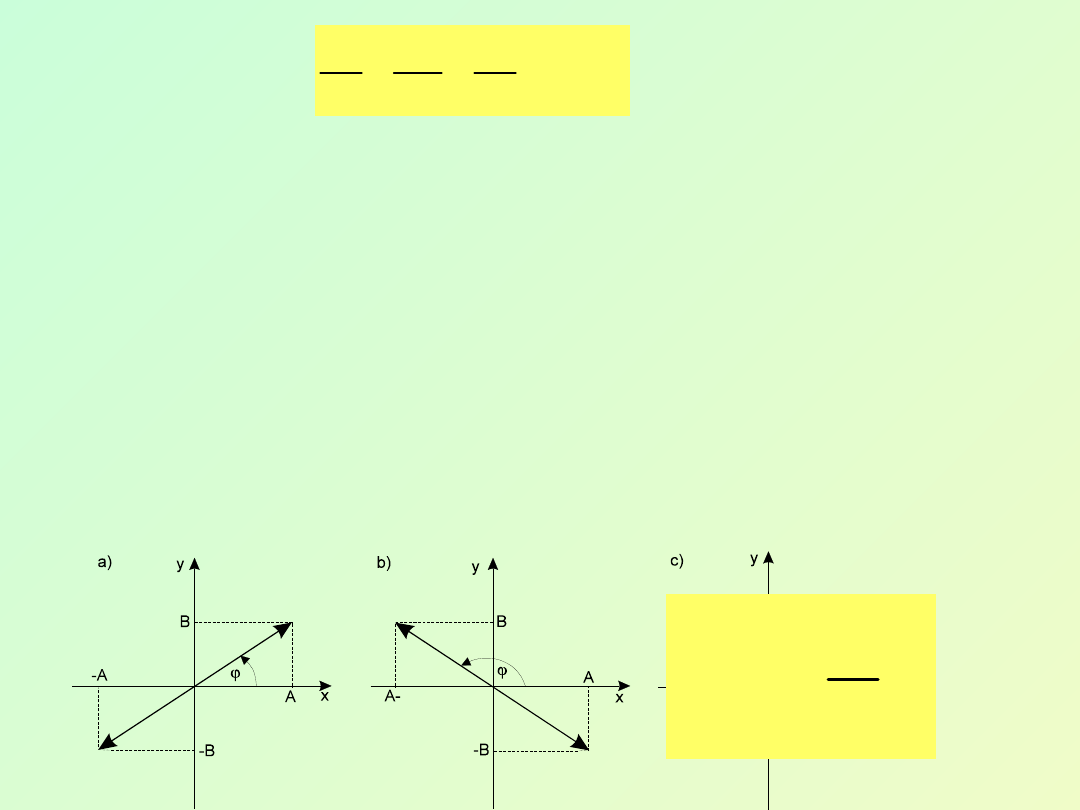
Drgający punkt porusza się po elipsie, więc
otrzymaliśmy przypadek tak zwanych drgań
eliptycznie spolaryzowanych.

Orientacja osi elipsy i jej rozmiary zależą od

amplitud drgań składowych i różnicy faz φ .
Rozpatrzymy niektóre szczególne przypadki:





,

,...

,

,

m

m

2

1

0













 w tym przypadku elipsa degeneruje się do odcinka

prostej

m  

0 2 4

,

,

m  

1 3 5

,

,

,

x

A

B

y 



30

m  

0 2 4

,

,

m  

1 3 5

,

,

,









,

,...

,

,

m

m

2

1

0

2

1

2























,

,...

,

,

m

m

2

1

0

2

1

2















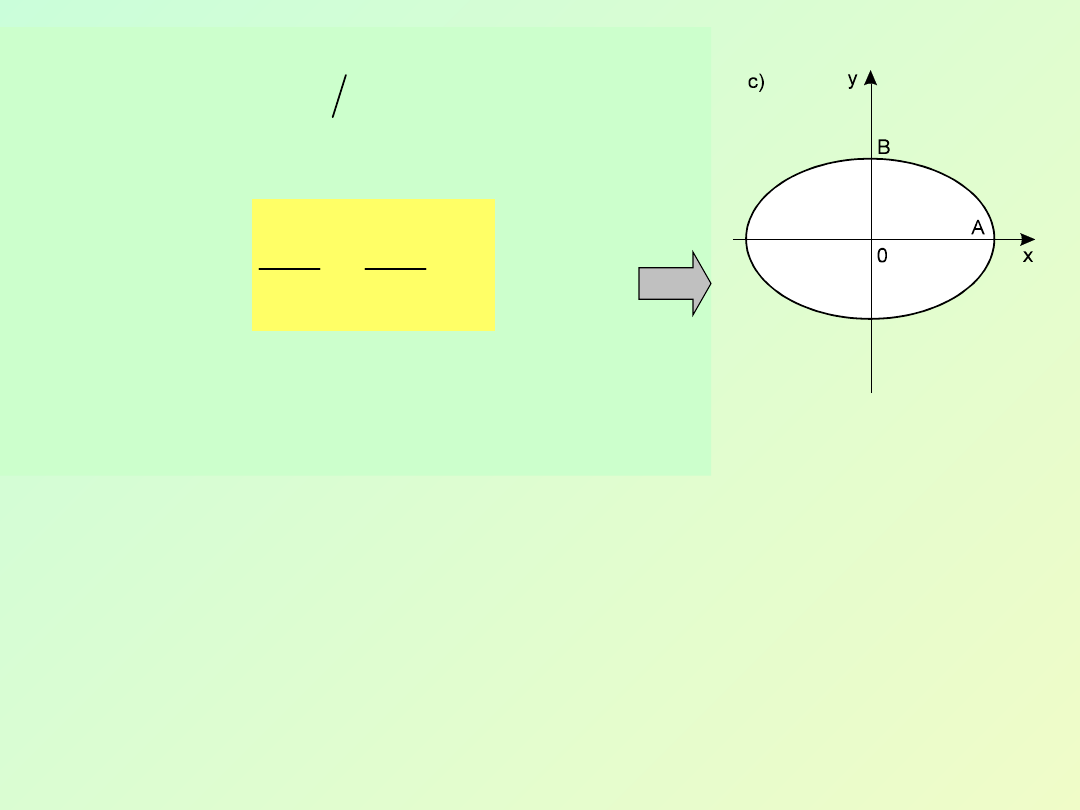
w tym przypadku otrzymujemy

1

2

2

2

2





B

y

A

x

Jest to równanie elipsy, której osie
pokrywają się z osiami współrzędnych,
a jej półosie są równe odpowiednim
amplitudom

31

6.4. Drgania tłumione

Jeżeli drgania ciała odbywają się w ośrodku

materialnym (np. w gazie, cieczy), to wskutek
występowania siły oporu ośrodka, którą będziemy
nazywać

siłą

tłumiącą,

drgania

będą

zanikać.

Niezależnie od natury ośrodka siła tłumiąca F

t

jest

proporcjonalna do prędkości  ciała drgającego (jeśli

prędkość ta jest niewielka). Zatem

(6.20)

Współczynnik

proporcjonalności

f

nazywa

się

współczynnikiem oporu ośrodka.

Znak minus w powyższym wzorze uwzględnia

fakt, że siła jest zawsze skierowana przeciwnie do
kierunku ruchu (kierunku prędkości).

dt

dx

f

F

t





32

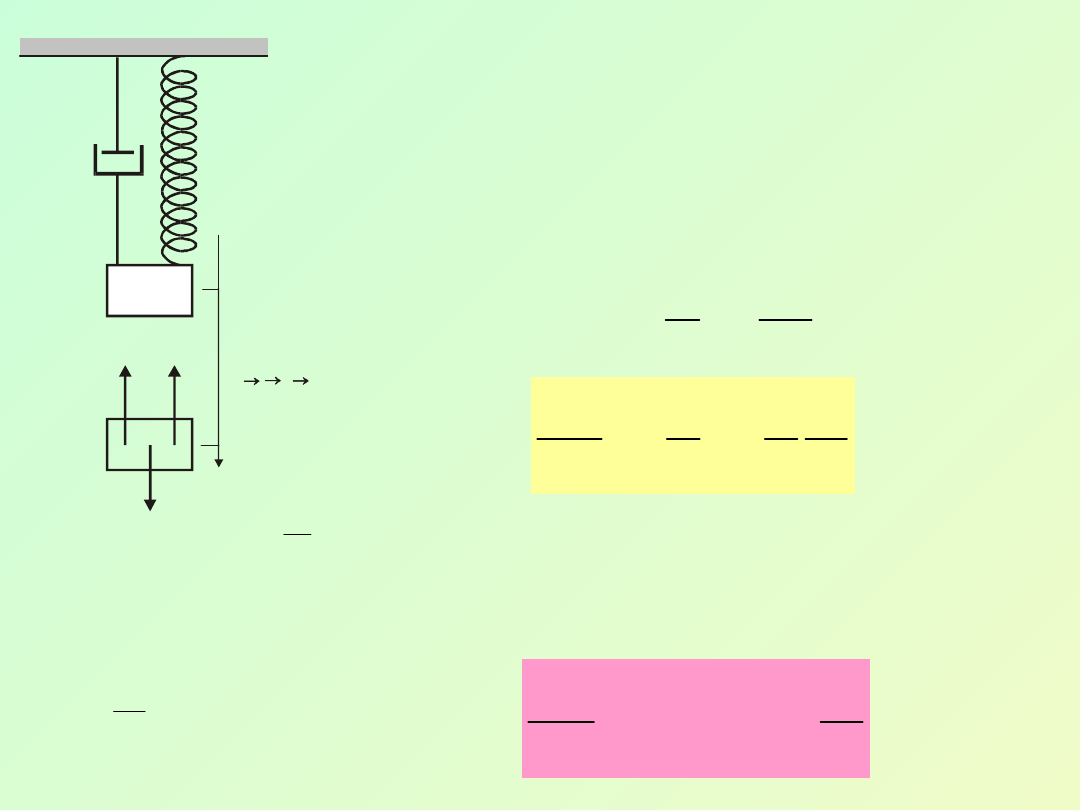
m

F

s

F

t

0

x

f k



 

F F + F

s

t

Uwzględniając działanie siły (6.20)
możemy dla drgań tłumionych,
zgodnie z II zasadą dynamiki,
napisać

Czyli

Albo

(6.21)

ma

F

F

;

ma

F

t

s









2

2

dt

x

d

m

dt

dx

f

kx







dt

dx

m

f

x

m

k

dt

x

d

2

2







Pamiętając, że

jest to częstość kołowa drgań

własnych (czyli częstość z jaką drgałby układ gdyby nie
było tłumienia) oraz oznaczając formalnie

2

o

m

k







2

m

f

Rnie
6.21
przyjmuj
e postać

dt

dx

2

x

dt

x

d

2

o

2

2











33

dt

dx

2

x

dt

x

d

2

o

2

2











Równanie to nosi nazwę równania ruchu drgań
harmonicznych tłumionych.

Jest to równanie

różniczkowe rzędu drugiego, jednorodne.

Rozwiązaniem tego równania jest funkcja

















t

cos

e

A

x

1

t

0

gdzie:

to tzw. współczynnik

tłumienia,

a

to pulsacja drgań tłumionych.

m

2

f





2

2

1

o











34

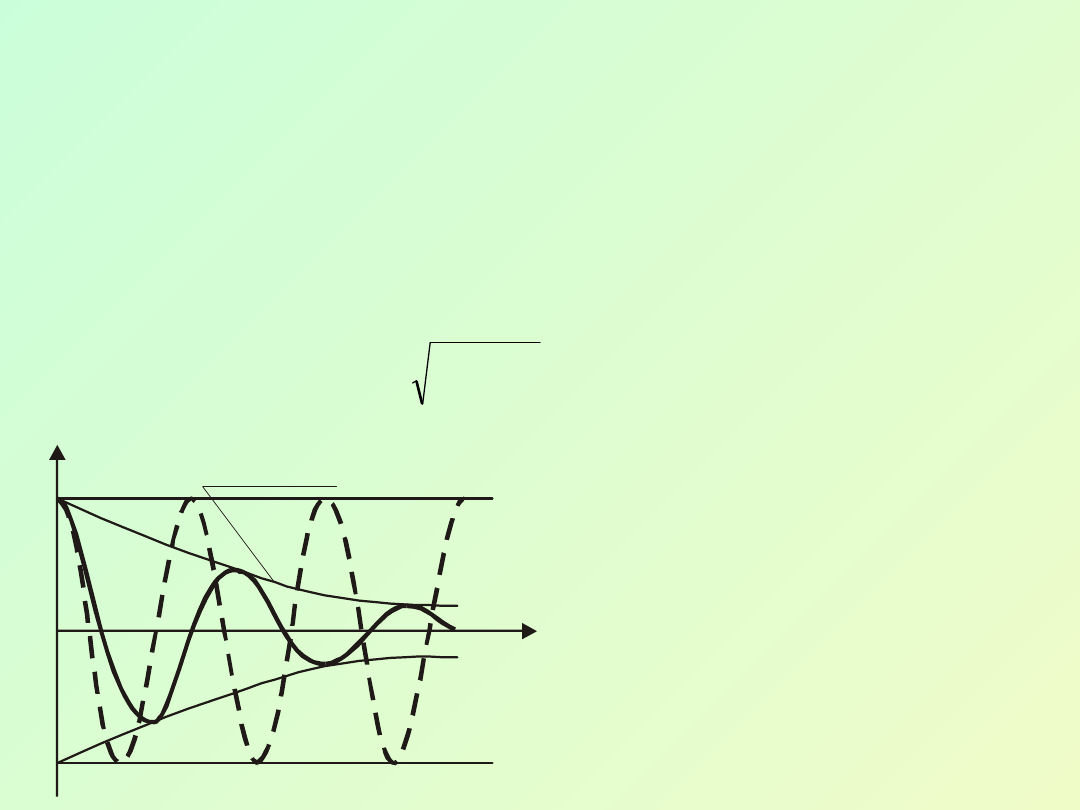
Porównując wzór (6.9) dla drgań swobodnych ze
wzorem (6.24) dla drgań tłumionych widzimy, że
wskutek działania siły tłumiącej:

1.      amplituda drgań tłumionych maleje z upływem
czasu według zależności

(6.25)

2.     pulsacja drgań tłumionych jest mniejsza niż dla
drgań swobodnych

(6.26)

t

0

e

A

A







o

2

2

1

o















x

A

0

- A

0

t

A = A e

0

- t



Na rysunku

przedstawiono wykres
drgań tłumionych ciała z
naniesionym dla
porównania z wykresem
drgań swobodnych tego
ciała.

35

Wielkością charakteryzującą drgania tłumione

jest tzw. logarytmiczny dekrement tłumienia.

Logarytmiczny

dekrement

tłumienia

jest

to

logarytm naturalny stosunku dwóch amplitud w
chwilach t i t+T. Oznaczając logarytmiczny dekrement
tłumienia literą  (lambda) możemy zapisać





T

e

ln

e

A

e

A

ln

T

T

t

o

t

o























Zależności od (6.24) do (6.27) mają sens tylko wtedy,
jeśli

, w przeciwnym razie ruch nie jest ruchem

drgającym, lecz ruchem pełzającym (aperiodycznym).

o







W

celu

scharakteryzowania

drgającego układu wprowadzono
pojęcie dobroci Q, która dla małych
wartości

logarytmicznego

dekrementu tłumienia jest równa













2

o

o

T

Q







36

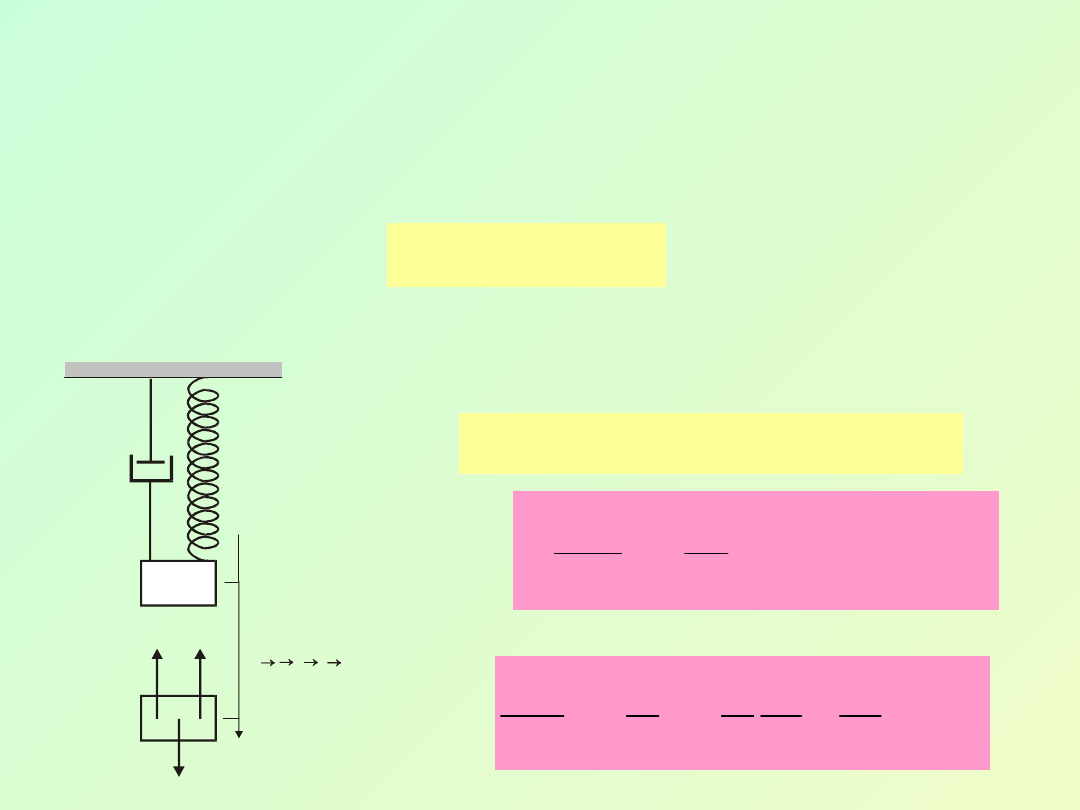
6.5. Drgania wymuszone

Jeżeli chcemy, aby opory ośrodka nie tłumiły drgań,

to na drgający punkt materialny należy działa
odpowiednio zmienną w czasie siłą. W przypadku drgań
harmonicznych siła ta ma postać:

(6.28)

Siłę tę nazywamy siłą wymuszającą.

t

cos

F

F

0

w





m

F

s

F

t

0

x

f k

 

F F + F + F

t

s

w

F

w

W przypadku drgań wymuszonych
mamy

Czyli

albo

ma

F

F

F

;

ma

F

w

t

s











t

cos

F

kx

dt

dx

f

dt

x

d

m

0

2

2









t

cos

m

F

dt

dx

m

f

x

m

k

dt

x

d

0

2

2











37

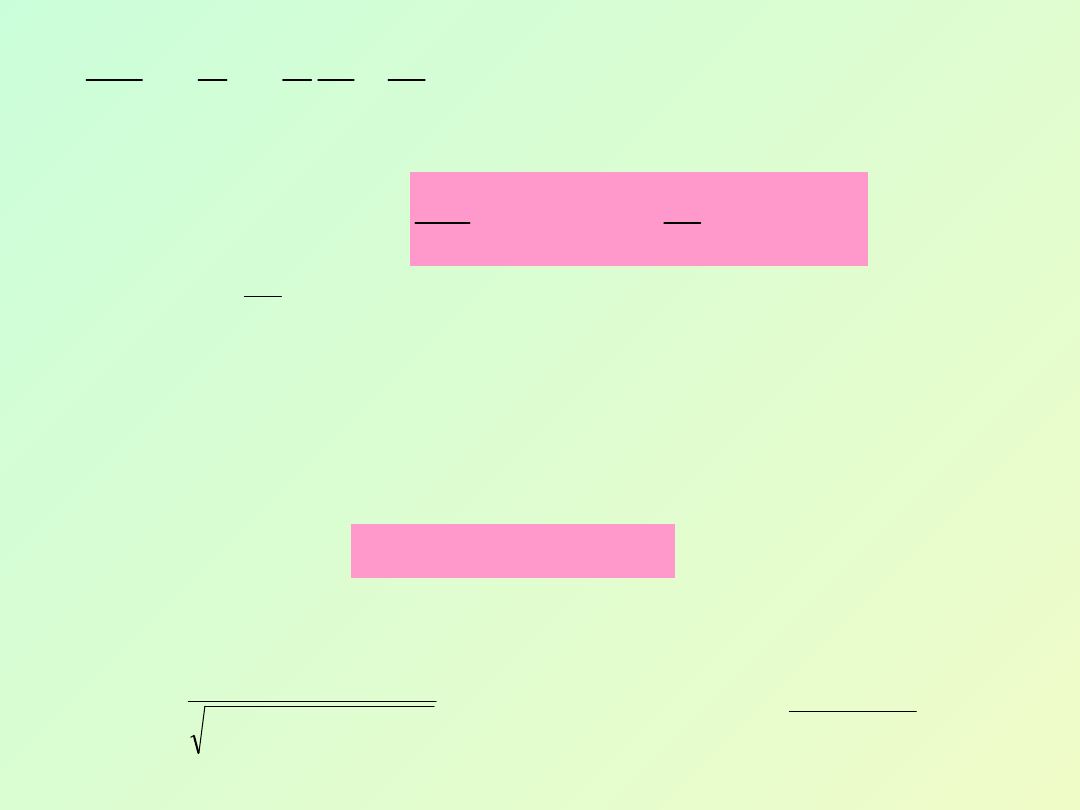
t

cos

m

F

dt

dx

m

f

x

m

k

dt

x

d

0

2

2











Co można zapisać

t

p

dt

dx

x

dt

x

d

o

o











cos

2

2

2

2





gdzie

jest amplitudą znormalizowaną

siły wymuszającej (przeliczoną na jednostkę masy).

Równanie (6.30) nosi nazwę równania ruchu drgań
wymuszonych.

Rozwiązaniem tego równania jest funkcja

(6.31)

m

F

p

o

o



(6.30
)





o

o

t

cos

A

x













2

2

2

2

2

o

o

o

4

p

A













































2

2

o

o

2

tg

arc

gdzie

38































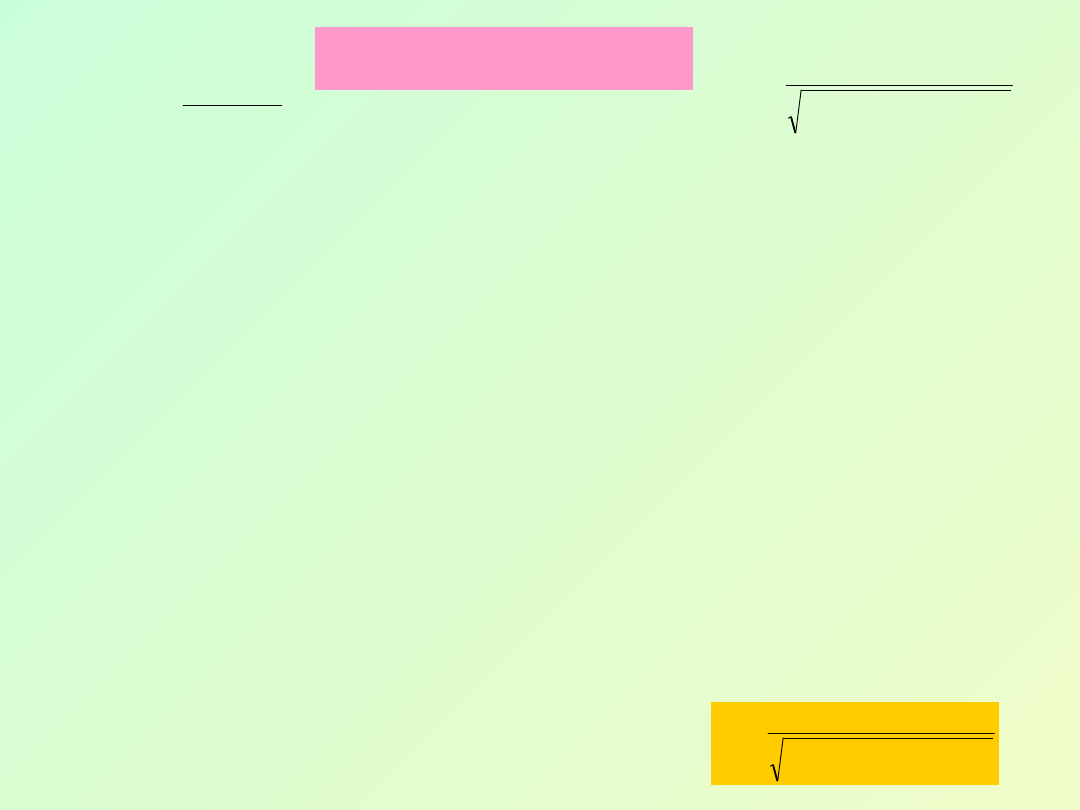
2

2

o

o

2

tg

arc





o

o

t

cos

A

x













2

2

2

2

2

o

o

o

4

p

A















Widzimy więc, że w wyniku działania siły wymuszającej
o postaci (6.28) punkt materialny wykonuje drgania
harmoniczne z pulsacją , tzn. z taką pulsacją, z jaką

zmienia się siła wymuszająca. Amplituda drgań
wymuszonych jest ściśle określona i zależy od amplitudy
siły wymuszającej p

o

oraz od jej pulsacji . Również

początkowa faza drgania 

o

zależy od pulsacji .

Gdy siła wymuszająca działa na drgające ciało z

odpowiednią częstotliwością, to amplituda drgań tego
ciała może osiągnąć bardzo dużą wielkość nawet przy
niewielkiej sile wymuszającej. Zjawisko to nazywamy
rezonansem. Przeanalizujemy obecnie wyrażenie (6.32)
na amplitudę

drgań wymuszonych.

 



o

A





2

2

2

2

2

o

o

o

4

p

A















39

A

A

r 1



r 1





r 2



r 3



1



0

= 0



2



3



4

A

r2

A

0



0

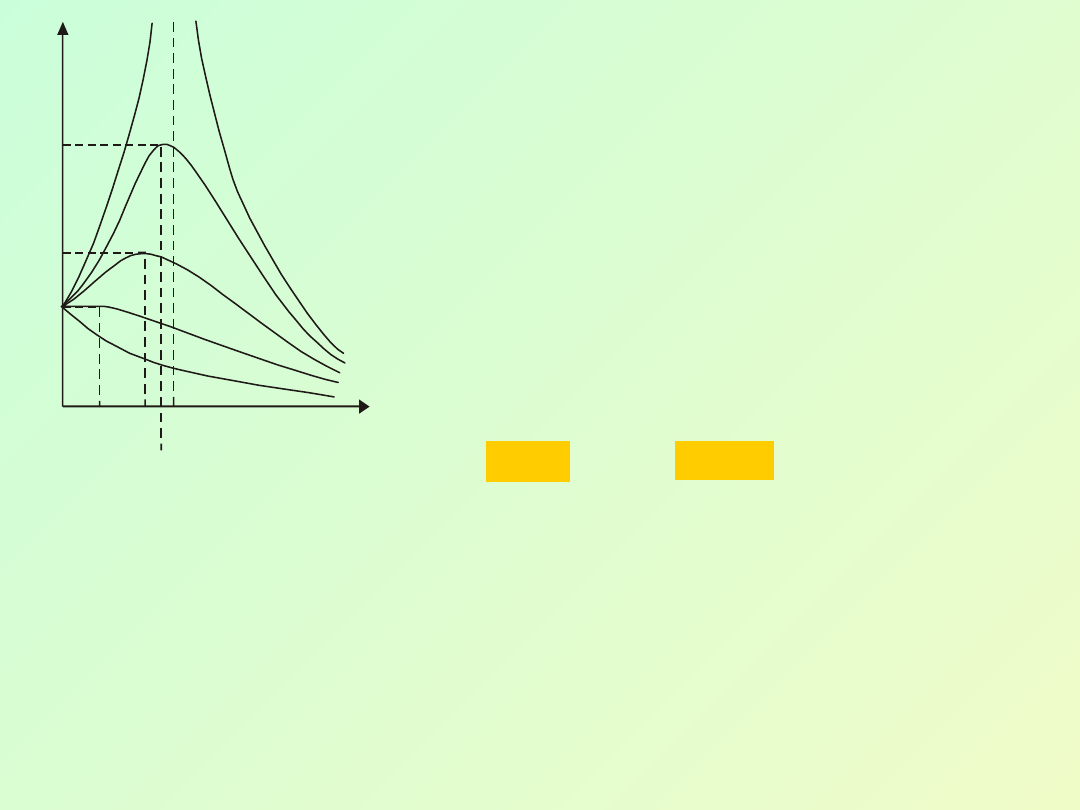
Wykres przedstawiający funkcję

nazywamy krzywą rezonansu. Na rysunku
przedstawiono krzywe rezonansu dla
różnych

wartości

współczynnika

tłumienia . Z rysunku tego wynikają

następujące wnioski:

>    Maksymalna wartość amplitudy A

r

jest tym większa, im mniejszy jest
współczynnik tłumienia , a gdy

, to

(patrz 

o

na rys.).

 



o

A

0









r

A

 

  >  Jeżeli tłumienie jest słabe (

1

i 

2

na rys.6.8) to A

r

osiąga

maksimum, gdy pulsacja  przyjmie wartości nieco mniejsze od

pulsacji drgań własnych 

o

. Im mniejsza jest wartość , tym bardziej



r

zbliża się do wartości 

o

.

   >  Przy bardzo silnym tłumieniu (

3

i 

4

na rys.6.8) rezonans nie

występuje; maksymalna amplituda drgań A

r

jest osiągana, gdy  jest

bliskie zera.

40

Wartość pulsacji siły wymuszającej 

r

, dla której

amplituda drgań jest maksymalna, nazywa się pulsacją
rezonansową. Odpowiadająca jej amplituda A

r

nazywa

się amplitudą rezonansową.

Wyrażenia na A

r

i 

r

można otrzymać ze wzoru (6.32).

Amplituda przyjmuje wartość maksymalną, gdy
wielomian pod pierwiastkiem osiąga minimum.

Obliczając jego pochodną względem  i przyrównując ją

do zera, znajdujemy

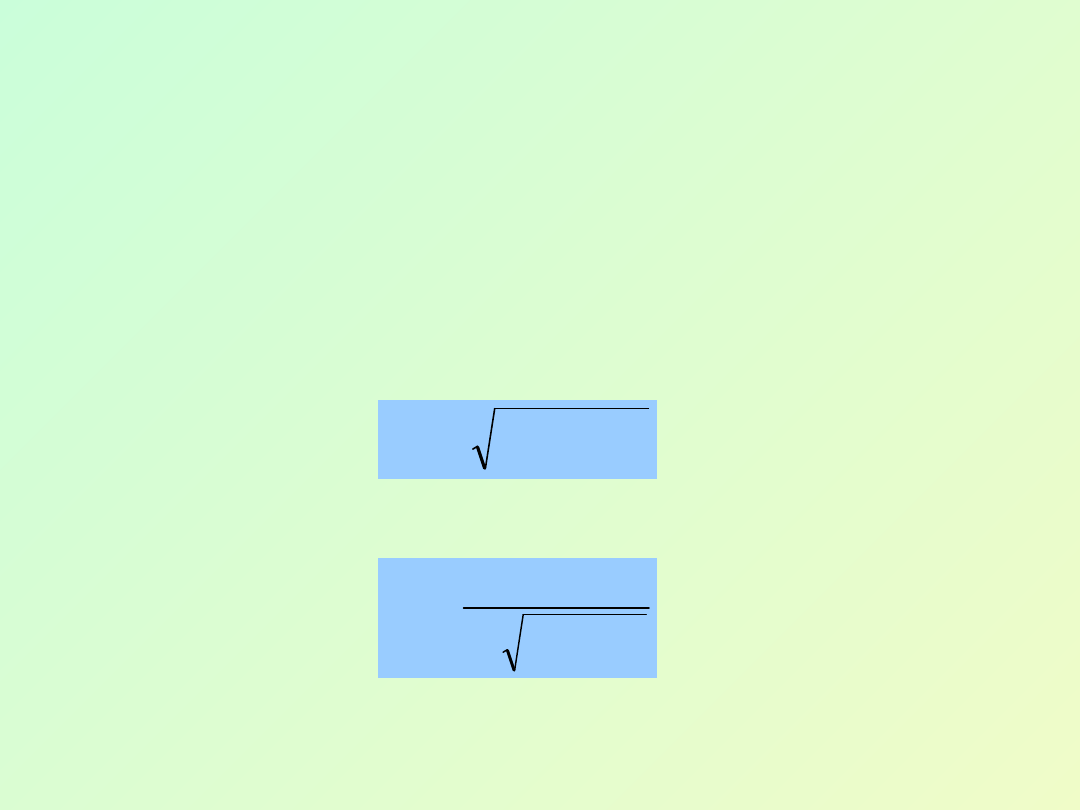
(6.34)

Podstawiając (6.34) do (6.32), otrzymujemy

(6.35)

2

2

o

r

2









2

2

o

o

r

2

p

A











41

Zjawisko rezonansu jest bardzo rozpowszechnione

w przyrodzie i technice. Skutki rezonansu mogą być
pozytywne lub negatywne. Na przykład, wirujące części
maszyny, jeżeli nie są dokładnie wyważone, wymuszają
drgania innych części maszyny i jeżeli jest spełniony przy
tym warunek rezonansu, to amplituda drgań
wymuszonych może być taka duża, że doprowadzi to do
zniszczenia drgających części.

Ze zjawiskiem rezonansu spotykamy się jadąc np.

autobusem: przy pewnej prędkości obrotów silnika szyby
lub niektóre części karoserii zaczynają silnie drgać.

42