Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie
Wydział Inżynierii Mechanicznej i Robotyki
TEROIA MASZYN I MECHANIZMÓW
Wykonał: Sprawdził:
Paweł Tomach dr inż. Józef Felis
Rok 2005/6 Grupa C11 Data……………
Ocena…………..
TEMAT PROJEKTU :
Synteza strukturalna i geometryczna mechanizmu
Zdefiniowanie wymiarów mechanizmu, oraz parametrów jednego jego położenia
Schemat mechanizmu
Wyznaczenie ruchliwości mechanizmu, podział na grupy strukturalne oraz klasyfikacja mechanizmu.
Podział mechanizmu
Analiza kinematyczna mechanizmu.
Analiza kinematyczna mechanizmu metoda grafoanalityczna.
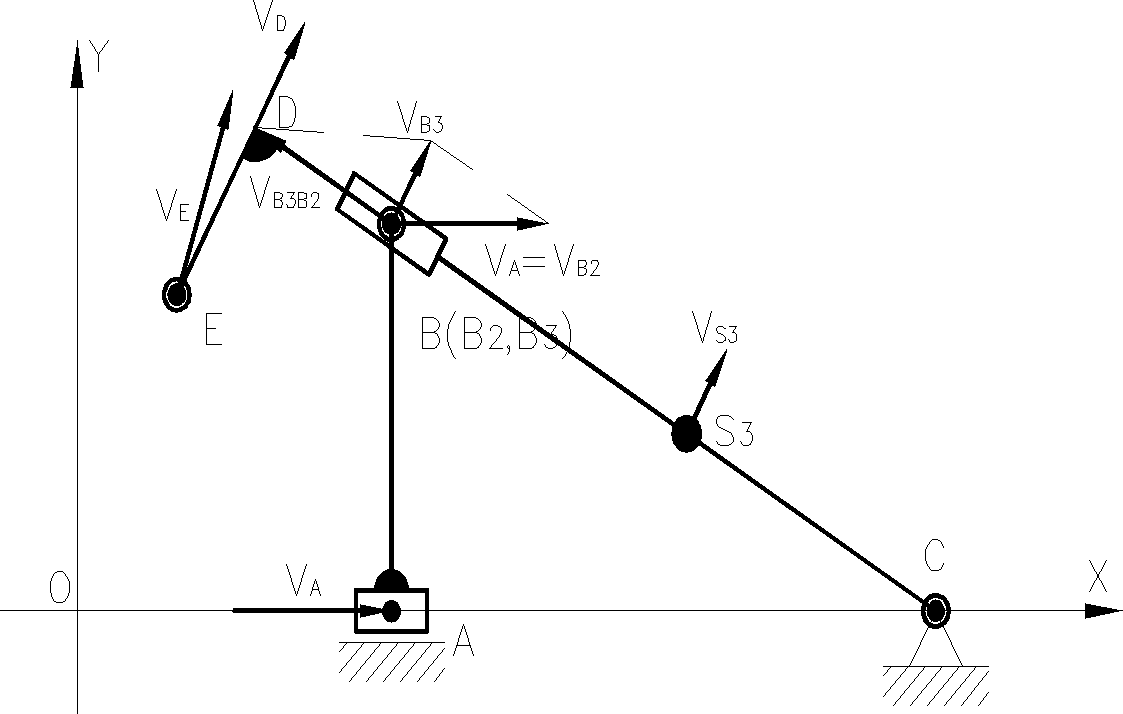
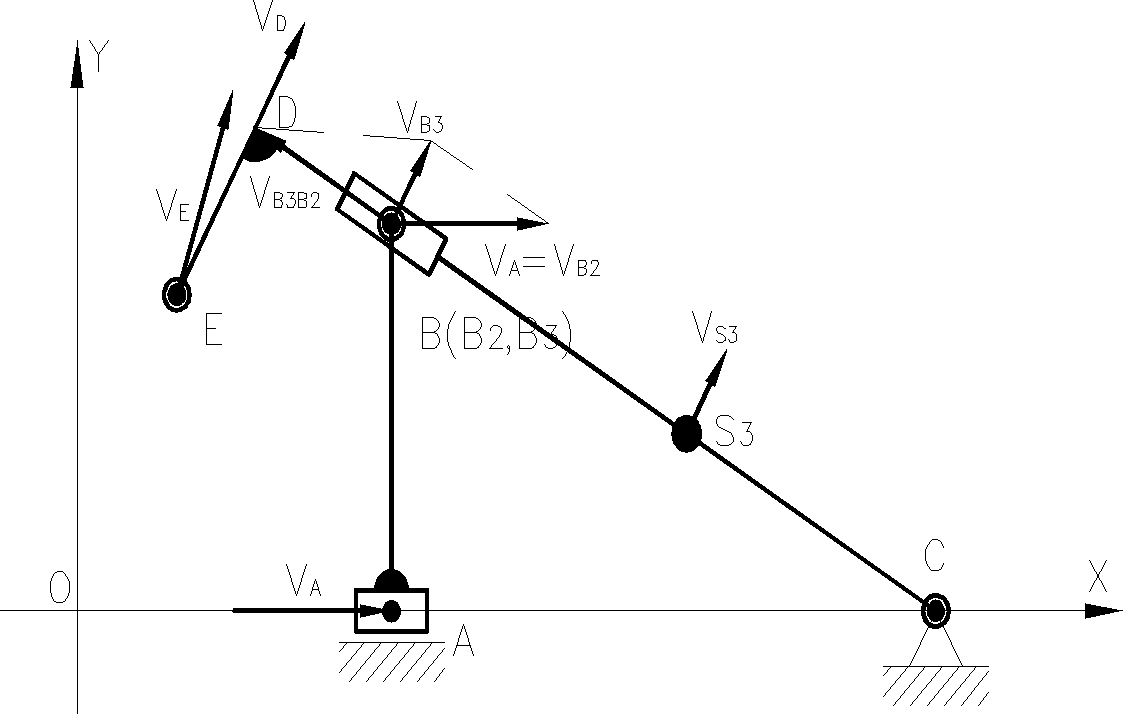
Schemat rozkładu prędkości
Grafoanalityczna analiza prędkości mechanizmu
Plan prędkości
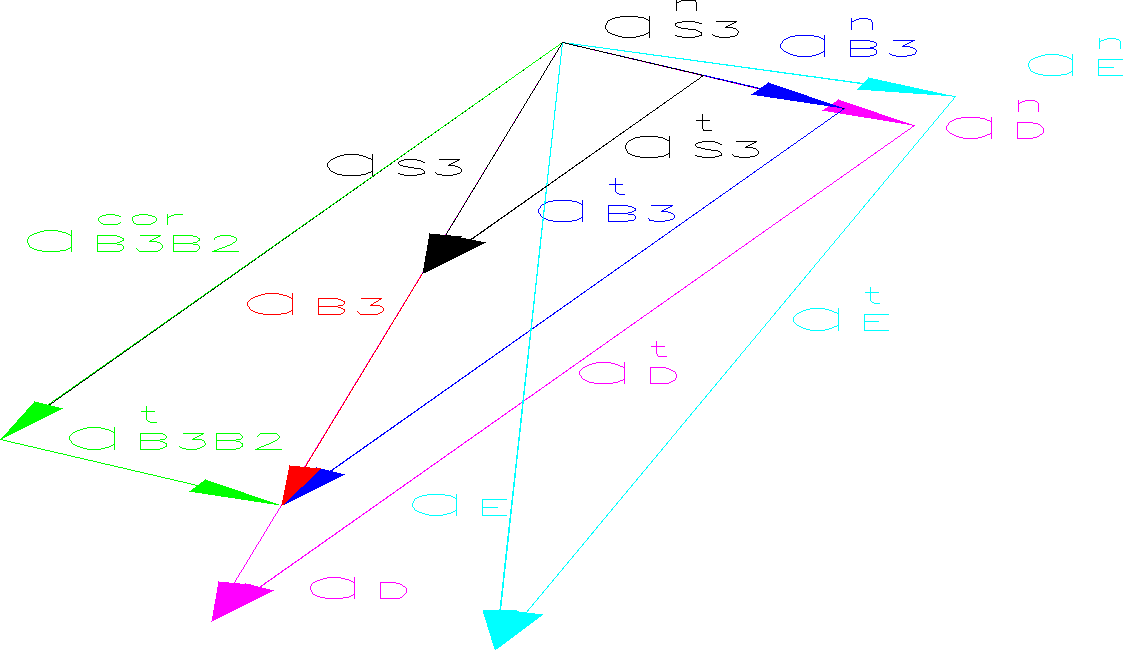
Grafoanalityczna analiza przyśpieszeń mechanizmu
Plan przyspieszeń
Analiza kinematyczna mechanizmu metoda analityczna.
Schemat mechanizmu do analizy metodą analityczną
Wyznaczenie nieznanych parametrów konstrukcyjnych mechanizmu
Analiza prędkości mechanizmu.
Analiza przyspieszeń mechanizmu
Analiza kinematyczna mechanizmu za pomocą programu SAM4.2
Schemat mechanizmu zamodelowany w programie SAM 4.2
Schemat mechanizmu w SAMie
Wyniki analizy kinematycznej w programie
Wyniki analizy
Podsumowanie analizy kinematycznej mechanizmu, oraz zestawienie wyników
Analiza kinetostatyczna mechanizmu.
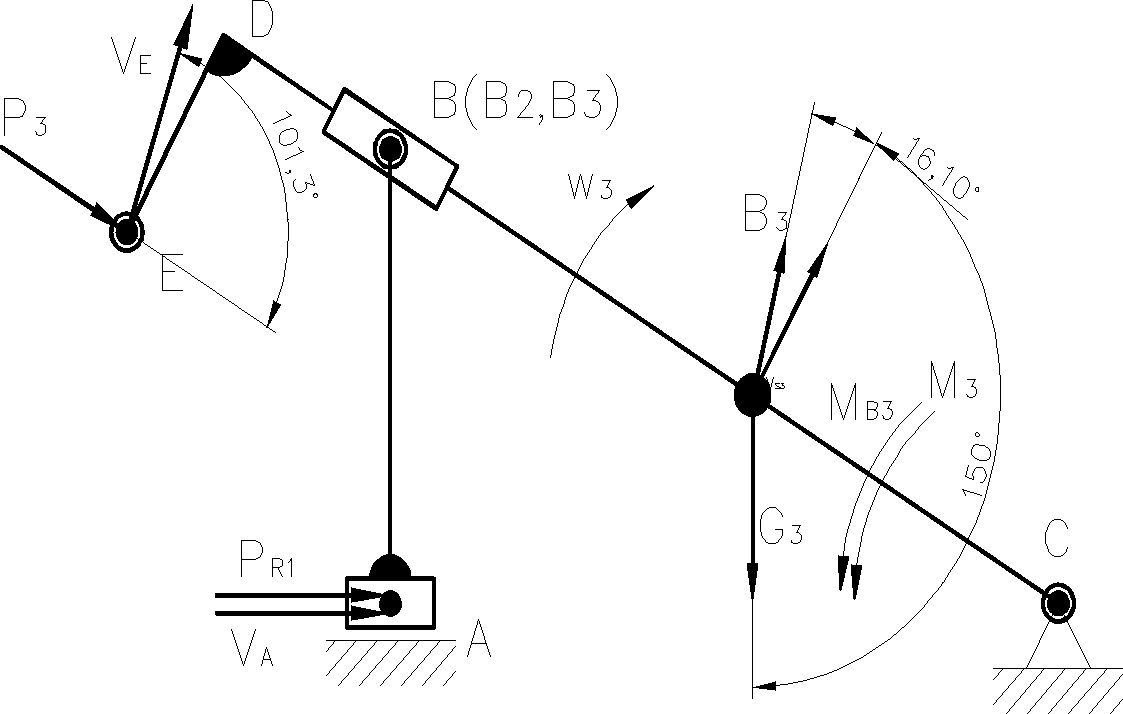
Mechanizm do analizy kienteostatycznej
Założenia analizy:
Wyznaczenie sił bezwładności działających na mechanizm:
Wyznaczenie sił grawitacji działających na mechanizm:
Odrzucenie członu napędzającego, oraz uwolnienie układu od więzów
Uwolnienie układu od więzów (odrzucenie członu napędzającego)
Równanie wektorowe równowagi sił działających na grupę strukturalną
Wyznaczenie nieznanych reakcji z równania momentów i planu sił
Plan sił
Wyznaczenie siły równoważącej działającej na człon napędzający
Wyznaczenie siły równoważącej działającej na człon metoda mocy chwilowych
Mechanizm do analizy metodą mocy chwilowych
Podsumowanie analizy kinetostatycznej
W poniższym podpunkcie zostały przyjęto, wymiary mechanizmu oraz ograniczenia warunkujące jego prawidłową prace i działanie. Również założyłem początkowe położenie mechanizmu, oraz prędkości i przyspieszenie członu napędzającego.
● Przyjęto wymiary:
|AB|=0,5[m] φ1=90[°]
|DE|=0,25[m] φ2=150[°]
|CD|=1,25[m] φ2=150[°]
oraz dla jednego położenia mechanizmu
|OA|=0,5[m]
● Zdefiniowano prędkość i przyspieszenie członu napędzającego:
![]()
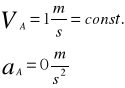
●Podział na grupy strukturalne.
●Grupa strukturalna analizowanego mechanizmu jest klasy II
●Ruchliwość mechanizmu:
![]()
w- ruchliwość mechanizmu
n- liczba członów mechanizmu
i- klasa par występujących w łańcuchu kinematycznym
p4- para kinematyczna klasy czwartej
p5- para kinematyczna klasy piątej
●Wyznaczenie ruchliwości analizowanego mechanizmu
n= 3
p4=0
p5=4
![]()
Ruchliwość mechanizmu w=1
Analiza kinematyczna wykonana jest dla jednego wybranego położenia mechanizmu.
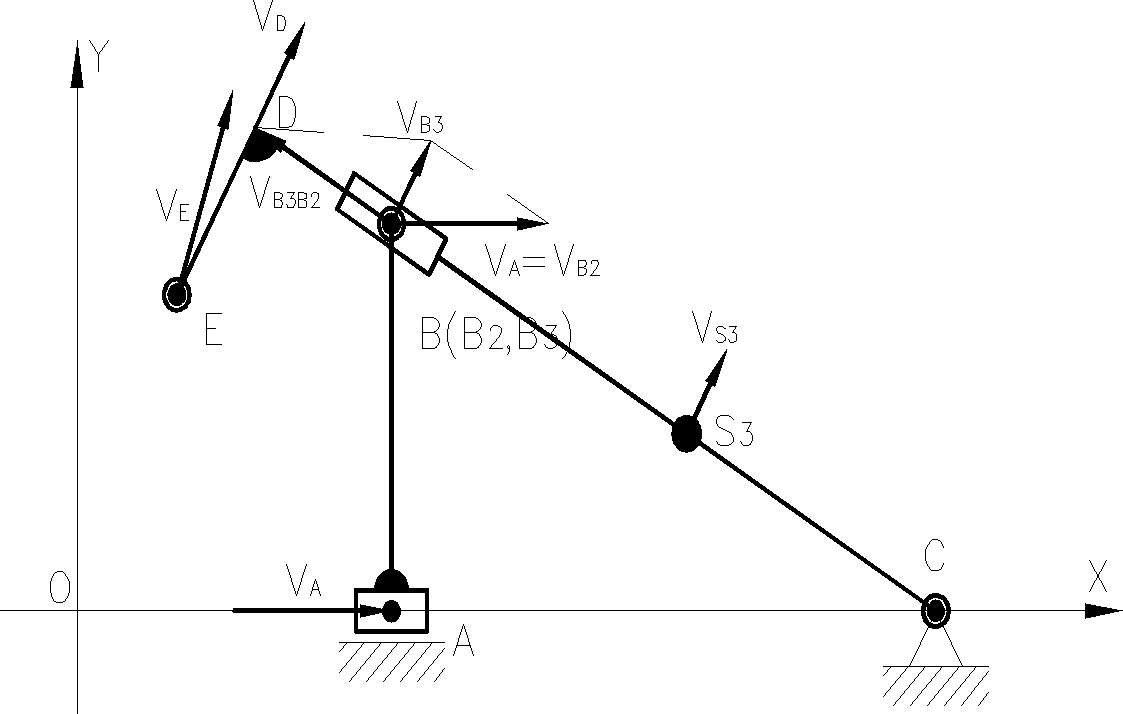
●Wyznaczenie prędkości VA(zdefiniowanie))
Prędkość VA=2![]()
●Wyznaczenie prędkości VB2
VA= VB2=2![]()
●Wyznaczenie prędkości VB3
![]()
Wektor prędkości VB2 jest zgodny z kierunkiem i zwrotem wektora VA
Wektor prędkości V B3B2 jest równoległy |BC|
Wektor prędkości V B3 jest prostopadły |BC|
●Wyznaczanie prędkości punktu VC
![]()
●Wyznaczenie prędkości VD
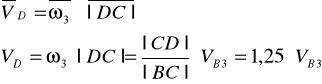
Wektor prędkości V D jest prostopadły |DC|
●Wyznaczenie prędkości VE
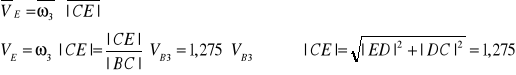
Wektor prędkości V E jest prostopadły |CE|
●Prędkość (m3) środka masy
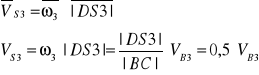
Wektor prędkości V S3 jest prostopadły |S3C|
●Przyjęcie podziałki rysunkowej dla planu prędkości:
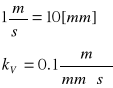
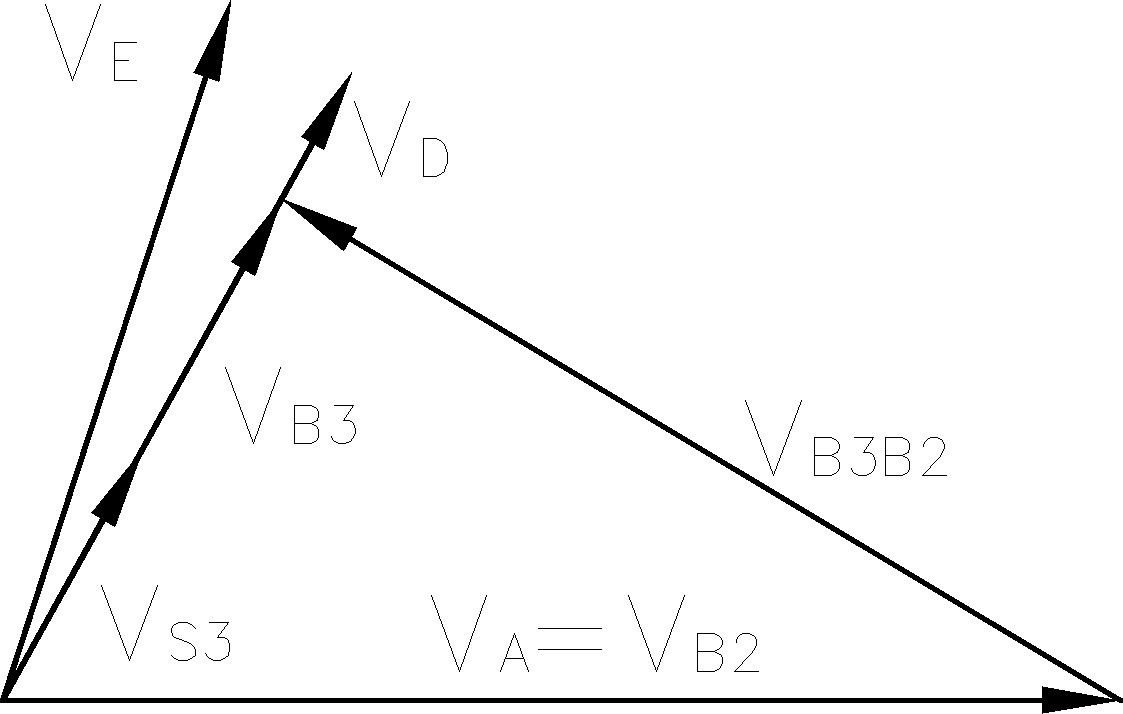
●Z planu prędkości odczytano następujące wartości:

●Wyznaczenie prędkości kątowej członu drugiego i trzeciego
![]()
●Przyspieszenie punktu A (członu napędzającego) zostało zdefiniowane w punkcie pierwszym i wynosi
![]()
●Wyznaczenie przyspieszenia pkt. B2
aA= aB2=0![]()
●Wyznaczenie przyspieszenia pkt. B3
![]()
gdzie
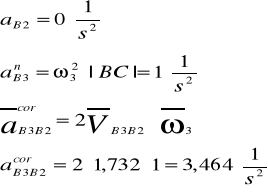
Wektor przyspieszenia aB3n jest równoległy do |BC|
Wektor przyspieszenia aB3t jest prostopadły do |BC|
Wektor przyspieszenia aB3B2cor jest prostopadły do |BC|
Wektor przyspieszenia aB3B2t jest równoległy do |BC|
●Wyznaczanie przyspieszenia punktu C
![]()
●Wyznaczanie przyspieszenia punktu D
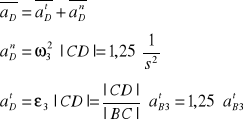
Wektor przyspieszenia aDn jest równoległy do |BC|
Wektor przyspieszenia aDt jest prostopadły do |BC|
●Wyznaczanie przyspieszenia punktu E
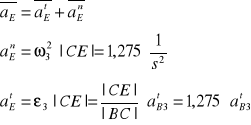
Wektor przyspieszenia aDn jest równoległy do |EC|
Wektor przyspieszenia aDt jest prostopadły do |EC|
●Wyznaczanie przyspieszenia punktu S3
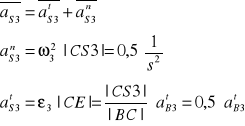
Wektor przyspieszenia aDn jest równoległy do |S3C|
Wektor przyspieszenia aDt jest prostopadły do |S3C|
●Przyjęcie podziałki rysunkowej dla planu przyśpieszeń:
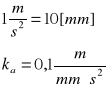
●Wyniki (najważniejsze -reszta na planie)
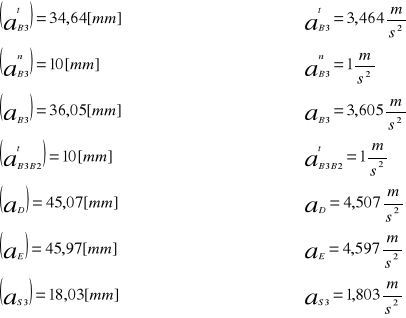
●Wyznaczenie przyspieszenia kątowego członu trzeciego
![]()
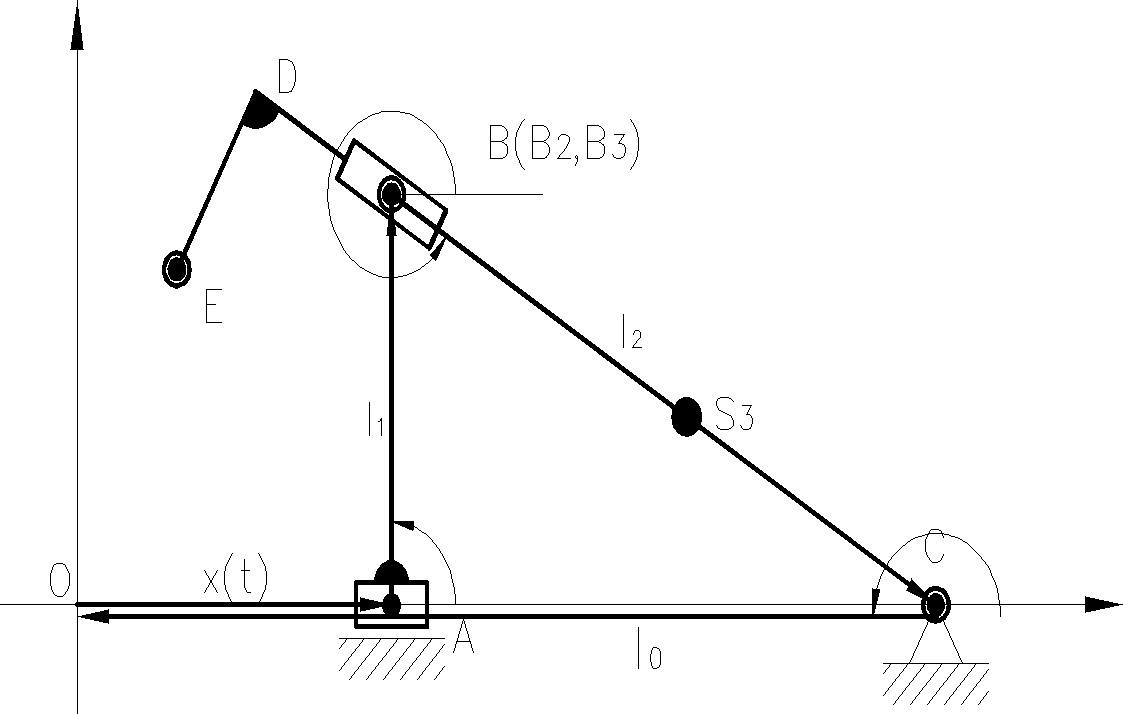
●x(t) definiuje ruch członu napędzającego
●φ3(t), l2(t), są funkcjami zmiennymi w czasie
●Poniższe funkcje są funkcjami stałymi i nie zależą od czasu, przyjmują zawsze stalą wartość:
φ1(t)= 90° l1(t)=0,5[m]
φ2(t)=330◦ l0(t)=1,366[m]
φ0(t)=180 ◦
● Dla zadanego położenia mamy
x1(t0=0)=0,5[m] v1(t0=0)=2 [m/s] a1(t0=0)=0 [m/s2]
●Wyznaczenie ogólnych równań ruchu
![]()
Po zrzutowaniu na osie układu wsp. otrzymujemy
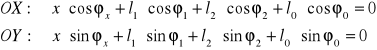
●Nieznany parametr φ2(t)
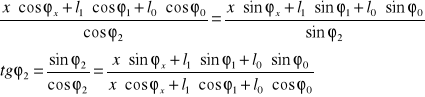
Po uwzględnieniu stałych parametrów otrzymujemy
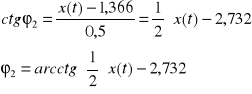
Dla jednego położenia mamy:
![]()
●Nieznany parametr l2(t)
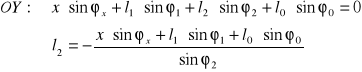
Po podstawieniu stałych parametrów mechanizmu otzrymujemy
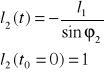
Po uwzględnieniu stałych parametrów otrzymujemy
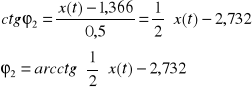
Dla jednego położenia mamy:
![]()
Różniczkując równania drogi po czasie otrzymamy zależność odpowiednich prędkości od czasu.
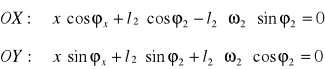
●Nieznany parametr a2(t)
Obracając układ o kąt φ2(t) wyznaczy nieznany parametr z równania OX
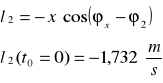
●Nieznany parametr ω2(t)
Obracając układ o kąt φ2(t) wyznaczymy nieznany parametr z równania OY
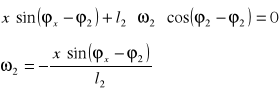
Dla jednego położenia
![]()
Różniczkując równania prędkości po czasie otrzymamy zależność odpowiednich przyspieszeń od czasu.
●Nieznany parametr a2(t)
Nieznaną wartość przyspieszania wyznaczymy bezpośrednio z równania prędkości od czasu przez wyznaczenie pochodnej tego równania
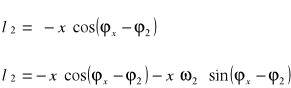
Dla jednego położenia mamy
![]()
●Nieznany parametr ε2(t)
Nieznaną wartość przyspieszania wyznaczymy bezpośrednio z równania prędkości od czasu przez wyznaczenie pochodnej tego równania
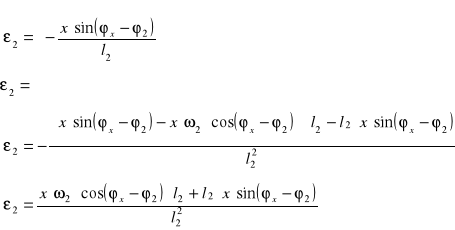
Dla jednego położenia mamy
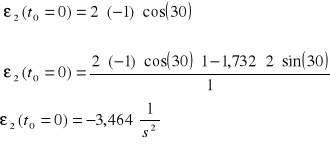
|
Metoda grafoanalityczna |
Metoda analityczna |
SAM |
Prędkości liniowe i kątowe mechanizmu |
|||
VA |
2 |
2 |
2 |
VB2 |
2 |
2 |
2 |
VB3B2 |
1,732 |
-1,732 |
- |
VB3 |
1 |
- |
1 |
VD |
1,25 |
- |
1,25 |
VE |
1,275 |
- |
1,275 |
VS3 |
0,5 |
- |
0,5 |
ω2 |
1 |
-1 |
-1 |
ω3 |
1 |
-1 |
-1 |
Przyspieszenia liniowe i kątowe mechanizmu |
|||
aA |
0 |
0 |
0 |
aB2 |
0 |
0 |
0 |
aB3 |
3,605 |
- |
3,606 |
acorB3B2 |
3,465 |
- |
- |
atB3B2 |
1 |
-1 |
- |
aD |
4,507 |
- |
4,507 |
atD |
4,33 |
- |
- |
anD |
1,25 |
- |
- |
aE |
4,597 |
- |
4,596 |
atE |
4,417 |
- |
- |
anE |
1,275 |
- |
- |
aS3 |
1,803 |
- |
1,803 |
ε2 |
3,464 |
-3,464 |
-3,464 |
ε3 |
3,464 |
-3,464 |
-3,464 |
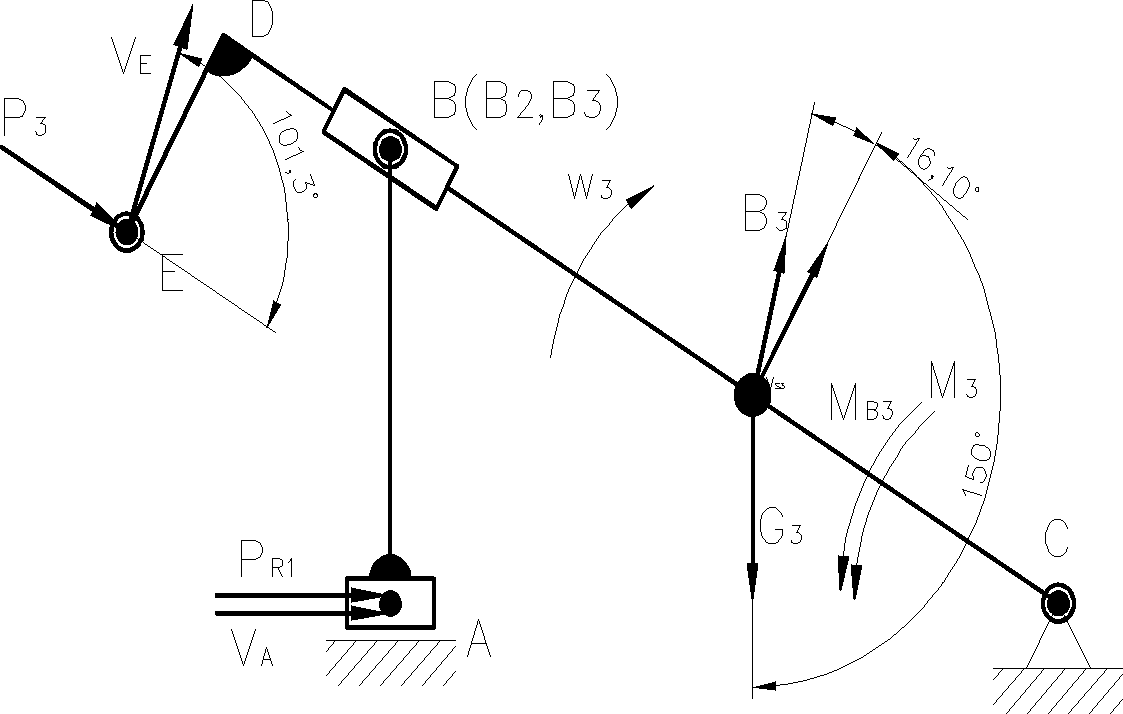
Dla mechanizmu przyjmuje:
●Wartości sił obciążających mechanizm:
M3=10Nm
P3=10N
●Człon drugi mechanizmu posiada: masę m2= 2 kg
●Moment bezwładności JS3
![]()
●Mechanizm znajduje się w polu grawitacyjnym ![]()
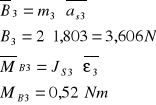
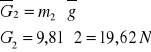
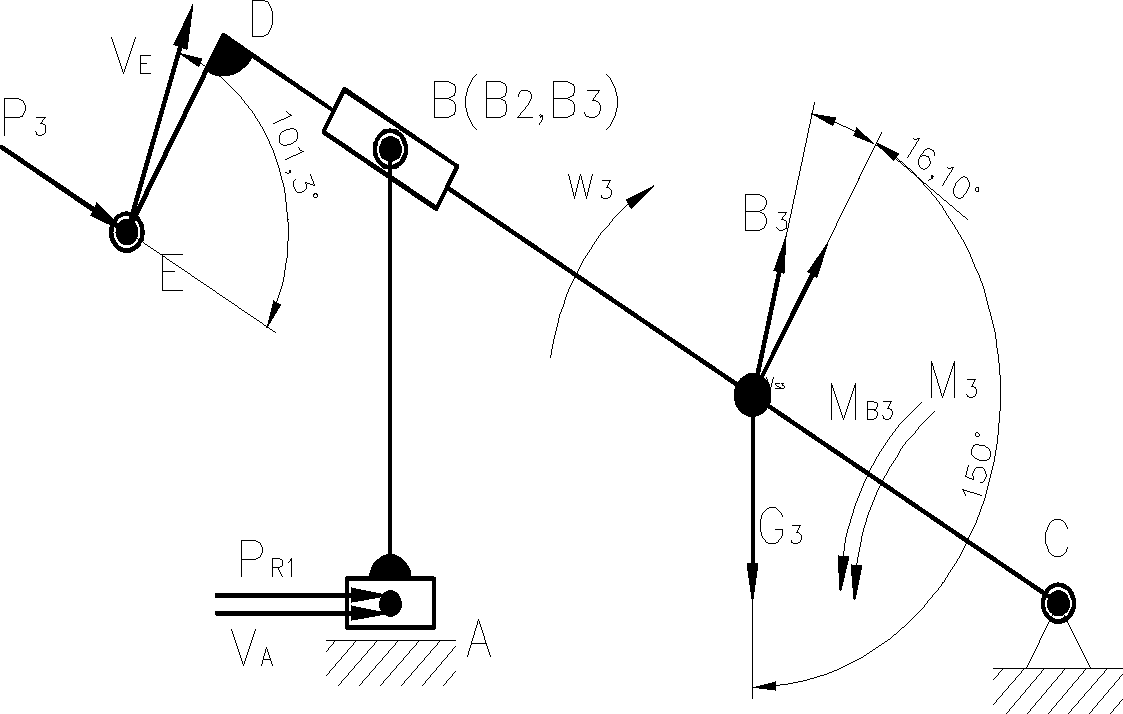
●Dla grupy strukturalnej
![]()
●Dla członu drugiego
![]()
●Dla członu trzeciego
![]()
●Wyznaczenie nieznanej reakcji M23 z równania momentów względem punktu B
![]()
●Wyznaczenie nieznanej reakcji R t12 z równania momentów względem punktu C
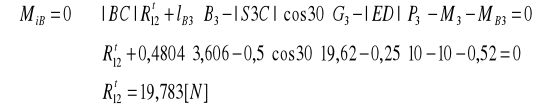
● Na podstawie planu sił wyznaczono
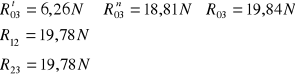
●Równanie sił dla członu napędzającego oraz siła równoważąca
![]()
R01=17,13[N]
PR1=9,89[N]
●Wyznaczenie momentu M01
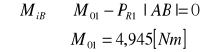
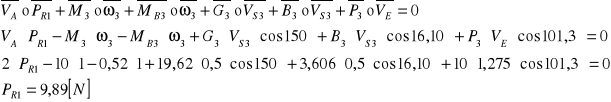
●Siła równoważąca:
![]()
|
Metoda wykreślna |
Metoda mocy chwilowych |
PR1 |
9,89 |
9,89 |
- 19 -
φ2
φ1
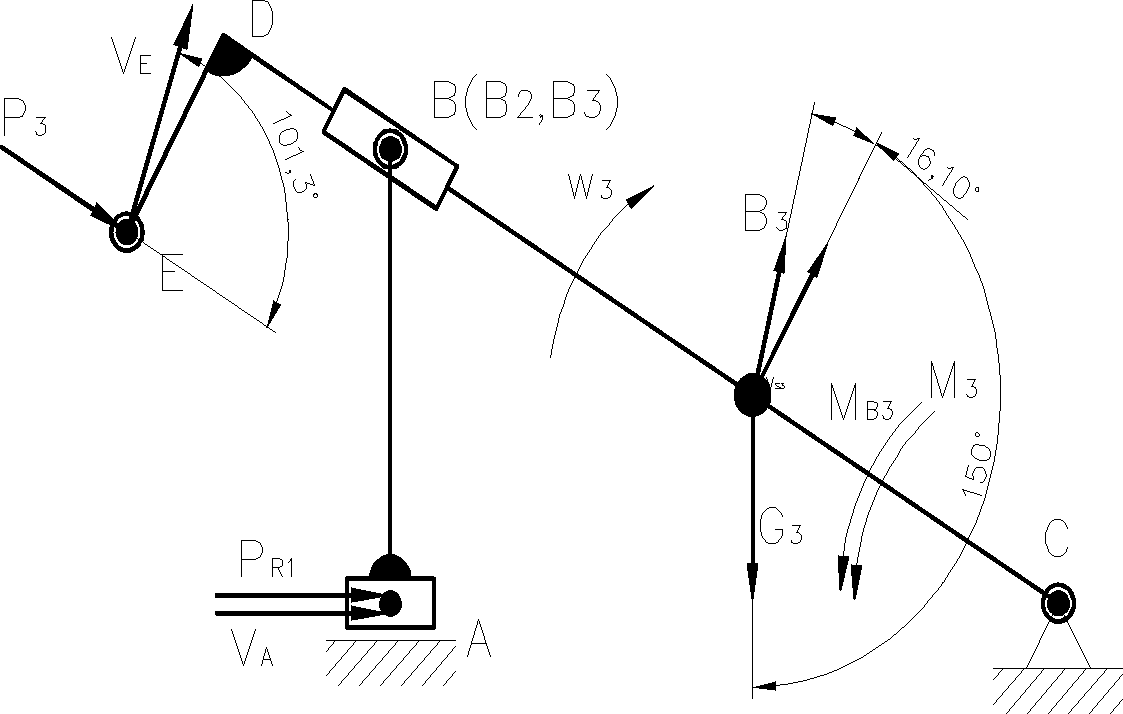
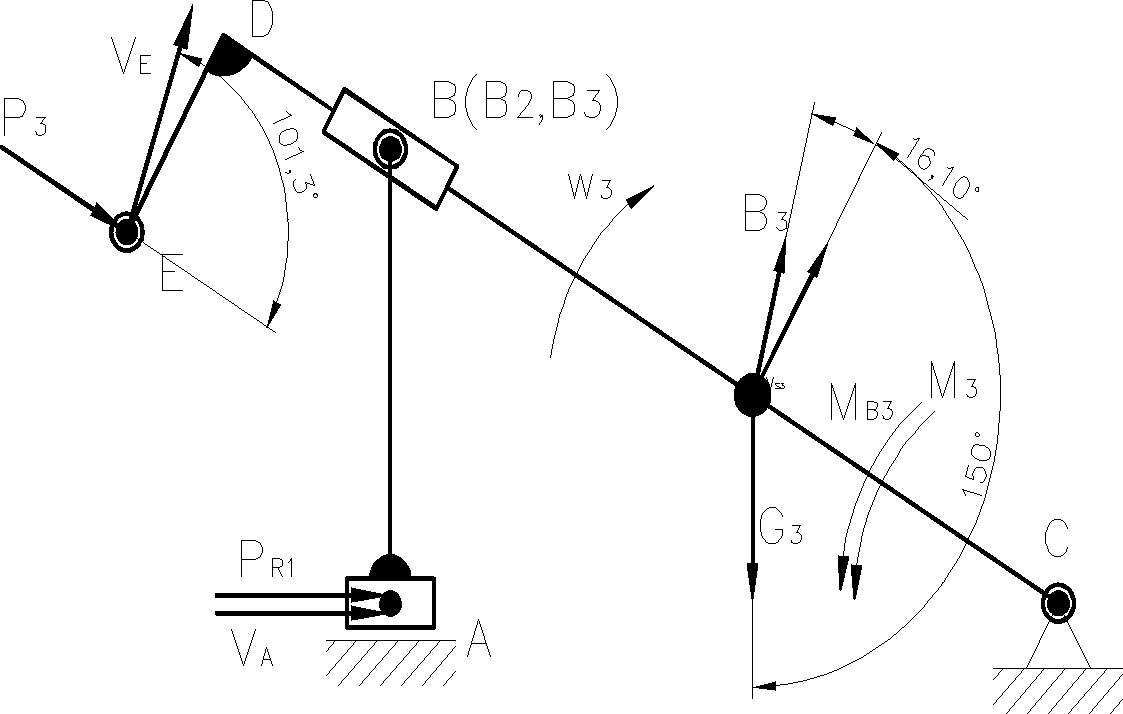
Rys. 12 Siły na człon napędzający
φ0
φ1
πV
πa
Wyszukiwarka
Podobne podstrony:
TMM projekt, Studia Mechatronika, Semestr 4, TMM, Projekty
najlepsz wersja chyba, Studia Mechatronika, Semestr 4, TMM, Projekty
2B-I, Studia Mechatronika, Semestr 4, TMM, Projekty
tmm3a odz, Studia Mechatronika, Semestr 4, TMM, Projekty
TMM+3b - zmieniony, Studia Mechatronika, Semestr 4, TMM, Projekty
TMM sprawko 1, Studia Mechatronika, Semestr 4, TMM
TMM+3b, Studia Mechatronika, Semestr 4, TMM, Projekty
TI -wyklad 2, Studia - Mechatronika, I semestr, Technologia Informacyjna
Elektronika 6, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw. 6
Sprawko nasze, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw. 5
sprawko metro, Studia Mechatronika, Semestr 4, Metrologia
Elektronika 5 protokół stary, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw. 5
Pytania na kolosa, Studia, Mechatronika, Semestr III, Techniki wytwarzania i systemy montażu, Wykład
Elektronika 6 protokół nowy, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw. 6
Sprawko stabilizacja napięcia, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw.
opracowanie 4 mechana, Studia - Mechatronika, III semestr, Mechanika Techniczna
więcej podobnych podstron