Zadanie 5

Wagon kolejowy o masie m, poruszający się z prędkością
, uderza o rampę zderzakami, które pod działaniem siły P uginają się o Δl. Wyznaczyć ugięcie zderzaków przy uderzeniu wagonu.

Dane: m, v, P, Δl

Szukane: s

Rozwiązanie

Przyjmujemy założenie, że ugięcie zderzaka jest wprost proporcjonalne do działającej siły, w wyniku czego zakładamy, że zderzak posiada sprężystość:
.

Sytuację zderzenia przedstawia poniższy rysunek:

Od momentu zetknięcia się zderzaka z rampą, na wagon zaczyna działać siła hamująca, która jest wprost proporcjonalna do ugięcia zderzaka. Wagon w wyniku działania tej siły porusza się ruchem niejednostajnie opóźnionym aż do zatrzymania się po przebyciu drogi s, która jednocześnie równa jest ugięciu się zderzaka.

Siłę hamującą, w funkcji przesunięcia x zapisać można jako:

Różniczkowe równanie ruchu wagonu podczas hamowania wywołanego zderzeniem ma postać:

czyli:

rozwiązujemy równanie:

/:m

równanie charakterystyczne:

niech

Równanie to ma dwa pierwiastki urojone:

Wobec tego całka ogólna równania przybiera postać:

stałe całkowania wyznaczamy z warunków początkowych:

dla t = 0:

stąd:

zatem:

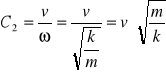
i ostatecznie:

prędkość:

Wagon zatrzyma się więc dla najmniejszego dodatniego t = t₁, dla którego
,

skąd:

Obliczamy przebytą w tym czasie przez wagon drogę:

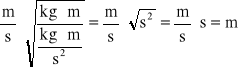
(jednostki się zgadzają)

Zatem ugięcie zderzaków wyniesie
.