Twierdzenie 2 - Stolz

Jeżeli:

a)
oraz

b) ciąg
gdzie
dla

posiada granicę skończoną lub nieskończoną wtedy

Np. znależć granice ciągu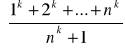
gdzie k jest ustaloną liczbą naturalną

Oznaczmy
jest widoczne, że

oraz

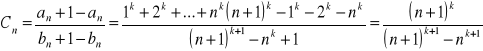
Dwumian Newtona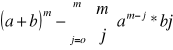
gdzie symbol Newtona: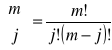

gdzie m!= 1,2,3,...

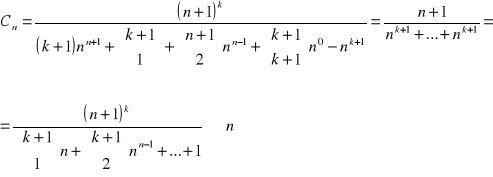
wtedy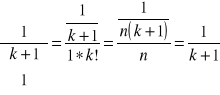
czyli

Z twierdzenia Stolza wynika następujące twierdzenie trzecie: (z granicy średniej arytmetycznej, wyrazów ciągu ) Jeżeli ciąg
jest zbieżny, to ciąg średnich arytmetycznych
jest zbieżny do tej samej granicy.

Dowód:

Wystarczy w twierdzeniu Stolza przyjąć
,
wtedy

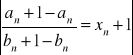
- zbieżny do g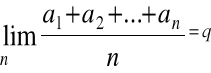

Twierdzenie 3 - odwrotne do twierdzenia Stolza o średniej arytmetycznej nie jest prawdziwe.

Np. Ciąg
gdzie
dla n=1,2,... jest rozbieżny.

Natomiast ciąg średnich arytmetycznych ma postać :

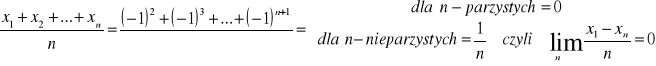
Twierdzenie o średniej arytmetycznej jest prawdziwerównież dla ciągów mających granicę niewłaściwą

PODCIĄGI- granica górna i dolna.

Niech będzie dany ciąg
oraz rosnący ciąg liczb naturalnych
tzn.

wtedy ciąg
nazywamy podciągiem ciągu
.

Podciąg
lub ciąg
są podciągami ciągu
.

Podciąg
różny od ciągu
nazywamy podciągiem właściwym.

Np.

Ciąg
lub ciąg
są podciągami ciągu
,

natomiast ciąg a1 a1 a2 a2 ... nie jest podciągiem ciągu

Jeżeli ciąg
i podciąg ciągu
jest zbieżny, to granicą

Nazywamy granicą częściową ciągu
.

Twierdzenie 4

Jeżeli ciąg
jest zbieżny g
R lub rozbieżny do
To wtedy jego podciąg
jest zbieżny do g lub rozbieżny do
. Oprócz ciągów rozbieżnych do
istnieją ciągi, których rozbieżność Jest spowodowana skupianiem się wyrazów ciągu dookoła więcej niż jednego punktu osi liczbowej.

Np.: Wyrazy ciągu
skupiają się wokół punktów 1,0 .

Definicja:

Ciąg
posiada punkt skupienia
jeżeli
Zatem wyżej wymieniony ciąg ma dwa punkty skupienia s1=1i s2=0 Jeżeli ciąg
ma granice q, to q jest punktem skupienia tego ciągu.

Twierdzenie 5- (Balzano - Weistloosa)

Każdy ciąg ograniczony liczbami żeczywistymi posiada co najmniej jeden punkt skupienia, oznaczony przez
, ciąg liczb żeczywistych. Niech E będzie zbiorem granic częściowych ciągu
. Wtedy granicą górną Ciągu
nazywamy wielkość
,

A granicą dolną ciągu
nazywamy wielość

Np.

Ciąg
=
ma następujące granice: górną i dolną

Ciągi monotoniczne:

Ciąg
nazywamy rosnącym bądź malejącym, jeżeli

Jeżeli zachodzą nierównowści nieostre
to mówimy o ciągu nimalejącym, nierosnącym.

Twierdzenie 6

a)Ciąg --> [Author:w.k]
niemalejący ograniczony z góry tzn.

jest zbieżny.

b) Jeżeli ciąg niemalejący
jest nieograniczony z góry to

a z dołu to

Dowód:

a) zakładamy, że ciąg niemalejący
spełnia warunek

Ponieważ zbiór
jest ograniczony, więc zbiór posiada kres górny

, zatem

oraz

dla k= 1,2,

Oznacza to, że

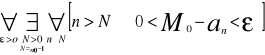
czyli

b) niech ciąg
będzie niemalejący i ograniczony z góry, tzn.

czyli korzystając monotoniczności ciągu otrzymujemy

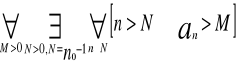
Definicja liczby e

e=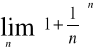

Można pokazać, że ciąg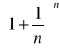
jest rosnący i ograniczony z góry przez 3

a więc jest to ciąg zbieżny.

Zachodzi twierdzenie ogólne:

Twierdzenie 7

Jeżeli
jest ciągiem dowolnym-rozbieżnym do

jest dowolnym ciągiem rozbieżnym do

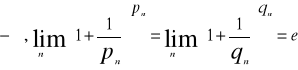
Dowód:

Niech
będzie dowolnym ciągiem liczb naturalnych rozbieżnym do

Ponieważ:

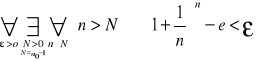
więc dla
>N otrzymujemy

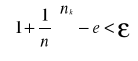
czyli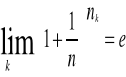

Jeżeli dowolny ciąg
, gdzie
>1 dla k=1,2, dąży do
,że

.

Z nierówności:

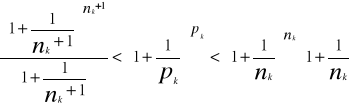
oraz z twierdzenia o trzech ciągach otrzymujemy

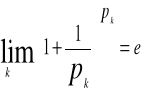
Jeżeli dowolny ciąg
gdzie
<-1 dla k=1,2, dąży do
to przedstawiając
otrzymujemy

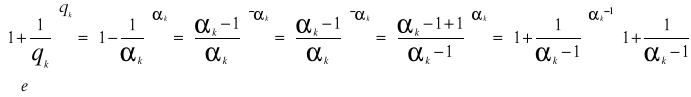
przy założeniu, że
.

Można wykazać, że liczba e jest liczbą nieogranuczoną ,ponadto

e=2,71828

Twierdzenie 8

a) jeżeli p>0,to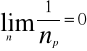

b) jeżeli p>0,to

c)

d) jeżeli p>0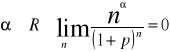

e) jeżeli

f)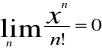
dla dowolnej liczby rzeczywistej x.

Dowód:

Skorzystamy ze wzoru dwumianowego newtona oraz z tego, że

Dla n=1,2, kolejno otrzymujemy

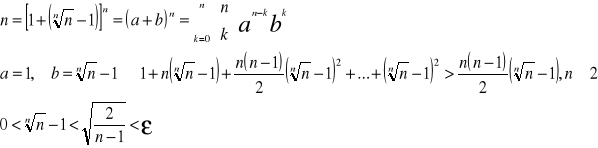
dla n takich, że n>1+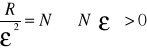

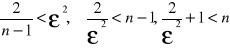
zatem z twierdzenia o trzech ciągach wynika, że

Twierdzenie 9- (zasada zbieżności ciągu liczb rzeczywistych)

Ciąg
jest zbieżny
gdy spełniony jest tzw. warunek

Cauchy'ego

Np.

a) znaleść

Podstawiając za n różne liczby naturalne otrzymujemy wyrażenie nieograniczone typu

Z twierdzenia 8 wynika, że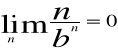
b>1.

Zatem dla dowolnie dużych n zachądzą nierównności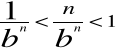

Oznaczamy przez
dowolnie małą llllliczbę dodatnią i podłóżmy

a>1 wtedy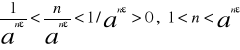

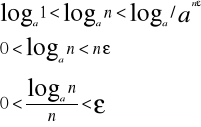
przy dostatecznie dużych n.

Zatem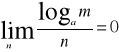

2) znaleźć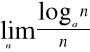
, gdy 0<a<1-w domu

Szeregi liczbowe-

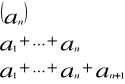
Niech będzie dany ciąg liczb rzeczywistych
. Dodajemy kolejno wyrazy ciągu
tworząc tzw. sumy częściowe postaci

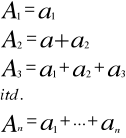
Funkcją lub operatorem nazywamy przyporządkowanie funkcyjne elementom zbioru x
Ø elementów zbioru y
Ø

Jeżeli operator ma wartości liczbowe rzeczywiste lub zespolone to nazywamy go funkcjonałem. Oznaczmy przez
zbiór tych wszystkich ciągów liczb rzeczywistych
dla których ciąg sum częściowych
, jest zbieżny tzn. ma skończoną granicę. Wtedy każdemu ciągowi
można przypożądkować granicę ciągu odpowiadających mu sum częściowych

Przyporządkowanie to jest funkcjonałem określanym na
o wartościach rzeczywistych. Funkcjonał ten nazywamy szeregiem liczbowym i oznaczamy symbolem
Wartość funkcjonału,
czyli szeregu liczbowego w punkcie

nazywamy sumą szeregu i piszemy
.

Niech zbiór
należą wszystkie ciągi liczb rzeczywistych (a_n) dla których ciągu sum częściowych (A_n) są zbieżne lub rozbieżna do +∞ V -∞. Rozszerzmy operator
na zbiór Ω przyjmując dla ciągu a_n, którego ciąg sum częściowych (A_n) dąży do (+∞,-∞)
. Funkcjonał
nazywamy szeregiem zbieżnym. Natomiast operator określamy na zbiorze
nazywamy szeregiem rozbieżnym.

Jeżeli dla ciągu A_n nie posiada granicy skończonej ani nieskończonej to mówimy, że szereg

jest rozbieżny. Mówiąc o szeregu nieskończonym
będziemy na ogół pisać
. Wtedy a_n n=1,2,3... nazywamy wyrazami szeregu.

Przykłady:

1. Szereg geometryczny:
dla xεR. Jest zbieżny dla |x|<1 oraz rozbieżny dla |x|≥1.

1. |x|<1 n-ta suma częściowa ma postać:
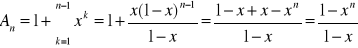
   a wiec szereg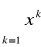
   jest równy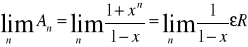
   czyli szereg jest zbieżny dla |x|<1

2. x=1
   
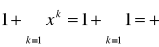
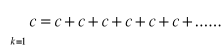
   suma nieskończonej ilości składników

3. x=-1
   ,
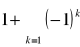
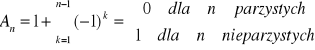
   czyli szereg jest rozbieżny dla x=±1

4. x≥1∨x<-1
   

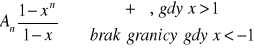
2. Szereg
jest rozbieżny gdy jest rozbieżny do +∞ ciąg sum częściowych.

3. Szereg
jest rozbieżny gdyż ciąg sum częściowych nie posiada granicy właściwej ani niewłaściwej.

Znaleźć sumę szeregu:
,

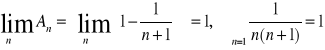
Twierdzenie 1.

Jeżeli szeregi
,
są zbieżne:

1. 
   

2. 
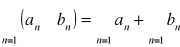
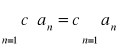
   , gdzie c jest stałą rzeczywistą

Dowód 1.

Ponieważ szeregi

są zbieżne więc ciągi sum częściowych: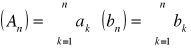
posiadają skończone granice odpowiednio A,B Zatem granica ciągu sum częściowych dla ciągu a_n±b_nwynosi.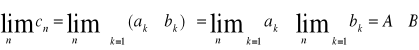
, Suma
, podobnie wykazujemy 2.

Definicja: N-tą resztą szeregu
nazywamy szereg postaci
gdzie n=0,1,2...

Twierdzenie 2.

1. Jeżeli szereg
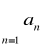
   jest zbieżny to jest zbieżna każda z jego reszt.

2. Jeżeli jedna z reszt szeregu
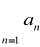
   jest zbieżna to szereg ten jest zbieżny.

WNIOSEK: Odrzucenie skończonej liczby początkowych wyrazów szeregu lub dołączenie na początku szeregu skończonej liczby wyrazów nie ma wpływu na zbieżność szeregu. Szereg
jest zbieżny wtedy i tylko wtedy, gdy.

Twierdzenie 3.

Szereg
jest zbieżny wtedy i tylko wtedy, gdy spełniony jest warunek:
Dowód wynika z zasady zbieżności ciągu liczbowego zastosowanej do ciągu sum częściowych (A_n) [Ćwiczenie do domu !]

Jeżeli w warunku zbieżności z twierdzenia 3 przyjąć m=n to otrzymujemy : warunek koieczny zbieżności szeregu. Jeśli szereg
jest zbieżny, to
.

Warunek a_n->0 nie wystarcza na to aby szereg
był zbieżny.

Kontrprzykład: Zbadać zbieżności szeregu:

Jest spełniony warunek konieczny zbieżności szeregu.

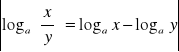
- przypomnienie

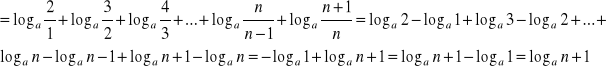
szereg rozbieżny

Przykład. Zbadać szereg harmoniczny

spełniony warunek konieczny zbieżności.

Przypuśćmy, że szereg ten jest zbieżny. Zatem istnieje skończona granica ciągu sum częściowych
. Ponieważ każdy podciąg ciągu zbieżnego jest zbieżny do granicy tego ciągu wiec:

Można napisać następujące oszacowania:

Czyli: Ciąg A_2n-A_n nie dąży do 0. Sprzeczność.

Zatem
=+∞

Twierdzenie 4. (Kryterium porównawcze)

Jeżeli
oraz szereg
jest zbieżny, to szereg
jest zbieżny.

Jeżeli
oraz szereg
o wyrazach mniejszych jest rozbieżny, to szereg
jest rozbieżny.

Dowód.

1. Ponieważ szereg
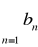
   jest zbieżny więc na podstawie twierdzenia 3 otrzymujemy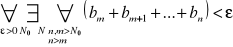
   . Zatem dla n≥m≥N₀ zachodzi nierówność: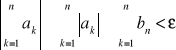
   , czyli z twierdzenia 3 szereg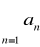
   jest zbieżn.

2. Przypuśćmy, że szereg
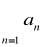
   jest zbieżny, wtedy na mocy a szereg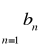
   jest zbieżny co jest sprzeczne z założeniem.

Przykłady:

Zbadać zbieżność szeregów:

1.

1. a>1,
   ;
   ;
   
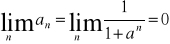
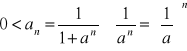
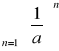
   szereg geometryczny o ilorazie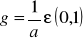
   jest to szereg rozbieżny

2. a=1
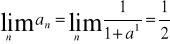
   Szereg jest rozbieżny, gdyż jest spełniony warunek konieczny

3. aε(0,1)
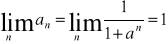
   Szereg rozbieżny, gdyż a_n nie dąży do 0

2.

;

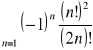
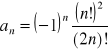
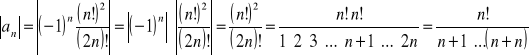
Skorzystamy z oszacowania.

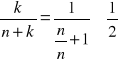
dla k=1,2,...,n

Wtedy
Ponieważ szereg
jest zbieżny, więc na mocy kryterium porównawczego dany szereg jest zbieżny.

3.
;

;

;
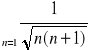
, z kryterium porównawczego wynika zbieżność szeregu.

4.

, zauważmy, że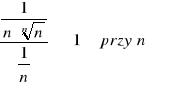
, a więc dla εε(0,1) istnieje N=N(ε)>0, takie, że dla n>N zachodzą nierówności: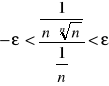
stąd
ponieważ szereg
, więc z kryterium porównawczego wynika zbieżność badanego szeregu.

Twierdzenie 5 (Kryterium pierwiastkowe Cauchy'ego)

Zakładamy, że wyrazy szeregu
są nieujemne:

1. Jeżeli istnieje taka liczba 0≤q≤1 oraz
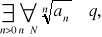
   to szereg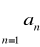
   jest zbieżny.

2. Jeśli istnieje taka liczba q≥1 oraz
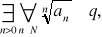
   to szereg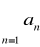
   jest rozbieżny.

Dowód:

1. Ponieważ dla n≥N
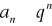
   oraz szereg geometryczny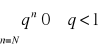
   jest zbieżny, więc na mocy kryterium porównawczego szereg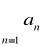
   jest zbieżny.

2. Dla n≥N
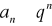
   oraz szereg geometryczny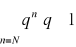
   a więc szereg a_n jest też rozbieżny (z kryterium porównawczego)

WNIOSEK:, Jeżeli wyrazy szeregu
są nieujemne oraz istnieje skończona granica
to:

1. Szereg
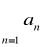
   jest zbieżny gdy q<1

2. Szereg
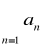
   jest rozbieżny gdy q>1

Dowód: Ponieważ istnieje granica
więc dla każdego ε>0 istnieje takie N>0, że dla n>N q-ε<
<q+ε

1. Jeżeli q<1 to przyjmując
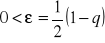
   oraz q=g+ε otrzymujemy: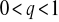
   
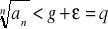
   dla n>N na mocy kryterium Caugh'ego szereg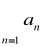
   jest zbieżny

2. Jeżeli q>1, to przyjmując
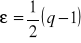
   , q=g-ε otrzymujemy q>1.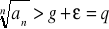
   czyli szereg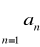
   jest rozbieżny

Twierdzenie 6 (Kryterium ilorazowe d'Alemberta)

Zakładamy, że wszystkie wyrazy szeregu
są dodatnie.

1. Jeżeli istnieje taka liczba 0≤q<1 oraz:
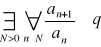
   to szereg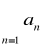
   jest rozbieżny

2. Jeśli istnieje taka liczba q≥1 oraz iloraz
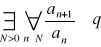
   to szereg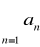
   jest rozbieżny

Dowód:

1. Dla n≥N mamy :
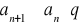
   ; podstawiamy za n kolejno N, N+1, N+2, N+p, pεN wtedy otrzymamy nierówność :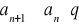
   ;
   ;
   ;
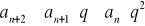
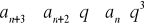
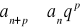
   dla dowolnego pεN. Ponieważ szereg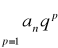
   jest szeregiem geometrycznym zbieżnym (0≤q≤1) więc z kryterium porównawczego wynika, że szereg a_n jest zbieżny

2. Ponieważ
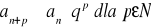
   więc z kryterium porównawczego wynika zbieżność szeregu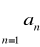
   (q>1)

Z kryterium iloczynowego wynika wniosek:, Jeśli wyrazy szeregu
są dodatnie oraz istnieje skończona granica
to:

1. Szereg
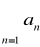
   jest zbieżny gdy q<1

2. Szereg
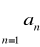
   jest rozbieżny gdy granica jest q>1

3. Gdy q=1 to nie jest wiadomo czy szereg jest zbieżny czy rozbieżny.

54

---