RODZIAŁ V RACHUNEK RÓŻNICZKOWY I CAŁKOWY FUNKCJI RZECZYWISTYCH WIELU ZMIENNYCH

Niech będzie dana przestrzeń metryczna
z metryką
tzn. dla dowolnych elementów
jest określona ich odległość
, przy czym:

1. 
   

2. 
   

3. 
   

.

W przestrzeni metrycznej
, kulą otwartą o środku
i promieniu r>0 nazywamy zbiór
.

Kulę otwartą
nazywamy także otoczeniem punktu x₀. Zbiór
nazywamy otwartym, jeżeli każdy punkt tego zbioru należy do A wraz z pewnym swym otoczeniem.

Punkt
nazywamy punktem skupienia zbioru
, jeżeli każde otoczenie
o dowolnie małym promieniu r zawiera, co najmniej jeden element zbioru A. Zbiór
nazywamy domkniętym, jeżeli A zawiera wszystkie swoje punkty skupienia.

1.GRANICA I CIĄGŁOŚĆ:

Niech
będą przestrzeniami metrycznymi odpowiednio z metryką
.

Niech
, funkcja
, p-punkt skupienia zbioru E.

DEFINICJA: Mówimy, że funkcja f posiada granicę
w punkcie p przy
, jeżeli:

.

Piszemy wtedy:
.

DEFINICJA: Mówimy, że funkcja
jest ciągła w punkcie
, jeżeli granica:

. W szczególności niech
.

Wtedy funkcję
nazywamy funkcją rzeczywistą n-zmiennych. Będziemy stosować zapis dla tych funkcji:

.

Z powyższych definicji: granicy i ciągłości wynika, że:

,

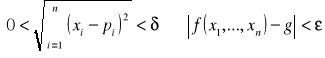
gdzie

f jest ciągła w punkcie p gdy:

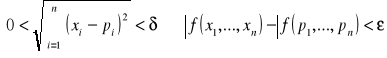
2.POCHODNE KIERUNKOWE ORAZ POCHODNE CZĄSTKOWE:

W dalszym ciągu wektorem
w przestrzeni euklidesowej
nazywamy odwzorowanie przestrzeni R^h na tę przestrzeń, przyporządkowującą każdemu punktowi

(1)gdzie
.

Wektor
oznaczamy symbolem:
przy czym liczby rzeczywiste a₁,...a_n to współrzędne wektora
.Zbiór wszystkich wektorów w R^h oznaczamy symbolem: W_n.Punkt (1) będziemy oznaczać symbolem: p+
tzn.
.

Wektor zerowy
.

DZIAŁANIA ALGEBRAICZNE NA WEKTORACH:

a)iloczyn liczby rzeczywistej
i wektora

:

b)suma wektorów

Niech:

dla dowolnego wektora:

zachodzi równość:

Wektory
nazywamy wersonami.

Niech
, gdzie G jest zbiorem otwartym w R^h.

DEFINICJA: Pochodną funkcji f w punkcie
w kierunku wektora
, nazywamy granicę:

przy założeniu istnienia granicy właściwej lub niewłaściwej.

Pochodną funkcji f w kierunku wektora
nazywamy funkcję
, która każdemu punktowi
, dla którego istnieje granica (1), przyporządkowuje wyrażenie
. Dla funkcji
, gdzie
, G zbiór otwarty, oznaczamy:

,

gdzie
.Ponieważ:

więc przy
otrzymujemy:
.

Ze względu na to, że:

.

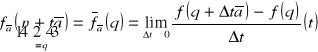
Otrzymaliśmy dla każdego
równość:

.

Ze względu na powyższy związek, między pochodną kierunkową i pochodną zwykłą funkcji rzeczywistej, zachodzą następujące równości: Dla funkcji
,
gdzie
, G zbiór otwarty.

1)

2)
, gdzie
-stała rzeczywista

3)

4)
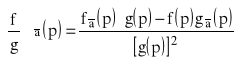
, przy czym

Powyższe równości rozumiemy następująco. Jeżeli istnieją skończone pochodne po prawej stronie wzorów to istnieje pochodna po lewej stronie i zachodzi równość:

, gdzie

stąd:

TWIERDZENIE 1:(o wartości średniej) Jeżeli:

a)odcinek o końcach
zawiera się w zbiorze otwartym

b)w każdym punkcie tego odcinka istnieje skończona pochodna kierunkowa
,to:

gdzie:
.

DOWÓD:Z założenia a) wynika, że funkcja pomocnicza f zbudowana dla funkcji f jest określona na przedziale
. Z założenia b) wynika, że posiada skończoną pochodną w każdym punkcie przedziału
.Z twierdzenia Lagrange'a o wartości średniej dla f otrzymujemy:

,gdzie
czyli:

.

POCHODNE CZĄSTKOWE:

Niech będzie dana funkcja
, gdzie
, G zbiór otwarty.

DEFINICJA: pochodne kierunkowe funkcji f w kierunku wektorów osi współrzędnych tzn. w kierunku wektorów:
nazywamy pochodnymi cząstkowymi funkcji f względem zmiennych odpowiednio:
i oznaczamy symbolami:

,

przy założeniu istnienia tych pochodnych.

Wartością skończonej pochodnej cząstkowej funkcji f względem j-tej zmiennej x_j w punkcie
jest liczbą:

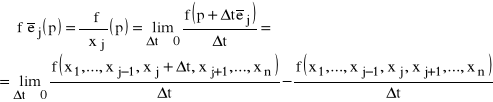
Zatem pochodna cząstkowa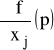
jest pochodną funkcji f jednej zmiennej x_j postaci:

gdzie zmienną jest x_j a
są ustalone

POCHODNE WYŻSZYCH RZĘDÓW:

W dalszym ciągu pochodne kierunkowe i cząstkowe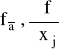
będziemy nazywać

pochodnymi kierunkowymi i cząstkowymi I-go rzędu.

Niech będzie dana funkcja
, gdzie
, zbiór otwarty posiada skończoną pochodną kierunkową
w pewnym otoczeniu punktu
.Można wtedy rozważać pochodną kierunkową funkcji
w punkcie p w kierunku wektora
.Jeżeli pochodna ta istnieje (w sensie właściwym lub niewłaściwym) to oznaczamy ją symbolem:
i nazywamy pochodną kierunkową II-rzędu funkcji f w kierunku

wektora
.Funkcję
określoną w zbiorze tych punktów
, w których istnieje pochodna
przyporządkowująca punktom
wartości
nazywamy pochodną kierunkową funkcji f II-rzędu, w kierunku wektorów
.

KOLEJNOŚĆ RÓŻNICZKOWANIA JEST WAŻNA!!!

Na ogół

są różne.

Zachodzi TWIERDZENIE SHWARZ'A:

Jeżeli pochodne kierunkowe II-go rzędu
,
istnieją i są ciągłe na zbiorze G, to są równe
, dla każdego
.

DEFINICJA: Pochodne cząstkowe II-rzędu funkcji f w kierunku wersorów
to pochodna postaci

. Oznaczamy ją symbolem:

.

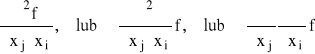
Symbol: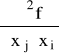
oznacza, że funkcję f zróżniczkowano względem x_i, a potem względem x_j.

Jeżeli
to pochodna cząstkową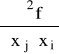
nazywamy pochodną zmienną.

Jeżeli
, to piszemy:
.

Jeżeli w otoczeniu punktu
istnieje skończona pochodna kierunkowa (m-1)-go rzędu funkcji f
to pochodną m-tego rzędu funkcji f w kierunku wektorów
definiujemy przyjmując:

,

przy założeniu istnienia granicy właściwej lub niewłaściwej.

Pochodne kierunkowe rzędu m w kierunku wersorów:
nazywamy pochodnymi cząstkowymi rzędu m funkcji f i oznaczamy symbolami:

.

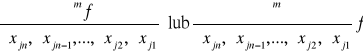
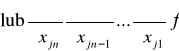
W przypadku gdy kilkakrotnie powtarza się różniczkowanie względem tej samej zmiennej, np. różniczkujemy funkcję f kolejne cztery razy względem x_j , stosujemy zapis: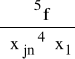
.

79

---