POCHODNA
Zad.1
Na podstawie definicji obliczyć pochodną funkcji f, jeżeli:
w ,
w
w
Zad.2
Zbadaj, czy istnieje jeżeli:
.
Zad.3
Dla jakich funkcja f jest ciągła i różniczkowalna w zbiorze R jeżeli:
a)
b) .
Zad.4
Obliczyć pochodne:
(a>0 - stała)
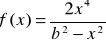
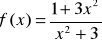
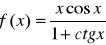
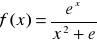
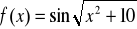
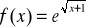
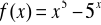

.
Zad.5
Napisać równanie stycznej do danej krzywej we wskazanych punktach:
w P(0,0)
w
w punktach przecięcia krzywej y = f(x) z prostą .
Zad.6
Wyznaczyć równanie stycznej do krzywej , wiedząc, że styczna jest
równoległa do prostej
Zad.7
Znaleźć kąt przecięcia krzywych:
z osią OX,
i g(x) = x.
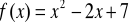
i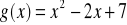
Wyszukiwarka
Podobne podstrony:
2 Pochodna calkaid 21156 ppt
Rozpuszczalniki organiczne pochodne alifatyczne (oprócz metanolu
potencjal spoczynkowy i jego pochodzenie
Klastry turystyczne, pochodzenie nazwy, co to
Naturalne źródła węglowodorów i ich pochodne
W 5 POCHODNE
3 Pochodne
Kr 029 Zieby Darwina umozliwiaja stestowanie rywalizujacych koncepcji pochodzenia
Pochodne zadania cz 2 id 364419
07 Pochodne WzoryPodstawowe
pochodne i całki
jednofunkcyjne pochodne weglowodorow odpowiedzi
Pochodne II IMiR
pochodne wyzszych rzedow id 364 Nieznany
2009 03 26 prezentacja pochodne Nieznany
4 pochodna funkcji jednej zmiennej
Pochodna
Kwasy i ich pochodne polecenai, Szkoła, Biologia
więcej podobnych podstron