1. Kalibracja termopary i termistora

Lp.	temperatura [°C]	napięcie termopary [mV]	oporność termistora [kΩ]
1	19,7	0,79	15,92
2	20,0	0,81	15,79
3	21,0	0,85	15,32
4	22,0	0,89	14,90
5	23,0	0,93	14,35
6	24,0	0,98	14,06
7	25,0	1,02	13,65
8	26,0	1,06	13,25
9	27,0	1,11	12,88
10	28,0	1,15	12,50
11	29,0	1,20	12,15
12	30,0	1,24	11,80
13	31,0	1,28	11,47
14	32,0	1,33	11,15
15	33,0	1,37	10,84
16	34,0	1,42	10,54
17	35,0	1,46	10,24
18	36,0	1,51	9,96
19	37,0	1,55	9,69
20	38,0	1,60	9,40
21	39,0	1,64	9,15
22	40,0	1,69	8,90
23	41,0	1,74	8,66
24	42,0	1,78	8,42
25	43,0	1,83	8,20

Wyniki pomiarów dla dłoni:

U _woltomierza = 1,35 mV

R _termistora = 10,78 kΩ

2. Rachunek błędów

Temperaturę wyznaczam korzystając z liniowej zależności U(t);

Równanie prostej (obliczam ze wzoru lub przy pomocy programu ORIGIN):

gdzie

S_a = 0,00453 ~0,0046 i S_b = 0,00014

a=-0,08834 ~0,0884 b=0,04440

równanie prostej ma postać :

U = 0,04440t_x -0,0884

Odczyt temperatury metodą algebraiczną:

t_x = (U - a) / b

t_x = (1,35 + 0,08834 ) / 0,0444 = 32,39504505 [°C]

Błędy standardowe współczynników prostej:

S_a = 0,00453 i S_b = 0,00014

Błąd systematyczny woltomierza:

Δx_S = A ∗ K / 100+V gdzie: A - zakres skali, K - klasa przyrządu

V- rozdzielczość przyrządu

dla użytego woltomierza: A = 100 mV, K = 0,2 V=0,1, V=0,01

ΔU = 100 ∗ 0,21 / 100 + 0,1= 0,21 [mV]

Niepewność standardową złożoną obliczam ze wzoru :

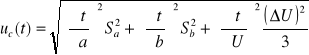
Za pomocą programu EXCEL otrzymuję
= 2,734084609

Niepewność standardowa złożona rozszerzona

U(t)=
*k

Dla α = 0,95 i m =15

k=2,06

U(t) =2,734084609

*2.06 =5,632214295

Wynik końcowy metoda algebraiczną 32,39504505±:5,632214295

33 ± 6[°C]

Wynik otrzymany za pomocą metody graficznej:

• odczyt z wykresu zależności napięcia od temperatury - 32,55

U(t)= 5,632214295

Odczytywanie wartości temperatury w porównaniu z metodą algebraiczną jest obarczone niepewnością wynikającą z rozdzielczości wykresu i grubości linii i niedoskonałości oka, a także z rozdzielczości skali a moim wykresie.

Tą „dodatkową” (q) niepewność szacuje: 0,25<q<0,3 ~q=0,3

5,882214295<U(t)+q<5,982214295

U(t)+q~5,982214295

Ostateczny wynik po zaokrągleniu

33 ± 6[°C]

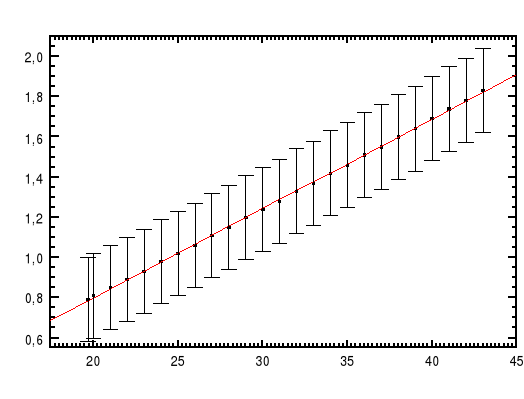
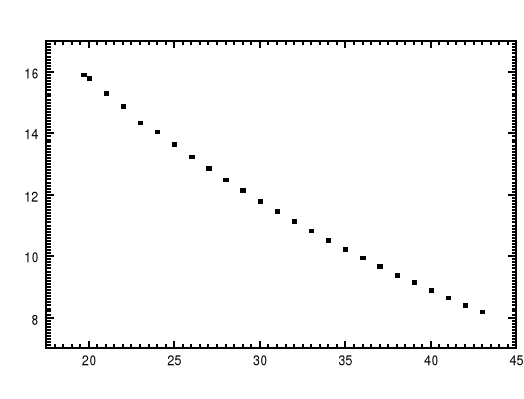
• odczyt z wykresu zależności oporu od temperaturu - 34,7

ΔR = 10 Ω = 0,01k Ω

Odczytywanie wartości temperatury w porównaniu z metodą algebraiczną jest obarczone niepewnością wynikającą z rozdzielczości wykresu i grubości linii i niedoskonałości oka, a także z rozdzielczości skali a moim wykresie.

Tą „dodatkową” (q) niepewność szacuje: 0,25<q<0,3 ~q=0,3

Zależność oporu od temperaturynie jest liniowa, dlatego wyznaczenie błędu związanego z tą metodą staje się bardziej skomplikowane. Otrzymany wynik (34,4) spełnia zależność x₁ - x₂ < Δx₁ + Δx₂ pomimo nie znanej niepewności dla termistora (nawet jeśli Δx₁ (termistora) jest bliskie zeru). Chciałbym też zwrócić uwagę że niepewność związana z klasą przyrządu w przypadku pomiarów oporu jest dużo mniejsza od tejże niepewności w przypadki pomiarów napięcia.

3. Porównanie dokładności i precyzji metody graficznej i algebraicznej pomiaru temperatury przy użyciu termopary

Jeśli zachodzi nierówność x₁ - x₂ < Δx₁ + Δx₂ to wyniki x₁ i x₂ są sobie równe w granicy błędu.

32,55 -32,39504505 < 5,982214295+5,632214295

nierówność jest prawdziwa więc otrzymane przeze mnie wyniki są sobie równe w granicy błędu.

niepewność względna: Δx/x

• dla metody graficznej: 5,982214295 /32,55 = 0,1837853 ~ 0,19

• dla metody algebraicznej: 5,632214295/ 32,39504505 = 0,173860 ~0,18

Zaokroąglenie niepewności wykonane niezgodnie z zasadami, gdyż powinoo wynosić 0,2 dla obu wartości ale w ten sposób zaostałaby zatarta różnica pomiędzy obiema metodami

Porównanie pomiarów temperatury termoparą:

	Graficzna	Algebraiczna
Wynik pomiaru [°C]	33 ± 6	33 ± 6
Niepewność względna	= 0,19 (19%)	0,18 (18%)

Metoda graficzna i algebriczna nie różnią się tylko sposobem odczytywania wyniku(ręcznie lub rachunkowo), metoda graficzna wydaje się metodą prostszą, ale przy zastosowaniu odpowiednich programów komputerowych w metodzie algebraicznej, metoda graficzna staje się sposobem mniej przydatnym w mierzeniu temeperatury.

Wykres zależności napięcia termopary od temperatury:

Linear Regression for Data1_B:

Y = A + B * X

Param Value sd

A -0,08834 0,00453

B 0,0444 0,00014

SD = 0,0051, N = 25

R = 0,99988

P = 3,2899E-43

Wykres zależności oporności termistora od temperatury

1

Przemysław Pepliński

---