![]()
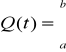
(wielomian interpolacyjny funkcji sklejanej)![]()
kwadratury
TWIERDZENIE
Kwadratury N-C oparte na n+ 1 węzłach są rzędu:
![]()
dla n parzystych
![]()
dla n nieparzystych
(Sprawdzenie z przykładu 3 - poprzedni wykład)
![]()
nieparzyste
![]()
- dla wielomianu stopnia 2 z resztą ![]()
gdyż zależą od ![]()
Przykład 4
![]()
węzły: ![]()
, ![]()
, ![]()
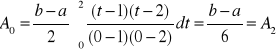
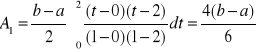
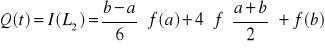
(7)
Wzór paraboliczny, wzór Simpsona
Kwadratura N-C dla ![]()
Reszta: ![]()
; ![]()
![]()
Zbieżność ciągu kwadratur
![]()
ciąg kwadratur
![]()
(8)
numer ciągu
przybliżających całkę 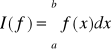
Załóżmy, że dane są skończone macierze trójkątne węzłów ![]()
i współczynników ![]()
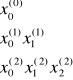
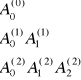
... ...
definiujące ciąg kwadratur ![]()
TWIERDZENIE
Ciąg kwadratur (8) jest rozbieżny dla dowolnych funkcji ciągłych na ![]()
czyli:
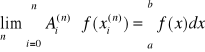
wtedy i tylko wtedy gdy:
ciąg (8) jest zbieżny dla dowolnego wielomianu
oraz
istnieje taka stała K, że dla n, (
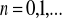
) zachodzi nierówność:
![]()
Istnieją funkcje, dla których ciąg kwadratur N-C nie jest zbieżny.
Akumulacja błędów.
Nie stosuje się kwadratur wyższych rzędów.
Złożone kwadratury Newtona-Cotesa
Przedział dzielimy na N części:
![]()
![]()
![]()
w każdym z nich kwadratura N-C niskiego rzędu.
Przykład 5 - złożona kwadratura
W każdym podprzedziale ![]()
stosujemy wzór trapezów (kwadratura N-C 2 rzędu z przykładu 1)
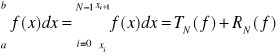
![]()
![]()
-->
[Author:JDz]
- złożony wzór trapezów
![]()
jeśli ![]()
dla ![]()
to
![]()
![]()
dla ![]()
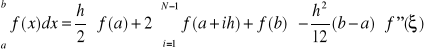
![]()
Przykład 6 (złożona kwadratura Simpsona)
Założenie: ![]()
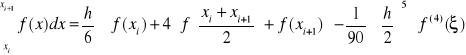
![]()
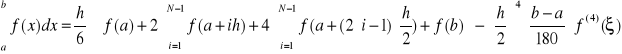
nieparzyste
błąd
![]()
![]()
Ogólnie złożone kwadratury N-C są postaci:
![]()
![]()
; ![]()
TWIERDZENIE
Dla dowolnego n ciąg złożonych kwadratur N-C ![]()
jest przy ![]()
(czyli ![]()
) zbieżny dla wszystkich funkcji ![]()
.
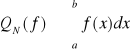
Praktycznie
Szukam przybliżenia ![]()
mając żądaną dokładność:
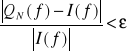
oszacowanie reszty często trudne lub niemożliwe. Jak wyznaczyć N?
Obliczyć kolejne kwadratury ![]()
, ![]()
, ..., ![]()
Ilość przedziałów
Zwykle ![]()
, potem każdy przedział dzielimy na m części, m dobieramy tak, aby w następnej kwadraturze korzystać z poprzednio obliczonych wartości f
![]()
np. dla złożonej kwadratury trapezów należy przyjąć m = 2, gdyż (z przykładu 5) dla ![]()
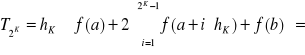
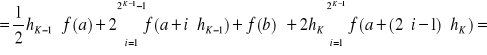
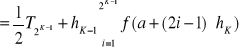
gdzie ![]()
Obliczenia kontynuujemy aż:
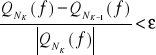
![]()
Skąd się wzięło to przejście?
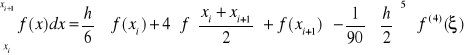
Wyszukiwarka
Podobne podstrony:
marcinka all, 20030121
marcinka all, 20021203, Ciąg dalszy:
marcinka all, 20021119
marcinka all, 20021008
marcinka all, 20021015, SZUKANIE ZER W FUNKCJACH NIELINIOWYCH
marcinka all, 20021126, (RYSUNEK)
marcinka all, 20021112, INTERPOLACJA FUNKCJAMI SKLEJANYMI:
IO ALL
ZLL ALL
All Flesh Must Be Eaten Two Rotted Thumbs Up
Jim Hall at All About Jazz
all
PDH, Broadband ISDN, ATM and all that
marcinstolp pro
mo all
Twarde dyski, Informatyka -all, INFORMATYKA-all
farmacja 12czerwca2007, Receptura, Farma - pytania, testy egzaminacyjne-all
Opis programu komputerowego Twierdzenie Pitagorasa-dowód i z, wrzut na chomika listopad, Informatyka
więcej podobnych podstron