Metoda najmniejszych kwadratów.

Służy do szacowania parametrów strukturalnych modeli liniowych bądź też sprowadzalnych do liniowych.

k - liczba zmiennych objaśniających

k+1 - liczba szacowanych parametrów

t = 1,...,T - liczba obserwacji

Zapis macierzowy:

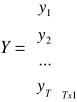
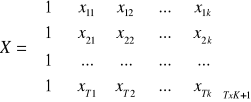
y - wektor obserwacji na zmiennej objaśnianej

x - macierz obserwacji na zmiennych objaśniających

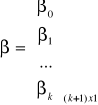
- wektor parametrów strukturalnych

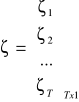
- wektor składników losowych

Warunki zastosowania metody najmniejszych kwadratów:

1. założenia stochastyczne (dotyczące składnika losowego)

1. model musi być sprowadzalny do postaci liniowej względem zmiennych

2. wartość oczekiwana składnika losowego jest równa zero
   
   

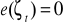
3. wariancja składników losowych jest stała w czasie
   
   

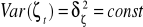
4. kowariancja pomiędzy składnikami losowymi jest równa zero
   
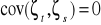
   , jeśli
   
   
   Składniki losowe z różnych okresów nie zależą od siebie - kowariancja.
   Brak autokorelacji składników losowych. Brak zależności pomiędzy czynnikami przypadkowymi.

5. kowariancja pomiędzy składnikami losowymi i zmiennymi objaśniającymi równa się zero
   
   

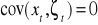
6. składnik losowy ma rozkład normalny
   
   

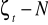
2. założenia numeryczne

1. rząd macierzy x = k+1
   n(x) = k+1
   Maksymalna liczba liniowo niezależnych wierszy, kolumn macierzy - rząd.
   Wszystkie kolumny macierzy x muszą być liniowo niezależne

2. k+1 < T
   k+1 - liczba parametrów strukturalnych
   T - liczba obserwacji
   Musimy mieć więcej obserwacji niż parametrów do oszacowania

Metoda najmniejszych kwadratów:

Szukamy minimum sumy kwadratów reszt:

Wzór na estymator metody najmniejszych kwadratów - narzędzie służące do szacowania parametrów
.

Przykład:

Dane są następujące szeregi:

X	Y
-1,5	0,5
-0,5	0,5
0,5	1
0,5	2
1	2,5

Oszacować parametry modelu:

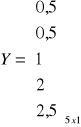
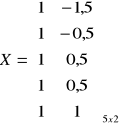
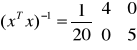
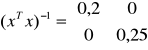
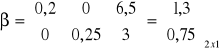
Przyczyny występowania składnika losowego:

1. występowanie czynników przypadkowych;

2. indeterminizm - w tych samych warunkach różne zachowanie się;

3. błędy w obserwacjach;

4. wady w konstrukcji modelu;

1