Wartość bezwzględna:

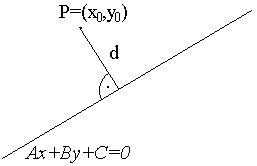
|x| = a x = a ∨ x = -a

|x| < a -a < x < a

|x| > a x > a ∨ x < -a

|x⋅y| = |x|⋅|y|

|x + y| ≤ |x| + |y|

√x² = |x|

Równanie ogólne prostej: Ax+By+C=0

Proste równoległe:

Ax+By+C=0 || Ax+By+C₁=0

P=(x₀,y₀)

Ax₀+By₀+C₁=0

C₁=- Ax₀-By₀

Warunki równoległości prostych:

1.
- proste pokrywają się

2.
- proste równoległe

3.
- proste przecinają się

Proste prostopadłe:

Ax+By+C=0 ⊥ Bx-Ay+C₁=0

P=(x₀,y₀)

Bx₀-Ay₀+C₁=0

C₁=- Ay₀-Bx₀

y₁=a₁x+b, y₂=a₂x+b

y₁||y₂ a₁=a₂

y₁⊥y₂ a₁=-1/a₂

Równanie prostej przechodzącej przez dwa punkty P(x₁,y₁) i Q(x₂,y₂), P≠Q:

Odcinek:

- długość odcinka AB

- współrzędne środka odcinka

Równania stopnia pierwszego: ax+b=0

I. a≠0 - równanie ma dokładnie jedno rozwiązanie

II. a=0 ∧ b=0 - równanie ma nieskończenie wiele rozwią-zań

III. a=0 ∧ b≠0 - równanie sprzeczne (nie ma rozwiązania)

Kąt między prostymi:

Odległość punktu od prostej:

Układy równań stopnia pierwszego:

,

I. W_g≠0 - układ równań niezależnych (jedno rozwiązanie)

II. W_g=0 ∧ W_x=0 ∧ W_y=0 - układ równań zależnych (nie-skończenie wiele rozwiązań)

III. W_g=0 ∧ (W_x≠0 ∨ W_y≠0) - układ równań sprzecznych (nie ma rozwiązań)

FUNKCJE TRYGONOMETRYCZNE

Miara w st.	0	30	45	60	90	180	270	360
sin	0				1	0	-1	0
cos	1				0	-1	0	1
tg	0		1		-	0	-	0
ctg	-		1		0	-	0	-
Miara w rad	0	π/6	π/4	π/3	π/2	π	3π/2	2π

Miara w st.	0 - 90	90 - 180	180 - 270	270 - 360
sinx	+	+	-	-
cosx	+	-	-	+
tgx	+	-	+	-
ctgx	+	-	+	-
Ćw. ukł.	I	II	III	IV

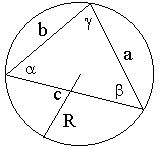
Twierdzenie cosinusów:

Twierdzenie sinusów:

Trójmian kwadratowy:

ax² + bx + c = 0 ∧ a≠0 ∧ x∈R

ax² + bx + c = a(x-x₁)(x-x₂)

I. Δ>0 - dwa rozwiązania

II. Δ=0 - jedno rozwiązanie

III. Δ<0 - brak rozwiązań

,

Aby pierwiastki x₁ i x₂ były równe sinusowi i cosinusowi tego samego kąta to:

Δ≥0 - aby istniał trójmian

x₁+x₂>0 - własność funkcji trygonometrycznej (I ćw)

x₁⋅x₂≥0 - własność funkcji trygonometrycznej (I ćw)

- jedynka trygonometryczna

Współrzędne wierzchołka paraboli:

Funkcja logarytmiczna:

Funkcja wykładnicza:

Przekształcenia wykresu funkcji: y=f(x)

y=-f(x) - symetria względem osi OX

y=f(-x) - symetria względem osi OY

y=|f(x)| - odbicie w osi OX

y=f(x-a) - przesunięcie w prawo o a

y=f(x+a) - przesunięcie w lewo o a

y=f(x)+a - przesunięcie w górę o a

Ciąg arytmetyczny:

,

Ciąg geometryczny:

,

gdy

Ciągłość funkcji w punkcie:

1. istnieje wartość funkcji f(x₀)

2. istnieje granica w tym punkcie

3. wartość funkcji w x₀ jest równa granicy

Pochodna funkcji w punkcie:

Styczna do wykresu funkcji w punkcie M(x₀,y₀):

Kąt między krzywymi:

Wzory skróconego mnożenia:

Symbol Newtona:

Dwumian Newtona:

- współczynnik rozwinięcia dwumianu Newtona

np. 81 - współczynnik wielomianu

Równanie okręgu o środku w punkcie (a,b) i promieniu r:

Równanie stycznej do okręgu O(S(a,b),R) w punkcie A(x₁,y₁):

Odległość między prostymi równoległymi Ax+By+C₁=0 i Ax+By+C₂=0:

Pole trójkąta w układzie współrzędnych:

A(x_A,y_A) B(x_B,y_B) C(x_C,y_C)

Wektory:

,

PRZEBIEG ZMIENNOŚCI FUNKCJI:

1. Dziedzina funkcji

2. Granice (w nieskończoności i punktach nieokreśloności)

Wyraz z najwyższą potęgą wyciągamy przed nawias.

Gdy mianownik ma taką samą lub większą potęgę niż licznik, to wszystkie wyrazy dzielimy przez najwyższą potęgę mianownika.

3. Asymptoty

asymptota pozioma y=d

asymptota pionowa x=c

Asymptota ukośna potęga licznika jest o 1 większa od potęgi mianownika:

y=ax+b

4. Punkty przecięcia z osiami

5. Pochodna i jej dziedzina

6. Ekstremum i monotoniczność

a) WK ⇒ f'(x₀)=0 - w tym punkcie f(x) może mieć ekstremum

b) WW - badam znak pochodnej

f'(x)>0 dla x∈… ⇒ f(x) rosnąca

f'(x)<0 dla x∈… ⇒ f(x) malejąca

z „-” na „+” ⇒ min

z „+”na „-” ⇒ max

f_max(x₀)=…

7. Tabelka (-∞, ↑, miejsca zerowe pochodnej, ↑, max, ↑, punkty nieokreśloności, ↑, +∞)

8. Wykres

FUNKCJE TRYGONOMETRYCZNE

---