Egzamin Ekonometria - Zadania zestaw A
Zadanie 1
Dana jest macierz kowariancji 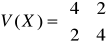
, wektora losowego ![]()
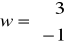
Oblicz wariancję D2(T) wektora
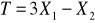
Oblicz
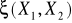
Rozwiązanie
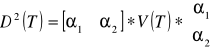
gdzie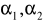
to współczynniki stojące przy parametrach X, V(T)=V(X)
Tego wzoru zupełnie nie jestem pewien. Próbowałem coś zaimprowizować na podstawie szczątkowych notatek z wykładów, bo nic innego nie mam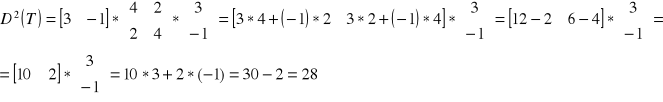
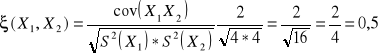
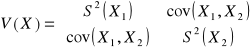
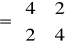
To jest dobry wzór
Zadanie 2
W modelu liniowym ![]()
na podstawie n=6 obserwacji otrzymano 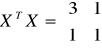
, 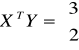
Oblicz NNK estymatora
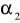
parametru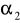
Dla danych ocen
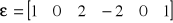
oblicz S2Dla danego S2=2 oblicz ocenę wariancji
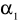
Rozwiązanie
Oblicz NNK estymatora
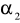
parametru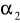
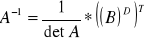
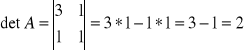
Obliczanie wyznaczników do macierzy dołączanej do XTX
(XTX)11 - oznacza wyznacznik z pierwszego wiersza i pierwszej kolumny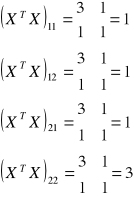
W macierzy dopełnień przed wartościami (XTX)12 i (XTX)21 stawiamy -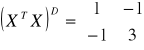
Transponowanie macierzy dołączanej
Obracamy macierz za oś symetrii biorąc przekątną macierzy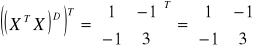
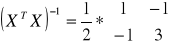
Obliczamy macierz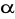
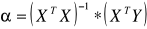
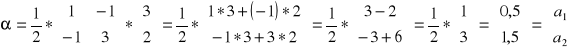
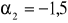
Dla danych ocen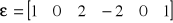
oblicz S2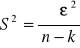
Na ćwiczeniach we wzorze było n-k-1, ale po sprawdzeniu wyniku wyszło mi, że na egzaminie obowiązuje powyższy wzór
n=6 - liczebność
k=2 - ilość X-ów w modelu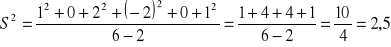
Dla danego S2=2 oblicz ocenę wariancji
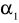
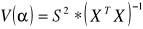
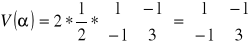
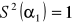
Tego w zasadzie nie trzeba obliczać
Zadanie 3
Na podstawie danych 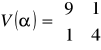
oraz 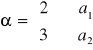
Oblicz wartość testu t-Studenta do weryfikacji hipotezy
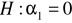
Oblicz lewy koniec przedziału ufności dla parametru
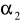
znając odczyt z tablic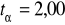
Rozwiązanie
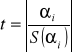
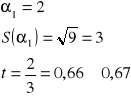
Oblicz lewy koniec przedziału ufności dla parametru
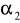
znając odczyt z tablic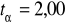
PL - lewy koniec przedziału ufności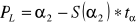
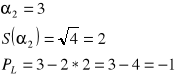
Zadanie 4
Dla stacjonarnego szeregu 1, -1, 0, 0, 1, -1, 0, 0, 1, -1, 0, 0
Oblicz autokorelację rzędu pierwszego r1
Oblicz autokorelację rzędu drugiego r2
Rozwiązanie
Oblicz autokorelację rzędu pierwszego r1
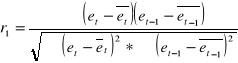
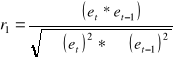
spotkałem się z takim wzorem i nie wiem czy jest dobry czekam na potwierdzenie od was
Postaci tego wzoru nie jestem pewien
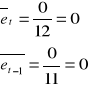
Oblicz autokorelację rzędu drugiego r2
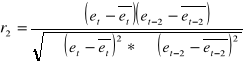
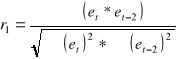
spotkałem się z takim wzorem i nie wiem czy jest dobry czekam na potwierdzenie od was
Postaci tego wzoru nie jestem pewien, ale podejrzewam, że coś chyba z tym wzorem jest nie tak,
bo zarówno w punkcie a jak i w b nie wychodzą wyniki z tabeli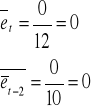
Oceń metodą Yula-Walkera parametr
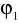
szereguOceń metodą Yula-Walkera parametr
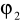
szereguWyznacz prognozę
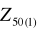
Wyznacz prognozę
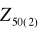
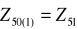
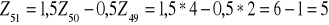
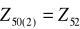
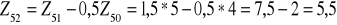
Podaj wartość elementu
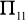
macierzy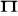
postaci zredukowanej modelu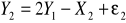
Podaj wartość elementu
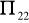
macierzy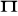
postaci zredukowanej modelu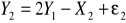
Doprowadzamy oba równania do postaci BY + ΓX = ε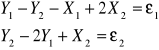
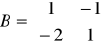
- macierz współczynników stojących przy Y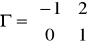
- macierz współczynników stojących przy X
Obliczamy B-1
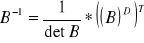
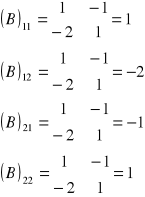
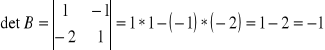
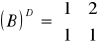
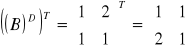
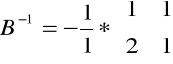
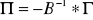
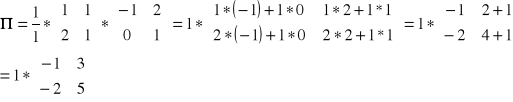
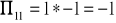
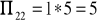
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
1 |
|
1 |
|
|
1 |
|
2 |
-1 |
1 |
- 1 |
1 |
-1 |
1 |
1 |
3 |
0 |
-1 |
0 |
-1 |
0 |
0 |
1 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
6 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
1 |
7 |
0 |
-1 |
0 |
-1 |
0 |
0 |
1 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
10 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
1 |
11 |
0 |
-1 |
0 |
-1 |
0 |
0 |
1 |
12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
∑ = - 3 |
∑ = 6 |
∑ = 6 |
![]()
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
1 |
|
|
|
|
1 |
|
2 |
-1 |
|
|
|
|
1 |
|
3 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
4 |
0 |
-1 |
-1 |
-1 |
1 |
0 |
1 |
5 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
6 |
-1 |
0 |
0 |
0 |
0 |
1 |
0 |
7 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
8 |
0 |
-1 |
-1 |
-1 |
1 |
0 |
1 |
9 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
10 |
-1 |
0 |
0 |
0 |
0 |
1 |
0 |
11 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
12 |
0 |
-1 |
-1 |
-1 |
1 |
0 |
1 |
|
|
|
|
|
∑ = 6 |
∑ = 6 |
∑ = 6 |
![]()
Nie jestem pewien czy to jest dobrze
Zadanie 5
Co prawda było to na wykładach, ale mam braki nie wiem jak to obliczyć
Dany jest szereg AR(2) ![]()
w którym r1=0,6 i r2=0,8
Zadanie 6
W szeregu ![]()
znamy Z49=2 i Z50=4
Rozwiązanie:
Zadanie 7
Dany jest model wielorównaniowy ze znanymi parametrami ![]()
Rozwiązanie
Tabela wyników nie dotyczy tego zestawu
1a |
1b |
2a |
2b |
2c |
3a |
3b |
4a |
4b |
5a |
5b |
6a |
6b |
7a |
7b |
8 |
0,50 |
2,00 |
2,50 |
2,86 |
2,00 |
0 |
-0,67 |
-0,83 |
0,19 |
-0,50 |
4 |
1,0 |
-2,0 |
1,5 |
26 |
0,19 |
0,00 |
3,00 |
4,00 |
0,75 |
-4 |
-0,50 |
0,50 |
-0,48 |
0,48 |
1 |
0,5 |
1,0 |
3,0 |
-2 |
0,75 |
3,00 |
2,00 |
1,50 |
0,67 |
-6 |
0,33 |
0,56 |
-0,50 |
-0,46 |
5 |
5,0 |
0,5 |
5,0 |
40 |
0,00 |
1,50 |
0,60 |
2,00 |
1,00 |
-1 |
0,00 |
0,00 |
0,27 |
0,33 |
3 |
5,5 |
-1,0 |
1,0 |
32 |
1,00 |
-1,50 |
1,00 |
1,00 |
1,50 |
-3 |
0,67 |
-0,80 |
0,10 |
0,69 |
2 |
2,0 |
3,0 |
-1,0 |
Odp. na zadanie 5
![]()
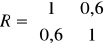
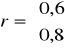
detR = 0,64 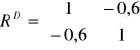
![]()
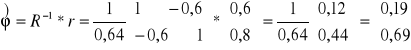
Tak to powinno być rozwiązane prawdopodobnie!!!!!!!!!!!!!!
Strona 2 z 6
Wyszukiwarka
Podobne podstrony:
Ekonometria sem3, Egzamin ekonometria, Zadanie 1
Cwiczenia 14, Ekonometria, Ekonometria, Egzaminy + Testy, Egzaminy, ekonometria 2009, Ekonometria za
ekonometria - zadania z egzaminu Wędzicha, Zadania z egzaminu - ekonometria
Przykładowe zadania na egzamin, Ekonomia, Wnioskowanie statystyczne, Wnioskowanie statystyczne
Ekonometria 08 09 sylabus, Ekonometria, Ekonometria, Egzaminy + Testy, Egzaminy, ekonometria 2009, E
Odpowiedzi grupa A, Ekonometria, Ekonometria, Egzaminy + Testy, Egzaminy, ekonometria 2009, Ekonomet
Wyk. zadania. analiza na egzamin, Ekonomia UWr WPAIE 2010-2013, Semestr II, Analiza Ekonomiczna
Cwiczenia 13, Ekonometria, Ekonometria, Egzaminy + Testy, Egzaminy, ekonometria 2009, Ekonometria za
ekonometria-zadania-ODPOWIEDZI, Studia UMK FiR, Licencjat, II rok - moduł Rachunkowość, Ekonometria
Egzamin praktyczny Zadanie Nr 4
na egzamin przykladowe zadania
Egzamin - propozycje pytan cz1, PKM Egzamin - teoria i zadania
egzamin z ekonomiki, Biotechnologia notatki, Ekonomika
świerk, Technikum PSBiG Lublin, Egzamin zawodowy, Zadania egzaminacyjne
egzamin ekonomika 2
egzamin ekonometria
Pytania z egzaminu ekonomika KTZ ORO 2010, OPRACOWANIE PYTAŃ NA EGZAMIN
więcej podobnych podstron