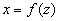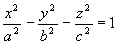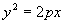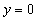
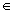
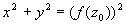
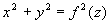
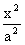
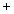
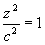
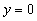
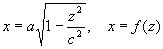
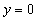
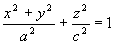
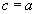
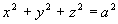
Powierzchnie stopnia 2-go w przestrzeni Powierzchnie obrotowe

Z: Krzywa k leży w płaszczyźnie Oxz i jest dana równaniem: (1)

,

Obracamy krzywą k dookoła osi Oz. Wtedy każdy punkt P0 k nie leżący na osi Oz zatoczy okrąg o równaniu:

2.

leżący w płaszczyźnie:

3. z = z0

Rugując z równań (2), (3) z0 otrzymujemy równanie powierzchni zatoczonej przez krzywą k daną równaniem (1) dookoła osi Oz: 4.

Elipsoida

Dana elipsa:

(5)

leżąca w płaszczyźnie Oxz:

k:

,

Obracamy dookoła osi Oz krzywą k: (6)

(6) – powierzchnia zwana elipsoidą obrotową powstała przez obrót elipsy (5) dookoła osi Oz.

Analogicznie gdy

(7)

(7) - równanie sfery kulistej o środku (0,0,0) i promieniu

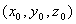
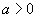
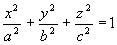
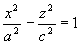
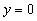
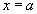
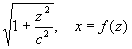
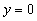
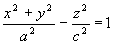
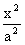
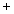
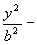
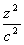
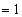
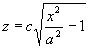
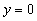
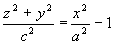
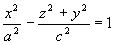
(8)

(8) - równanie sfery kulistej o środku i promieniu

(9)

(9) - równanie elipsoidy 3-osiowej (to nie jest powierzchnia obrotowa) Hiperboloida jednopowłokowa i dwupowłokowa Dana hiperbola:

(10)

leżąca w płaszczyźnie Oxz:

k:

,

Obracamy krzywą k dookoła osi Oz, otrzymujemy powierzchnię (11)

(11) – powierzchnia zwana hiperboloidą jednopowłokową powstała przez obrót dookoła osi Oz hiperboli (10).

12.

(12) - hiperboloida jednopowłokowa Obracamy hiperbolę (10) dookoła osi Ox (krzywą k:

, z = f(x),

),

otrzymamy powierzchnię:

(13)

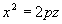
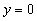
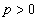
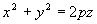
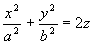
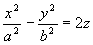
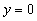
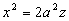
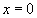
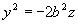
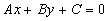
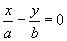
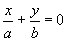
zwaną hiperboloidą obrotową 2-powłokową 14.

(14) - hiperboloida 2-powłokowa Paraboloida eliptyczna i hiperboliczna Dana parabola

(15)

leżąca w płaszczyźnie

,

Obracamy krzywą dookoła osi Oz (16)

(16) - paraboloida obrotowa

17.

(17) - paraboloida eliptyczna.

Równanie postaci

18.

przedstawia powierzchnię zwaną paraboloidą hiperboliczną (siodło).

1) Płaszczyzna

przecina powierzchnię po paraboli

.

2) Płaszczyzna

przecina powierzchnię po paraboli

.

3) Płaszczyzny przechodzące przez oś Oz przecinają powierzchnię po parabolach (

z dowol.) z wyjątkiem płaszczyzn: i

które przecinają powierzchnie po prostych

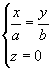
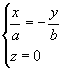
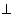
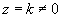
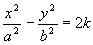
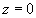
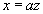
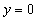
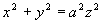
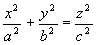
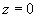
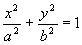
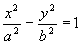
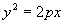
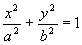
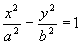
4) Płaszczyzna do osi Oz

przecina powierzchnię po hiperbolach

, gdy

hiperbola redukuje się do 2-ch prostych.

Powierzchnie stożkowe

Prosta

(19)

leżąca w płaszczyźnie Oxz:

obraca się dookoła osi Oz. Otrzymamy powierzchnię zwaną stożkiem kołowym.

(20)

(20) - stożek kołowy

(21)

(21) - stożek eliptyczny

Powierzchnie walcowe

Na płaszczyźnie Oxy:

dana jest elipsa, hiperbola, parabola:

,

,

p – prosta || do osi Oz i poruszająca się przez wszystkie punkty krzywej opisze:

(22)

(z – dowolne)

(22) – walec eliptyczny,

(23)

(z – dowolne)

(23) - walec hiperboliczny

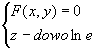
(24)

(z – dowolne)

(24) - walec paraboliczny

Ogólnie:

25.

(25) - równanie powierzchni walcowej o kierownicy i tworzących || do osi Oz.