Egzamin dla Aktuariuszy z 2 czerwca 2001 r.
Prawdopodobieństwo i Statystyka Zadanie 1
Metodą eliminacji wystarczy sprawdzić Dla n=0 i n=1
b
Dla n=0 0 pasują wszystkie odpowiedzi m
2
b + 1 m − b
b
b m + m − b Dla n=1:
0
0
0
0
0
p =
+ =
i pasuje tylko odpowiedź (B)
1
2
m
m
m
m
Zadanie 2
1 2 2
tµ+ t σ
tZ
2
EX = EN ⋅ Ee
= λe
2
EX
= E( 2 2 tZ
N e
)
2
2 tZ
= EN Ee
= (
2
λ + λ )
2 2
2 tµ+2 t σ
e
X = (
2
var
λ + λ )
2 2
2 2
2 tµ+2 t σ
2 2 µ
t + t σ
e
− λ e
( 2
λ + λ ) 2 tµ+2 2 2
t σ
2 2
2 2
e
−
µ
t +
λ e
t σ
1
ODP =
= exp σ t +
σ t
−
2 2
( 2 2) exp( 2 2) 1
2 2 tµ+ t σ
λ
λ e
Zadanie 3
∑( X − X
∑
−
k
)2
X
X
2
(
)2
σ
k
=
≅ χ )
8
(
2
χ
= ,
2 733
2
σ
0,05
(ale jak dokładnie?)
≅ t(8)− N (0 ) 1
, ;var (8)=..
8
7
6
t
3
≅ N (0 )
1
,
}
9
,
1
8
6
9
,
1 6
X 8
4
po przekształceniach: P
X
≤
χ )
8
(
=
P
≤
,
2 733
χ )
8
(
,
2 733
= F
( 9
,
2 )
N
≈ 9
,
0 9
(0 )
1
,
Zadanie 4
∞
λt
t
λx
λy
λy 1
P min( W , W
, W
W
t
λ e
e
dxdy
λ e
e
1
2 )
−
>
1 +
2 >
= ∫ ∫ 2 − −
= ∫ 2 −
2 =
2
λ
t t
t
2 2
2
λt ∞
−
− λt
− λt
=
λy
1
2
λe
∫ −
2
2
−
e
= λe
e
= λt
e
λ
t
2
t
∞
1
P(
t
W
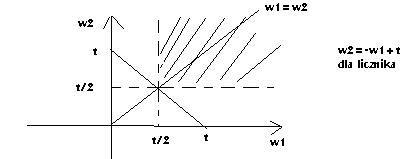
1 + W 2 > t ) = ∫ ∫
2 − λx − λy
λ e
e
dydx = ∫ 2 − λx
− λ(− x+ t)
−
λ e
e
dx =
λt
λe
t
0 −
λ
x+ t
0
−
e λt
1
lim
= lim
= 0
−
t→∞
λt
t→∞
λe
t
t
λ
Zadanie 5
EX = 0 = α(2 ⋅ 0 + 0) + EU → EU = 0
9 = α 2 40 + var U
1 − 2 α
W
U =
(2 X + W ) −
= 1
( − 2 α) X − αW
2
2
1
( − 2 α)2 9 + α 2 4 = var U
czyli
2
2
2
9 − 40 α = 9 − 36 α + 36 α + 4 α
80 2
α − 36 α = 0
α = 0 odpada bo wtedy X=U, z tego X i Y nzl, z tego sprzeczność bo Y=2X+W
80 α = 36
36
9
α =
=
80
20
Zadanie 6
S = X X
Dla parzystych def: 1
1
2
X = X
X
−
S = X X + X X
n
2 n 1
2 n
2
1
2
3
4
i E( X
X
n−
n
=
2
1
) 0
2
var( X
X
EX
EX
EX
EX
n−
n
=
n−
n −
n−
n
=
2
1
2 )
2
2
2
1
2
( 2 1 2 )2 1
1
n
→∞
i z CTG: P
S ≤ a
→ Φ( a)
n
n
dla nieparzystych to samo i z tego odpowiedź (B) prawidłowa Zadanie 7
∞
5
∞
k
L = ∑∏
k
i
k
λ
f
k
P
X
f k
α e
e
e
wykl (⋅
) −5
5
α
k
∑ x
!
k 5
10 α
λ
(
< 10) ( ) = ∑
−
(1− ) −
−
− =
k
k
k =
5
!
5 (
)
5 !
!
5 i=1
k =5
−
∞
k
∞
n+5
k
k
λ
n
5
5 −100 α −
=
λ
α e
e
∑
5
10 α
5
100 α
λ
10
n
α
λ
(1 − e
) −
−
−
−
= k − 5 = n = α e e
∑ +
(
−
1 − e
)
=
k
n
k =
5
!
5
(
)
5 !
5
n=0
+
n
10
n
α
5 −100 α −
=
λ 1
λ
5
α e
e
λ (
−
n
α
α
λ
e
1 −
10 α
e
)
∞
5 −100 α
λ
1
5
[ ( −
−
1 −
)] − λ(− −
1
10
e
) λ( − −
1
10
e
)
∑
= α e
e
λ ∑
e
e
=
!
5
n
n
n=
!
120
!
0
n=0
5
1
− 00 α − λ 1
−
5
λ − λ exp( 1
− 0 α)
10 α
1
5 5
1
− 00 α − λe
= α e
e
λ e e
=
α λ e
e
120
120
−10 α
ln L = − ln120 + 5ln α + 5ln λ −10 α
0 − e
λ
∂
5
= −100 +10
1
− 0 α
λe
= 0
∂ α α
1
− 0
→
α
λe
= 5
∂
5
1
− 0
= −
α
e
= 0
∂ λ λ
5 −100 + 5⋅10 = 0
α
5
1
−
=
λe
= 5
50 5
; 0 α = 5
α
λ = e
5
α = 1
,
0
moŜna sprawdzić, Ŝe to max
∂
∂
2
∂ α
∂ α∂ λ
∂
tzn:
>
0
i
< 0 → max
2
∂
∂
∂ α
2
∂ α∂ λ
∂ λ
Zadanie 8
1
P( X
EX =
k =
) 1
1 = 10
1
10
1
P( X
ES =
k =
) 9
0 = 10
5
2
E( X X + X + X + X + X
= ⋅ P X = =
1 (
1
2
3
4
5 )
1
( 1 )1 1,
0
cov( X , S =
−
⋅
=
=
1
5 )
1
1
,
0
1
,
0
5
,
0
,
0 05
20
Zadanie 9
n
∑ X
N nµ nσ 2
,
i ≅
(
)
i=1
2
σ
X
,
m ≅ N µ
m
n
n
n
2
E
2
2
.
1
∑ ( X
X
E
X
2 X
X
X
n
i −
m )
=
∑ i −
m ∑
i +
m
i=1
i=1
i=1
n
2
E ∑ X
= n
+
i
( 2 2
σ
µ )
i 1
=
1
n
n 1
E
m
(
1
X + ... + X
=
nσ + n µ + ( m − n) nµ
1
n )
[ 2 2 2
2 ]
m
m
E( X
=
+
m )
2
2
σ
2
µ
m
2
2
nσ
teraz 1. równa si
2
n σ + 2
µ
− ( 2
nσ + 2 2
n µ + mn − 2
2
n µ )
ę = (
)
(
) + + 2
nµ =
m
m
=
6
4
4
4
4
7
0
4
4
4
4
8
2 n
n
2
2
2
2
2 n
2 n
= σ n −
+ + µ n −
− 2 n +
+
n
m
m
m
m
n
n −
= c
n, m
m
1
c
1
n, m = n
−
m
Zadanie 10
µ > µ
2
1
2
9
∑( Xi− µ i
2
)
1 −
2
2
−
2
∑ Xi +2 µ 2∑ iXi− µ 2 ∑ i e
µ 2
µ 2
2Π
2
µ
e
2 ∑
i X
2
1
i −
∑ i− µ 1∑ iXi+ ∑ i e
2
2
2
2
2
9
∑( X
2
i − µ
i
1
) =
=
→
−∑ Xi + µ 1∑ iXi − µ 1 ∑ i
1 −
e
2
e
2
2Π
9
→ ∑ iX - STATYSTYKA
i
i=1
9
9
9
∑
i X
N
i µ i
i
N
µ
i ≅
∑
; ∑ ≅
(45 ;4 )
5
i=1
i=1
i=1
≅ N
9
}
(0 )
1
,
c
c
P
µ=
∑ iXi > c = ,0025 = P X >
→
= 9
,
1 6 → c = 9
,
1 6 45
0
i 1
=
45
45
ODPOWIEDŹ (E) jest prawidłowa