
ALGEBRA
1
Algebra
WYKŁAD 4

ALGEBRA
2
Własności działań macierzowych
Twierdzenie
Działania dodawania i mnożenia macierzy mają następujące własności:
A + B = B + A
(przemienność dodawania);
(
A + B) + C = A + (B + C)
(łączność dodawania);
A + 0 = 0 + A
gdzie
0
jest macierzą zerową;
A
(B
C) = (A
B)
C
(łączność mnożenia);
A
(B + C) = A
B + A
C
(rozdzielność dodawania względem
mnożenia);
(A + B)
C = A
C + B
C
(rozdzielność mnożenia względem
dodawania);
Jeśli
A
= [
a
ij
]
nxn
i
I
jest macierzą jednostkową stopnia
n
, to
A
I = A = I
A.
Własności te wynikają bezpośrednio z definicji działań na macierzach.
Macierze

ALGEBRA
3
Twierdzenie
Niech
-A
=
[
-
a
ij
]
mxn
oznacza
macierz przeciwną do macierzy
A
.
Dla dowolnych macierzy
A
i
B
zachodzą następujące związki:
- ( A + B) = ( - A) + ( - B );
- A
= (
-1
)
A;
A - B
=
A +
(-
B
).
Macierze
ALGEBRA
4
Definicja
Jeżeli
A
= [
a
ij
]
jest macierzą wymiaru
m
n
, wtedy macierz wymiaru
n
m
,
oznaczoną przez
]
[a
A
T
ij
T
, gdzie
a
a
ji
T
ij
,
1
i
m
,
1
j
n
,
nazywamy
macierzą transponowaną do macierzy
A
.
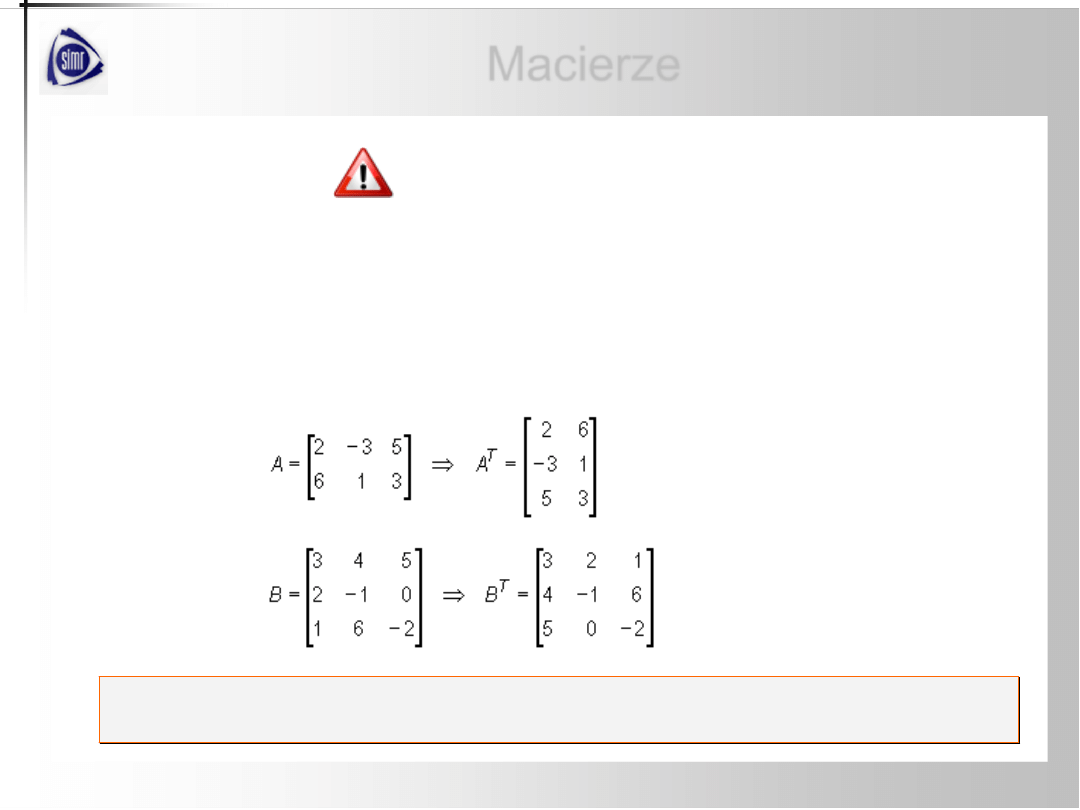
Przykład
Znaleźć macierze transponowane do danych macierzy.
Transpozycja macierzy polega więc na zamianie miejscami kolumn i wierszy
macierzy w ten sposób, że pierwszy wiersz staje się pierwszą kolumną itd.
Macierze

ALGEBRA
5
Twierdzenie
Dla macierzy
A
i
B
zachodzą równości:
(
A
T
)
T
=
A
,
(
A
+
B
)
T
=
A
T
+
B
T
,
(
A
B
)
T
=
B
T
A
T
.
Definicja
Macierz
A
nazywamy
macierzą symetryczną, gdy
A
T
=
A
.
Macierze

ALGEBRA
6
WYZNACZNIK MACIERZY

ALGEBRA
7
Rozpatrzmy układ równań liniowych z dwiema niewiadomymi
Rozwiązanie układu metodą eliminacji
Mnożymy pierwsze równanie przez b
2
,
Mnożymy drugie równanie przez (- b
1
),
Dodaj
emy równania stronami.
Stąd
.
Podobnie
.
Pzy założeniu
r
ozwiązanie układu równań jest postaci:
Wyznacznik macierzy

ALGEBRA
8
Macierz główna układu dwóch równań ma postać
Definicja
Wyznacznikiem
macierzy głównej układu dwóch równań nazywamy liczbę
równą
a
1
b
2
- a
2
b
1
i oznaczamy przez
Wyznacznik macierzy

ALGEBRA
9
Wyznaczaj
ąc dodatkowo dwa następujące wyznaczniki
możemy rozwiązanie układu równań zapisać w postaci
Wyznacznik macierzy

ALGEBRA
10
Niech
A
będzie dowolną macierzą kwadratową o wymiaru
n
n
(stopnia
n
)
nn
n
n
a
a
a
a
a
a
a
a
A
21
2
21
21
1
12
11
Dla macierzy
A
zdefiniujemy liczbę nazywaną wyznacznikiem
A
,
oznaczaną
jako
det A
, lub |
A
|.
Możemy zatem wyznacznik traktować jako funkcję, która każdej macierzy
kwadratowej przypisuje liczbę rzeczywistą.
Wyznacznik macierzy

ALGEBRA
11
Definicja
(indukcyjna wyznacznika -
rozwinięcie względem pierwszego wiersza)
Niech
A
oznacza macierz kwadratową wymiaru
n
n
.
Krok 1. Dla
n = 1
,
det A = a
.
Krok 2.
Zakładając, że mamy zdefiniowany wyznacznik macierzy
A
wymiaru
n
n
definiujemy wyznacznik macierzy
A
wymiaru
(n+1)
(n+1)
postaci:
1
,
1
,
1
2
,
1
1
,
1
1
,
2
2
21
21
1
,
1
1
12
11
n
n
n
n
n
n
n
n
n
n
a
a
a
a
a
a
a
a
a
a
a
a
W tym celu dla
j
= 1, 2, ...,
n
+
1:
w
ykreślamy z macierzy
A
wiersz
1
i
kolumnę
j
,
d
la pozostałej macierzy
A
1,j
obliczamy det
A
1j
,
t
worzymy sumę
1
,
1
1
,
1
1
1
,
1
1
1
2
,
1
12
2
1
1
,
1
11
1
1
det
)
1
(
det
)
1
(
det
)
1
(
det
)
1
(
n
n
n
j
j
j
A
a
A
a
A
a
A
a
S
Krok 3. Przyjmujemy
det A = S
.
Wyznacznik macierzy
ALGEBRA
12
det A
jest więc sumą następujących iloczynów:
każdy element
a
1j
pierwszego wiersza
mnożymy przez (-1)
1+j
i przez wyznacznik macierzy otrzymanej przez wy
kreślenie
pierwszego wiersza i
j
-tej kolumny.
Wyznacznik macierzy

ALGEBRA
13
Zauważmy, że stosując definicję indukcyjną do macierzy
kwadratowej A
stopnia 2 otrzymamy wynik zgodny z pierwszą
definicją przedstawioną w tym wykładzie tzn.:
12
21
22
11
22
21
12
11
a
a
a
a
a
a
a
a
Wyznacznik macierzy

ALGEBRA
14
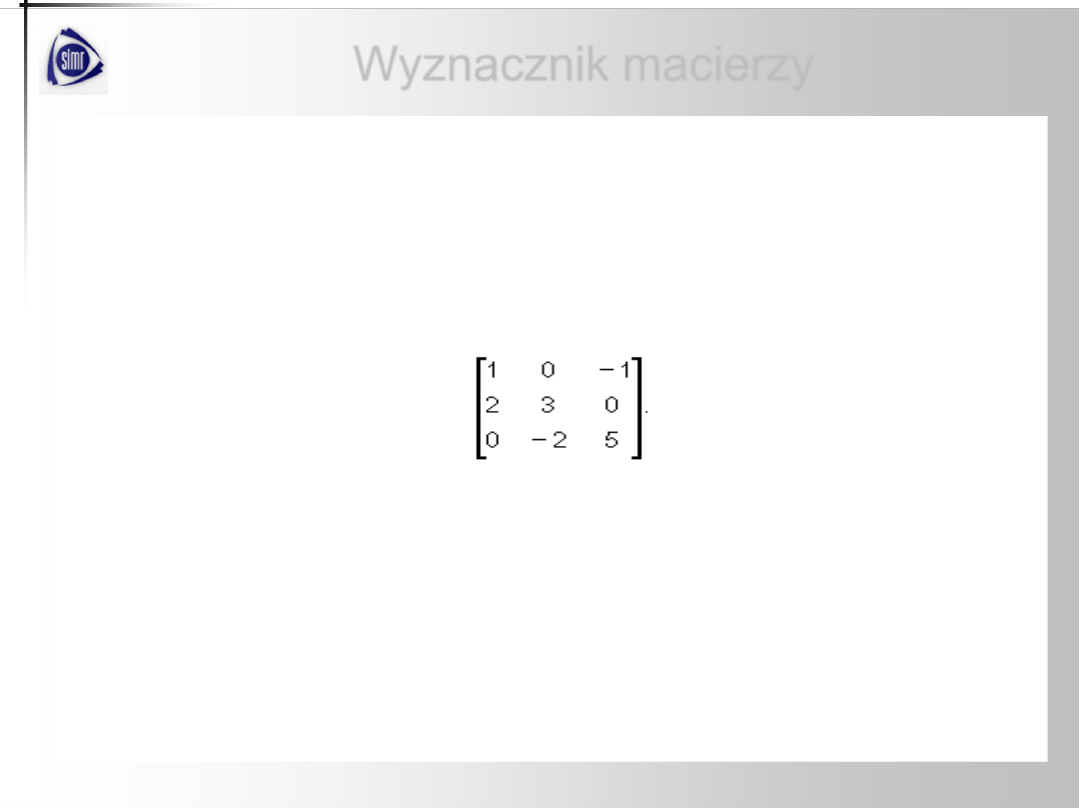
Przykład
Obliczyć z definicji wyznacznik macierzy:
.
Wyznacznik macierzy
24
ALGEBRA
15
Wyznacznik macierzy kwadratowej oznaczamy również symbolem:
nn
n
n
a
a
a
a
a
a
a
a
21
2
21
21
1
12
11
Podobnie jak w przypadku macierzy,
dla wyznacznika definiuje się stopień,
wiersze i kolumny.
Wyznacznik jest
określony tylko dla macierzy kwadratowych!
Wyznacznik macierzy
ALGEBRA
16
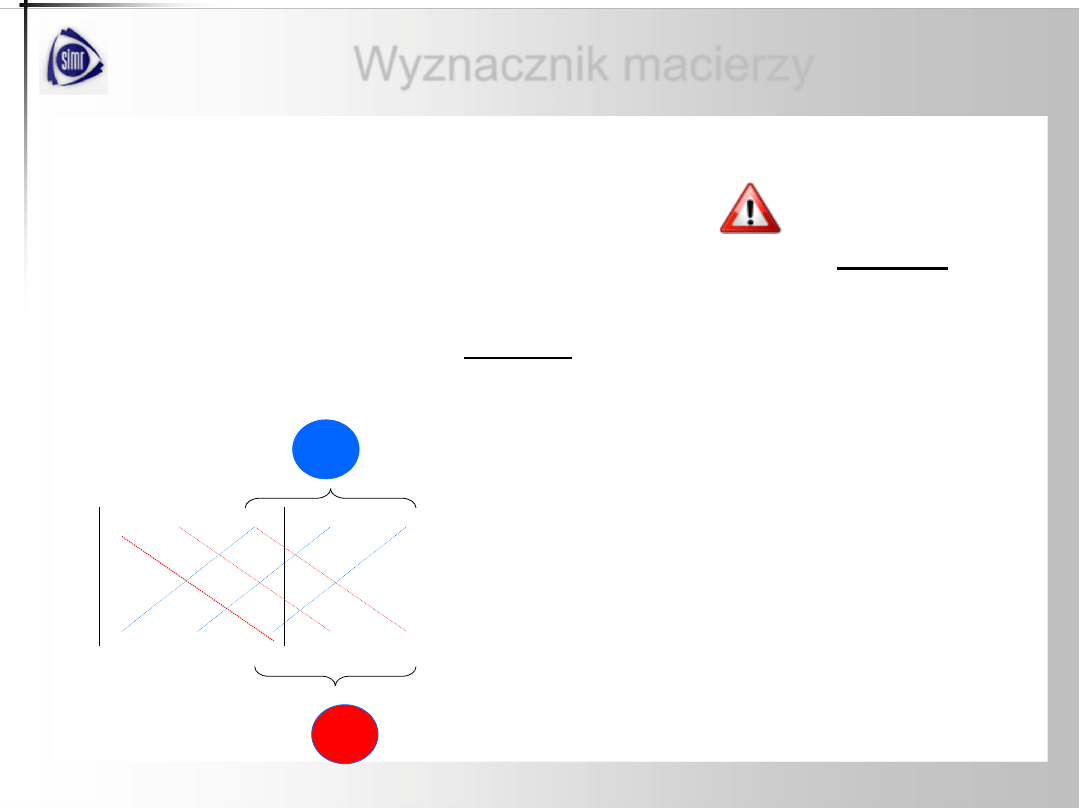
Metoda (wzór) Sarrusa
Jest to metoda rachunkowa obliczania wyznacznika macierzy stopnia 3.
Do macierzy dopisujemy dwie pierwsze kolumny
i obliczamy sumę
następujących iloczynów:
)
(
12
21
33
11
23
32
13
22
31
32
21
13
31
23
12
33
22
11
32
22
12
31
21
11
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
-
+
Wyznacznik macierzy

Przykład
Obliczyć wyznacznik
48
2
0
4
3
2
1
1
5
6
1
0
1
6
2
2
4
5
3
1
6
5
0
2
3
4
1
6
2
5
0
1
2
3
A
Wyznacznik macierzy

ALGEBRA
18
Wzór Sarrusa
48
1
2
3
4
0
2
6
5
1
6
2
2
1
1
0
4
5
3
4
1
6
2
5
0
1
2
3
4
1
6
2
5
0
1
2
3
4
1
6
2
5
0
1
2
3
4
1
6
2
5
0
1
2
3
4
1
6
2
5
0
1
2
3
4
1
6
2
5
0
1
2
3
A
.
Wyznacznik macierzy
ALGEBRA
19
Uwaga
Zamiast kolumn
można dopisać dwa pierwsze wiersze
i zastosować opisaną procedurę
Przyk
ład
O
blicz wyznacznik metodą Sarrusa
48
4
2
0
2
1
3
1
5
6
2
2
6
1
1
0
4
5
3
2
5
0
1
2
3
4
1
6
2
5
0
1
2
3
A
Wyznacznik macierzy
+
-
ALGEBRA
20
Zadanie
Obliczyć wyznacznik macierzy
Wyznacznik macierzy

ALGEBRA
21
Twierdzenie
Wyznacznik macierzy mającej wiersz (kolumnę) zerową
jest równy 0.
Twierdzenie
Przestawienie dwóch wierszy (kolumn) w macierzy jest
równoważne pomnożeniu wyznacznika przez -1.
Przykład
c
d
a
b
ad
bc
bc
ad
d
c
b
a
)
(
Własności wyznaczników

ALGEBRA
22
Twierdzenie
Wyznacznik macierzy o dwóch jednakowych wierszach
(kolumnach) jest równy 0.
Przykład
0
ab
ab
b
a
b
a
Twierdzenie
Wyznacznik macierzy jest równy wyznacznikowi macierzy
względem niej transponowanej
det A = det A
T
Przykład
d
b
c
a
bc
ad
d
c
b
a
Własności wyznaczników

ALGEBRA
23
Twierdzenie
Mnożąc wiersz (kolumnę) macierzy przez liczbę
mnożymy wyznacznik tej macierzy przez tę liczbę.
Przykład
d
c
b
a
d
c
b
a
Twierdzenie
Wyznacznik macierzy o dwóch proporcjonalnych
wierszach (kolumnach) jest równy 0.
Przykład
0
0
b
a
b
a
b
a
b
a
Własności wyznaczników

ALGEBRA
24
Twierdzenie
Jeżeli w macierzy jeden z wierszy (lub jedna z kolumn)
jest kombinacją liniową pozostałych wierszy (lub kolumn),
to wyznacznik tej macierzy jest równy 0.
Przykład
0
0
0
3
3
3
2
2
2
1
1
1
3
3
3
2
2
2
1
1
1
3
3
3
3
2
2
2
2
1
1
1
1
b
b
a
b
b
a
b
b
a
a
b
a
a
b
a
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
Własności wyznaczników
ALGEBRA
25
Twierdzenie
Wyznacznik macierzy nie zmieni wartości, jeżeli do wiersza
(lub kolumny) macierzy dodamy kombinację liniową
pozostałych wierszy (lub kolumn).
Przykład
3
3
3
3
3
2
2
2
2
2
1
1
1
1
1
3
3
3
3
2
2
2
2
1
1
1
1
3
3
3
2
2
2
1
1
1
3
3
3
2
2
2
1
1
1
b
a
c
b
a
b
a
c
b
a
b
a
c
b
a
b
a
b
a
b
a
b
a
b
a
b
a
c
b
a
c
b
a
c
b
a
c
b
a
c
b
a
c
b
a
= 0
Własności wyznaczników

ALGEBRA
26
W przyjętej definicji wyznacznika macierzy
wykorzystaliśmy tzw. rozwinięcie względem pierwszego
wiersza. Można wykazać, że ten sam wynik uzyskamy
stosując rozwinięcie względem dowolnego wiersza,
lub kolumny.
Własności wyznaczników

ALGEBRA
27
Niech
A
będzie macierzą kwadratową stopnia
n
Definicja
Wyrażenie
D
i j
= (-1)
i +j
det A
i j
,
1
i , j
n
,
gdzie
A
i j
oznacza macierz stopnia
n
-1
otrzymaną przez
skreślenie
i
-tego wiersza i
j
-tej kolumny macierzy
A
,
nazywamy
dopełnieniem algebraicznym elementu
a
i j
.
Własności wyznaczników

ALGEBRA
28
Twierdzenie
(
Laplace'a o rozwinięciu wyznacznika względem
wiersza, lub kolumny )
Dla macierzy
A
stopnia
n
zachodzi:
det A = a
i 1
D
i 1
+ a
i 2
D
i 2
+ ... + a
i n
D
i n
i
det A = a
1j
D
1j
+ a
2 j
D
2 j
+ ... + a
n j
D
n j
dla dowolnych liczb
i
,
j
takich, że 1
i
,
j
n
.
Zatem wyznacznik jest równy sumie iloczynów elementów
i
-tego
wiersza i ich dopełnień algebraicznych, bądź sumie iloczynów
elementów
j
-
tej kolumny i ich dopełnień algebraicznych.
Własności wyznaczników

ALGEBRA
29
Uwagi
Stosując rozumowanie indukcyjne i twierdzenie Laplace'a łatwo
uzasadnić, że wyznacznik macierzy diagonalnej oraz dolno
lub górnotrójkątnej jest równy
iloczynowi elementów leżących na głównej przekątnej.
Korzystając z twierdzenia Laplace’a należy rozwijać wyznacznik
względem wiersza (lub kolumny) zawierającego najwięcej
elementów zerowych.
Liczbę elementów zerowych w wierszu, względem którego
rozwijany jest wyznacznik,
można zwiększyć dodając do wierszy
(kolumn
) inne wiersze (kolumny) pomnożone przez odpowiednio
dobrane liczby (operacje te nie zmieniają wartości wyznacznika).
Własności wyznaczników

ALGEBRA
30
Przykład
Obliczyć wyznacznik
5
1
1
1
1
1
4
1
1
1
1
1
3
1
1
1
1
1
2
1
1
1
1
1
1
Odejmując pierwszy wiersz od pozostałych otrzymujemy wyznacznik o niezmienionej
wartości
4
0
0
0
0
0
3
0
0
0
0
0
2
0
0
0
0
0
1
0
1
1
1
1
1
J
est on równy
1
1
2
3
4 = 24.
Własności wyznaczników

Dziękuję za uwagę
Wyszukiwarka
Podobne podstrony:
SIMRAlgebra W04
SIMRAlgebra W04
RBD W04
W04 2
W04 3
W04 4
cps w04 v9
PI w04
Elektronika W04
zj w04
gs w04 id 197501 Nieznany
223 B8 4 A W04 zestawienie slus Nieznany
bal w04
krs form w04
KZ BD w04
Gazownictwo w04
c cxx w04
więcej podobnych podstron