CPS 1

2006/2007

PRZEKSZTAŁCENIE ZET

Definicja przekształcenia „Z”

Przekształcenie ZET jest w dziedzinie czasu dyskretnego odpowiednikiem ciągłego

przekształcenia Laplace’a w dziedzinie czasu ciągłego. Podamy dwie równoważne definicje
przekształcenia ZET różniące się jedynie sposobem zapisu matematycznego sygnału
dyskretnego:

• Dla sygnału zapisanego w

U

postaci ciągu

U

U

wartości

U

f[n]:

( )

[ ]

definicja

n

F z

f n z

∞

−∞

−

=

∑

• Dla

U

sygnału spróbkowanego

U

f*(t) ( wykorzystując przekształcenie Laplace’a )

( )

( )

{

}

*

sTp

definicja

e

z

F z

L f

t

=

=

U

Sygnał dyskretny

( )

( ) (

*

p

p

)

f

t

f nT

t nT

δ

∞

−∞

=

⋅

−

∑

Transformata Laplace’a (dwustronna) sygnału dyskretnego:

( )

( )

*

p

sTp

nsT

II

p

e

z

F

s

f nT

e

∞

−

=

−∞

=

⋅

∑

Stąd po dokonaniu podstawienia zgodnie z definicją otrzymamy wyrażenie jak dla ciągu

( )

( )

n

p

F z

f nT

z

∞

−

−∞

=

⋅

∑

Obszar zbieżności

Ponieważ przekształcenie

Z

ciągu f[n] jest zdefiniowane jako suma szeregu

nieskończonego, zatem

U

istnieje tylko dla tych wartości dla których szereg jest zbieżny

U

.

Suma zawiera zarówno dodatnie jak i ujemne potęgi zmiennej

z

. Jak wiadomo z teorii

szeregów potęgowych suma ujemnych potęg szeregu zbieżna dla |z| większego niż pewna stała
r

B

1

B

, a suma potęg dodatnich szeregu jest zbieżna dla |z| mniejszego niż pewna stała r

B

2

B

.

CPS 2

2006/2007

U

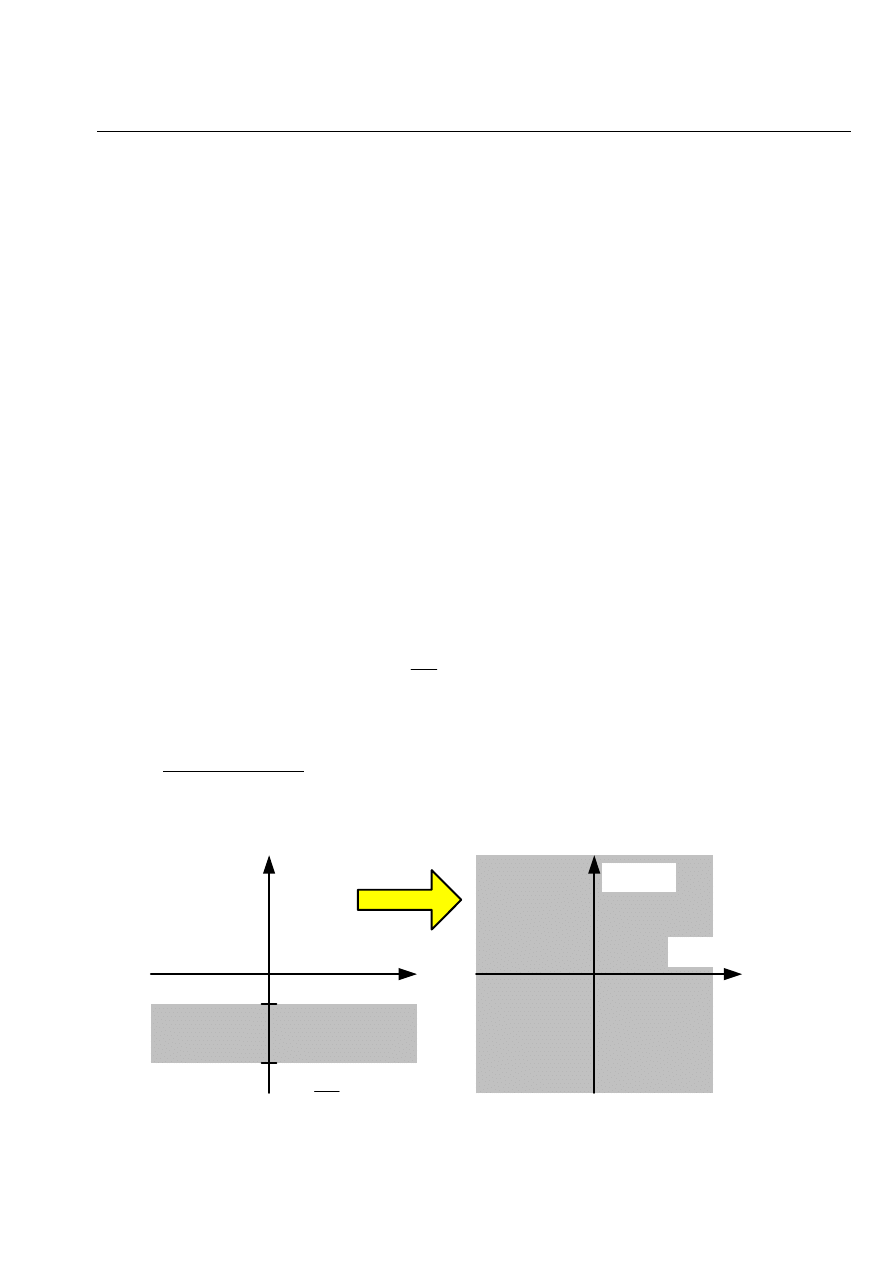
Wynika stąd, że obszar zbieżności (istnienia) transformaty

Z

ma kształt pierścienia

U

o promieniach r

B

1

B

, r

B

2

B

zależnych od funkcji f[n].

W celu dokładniejszego wyjaśnienia tego zagadnienia wykorzystamy przekształcenie

Laplace’a. Rozpatrzymy odwzorowanie punktów płaszczyzny zmiennej zespolonej

s

na punkty

płaszczyzny zmiennej zespolonej

z

.

Zgodnie z definicją przekształcenia

Z

związek między zmienną

z

i

s

opisuje równanie:

p

sT

z e

=

Ponieważ

s

j

σ

ω

= +

Stąd

(

)

p

p

p

j T

T

j T

z e

e e

σ ω

σ

ω

+

=

=

Czynnik

p

j T

e

ω

jest okresowy, zatem odwzorowanie nie jest jednoznaczne.

(

)

2

p

p

p

p

j T

T

T

j T

z e e

e e

ω

π

σ

σ

ω

+

=

=

Oznacza to, że każdy dowolny pas na płaszczyźnie zmiennej

s określony następująco

0

0

2

p

T

π

ω

ω ω

< <

+

σ

−∞ < < ∞

odwzorowuje

U

całą płaszczyznę

U

zmiennej

z

.

Re{s}

Im{s}

Im{z}

Re{z}

0

ω

p

T

π

ω

2

0

+

CPS 3

2006/2007

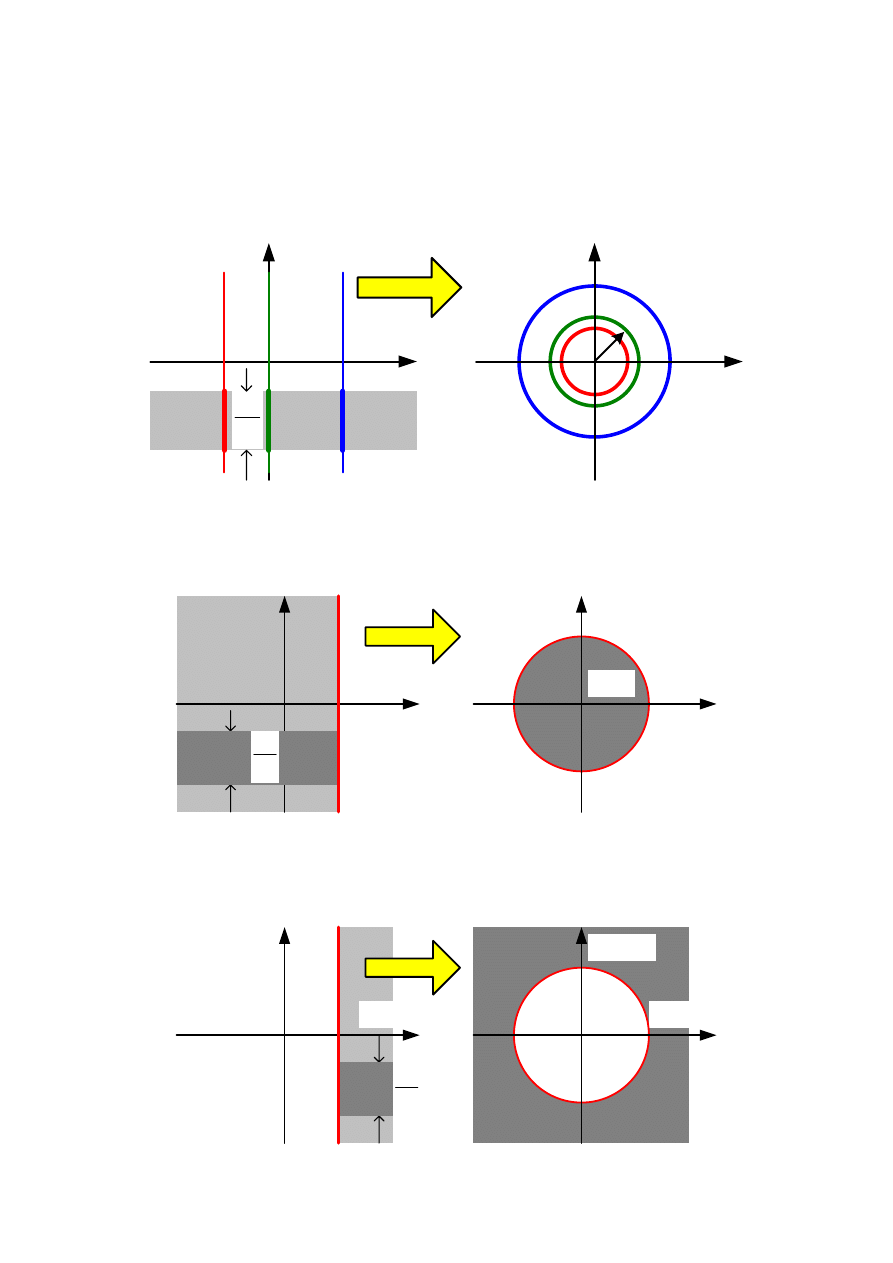
Rozpatrzymy szczególne przypadki odwzorowań:

Obrazem prostej o równaniu s=a (pionowa) na płaszczyźnie s będzie okrąg o promieniu

p

aT

e na

płaszczyźnie zmiennej

z

. Oś urojonych ma płaszczyźnie s odwzorowuje się na okrąg

jednostkowy na płaszczyźnie

z

.

Re{s}

Im{s}

Im{z}

Re{z}

p

T

π

2

0

1

Półpłaszczyzna na lewo od prostej s=a na płaszczyźnie s będzie wnętrzem koła o
promieniu

p

aT

e

Re{s}

Im{s}

Im{z}

Re{z}

0

p

T

π

2

r>1

Półpłaszczyzna na prawo od prostej

s=a

na płaszczyźnie

s

będzie zewnętrzem koła o promieniu

p

aT

e

Im{s}

Im{z}

Re{z}

0

p

T

π

2

r>1

Re{s}

CPS 4

2006/2007

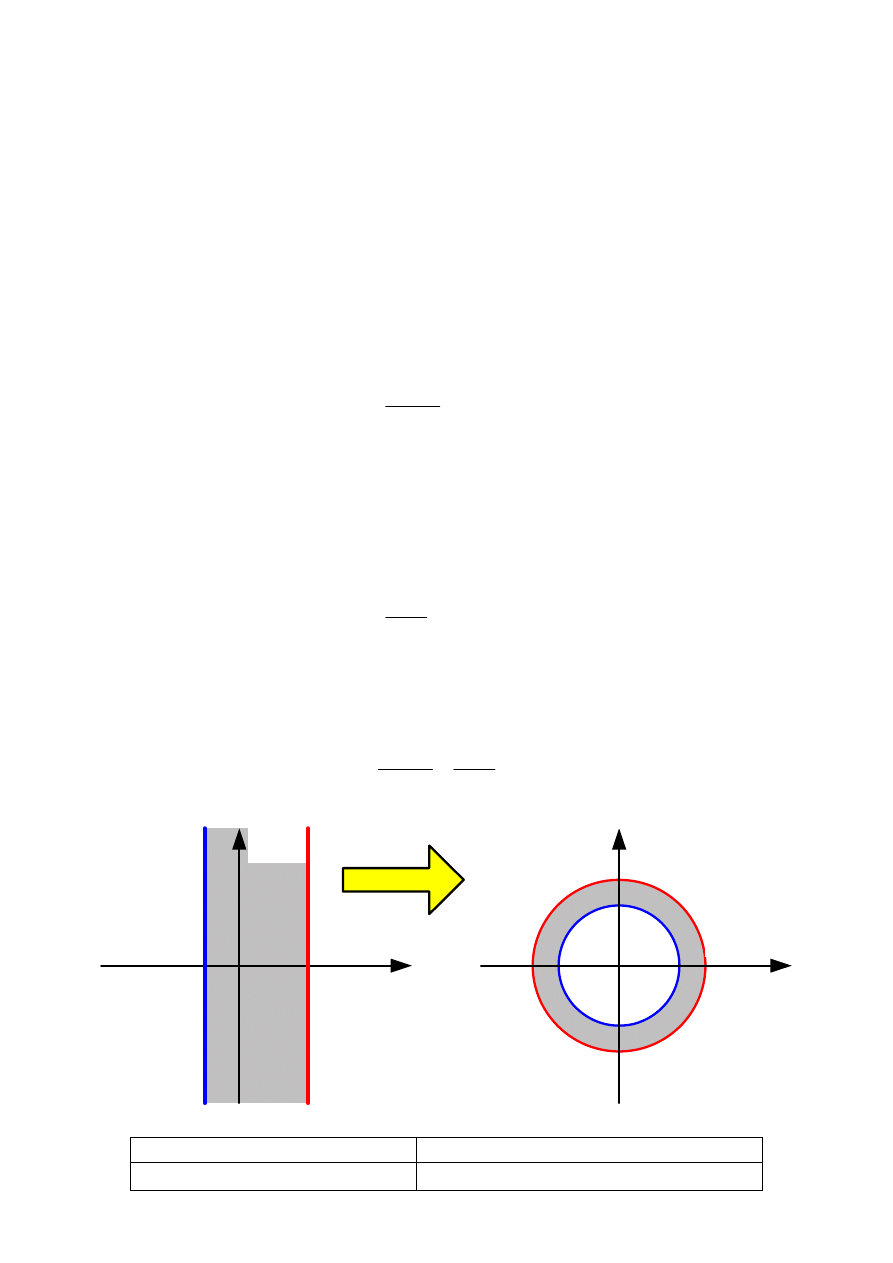
Rozpatrzymy przykład, który do wyznaczania przekształcenia Z wykorzystuje analogie z
transformacją Laplace’a

Obliczymy dwustronną transformatę Laplace’a sygnału o ciągłym czasie:

( )

( )

( )

1

1

at

bt

x t

e

t

e

t

−

=

− +

( )

( )

( )

x t

x t

x t

−

+

=

+

( )

( )

{

}

s

s

X s

L x t

−

=−

=

−

( )

1

X s

s a

−

=

− +

Obszar zbieżności dla tego składnika leży na lewo od punktu a na płaszczyźnie s, czyli
wewnątrz okręgu o promieniu

p

aT

e >1

( )

( )

{ }

X s

L x t

+

=

( )

1

X s

s b

+

=

+

Obszar zbieżności dla tego składnika leży na prawo od punktu –b na płaszczyźnie s, czyli na
zewnątrz koła o promieniu

p

bT

e

−

<1

( )

1

1

X s

s a

s b

=

+

− +

+

Im{s}

Im{z}

Re{z}

0

Re{s}

a

-b

p

bT

e

−

p

aT

e

S Z

Pas zbieżności pomiędzy –b i a

pierścień o promieniach

p

bT

e

−

,

p

aT

e

CPS 5

2006/2007

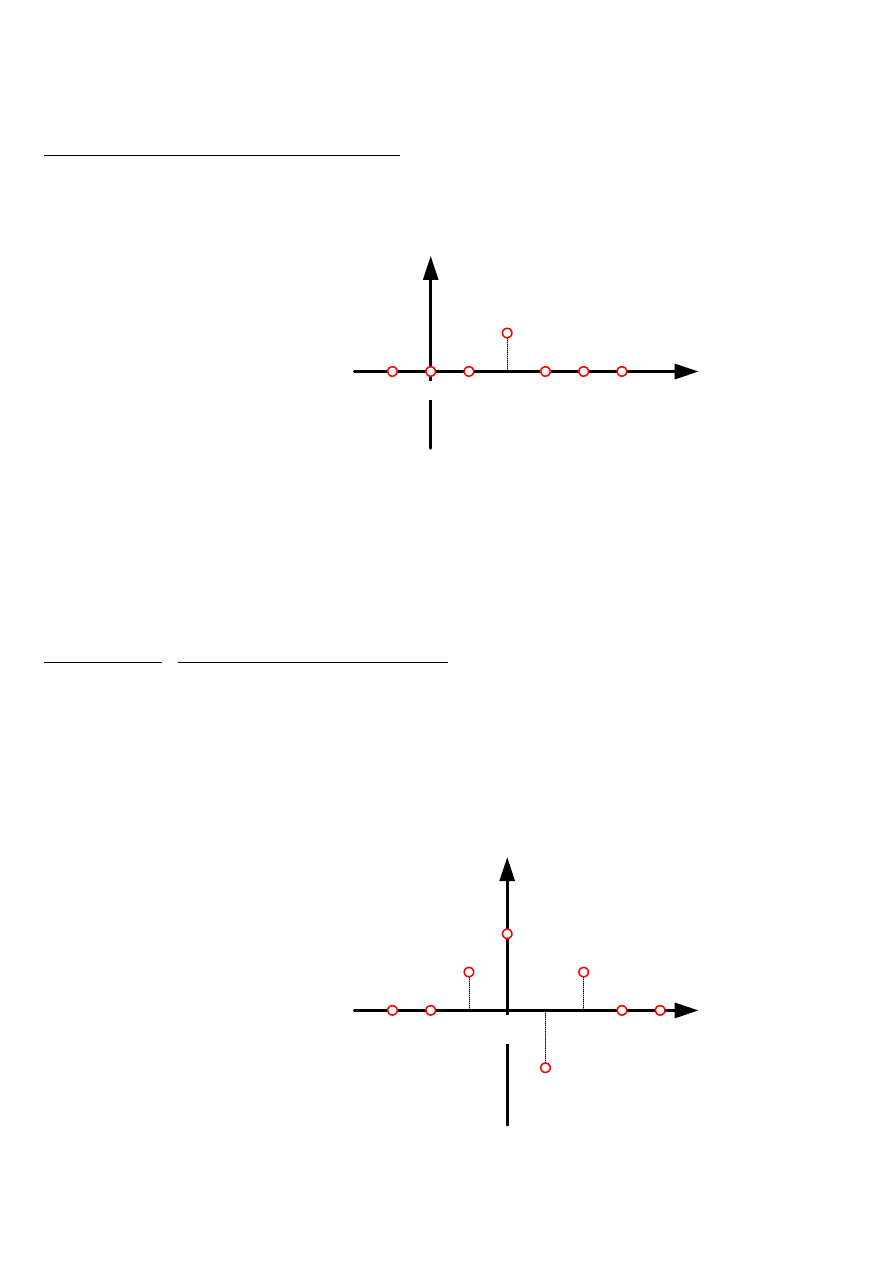
Przykłady wyznaczania transformaty Z podstawowych sygnałów:

U

Transformata „zet” (Z) delty Kroneckera:

[ ]

1

0

0

0

dla n

n

dla n

δ

=

⎧

= ⎨

≠

⎩

f[n]

0

n

1 2 3

-1

-3

1

-2

[ ]

{

}

[ ]

[ ]

0

0

0

1

n

n

n

n

f n

f n z

f n z

z

∞

−

−

=−∞

=

=

=

=

∑

∑

Z

=

[ ]

1

n

δ

⎯⎯

→

Z

U

Transformata

U

Z

U

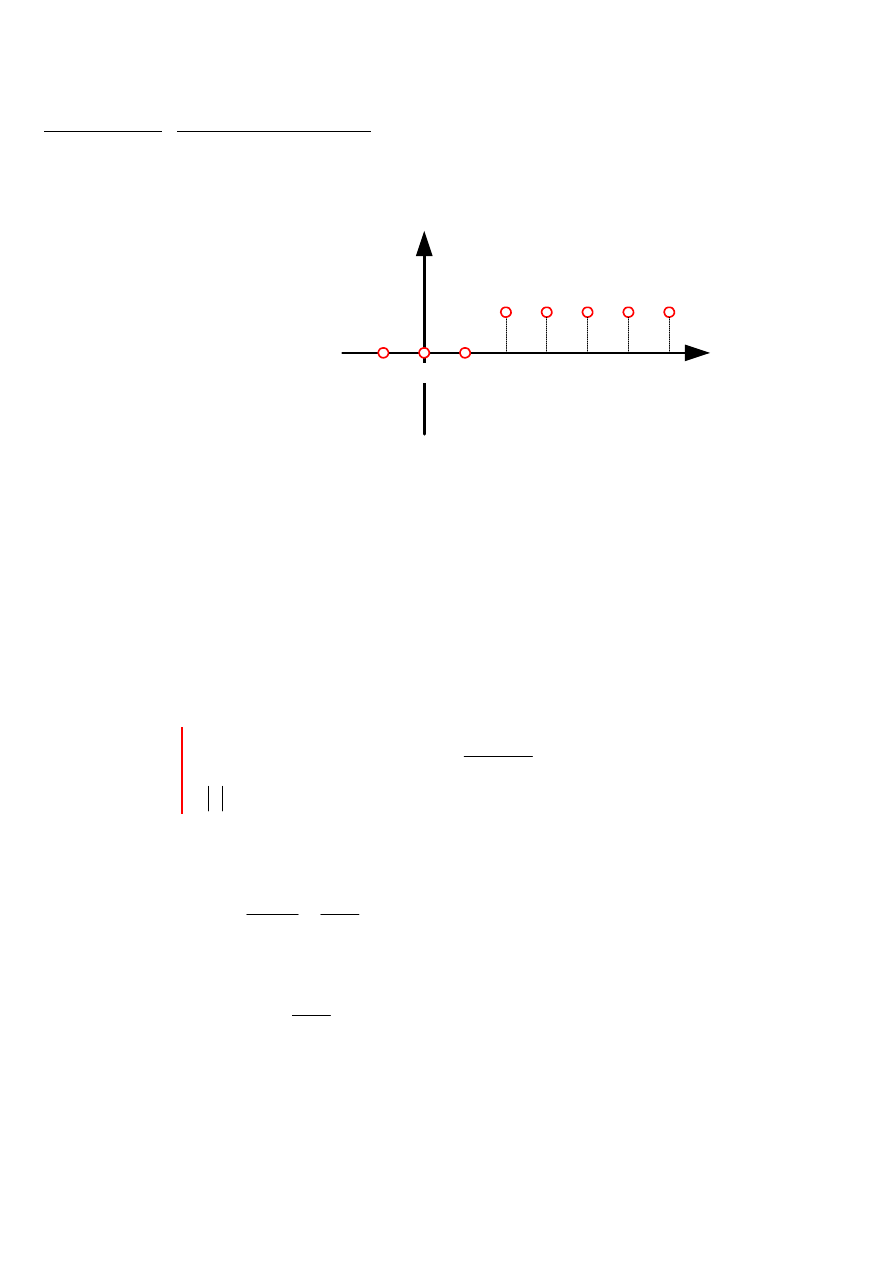
dowolnego ciągu skończonego:

[ ]

1,

1

2,

0

1,

1

1,

2

0,

n

n

x n

n

n

inne

= −

⎧

⎪

=

⎪⎪

= −

=

⎨

⎪

=

⎪

⎪⎩

f[n]

n

1 2 3

-1

-2

-3

1

2

0

-1

[ ]

{

}

[ ]

1

2

2

n

n

f n

f n z

z

z

∞

−

−

=−∞

=

= + −

∑

Z

z

−

+

CPS 6

2006/2007

U

Transformata

U

Z

U

skoku jednostkowego:

[ ]

1

0

1

0

0

dla n

n

dla n

≥

⎧

= ⎨

<

⎩

f[n]

0

n

1 2 3

-1

-3

1

-2

[ ]

{

}

[ ]

( )

0

1

0

1

n

n

n

n

n

n

f n

f n

z

z

∞

−

=−∞

∞

−

=

∞

−

=

=

=

⋅

=

∑

∑

∑

Z

z

Wykorzystamy zależność na sumę ciągu geometrycznego:

1

1

0

...

1

n

N

N

n

n

A Ax

A Ax

Ax

Ax

x

−

−

=

−

+

+ +

=

=

−

∑

1

0

N

x

oraz N

x

<

→ ∞ ⇒

→

[ ]

{

}

1

1

1

1

z

f n

z

z

−

=

=

−

−

Z

[ ]

1

1

z

n

z

⎯⎯

→

−

Z

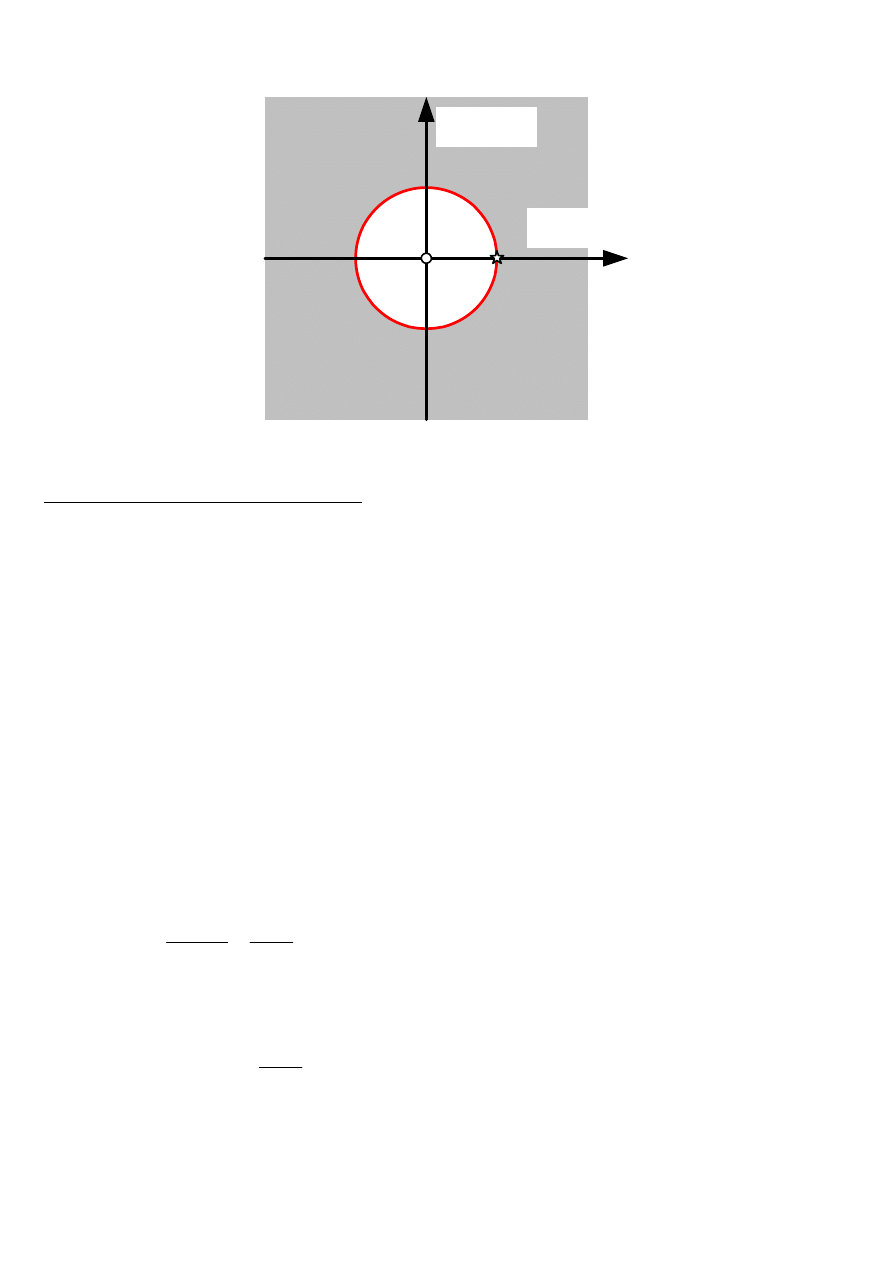
Transformata F(z) posiada biegun w punkcie z=1, oraz pierwiastek w punkcie z=0. Obszar
zbieżności opisuje zależność |z| >|1|, leży na zewnątrz okręgu o promieniu 1.

CPS 7

2006/2007

Im{z}

Re{z}

0

1

U

Transformata

Z

funkcji wykładniczej

U

(

):

0

n

≥

[ ]

[ ]

1

n

x n

a

n

=

⋅

( )

[ ]

( )

0

1

0

n

n

n

n

n

n

n

X z

x n z

a z

az

∞

−

=−∞

∞

−

=

∞

−

=

=

=

=

∑

∑

∑

Suma jest zbieżna gdy |a/z|<1 lub |z|>|a|

( )

1

1

1

z

X z

az

z a

−

=

=

−

−

[ ]

1

n

z

a

n

z a

⎯⎯

→

−

Z

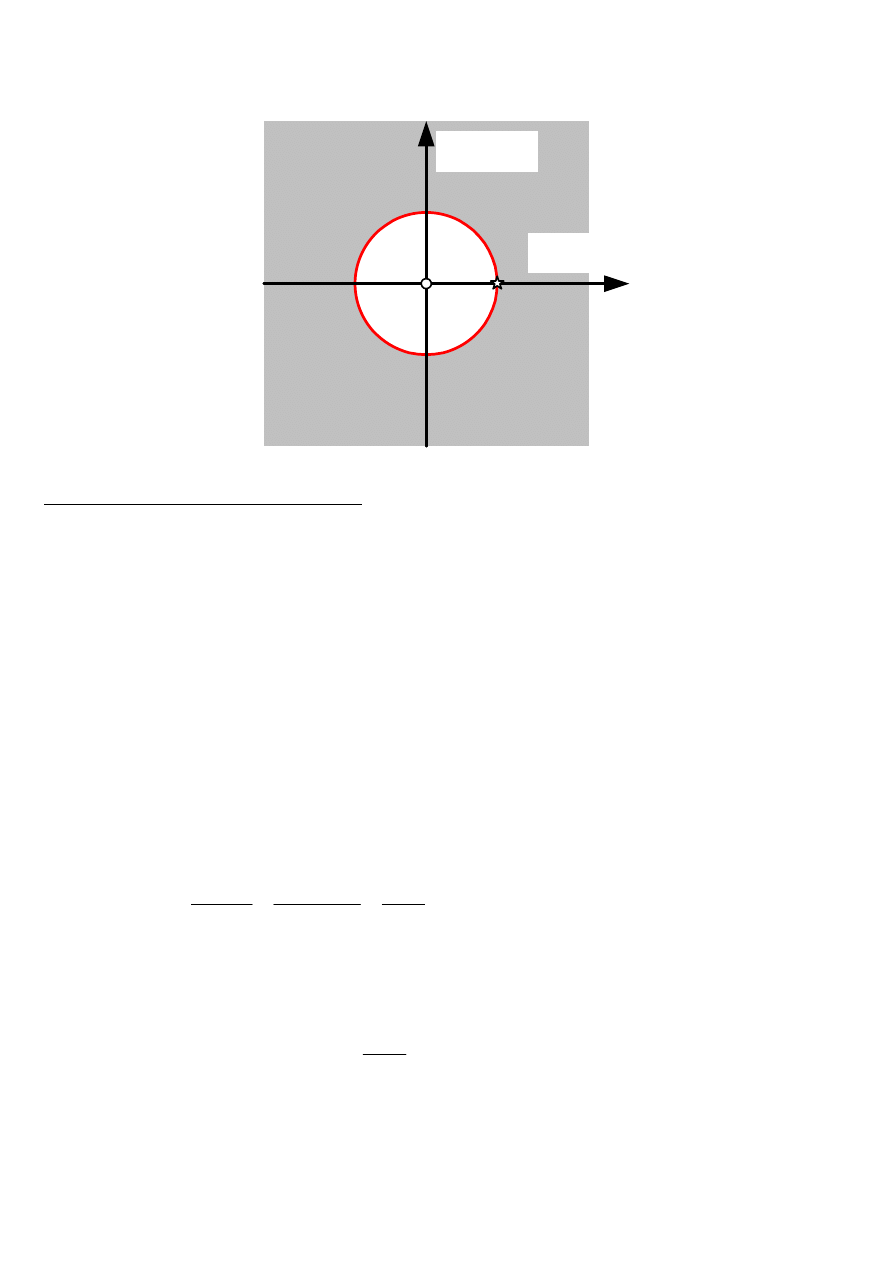
Transformata X(z) posiada biegun w punkcie z=a, oraz pierwiastek w punkcie z=0. Obszar
zbieżności opisuje zależność |z| >|a|, leży na zewnątrz okręgu o promieniu a.

CPS 8

2006/2007

Im{z}

Re{z}

0

a

U

Transformata

Z

funkcji wykładniczej

U

(

0

n

< ):

[ ]

[

]

1

1

n

y n

a

n

= − ⋅ − −

( )

[ ]

( )

( )

1

1

1

1

0

1

n

n

n

n

n

n

n

n

n

Y z

y n z

a z

az

a z

∞

−

=−∞

−

−

=−∞

−

−

=−∞

∞

−

=

=

= −

= −

= −

∑

∑

∑

∑

Suma jest zbieżna gdy |z/a|<1 lub |z|<|a|

( )

1

1

1

1

1

1

1

1

1

za

z

X z

za

za

z a

−

−

−

−

−

= −

=

=

−

−

−

[

]

1

1

n

z

a

n

z a

−

− − ⎯⎯

→

−

Z

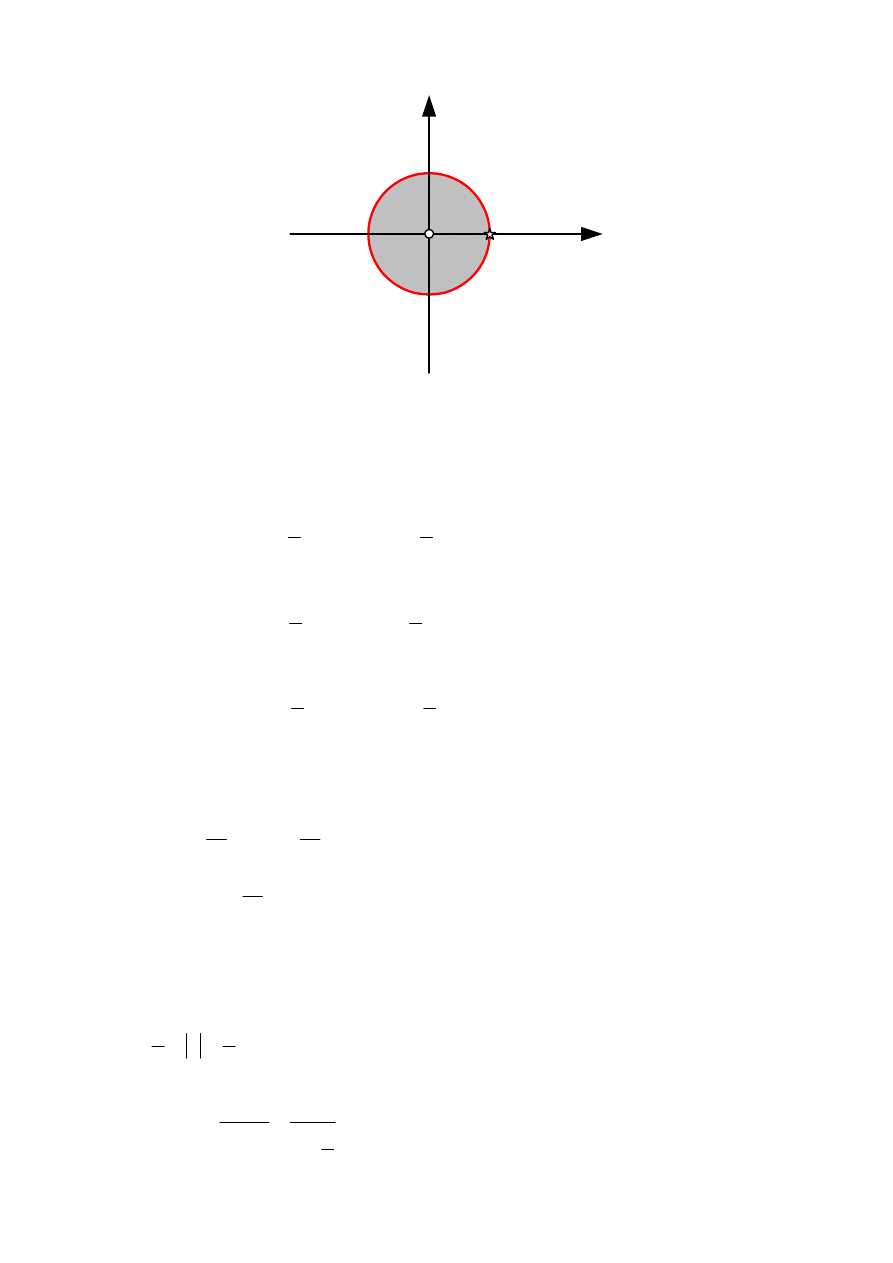
Transformata X(z) posiada biegun w punkcie z=a, oraz pierwiastek w punkcie z=0. Obszar
zbieżności opisuje zależność |z| <|a|, leży wewnątrz okręgu o promieniu a.

CPS 9

2006/2007

Im{z}

Re{z}

0

a

Przykład

Zidentyfikujemy obszary istnienia transformaty Z dla następujących sygnałów:

[ ]

[ ]

[ ]

1

1

1

2

1

2

4

n

n

x n

n

⎛

⎞

⎛ ⎞

= −

⋅ − +

⋅

⎜

⎟

⎜ ⎟

⎝

⎠

⎝ ⎠

n

[ ]

[ ]

[ ]

1

1

1

2

1

2

4

n

n

y n

n

n

⎛

⎞

⎛ ⎞

= −

⋅

+

⋅

⎜

⎟

⎜ ⎟

⎝

⎠

⎝ ⎠

[ ]

[ ]

[ ]

1

1

1

2

1

2

4

n

n

w n

n

n

⎛

⎞

⎛ ⎞

= −

⋅ − +

⋅ −

⎜

⎟

⎜ ⎟

⎝

⎠

⎝ ⎠

X(z)

( )

(

)

0

0

0

0

1

1

2

2

4

1

2

2

4

n

n

n

n

n

n

n

n

X z

z

z

z

z

∞

=−∞

=

∞

∞

=

=

⎛

⎞

⎛

=

−

+

⎜

⎟

⎜

⎝

⎠

⎝

⎛

⎞

=

−

+

⎜

⎟

⎝

⎠

∑

∑

∑

∑

⎞

⎟

⎠

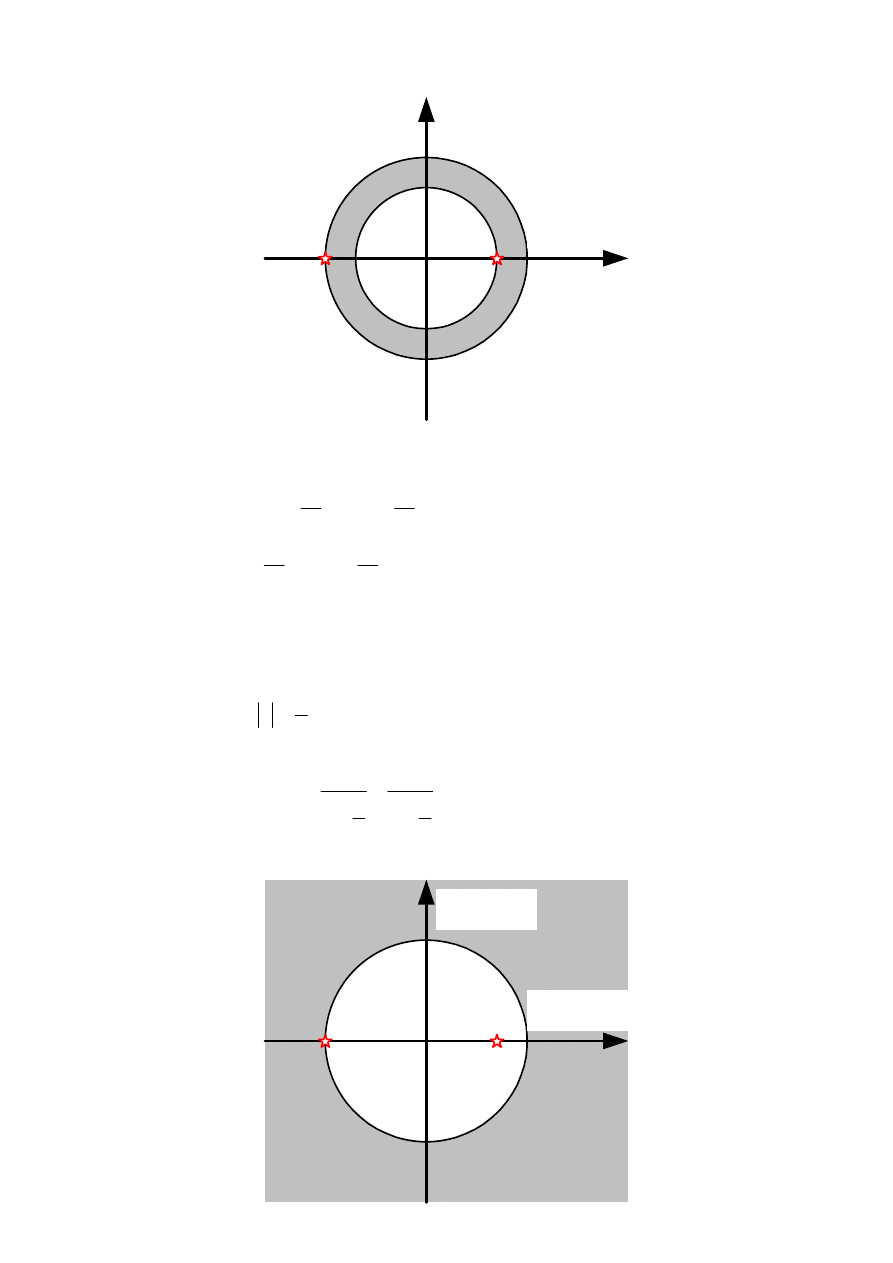
Pierwsza suma jest zbieżna dla |2z|<1 lub |z|<1/2. Druga suma jest zbieżna dla |1/(4z)|<1 lub
|z|>1/4. Wspólny obszar zbieżności dla tych szeregów stanowi pierścień:

1
4

2

z

< <

1

( )

1

2

1

1 2

4

z

X z

z

z

=

+

+

−

CPS 10

2006/2007

Im{z}

Re{z}

1/4

-1/2

Y(z)

( )

0

0

0

0

1

1

2

2

4

1

1

2

2

4

n

n

n

n

n

n

n

n

Y z

z

z

z

z

∞

∞

=

=

∞

∞

=

=

⎛

⎞

⎛

⎞

=

−

+

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

⎛

⎞

⎛

⎞

=

−

+

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

∑

∑

∑

∑

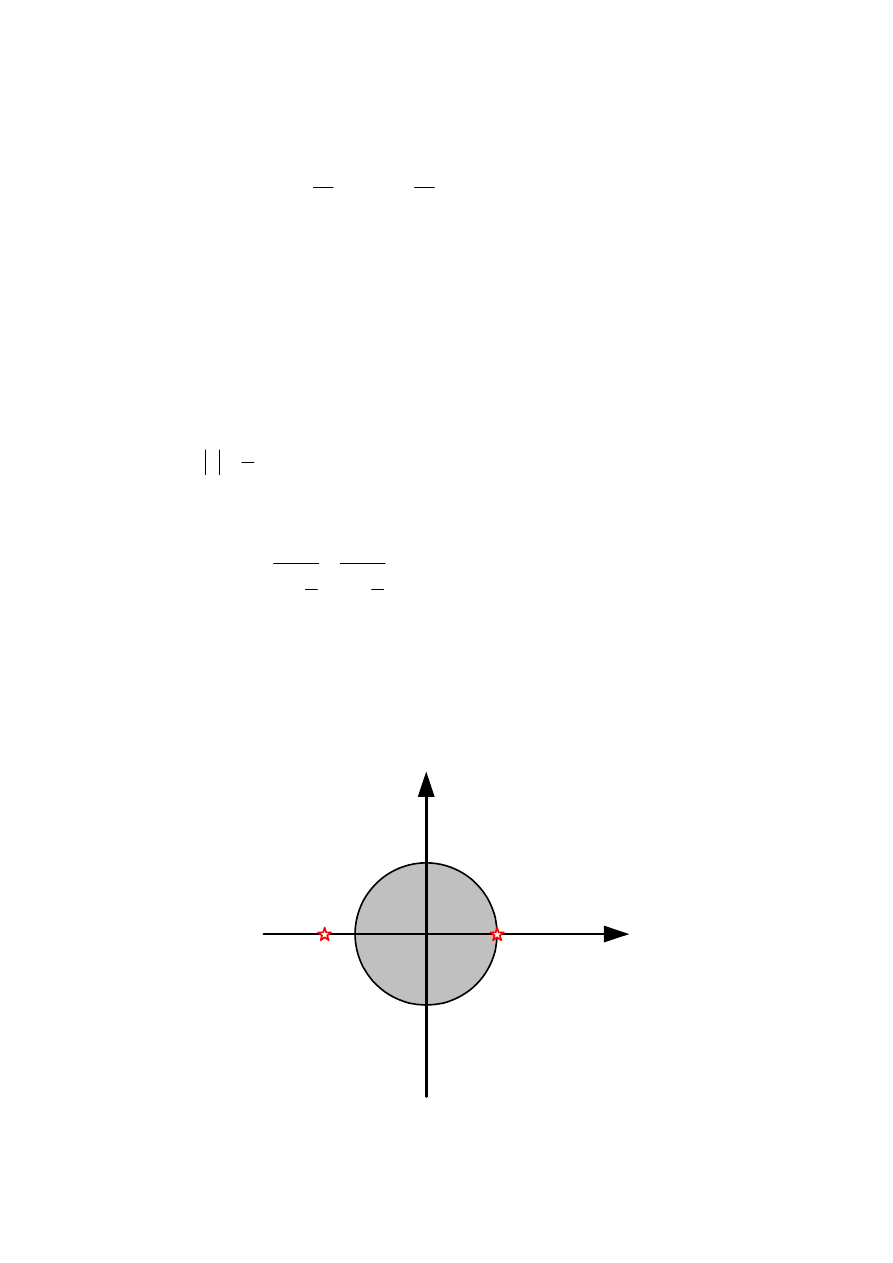
Pierwsza suma jest zbieżna dla |1/(2z)|<1 lub |z|>1/2. Druga suma jest zbieżna dla |1/(4z)|<1 lub
|z|>1/4. Wspólny obszar zbieżności dla tych szeregów stanowi zewnętrze okręgu:

1

2

z

>

( )

2

1

1

2

4

z

z

Y z

z

z

=

+

+

−

Im{z}

Re{z}

1/4

-1/2

CPS 11

2006/2007

W(z)

( )

(

)

( )

0

0

0

0

1

1

2

2

4

2

2

4

n

n

n

n

n

n

n

n

W z

z

z

z

z

=−∞

=−∞

∞

∞

=

=

⎛

⎞

⎛

⎞

=

−

+

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

=

−

+

∑

∑

∑

∑

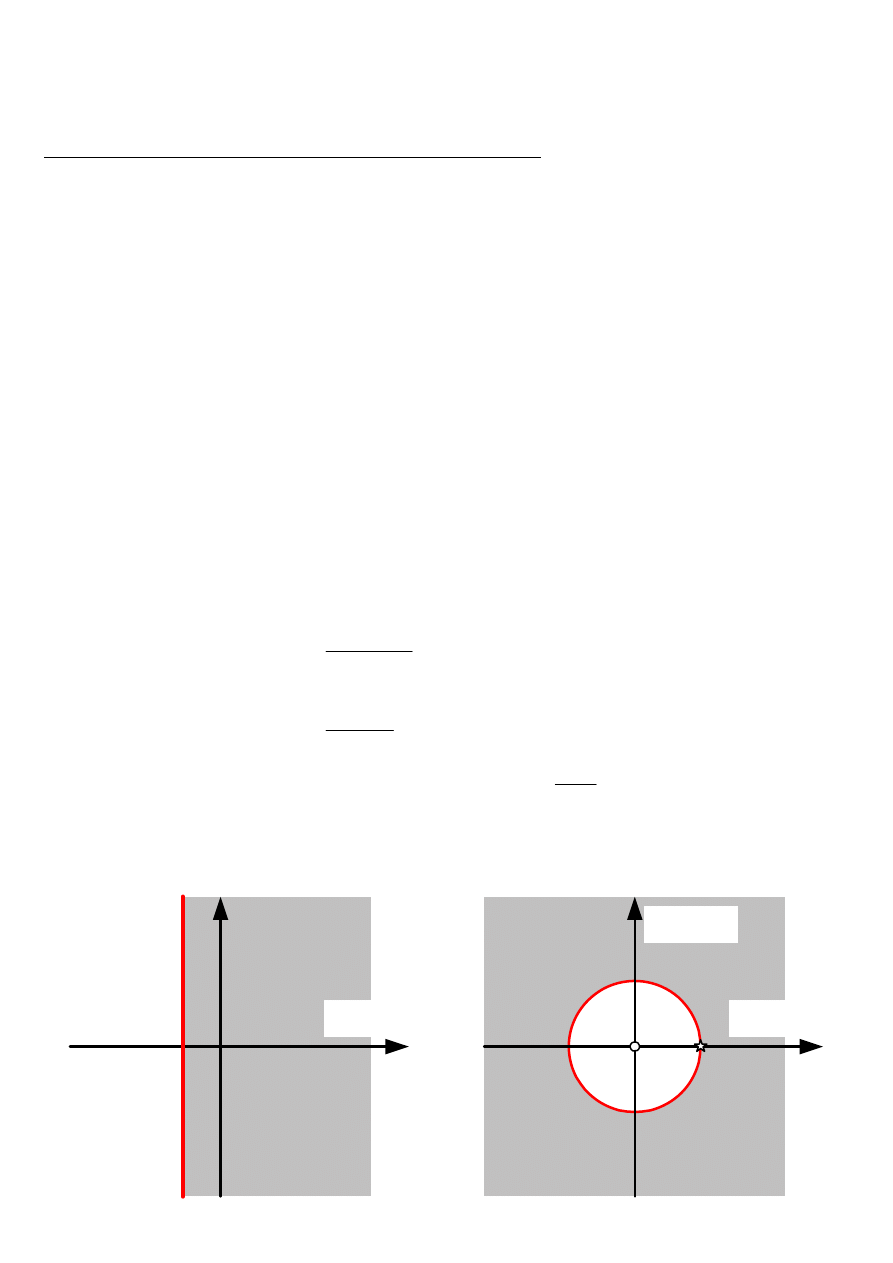
Pierwsza suma jest zbieżna dla |2z|<1 lub |z|<1/2. Druga suma jest zbieżna dla |4z|<1 lub
|z|<1/4. Wspólny obszar zbieżności dla tych szeregów stanowi wnętrze okręgu:

1
4

z

<

( )

2

1

1

2

4

z

z

W z

z

z

=

+

+

−

Im{z}

Re{z}

1/4

-1/2

CPS 12

2006/2007

Wykorzystanie przekształcenia Laplace’a od wyznaczania transformaty Z:

U

Transformata Z wykładniczego przebiegu prawostronnego

U

(

):

0

t

≥

( )

( )

1

bt

x t

e

t

−

=

( )

(

)

0

*

bt

p

k

x

t

e

t kT

δ

∞

−

=

=

⋅

−

∑

( )

(

)

0

*

p

bkT

p

k

x

t

e

t kT

δ

∞

−

=

=

−

∑

Korzystając z transformaty Laplace’a

( )

0

*

p

p

bkT

skT

k

X

s

e

e

∞

−

−

=

=

∑

( )

(

)

0

*

p

p

k

bT

sT

k

X

s

e

e

∞

−

−

=

=

∑

( )

(

)

1

0

p

k

bT

k

X z

e

z

∞

−

−

=

=

∑

( )

1

1

1

p

bT

X z

e

z

−

−

=

−

( )

p

bT

z

X z

z e

−

=

−

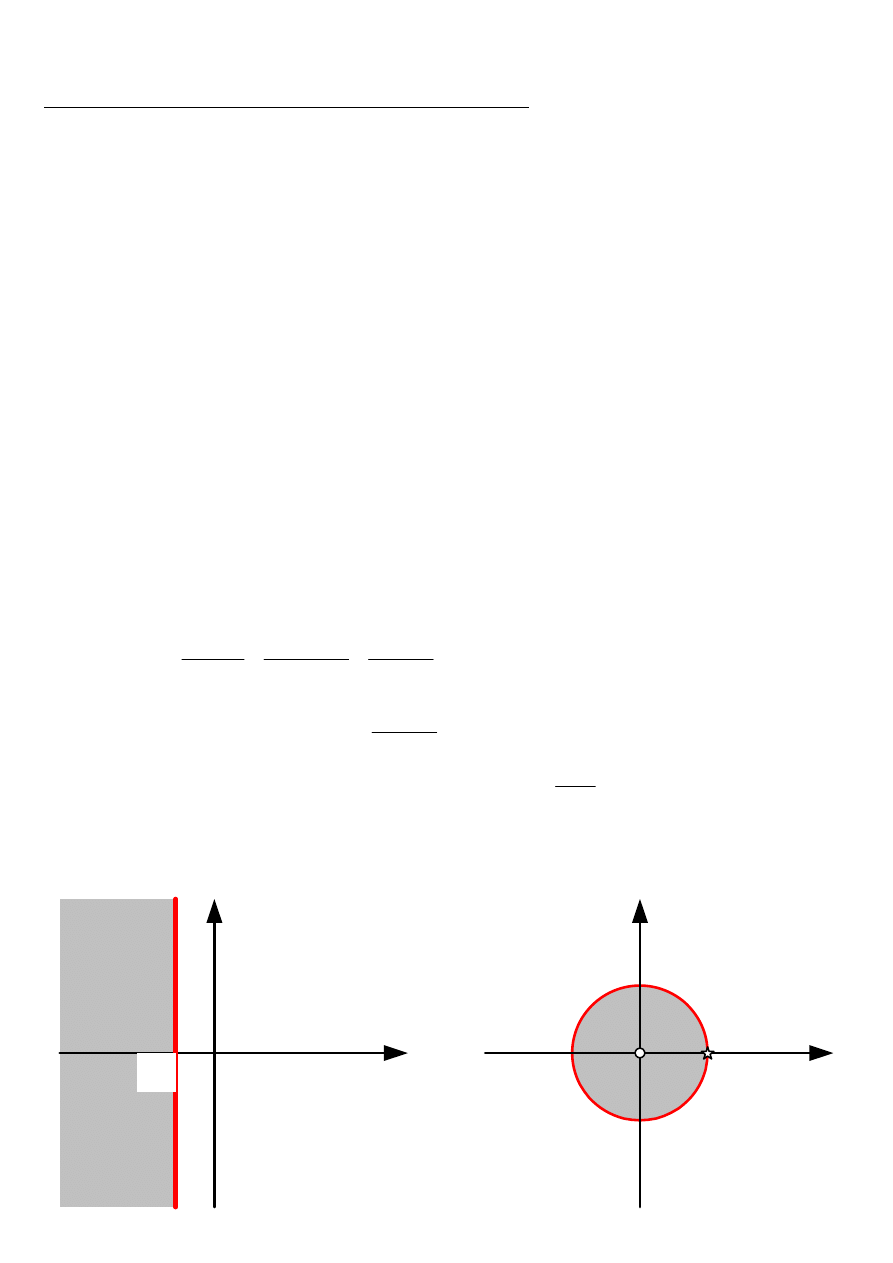
Ponieważ obszar zbieżności transformaty Laplace’a

( )

1

X s

s b

=

+

jest półpłaszczyzną położoną

na prawo od prostej s=-b dlatego obszarem zbieżności transformaty Z jest zewnętrze okręgu o
promieniu

p

bT

e

−

Im{s}

Im{z}

Re{z}

0

Re{s}

-b

p

bT

e

−

0

CPS 13

2006/2007

U

Transformata Z wykładniczego przebiegu lewostronnego

U

(t 0

< ):

( )

( )

1

bt

x t

e

−

= −

−t

( )

(

)

1

*

bt

p

k

x t

e

t kT

δ

−

−

=−∞

= −

⋅

−

∑

( )

(

)

1

*

p

bkT

p

k

x

t

e

t k

δ

−

−

=−∞

=

−

−

∑

T

Korzystając z transformaty Laplace’a

( )

1

*

p

p

bkT

skT

k

X

s

e

e

−

−

−

=−∞

=

−

∑

( )

1

*

p

p

bkT

skT

k

X

s

e e

∞

=

= −

∑

( )

(

)

1

*

p

p

k

bT

sT

k

X

s

e e

∞

=

= −

∑

( )

( )

1

p

k

bT

k

X z

e z

∞

=

= −

∑

( )

( )

0

1

p

k

bT

k

X z

e z

∞

=

= −

∑

( )

1

1

1

1

1

1

p

p

p

bT

bT

bT

bT

e z

z

X z

e z

e z

e

z

−

−

−

−

= −

=

=

−

−

p

−

( )

p

bT

z

X z

z e

−

=

−

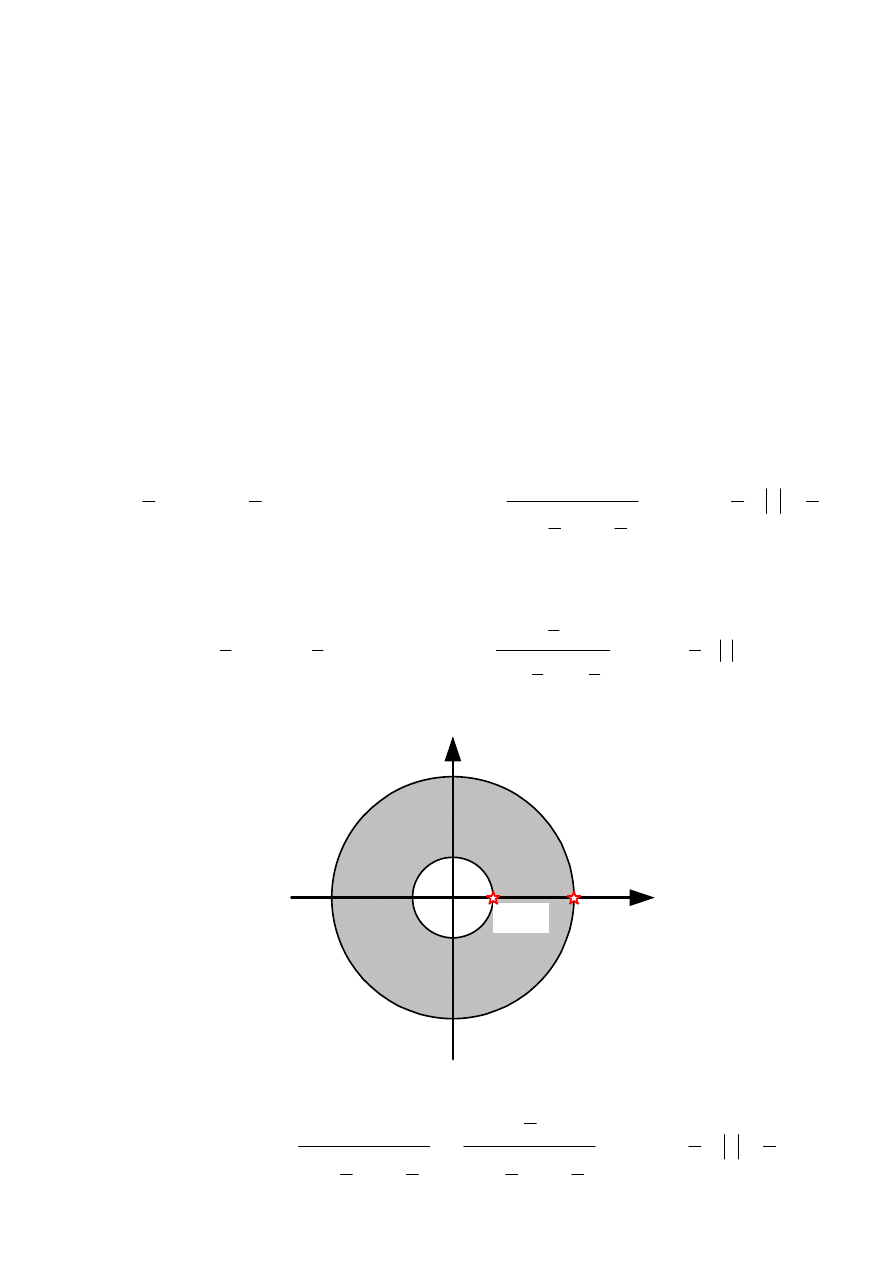
Ponieważ obszar zbieżności transformaty Laplace’a

( )

1

X s

s b

=

+

jest półpłaszczyzną położoną

na lewo od prostej s=-b, dlatego obszarem zbieżności transformaty zet jest wnętrze okręgu o
promieniu

p

bT

e

−

Im{s}

Im{z}

Re{z}

0

Re{s}

-b

p

bT

e

−

0

CPS 14

2006/2007

Podstawowe właściwości przekształcenia Z:

Przyjmiemy skrótowe oznaczenie transformaty zet sygnału x[n], istniejącej w obszarze
zbieżności o promieniu R

B

x

B

[ ]

( )

x

x n

X z dla OZ

←⎯→

Z

R

Liniowość

[ ]

[ ]

( )

( )

x

y

ax n

by n

aX z

bY z dla OZ R

R

+

←⎯→

+

∩

Z

(wspólny obszar zbieżności)

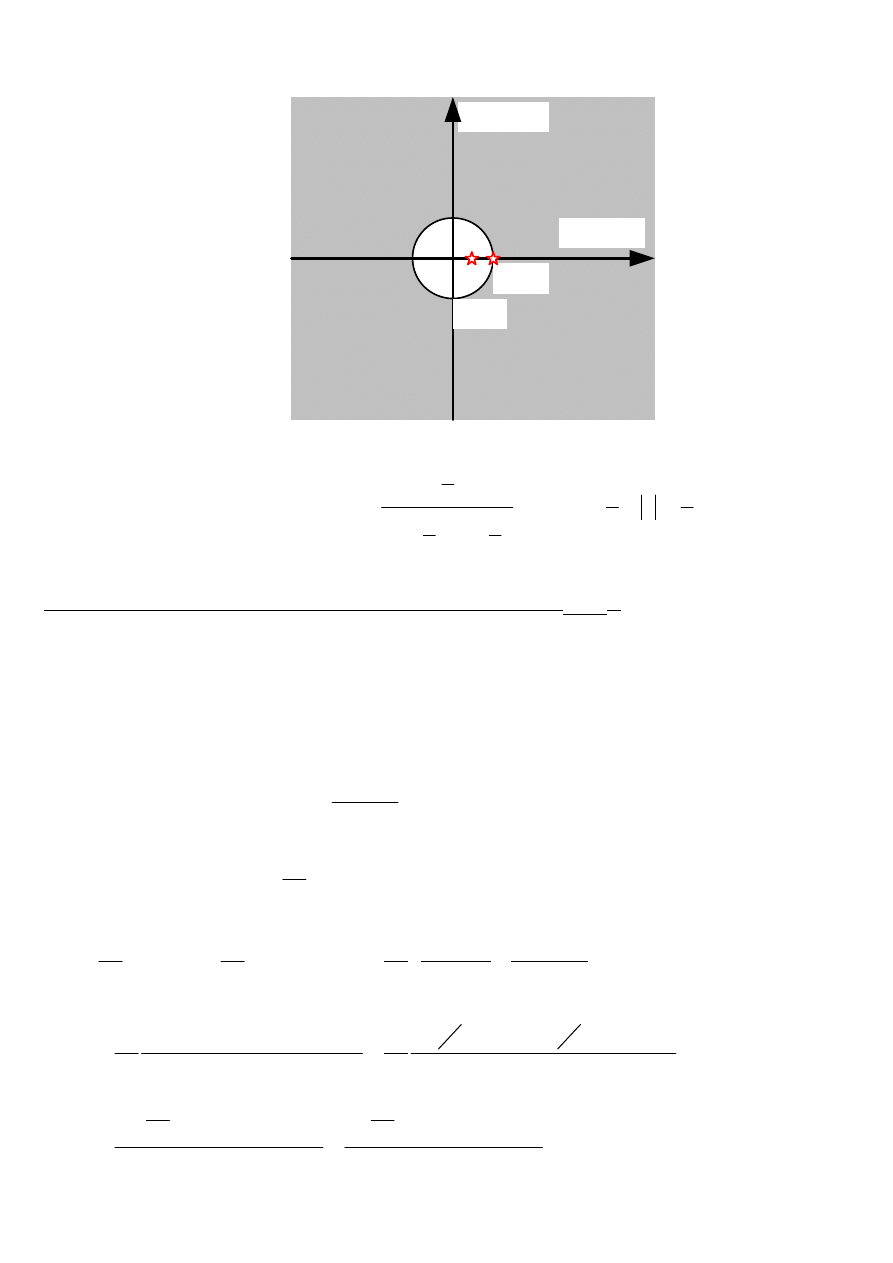
Przykład

[ ]

[ ]

[

]

( )

1

3

1

1

1

1

1

3

2

2

2

2

2

n

n

Z

z

x n

n

n

X z

dla OZ

z

z

z

−

⎛ ⎞

⎛ ⎞

=

⋅

−

⋅ − −

←⎯→

=

<

<

⎜ ⎟

⎜ ⎟

⎛

⎞⎛

⎞

⎝ ⎠

⎝ ⎠

−

−

⎜

⎟⎜

⎟

⎝

⎠⎝

⎠

3
2

oraz

[ ]

[ ]

[ ]

( )

1

1

1

1

4

1

1

1

1

4

2

2

4

2

n

n

Z

z

y n

n

n

Y z

dla OZ

z

z

−

⎛ ⎞

⎛ ⎞

=

⋅

−

⋅

←⎯→

=

<

⎜ ⎟

⎜ ⎟

⎛

⎞⎛

⎞

⎝ ⎠

⎝ ⎠

−

−

⎜

⎟⎜

⎟

⎝

⎠⎝

⎠

z

Im{z}

Re{z}

3/2

1/2

[ ]

[ ]

1

1

3

4

1

3

1

1

2

2

2

2

4

2

Z

z

z

ax n

by n

a

b

dla OZ

z

z

z

z

z

−

−

+

←⎯→

+

⎛

⎞⎛

⎞

⎛

⎞⎛

⎞

−

−

−

−

⎜

⎟⎜

⎟

⎜

⎟⎜

⎟

⎝

⎠⎝

⎠

⎝

⎠⎝

⎠

<

<

CPS 15

2006/2007

Im{z}

Re{z}

1/4

1/2

W przypadku gdy a=b

[ ]

[ ]

5

1

3

4

1

3

4

2

4

2

Z

z

ax n

ay n

a

dla OZ

z

z

z

−

+

←⎯→

<

⎛

⎞⎛

⎞

−

−

⎜

⎟⎜

⎟

⎝

⎠⎝

⎠

<

U

Transformata zet sinusoidalnego przebiegu prawostronnego (

0

t

≥ ):

[ ]

(

)

[ ]

0

sin

1

p

x n

n T

ω

=

⋅ n

Wykorzystamy właściwość liniowości przekształcenia oraz wyprowadzoną wcześniej
transformatę sygnału wykładniczego:

[ ]

1

p

p

nbT

bT

z

e

n

z e

−

−

←⎯→

−

Z

Ponieważ

( )

(

)

1

sin

2

e

e

j

α

α

α

−

=

−

[ ]

[ ]

0

0

0

0

1

1

1

1

1

2

2

2

p

p

p

p

jn T

jn T

j T

j T

z

z

e

n

e

n

j

j

j z e

z e

ω

ω

ω

ω

−

−

⎛

⎞

−

←⎯→

−

⎜

⎟

−

−

⎝

⎠

Z

=

(

) (

)

(

)(

)

0

0

0

0

2

1

1

2

2

p

p

p

p

j T

j T

j T

j T

z z e

z z e

z

j

j

z e

z e

ω

ω

ω

ω

−

−

−

−

−

=

=

−

−

0

2

p

j T

ze

z

ω

−

−

−

0

0

0

0

0

2

p

p

p

p

j T

j T

j T

j T

j T

ze

z

ze

ze

e

e

ω

ω

ω

ω

ω

−

−

+

=

−

−

+

p

(

)

(

)

(

)

(

)

0

0

0

0

0

0

0

0

2

0

2

2

2

1

p

p

p

p

p

p

p

p

j T

j T

j T

j T

j T

j T

j T

j T

z

z

e

e

e

e

j

j

z

z e

e

e

z

z e

e

ω

ω

ω

ω

ω

ω

ω

ω

−

−

−

−

−

−

=

=

−

+

+

−

+

+

CPS 16

2006/2007

(

)

[ ]

(

)

(

)

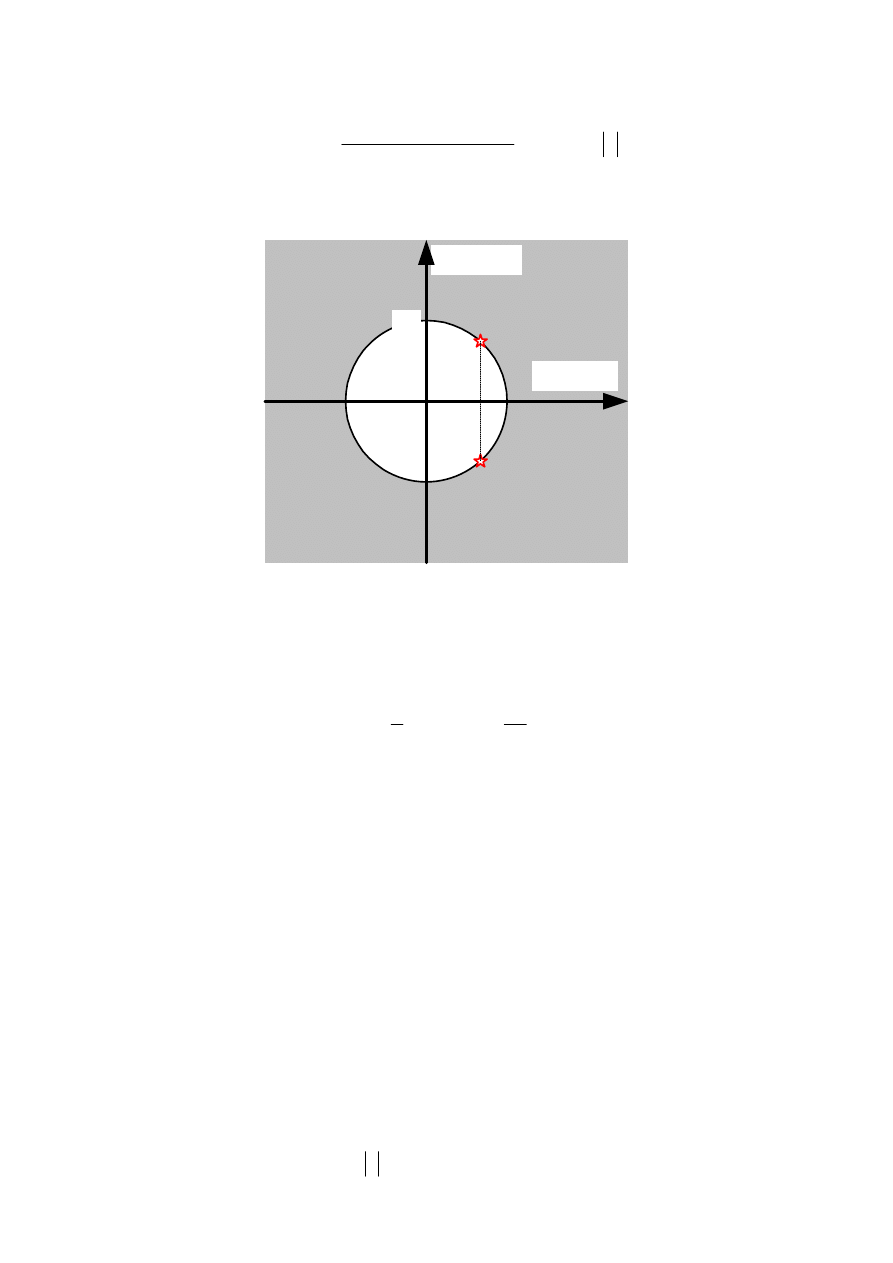
0

0

2

0

sin

sin

1

1

2 cos

1

p

Z

p

p

z

T

n T

n

dla OZ z

z

z

T

ω

ω

ω

⋅

←⎯→

>

−

+

Im{z}

Re{z}

1

Odwrócenie sygnału w czasie

[ ]

1

1

x

x n

X

dla OZ

z

R

⎛ ⎞

− ←⎯→ ⎜ ⎟

⎝ ⎠

Z

Odwrócenie sygnału w dziedzinie czasu odpowiada zmianie zmiennej z na z

P

-1

P

. Zmianie ulega

także obszar zbieżności. Jeżeli R

B

x

B

jest pierścieniem a<|z|<b to obszar zbieżności sygnału

odwróconego a<|1/z|<b lub 1/b<|z|<1/a

Przesunięcie sygnału w czasie

[

]

( )

0

0

n

x

x n n

z X z dla OZ R

−

−

←⎯→

Z

Mnożenie przez

wprowadza n

B

0

B

biegunów w z=0 gdy n

B

0

B

>0. W tym przypadku jeżeli

bieguny nie są redukowane przez pierwiastki

X

(

z

), nowy obszar zbieżności nie może zawierać

punktu z=0. Natomiast gdy n

B

0

B

<0 mnożenie przez

wprowadza n

B

0

B

biegunów w

nieskończoności. Jeżeli bieguny te nie są redukowane przez pierwiastki

X

(

z

), nowy obszar

zbieżności nie może zawierać punktu

0

n

z

−

0

n

z

−

z

= ∞

CPS 17

2006/2007

Przykład:

f[n]

n

1 2 3

-1

-2

-3

0

g[n]=f[n-1]

n

1 2 3

-1

-2

-3

0

g[0]=f[-1]
g[1]=f[0]

( )

[ ]

[ ] [ ]

[ ]

[ ]

[ ]

[ ]

[ ]

[ ]

[ ]

1

2

0

1

2

1

1

( )

0

1

2

...

1

0

1

...

1

0

1

...

n

n

F z

G z

g n z

g

g

z

g

z

f

f

z

f

z

f

z

f

z

f

z

∞

−

−

=

−

−

−

−

=

=

+

+

=

− +

+

+

⎧

⎫

⎪

⎪

=

− +

+

+

⎨

⎬

⎪

⎪

⎩

⎭

∑

−

+

Stąd otrzymujemy zależności:

[

]

( )

[ ]

1

1

1

Z

f n

z F z

f

−

− ←⎯→

+

−

[

]

( )

[ ]

(

)

[ ]

( )

[ ] [ ]

1

1

2

1

2

1

2

Z

f n

z

z F z

f

f

z F z

z f

f

−

−

−

−

− ←⎯→

+

−

+

− =

+

− +

1

2

−

[

]

{

}

[ ]

(

)

[ ]

{

}

[ ]

{

}

[ ]

(

)

[

]

{

}

1

1

0

1

z Z f n

f

Z f n

z Z f n

f

Z f n

−

−

−

=

−

=

+

[

]

( )

[ ]

(

)

1

0

Z

f n

z F z

f

+ ←⎯→

−

[

]

( )

[ ]

(

)

[ ]

( )

[ ]

[ ]

2

2

2

0

1

Z

0

1

f n

z z F z

f

f

z F z

z f

⎛

⎞

⎜

⎟

+ ←⎯→ =

−

−

=

−

−

⎜

⎟

⎝

⎠

zf

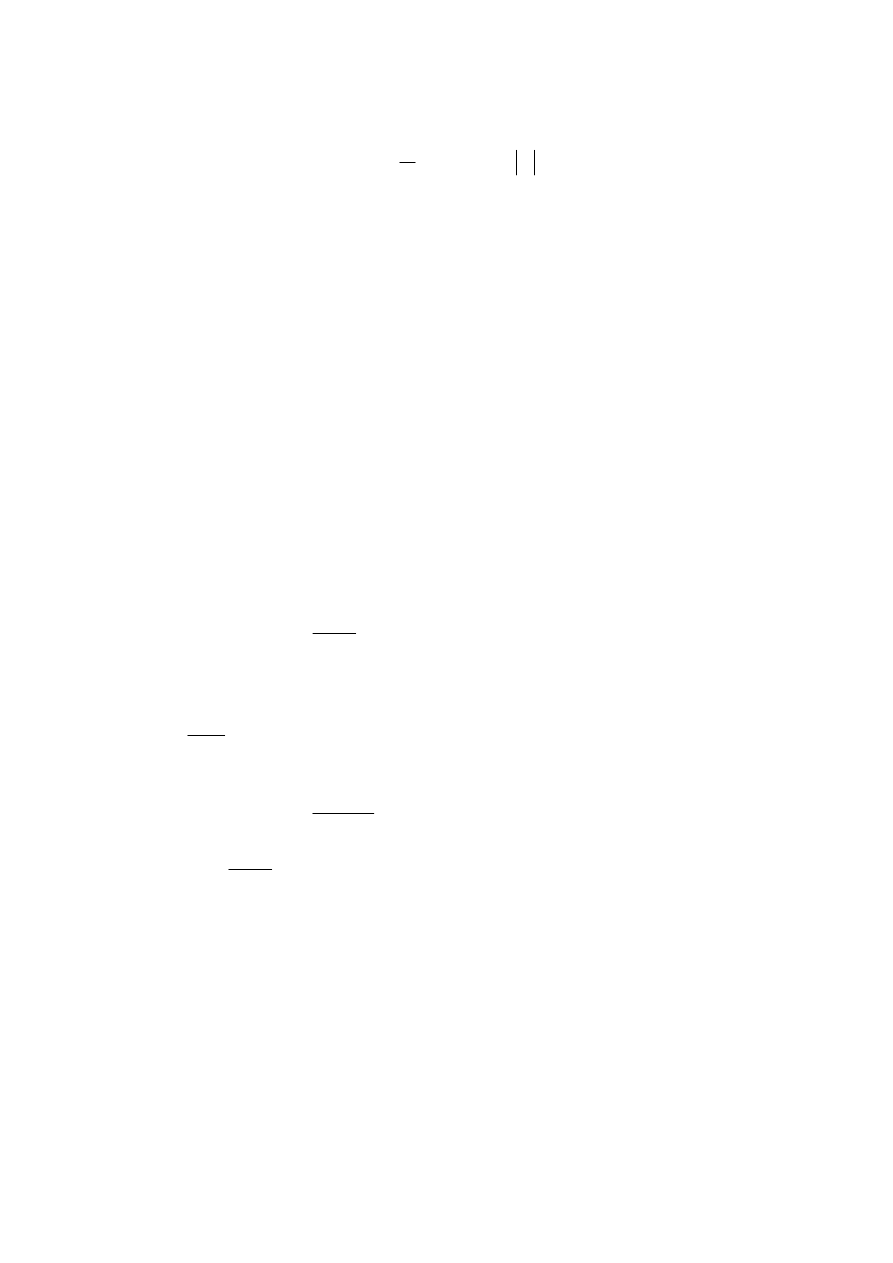
CPS 18

2006/2007

Mnożenie przez ciąg wykładniczy

[ ]

n

x

z

x n

X

dla OZ

α

α

α

⎛ ⎞

←⎯→ ⎜ ⎟

⎝ ⎠

Z

R

n

Jeżeli

R

B

x

B

jest pierścieniem

a

<|

z

|<

b

to obszar zbieżności sygnału |

a

|

a

<|

z

|<|

a

|

b

. Zmiana obszaru

zbieżności wynika z przesuwania się biegunów funkcji

X

(

z

). Wszystkie bieguny zostają w

jednakowej skali równej |

a

| przesunięte względem

z

=

0

.

Wyprowadzimy z definicji przekształcenia ZET powyższą własność

[ ] [ ]

[ ]

[ ]

[ ]

( )

( )

0

0

1

0

1

1

n

n

Z

n

n

n

n

n

n

a x n

n

a x n z

x n a z

x n a z

X a z

∞

−

=

∞

−

=

∞

−

−

=

−

←⎯→

=

=

=

∑

∑

∑

Przykład

[ ]

1

n

Z

z

a

n

z a

←⎯→

−

Ponieważ

[ ]

1

1

Z

z

n

z

←⎯→

−

to

[ ]

1

1

1

1

n

Z

a z

a

n

a z

z

z a

−

−

←⎯→

=

−

=

−

Splot

[ ] [ ]

( ) ( )

x

y

x n

y n

X z Y z dla OZ R

R

∗

←⎯→

∩

Z

Splot przebiegów czasowych odpowiada mnożeniu transformat. Z liniowości

przekształcenia wynika, że obszar zbieżności może być większy niż część wspólna obszarów
dla transformat splatanych sygnałów. Taki przypadek zachodzi wtedy wystepuje redukcja
pierwiastków i biegunów.

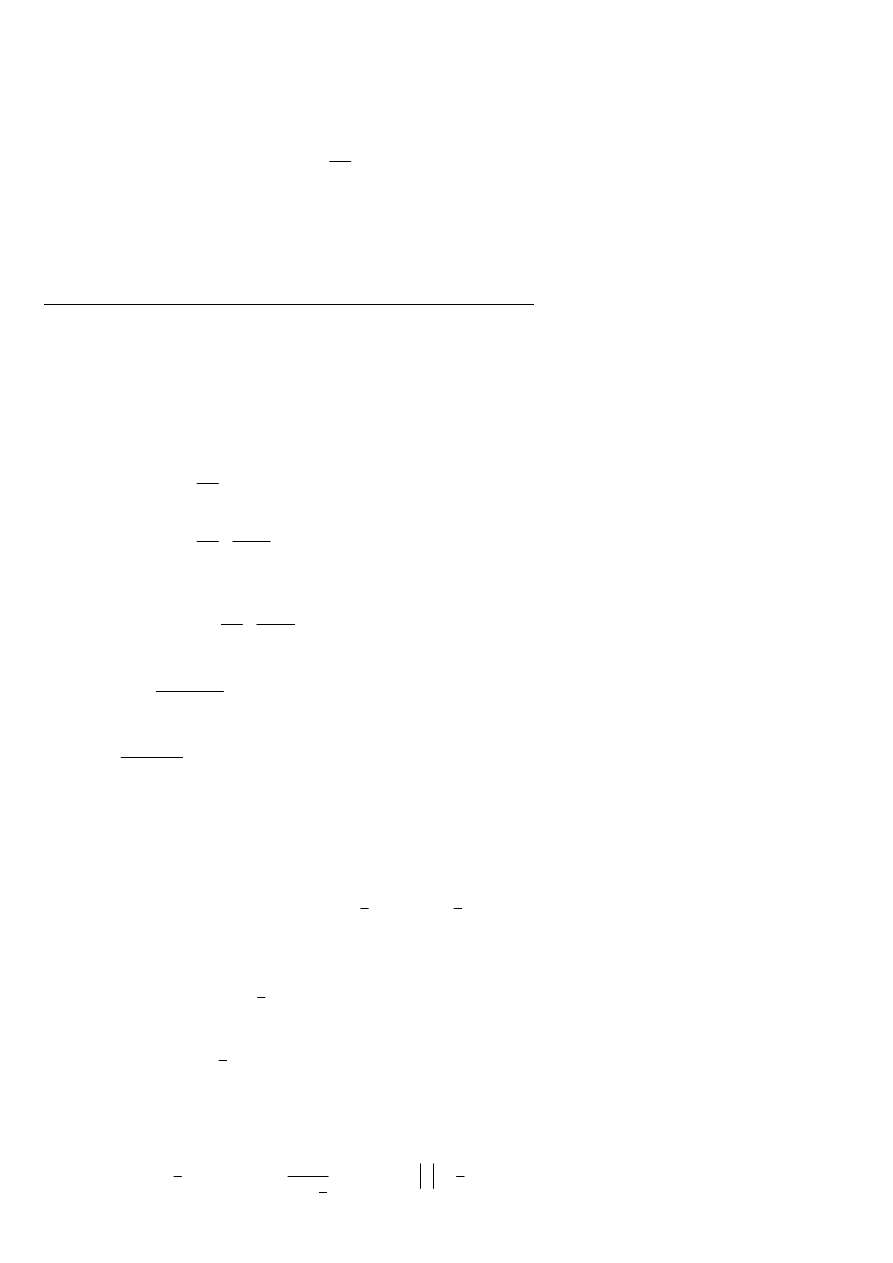
CPS 19

2006/2007

Różniczkowanie w dziedzinie zet

[ ]

( )

x

d

nx n

z

X z dla OZ R

dz

←⎯→−

Z

Mnożenie sygnału przez n w dziedzinie czasu odpowiada różniczkowaniu oraz mnożeniu przez
–z w dziedzinie zet. Operacja ta nie zmienia obszaru zbieżności.

U

Wyprowadzimy tę własność z definicji przekształcenia zet:

[ ]

{

}

{

}

0

1

2

3

2

3

4

1

2

3

1

0

2

3

...

2

3

...

1

2

3

1

n

Z

n

n n

nz

z

z

z

z

z

z

z

d

z

z

z

z

dz

d

z

z

dz z

∞

−

=

−

−

−

−

−

−

−

−

−

←⎯→

=

= +

+

+

+

= − −

−

−

−

= −

+

+

+

+

⎧

⎫

= −

⎨

⎬

−

⎩

⎭

∑

...

stąd

[ ]

(

)

(

)

2

2

1

1

1

1

1

Z

d

z

n n

z

dz z

z

z

z

z

z

z

⎧

⎫

←⎯→−

=

⎨

⎬

−

⎩

⎭

⎧

⎫

− −

⎪

⎪

= − ⎨

⎬

−

⎪

⎪

⎩

⎭

=

−

Przykład:
Znajdziemy transformatę sygnału

[ ]

( )

[ ]

(

)

( )

[ ]

1

1

2

4

1

1

n

n

x n

n

n

n

−

=

−

∗

−

Oznaczymy:

[ ]

( )

[ ]

(

)

1

2

1

n

w n

n

n

=

−

[ ]

( )

[ ]

1

4

1

n

y n

n

−

=

−

Obliczenia dla w[n]:

( )

[ ]

1

1

2

2

1

2

1

n

Z

z

n

dla OZ

z

−

←⎯→

>

+

z

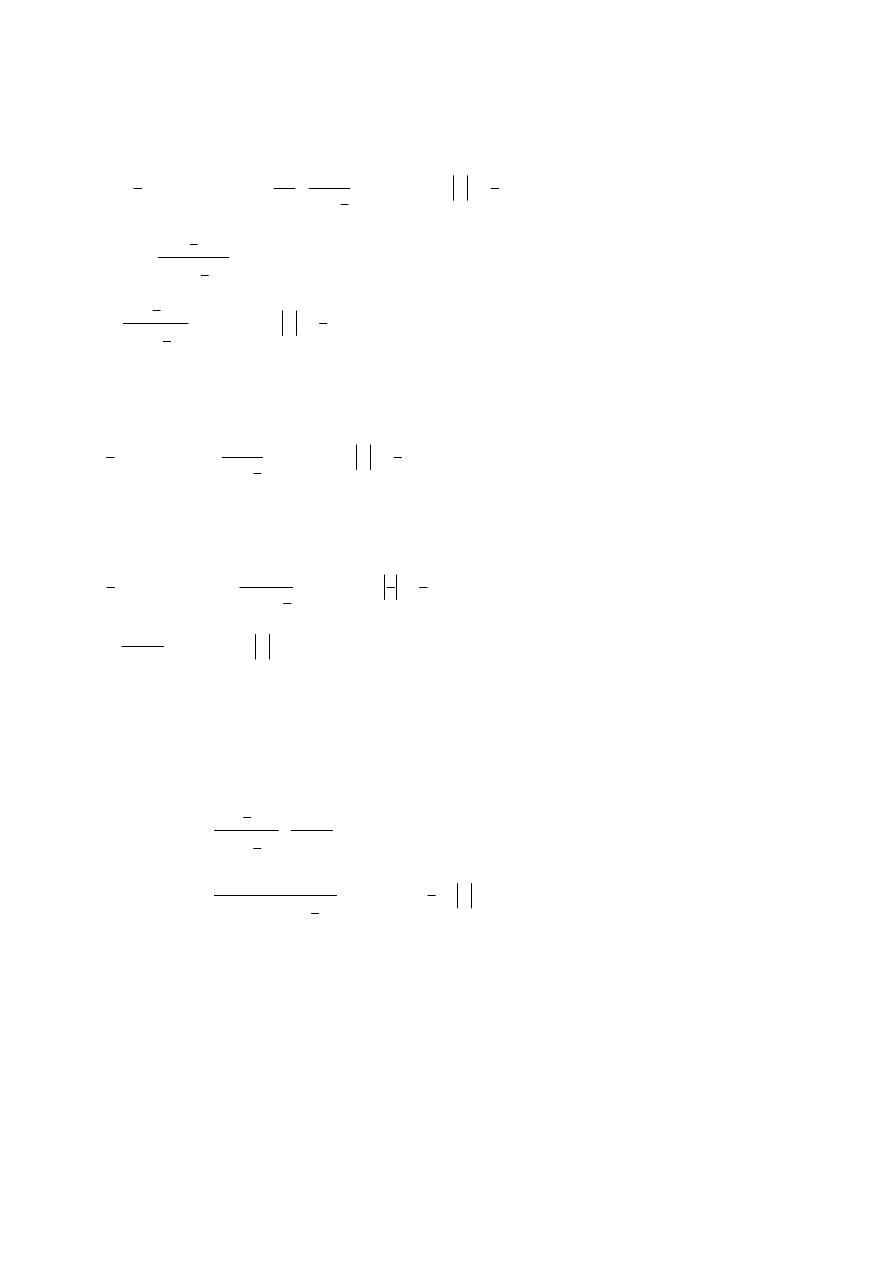
CPS 20

2006/2007

Wykorzystamy właściwość różniczkowania w dziedzinie zet:

( )

[ ]

(

)

(

)

1

1

2

2

1

2

1

2

2

1

2

1

2

1

2

2

1

2

1

n

Z

d

z

n

n

z

dla OZ z

dz z

z

z

z

z

z

dla OZ z

z

⎛

⎞

−

←⎯→−

>

⎜

⎟

+

⎝

⎠

⎛

⎞

+ −

= − ⎜

⎟

⎜

⎟

+

⎝

⎠

−

=

>

+

Obliczenia dla y[n]:

( )

[ ]

1

1

4

4

1

4

1

n

Z

z

n

dla OZ

z

←⎯→

>

−

z

Wykorzystamy właściwość inwersji w czasie:

( )

[ ]

1

1

1

4

4

1

1

4

1

4

4

4

n

Z

z

z

n

dla OZ

z

z

dla OZ z

z

−

−

−

− ←⎯→

>

−

−

=

<

−

1

Wykorzystamy właściwość transformaty splotu:

[ ]

[ ] [ ]

( )

( ) ( )

(

)

(

)(

)

1

2

2

1

2

2

1

2

2

1

2

4

4

2

4

4

Z

W

Y

x n

w n

y n

X z

W z Y z dla OZ R

R

z

z

z

z

z

dla OZ

z

z

z

=

∗

←⎯→

=

−

−

=

⋅

−

+

=

< <

−

+

∩