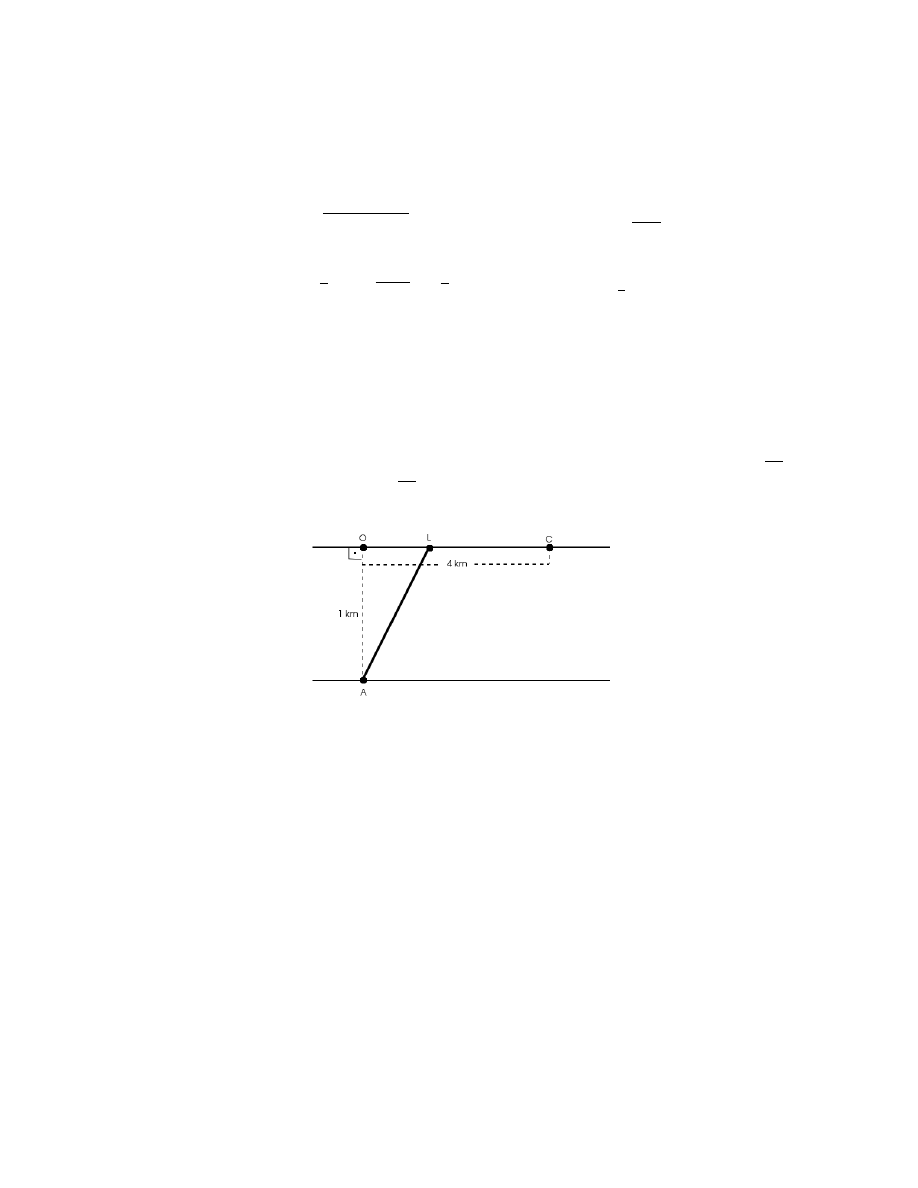
SiMR  Kolokwium z Analizy Matematycznej 1

Grupa 1.9 β

13 grudnia 2007

1. [4p] Obliczy¢ granice ci¡gów:

(a) [2p] lim

n→∞

n

√

2 · 3

n

+ 4 · 7

n

(b) [2p] lim

n→∞

n

2

−3

n

2

+3

n

2

+n

2. [5p] Obliczy¢:

(a) [3p] lim

x→∞

√

x · sin(

√

x + 1 −

√

x)

(b) [2p] (arctan

1

x

)

0

3. [4p] Dobra¢ a, b, c, d tak, aby funkcja

f (x) =







x + a

dla x ≤ −1

−bx

2

+ 2

dla − 1 < x ≤ 0

c cos x + d

dla 0 < x

byªa ci¡gªa i ró»niczkowalna na R.

4. [4p] Czªowiek mo»e wiosªowa¢ z punktu A do punktu na drugim brzegu kanaªu z pr¦dko±ci¡ 4

km

h

i

biec po drugim brzegu z pr¦dko±ci¡ 16

km

h

. W którym punkcie L powinien przybi¢ do brzegu, aby

punkt C osi¡gn¡¢ w jak najkrótszym czasie?

Powodzenia!