METODY ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH

Rozwiązanie równania f(x)=0 jest równoważne lokalizacji miejsca zerowego, x^*, funkcji f(x);

Jeśli f(x) jest ciągła i f(a)·f(b)<0 to x^* ∈ [a,b].

METODA BISEKCJI (połowienia przedziału)

, jeśli f(x_k)·f(x_k-1)<0

Zakończenie obliczeń:

iteracja	a	b	f(a)	f(b)	c=(a+b)/2	f(c)		koniec obliczeń
1 2 . k					xk	f(xk)		nie . . tak

Przedział (a,b) w k-tej iteracji wyznaczamy za pomocą wzorów:

a_k-1 jeśli f(a_k-1)f(c_k-1)<0

a_k =

c_k-1 jeśli f(ak-1)f(c_k-1)≥0

METODA NEWTONA (stycznych)

Warunki, które musi spełniać funkcja:

1. funkcje f(x), f'(x), f”(x) są określone i ciągłe w przedziale [a,b]

2. f(a)·f(b)<0

3. f'(x) I f”(x) nie są równe zeru I nie zmieniają znaku w domkniętym przedziale [a,b] , tzn. w rozważanym przedziale funkcja f(x) jest ściśle monotoniczna oraz wklęsła lub wypukła.

Algorytm metody stycznych:

1. w charakterze przybliżenia początkowego, x₀, przyjmujemy ten koniec a lub b przedziału, który spełnia warunek: f(x₀)·f”(x₀)>0.

2. kolejne przybliżenia obliczamy ze wzoru

3. obliczenia kończymy, jeśli spełniona jest nierówność

METODA SIECZNYCH (reguła falsi, metoda interpolacji liniowej)

Algorytm tej metody:

1. w charakterze przybliżenia początkowego x₀ przyjmujemy ten koniec a lub b przedziału, który spełnia warunek: f(x₀)·f”(x₀)<0.

2. kolejne przybliżenia obliczamy ze wzoru

d = a, gdy x₀=b lub d = b, gdy x₀=a

3. obliczenia kończymy, jeśli spełniona jest nierówność

METODA ITERACJI PROSTEJ

Równanie f(x) = 0

należy przekształcić do równoważnego równania x = g(x)

Znajdowanie pierwiastka jest realizowane w dwóch etapach:

1. wybór funkcji iteracyjnej
   

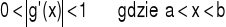
2. obliczenia wg schematu:

• przybliżenie zerowe x₀ = (a+b)/2

• kolejne przybliżenia x_k+1 = g(x_k)

• zakończenie obliczeń:

,

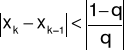
gdzie

b_k-1 jeśli f(b_k-1)f(c_k-1)<0

b_k =

c_k-1 jeśli f(b_k-1)f(c_k-1)≥0