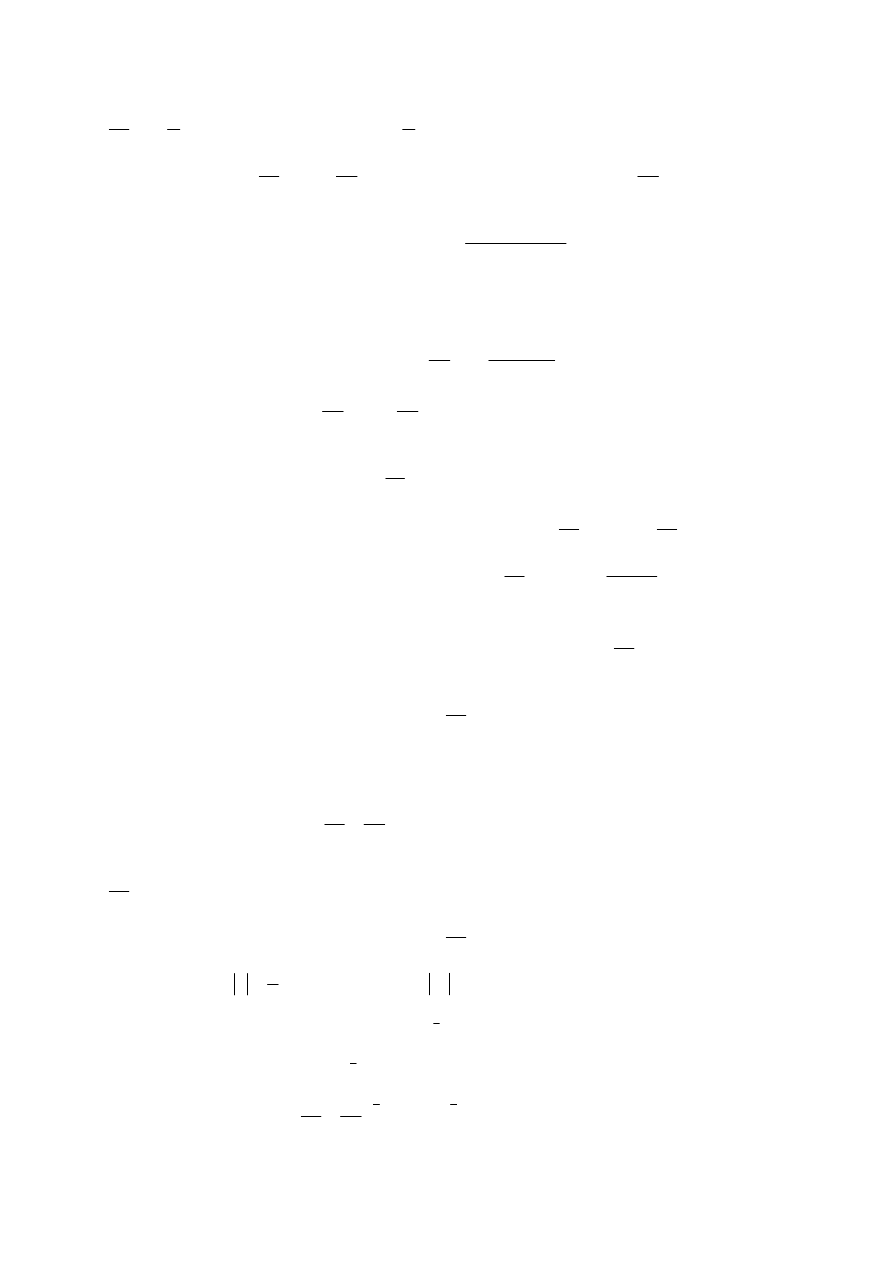
RÓWNANIA RÓŻNICZKOWE JEDNORODNE WZGLĘDEM X i Y
)
(
x
y
f
dx
dy
=
stosujemy podstawienie
x
y
u
=
==>
xu
y
=
po zróżniczkowaniu
dx
du
x
u
dx
dy
+
=
i po podstawieniu do równania
)
(u
f
dx
du
x
u
=
+
RÓWNANIA RÓŻNICZKOWE TYPU
)
(
`
2
2
2
1
1
1
c
y
b
x
a
c
y
b
x
a
f
y
+
+
+
+
=
Przypadek I : a
1
b
2
– b
1
a
2
≠≠≠≠
0
Wtedy układ równań ma jedno rozwiązanie x=
α
i y=
β
Wprowadzamy nowe zmienne : x -
α
= u; y -
β
= v
Równanie różniczkowe przekształci się na :
)
(
2
2
1
1
v
b
u
a
v
b
u
a
f
du
dv
+
+
=
Za v podstawiamy
tu
v
=
=>
du
dt
u
t
du
dv
+
=
Rozdzielamy zmienne i całkujemy.
Przypadek II : a
1
b
2
– b
1
a
2
= 0
współczynnik proporcjonalności :
1
2
a
a
k
=
wprowadzamy nową zmienną :
y
b
x
a
z
1
1
+
=
=> po różniczce
dx
dy
f
b
a
dx
dz
1
1
+
=
po uwzględnieniu wzorów równanie przyjmie postać :
)
(
2
1
1
1
c
kz
c
z
f
b
a
dx
dz
+
+
+
=
rozwiązujemy metodą rozdzielenia zmiennych
RÓWNANIA RÓŻNICZKOWE LINIOWE NIEJEDNORODNE
)
(
)
(
x
q
y
x
p
dx
dy
=
+
rozwiązujemy tzw.
metodą uzmienniania stałej.
Rozwiązujemy najpierw równanie jednorodne
0
)
(
=
+
y
x
p
dx
dy
Całką tego równania jest
)
( x
P
Ce
y
−
=
Teraz stałą C zastępujemy funkcją
)
(x
u
i mamy
)
(
)
(
x
P
e
x
u
y
−
=
Obliczamy z tego pochodną :
)
(
)
(
)
(
x
P
x
P
e
x
u
e
dx
du
dx
dy
−
−
+
=
podstawiamy, redukujemy i liczymy
PRZYKŁAD :
2
x
xe
xy
dx
dy
=
−
Rozwiązujemy najpierw równanie jednorodne
0
=
−
xy
dx
dy
(przez rozdzielenie zmiennych)
Wynikiem jest
C
x
y
+
=
2
2
1
ln
gdzie
1
ln C
C
=
uwalniając się od logarytmów mamy
2
2
1
1
x
e
C
y
=
uzmienniamy stałą C
1
:
2
2
1
)
(
x
e
x
u
y
=
(**)
obliczamy pochodną :
x
e
x
u
e
dx
du
dx
dy
y
x
x
2
2
2
1
2
1
)
(
`
+
=
=
wartości y i y` wstawiamy do pierwszego równania
2
2
2
2
2
1
2
1
2
1
)
(
)
(
x
x
x
x
xe
e
x
xu
e
x
xu
e
dx
du
=
−
+
skąd po redukcji otrzymamy
2
2
2
1
x
x
xe
e
dx
du
=
czyli
2
2
1
x
e
dx
du
=
2
2
1
2
1
2
2
)
(
C
e
dx
e
x
u
x
x
+
=
=
∫
podstawiamy to do równania (**) otrzymując końcowy wynik
2
2
2
1
2
x
x
e
C
e
y
+
=
RÓWNANIA RÓŻNICZKOWE TYPU
cx
be
ay
y
=
+
`
Przewidzenie :
y
1
= me
Cx
lub
y
1
= (mx+n)e
Cx
PRZYKŁAD
x
e
y
dx
dy
3
2
2
=
−
Przewidujemy :
x
me
y
3
1
=
Obliczamy z tego pochodną
x
me
dx
dy
3
1
3
=
Wartości
1
y
i
dx
dy
1
podstawiamy do pierwszego równania :
x
x
x
e
me
me
3
3
3
2
2
3
=
−
Skąd po uproszczeniu przez e
3x
znajdujemy m=2
Podstawiając m do równania na
1
y
otrzymujemy
x
e
x
y
3
1
2
)
(
=
Obliczamy teraz całkę ogólną równania uproszczonego :
0
2
=
−
y
dx
dy
Po rozwiązaniu mamy :
x
e
C
y
2
1
2
=
Całka ogólna całego równania to y
1
+y
2
czyli
x
x
e
C
e
y
2
1
3
2
+
=
RÓWNANIA RÓŻNICZKOWE TYPU
)
(
`
x
W
ay
y
n
=
+
gdzie a jest liczbą stałą, a W
n
(x)
jest wielomianem stopnia n
PRZYKŁAD:
2
2
x
y
dx
dy
=
+
Przewidzenie :
c
bx
ax
y
+
+
=
2
1
Obliczamy pochodną
b
ax
dx
dy
+
=
2
1
Podstawiamy powyższe wartości do pierwszego równania:
2
2
2
2
2
2
x
c
bx
ax
b
ax
=
+
+
+
+
Przyrównując współczynniki przy tych samych potęgach zmiennej x otrzymujemy związki:
2a=1; 2a+2b=0; b+2c=0; z tego mamy :
4
1
2
1
2
1
2
1
+
−
=
x
x
y
Rozwiązujemy teraz równanie jednorodne
0
2
=
+
y
dx
dy
i z tego mamy
x
Ce
y
2
2
−
=
Całka ogólna ma więc postać y
1
+ y
2
tj.
x
Ce
x
x
y
2
2
4
1
2
1
2
1
−
+
+
−
=
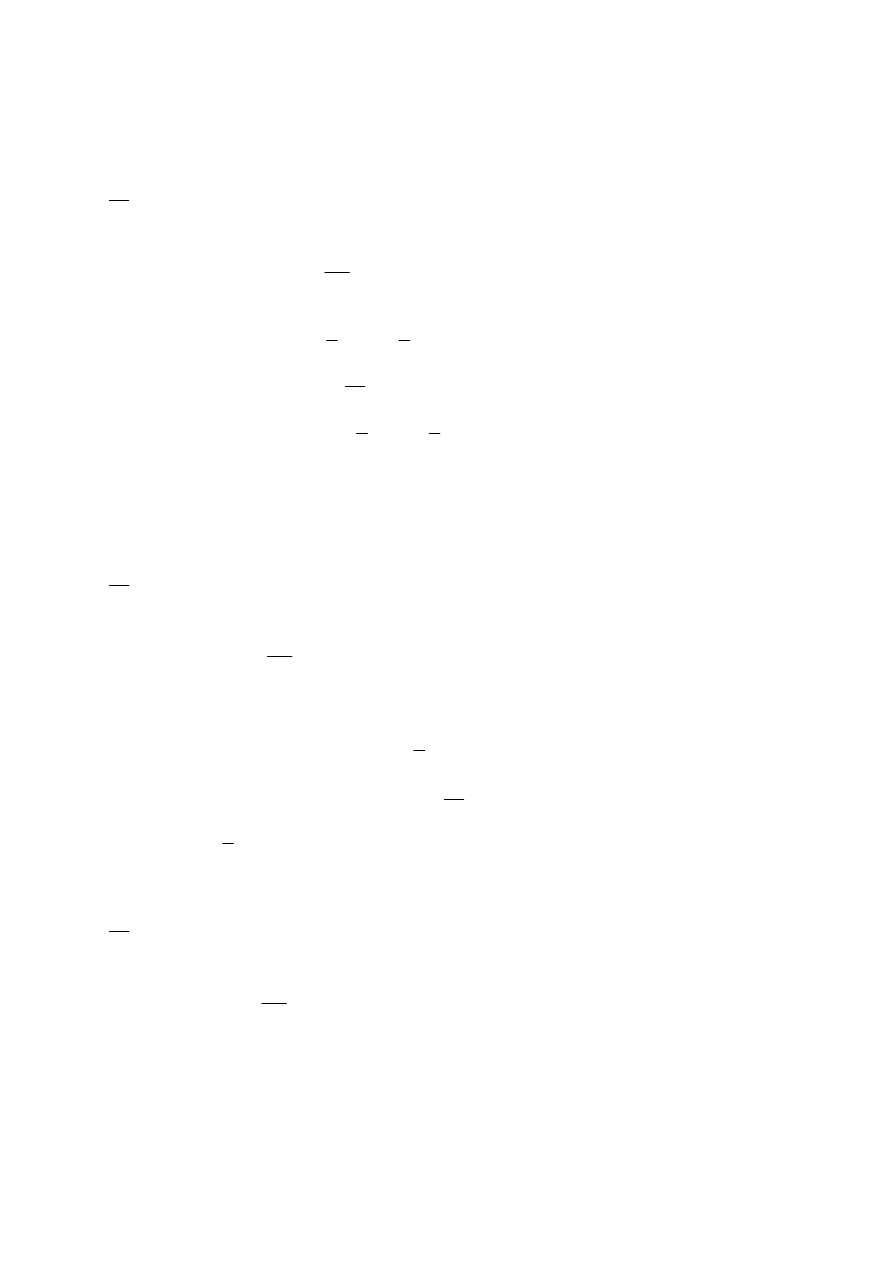
RÓWNANIA RÓŻNICZKOWE TYPU
ax
n
ax
c
by
y
cos
sin
`
+
=
+
PRZEWIDZENIE :
ax
n
ax
m
y
cos
sin
1
+
=
PRZYKŁAD
x
y
dx
dy
3
sin
5
=
+
Przewidujemy :
x
n
x
m
y
3
cos
3
sin
1
+
=
Obliczamy z tego pochodną :
x
n
x
m
dx
dy
3
sin
3
3
cos
3
1
−
=
Wstawiamy to do pierwszej równości :
x
x
n
x
m
x
n
x
m
3
sin
5
3
cos
3
sin
3
sin
3
3
cos
3
=
+
+
−
Obliczamy
n i m i mamy
x
x
y
3
cos
2
3
3
sin
2
1
1
−
=
Obliczamy równanie jednorodne
0
=
+
y
dx
dy
z czego mamy
x
Ce
y
−
=
2
No i całka ogólna ma postać :
x
Ce
x
x
y
−
+
−
=
3
cos
2
3
3
sin
2
1
RÓWNANIA RÓŻNICZKOWE INNYCH TYPÓW
PRZYKŁAD 1
x
e
x
y
dx
dy
3
2
25
2
=
+
PRZEWIDZENIE :
x
e
c
bx
ax
y
3
2
1
)
(
+
+
=
Obliczamy pochodną
x
x
e
c
bx
ax
e
b
ax
dx
dy
3
2
3
1
)
(
3
)
2
(
+
+
+
+
=
wstawiamy to do równania pierwszego i dzielimy od razu przez e
3x
,
otrzymujemy :
2
2
2
25
)
(
2
)
(
3
2
x
c
bx
ax
c
bx
ax
b
ax
≡
+
+
+
+
+
+
+
znajdujemy a,b,c i mamy
x
e
x
x
y
3
2
1
)
5
2
2
5
(
+
−
=
Liczymy całkę ogólną równania jednorodnego
0
2
=
+
y
dx
dy
i mamy ostatecznie
x
x
Ce
e
x
x
y
2
3
2
)
5
2
2
5
(
−
+
+
−
=
PRZYKŁAD 2
x
x
y
dx
dy
cos
2
=
+
PRZEWIDUJEMY :
x
d
cx
x
b
ax
y
cos
)
(
sin
)
(
1
+
+
+
=
Liczymy pochodną :
x
d
cx
x
c
x
b
ax
x
a
dx
dy
sin
)
(
cos
cos
)
(
sin
1
+
−
+
+
+
=
Wstawiamy to do pierwszego równania i mamy równanie, obliczamy współczynniki
x
x
x
x
y
cos
sin
)
1
(
1
+
−
=
liczymy całkę ogólną równania jednorodnego i ostatecznie mamy :
x
Ce
x
x
x
x
y
−
+
+
−
=
cos
sin
)
1
(
RÓWNANIA RÓŻNICZKOWE RZĘDU DRUGIEGO
TYP :
0
``)
`,
,
(
=
y
y
x
F
Podstawienie :
)
(
`
x
p
y
=
PRZYKŁAD
`
``
)
1
(
y
y
x
=
+
Robimy podstawienie :
)
(
`
x
p
y
=
i otrzymujemy
p
dx
dp
x
=
+
)
1
(
rozdzielamy zmienne
x
dx
p
dp
+
=
1
skąd mamy lnp = ln(1+x) +lnC, a wiec
)
1
(
x
C
p
+
=
to znaczy
Cx
C
dx
dy
+
=
czyli
∫
+
=
dx
C
Cx
y
)
(
ostatecznie otrzymujemy
1
2
2
1
C
Cx
Cx
y
+
+
=
TYP :
0
``)
`,
,
(
=
y
y
y
F
Podstawienie :
)
(
`
y
p
y
=
wówczas
)
(
``
y
u
dy
du
dx
dy
dy
du
dx
du
y
=
⋅
=
=
a równanie przekształci się na równanie rzędu
pierwszego