DROGI SZYNOWE cz. 5
DROGI SZYNOWE cz. 5
KSZTAŁTOWANIE UKŁADÓW GEOMETRYCZNYCH TORU
KOLEJOWEGO
Układ geometryczny toru kolejowego ma charakter
przestrzenny i dlatego należy go rozpatrywać w trzech
płaszczyznach:
• poziomej,
• pionowej i
• poprzecznej do osi toru.
W płaszczyźnie poziomej (in. w planie) podstawowymi
elementami układu są:
• odcinki proste toru,
• odcinki ułożone w łuku kołowym oraz
• odcinki w łukach o zmiennej krzywiźnie (tzw. krzywe
przejściowe).
Ponadto wyróżnia się tzw. wstawki proste, czyli krótkie odcinki
proste toru ułożone między dwiema krzywymi przejściowymi lub
dwoma łukami kołowymi.
W płaszczyźnie pionowej (in. w profilu podłużnym)
wyróżnia się:
• odcinki toru o jednostajnym pochyleniu oraz
• kołowe łuki wyokrąglające tzw. załomy profilu
podłużnego.
W płaszczyźnie poprzecznej do osi toru (in. w przekroju
poprzecznym) występuje :
• szerokość toru oraz
• różnica wysokości toków szynowych (która na
długości łuku kołowego jest stała i nosi nazwę
przechyłki).
Najkorzystniejszym rozwiązaniem geometrycznym trasy
kolejowej w płaszczyźnie poziomej byłaby prosta.
Ponieważ na skutek istniejących uwarunkowań
terenowych nie jest to możliwe, występuje konieczność
zmiany kierunku trasy i zastosowania w tym rejonie łuku
kołowego w celu zapewnienia płynnego przejazdu
pojazdu szynowego.
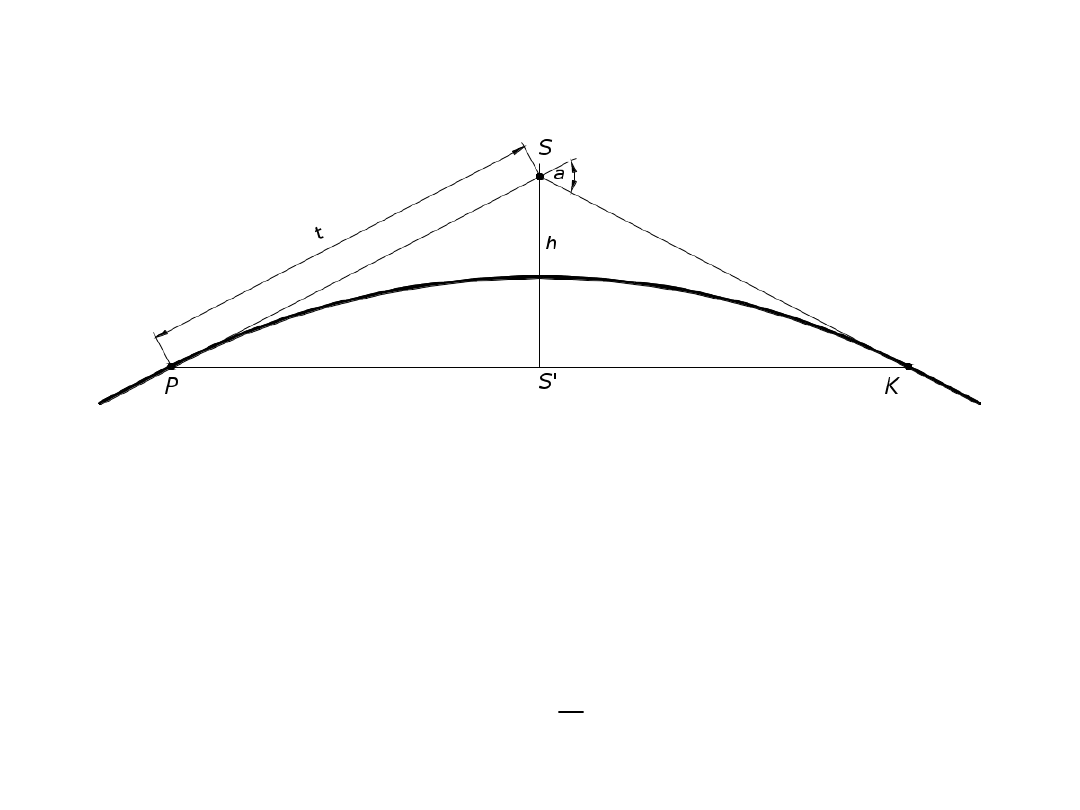
Schemat połączenia kierunków głównych trasy za pomocą łuku kołowego
Długość połączenia kierunków głównych trasy zależy od
kąta zwrotu
i zastosowanego promienia łuku
kołowego R. Wartości stycznych t wynikają z zależności
2
tg
R
t
Projektowanie łuku kołowego
Dla nowo projektowanej linii kolejowej ustala się jej
podstawowe wymagane parametry eksploatacyjne:
• maksymalną prędkość pociągów pasażerskich v
p
[km/h],
• prędkość pociągów towarowych v
t
[km/h],
• natężenie przewozów q [Tg/rok].
Promień łuku kołowego o prędkości jazdy pociągów.
Występuje na nim bowiem przyspieszenie poprzeczne
(odśrodkowe), którego wartość nie może przekroczyć
określonej wartości dopuszczalnej.
Aby można było zmniejszyć wartość tego
przyspieszenia i zastosować jak największą prędkość,
najczęściej podnosi się na łuku tok zewnętrzny toru
(poprzez odpowiednie przechylenie podkładów),
tworząc tzw. przechyłkę.
Pierwszym zadaniem projektanta jest określenie
minimalnej wartości promienia łuku kołowego R.
Wyznacza się ją na podstawie odpowiednich
warunków, łączących parametry kinematyczne i
geometryczne.
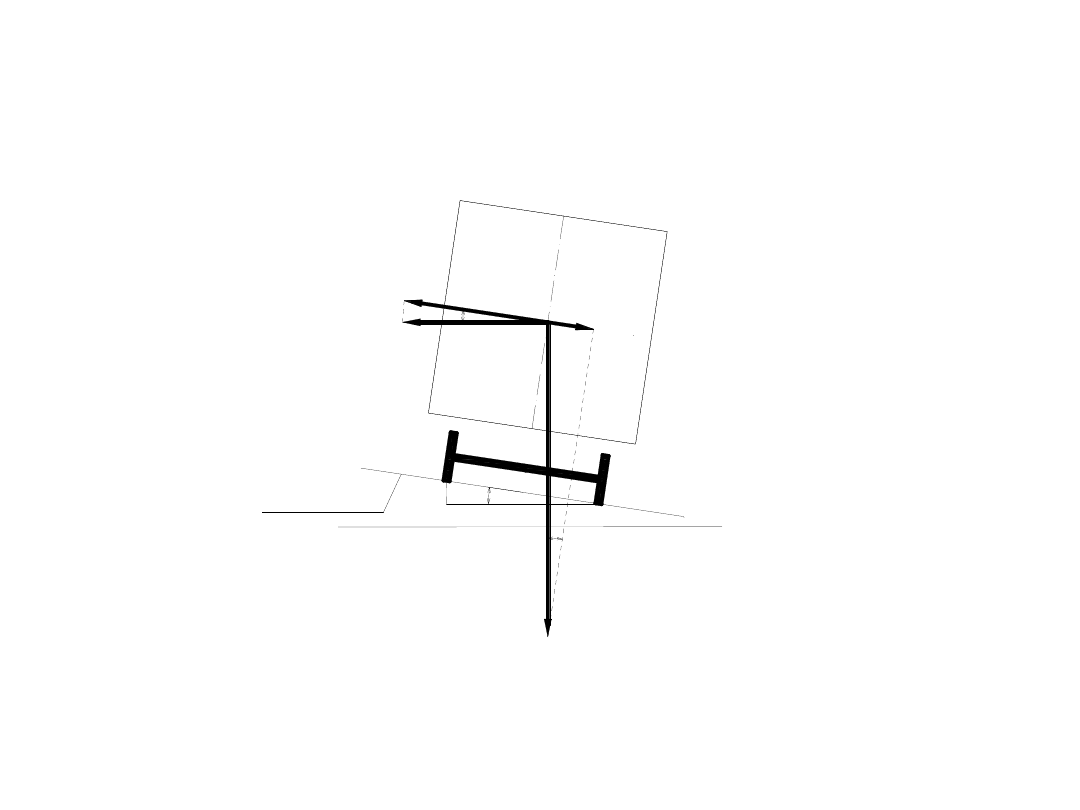
Ponieważ, zgodnie z wieloletnią tradycją, jako model
pojazdu szynowego przyjmuje się punkt materialny, na łuku
kołowym powstaje sytuacja przedstawiona na rysunku
poniżej.
h
s
0
g
Płaszczyzna toru
a
W
a
Z
a
R
0
Przyspieszenia poprzeczne działające na pojazd
szynowy
poruszający się po łuku kołowym
Przyspieszenia poprzeczne są one opisywane
następującymi wzorami:
Występujący w tych wzorach kąt
jest bezpośrednio
związany z wartością przechyłki h
0
. Sinus tego kąta (przy
obowiązującym rozstawie toków szynowych s) wynosi
cos
)
6
,
3
(
2
2
R
v
a
p
z
sin
g
a
w
s
h
0
sin
Obowiązują zatem następujące zależności:
2
0
2
2
1
)
6
,
3
(
s
h
R
v
a
p
z
s
h
g
a
w
0
Ponieważ relacja h
0
/s nie przekracza 0,1, przyjmuje się,
że występujący we wzorze na a
z
pierwiastek
kwadratowy jest równy 1.
Łuk powinien zostać tak zaprojektowany, aby wypadkowa
przyspieszeń nie przekroczyła odpowiedniej wartości
dopuszczalnej, przy czym obowiązują następujące
warunki:
•
jeżeli a
z
> a
w
dop
p
a
g
s
h
R
v
0
2
2
)
6
,
3
(
•
jeżeli a
z
< a
w
t
t
a
R
v
g
s
h
2
2
0
)
6
,
3
(
Stosowane oznaczenia:
R promień łuku kołowego [m],
h
0
wartość przechyłki na łuku [mm],
g przyspieszenie ziemskie [m/s
2
],
s rozstaw osi toków szynowych [mm],
a
dop
dopuszczalna wartość niezrównoważonego
przyspieszenia [m/s
2
],
a
t
dopuszczalna wartość przyspieszenia
skierowanego do
wewnątrz łuku (zależna
od natężenia przewozów q) [m/s
2
].
Wartości dopuszczalne przyspieszeń są określone przez
obowiązujące przepisy projektowania.
Wartości a
dop
zależą od rodzaju układu
geometrycznego, natomiast a
t
- od obciążenia linii
przewozami.
Dopuszczalne wartości przyspieszenia niezrównoważonego
a
dop
dla pociągów pasażerskich:
•
poszerzenia międzytorzy w dogodnych warunkach
terenowych
a
dop
= 0,3 m/s
2
• łuki i pojedyncze krzywe przejściowe dla torów, po
których odbywa się ruch z v < 160 km/h
a
dop
= 0,8 m/s
2
•
łuki i pojedyncze krzywe przejściowe dla torów, po
których odbywa się ruch z v 160 km/h
a
dop
= 0,6 m/s
2
•
tory zwrotne rozjazdów zwyczajnych
a
dop
=
0,65 m/s
2
• tory boczne na stacjach (v
40 km/h)
a
dop
=
0,65 m/s
2
• łuki o promieniach: 200 m < R
250 m
a
dop
=
0,5 m/s
2
• łuki o promieniach: R
200 m
a
dop
=
0,45 m/s
2
• poszerzenia międzytorzy w trudnych warunkach
terenowych
a
dop
= 0,45
m/s
2
Dopuszczalne wartości przyspieszenia niezrównoważonego
a
t
dla pociągów towarowych przy obciążeniu przewozami q
[Tg/rok]:
• dla 0
T < 5
a
t
= 0,6 m/s
2
• dla 5
T < 10
a
t
= 0,5 m/s
2
• dla 10
T < 15
a
t
= 0,4 m/s
2
• dla 15
T < 20
a
t
= 0,3 m/s
2
• dla T
20
a
t
= 0,2 m/s
2
Jeśli założymy, że g = 9,81 m/s
2
i s = 1500 mm,
otrzymujemy:
• z warunku
t
t
dop
p
a
R
v
h
a
R
v
153
8
,
11
153
8
,
11
2
0
2
dop
p
a
g
s
h
R
v
0
2
2
)
6
,
3
(
dop
p
a
R
v
h
153
8
,
11
2
0
• z warunku
t
t
a
R
v
g
s
h
2
2
0
)
6
,
3
(
t
t
a
R
v
h
153
8
,
11
2
0
stąd
t
t
dop
p
a
R
v
h
a
R
v
153
8
,
11
153
8
,
11
2
0
2
Wynika stąd przedział, z którego możemy przyjmować
wartość przechyłki h
0
dla różnych wartości promienia
R.
W myśl obowiązujących przepisów wartość przechyłki
powinna mieścić się w granicach 20 mm h
0
150
mm.
Przepisy określają też minimalne promienie łuku,
uzależniając je od kategorii linii kolejowych i
ukształtowania terenu.
Minimalne promienie łuku R[m]
Linia magistralna
• w terenie nizinnym
1400
• w terenie podgórskim
1200
• w terenie górskim
600
Linia pierwszorzędna
• w terenie nizinnym
1200
• w terenie podgórskim
600
• w terenie górskim
400
Linia drugorzędna
• w terenie nizinnym
600
• w terenie podgórskim
400
• w terenie górskim
300
Linia znaczenia miejscowego
• w terenie nizinnym
400
• w terenie podgórskim
250
• w terenie górskim
200
Minimalna długość toru w łuku kołowym powinna wynosić:
• w torach głównych linii magistralnych i
pierwszorzędnych
5
,
2
max
min
v
l
lecz nie mniej niż 30 m,
• w torach głównych linii drugorzędnych – 30
m,
•
w pozostałych torach – 10 m.
Pomiędzy odcinkiem prostym toru i zaprojektowanym łukiem
poziomym o promieniu R powinna zostać wykonana tzw.
krzywa przejściowa, na długości której będzie występowała
ciągła zmiana krzywizny toru.
Takie rozwiązanie zapewnia płynny przyrost
niezrównoważonego przyspieszenia od wartości zerowej na
prostej do wartości am na łuku kołowym.
Projektowanie krzywej przejściowej
R
v
a
p
m
2
2
)
6
,
3
(
Wartość przyspieszenia a
m
wynika z zależności
:
• w przypadku braku przechyłki na łuku
s
h
g
R
v
a
p
m
0
2
2
)
6
,
3
(
• w przypadku występowania na łuku przechyłki h
0
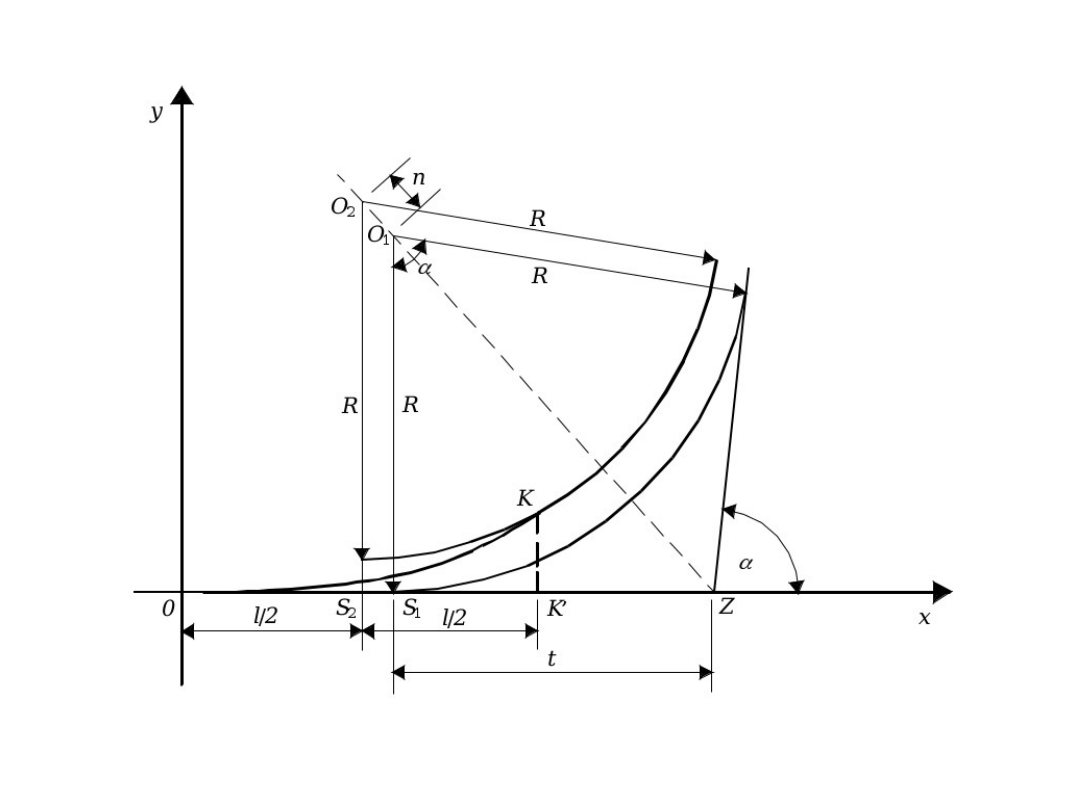
Ścisły sposób kształtowania krzywej przejściowej
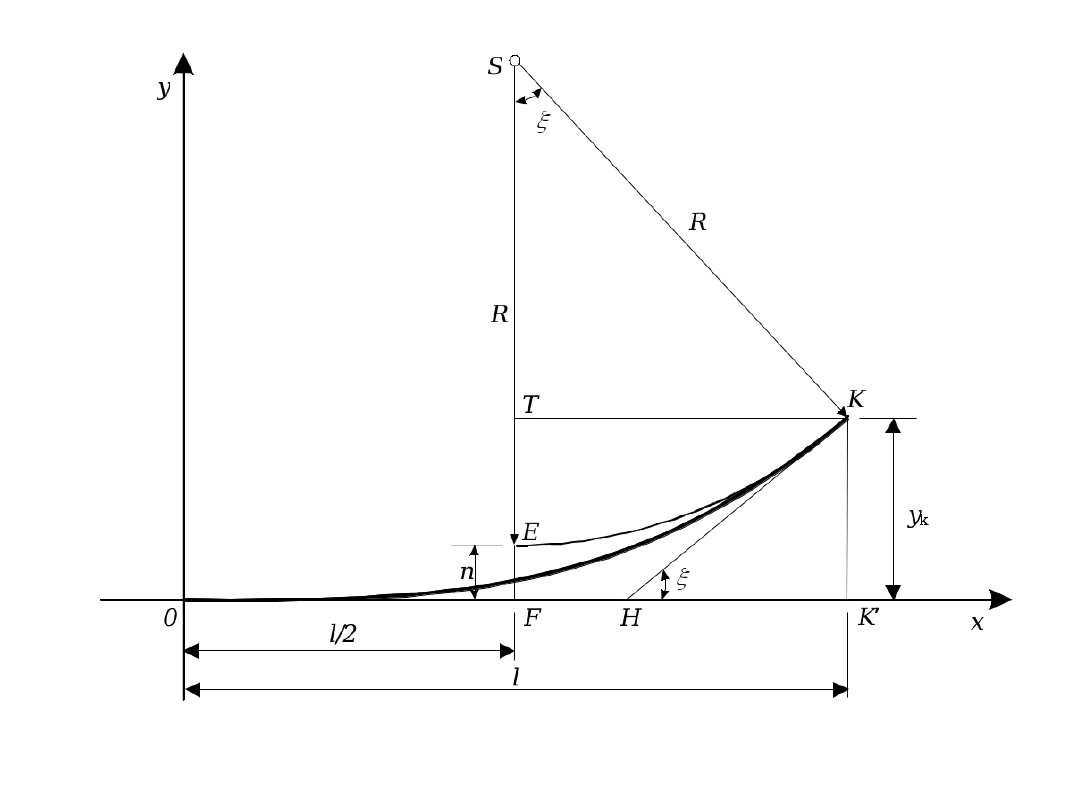
Stosowany sposób kształtowania krzywej przejściowej
Projektowanie układu geometrycznego ma na celu uzyskanie
takiego rozwiązania, które zapewni korzystny rozkład
przyspieszeń, działających na przejeżdżający tabor w
kierunku poprzecznym do osi toru.
O wielkości tych przyspieszeń decyduje krzywizna toków
szynowych w płaszczyźnie poziomej i właściwe
kształtowanie krzywizny stanowi podstawowe zadanie
procesu projektowego.
Miarą zakrzywienia łuku toru kolejowego jest stosunek kąta,
o jaki zmienia się kierunek osi podłużnej wagonu po
przebyciu pewnego łuku, do długości tegoż łuku.
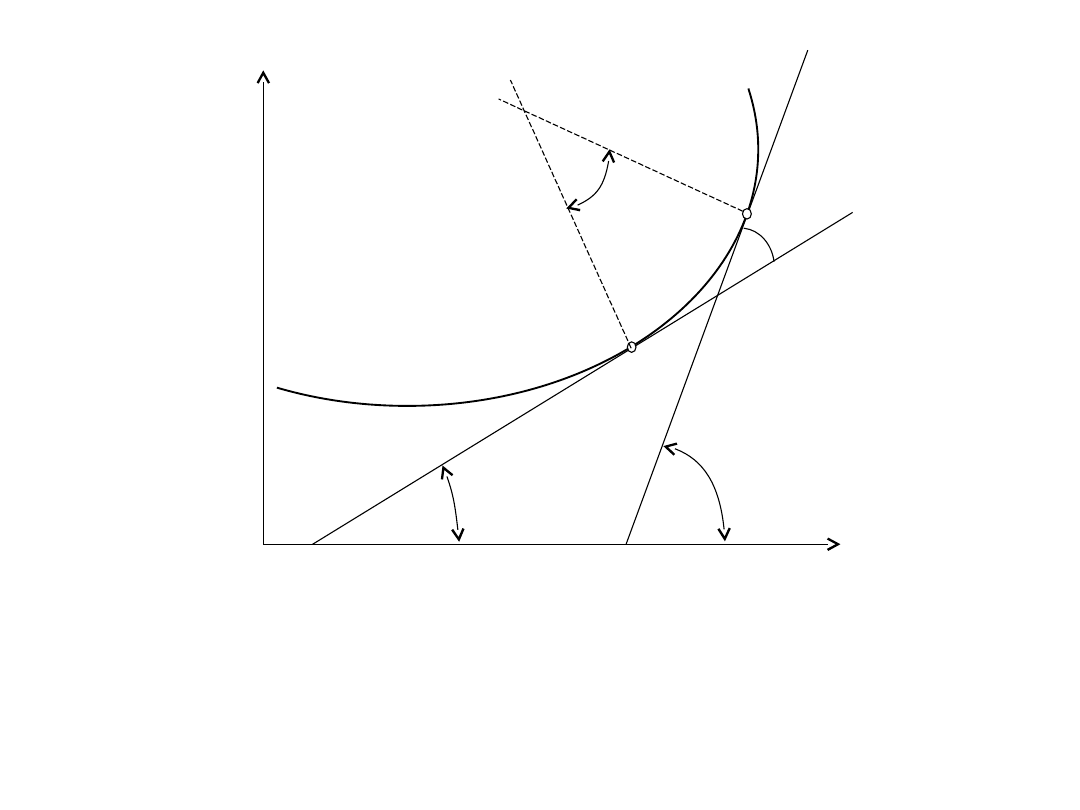
Schemat ideowy do wyjaśnienia pojęcia krzywizny toru
Krzywizną krzywej K w punkcie M nazywamy granicę, do której
dąży stosunek kata ostrego Δα zawartego między stycznymi do
krzywej K w punktach M i M
1
do długości Δl łuku MM
1
, gdy
punkt M
1
dąży po krzywej K do punktu M.
1
M
l
x
y
M
1
l
k
l
lim
0
Dla łuku kołowego (tj. okręgu) o promieniu R kąt Δα jest
równy kątowi między promieniami dochodzącymi do
punktów styczności i posiada miarę łukową
R
l
R
l
1
Tak więc
stąd dla łuku
kołowego
R
k
1
Znacznie bardziej złożona jest kwestia określania krzywizny na
innych krzywych. Generalnie mówiąc, jest ona zmienna na
długości krzywej; pokażemy sposób jej wyznaczania dla krzywej
danej równaniem jawnym y = y(x).
Niech α oznacza skierowany kąt nachylenia stycznej do
krzywej w punkcie M o odciętej x do osi Ox .
Przy przejściu od M do M
1
: Δα = α
1
– α , Δx = x
1
– x , Δl = l
1
– l (mierzone po krzywej K od punktu M
0
).
Granica
stosunku
l
gdy
1
M
M
x
l
x
x
l
x
l
k
l
l
l
l
lim
lim
lim
lim
0
0
0
0
czyli
ostatecznie
dx
dl
dx
d
k
Żeby
wyznaczyć
dx
d
należy określić kąt α .
Wykorzystujemy związek y’(x) = tg α α(x) = arc tg y’(x).
Tak więc
2
)
(
1
)
(
x
y
x
y
dx
d
Do określenia
pochodnej
dx
dl
wykorzystujemy wzór na długość
krzywej
dx
x
y
l
2
)
(
1
stą
d
2
)
(
1
x
y
dx
dl
Po podstawieniu
otrzymujemy
2
2
2
2
)
(
1
)
(
1
)
(
)
(
1
)
(
1
)
(
)
(
x
y
x
y
x
y
x
y
x
y
x
y
x
k
i ostatecznie
2
3
2
)
(
1
)
(
)
(
x
y
x
y
x
k
Jak widać, struktura wzoru na krzywiznę jest więc dość
złożona. Nie ma też podstaw, żeby traktować dowolną krzywą
jako ciąg łuków kołowych o zmieniającym się promieniu (co
uzasadniałoby wykorzystywanie wzoru na krzywiznę łuku
kołowego i jest niekiedy praktykowane).
Należy również zaznaczyć, że wzór opisuje krzywiznę
odniesioną do osi odciętych, nie zaś do długości samej
krzywej. Tymczasem ruch pojazdów szynowych odbywa się
po krzywej i właśnie na długości krzywej należy formować
rozkład krzywizny.
Wyznaczanie krzywizny na krzywych przejściowych
Spróbujmy skupić się na samej krzywiźnie i zająć się jej
rozkładem na długości krzywej.
Nie będziemy więc wyznaczać krzywizny k(x), zależnej od
przyjętego układu współrzędnych, lecz krzywiznę k(l), dla
której wymagania jesteśmy w stanie określić jednoznacznie.
Krzywizna k(l) powinna być opisana funkcją odpowiedniej
klasy, żeby wywoływała mniejsze (a więc korzystniejsze)
oddziaływania dynamiczne.
Przedstawiony zapis matematyczny stanowi identyfikacje kształtu
krzywych przejściowych równaniami różniczkowymi i określa
sposób na znalezienie rozwiązań spełniających dowolną liczbę
założonych warunków, przy czym dla danych warunków mogą to
być rozwiązania zupełnie różnej postaci.
Funkcji k(l) należy poszukiwać wśród rozwiązań równania
różniczkowego
)
1
(
)
(
,...,
,
,
)
(
m
m
k
k
k
l
f
l
k
z warunkami na początku (dla l = 0) i na końcu (dla l = l
k
)
krzywej przejściowej
1
)
(
,...,
2
,
1
,
0
0
)
0
(
n
i
dla
k
i
2
)
(
,...,
2
,
1
0
0
1
)
(
n
j
j
dla
dla
R
l
k
k
j
Otrzymana funkcja k(l) jest funkcja klasy C
n
w przedziale ,
gdzie
n = min (n
1
, n
2
).
Ze względów praktycznych korzystne będzie zapisywanie k(l)
w postaci
)
(
1
)
(
l
g
R
l
k
gdzie g(l) – funkcja zmiennej l , zależna od rodzaju krzywej
przejściowej, przy czym
g(0) = 0,
g(l
k
) = 1.
Możemy wówczas łatwo określić rzędne rampy
przechyłkowej (jeśli taka występuje)
)
(
)
(
0
l
g
h
l
h
oraz
przyspieszenie
)
(
)
(
l
g
a
l
a
m
Identyfikacja znanych rozwiązań
k(0
+)
= 0
k(l
k
) = 1/R
0
)
(
l
k
l
c
c
l
k
2
1
)
(
k
l
l
R
l
k
1
)
(
k
l
l
l
g
)
(
0
1
c
k
l
R
c
1
1
2
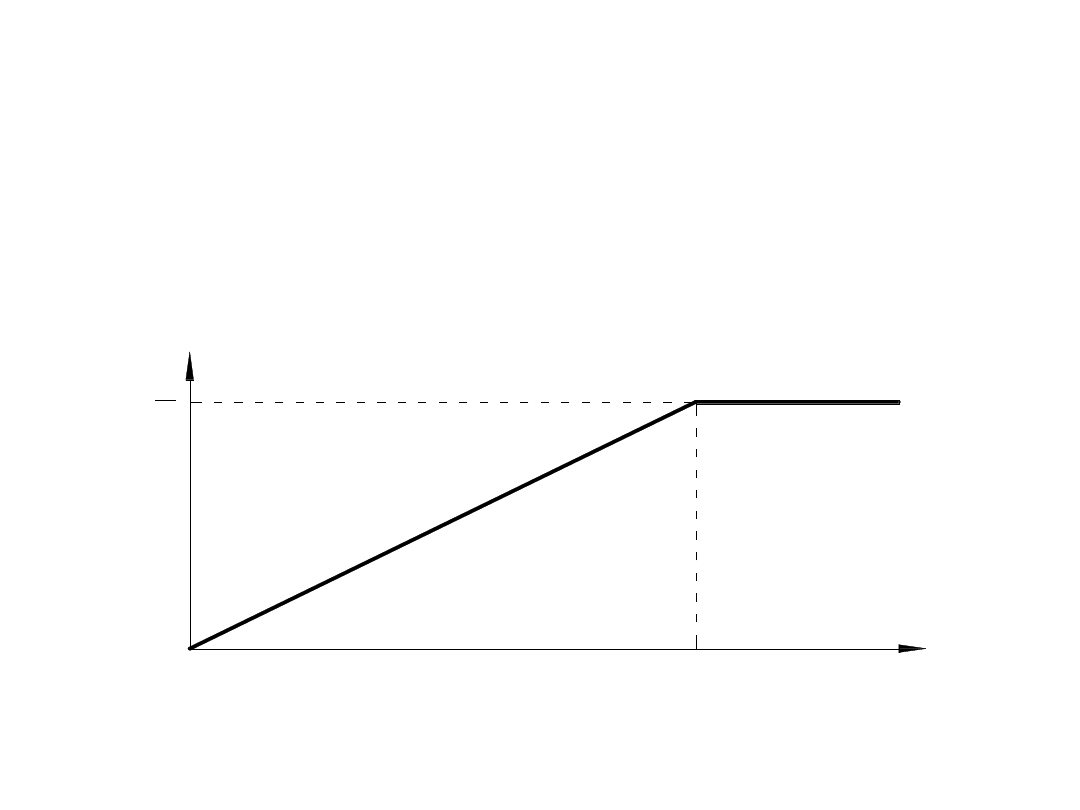
W stosownych w kolejnictwie krzywych przejściowych –
gdy przyjmujemy układ współrzędnych, w którym
początek krzywej jest styczny do osi odciętych – wartość
stycznej na długości jest niewielka. Dlatego też możemy
zastosować pewne przybliżenie. Standardowo
przyjmujemy, że zamodelowana krzywizna k(l) odnosi
się do swego rzutu na oś x , czyli że l = x .
Wykres krzywizny liniowej
k
1
R
0
l
x
W wyniku takich założeń otrzymujemy równanie krzywizny
)
(
1
)
(
0
x
g
R
x
k
k
l
x
x
g
)
(
Znamy też równanie rampy przechyłowej
)
(
)
(
0
x
g
h
x
h
Rzędna końcowa krzywej przejściowej wynosi
Traktujemy k
0
(x) jako krzywiznę wyjściową, będącą
przybliżeniem krzywizny docelowej k(x); pozwala nam to
na znalezienie szukanej funkcji y(x), jako rozwiązania
równania różniczkowego
k
l
x
R
x
y
1
)
(
Równanie to następnie dwukrotnie całkujemy,
uwzględniając warunki: y(0) = 0 i y’(0) = 0 .
Otrzymujemy w ten sposób równanie krzywej
przejściowej w postaci paraboli trzeciego stopnia.
k
l
R
x
x
y
6
)
(
3
R
l
l
x
y
k
k
6
)
(
2
a nachylenie stycznej na końcu
R
l
l
x
y
k
k
2
)
(
Powszechnie uznaje się, że liniową krzywiznę posiada
krzywa przejściowa w postaci paraboli trzeciego stopnia.
Jest to tradycyjnie podstawowy rodzaj krzywej przejściowej
stosowany na drogach kolejowych.
Należy jeszcze wspomnieć o pewnej nieprawidłowości,
która dotyczyć będzie również innych rozpatrywanych
krzywych przejściowych. Równanie paraboli trzeciego
stopnia nie spełnia warunku styczności krzywej
przejściowej z łukiem kołowym, tj.
)
(
)
(
k
k
l
y
l
y
Powiększamy dalej liczbę warunków
0
0
0
k
k
R
l
k
k
/
1
0
k
l
k
i przyjmujemy równanie różniczkowe
0
)
(
)
4
(
x
k
3
4
2
3
2
1
)
(
x
c
x
c
x
c
c
x
k
c
1
= 0 c
2
= 0
2
3
3
1
k
l
R
c
3
4
2
1
k
l
R
c
3
5
2
4
10
4
1
)
(
k
k
l
x
l
x
R
x
y
3
3
2
2
2
3
1
)
(
k
k
l
x
l
x
R
x
k
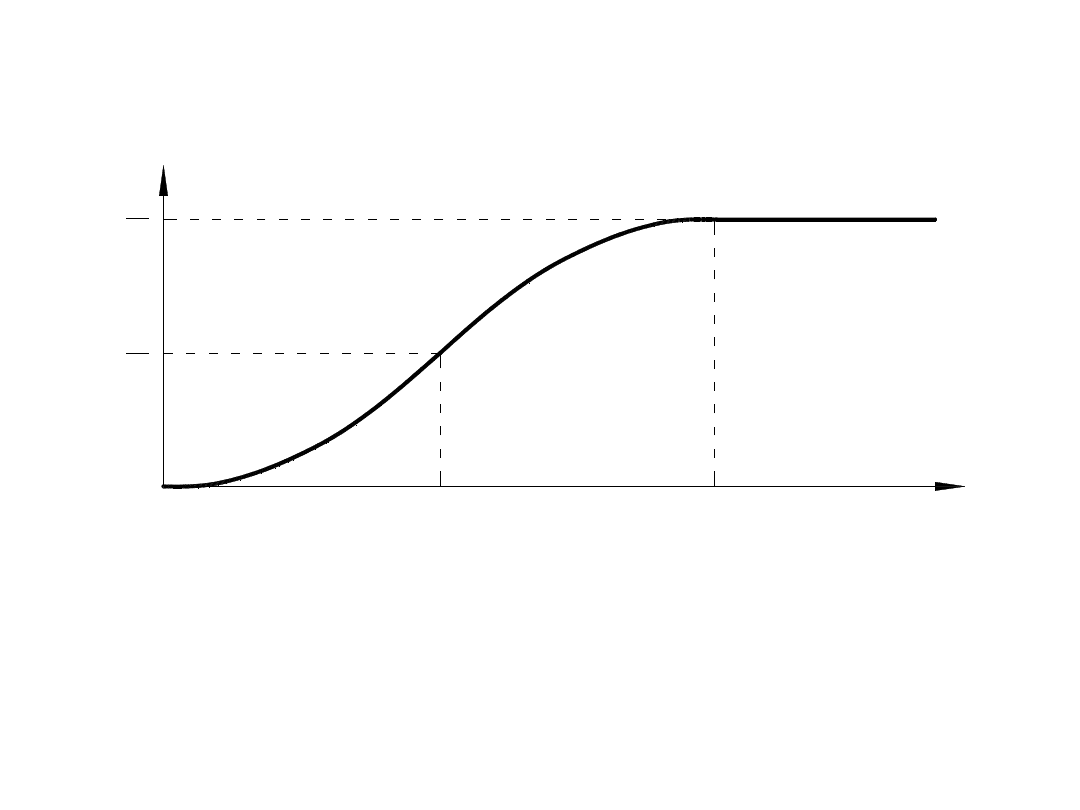
Przykładowa krzywizna o nieliniowym rozkładzie na
długości
k
1
R
1
2R
0
l/2
l
x
Zachowując cztery warunki zidentyfikujmy krzywiznę
innym równaniem różniczkowym
x
l
c
x
l
c
x
c
c
x
k
k
k
cos
sin
)
(
4
3
2
1
R
c
1
2
1
1
c
2
= 0 c
3
= 0
R
c
1
2
1
4
k
l
x
R
x
k
cos
1
2
1
)
(
1
cos
2
2
1
)
(
2
2
2
k
k
l
x
l
x
R
x
y
0
)
(
)
(
2
2
)
4
(
x
k
l
x
k
k
Zakładamy jeszcze większą liczbę warunków
c
1
=
0
0
)
0
(
0
0
k
k
k
R
l
k
k
/
1
0
)
(
k
k
l
k
l
k
0
)
(
4
)
(
)
4
(
2
2
)
6
(
x
k
l
x
k
k
x
l
c
x
l
c
x
c
x
c
x
c
c
x
k
k
k
2
cos
2
sin
)
(
6
5
3
4
2
3
2
1
k
l
R
c
1
1
2
c
3
= c
4
= 0
2
1
1
5
R
c
c
6
=
0
k
k
l
x
l
x
R
x
k
2
sin
2
1
1
)
(
l
x
l
x
l
l
x
R
x
y
2
sin
4
2
3
2
1
)
(
3
2
2
3
Rampa przechyłkowa
Jeśli na łuku kołowym została zastosowana przechyłka,
wówczas na długości krzywej przejściowej wykonuje się
rampę przechyłkową, czyli łagodne przejście od toru
bez przechyłki na prostej do toru na łuku z
podniesionym tokiem zewnętrznym.
Rzędne rampy przechyłkowej h(x) muszą
odpowiadać krzywiźnie k(x) krzywej przejściowej, od
której zależy charakter występującego przyspieszenia
odśrodkowego.
h(x) = h
0
g(x)
• dla paraboli trzeciego stopnia
• dla krzywej Blossa
• dla cosinusoidy
• dla sinusoidy
k
l
x
x
g
)
(
k
l
x
h
x
h
0
)
(
3
3
2
2
2
3
)
(
k
k
l
x
l
x
x
g
3
3
2
2
0
2
3
)
(
k
k
l
x
l
x
h
x
h
k
l
x
x
g
cos
1
2
1
)
(
k
l
x
h
x
h
cos
1
2
)
(
0
k
k
l
x
l
x
x
g
2
sin
2
1
)
(