Plan prezentacji:

Plan prezentacji:



Entalpie przemian fizycznych i entropia
reakcji



Warunek termodynamicznej samorzutności
reakcji



Stała równowagi a samorzutność reakcji



Diagram Ellinghama



Zmiany entalpii swobodnej reakcji
utleniania węgla i tlenku węgla w funkcji
temperatury

2

Przypomnienie:

Przypomnienie:

II zasada termodynamiki

W przemianach samorzutnych entropia

W przemianach samorzutnych entropia

układu izolowanego rośnie:

układu izolowanego rośnie:

Δ

Δ

S

S

cał

cał

>0

>0

III zasada termodynamiki

W temperaturze zera bezwzględnego 0K

W temperaturze zera bezwzględnego 0K

entropia kryształu doskonałego równa

entropia kryształu doskonałego równa

się zeru.

się zeru.

3

Entalpie przemian fizycznych

Entalpie przemian fizycznych

4

Entalpie przemian fizycznych

Entalpie przemian fizycznych

5

Entalpie przemian fizycznych

Entalpie przemian fizycznych

6

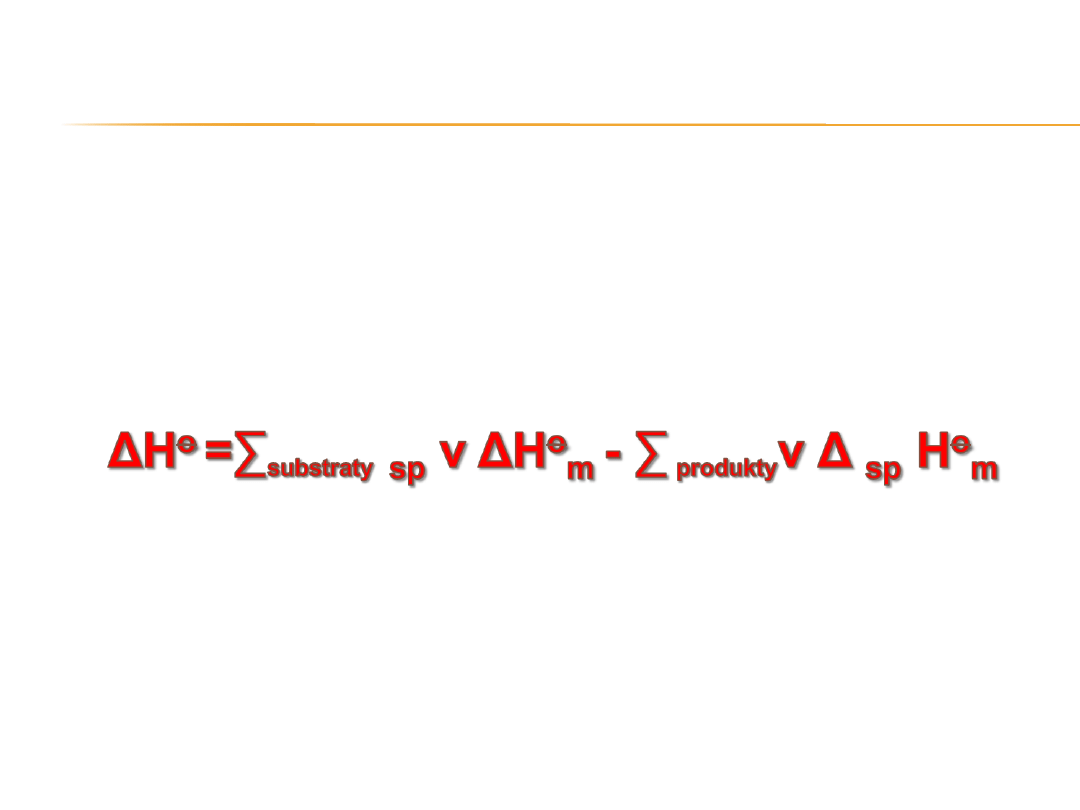
7

Standardowa molowa entalpia spalania
związku chemicznego jest to entalpia
towarzysząca reakcji spalania 1 mola
związku chemicznego.

Molowe entalpie spalania pierwiastków nie są

Molowe entalpie spalania pierwiastków nie są

równe 0 !!!

równe 0 !!!

Entalpie przemian fizycznych

Entalpie przemian fizycznych

8

Funkcja ta związana jest z podziałem energii

wewnętrznej układu na poszczególne drobiny

występujące w układzie

oraz różne rodzaje ruchu tych drobin.

Jest więc miarą wewnętrznej różnorodności układu

(„nieporządku” panującego w układzie).

Entropia reakcji (S)

Entropia reakcji (S)

Entropia przyjmuje tym większą wartość, im :

 więcej jest różnych substancji w układzie,

 większa jest liczba cząstek,

 więcej jest faz (np. substancja o różnym stanie
skupienia)

S

kryst



S

cieczy



S

gazów

 większa jest swoboda ruch cząstek.

9

Entropia jako funkcja stanu zależeć musi od parametrów
opisujących jego stan, a w szczególności od :

temperatury – wzrost temperatury zwiększa energię,
a w konsekwencji swobodę ruchu
cząstek,
a wiec i entropię układu

ciśnienia – zwiększenie ciśnienia ogranicza swobodę
ruchu
cząstek przez co maleje entropia

liczby moli – im więcej moli tym większa entropia .

Entropia reakcji (S)

Prawo Hessa

Efekt cieplny reakcji nie zależy od drogi
przemiany pod warunkiem, że wszystkie
procesy są izobaryczne lub izochoryczne, a
jedyną formą wymiany energii na sposób
pracy jest praca objętościowa.

ΔH = q

p

p = const

Entalpia reakcji sumarycznej jest sumą entalpii
etapów, na które reakcje tą można podzielić.

10

Entalpie przemian fizycznych

Entalpie przemian fizycznych

Prawo Lavosiera i Laplace’a

Efekt cieplny reakcji przebiegającej w

danym kierunku równy jest efektowi
cieplnemu reakcji odwrotnej z przeciwnym
znakiem.

A + B → C + D

A + B → C + D

Δ

Δ

H

H

C + D → A + B

C + D → A + B

–

–

Δ

Δ

H

H

11

Entalpie przemian fizycznych

Entalpie przemian fizycznych

Entalpie przemian fizycznych

Entalpie przemian fizycznych

12

Standardowa molowa entalpia swobodna

Standardowa molowa entalpia swobodna

reakcji

reakcji

13

Δ G < 0

Δ G < 0

proces samorzutny

proces samorzutny

Δ G > 0 - proces wymuszony

Δ G = 0 - stan równowagi

termodynamicznej

14

Warunek samorzutności reakcji

Warunek samorzutności reakcji





G

G

r

r

o

o

=

=





H

H

r

r

o

o

-

-

T

T





S

S

r

r

o

o

15

Z definicji zmiany entalpii swobodnej Δ G
wynika,
że o samorzutności procesu decydują trzy
czynniki :

Efekt energetyczny

Efekt energetyczny

-

tj. tendencja do

obniżenia

energii układu

Efekt entropowy

Efekt entropowy

-

czyli skłonność do

zwiększenia

entropii

Temperatura

Temperatura

Warunek samorzutności reakcji

Warunek samorzutności reakcji

Warunek samorzutności reakcji

Warunek samorzutności reakcji

16

Entalpia Entropia

Samorzutność

Reakcje egzotermiczne

Н < 0

Н < 0

Reakcje endotermiczne

Н > 0

Н > 0

.

S > 0
S < 0

.

S > 0
S < 0

.

+

+

(G < 0)

+

+

jeśli |TS| < |Н|

to (G

< 0)

.

+

+

jeśli TS > Н

to

(G < 0)

-

-

(G > 0)

Udziały decydujące o samorzutności procesu:

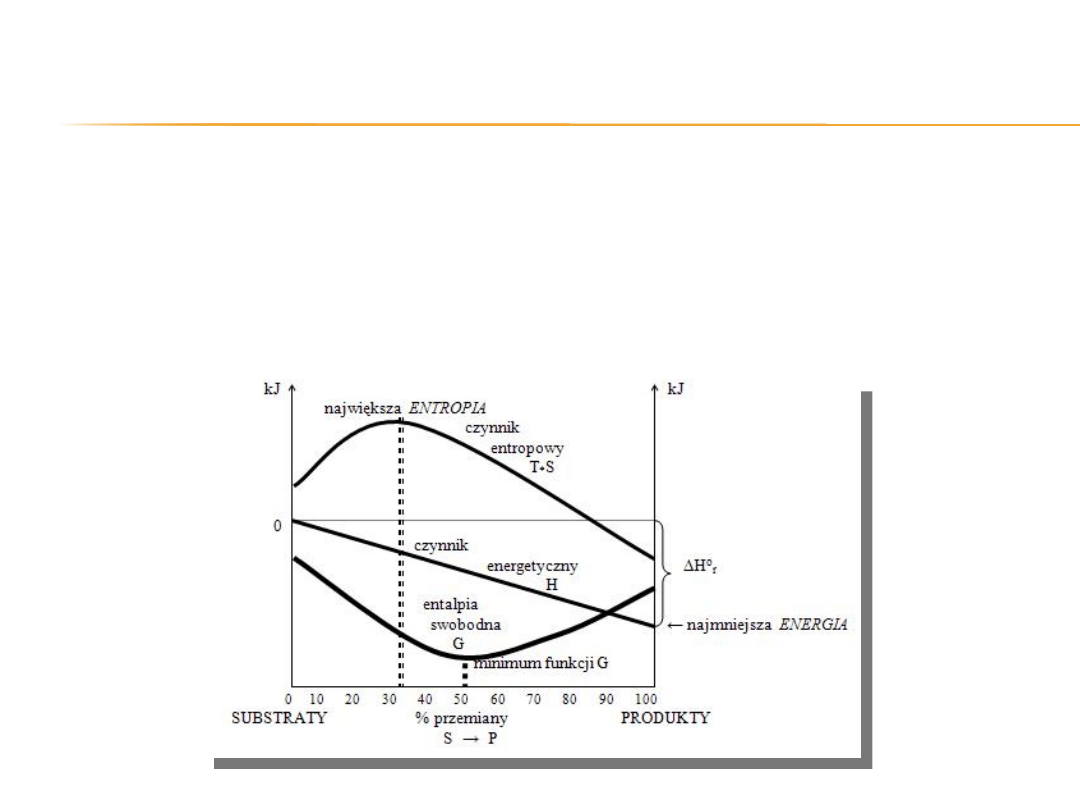
Stała równowagi a

Stała równowagi a

samorzutność reakcji

samorzutność reakcji



Układ w którym entalpia swobodna osiąga
minimum (∆G) znajduje się w stanie
równowagi termodynamicznej, czyli w takim
stanie w którym nie działają na układ
czynniki entropowy i energetyczny.

17

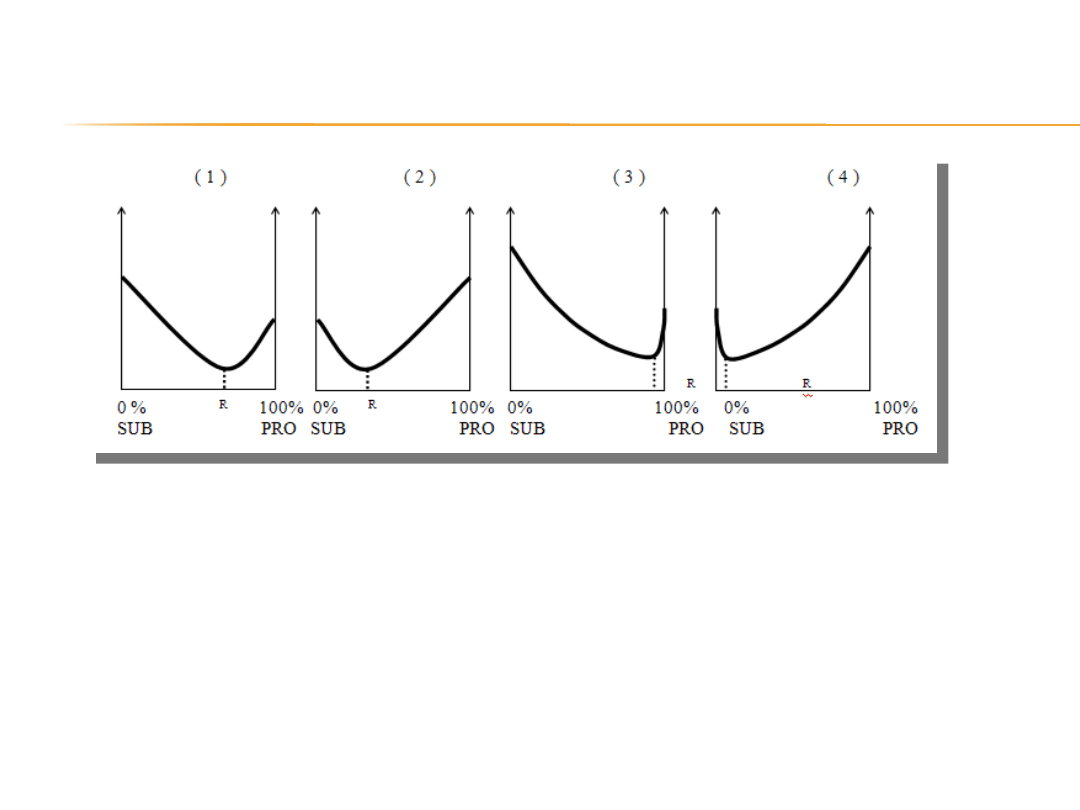
18

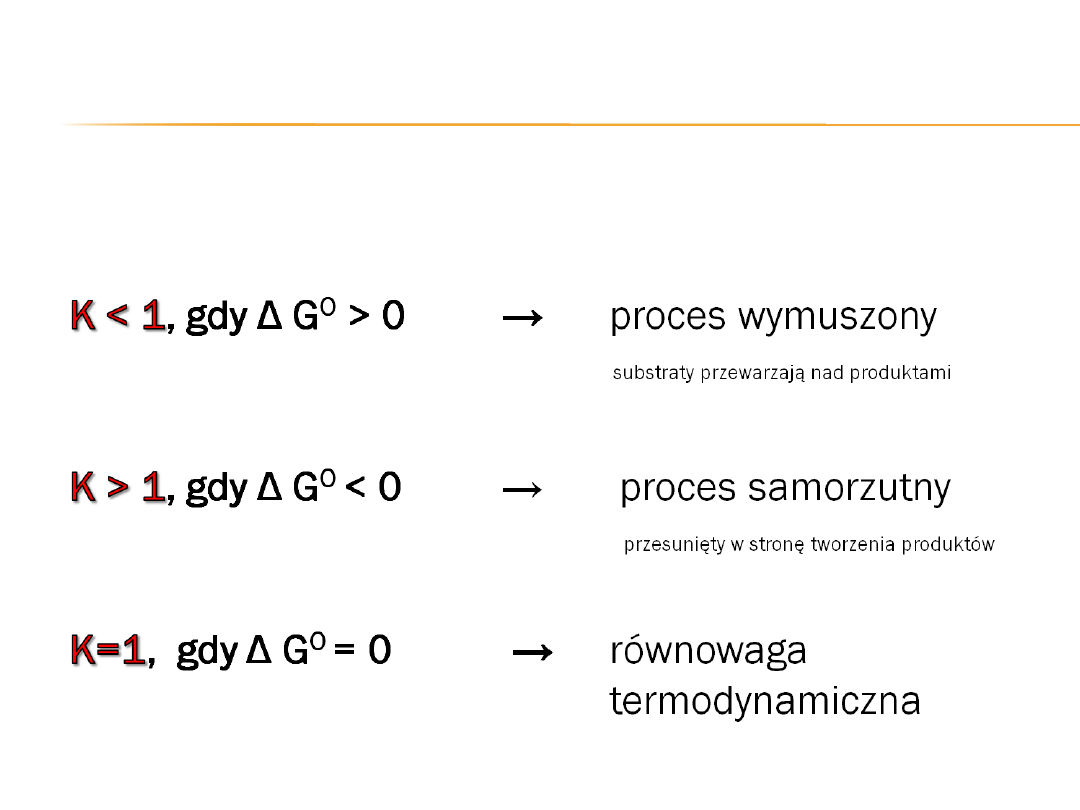
( 1 ) reakcja z dużą wydajnością (tj. głównie biegnie w prawo)

( 2 ) reakcja z małą wydajnością (tj. głównie biegnie w lewo)

( 3 ) reakcja z praktycznie 100 % wydajnością (prawie do wyczerpania
substratów)

( 4 ) reakcja praktycznie nie zachodzi (wydajność bliska 0 %)

Analizując uzyskane w praktyce kształty krzywej funkcji G zaobserwować
można cztery typowe przypadki przebiegu przemiany

SUBSTRATY ⇄ PRODUKTY :

Stała równowagi a

Stała równowagi a

samorzutność reakcji

samorzutność reakcji

19

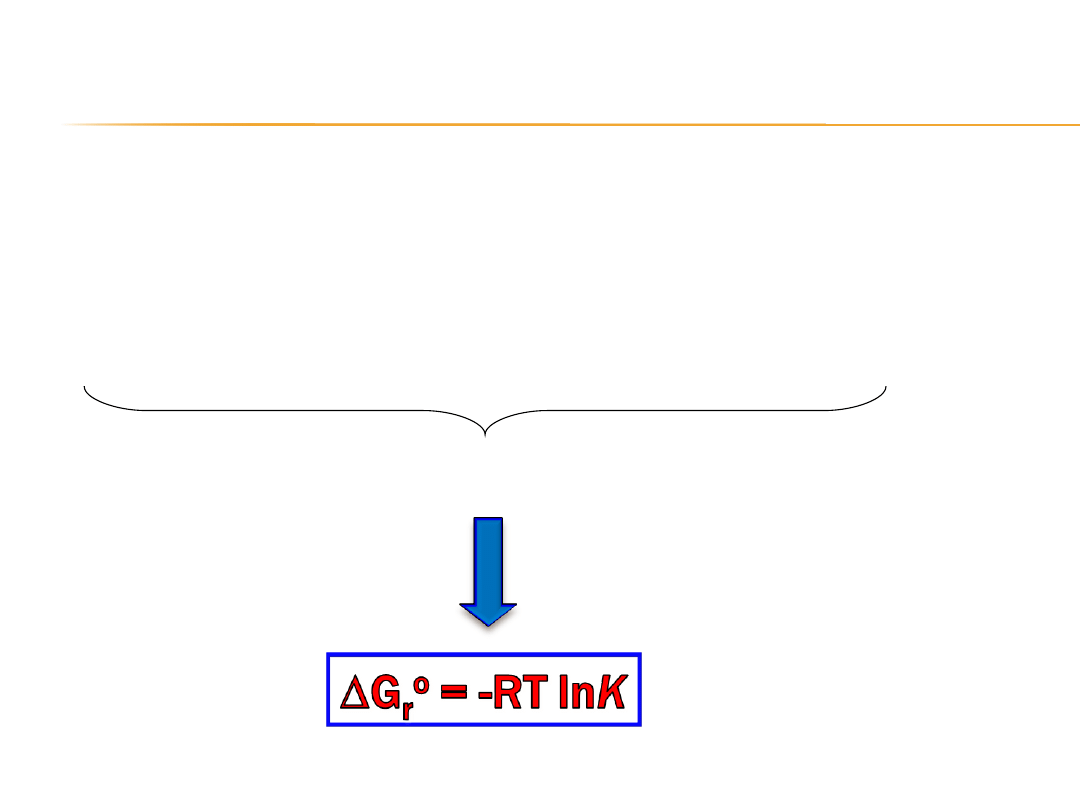
Gdy reakcja osiąga stan równowagi chemicznej to:

G

r

= 0

Iloraz reakcji Q = K

G

r

= G

r

o

+ RT lnQ

0 = G

r

o

+ RT lnK

Stała równowagi a samorzutność

Stała równowagi a samorzutność

reakcji

reakcji

20

Diagram Ellinghama

Diagram Ellinghama

Diagram Ellinghama:

Diagram Ellinghama:



określa zakres temperatur, w których mogą

zachodzić procesy redukcji.



przedstawia graficzną zależność zmiany entalpii

swobodnej reakcji (Δ G

0

) od temperatury (T).



wykorzystywany jest do analizy redukcji rud

metali.

21

Diagram Ellinghama

Diagram Ellinghama

Przeanalizujmy

równowagi

reakcji

na

podstawie

funkcji

termodynamicznych

następujących reakcji:

22

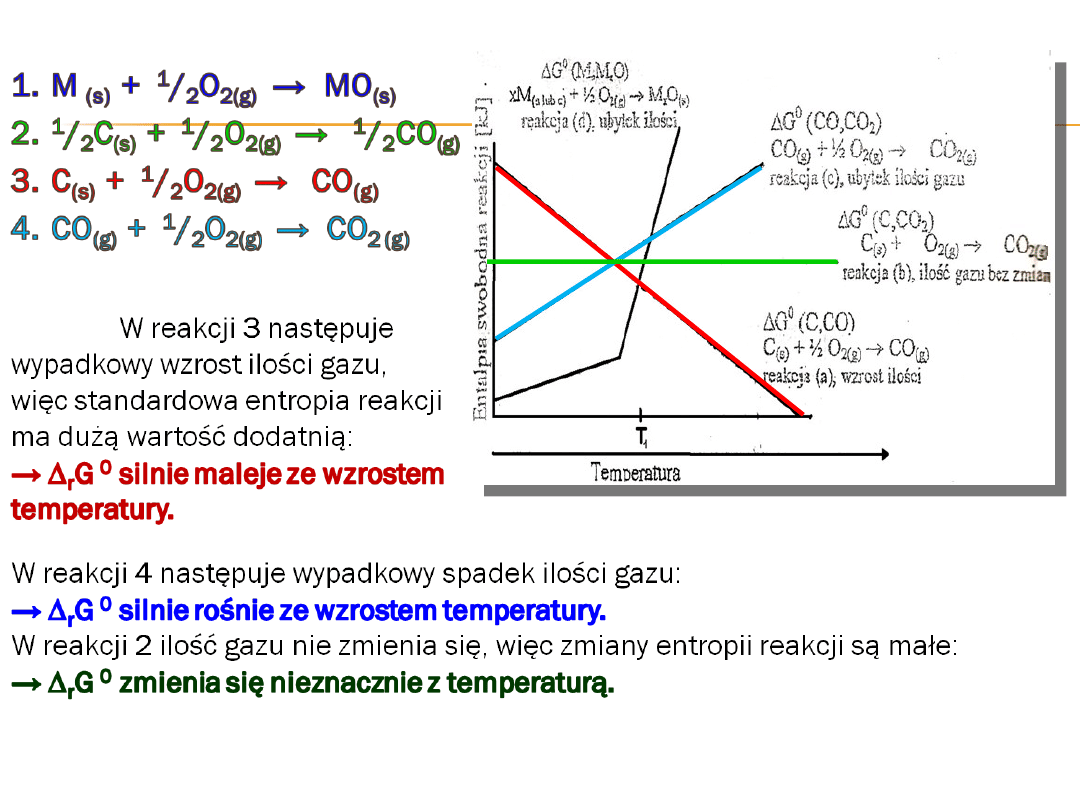
1.

1.

M

M

(s)

(s)

+

+

1

1

/

/

2

2

O

O

2(g)

2(g)

→ MO

→ MO

(s)

(s)

2.

2.

1

1

/

/

2

2

C

C

(s)

(s)

+

+

1

1

/

/

2

2

O

O

2(g)

2(g)

→

→

1

1

/

/

2

2

CO

CO

(g)

(g)

3.

3.

C

C

(s)

(s)

+

+

1

1

/

/

2

2

O

O

2(g)

2(g)

→ CO

→ CO

(g)

(g)

4.

4.

CO

CO

(g)

(g)

+

+

1

1

/

/

2

2

O

O

2(g)

2(g)

→ CO

→ CO

2 (g)

2 (g)

23

Diagram

Diagram

Ellinghama

Ellinghama

24

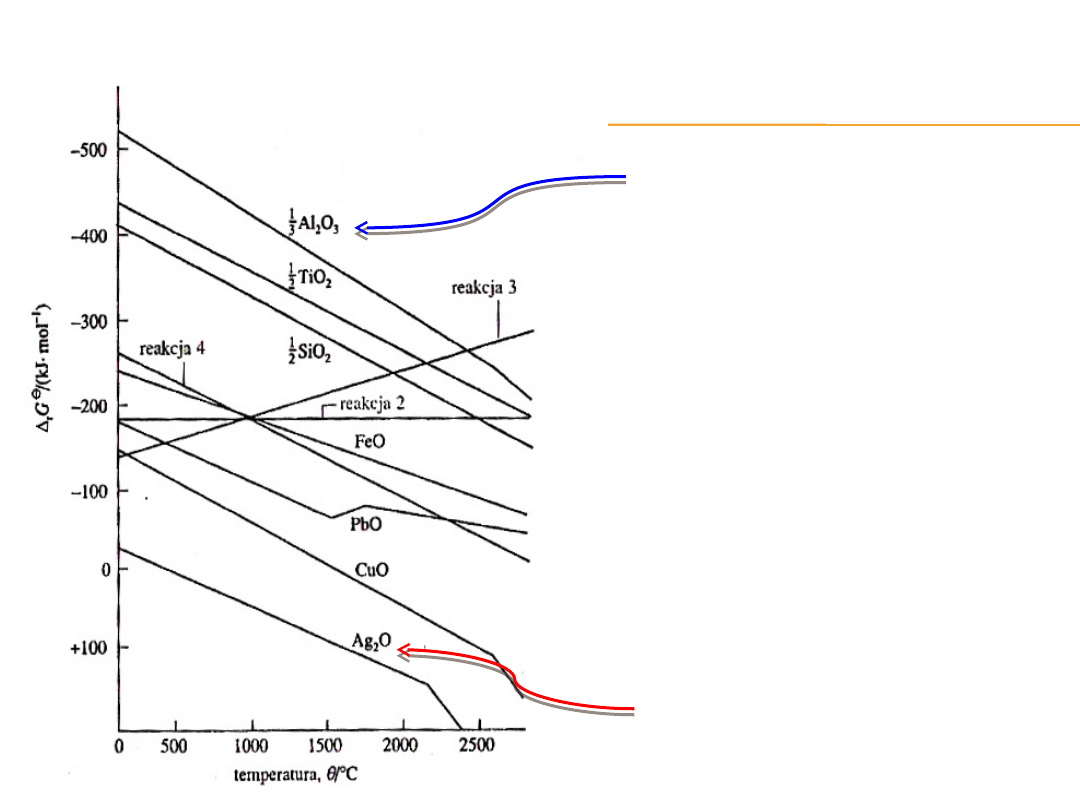
Proces najbardziej
egzotermiczny

Proces najmniej
egzotermiczny

Standardowa entropia
tych reakcji jest
porównywalna dla
wszystkich metali,
ponieważ w każdej z
nich usuwany jest tlen
gazowy, a powstający
tlenek jest zwartym
ciałem stałym.

Diagram Ellinghama

Diagram Ellinghama

25

26

Aby reakcja redukcji tlenku metalu

zachodziła to entalpia swobodna reakcji

sumarycznej ( ΔG

0

)

musi być mniejsza od zera

.

ΔG

0

tw

= Σ ΔG

0

prod

- Σ ΔG

0

subst

MO + C M + CO

ΔG

0

= ΔG

0

tw

(M) + ΔG

0

tw

(CO) - ΔG

0

tw

(C) - ΔG

0

tw

(MO)

< 0

ΔG

0

tw

pierwiastków w stanie podstawowym

równa jest 0

i dlatego:

ΔG

0

tw

(CO) - ΔG

0

tw

(MO)

< 0

ΔG

0

tw

(CO) < ΔG

0

tw

(MO)

Diagram

Diagram

Ellinghama

Ellinghama

27

28

Diagram

Diagram

Ellinghama

Ellinghama

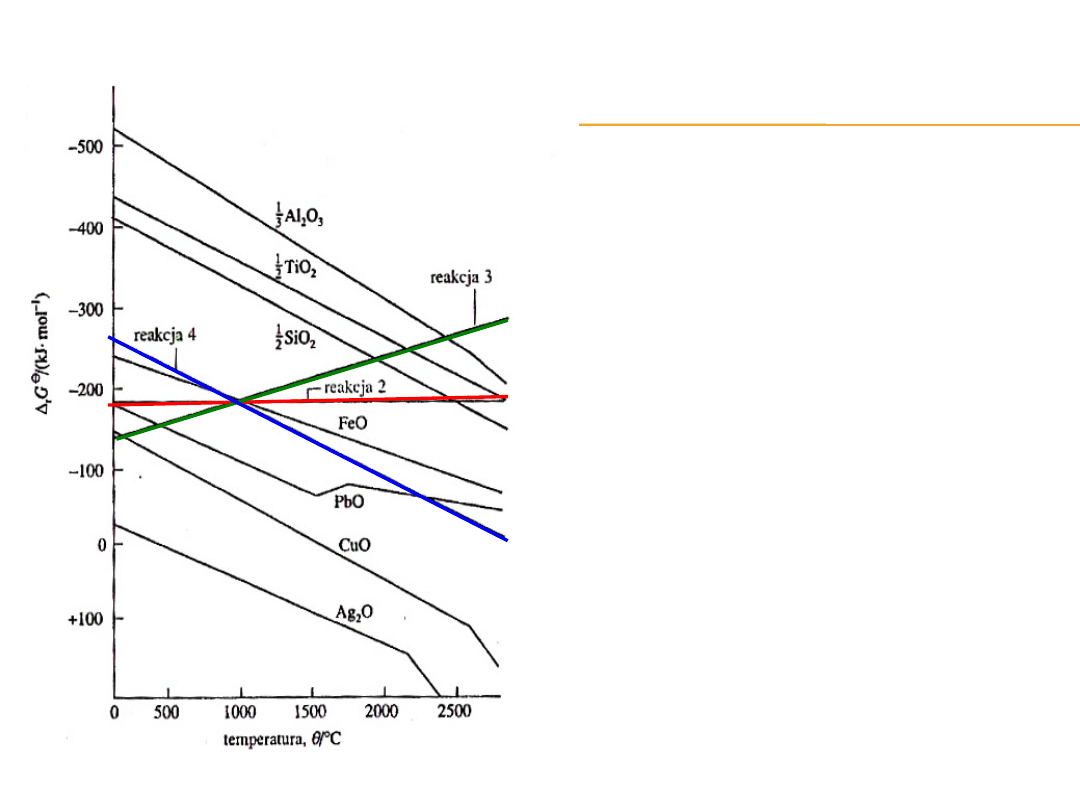
Gdy



r

G

0

< 0

, to równowaga

jest przesunięta w prawo, czyli
w układzie przeważają
produkty nad substratami.
Taki przypadek ma miejsce,
gdy linia odpowiadająca
reakcji:

1. M

(s)

+

1

/

2

O

2(g)

→ MO

(s)

Leży poniżej linii opisującej
jedną z reakcji :

2.

1

/

2

C

(s)

+

1

/

2

O

2(g)

→

1

/

2

CO

(g)

3. C

(s)

+

1

/

2

O

2(g)

→ CO

(g)

4. CO

(g)

+

1

/

2

O

2(g)

→ CO

2 (g)

to znaczy odpowiada bardziej
dodatnim wartościom 

r

G

0

.

29

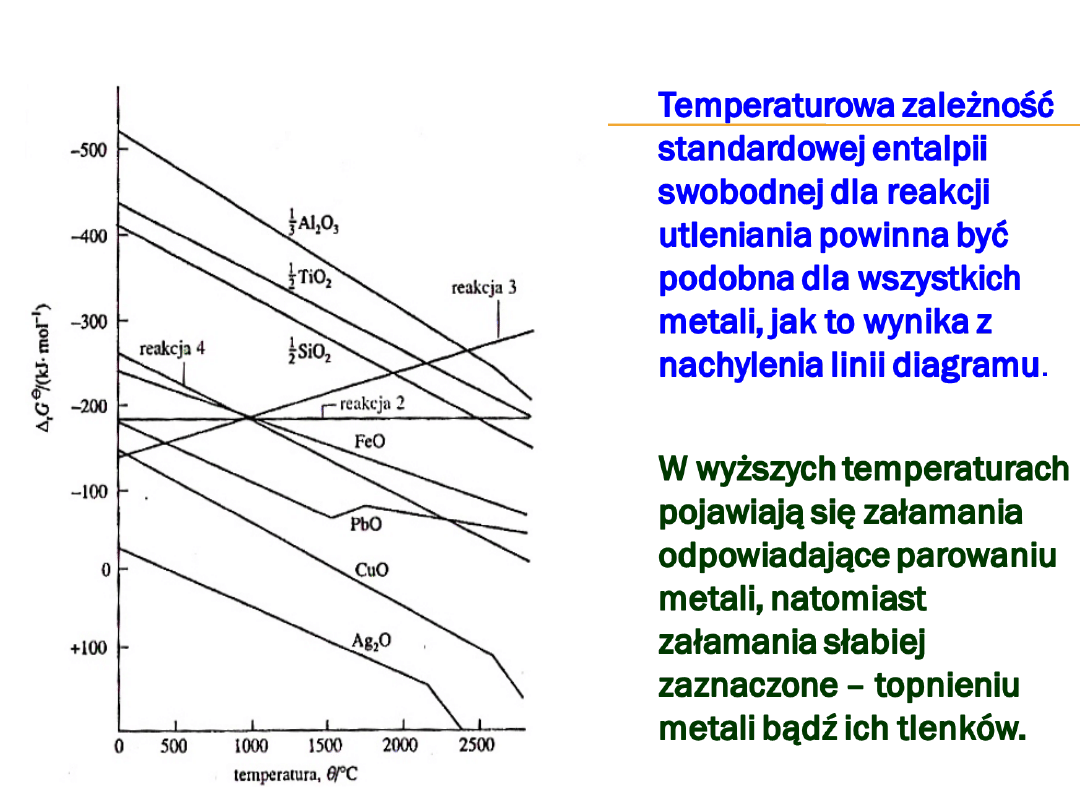
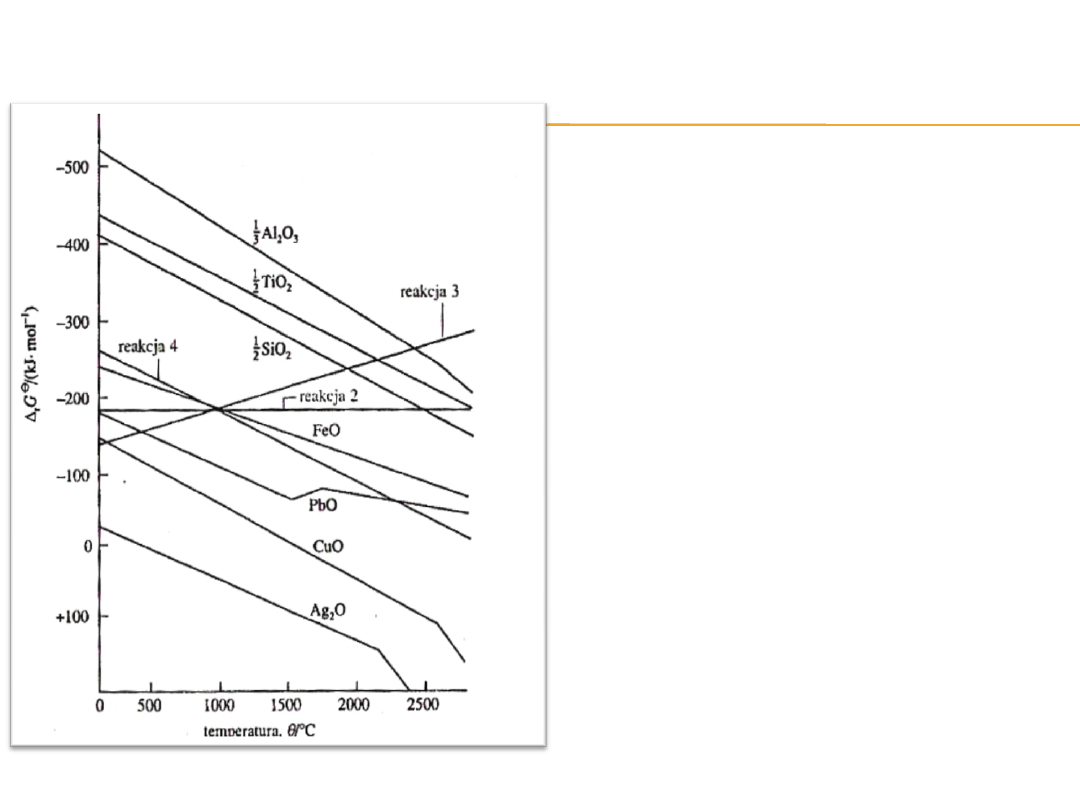
Samorzutność reakcji w dowolnej
temperaturze można przewidzieć
w prosty sposób, korzystając z
diagramu.

 Tlenek metalu można
zredukować
w każdej reakcji z węglem, której
linia



r

G

0

leży powyżej, ponieważ

wówczas
dla sumarycznej reakcji



r

G

0

<

0.

Na przykład CuO można
zredukować do Cu w każdej
temperaturze wyższej od
pokojowej.

 Natomiast Ag

2

O ogrzany

powyżej 200ºC ulega rozkładowi
nawet pod nieobecność węgla,
ponieważ standardowa entalpia
swobodna reakcji (1) staje się
dodatnia,
a więc samorzutny staje się
proces odwrotny.

 Z kolei Al

2

O

3

nie ulega redukcji

węglem zanim temperatura nie
przekroczy 2300ºC.

30

Przebieg reakcji redukcji tlenków metali pod działaniem węgla elementarnego
lub tlenku węgla możemy przewidzieć rozpatrując odpowiednie zmiany entalpii
swobodnej.

Rozpatrzmy w tym celu najpierw następujące reakcje:

Dla każdej z nich możemy obliczyć ∆G⁰ w zależności od temperatury. W
przybliżeniu możemy przyjąć, że wartości ∆H i ∆S nie zależą od temperatury i
zamiast trudniej dostępnymi
danymi odnoszącymi się do dowolnej temperatury, posłużyć się wartościami
∆H⁰

298

i ∆S⁰

298

podanymi przy równaniach (a), (b) i (c).

31

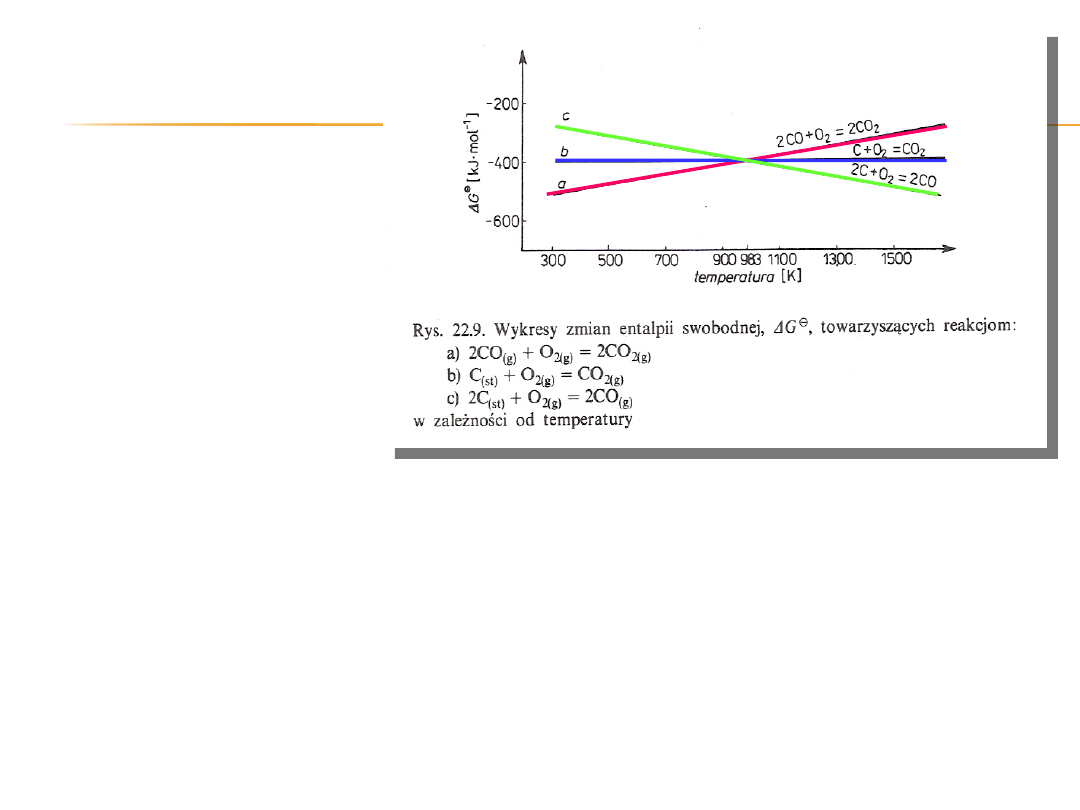
Zależności uzyskanych w ten
sposób przedstawiono
na diagramie.
Zgodnie z równaniem

∆G⁰

T

= ∆H⁰

298

– T∆S⁰

298

mają one przebieg liniowy.

 We wszystkich trzech
przypadkach w zakresie
temperatur 300 – 1500 K
wartość ∆G⁰

T

są ujemne, co oznacza, że reakcje te mogą zachodzić w

sposób samorzutny w warunkach standardowych.

 Niemniej jednak zmiana ∆G towarzysząca reakcji (a) rośnie z temperaturą
i w temperaturach powyżej 3300 K przyjmuje wartości dodatnie, a to
oznacza, że w warunkach standardowych może zachodzić wówczas
samorzutnie tylko reakcja odwrotna czyli rozpad CO

2

na CO i tlen. Wzrost

∆G⁰

T

dla reakcji (a) spowodowany jest ujemną ∆S⁰

298

.

 W przypadku reakcji (b) ∆G⁰

T

nieznacznie zmienia się z temperaturą.

 Reakcji (c) odpowiada dodatnia wartość ∆S⁰

298,

a to pociąga zmniejszenie

się ∆G⁰

T

w miarę wzrostu temperatury.

32

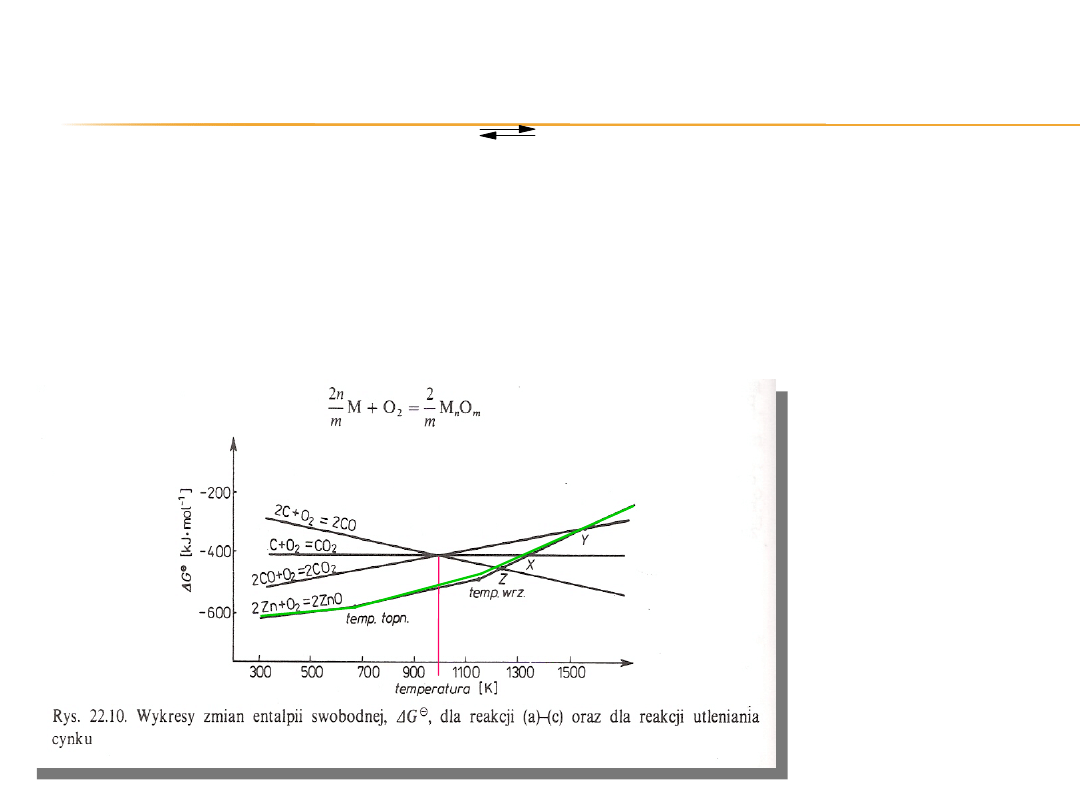
Odejmując równanie reakcji (b) od równania reakcji (c) dochodzimy do
równania wyrażającego tzw. równowagę Boudouarda:

2 CO

(g)

CO

2(g)

+ C

(s)

Wartość ∆G⁰

T

dla tej reakcji stanowi różnicę ∆G⁰

T(c)

i ∆G⁰

T(b)

i wobec tego

możemy
na podstawie poprzedniego diagramu stwierdzić, że w zakresie temperatur
poniżej 983 K
dla powyższej reakcji ∆G⁰

T

> 0 oraz w zakresie temperatur powyżej 983 K

∆G⁰

T

< 0.

Oznacza to, że w wyższych temperaturach w równowadze przeważać
będzie CO,
a w niższych CO

2 .

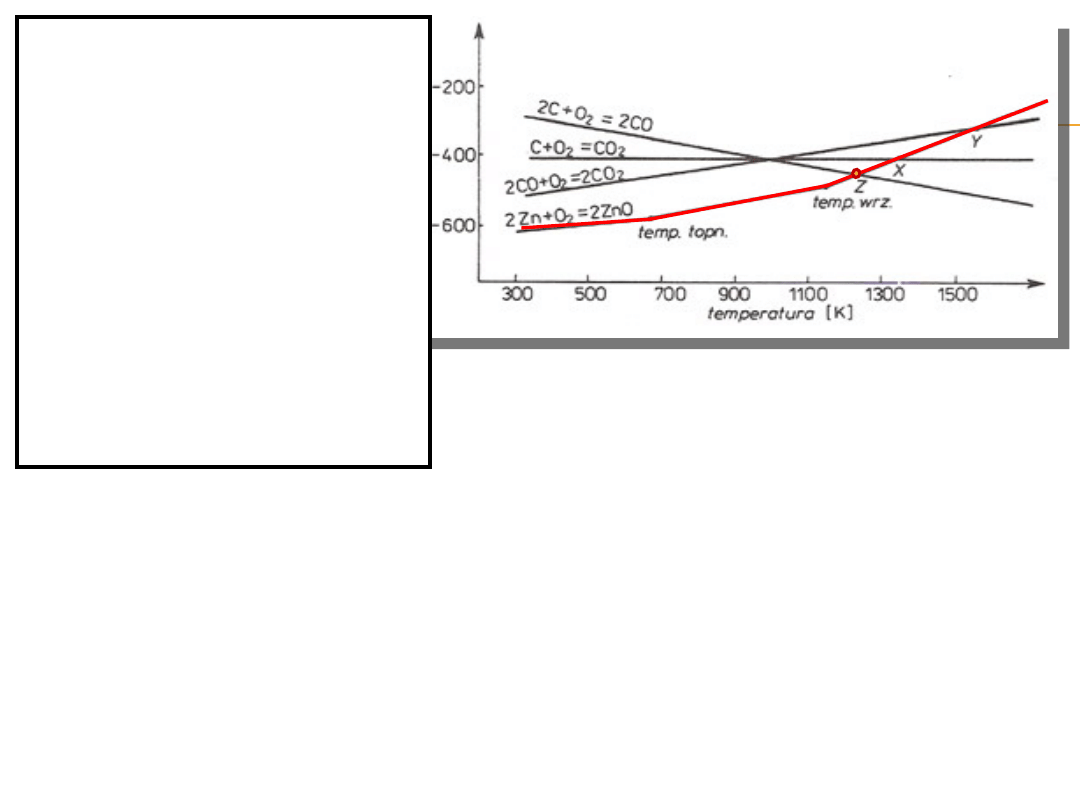
Na poniższym diagramie dodano linię ∆G⁰

T

(T) dla reakcji

tworzenia się tlenku cynku w reakcji typu:

Załamania linii
prostej następują w
punktach
odpowiadających
temperaturze
topnienia
i wrzenia metalu
(lub tlenku).
Wewszystkich
przypadkach wraz
ze wzrostem
temperatury
wartość ∆G⁰

T(M)

rośnie.

CO

CO

2

33

Biorąc pod uwagę punkt Z,
w którym to przecinają
się wykresy odpowiadające
reakcjom:
2 Zn + O

2

= 2 ZnO (e)

2 C + O

2

= 2 CO (c)

W punkcie tym ∆G⁰

T

dla reakcji

2 ZnO + 2 C = 2 Zn + 2 CO (f)
wynosi 0.

 W temperaturze odpowiadającej punktowi Z mamy do
czynienia z równowagą
pomiędzy stałym węglem, ciekłym cynkiem, stałym tlenkiem
cynku oraz gazowym
tlenkiem węgla pod ciśnieniem 1 atm.

 W temperaturach wyższych ∆G⁰

T

przyjmuje wartości ujemne, co

oznacza,
że następuje redukcja ZnO węglem w obecności tlenku węgla pod
ciśnieniem atmosferycznym.

 W temperaturach niższych od temperatury odpowiadającej
punktowi Z reakcja
taka nie może zachodzić samorzutnie.

 Samorzutnie może zajść reakcja odwrotna do reakcji (f), czyli
utleniania cynku
przez CO z wydzieleniem węgla.

Z

Reakcja redukcji ZnO

węglem:

ZnO + C  CO + Zn

ΔG

0

tw

= ΔG

0

tw

(CO) + ΔG

0

tw

(Zn) - ΔG

0

tw

(C) - ΔG

0

tw

(ZnO)

< 0

ΔG

0

tw

(CO) - ΔG

0

tw

(ZnO)

<

0

ΔG

0

tw

(CO)

<

ΔG

0

tw

(ZnO)

34

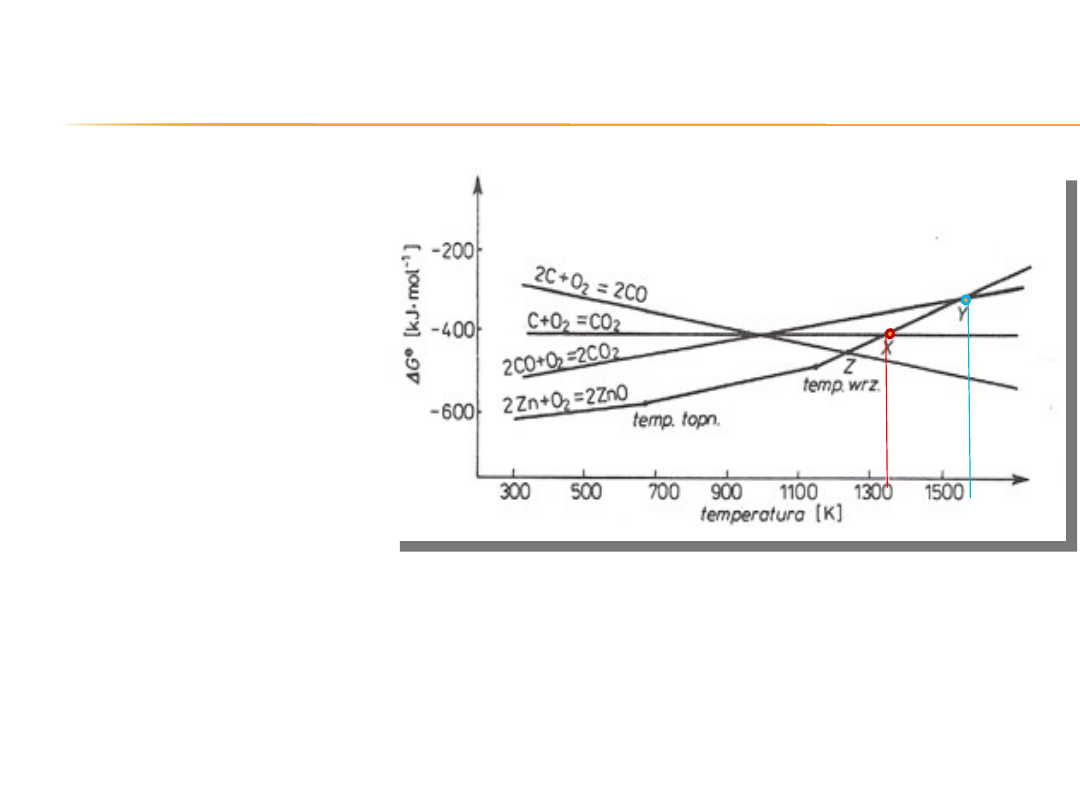
 Analogicznie możemy wykazać,
że powyżej temperatury dla
punktu X może nastąpić
redukcja ZnO węglem
z utworzeniem CO

2

.

2 ZnO + C = 2 Zn + CO

2

 Ponad to w temperaturze
wyższej od temperatury
wyznaczonej przez punkt Y
możliwa staje się redukcja ZnO przez CO.

2 ZnO + 2 CO = 2 Zn + 2 CO

2

X

Y

Y

35

M

1

O + M

2

M

2

O + M

1

ΔG

0

tw

= ΔG

0

tw

(M

2

O) + ΔG

0

tw

(M

1

) - ΔG

0

tw

(M

1

O) -

ΔG

0

tw

(M

2

)

< 0

ΔG

0

tw

(M

2

O) - ΔG

0

tw

(M

1

O)

< 0

ΔG

0

tw

(M

2

O)

<

ΔG

0

tw

(M

1

O)

36

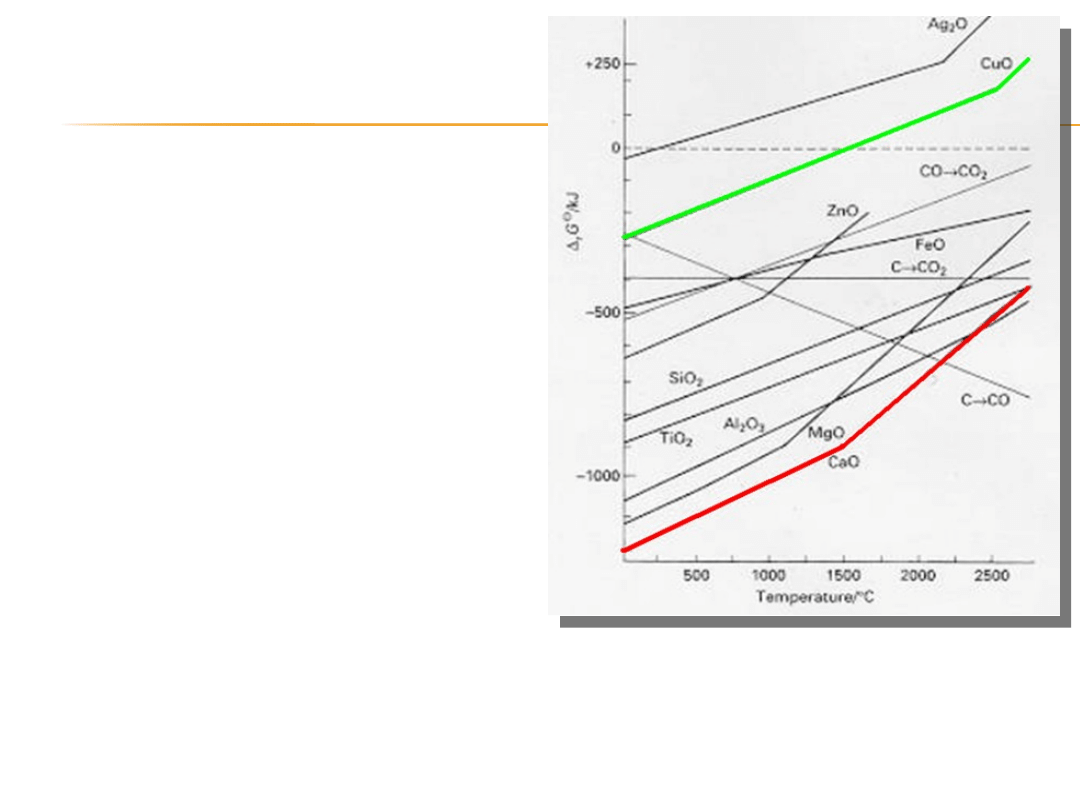
 Z diagramu Ellinghama
można odczytać, który
pierwiastek zredukuje dany
tlenek.
Okazuje się że pierwiastkiem
tworzącym najtrwalsze tlenki
jest wapń. Redukuje on takie
tlenki jak:
FeO, ZnO, CuO, SiO

2

 Przykładowa reakcja przedstawia
się następująco:

CuO + Ca CaO + Cu

ΔG

0

tw

= ΔG

0

tw

(CaO) + ΔG

0

tw

(Cu) – ΔG

0

tw

(Ca) – ΔG

0

tw

(CuO)

< 0

ΔG

0

tw

(CaO) – ΔG

0

tw

(CuO)

< 0

ΔG

0

tw

(CaO)

<

ΔG

0

tw

(CuO)

 Po naniesieniu na jeden wykres
zależności dla różnych tlenków
możemy porównywać ich trwałość.
Tlenki dla których linie leżą niżej na
wykresie są bardziej stabilne.

37

1.

„ Chemia fizyczna” P.W. Atkins, Wydawnictwo Naukowe PWN

2.

„ Podstawy chemii nieorganicznej” A. Bielański, Wydawnictwo
Naukowe PWN

3.

Internet:

http://www.doitpoms.ac.uk/tlplib/ellingham_diagrams/thermodynamics.php

http://www.engr.sjsu.edu/ellingham/tutorial.html

BIBLIOGRAFIA:

BIBLIOGRAFIA:

38