Ćwiczenia

WARTOŚĆ PIENIĄDZA W CZASIE

Wartość pieniądza w czasie

Mówimy zwykle o zmiennej wartości pieniądza w czasie. 

Wynika ona z działania czterech czynnikiów:

1.

Spadku siły nabywczej

2.

Możliwości zainwestowania

3.

Występowanie ryzyka

4.

Preferowanie bieżącej konsumpcji

Wartość pieniądza w czasie

Przy określaniu (i podawaniu do publicznej wiadomości) 

stopy procentowej są istotne pewne kwestie 

formalnometodyczne, o których trzeba pamiętać, a 

mianowicie:

1.

Stopa procentowa w skali okresu

2.

Stopa procentowa dotycząca okresu

3.

Kapitalizacja i reinwestycja

Wartość pieniądza w czasie

Wartość przyszła (FV) i wartość bieżąca (PV)

Renta (annuity) – to płatność występująca w stałych 

okresach, np. ta sama kwota płacona co miesiąc. 

Renta (annuity) – to płatność występująca w 

stałych okresach, np. ta sama kwota płacona co 

miesiąc. 

Wartość pieniądza w czasie – wart0ść 
przyszła

)

1

(

nr

PV

FV





Wartość przyszła – kapitalizacja 
prosta (zgodna z okresem inwestycji)

n

r

PV

FV

)

1

( 



Wartość przyszła – kapitalizacja 
roczna

nm

m

r

PV

FV











 



1

Wartość przyszła – kapitalizacja 
złożona

nr

PVe

FV 

Wartość przyszła – kapitalizacja ciągła

Wartość pieniądza w czasie – wart0ść 

bieżąca (teraźniejsza, obecna, present value)

)

1

(

nr

FV

PV





Wartość bieżąca – kapitalizacja prosta 
(zgodna z okresem inwestycji)

n

r

FV

PV

)

1

( 



Wartość bieżąca– kapitalizacja roczna

nm

m

r

PV

FV











 



1

Wartość bieżąca – kapitalizacja 
złożona

nr

PVe

FV 

Wartość bieżąca – kapitalizacja ciągła

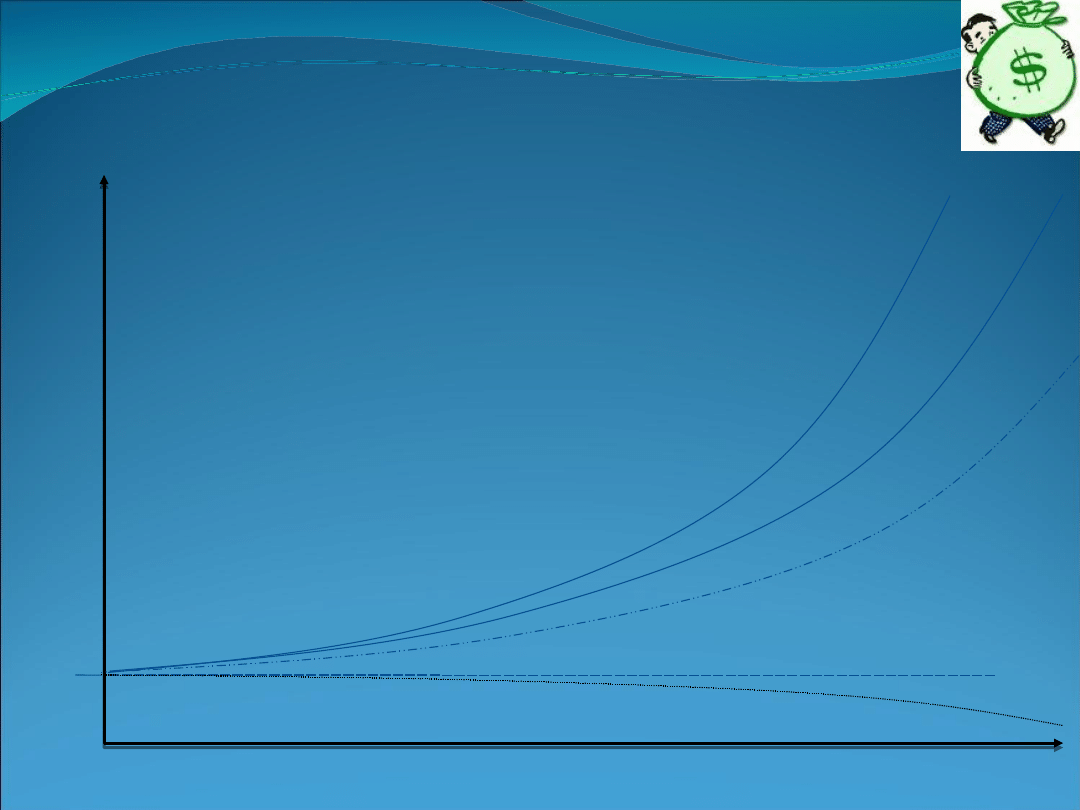
Wart0ść przyszła jako funkcja liczby 
okresów

PV

n 
okresów

FV

A

B

C

D

E

A – kapitalizacja ciągła, r >0,
B – kapitalizacja roczna, r>0,
C – kapitalizacja prosta, r>0,
D  –  dowolna  kapitalizacja, 
r=0,
E – kapitalizacja roczna, r<0. 

Wartość pieniądza w czasie

+

+

_

_

Strona długa

Strona krotka

Wartość pieniądza w czasie – schemat renty 
płatnej z dołu

Ze schematem renty płatnej z dołu mamy do 

czynienia wtedy, kiedy występują równe przepływy 

pieniężne na końcu każdego podokresu (o równej 

długości); na końcu lub na początku każdego 

podokresu.

Wartość pieniądza w czasie – schemat renty 
płatnej z dołu

Określona suma jest regularnie inwestowana co pewien okres (na 

końcu każdego podokresu), zwiększając dochody:

…

Wartość pieniądza w czasie – schemat renty płatnej 
z dołu

…

Lub pewna suma jest pożyczana (na końcu każdego podokresu), 

zwiększając zadłużenie:

Wartość pieniądza w czasie – schemat renty płatnej 
z góry

Występuje wówczas wtedy, kiedy następują równe przepływy  na 

początku każdego podokresu, na które to podokresy (o równej 

długości) jest podzielony cały okres, a na początku lub na końcu 

całego okresu występuje jeden przepływ pieniężny (ma on odwrotny 

znak niż te pozostałe przepływy).

 Są tu następujące możliwości:

Wartość pieniądza w czasie – schemat renty płatnej 
z góry

Określona suma jest regularnie inwestowana co pewien okres (na 

początku każdego podokresu), zwiększając dochody:

…

Wartość pieniądza w czasie – schemat renty płatnej 
z góry

…

Lub pewna suma jest pożyczana regularnie co pewien okres (na 

początku każdego podokresu):

Wartość pieniądza w czasie – schemat renty płatnej 
z góry przypadek 2

Na początku jest pożyczana pewna suma, która jest następnie 

spłacana w równych ratach na początku każdego podokresu:

…

Lub na początku jest inwestowana pewna suma, która następnie 

przynosi regularne równe płatności na początku każdego podokresu:

Wartość pieniądza w czasie – schemat renty płatnej 
z góry przypadek 2

…

Stopa procentowa i stopa zwrotu a wartość 
przyszła

Z wartością przyszłą niedłącznie wiąże się zagadnienie tzw. 

efektywnej stopy zwrotu (effective interest rate). 

W najprostszym ujęciu efektywna stopa procentowa jest to stopa 

uwzględniająca kapitalizację.

1

1













 



m

ef

m

r

r

1





r

ef

e

r

Kapitalizacja częstsza niż raz w 
roku

Kapitalizacja ciągła

EFEKTYWNA STOPA PROCENTOWA

Stopa procentowa i stopa zwrotu a wartość 
przyszła

Z wartością przyszłą niedłącznie wiąże się zagadnienie tzw. 

efektywnej stopy zwrotu (effective interest rate). 

W najprostszym ujęciu efektywna stopa procentowa jest to stopa 

uwzględniająca kapitalizację.

1

1













 



m

ef

m

r

r

1





r

ef

e

r

Kapitalizacja częstsza niż raz w 
roku

Kapitalizacja ciągła

EFEKTYWNA STOPA PROCENTOWA

Stopa zwrotu – skończony okres inwestycji

W poprzednio przedstawionych wzorach stopa procentowa była 

znana, teraz rozpatrujemy zagadnienie odwrotne, czyli wyznaczamy 

nieznaną stopę procentową.

Przy obliczaniu wartości bieżącej przyjmowana stopa procentowa 

nazywana jest wymaganą stopą zwrotu z alternatywnych 

inwestycji.

Stopa zwrotu jest szczególnym przypadkiem pojęcia stopa 

procentowa

Brak  przepływów  pieniężnych  w  okresie  trwania 
inwestycji

Stopa zwrotu – skończony okres inwestycji

Zainwestowana kwota pieniężna przynosi wartość na koniec okresu. 

Jest to zatem standardowe zagadnienie, w którym są znane: 

•

   wartość bieżąca,

•

   wartość przyszła,

•

  okres trwania inwestycji

Brak  przepływów  pieniężnych  w  okresie  trwania 
inwestycji

Stopa zwrotu – skończony okres inwestycji

W praktyce rozważa się trzy możliwości: kapitalizację prostą (prosta 

stopa zwrotu), kapitalizację roczną (efektywna stopa zwrotu) i 

kapitalizację ciągłą (logarytmiczna stopa zwrotu.

Stopa zwrotu jako dochód z inwestycji (iloraz 

















1

1

PV

FV

n

r

1

1

















n

PV

FV

r















PV

FV

n

r

ln

1

•

  Logarytmiczna stopa zwrotu jest najniższa spośród 

tych stóp, gdyż zakłada „najbardziej rygorystyczną 
kapitalizację ciągłą

•

  prosta stopa zwrotu jest wyższa od efektywnej stopy 

zwrotu, gdy horyzont inwestycji jest dłuższy niż rok, a 
niższa, gdy horyzont inwestycji jest krótszy niż rok

•

  w przypadku rocznego horyzontu inwestycji prosta 

stopa zwrotu i efektywna stopa zwrotu są sobie równe.

Stopa terminowa

Stopa procentowa spot (natychmiastowa) – jest to stopa 

procentowa obowiązująca od danego momentu przez okres, którego 

dotyczy.

Stopa procentowa forward (terminowa) jest to stopa 
procentowa obowiązująca od pewnego momentu w 
przeszłości przez okres, którego dotyczy