PODSTAWY TEORII STANU NAPRĘŻENIA

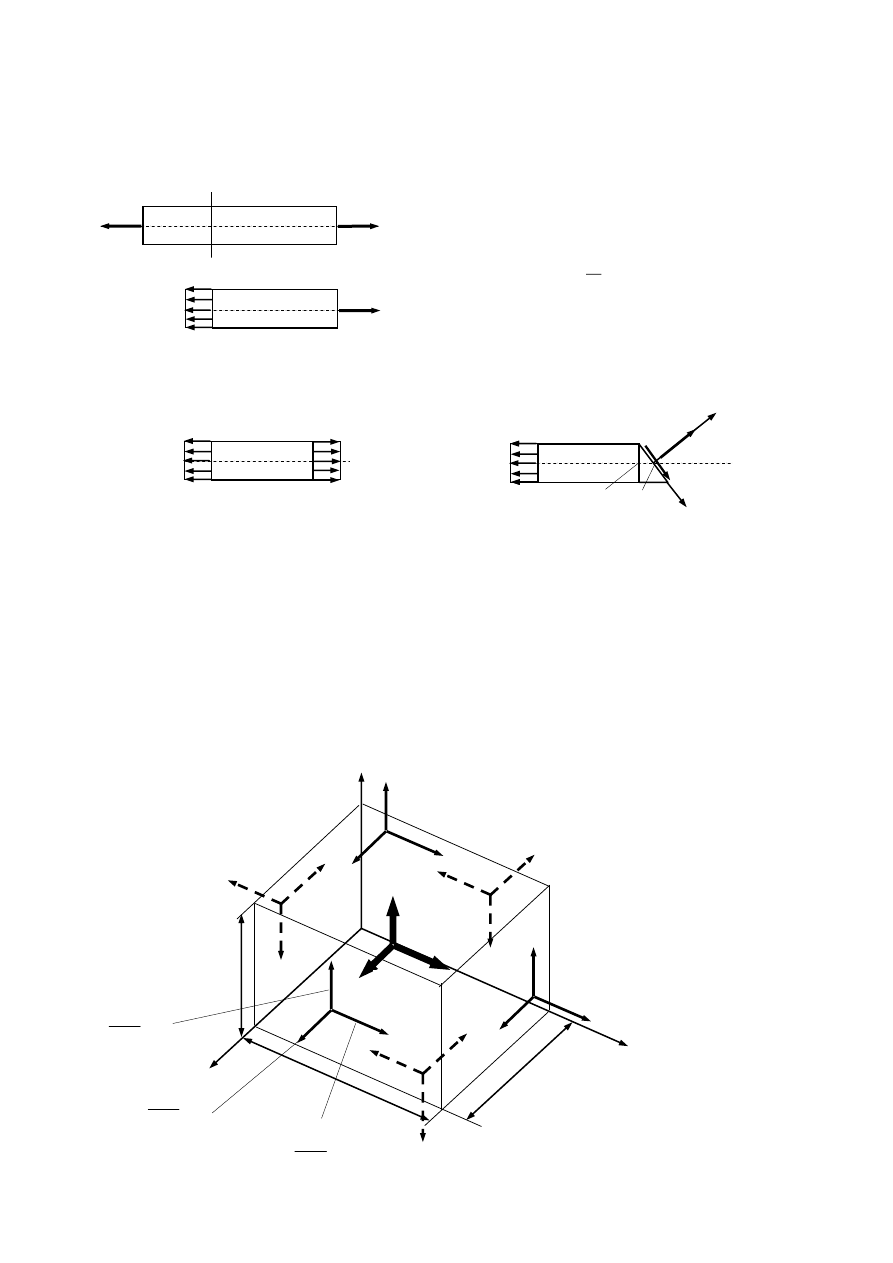
1. Stan naprężenia przy jednoosiowym rozciąganiu (stan jednorodny)

Przez każdy punkt pręta można przeprowadzić nieskończoną liczbę przekrojów pod różnymi
kątami do jego osi i każdemu przekrojowi odpowiada inne naprężenie.

W przekroju prostopadłym

A

P

x





Wytnijmy z pręta element dwoma przekrojami prostopadłymi i przetnijmy go pod kątem



do

przekroju prostopadłego.






Ułóżmy równania równowagi:



P

n

=





A -



x

A cos



cos



= 0







=



x

cos

2





P

t

=





A -



x

A cos



sin



= 0







=



x

sin



cos



= ½



x

sin2









max





= 0







=



x







max





= 45







= ½



x

2. Równania równowagi wewnętrznej

W przypadku niejednorodnego stanu naprężenia, wartości składowych naprężeń zmieniają
si

ę ze zmiana położenia.

Rozpatrzmy prostopadłościan o krawędziach dx, dy, dz będący w równowadze

Znaki naprężeń:



-

rozciągające ( + )

ściskające ( – )



xy

– x –wskazuje oś



y -

wskazuje oś II

X, Y, Z

– siły masowe



x

,



xy

,



xz

– naprężenia na

ściance



do osi x

naprężenia na ściance przesuniętej o dx.

P

P

B

B

P



x



x



x



x



x









t

Aco

s



A

n

dz

dx

dy

z

x

y

X

Y

Z



x



y



z



xy



xz



zx



zy



yz



yx

dx

x

xz

xz











dx

x

x

x











dx

x

xy

xy











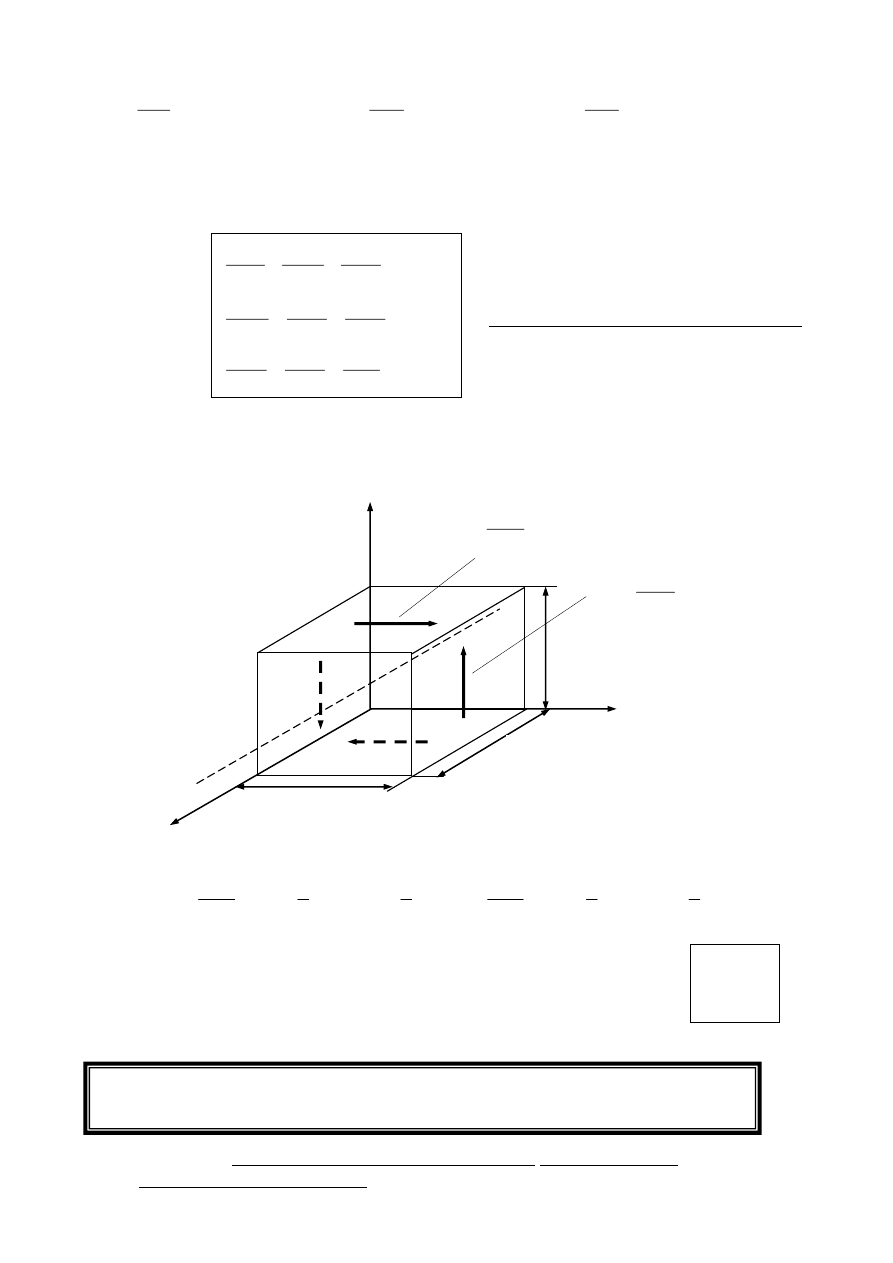
Pisząc równania równowagi (sumy rzutów wszystkich sił na poszczególne osie)

0

)

(

)

(

)

(



































Xdxdydz

dxdy

dxdy

dz

z

dxdz

dydz

dx

y

dydz

dydz

dx

x

X

zx

zx

zx

yx

yz

yz

x

x

x



















podobnie





0

Y

i





0

Z

po uporządkowaniu i uproszczeniu otrzymamy układ równań:

0





















X

z

y

x

zx

yx

x







0





















Y

z

y

x

zy

y

xy







są to równania równowagi wewnętrznej

0





















Z

z

y

x

z

zx

xz







3. Twierdzenie o wzajemności naprężeń stycznych

Wykorzystamy pozostałe równania równowagi – równania momentów

0

2

1

2

1

)

(

2

1

2

1

)

(

'

























dz

dxdy

dz

dxdy

dz

z

dy

dzdx

dy

dxdz

dy

y

M

zy

zy

zy

yz

yz

yz

x













po uproszczeniu i pominięciu wyrażeń małych wyższego rzędu otrzymamy:



yz

=



zy

z pozostałych równań momentów mamy



xz

=



zx



yx

=



xy

słownie tzw. aksjomat Boltzmanna brzmi:

„Składowe naprężeń stycznych prostopadłe do krawędzi przecięcia się dwóch
przekrojów elementarnych wzajemnie prostopadłych są zawsze równe”

Mamy zatem w

układzie przestrzennym 6 składowych stanu naprężenia,

a w

układzie płaskim 3 składowe -



x

,



y

i



xy

=



yx

z

y

x’

x

dy

dx

dz



zy



yz

dz

z

zy

zy











dy

y

yz

yz











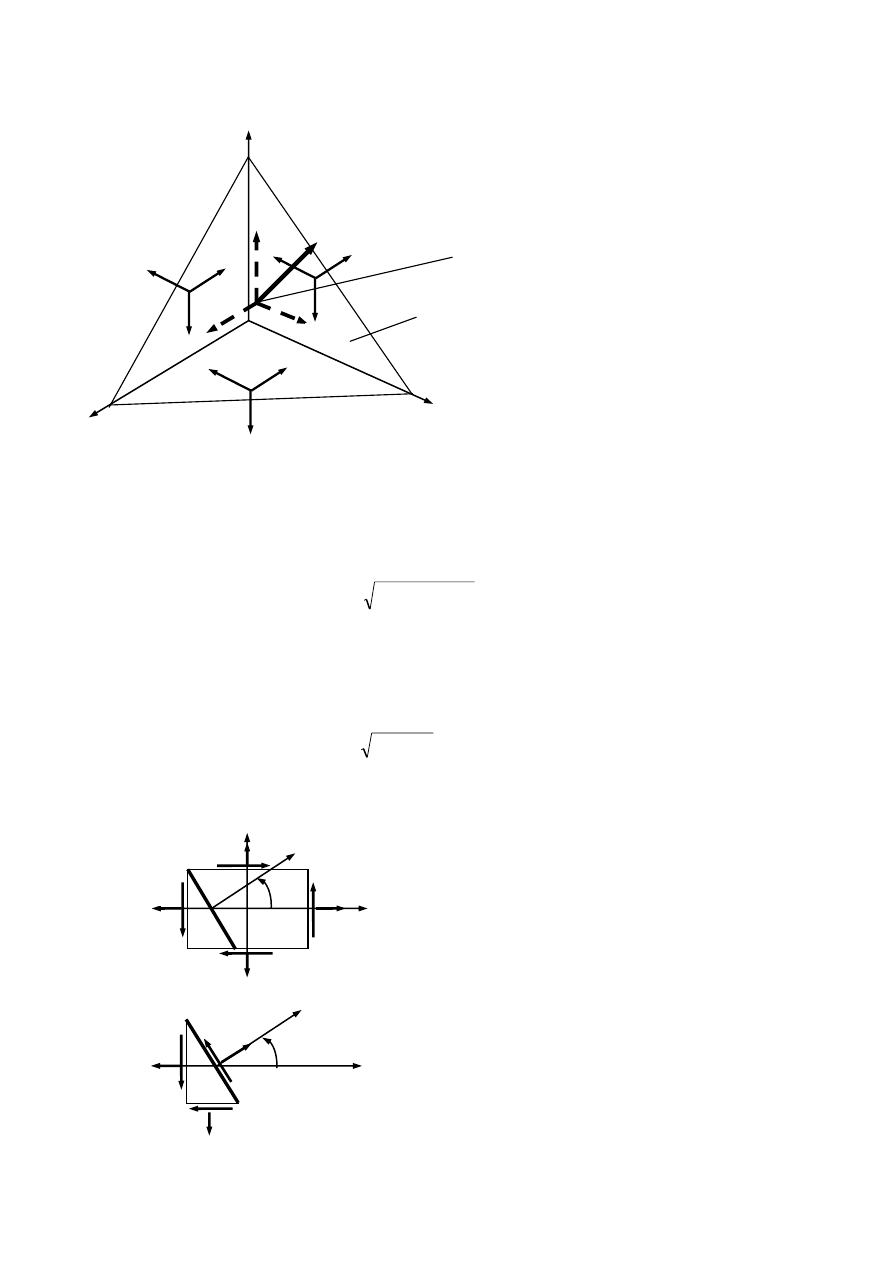
4. Warunki powierzchniowe

– naprężenia w punkcie zależnie od orientacji przekroju.

Rozpatrzmy równowagę czworościanu pod wpływem sił powierzchniowych.

Znamy w punkcie 0 naprężenia w
trzech wzajemnie prostopadłych
przekrojach.

Chcemy wyznaczyć naprężenia w
tym punkcie w przekroju o kierunku
określonym osią normalną o
cosinusach kierunkowych:

l = cos(



x), m = cos(



y), n = cos(



z),

Z sumy rzutów otrzymamy;















0

dA

p

dA

dA

dA

Y

y

z

zy

x

xy

y

y







podobnie:









0

0

X

i

Z

p

x

=



x

l +



yx

m +



zx

n

p

y

=



xy

l +



y

m +



zy

n

p

z

=



xz

l +



yz

m +



z

n

Całkowite naprężenie:

2

2

2

z

y

x

p

p

p

p







Naprężenie normalne

n

p

m

p

l

p

z

y

x









a po rozwinięciu i uporządkowaniu i wykorzystaniu postulatu Boltzmanna:

nl

mn

lm

n

m

l

zx

yz

xy

z

y

x















2

2

2

2

2

2













naprężenie styczne

2

2









p

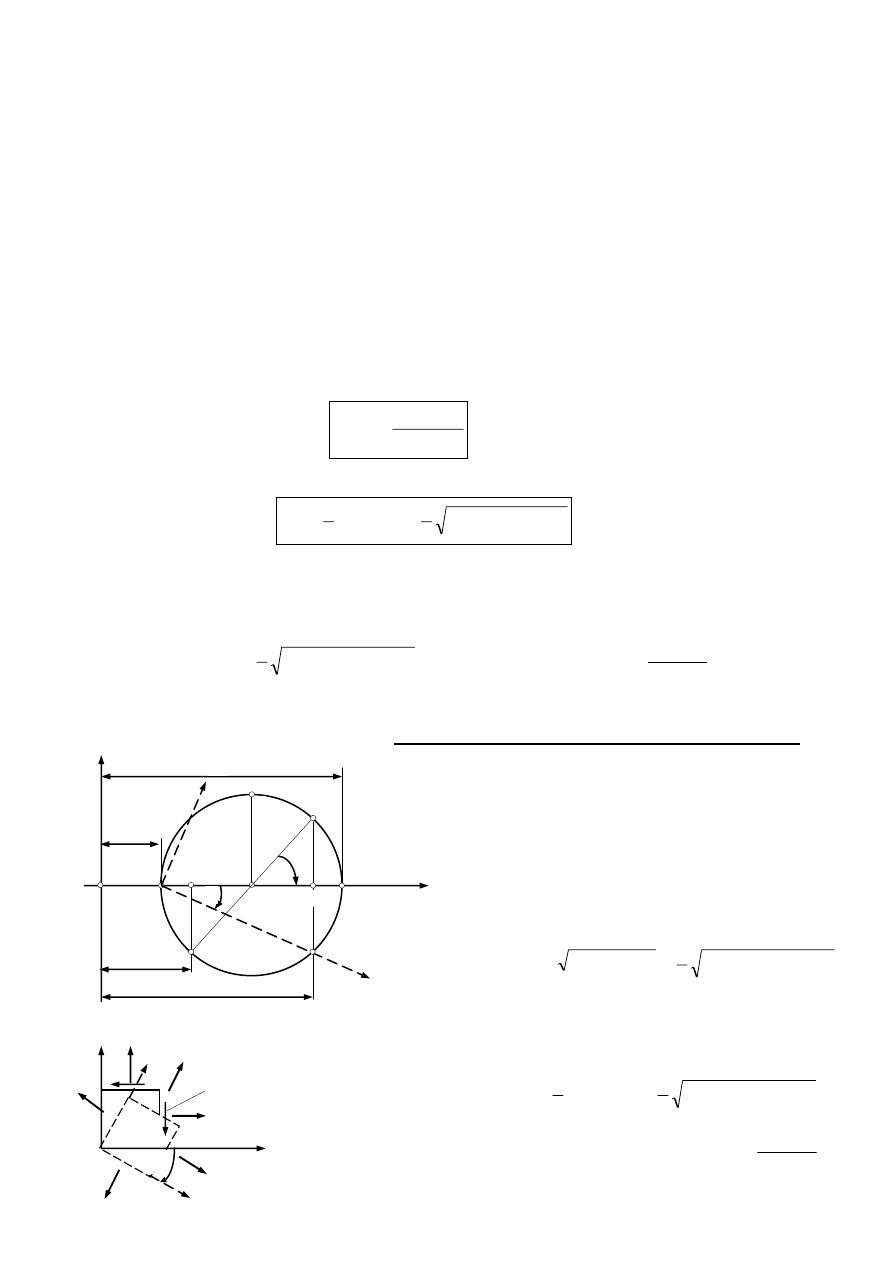
Transformacja składowych płaskiego stanu naprężenia

Rozpatrzmy cienką płaska tarczę poddaną działaniu naprężeń:



x

,



y

i



xy

=



yx

.

Przyjmijmy grubość tarczy równą 1.
Poprowadźmy myślowy przekrój pod
kątem



do kierunku osi x.

Niech powierzchnia przekroju wynosi A



zatem

A

x

= A



cos



; A

y

= A



sin



;

Odrzućmy część prawą i rozpatrzmy
równowagę pozostałej (lewej) części elementu.



F



=





A -



x

A



cos



cos



-



y

A



sin



sin



-



xy

A



cos



sin



-



xy

A



sin



cos



= 0



F



+90

=





A +



x

A



cos



sin



-



y

A



sin



cos



+



xy

A



sin



sin



-



xy

A



cos



cos



= 0

dA

y

x

z





x



xy

P

P

z

P

y

P

x

0



yx



yz



zy



zx



y



z



xz

x

x

n
]
n

n
]
n



x



xy



x



xy



yx

y
]
n



y



y







xy



x



yx



y









po uporządkowaniu otrzymamy:





=



x

cos

2



+



y

sin

2



+ 2



xy

sin



cos







= - (



x

-



y

) sin



cos



+



xy

(cos

2



- sin

2



)

lub po wprowadzeniu kąta podwójnego 2



:





= ½(



x

+



y

) + ½(



x

-



y

) cos2



+



xy

sin2







=



x

cos

2



+



y

sin

2



+



xy

sin2



wzory transformacyjne





= -

½ (



x

-



y

) sin2



+



xy

cos2



:

- Naprężenia główne – ekstremalne wartości naprężeń normalnych dla których



= 0,

- Płaszczyzny główne – płaszczyzny na których działają naprężenia główne,

- Osie główne (kierunki główne) – normalne do płaszczyzn głównych

Położenie kierunków głównych wyznaczymy z





= 0 lub z d





/d



=0

)

(

2

2

tg

y

x

xy

















1

i



1

+90



a ich wartość ze wzoru

2

2

2

,

1

4

)

(

2

1

)

(

2

1

xy

y

x

y

x

























1

=



max

,



2

=



min

,

(



3

= o)

Ekstremalne naprężenia styczne występują w przekrojach obróconych względem
przekrojów głównych o kąt 45



, a ich wartość wynosi:

2

2

min

max,

4

)

(

2

1

xy

y

x

















lub

2

2

1

max











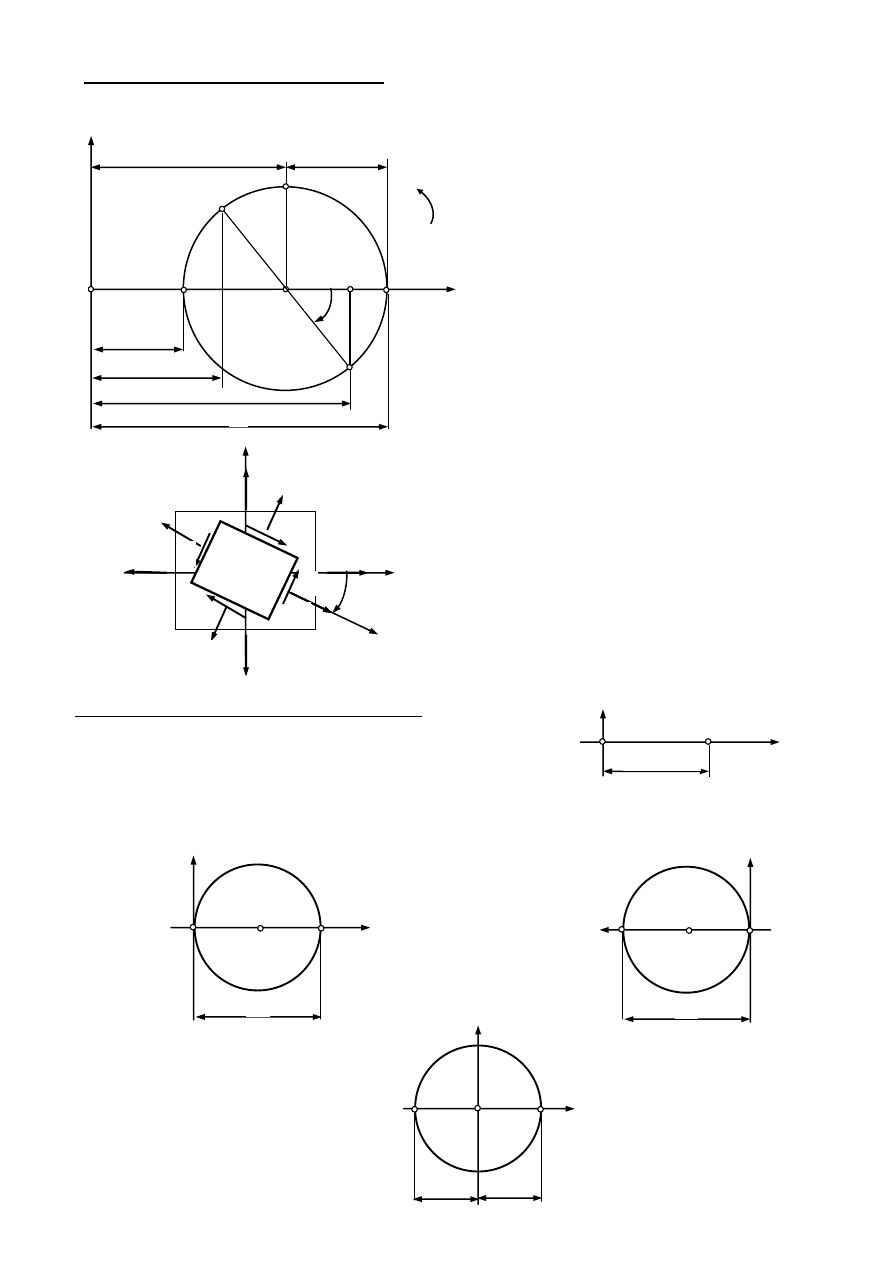
Koło Mohra i jego zastosowanie do transformacji składowych płaskiego stanu naprężenia

I. Dane



x

,



y

i



xy

,



x

>



y

,



xy

>0,

-

szukamy kierunków głównych i naprężeń głównych

1. Rysujemy osie



i



.

2.

Na osi poziomej odkładamy:



x

= 0A,



y

= 0B,

3.

Wyznaczamy środek koła:
0S = ½(0A+0B) = ½(



x

+



y

)

4. Zaznaczamy odcinek AC=



xy

5.

Promieniem SC kreślimy koło

2

2

2

2

4

)

(

2

1

xy

y

x

AC

SA

SC

















6.

Kierunki główne określa kąt 2



0

zawarty

między osią



a SC.

7.

Naprężenie główne



1

=0S+SF

2

2

1

4

)

(

2

1

)

(

2

1

xy

y

x

y

x

























2

=0S

–SE

2

2

1

max













SG







y



x



2

1

2



xy



max



2



0

E

B

S

A

C

G

F



1



xy

x

y



2



2

1

2



1



1



x



y



0

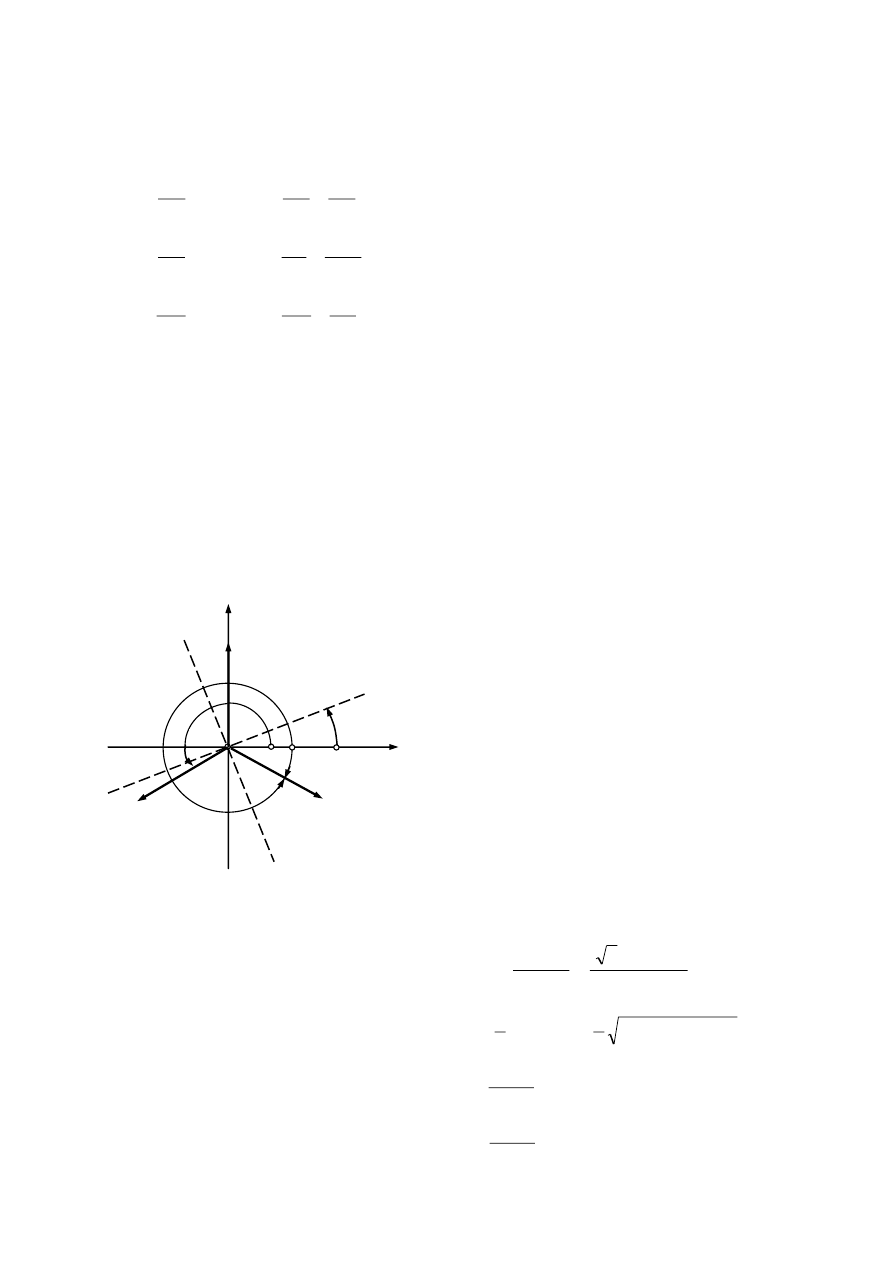
II. Transformacja z kie

runków głównych.

Dane



1

>



2

> 0, oraz ich położenie - szukamy naprężeń w dowolnym przekroju



.

Odkładamy



1

= 0A,



2

= 0B

Znajdujemy środek koła:

0S = ½(



1

+



2

)

i promieniem

SA = ½(



1

-



2

)

kreślimy koło.

Odmierzamy od promienia SA kąt 2



i ze

środka S prowadzimy prostą do

przecięcia się z kołem (D).

Przykłady szczególnych stanów naprężenia

1.

Równomierne rozciąganie



1

=



2

=



3

>0

2.

Płaskie równomierne rozciąganie



1

=



2

> 0



3

=0

3.

Jednoosiowe rozciąganie (ściskanie)

4.

Płaskie ścinanie



1

= -



2





2





+90







1

A

R
T

P

S

B

0







½(



1

+



2

)

½(



1

-



2

)

-2



+



-



2





+90



1

1



1



1



2



2









+90













+90









+90



S





1

=



2

=



3



S





1



S





2



1

>0



2

=0



1

=0



2

<0





S



2



1

PODSTAWY TEORII STANU ODKSZTAŁCENIA

Warunki geometryczne

– związki przemieszczeń i odkształceń.

Jeżeli przez u, v, w oznaczymy składowe przemieszczenia dowolnego punktu w kierunkach osi
x, y, z, to



,



-

składowe stanu odkształcenia wynoszą:

x

v

y

u

x

u

xy

x

























-

wydłużenie właściwe

xy

vw

z

v

y

v

yz

y

























-

odkształcenie poprzeczne

z

u

x

w

z

w

zx

z























(kąt odkształcenia postaciowego)

Transformacja składowych płaskiego stanu odkształcenia

Zależności opisujące transformacje odkształceń mają taką samą postać jak zależności
opisujące transformację naprężeń, jeżeli dokona się zamiany wielkości:











½



Przykład Stan określono trzema wydłużeniami



a

,



b

,



c

na powier

zchni ciała mierzonymi w

kierunkach trzech osi a, b, c, nachylonych wzajemnie pod kątem ⅔



. Wyznaczyć

składowe stanu odkształcenia



x

,



y

,



xy

w prostokątnym układzie osi x, y (y=a),

kierunki główne i odkształcenia główne, a także wartości naprężeń głównych



1

,



2

.



a

=



y



c

= ½(



x

+



y

)+½(



x

-



y

)cos2 210°+½



xy

sin2 210°



b

= ½(



x

+



y

)+½(



x

-



y

)cos2(-

30°)+½



xy

sin2(-

30°)

cos420°=cos(2



+60°)=½

sin420°=sin(2



+60°)=√3/2

cos(-

60°)= cos(60°)=½

sin(-

60°)= -sin(60°)=-√3/2



c

= ½(



x

+



y

) + ½(



x

-



y

) ½ + ½



xy

√3/2



b

= ½(



x

+



y

) + ½(



x

-



y

) ½ - ½



xy

√3/2



x

= ⅓(-



a

+2



b

+2



c



xy

= ⅔√3(



c

-



b

)

położenie kierunków głównych

c

b

a

c

b

y

x

xy

tg































2

)

(

3

2

0

odkształcenia główne

2

2

2

,

1

)

(

2

1

)

(

2

1

xy

y

x

y

x























naprężenia główne

)

(

1

2

1

2

1

 













E

)

(

1

1

2

2

2

 













E

kier. główne

y

x

a

b

c

210



330



-30



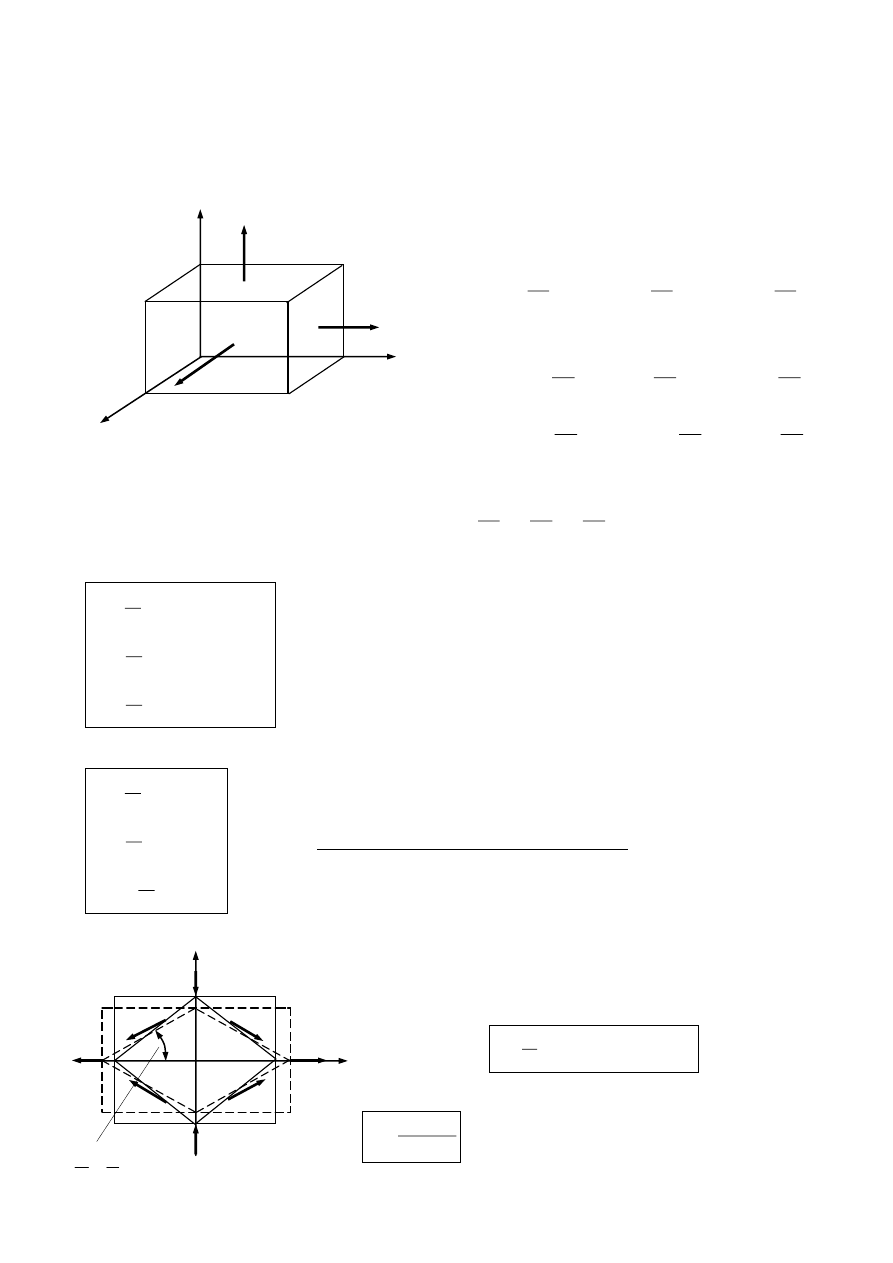
Uogólnione prawo Hooke’a – określa związki miedzy składowymi stanu naprężenia i stanu

odkształcenia dla dowolnego przestrzennego stanu.

Rozpatrzmy jednostkowy sześcian na który działają naprężenia główne



1

,



2

,



3

.

Korzystając z zasady superpozycji rozkładamy
ten stan na trzy stany proste.

Gdy działa tylko



1

(



2

=



3

=0) to odkształcenia:

E

E

E

1

'

3

1

'

2

1

'

1

;

;



























podobnie:

E

E

E

2

'

3

2

'

2

2

'

'

1

;

;



























i

E

E

E

3

'

3

3

'

2

3

'

'

'

1

;

;



























Całkowite odkształcenie względne w kierunku osi 1 wyznaczymy:

E

E

E

3

2

1

'

'

'

1

'

'

1

'

1

1































analogiczni

e wyznaczając wydłużenia w kierunku 2 i 3 otrzymamy:













)

(

1

)

(

1

)

(

1

1

2

3

3

3

1

2

2

3

2

1

1

















































E

E

E

-

uogólnione prawo Hooke’a dla przestrzennego stanu naprężenia

dla płaskiego stanu naprężenia (



3

=0):













1

2

3

1

2

2

2

1

1

1

1









 





 



















E

E

E

-

mamy przestrzenny stan odkształcenia

Zal

eżność między kątem odkształcenia postaciowego a naprężeniem stycznym

Możemy ją uzyskać rozpatrując odkształcenia
elementu znajdującego sie w stanie czystego
ścinania



=

















G

G

lub

jest to prawo Hooke’a dla czystego ścinania

)

1

(

2







E

G

moduł sprężystości postaciowej (Kirchhoffa)

ponieważ 0<



<0,5

E/3



G



E/2 dla stali G



0,4E

2

1

3



2



1



3

2

4







1

2



2

=-





1

=





W przypadku trójwymiarowego stanu naprężenia określonego przez



x

,



y

,



z

,



xy

,



yz

,



zx

przestrzenny stan odkształcenia jest opisany przez 9 wielkości:



x

,



y

,



z

,



xy

,



yx

,



xz

,



zx

,



yz

,



zy

, lecz wobec



ij

,



ji

,

przestrzenny stan odkształcenia określa 6 składowych:



x

,



y

,



z

,



xy

,



xz

,



yz

,

oraz













G

E

G

E

G

E

zx

zx

x

y

z

z

yz

yz

z

x

y

y

xy

xy

z

y

x

x



































































)

(

1

)

(

1

)

(

1

-

uogólnione prawo Hooke’a

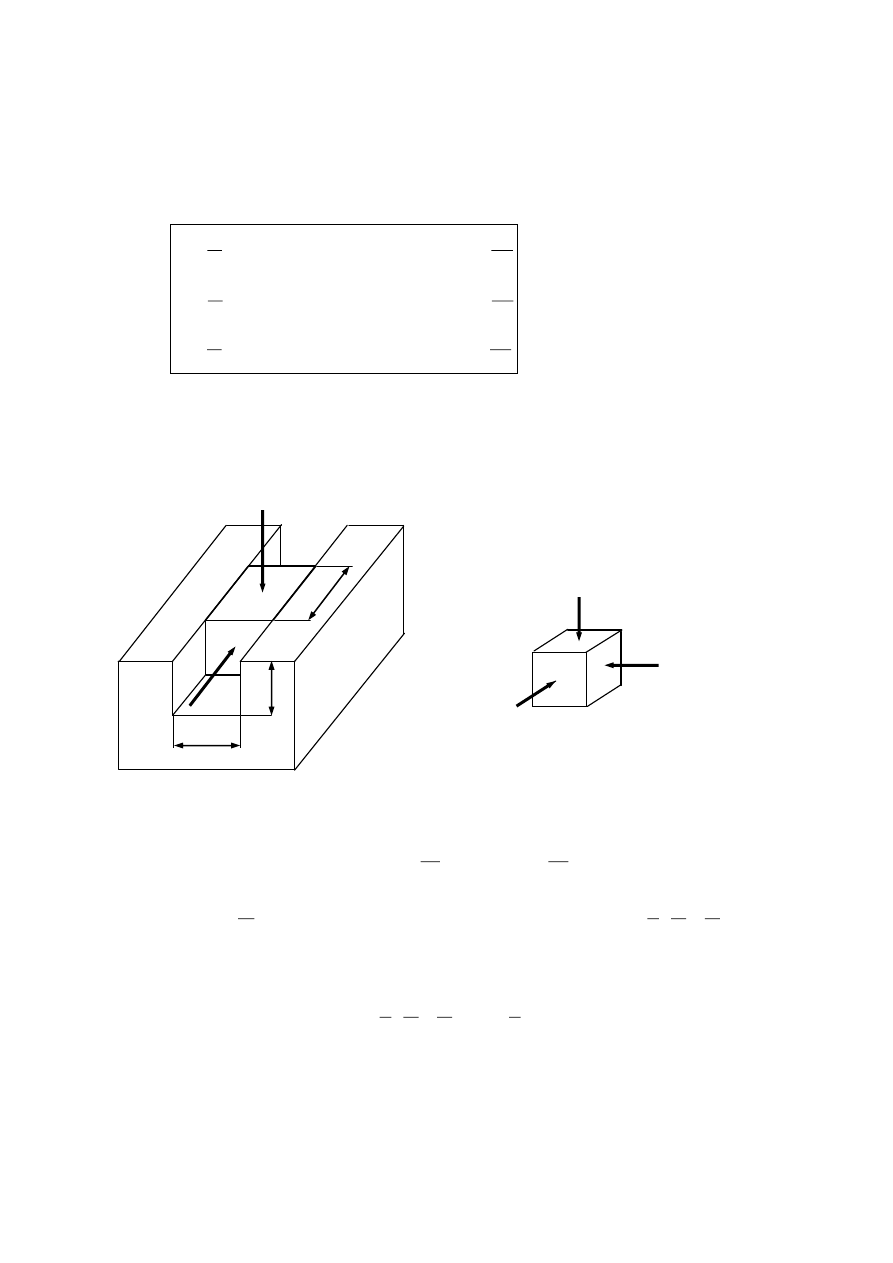
Przykład Wyznaczyć siłę z jaką prostopadłościan abc oddziaływuje na boczne ściany

kanału płyty doskonale sztywnej. Prostopadłościan mieści się w kanale bez luzu i
wcisku. Dane: P, Q, a, b, c,



.

Prostopadłościan znajduje się w
przestrzennym stanie naprężenia



1



0



2



0



3



0

i w płaskim stanie odkształcenia



1



0



2



0



3



0

Naprężenia składowe:

ab

Q

ac

P





3

1



















 

















b

Q

c

P

a

E





















)

(

)

(

1

0

1

3

2

1

3

2

2

Siła naporu prostopadłościanu na boczne ścianki płyty:

)

(

2

Qc

Pb

a

bc

b

Q

c

P

a

bc

R

















 













c

P

Q

a

b



3



1



2

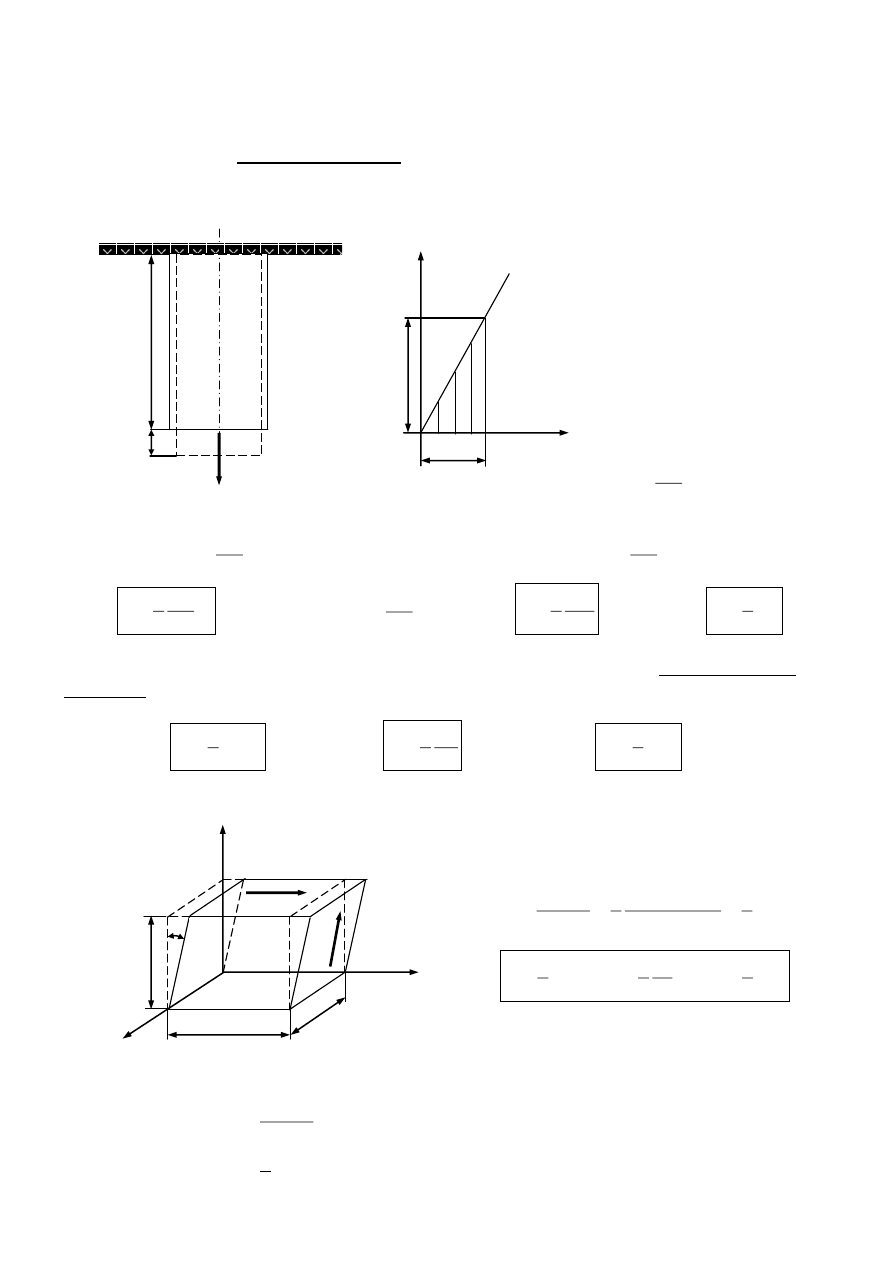
Energia sprężysta
Ważną własnością materiału jest zdolność gromadzenia w odkształconym sprężyście ciele
energii sprężystej, w którą przemienia się praca sił zewnętrznych L obciążających ciało.
Określa się ją jako energię sprężystości.

Obliczmy energię sprężystą pręta rozciągniętego siłą P o wydłużeniu



.

L

– praca sił zewnętrznych

V

– energia sprężysta

Praca elementarna

dL = P d



podstawiając:

V

L

i

l

EA

P







otrzymamy:





d

l

EA

dV



po scałkowaniu











0

d

l

EA

V

2

2

1



l

EA

V



podstawiając

EA

Pl





mamy

EA

l

P

V

2

2

1



lub



P

V

2

1



Dzieląc całkowita energię sprężystą V przez objętość pręta A



l otrzymamy

właściwą energię

sprężystą



dla stanu jednoosiowego:

2

2

1









E

E

2

2

1

















2

1

obliczmy energie sprężystą ścinania

siła -



zy

dydx

przesunięcie BB’ -



yz

dz

zy

zy

yz

zy

dxdydz

dz

dydx

dxdydz

V









2

1

2

1









2

2

2

1

2

1

2

1







G

G













W przypadku ogólnego stanu naprężenia:

dL = ½(



x

dydz



x

dx+



y

dxdz



y

dy+



z

dxdy



x

dz+



xy

dydz



xy

dx+



yz

dzdx



yz

dy+



zx

dxdy



zx

dz)

dxdydz

dL









zx

zx

yz

yz

xy

xy

z

z

y

y

x

x







































2

1

P

P



l

P





y

z

x



zy



zx

d

y

dx

dz

B

B’



yz