MO

Z2/6. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 6

1

Z2/6. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 6

Z2/6.1. Zadanie 6

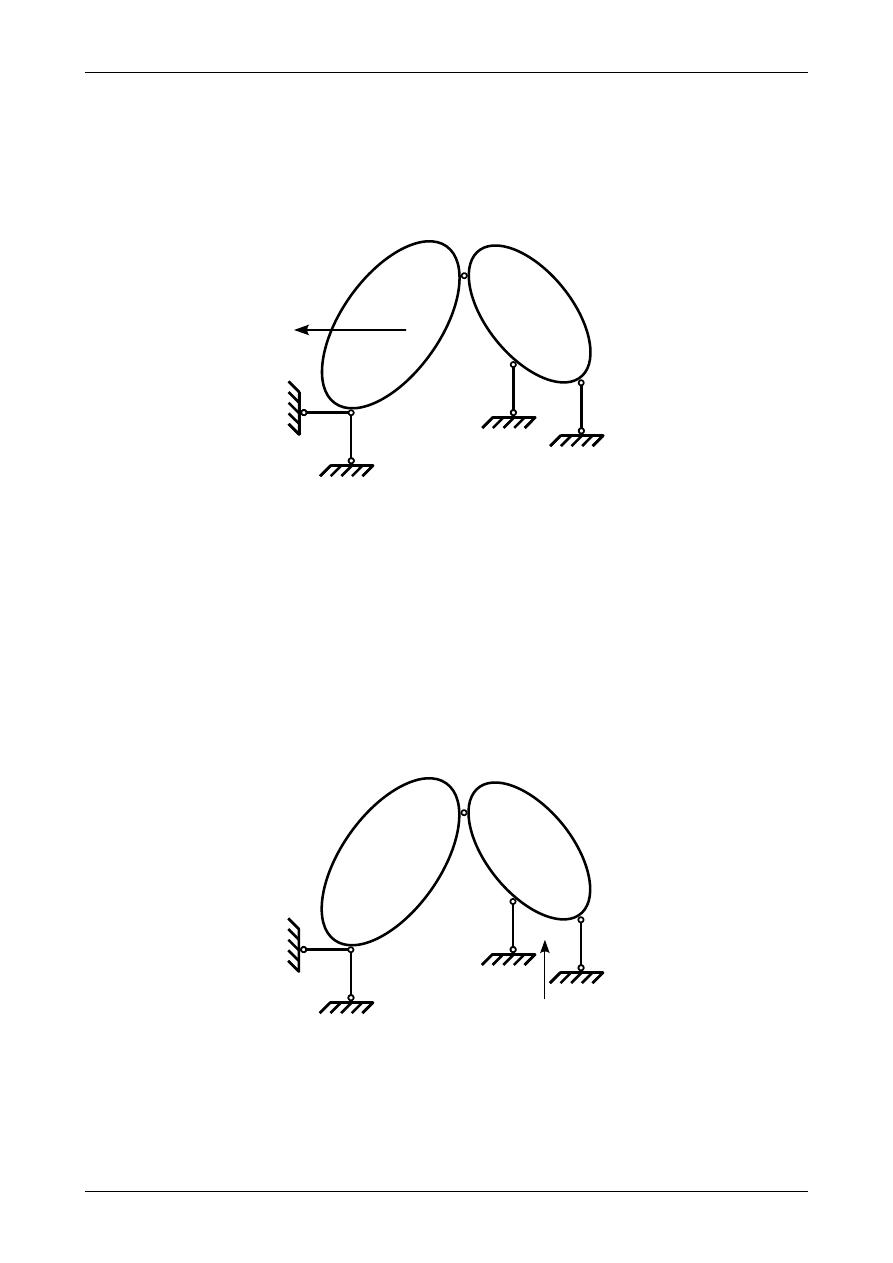
Metodą wykreślną wyznaczyć reakcje we wszystkich przegubach układu trójprzegubowego

przedstawionego na rysunku Z2/6.1. Kierunki prętów podporowych numer 1 i 2 są do siebie równoległe.

B

P

I

II

4

3

1

2

Rys. Z2/6.1. Układ trójprzegubowy

Z2/6.2. Analiza kinematyczna układu tarcz sztywnych

Układ trójprzegubowy na rysunku Z2/6.2 składa się z dwóch tarcz sztywnych, które mają sześć stopni

swobody. Cztery pręty podporowe numer 1, 2, 3 i 4 oraz przegub rzeczywisty B odbierają obu tarczom
sztywnym wszystkie sześć stopni swobody. Został więc tym samym spełniony warunek konieczny
geometrycznej niezmienności.

Pręty podporowe numer 1 i 2 sprowadzamy do przegubu fikcyjnego A. Pręty podporowe numer 3 i 4

sprowadzimy do przegubu fikcyjnego C znajdującego się pionowo w nieskończoności. Przeguby A, B i C
nie leżą na jednej prostej. Został więc spełniony także i warunek dostateczny geometrycznej niezmienności.
Układ trójprzegubowy jest więc układem geometrycznie niezmiennym i statycznie wyznaczalnym.

A

C

∞

B

I

II

4

3

1

2

Rys. Z2/6.2. Układ trójprzegubowy

Z2/6.3. Analiza statyczna układu tarcz sztywnych

Rysunek Z2/6/3 przedstawia tarczę sztywną numer II. Tarcza ta będzie w równowadze wtedy, gdy

reakcje w przegubach B i C będą działały na jednej prostej. Reakcja w przegubie rzeczywistym B będzie

Dr inż. Janusz Dębiński

Zaoczni

MO

Z2/6. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 6

2

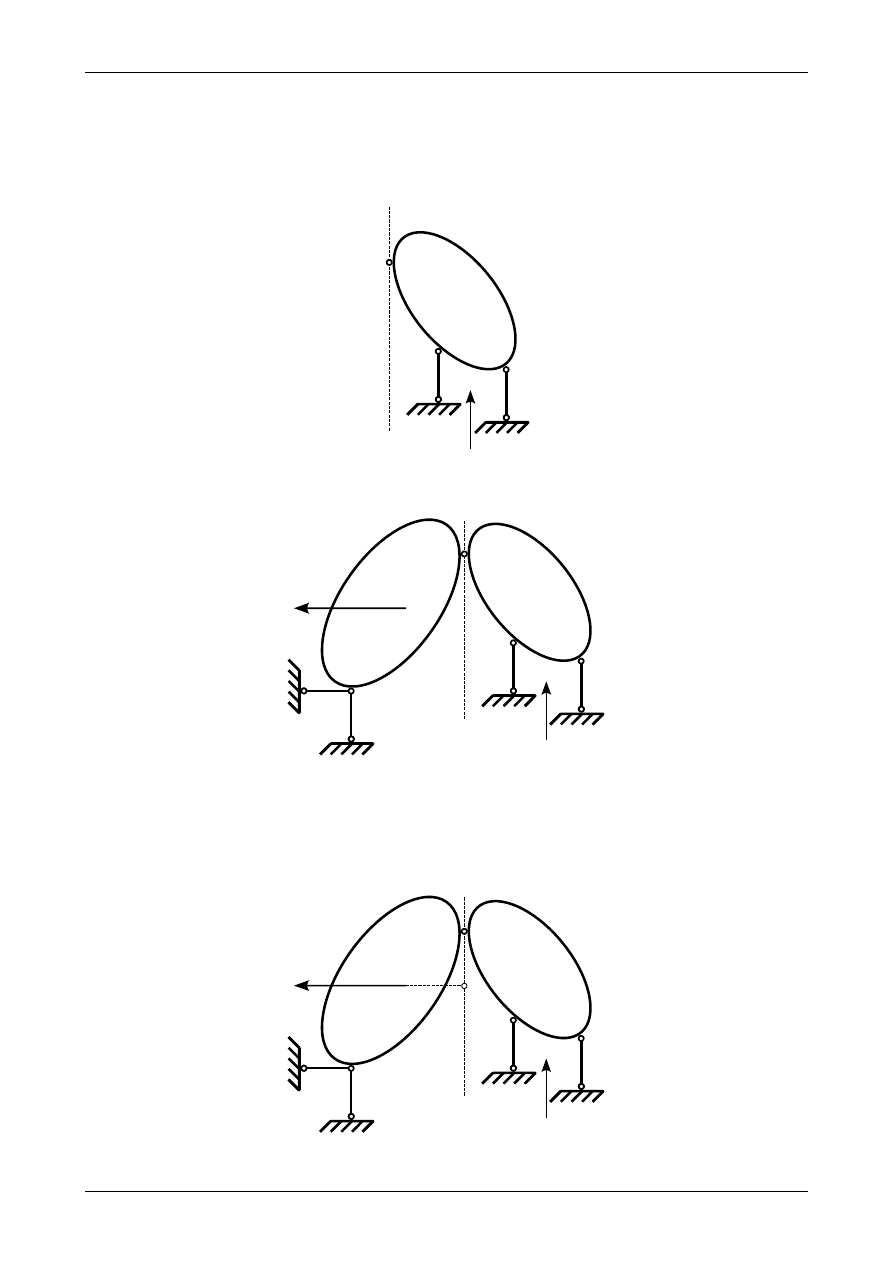
przechodzić przez punkt B. Natomiast reakcja w przegubie fikcyjnym będzie pionowa. Na tej podstawie
możemy stwierdzić, że reakcja w przegubie fikcyjnym w nieskończoności C będzie pionowa a jej kierunek
będzie przechodził przez punkt B. Kierunek reakcji w przegubie fikcyjnym w nieskończoności C
przedstawia rysunek Z2/6.4.

B

II

4

3

C

∞

Rys. Z2/6.3. Tarcza numer II

B

P

I

II

4

3

1

2

C

∞

A

Rys. Z2/6.4. Kierunek reakcji w przegubie fikcyjnym C

Łącząc kierunek reakcji w przegubie fikcyjnym C i kierunek siły P otrzymujemy punkt D

przedstawiony na rysunku Z2/6.5.

B

P

I

II

4

3

1

2

D

C

∞

A

Rys. Z2/6.5. Punkt przecięcia kierunków siły P oraz reakcji w przegubie C

Dr inż. Janusz Dębiński

Zaoczni

MO

Z2/6. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 6

3

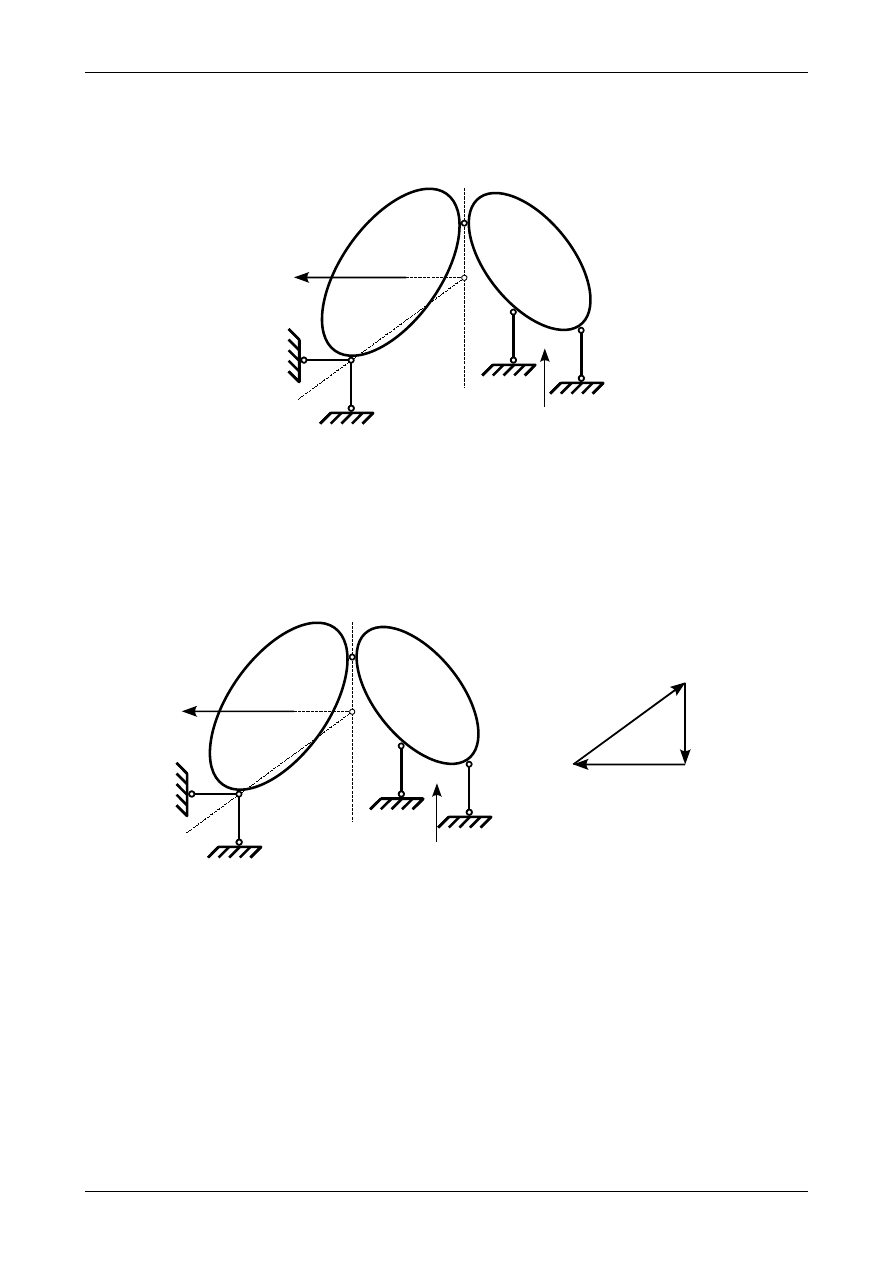
Aby układ trójprzegubowy znajdował się w równowadze kierunki wszystkich sił działających na

niego muszą się przeciąć w jednym punkcie. Punktem tym będzie punkt D. Łącząc punkt A z punktem D
otrzymamy więc kierunek reakcji w przegubie fikcyjnym A. Przedstawia to rysunek Z2/6.6.

B

P

I

II

4

3

1

2

D

C

∞

A

Rys. Z2/6.6. Kierunki reakcji w przegubach fikcyjnych A i C

Skoro znamy kierunki reakcji w przegubach fikcyjnych A i C możemy zacząć budować wielobok sił.

Przedstawia go rysunek Z2/6.7. W tym celu przenosimy równolegle siłę P. Do jednego końca przykładamy
kierunek reakcji w przegubie fikcyjnym A natomiast do drugiego końca kierunek reakcji w przegubie
fikcyjnym C. Ich punkt przecięcia wyznaczy nam wartości poszczególnych reakcji. Natomiast ich zwroty
muszą być takie aby siła wypadkowa z wieloboku sił była równa zero. Siły te muszą się więc gonić.

B

P

I

II

4

3

1

2

D

P

R

C

R

A

C

∞

A

Rys. Z2/6.7. Wielobok sił w równowadze

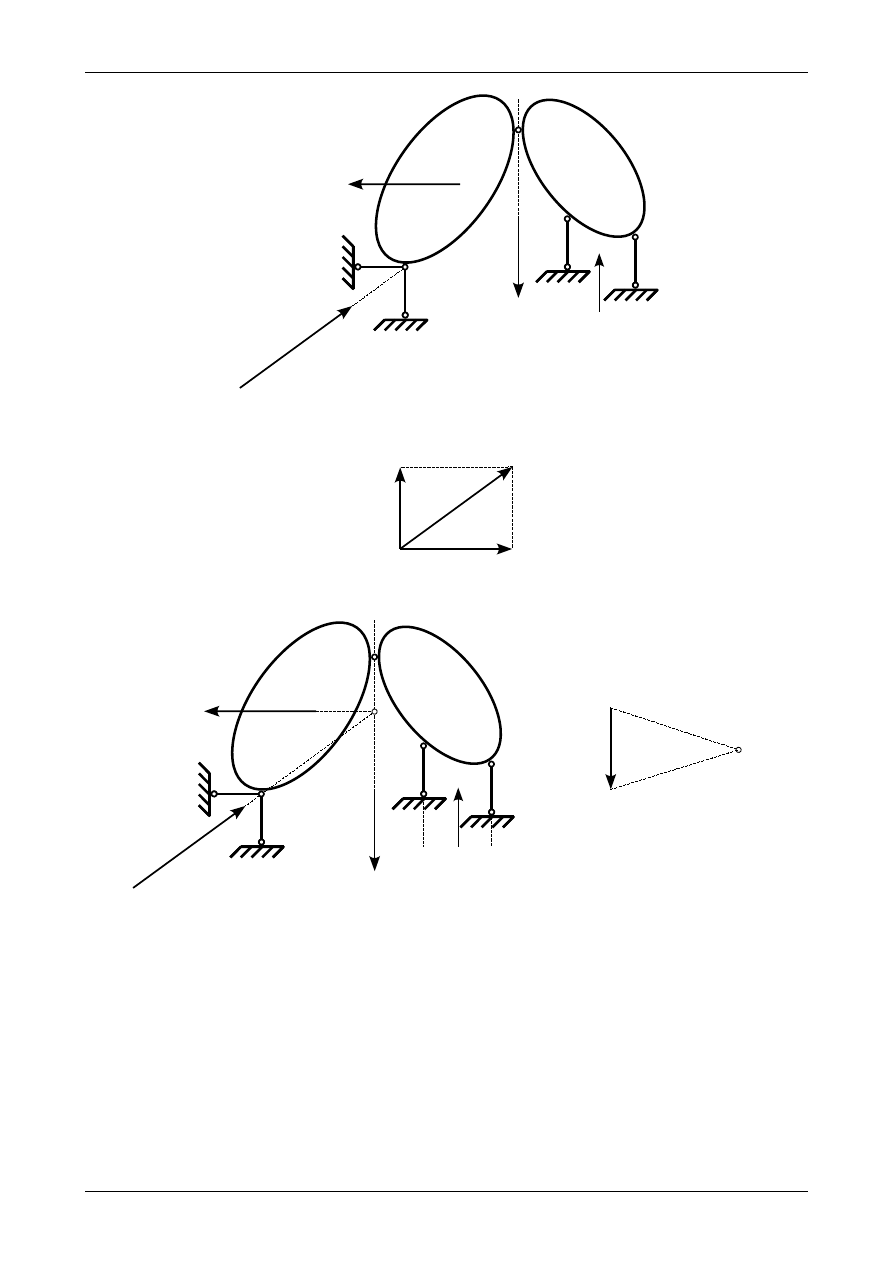
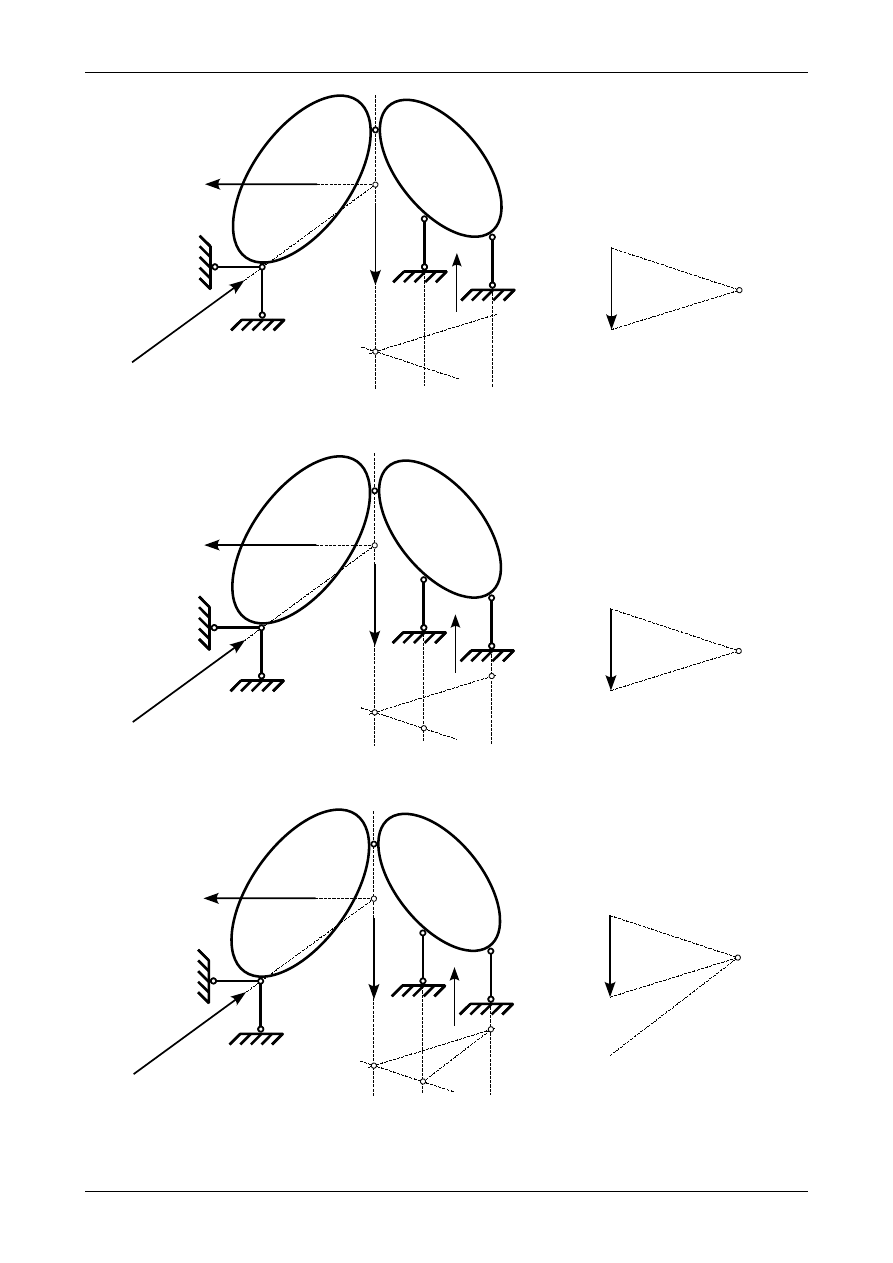
Rysunek Z2/6.8 przedstawia siłę czynną P oraz reakcje działające w przegubach fikcyjnych A i C na

układ trójprzegubowy będące w równowadze.

Reakcję w przegubie fikcyjnym A należy rozłożyć na składowe po kierunkach reakcji w prętach

podporowych numer 1 i 2. Reakcja w przegubie musi być przekątną równoległoboku, którego bokami są
reakcje w prętach podporowych numer 1 i 2. Reakcje w prętach podporowych przedstawia rysunek Z2/6.9.

Reakcję w przegubie fikcyjnym C należy rozłożyć na składowe po kierunkach reakcji w prętach

podporowych numer 3 i 4. Ponieważ oba pręty podporowe są równoległe do siebie musimy zastosować
wielobok sznurowy. W tym celu przenosimy równolegle reakcję R

C

i obieramy biegun O. Łączymy początek

i koniec reakcji R

C

z biegunem O promieniami 1 i 2. Przedstawia to rysunek Z2/6.10.

Reakcja R

C

znajduje się pomiędzy promieniami 1 i 2. Promienie te muszą się więc przeciąć w punkcie

E na kierunku reakcji R

C

. Przedstawia to rysunek Z2/6.11.

Dr inż. Janusz Dębiński

Zaoczni

MO

Z2/6. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 6

4

B

P

I

II

4

3

1

2

R

C

R

A

C

∞

A

Rys. Z2/6.8. Reakcje w przegubach A i C

R

1

R

2

R

A

Rys. Z2/6.9. Rozkład reakcji w przegubie fikcyjnym A

B

P

I

II

4

3

1

2

D

R

C

R

A

R

C

O

1

2

A

C

∞

Rys. Z2/6.10. Biegun O i promienie 1 i 2

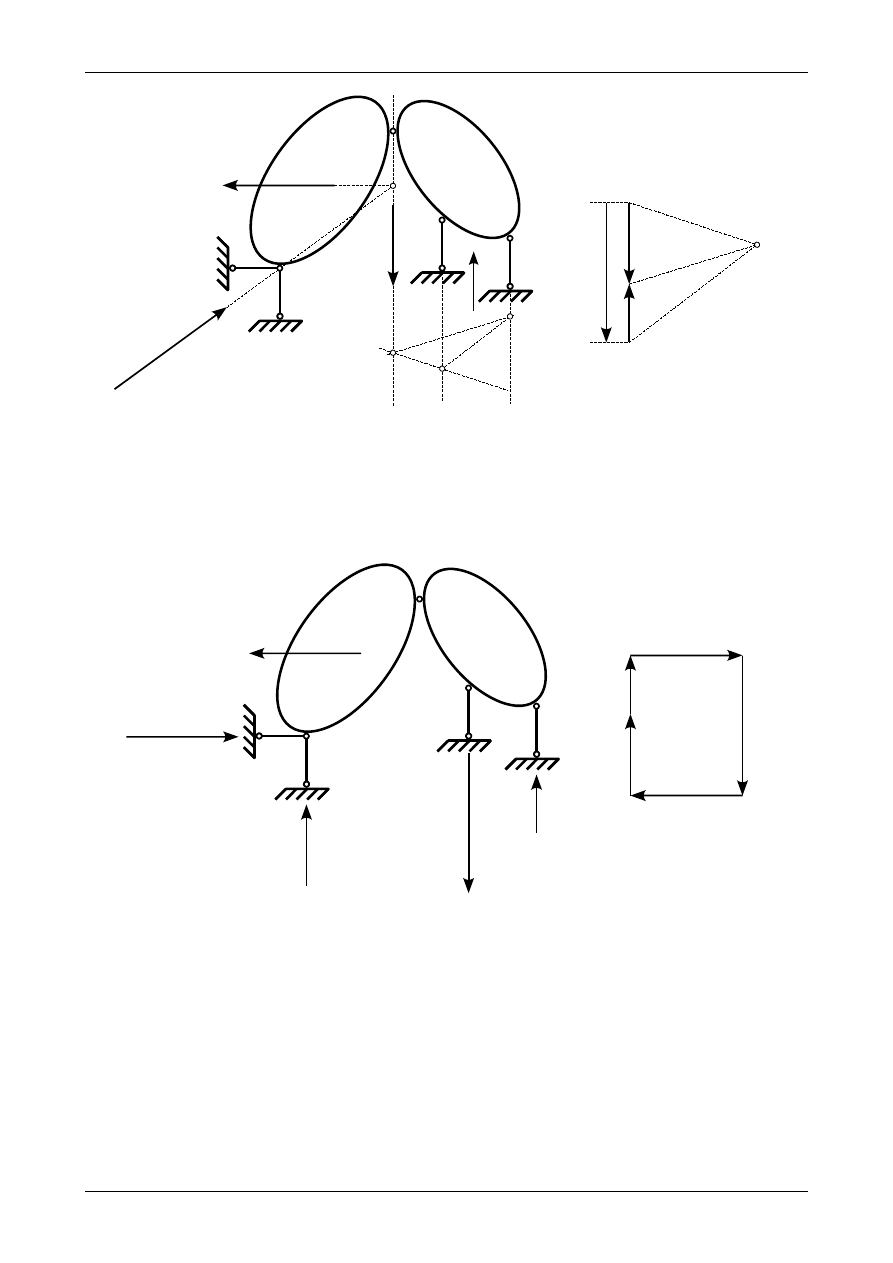
Promień 1 przecina kierunek reakcji w pręcie podporowym numer 3 w punkcie F natomiast promień 2

przecina kierunek reakcji w pręcie podporowym numer 4 w punkcie G. Przedstawia to rysunek Z2/6.12.

Łącząc punkty F i G otrzymamy promień 3, który przenosimy do bieguna O. Przedstawia to rysunek

Z2/6.13.

Promień 3 wyznacza nam wartości reakcji w prętach podporowych numer 3 i 4. Reakcje te

przedstawia rysunek Z2/6.14. Kierunki tych reakcji wynikają z faktu, że siła wypadkowa R

C

jest sumą

swoich reakcji składowych R

3

i R

4

. Na kierunku reakcji w pręcie podporowym R

3

przecinają się promienie 1

i 3 czyli pomiędzy tymi promieniami występuje ta reakcja. Na kierunku reakcji w pręcie podporowym
numer 4 R

4

przecinają się promienie 2 i 3 czyli pomiędzy tymi promieniami występuje ta reakcja.

Dr inż. Janusz Dębiński

Zaoczni

MO

Z2/6. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 6

5

B

P

I

II

4

3

1

2

D

R

C

R

A

R

C

O

1

2

1

2

E

A

C

∞

Rys. Z2/6.11. Promienie 1 i 2 przecinające się na kierunku reakcji R

C

w punkcie E

B

P

I

II

4

3

1

2

D

R

C

R

A

R

C

O

1

2

1

2

E

F

G

A

C

∞

Rys. Z2/6.12. Promień 1 i 2 przecinające kierunki reakcji w prętach podporowych numer 3 i 4

3

B

P

I

II

4

3

1

2

D

R

C

R

A

R

C

O

1

2

1

2

E

F

G

3

A

C

∞

Rys. Z2/6.13. Promień 3

Dr inż. Janusz Dębiński

Zaoczni

MO

Z2/6. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 6

6

3

B

P

I

II

4

3

1

2

D

R

C

R

A

R

C

O

1

2

1

2

E

F

G

3

R

4

R

3

A

C

∞

Rys. Z2/6.14. Reakcje w prętach podporowych numer 3 i 4

Rysunek Z2/6.15 przedstawia siłę czynną P oraz reakcje we wszystkich prętach podporowych. Jak

widać na tym rysunku wszystkie siły działające na układ trójprzegubowy znajdują się w równowadze,
ponieważ siła wypadkowa z wieloboku sił wynosi zero. Wszystkie siły w wieloboku sił gonią się.

B

P

I

II

4

3

1

2

R

4

R

3

R

1

R

2

P

R

4

R

3

R

1

R

2

Rys. Z2/6.15. Wszystkie siły działające na układ trójprzegubowy w równowadze

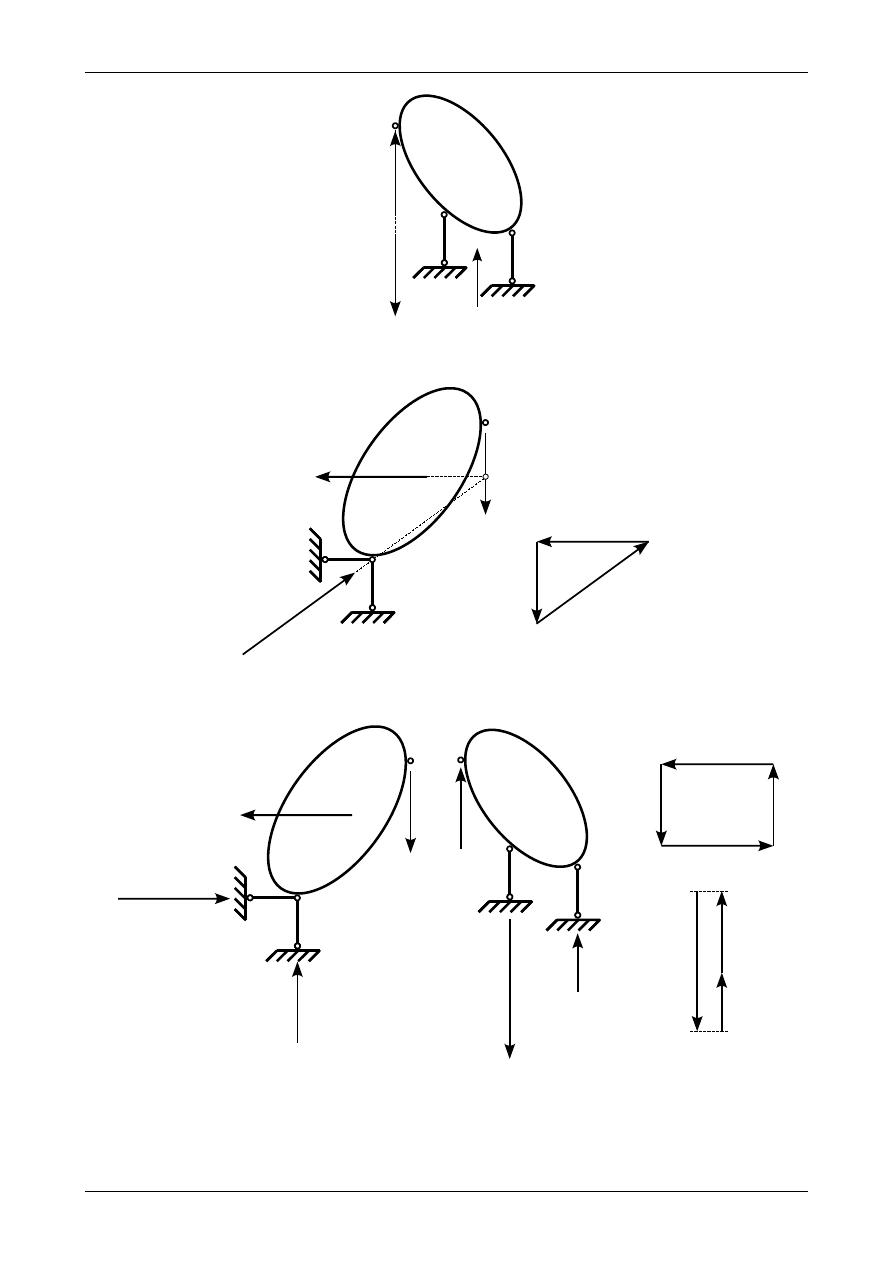
Na koniec musimy określić reakcję w przegubie B. Rysunek Z2/6.16 przedstawia równowagę tarczy

sztywnej numer II. Jak widać reakcja w przegubie B działająca na tarczę sztywną numer II ma taką samą
wartość ale przeciwny zwrot jak reakcja w przegubie fikcyjnym C. Obie te reakcje działają na jednej prostej.

Rysunek Z2/6.17 przedstawia równowagę sił działających na tarczę sztywną numer I. Jak widać

kierunki wszystkich sił przecinają się w jednym punkcie H a także siła wypadkowa z wieloboku sił wynosi
zero. Wszystkie siły gonią się.

Rysunek Z2/6.18 przedstawia siły działające na każdą z tarcz układu trójprzegubowego z osobna. Siły

te tworzą dwa zamykające się wieloboki sił.

Dr inż. Janusz Dębiński

Zaoczni

MO

Z2/6. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 6

7

B

II

4

3

R

C

R

B

(II)

C

∞

Rys. Z2/6.16. Równowaga sił działających na tarczę sztywną numer II

B

P

I

1

2

R

B

(I)

R

A

H

P

R

B

(I)

R

A

A

Rys. Z2/6.17. Równowaga sił działających na tarczę sztywną numer I

B

P

I

1

2

R

B

(I)

B

II

4

3

R

B

(II)

R

1

R

2

R

4

R

3

R

4

R

3

R

B

(II)

R

2

P

R

B

(I)

R

1

Rys. Z2/6.18. Równowaga tarcza sztywnych numer I i II

Dr inż. Janusz Dębiński

Zaoczni