KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Ćwiczenie 8
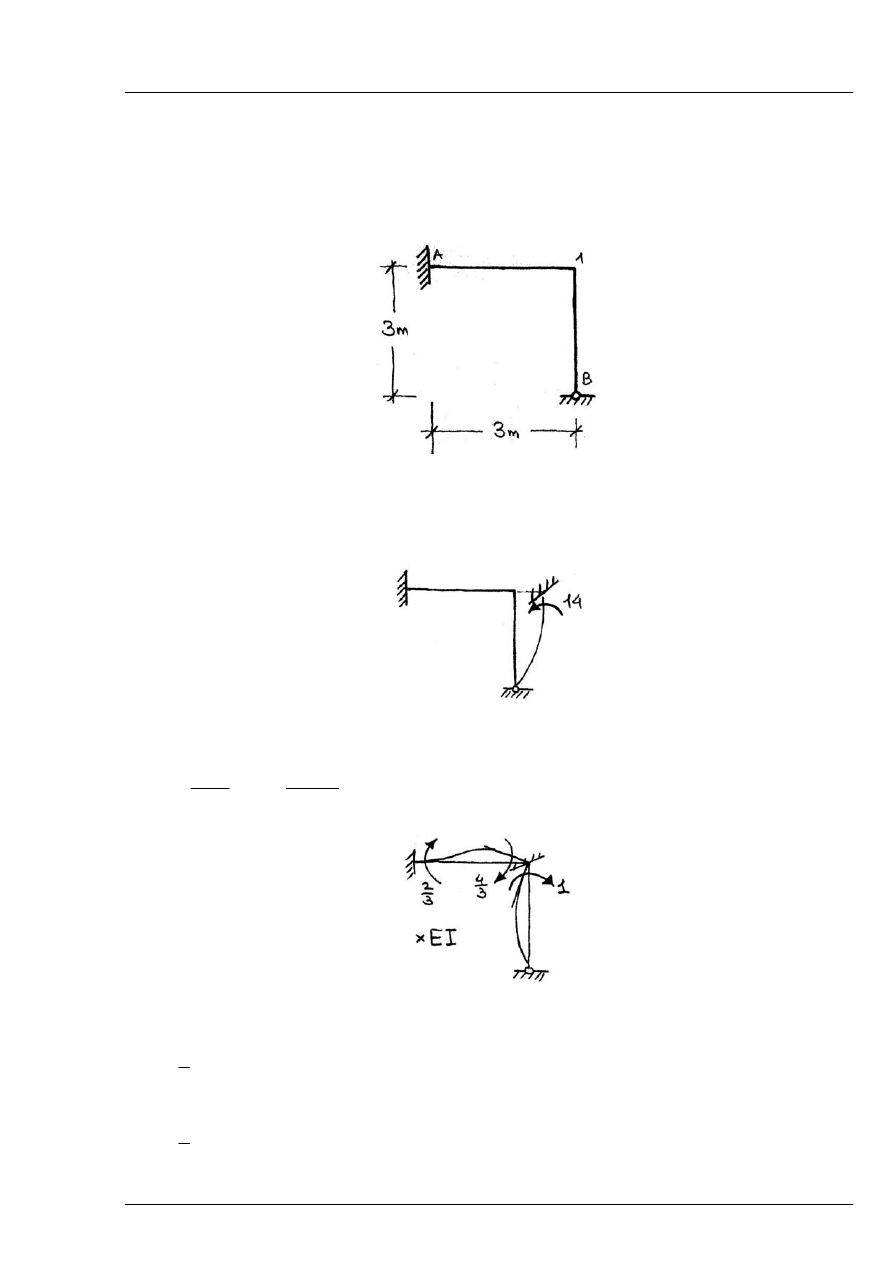
Zad. 8.1
Wyznaczyć siły wewnętrzne powstałe na skutek wmontowania pręta A-1 dłuższego o
3[
]
l
cm
∆ =
.
2
1400 [
]
EI
kNm
=
Rys. 8.1.1
Stopień geometrycznej niewyznaczalności układu
1( )
g
n
ϕ
=
Schemat geometrycznie wyznaczalny:
Rys. 8.1.2
Momenty wyjściowe:
0
1
2
2
3
3 1400
0,03
14 [
]
3
3
B
EI
M
l
k
⋅
⋅
= −
⋅ ∆ = −
⋅
= −
Nm
Momenty przywęzłowe powstałe na skutek kąta obrotu
1
ϕ
= :
Rys. 8.1.3
Sumaryczne momenty przywęzłowe:
1
1
1
4
3
14
2
3
A
B
A
M
EI
M
EI
M
EI
ϕ
ϕ
ϕ
=
= − +
=
C16-2005-cw08
64
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Równanie równowagi :
1
1
1
0
A
B
M
M
M
Σ
=
+
=
Stąd:
7
6
14
0
3
EI
EI
ϕ
ϕ
− +
=
⇒
=
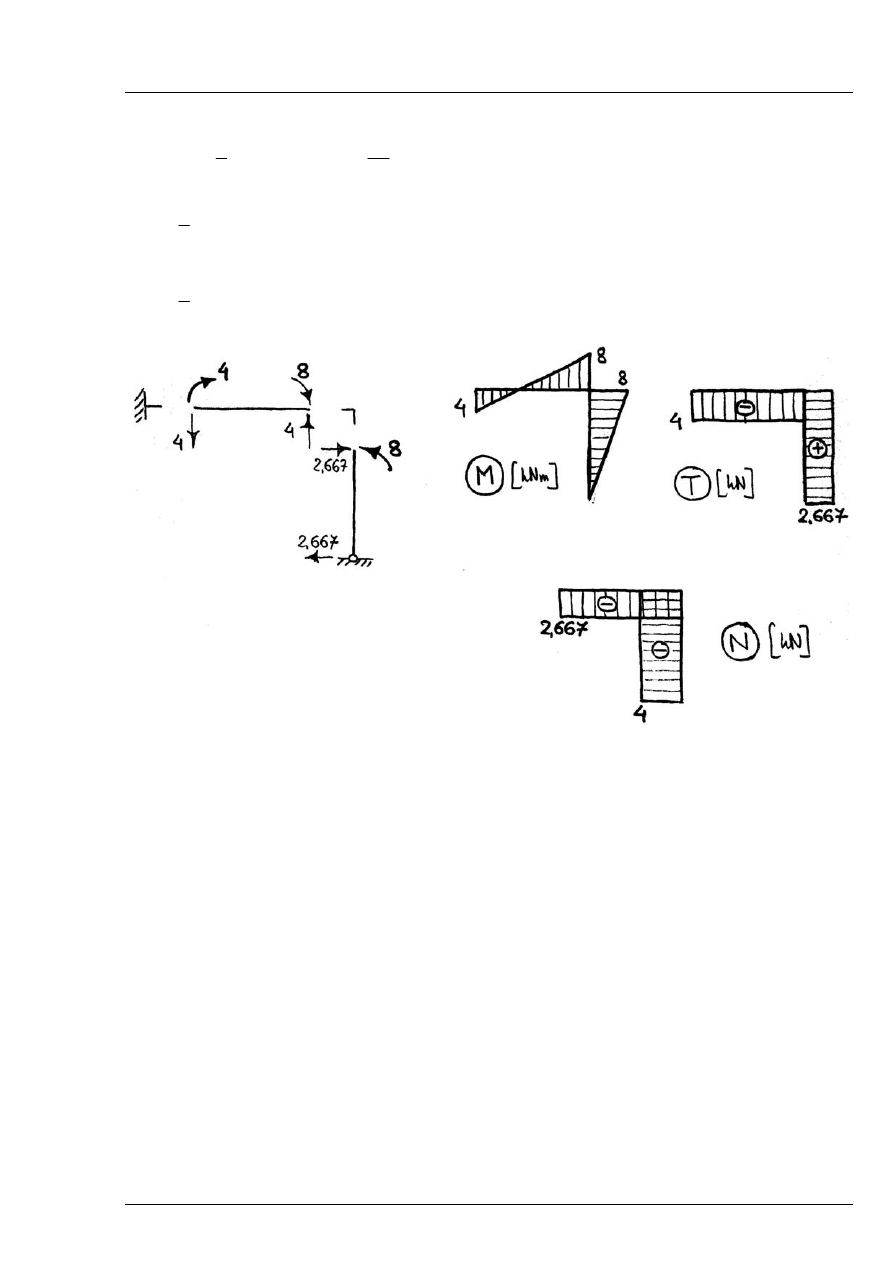
Wartości momentów przywęzłowych:
1
1
1
4
6 8 [
]
3
14 6
8 [
]
2
6 4 [
]
3
A
B
A
M
kNm
M
kNm
M
kNm
= ⋅ =
= − + = −
= ⋅ =
Rozwiązanie:
Rys. 8.1.4
C16-2005-cw08
65
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
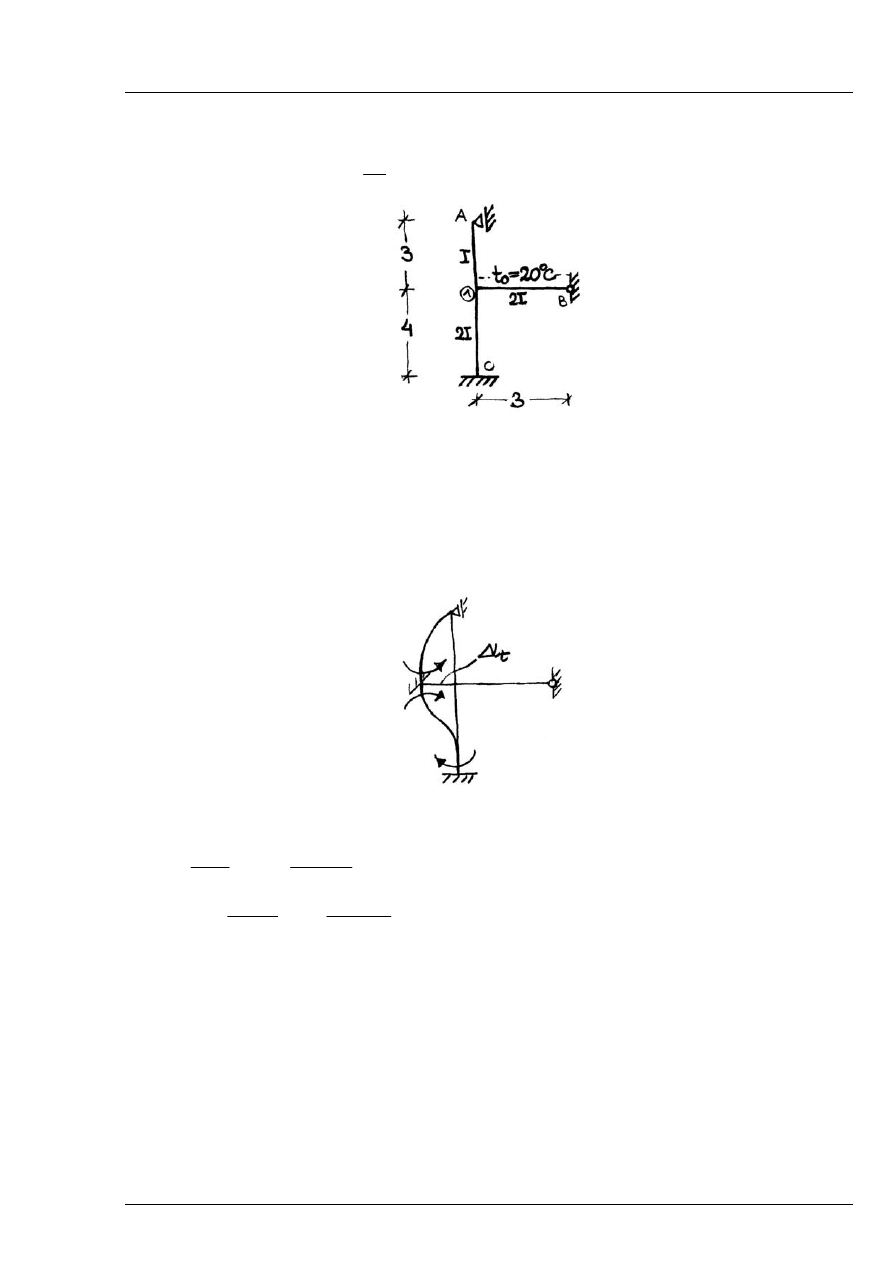
Zad. 8.2
Wyznaczyć siły wewnętrzne powstałe na skutek równomiernego ogrzania jednego z elementów.
2
5
1
10000 [
],
10
t
o
EI
kNm
C
α
−
⎡
⎤
=
=
⎢
⎥
⎣
⎦
Rys. 8.2.1
Stopień geometrycznej niewyznaczalności układu
1( )
g
n
ϕ
=
Wydłużenie termiczne elementu 1-B:
5
4
0
10
20 3 6 10 [ ]
t
t
l
t l
α
−
−
∆ =
⋅ ⋅ =
⋅
⋅ = ⋅
m
Schemat geometrycznie wyznaczalny:
Rys. 8.2.2
Momenty wyjściowe:
0
4
1
2
2
0
0
4
1
1
2
3
3 10000
6 10
2 [
]
3
3
6
2
6 20000
6 10
4,5 [
]
4
16
A
t
C
C
t
EI
M
l
kNm
E
I
M
M
l
−
−
⋅
⋅
= −
⋅ ∆ = −
⋅ ⋅
= −
⋅
⋅
=
=
⋅ ∆ =
⋅ ⋅
=
kNm
C16-2005-cw08
66
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Momenty przywęzłowe:
1
1
1
1
3
2
2
3
3
2
2
3
4
2
4,5
4,5 2
4
2
2
4,5
4,5
4
A
B
C
C
EI
M
E
E
I
M
EI
E
I
I
M
EI
E
I
M
EI
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
= − +
= − +
⋅
=
=
⋅
=
+
=
+
⋅
=
+
=
+
Równanie równowagi :
1
1
1
1
0
A
B
C
M
M
M
M
Σ
=
+
+
=
Stąd:
1
2,5 5
0
2
EI
EI
ϕ
ϕ
+
=
⇒
= −
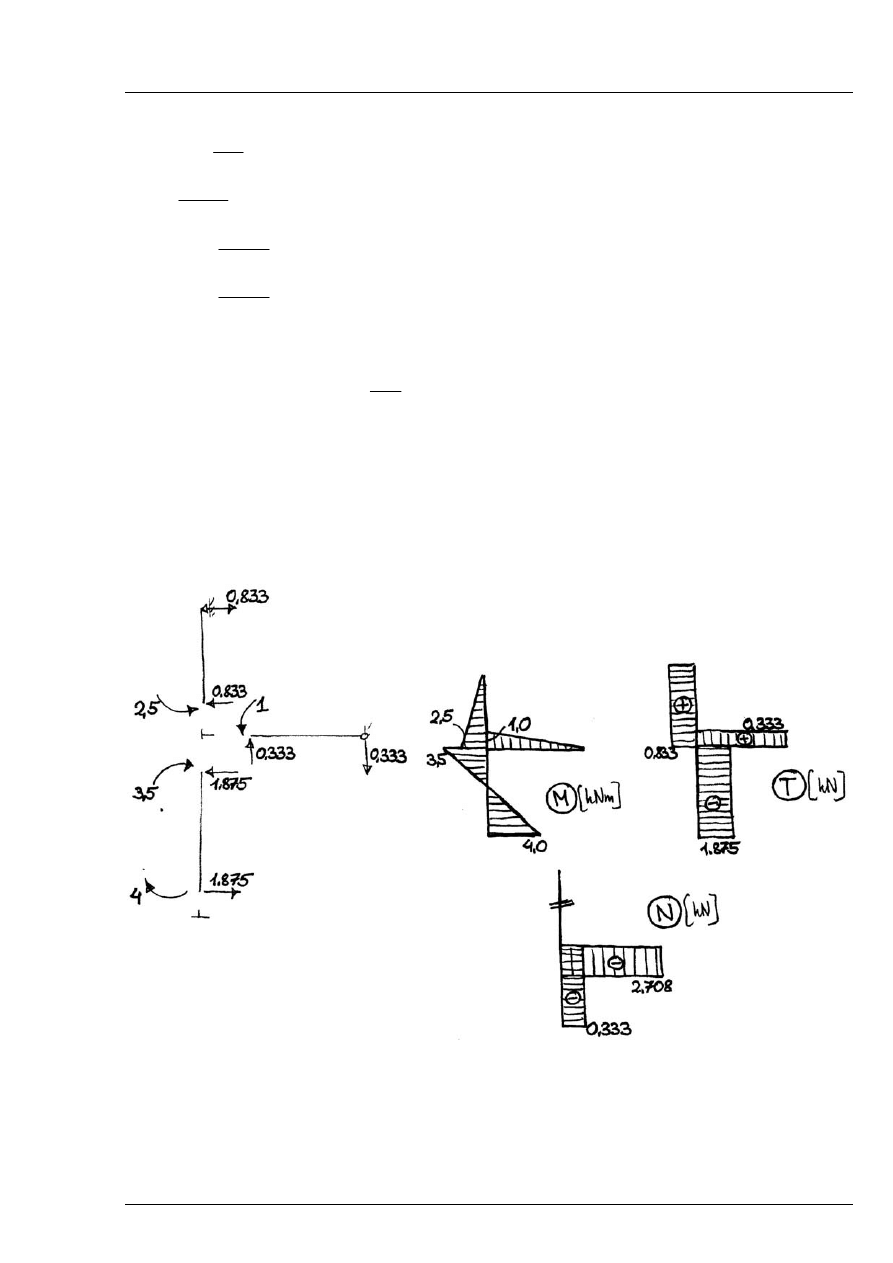
Wartości momentów przywęzłowych:
1
1
1
1
2 0,5
2,5 [
]
1[
]
4,5 1 3,5 [
]
4,5 0,5 4 [
]
A
B
C
C
M
kNm
M
kNm
M
k
M
k
= − −
= −
= −
=
− =
=
−
=
Nm
Nm
Rozwiązanie:
Rys. 8.2.3
C16-2005-cw08
67
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
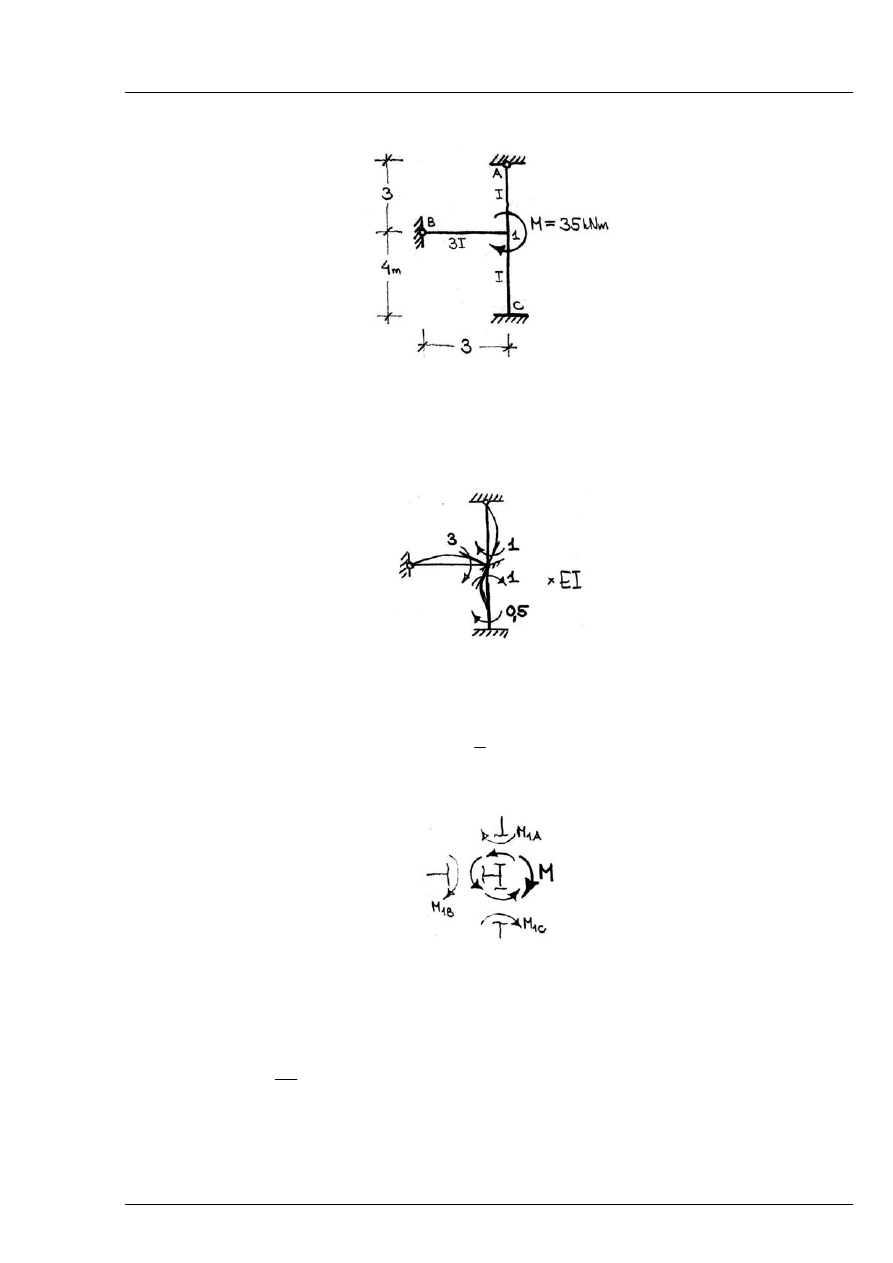
Zad. 8.3
Sporządzić wykresy sił wewnętrznych N, T, M.(pręty A-1 i 1-C mają jednakowy przekrój)
Rys. 8.3.1
Układ jest jednokrotnie geometrycznie niewyznaczalny.
1( )
g
n
ϕ
=
Brak momentów wyjściowych – nie ma obciążenia przęsłowego.
Wpływ kąta obrotu
1
ϕ
= :
Rys. 8.3.2
Momenty przywęzłowe pochodzące od kata obrotu
1
ϕ
= :
1
1
1
1
1
3
2
A
B
C
C
M
EI
M
EI
M
EI
M
EI
ϕ
ϕ
ϕ
=
=
=
=
ϕ
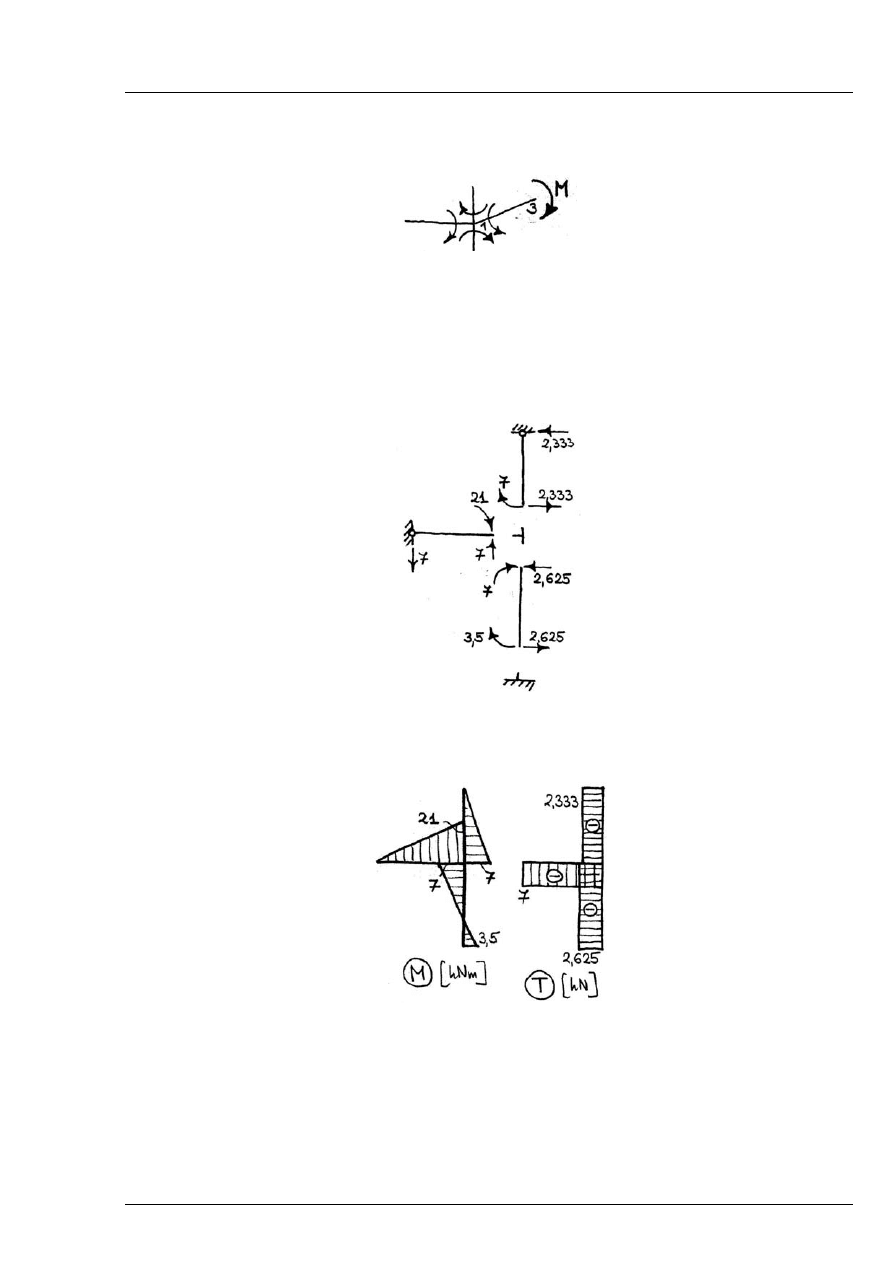
Równanie równowagi :
Rys. 8.3.3
1
1
1
1
1
1
1
0
lub
A
B
C
A
B
C
M
M
M
M
M
M
M
M
M
Σ
= −
−
−
+
=
+
+
=
Stąd:
7
5
35 0
EI
EI
ϕ
ϕ
−
=
=
C16-2005-cw08
68
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Inna interpretacja:
Dodatkowy element 1-3 obciążony momentem skupionym M , powstaje moment wyjściowy
13
M
M
= −
Rys. 8.3.4
Wartości momentów przywęzłowych:
1
1
1
1
7 [
]
21[
]
7[
]
3,5 [
]
A
B
C
C
M
kNm
M
kNm
M
kNm
M
kNm
=
=
=
=
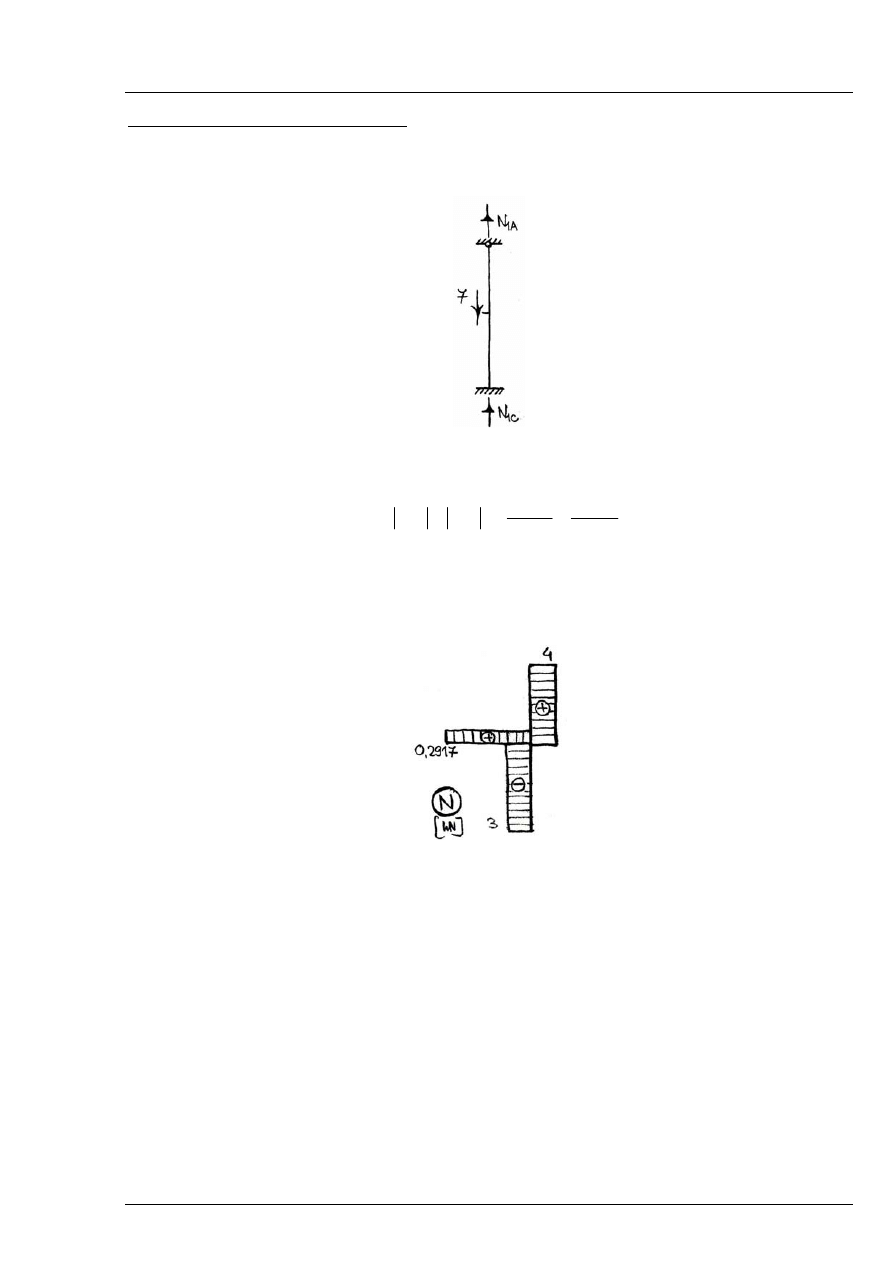
Rys. 8.3.5
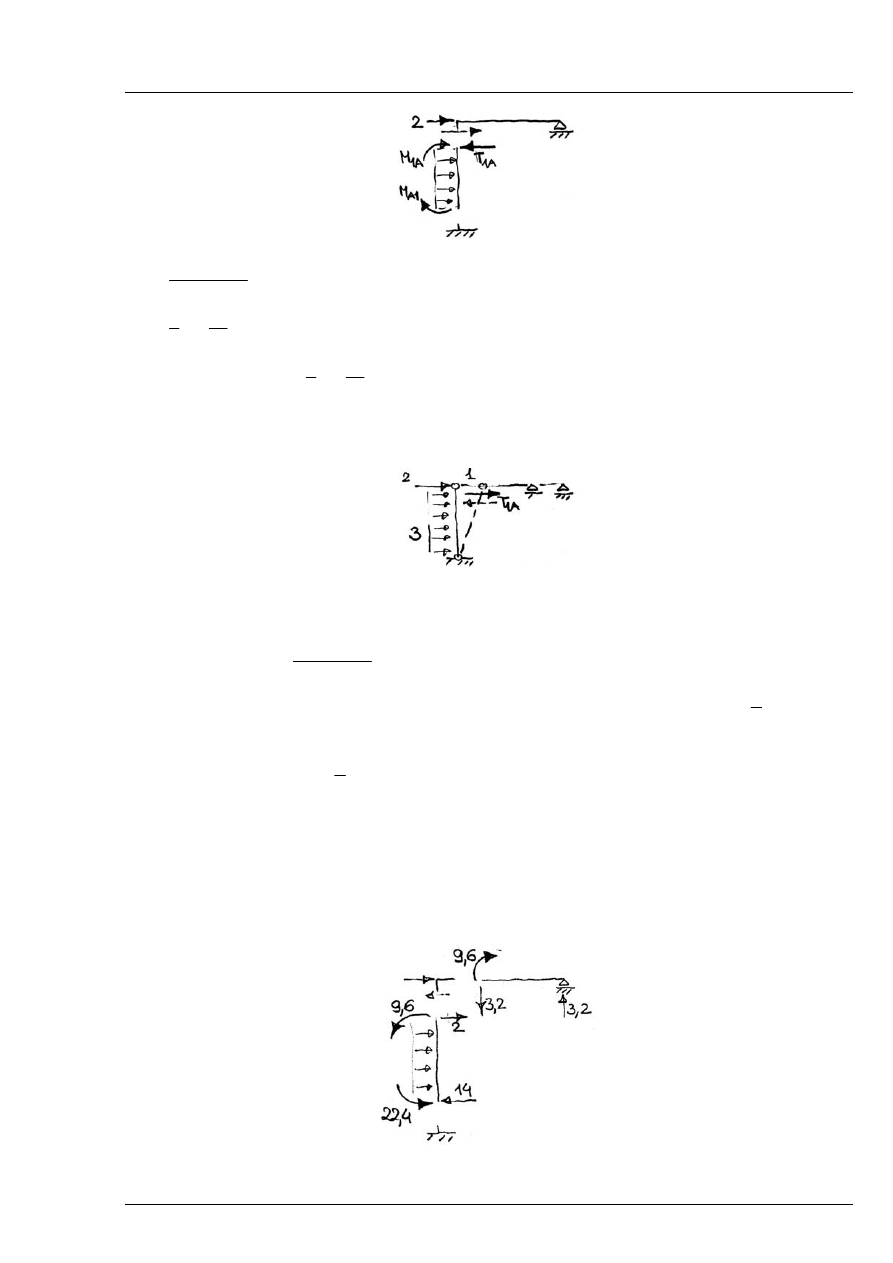
Rozwiązanie M, T:
Rys. 8.3.6
C16-2005-cw08
69
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
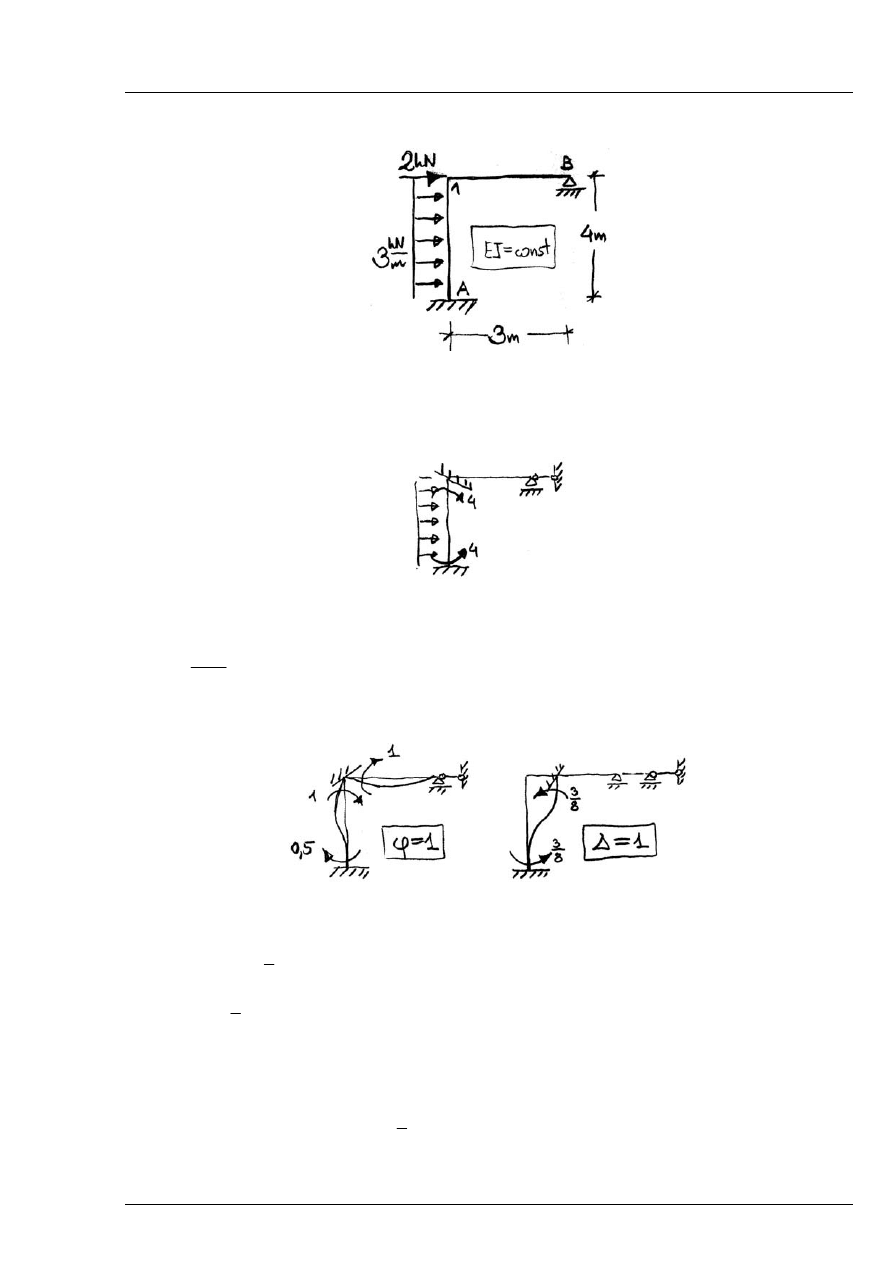
Siły normalne w elementach A-1 i 1-C:
Przyjmujemy że siła
jest rozciągająca, zaś siła
ściskająca.
1A
N
1C
N
Rys. 8.3.7
Równanie równowagi:
1
1
0
7
y
A
C
P
N
N
∑
= ⇒
+
=
(1)
Warunek zgodności przemieszczeń:
1
1
1
1
1
1
4
3
3
4
(
C
A
A
C
A
C
N
N
l
l
N
N
EA
EA
2)
⋅
⋅
∆
= ∆
⇒
=
=
Z (1) i (2) mamy:
[ ]
1
1
1
4
3[
]
2,625 2,333 0, 2917 [
]
A
C
B
N
kN
N
kN
N
k
=
=
=
−
=
N
Rys. 8.3.8
C16-2005-cw08
70
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
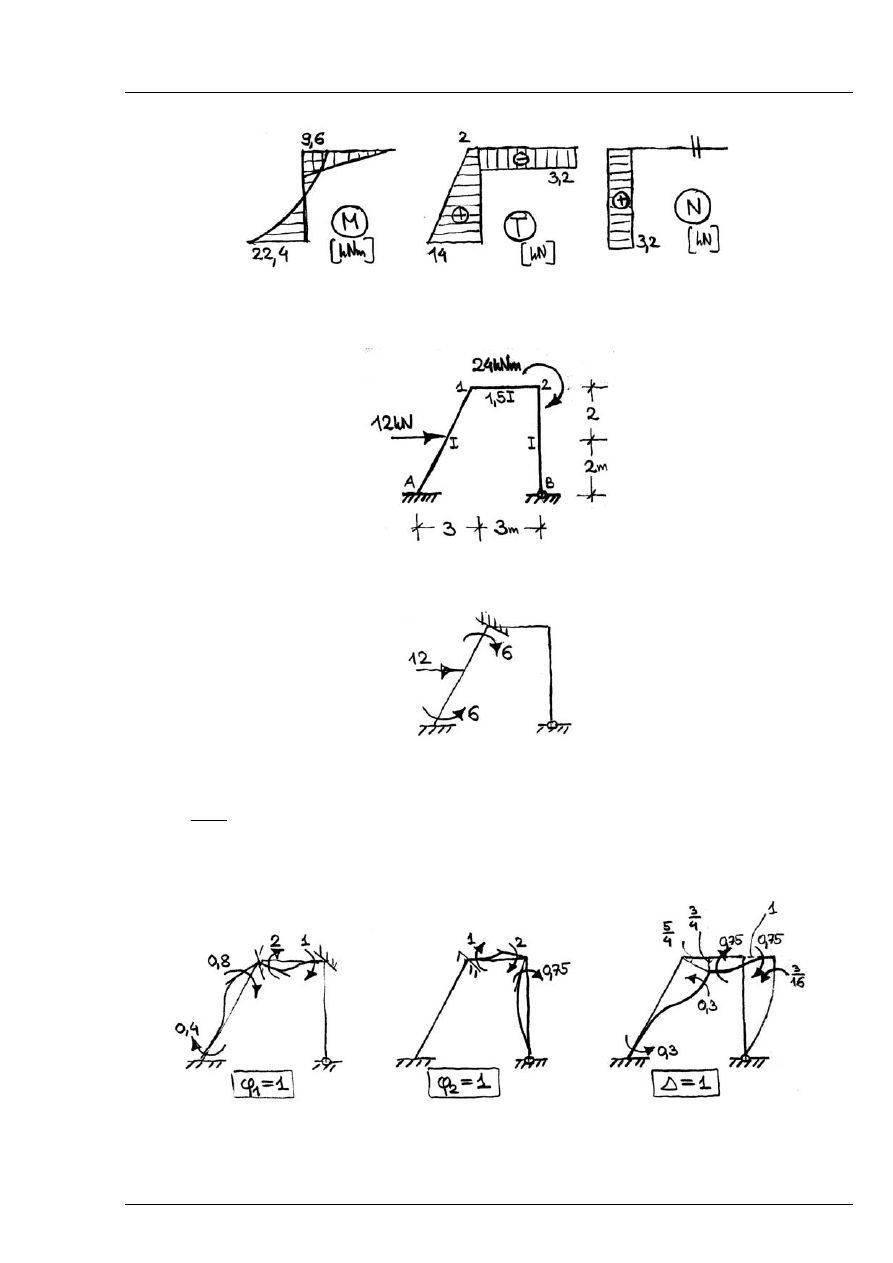
Zad. 8.4
Sporządzić wykresy sił wewnętrznych
Rys. 8.4.1
Układ jest dwukrotnie geometrycznie niewyznaczalny, przesuwny.
2( , )
g
n
ϕ
=
∆
Schemat geometrycznie wyznaczalny z obciążeniem zewnętrznym:
Rys. 8.4.2
Momenty wyjściowe:
2
0
1
0
1
3 4
4 [
]
12
4 [
]
A
A
M
kNm
M
kNm
⋅
= −
= −
=
Momenty zginające wywołane jednostkowymi wymuszeniami
1
1
i
ϕ
=
∆ =
Rys. 8.4.3
W obliczeniach przyjmujemy EI=1.
Momenty przywęzłowe:
1
1
1
3
4 0,5
8
3
4
8
A
A
B
M
M
M
ϕ
ϕ
ϕ
= − +
− ∆
= + − ∆
=
Równania równowagi :
(1)
1
1
1
3
0
2
4 0
16
3
32
8
A
B
M
M
M
ϕ
ϕ
Σ
=
+
=
⇒
− ∆ + =
⇒
− ∆ = −
(1)
(2) Równowaga sił w elemencie 1-B w kierunku przesuwu
C16-2005-cw08
71
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Rys. 8.4.4
0
0
1
1
1
1
1
1
1
,
6
4
3
3
6
8
16
3
3
0
2 0
8
8
16
6
3
128 (2)
A
A
A
A
A
A
x
A
M
M
T
T
T
T
P
T
ϕ
ϕ
ϕ
+
=
+
=
=
−
∆ +
Σ = ⇒
+ = ⇒
−
∆ + =
− ∆ = −
0
Równanie (2) można otrzymać tworząc układ przegubowy (mechanizm) i zadając w nim
przemieszczenie wirtualne
1
∆ =
Rys. 8.4.5
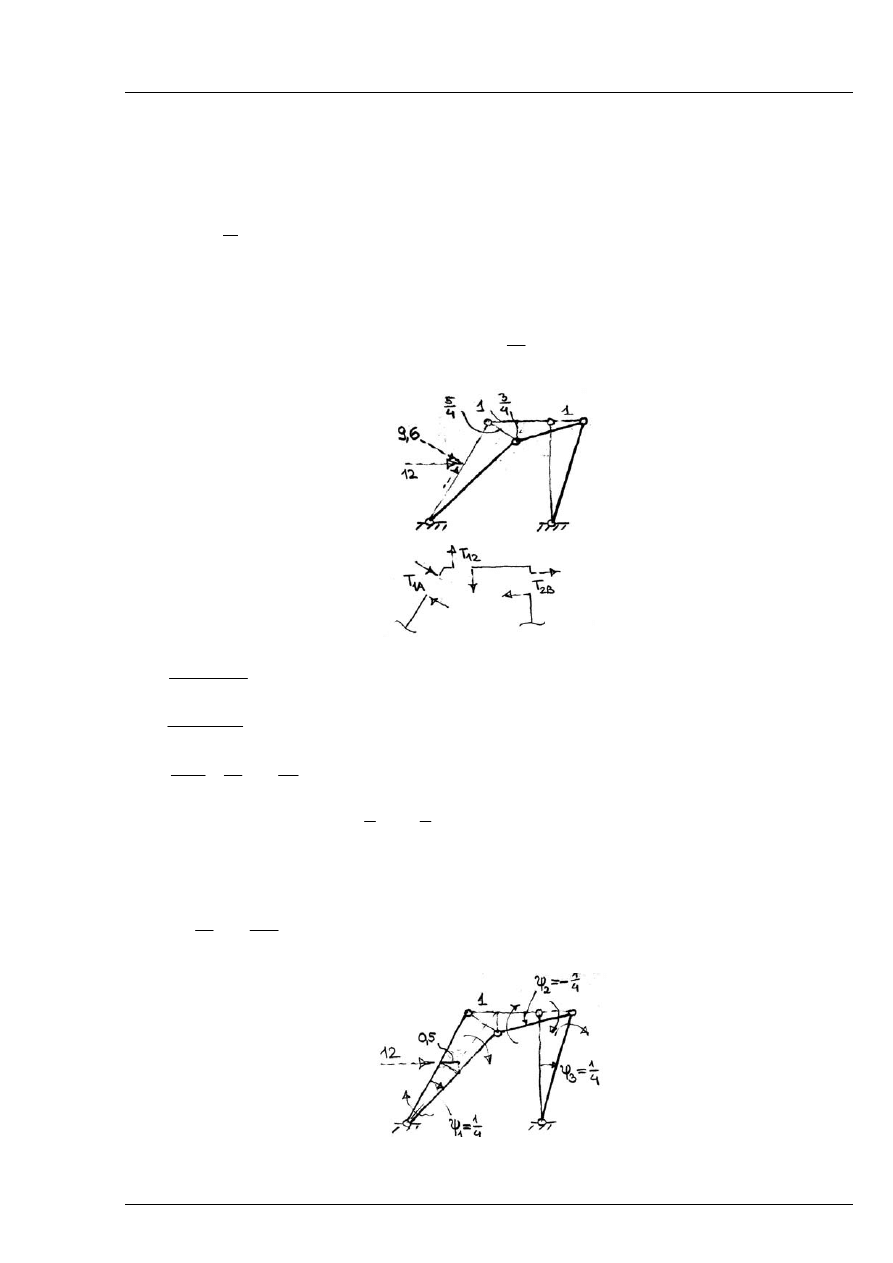
Równanie równowagi wyciętego elementu 1 – B:
1
0
1 2 1 0
x
A
P
T
= ⇒
⋅ + ⋅ =
∑
1A
(T - od strony węzła)
Po podstawieniu
1
1
1
6
4
A
A
A
M
M
T
+
=
+ otrzymujemy (2)
Do tego samego rezultatu można dojść wprowadzając kąt obrotu pręta A-1:
1
1
4
A
−
Ψ
= i zapisując
równanie pracy wirtualnej:
1
1
1
1
(
) 2 1 3
1 4 0
2
A
A
A
M
M
−
Ψ
⋅
+
+ ⋅ + ⋅ ⋅ ⋅ =
⇒ (2)
Z (1) i (2)
9,6
61,8667
ϕ
⇒
=
∆ =
Wartości momentów przywęzłowych:
1
1
1
4 4,8 23, 2
22, 4 [
]
4 9,6 23, 2
9,6 [
]
9,6 [
]
A
A
B
M
kNm
M
k
M
kNm
= − +
−
= −
= +
−
= −
= −
Nm
Rys. 8.4.6
C16-2005-cw08
72
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Rozwiązanie:
Rys. 8.4.7
Zad. 8.5
Sporządzić wykresy sił wewnętrznych N, T, M
Rys. 8.5.1
Układ jest trzykrotnie geometrycznie niewyznaczalny.
1
2
3( , , )
g
n
ϕ ϕ
=
∆
Rys. 8.5.2
Momenty wyjściowe:
0
1
0
1
12 4
6 [
]
8
6 [
]
A
A
M
kNm
M
kNm
⋅
= −
= −
=
Momenty przywęzłowe wywołane stanami:
1
2
1,
1,
1
ϕ
ϕ
=
=
∆ = :
Rys. 8.5.3
C16-2005-cw08
73
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Momenty przywęzłowe:
1
1
1
1
12
1
2
21
1
2
2
2
6 0, 4
0,3
6 0,8
0,3
2
0,75
2
0,75
3
0, 75
16
A
A
B
M
M
M
M
M
ϕ
ϕ
ϕ ϕ
ϕ
ϕ
ϕ
= − +
−
∆
= +
−
∆
=
+
+
∆
=
+
+
∆
=
−
∆
Równania równowagi :
(1)
1
1
12
1
2
0
2,8
0, 45
6
A
M
M
M
(1)
ϕ ϕ
Σ
=
+
=
⇒
+
+
∆ = −
(2)
2
21
2
1
2
9
24
2,75
24 (2)
16
B
M
M
M
M
ϕ
ϕ
Σ
=
+
=
=
⇒
+
+
∆ =
(3) Tworzymy układ przegubowy i zadajemy przemieszczenie wirtualne
1
∆ =
Rys. 8.5.4
1
1
1
1
12
21
12
1
2
2
2
2
4,8 0, 24
0,12
4,8
5
0,5
3
3
3
4
16
64
A
A
A
B
B
M
M
T
M
M
T
M
T
ϕ
ϕ ϕ
ϕ
+
=
+
=
−
∆
+
=
=
+
+
∆
=
=
−
∆
+
Równanie pracy wirtualnej:
1
12
2
5
3
1 0
4
4
A
B
T
T
T
⋅ −
⋅ +
⋅ =
(zwrot sił – od strony węzłów, w przypadku braku obciążenia węzłowego można podstawić siły T
od strony elementów)
Po podstawieniu otrzymujemy:
1
2
9
183
0, 45
6 (3)
16
320
ϕ
ϕ
+
+
∆ =
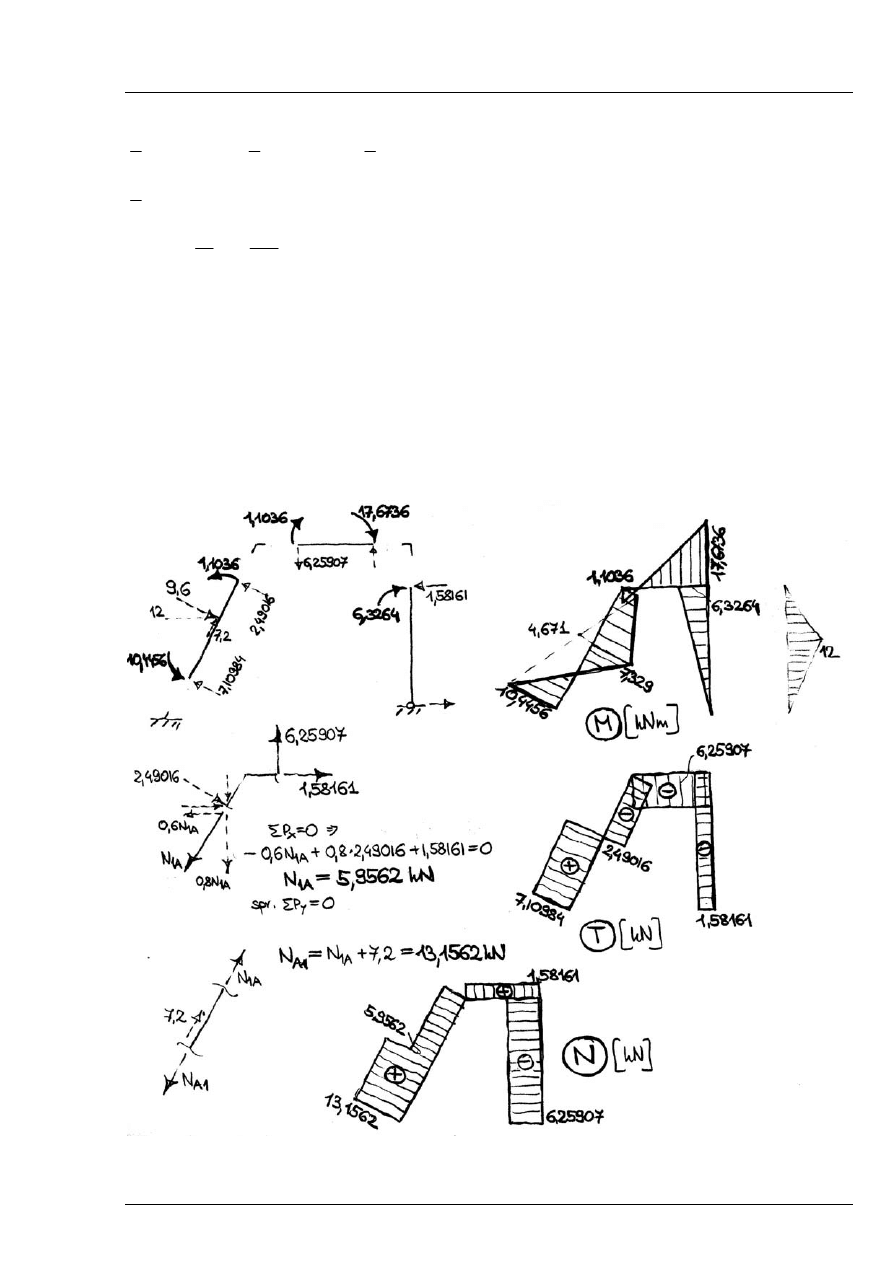
Inny wariant: obliczamy kąty obrotu poszczególnych prętów układu przegubowego (mechanizmu)
Rys. 8.5.4
C16-2005-cw08
74
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Równanie pracy wirtualnej:
1
1
21
12
2
1
1
21
12
2
1
2
1
1
1
(
)
(
)
12 0,
4
4
4
1
(
) 6
4
9
183
0, 45
6 (3)
16
320
A
A
B
A
A
B
M
M
M
M
M
M
M
M
M
M
ϕ
ϕ
+
−
+
+
+ ⋅
=
+
−
−
+
+ =
+
+
∆ =
5 0
0
Po rozwiązaniu układu równań (1), (2), (3) otrzymujemy:
1
2
6,64506,
9,92489,
5,95861
ϕ
ϕ
= −
=
∆ =
Momenty przywęzłowe:
1
1
12
21
2
10, 4456 [
]
1,1036 [
]
1,1036 [
]
17,6736 [
]
6,3264 [
]
A
A
B
M
kNm
M
kNm
M
kNm
M
kNm
M
kN
= −
= −
=
=
=
m
Rozwiązanie:
Rys. 8.3.6
C16-2005-cw08
75
Document Outline