 | Pobierz cały dokument 2007 05 14 praid 25651 Nieznany .pdf Rozmiar 179,1 KB |
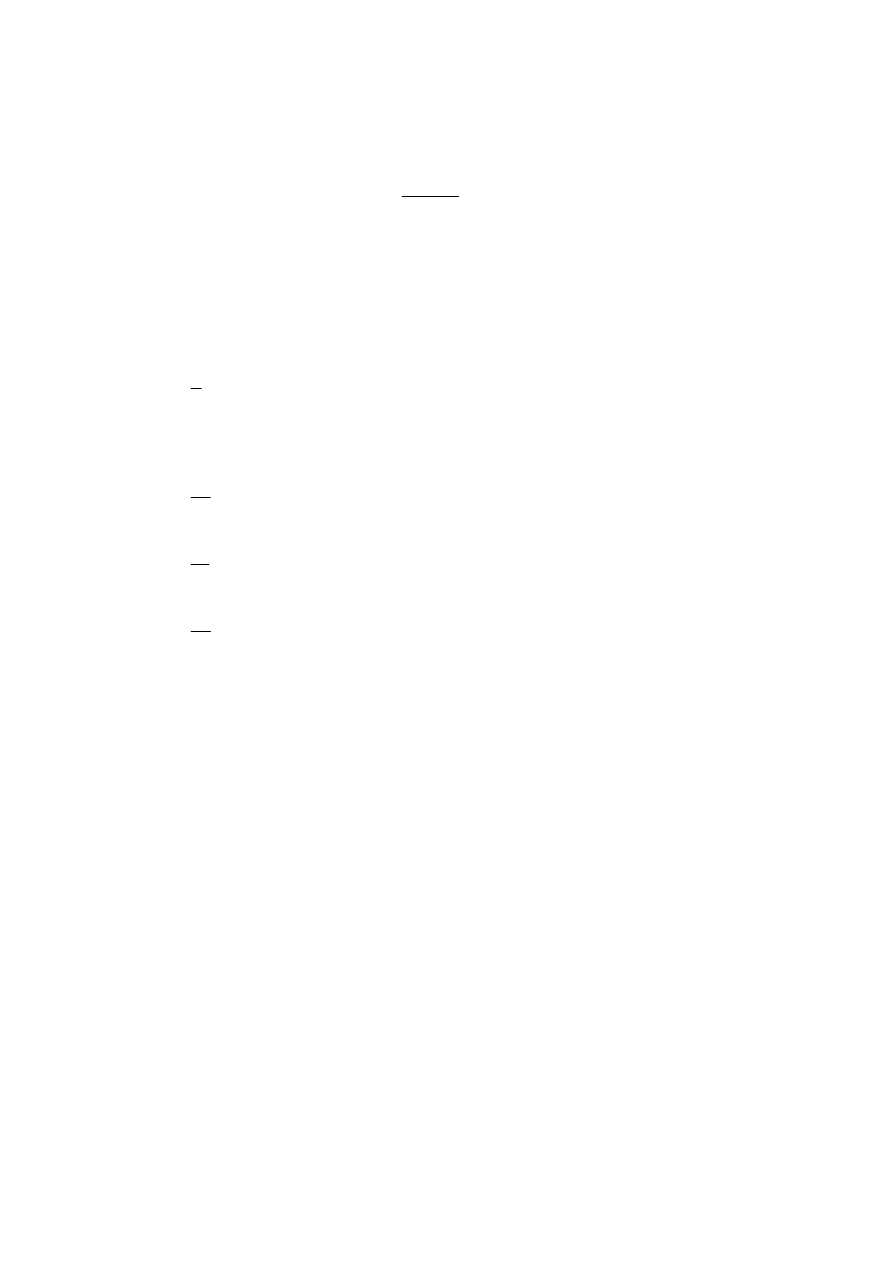
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie 1.
Niech X będzie zmienną losową o rozkładzie Pareto o gęstości
⎪⎩
⎪
⎨
⎧
≤
>
+
=
0
0
0
)
2
(
64
)
(
5
x
gdy
x
gdy
x
x
f
.
Niech Y będzie zmienną losową równą
⎩
⎨
⎧
>
−
≤
=
3
3
3
0
x
gdy
X
x
gdy
Y
.
Wyznaczyć
).
3
|
(
>
X
Y
Var
(A)
9
8
(B) 1
(C)
9
50
(D)
9
12
(E)
9
75
1
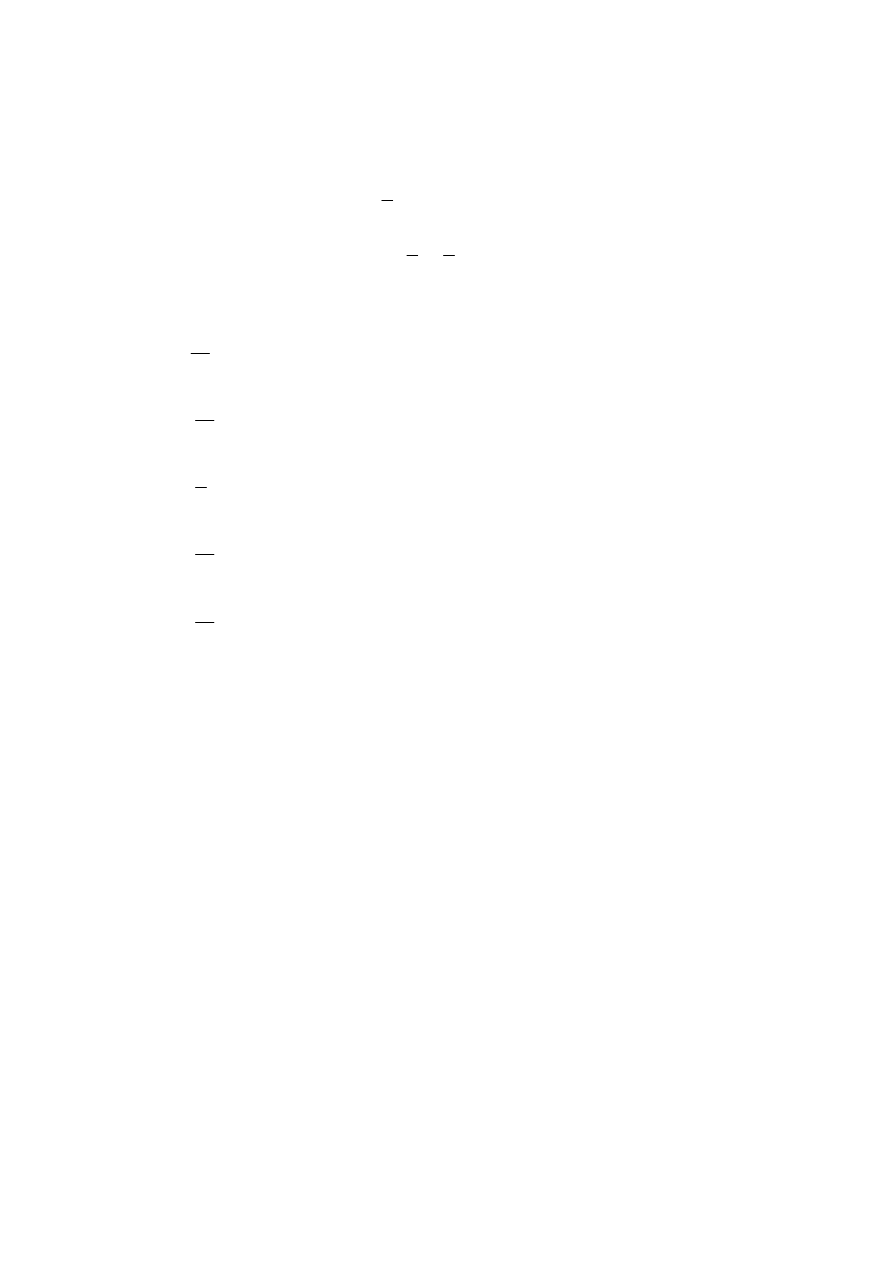
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie 2.
Niech
będą niezależnymi zmiennymi losowymi o tym samym rozkładzie
ujemnym dwumianowym
2
1
, X
X
⎟
⎠
⎞
⎜
⎝
⎛
−
4
3
,
2
bin
(
)
K
,
2
,
1
,
0
dla
4
1
4
3
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛ +
=
=
n
n
n
n
X
P
n
i
,
Wyznaczyć
)
6
|
3
(
2
1
1
=
+
=
X
X
X
P
.
(A)
21
10
(B)
21
4
(C)
2
1
(D)
21
6
(E)
21
11
2
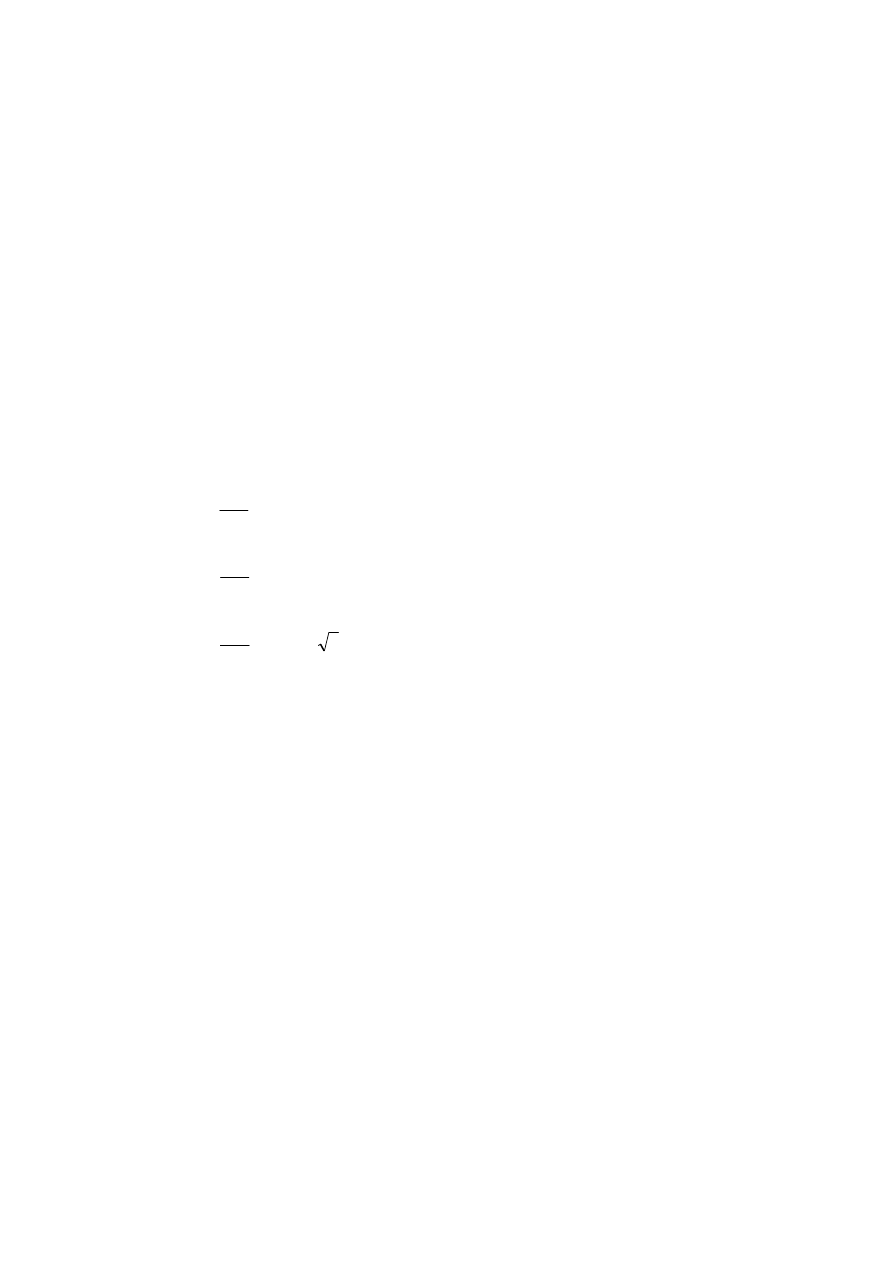
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie 3.
Zmienna losowa N ma rozkład Poissona z parametrem
0
>
λ
. Rozważamy losową
liczbę zmiennych losowych
, przy czym zmienne losowe
są niezależne wzajemnie i niezależne od zmiennej losowej N. Każda ze
zmiennych losowych
ma rozkład Weibulla o gęstości
N
X
X
X
,
,
,
2
1
K
N
X
X
X
,
,
,
2
1
K
i
X
⎩
⎨
⎧
≤
>
−
=
0
0
0
)
exp(
2
)
(
2
x
gdy
x
gdy
x
x
x
p
θ
θ
θ
,
gdzie
0
>
θ
jest nieznanym parametrem. Obserwujemy tylko te spośród zmiennych
, które są większe od 10. Nie wiemy ile jest pozostałych zmiennych ani
jakie są ich wartości. Przypuśćmy, że zaobserwowaliśmy cztery wartości większe od
10 i suma ich kwadratów jest równa 1200. Na podstawie tych danych wyznaczyć
estymatory największej wiarogodności parametrów
N
X
X
X
,
,
,
2
1
K
θ
i
λ
.
(A)
i
4
ˆ
−
= e
θ
4
ˆ =
λ
(B)
300
1
ˆ =
θ
i
e
4
ˆ =
λ
(C)
300
1
ˆ =
θ
i
3
/
1
4
ˆ
e
=
λ
(D)
200
1
ˆ =
θ
i
e
4
ˆ =
λ
(E)
i
4
ˆ
−
= e
θ
e
4
ˆ =
λ
3
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie 4.
W urnie znajdują się trzy kule białe i dwie czarne. Powtarzamy następujące
doświadczenie: losujemy z urny kulę, odkładamy na bok i dorzucamy do urny kulę
białą. Dopiero po trzykrotnym powtórzeniu doświadczenia w urnie nie było już kul
czarnych. Obliczyć prawdopodobieństwo, że w pierwszym doświadczeniu
wylosowano kulę czarną.
(A)
4
3
(B)
7
3
(C)
125
6
(D)
125
8
(E)
7
4
4
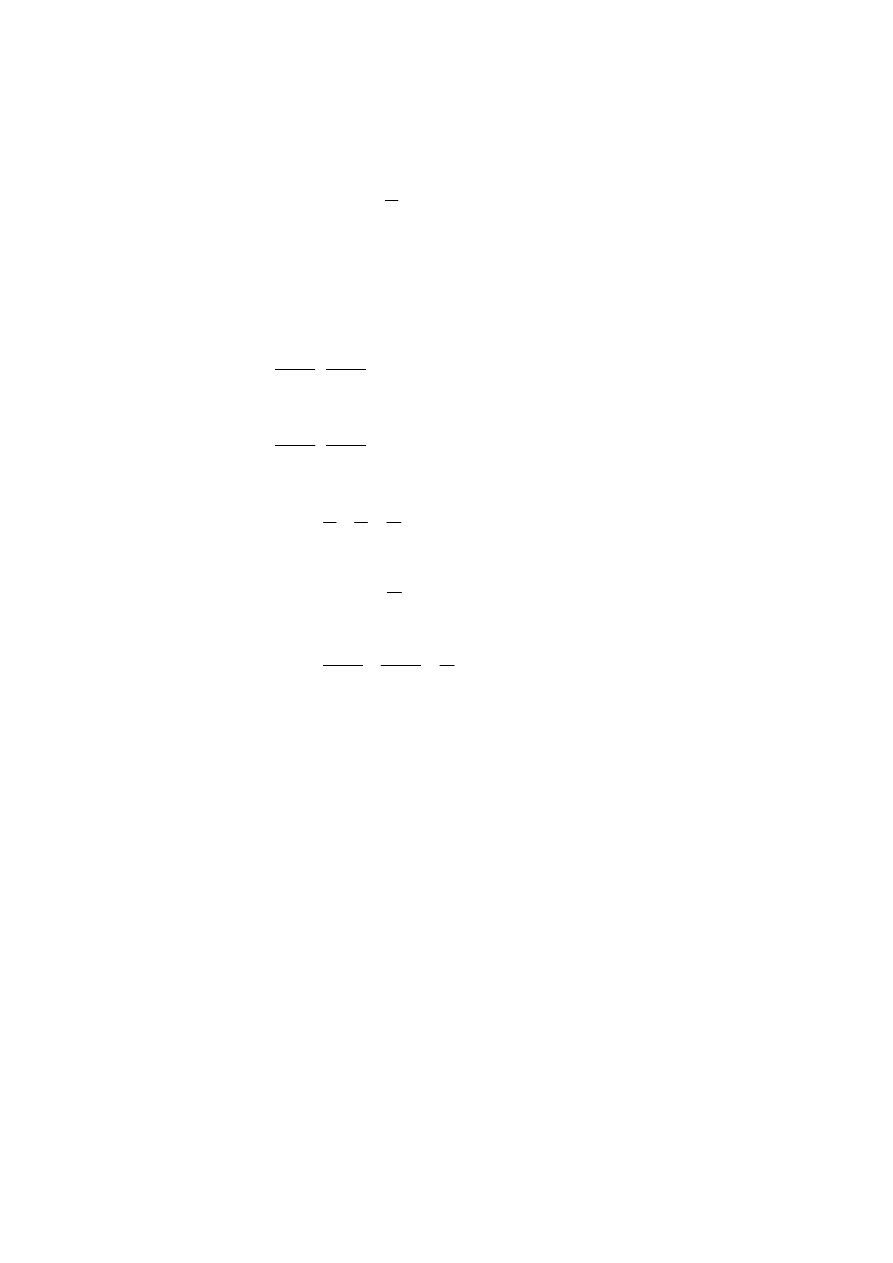
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie 5.
Załóżmy, że
są niezależnymi zmiennymi losowymi o tym samym
rozkładzie wykładniczym i
K
K
,
,
,
,
1
0
n
X
X
X
λ
1
=
i
EX
. Niech
⎭
⎬
⎫
⎩
⎨
⎧
>
≥
=
∑
=
k
i
i
a
X
k
N
0
:
0
min
,
gdzie
a
jest ustaloną liczbą dodatnią. Podać rozkład prawdopodobieństwa zmiennej
N.
(A)
(
)
k
a
a
a
k
N
P
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
=
λ
λ
λ
dla
K
,
2
,
1
,
0
=
k
(B)
(
)
k
a
a
a
k
N
P
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
=
λ
λ
λ
dla
K
,
2
,
1
,
0
=
k
(C)
(
)
!
1
exp
k
a
a
k
N
P
k
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛−
=
=
λ
λ
dla
K
,
2
,
1
,
0
=
k
(D)
(
)
(
)( )
!
1
exp
k
a
a
k
N
P
k
λ
λ
−
=
=
dla
K
,
2
,
1
,
0
=
k
(E)
(
)
!
1
exp
k
a
a
a
a
k
N
P
k
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
=
λ
λ
dla
K
,
2
,
1
,
0
=
k
5
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie 6.
Niech
będą niezależnymi zmiennymi losowymi o tym samym
rozkładzie jednostajnym na przedziale
K
K
,
,
,
,
2
1
n
X
X
X
[ ]
θ
,
0
, gdzie
0
>
θ
jest nieznanym parametrem.
Rozważamy estymator nieobciążony parametru
θ
postaci
(
)
n
n
n
n
aX
T
X
X
X
T
:
1
2
1
,
,
,
=
=
K
,
gdzie
i a jest pewną stałą. Wtedy
{
n
n
X
X
X
X
,
,
,
min
2
1
:
1
K
=
}
(A)
(
0
lim
0
0
=
>
−
>
∀
>
∀
∞
→
ε
θ
θ
ε
θ
n
n
T
P
)
(B)
(
)
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
>
−
>
∀
>
∀
∞
→
θ
ε
ε
θ
θ
ε
θ
1
exp
lim
0
0
n
n
T
P
(C)
(
)
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
>
−
>
∀
>
∃
∞
→
θ
ε
ε
θ
θ
ε
θ
1
exp
lim
0
0
n
n
T
P
(D)
(
)
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
=
>
−
>
∃
>
∃
∞
→
θ
ε
θ
ε
ε
θ
θ
ε
θ
1
exp
1
exp
1
lim
0
0
n
n
T
P
(E)
(
)
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
=
>
−
>
∀
>
∀
∞
→
θ
ε
θ
ε
ε
θ
θ
ε
θ
1
exp
1
exp
1
lim
0
0
n
n
T
P
6
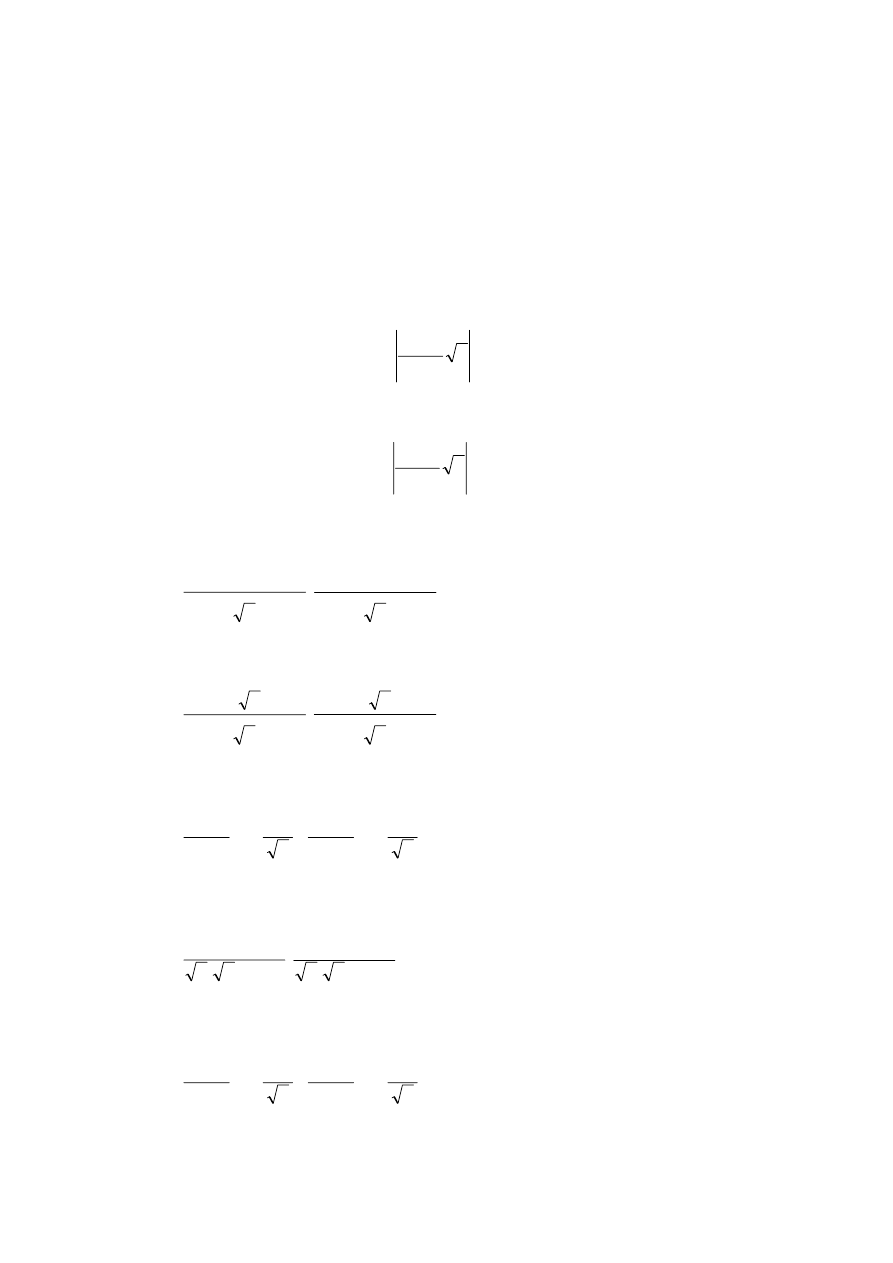
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie
7.
Niech
będą niezależnymi zmiennymi losowymi z rozkładu Weibulla o
gęstości
n
X
X
X
,
,
,
2
1
K
(
)
⎩
⎨
⎧
≤
>
−
=
0
0
0
exp
3
)
(
3
2
x
gdy
x
gdy
x
x
x
f
θ
θ
θ
,
gdzie
0
>
θ
jest nieznanym parametrem. Przedział ufności dla parametru
θ
w oparciu
o estymator największej wiarogodności
(
)
n
n
n
X
X
X
,
,
,
ˆ
ˆ
2
1
K
θ
θ
=
parametru
θ
otrzymujemy rozwiązując nierówność
z
n
n
≤
−
)
(
ˆ
θ
σ
θ
θ
,
gdzie )
(
θ
σ
jest wariancją asymptotyczną statystyki
(
)
n
n
n
X
X
X
,
,
,
ˆ
ˆ
2
1
K
θ
θ
=
i liczba z
spełnia
95
,
0
)
(
ˆ
lim
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
≤
−
+∞
→
z
n
P
n
n
θ
σ
θ
θ
.
Tak otrzymany przedział ma postać
(A)
(
)
(
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
+
∑
∑
=
=
n
i
i
n
i
i
n
X
n
n
X
n
1
3
1
3
96
,
1
,
96
,
1
(B)
(
)
(
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
+
∑
∑
=
=
n
i
i
n
i
i
n
X
n
n
n
X
n
n
1
3
1
3
96
,
1
,
96
,
1
(C)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ +
⎟
⎠
⎞
⎜
⎝
⎛ −
∑
∑
=
=
n
X
n
n
X
n
n
i
i
n
i
i
96
,
1
1
,
96
,
1
1
1
3
1
3
(D)
(
) (
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
+
∑
∑
=
=
96
,
1
,
96
,
1
1
3
1
3
n
n
X
n
n
X
n
i
i
n
i
i
(E)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ +
⎟
⎠
⎞
⎜
⎝
⎛ −
∑
∑
=
=
n
n
X
n
n
X
n
i
i
n
i
i
96
,
1
1
,
96
,
1
1
1
3
1
3
7
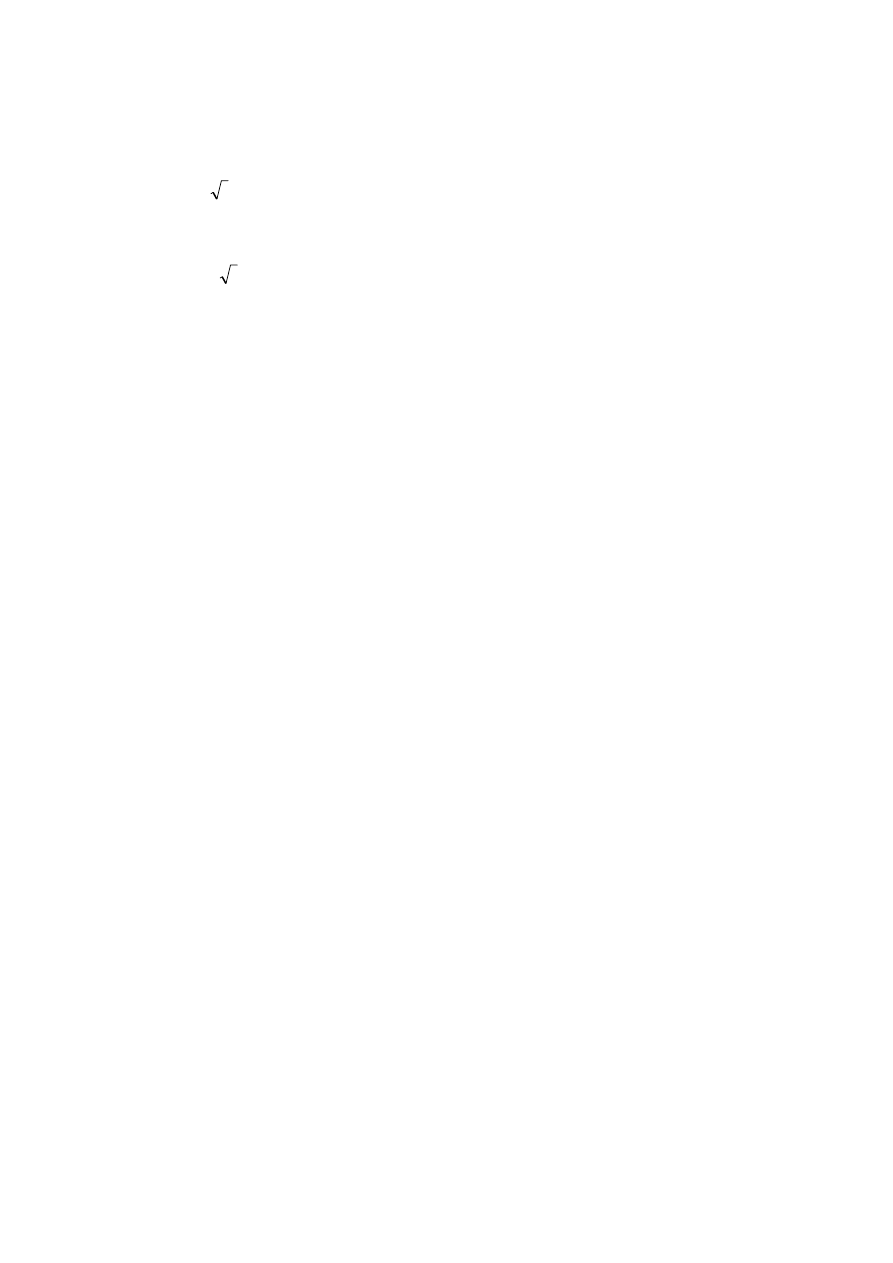
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie
8.
Zakładając, że zmienne losowe
są niezależne i mają rozkłady normalne
5
2
1
,
,
,
X
X
X
K
)
1
,
(
~
i
m
N
X
i
zbudowano test jednostajnie najmocniejszy dla weryfikacji hipotezy
przy alternatywie
na poziomie istotności 0,05.
0
:
0
=
m
H
0
:
1
>
m
H
W rzeczywistości okazało się, że wektor
ma rozkład normalny taki,
że
)
,
,
,
(
5
2
1
X
X
X
K
i
m
EX
i
=
,
⎪
⎩
⎪
⎨
⎧
=
=
−
=
0
1
1
|
|
5
,
0
)
,
(
pp
w
j
i
gdy
j
i
gdy
X
X
Cov
j
i
Wyznaczyć rzeczywisty rozmiar testu.
(A) 0,11
(B) 0,08
(C) 0,15
(D) 0,07
(E) 0,02
8
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie
9.
Obserwujemy
niezależnych zmiennych losowych o tym samym
rozkładzie Pareto o gęstości
4
3
2
1
,
,
,
X
X
X
X
⎪⎩
⎪
⎨
⎧
≤
>
+
=
+
0
0
0
)
1
(
)
(
1
1
1
1
x
gdy
x
gdy
x
x
f
θ
θ
θ
i
niezależnych zmiennych losowych o tym samym rozkładzie Pareto o
gęstości
5
2
1
.
,
,
Y
Y
Y
K
⎪⎩
⎪
⎨
⎧
≤
>
+
=
+
0
0
0
)
1
(
)
(
1
2
2
2
x
gdy
x
gdy
x
x
f
θ
θ
θ
gdzie
1
θ
i
2
θ
są nieznanymi parametrami dodatnimi.
Wszystkie zmienne losowe są niezależne. Testujemy hipotezę
2
:
2
1
0
=
θ
θ
H
przy
alternatywie
2
:
2
1
1
<
θ
θ
H
za pomocą testu o obszarze krytycznym
⎭
⎬
⎫
⎩
⎨
⎧
<
=
t
K
2
1
ˆ
ˆ
θ
θ
gdzie
i są estymatorami największej wiarogodności odpowiednio parametrów
1
ˆ
θ
2
ˆ
θ
1
θ
i
2
θ
wyznaczonymi na podstawie prób losowych
i
.
Dobrać stałą t tak, aby otrzymać test o rozmiarze 0,05.
4
3
2
1
,
,
,
X
X
X
X
5
2
1
.
,
,
Y
Y
Y
K
(A)
1628
,
0
=
t
(B)
5358
,
1
=
t
(C)
6511
,
0
=
t
(D)
6736
,
1
=
t
(E)
3852
,
0
=
t
9
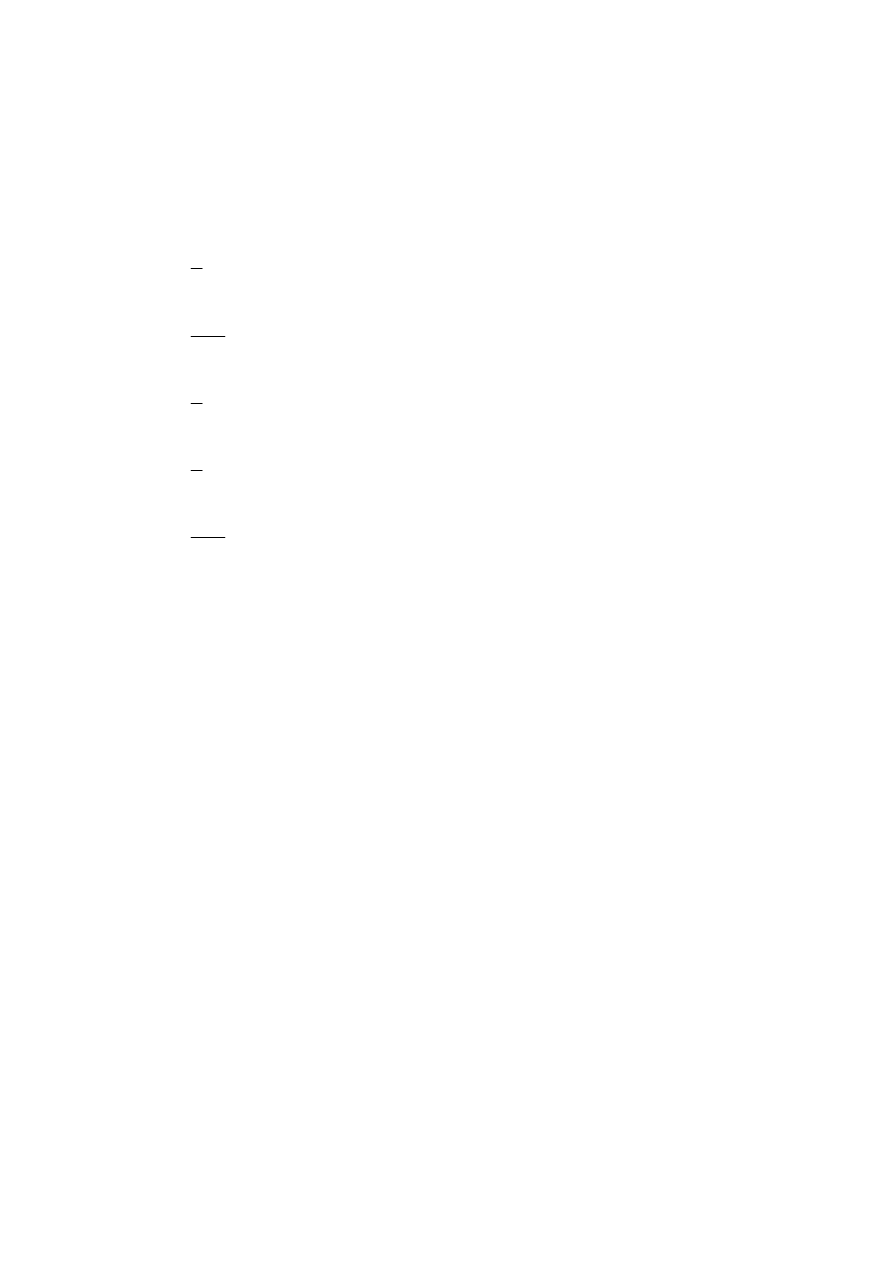
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Zadanie
10.
Niech
będą niezależnymi zmiennymi losowymi o tym samym
rozkładzie wykładniczym o wartości oczekiwanej 1. Obliczyć
n
X
X
X
X
,
,
,
,
2
1
0
K
{
}
(
)
0
1
0
|
,
,
,
min
X
X
X
X
E
n
K
(A)
(
)
(
)
(
0
0
0
exp
exp
1
1
nX
X
nX
n
−
+
−
−
)
(B)
(
)
(
)
(
0
0
0
)
1
(
exp
)
1
(
exp
1
1
1
X
n
X
X
n
n
+
−
+
+
−
−
+
)
(C)
(
)
(
)
(
0
0
0
exp
exp
1
1
nX
X
nX
n
−
−
−
−
)
(D)
(
)
(
)
0
exp
1
1
nX
n
−
−
(E)
1
1
+
n
10
Prawdopodobieństwo i statystyka
14.05.2007 r.
___________________________________________________________________________
Egzamin dla Aktuariuszy z 14 maja 2007 r.
Prawdopodobieństwo i statystyka
Arkusz odpowiedzi
Imię i nazwisko : ........................ K L U C Z O D P O W I E D Z I ..............................
Pesel ...........................................
Zadanie nr
Odpowiedź Punktacja
1 C
2 B
3 D
4 E
5 D
6 D
7 B
8 A
9 C
10 D
*
Oceniane są wyłącznie odpowiedzi umieszczone w Arkuszu odpowiedzi.
♦
Wypełnia Komisja Egzaminacyjna.
11
| Pobierz cały dokument 2007 05 14 praid 25651 Nieznany .pdf Rozmiar 179,1 KB |