Akademia Górniczo-Hutnicza

Katedra Robotyki i Mechatroniki

Identyfikacja i analiza sygnałów

Laboratorium 2

Wprowadzenie do przetwarzania sygnałów w dziedzinie

czasu

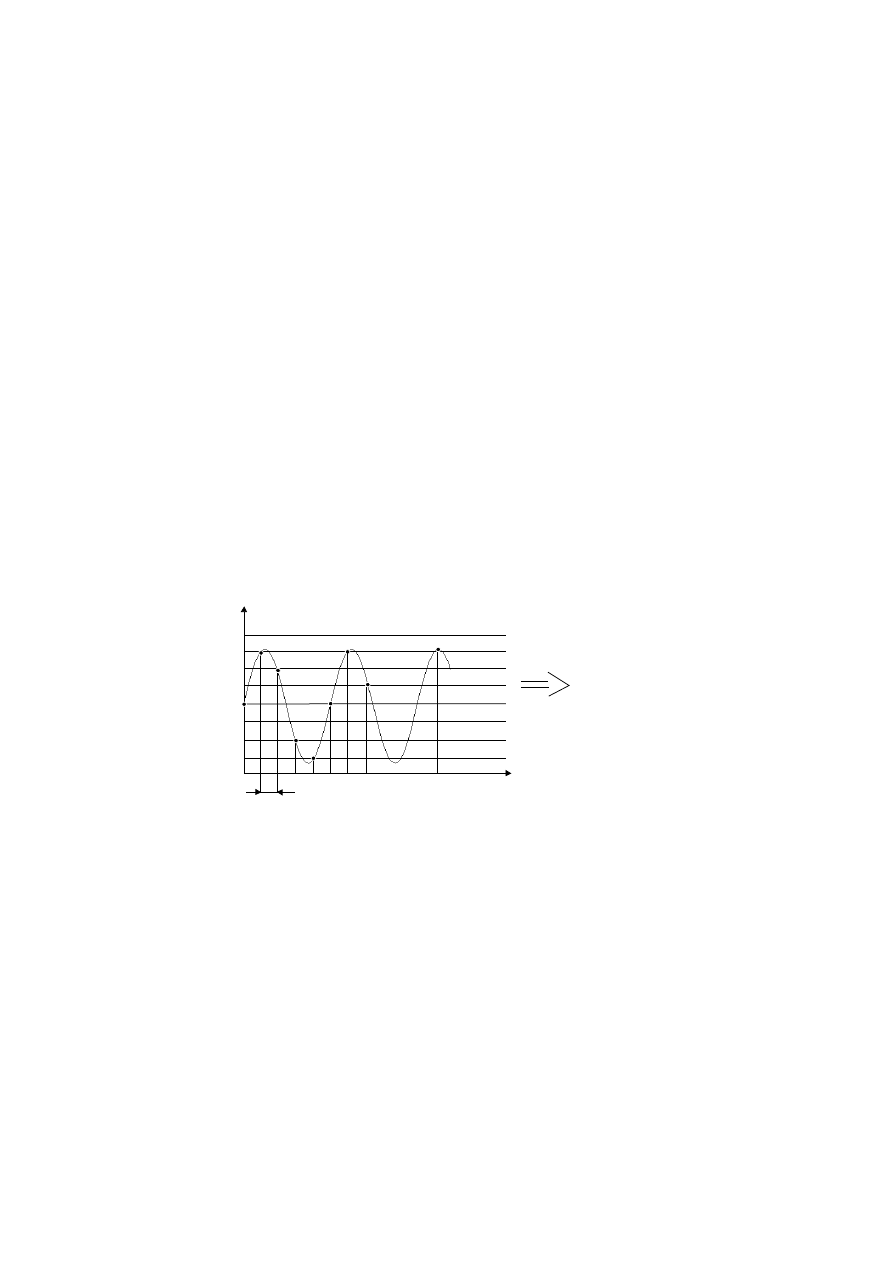
Przetwarzanie sygnału dla potrzeb badania dynamiki układów
mechanicznych

Problemy wstępnego przetwarzania sygnału w dziedzinie czasu

Podstawową czynnością w przetwarzaniu sygnałów jest przetwarzanie sygnału o naturze
analogowej do postaci cyfrowej. Proces ten polega na zamianie wielkości analogowej na ciąg
dyskretnych wartości w zadanych chwilach czasowych. Operacja ta nie wnosi nowych
informacji o sygnale, czasem może prowadzić do utraty pewnej ilości informacji.
Przetwarzanie analogowo-cyfrowe sygnałów składa się z dwóch podstawowych czynności:

−

kwantowanie sygnału,

−

dyskretyzacja sygnału.

0

1

2

3

4

5

6

7

8

n

∆

t

t

1

2

3

4

5

6

7

(0,4) (1,7) (2,6) (3,2)

(4,1) (5,4) (6,7) (7,5)...(n,7)

X

Rys. 1 Schematyczne przedstawienie procesu przetwarzania analogowo

−

cyfrowego.

Dyskretyzacja sygnału polega na wyborze na osi czasu dyskretnych chwil czasowych, w
których określona jest wartość amplitudy sygnału w procesie przetwarzania. Dyskretyzacja
sygnału odbywa się z okresem próbkowania zależnym od wymaganych parametrów analizy,
zakresu częstości w analizowanym sygnale tak, aby spełnione było twierdzenie Shanona o
próbkowaniu sygnałów. Twierdzenie to mówi, że: "Sygnał nie zawierający częstości
większych niż f

N

(częstość graniczna) może być jednoznacznie opisany za pomocą

dyskretnych próbek, otrzymanych przez próbkowanie analizowanego sygnału z częstością

f

f

S

N

≥

2

" W praktyce częstość f

S

jest 4 do 10 razy większa niż częstość f

N

.

Kolejną czynnością jest kwantyzacja polegająca na zamianie wartości analogowej na postać
cyfrową o wartości całkowitej związanej z ustalonym poziomem kwantyzacji.. Przetwarzanie
analogowo-cyfrowe sygnałów jest wykonywane za pomocą specjalizowanych układów
elektronicznych.

Przykłady związane z doborem częstotliwości próbkowania

Odpowiedni dobór częstotliwości próbkowania:

f1 = 1; % Częstotliwości przykładowych przebiegów sinusoidalnych
f2 = 4;

f3 = 6;

fs = 200; % Częstotliwość próbkowania sygnału
t=0:(1/fs):1; % Wektor czasu

% Definicje przykładowych przebiegów sinusoidalnych

x1 = sin(2*pi*f1*t);
x4 = -sin(2*pi*f2*t);

x6 = sin(2*pi*f3*t);
plot(t,x1,t,x4,t,x6)

Wybór zbyt niskiej częstotliwości próbkowania:

fs = 5; % Częstotliwość próbkowania sygnału
t=0:(1/fs):1; % Wektor czasu

% Definicje przykładowych przebiegów sinusoidalnych

x1 = sin(2*pi*f1*t);
x4 = -sin(2*pi*f2*t);

x6 = sin(2*pi*f3*t);
plot(t,x1,t,x4,t,x6)

Kolejny przykład złego doboru częstotliwości próbkowania zawarty jest poniżej.

fs = 20; % Częstotliwość próbkowania sygnału

t=0:(1/fs):10; % Wektor czasu

x = sin(2*pi*40*t);
plot(t,x)

Przedstawiona w powyższych przykładach niejednoznaczność przetwarzania analogowo
cyfrowego jest podstawowym problemem przetwarzania sygnałów. Wynika ona z faktu, że w
przypadku gdy w sygnale znajdują się składowe o częstości większej niż f

S

/ 2 wówczas nie

mogą one być odtworzone w sposób jednoznaczny, a mogą mieć wpływ na wartość amplitudy
sygnału. Zjawisko to jest nazywane aliazingiem.
Aby uniknąć zjawiska aliazingu należy przed przetwarzaniem usunąć z sygnału wszystkie
składowe o częstości większej niż f

S

/ 2 . W tym celu stosuje się na etapie kondycjonowania

sygnału filtrację analogową za pomocą filtru dolnoprzepustowego, o częstości przepuszczania

mniejszej niż

f

S

2

. Ze względu na to, że nie istnieją filtry idealne o pionowym nachyleniu

zbocza, częstość graniczną filtru przyjmuje się w praktyce ok. 40 % f

S

. Nachylenie zbocza

filtru zależy od jego rzędu i dla najczęściej stosowanych filtrów typu Buttworta 6 rzędu
wynosi 48 dB na oktawę. Do bardzo efektywnych filtrów należą filtry Cautera, dla których
nachylenie zbocza wynosi 96 dB/oktawę.

Zastosowanie filtracji cyfrowej

W tej części przedstawiono możliwości toolboxu Signal Processing Toolbox (SPT) z zakresu
analizy i projektowania filtrów cyfrowych.

Splot i filtrowanie
Matematyczną podstawą filtracji jest splot. Matlabowska funkcja

conv

dokonuje

standardowego jednowymiarowego splotu dwóch wektorów.

conv([1 1 1],[1 1 1])

•

ans =

•

1 2 3 2 1

Splotu macierzy prostokątnych dla dwuwymiarowego przetwarzania sygnałów można
natomiast dokonać za pomocą funkcji

conv2

.

Sekwencja danych y(n) otrzymywana na wyjściu filtru cyfrowego jest splotem ciągu danych
wejściowych x(n) przez splot z odpowiedzią impulsowego filtru h(n):

∑

∞

− ∞

=

−

=

∗

=

m

)

m

(

x

)

m

n

(

h

)

n

)(

x

h

(

)

n

(

y

( 1 )

i może być interpretowana jako ruchoma średnia ważona wejścia.
Jeżeli odpowiedź impulsowa filtru cyfrowego h(n) oraz sygnał wejściowy x(n) mają
skończone długości, można wtedy dokonać filtracji za pomocą funkcji

conv

. Przykładowo

utworzono sygnał wejściowy x(n) jako wektor x, sygnał h(n) jako wektor h, a następnie
dokonano ich splotu.

x=randn(5,1);

h=[1 1 1 1]/4;
y=conv(h,x);

Funkcja przejścia filtru
Definicja funkcji przejścia filtru oparta jest na własnościach przekształcenia Z. Transformata
Z Y(z) z cyfrowego wyjścia filtru y(n) jest powiązana z transformacją Z X(z) wejścia x(n)
następującym wzorem:

)

z

(

X

z

)

1

na

(

a

...

z

)

2

(

a

1

z

)

1

nb

(

b

...

z

)

2

(

b

)

1

(

b

)

z

(

X

)

z

(

H

)

z

(

Y

na

1

nb

1

⋅

⋅

+

+

+

⋅

+

⋅

+

+

+

⋅

+

=

⋅

=

−

−

−

−

( 2 )

gdzie H(z) jest funkcją przejścia filtru. Stałe b(i) oraz a(i) są współczynnikami filtru, a
wartość na i nb reprezentuje rząd filtru. Współczynniki filtru są zebrane w dwóch wektorach:
b - dla licznika i a - dla mianownika. Według przyjętej konwencji Matlab używa wektora
wierszowego dla zapamiętania współczynników.

Uwaga: Indeksowanie współczynników w wektorach rozpoczyna się od liczby 1, zamiast od
0. Jest to standardowy schemat stosowanego w Matlabie sposobu indeksowania wektorów.

Filtrowanie przy pomocy funkcji

filter

W celu przedstawienia sposobu działania funkcji

filter

cofnijmy się do zależności (2). Po

pomnożeniu równania (2) przez mianownik ułamka i dokonaniu odwrotnej transformaty Z
otrzymuje się następującą zależność:

)

nb

n

(

x

)

1

nb

(

b

)

1

n

(

x

)

2

(

b

...

)

n

(

x

)

1

(

b

)

na

n

(

y

)

1

na

(

a

...

)

1

n

(

y

)

2

(

a

)

n

(

y

−

⋅

+

+

+

−

⋅

+

+

⋅

=

−

⋅

+

+

+

−

⋅

+



( 3 )

Z równania (3) wynika, że wartość y(n) można wyznaczyć znając wartości wejściowe x(n),
x(n-1), ...,x(n-nb):

)

na

n

(

y

)

1

na

(

a

...

)

1

n

(

y

)

2

(

a

)

nb

n

(

x

)

1

nb

(

b

...

)

1

n

(

x

)

2

(

b

)

n

(

x

)

1

(

b

)

n

(

y

−

⋅

+

−

−

−

⋅

−

−

⋅

+

+

+

−

⋅

+

⋅

=

( 4 )

( )

)

k

n

(

y

)

1

k

(

a

)

m

n

(

x

)

1

m

(

b

n

y

na

0

k

nb

0

m

−

⋅

+

−

−

⋅

+

=

∑

∑

=

=

Równanie (4) jest standardową reprezentacją filtru cyfrowego w dziedzinie czasu i nosi
nazwę tzw. równania różnicowego. Obliczenia rozpoczyna się dla y(1), zakładając zerowe
warunki początkowe. Algorytm obliczeń przedstawiają równania (5):

⋮

)

1

(

y

)

3

(

a

)

2

(

y

)

2

(

a

)

1

(

x

)

3

(

b

)

2

(

x

)

2

(

b

)

3

(

x

)

1

(

b

)

3

(

y

)

1

(

y

)

2

(

a

)

1

(

x

)

2

(

b

)

2

(

x

)

1

(

b

)

2

(

y

)

1

(

x

)

1

(

b

)

1

(

y

−

−

+

+

=

−

+

=

=

( 5 )

W tej formie filtr cyfrowy jest wprowadzany przez funkcję

filter

. Dla przykładu, prosty

rekurencyjny filtr dolnoprzepustowy z pojedynczym biegunem (zero wielomianu mianownika
funkcji przejścia H(z) (2)) jest dany jako:

b=1;

a=[1 -0.9];

gdzie wektory a i b reprezentują współczynniki filtru w formie funkcji przejścia. Filtr
realizowany jest poprzez wyrażenie:

y=filter(b,a,x);

Funkcja

filter

oblicza tyle próbek wyjściowych, ile jest próbek wejściowych, znaczy to, że

długość wektora y jest taka sama, jak długość wejściowego wektora x. Jeśli pierwszy element
a(1) nie jest 1, funkcja

filter

dzieli przez niego współczynniki uprzednio wyprowadzonych

równań różnicowych postaci (4).

Odpowiedź impulsowa
Odpowiedź impulsową (charakterystykę czasową) filtru cyfrowego otrzymujemy podając na
wejście filtru następujący ciąg próbek:









≠

=

=

1

n

dla

0

1

n

dla

1

)

n

(

x

W Matlabie funkcję impulsową, można wygenerować na wiele sposobów. Najprostszy to
wykonanie poniższego polecenia:

imp=[1 zeros(1,49)];

Odpowiedź impulsową prostego filtru o współczynnikach

b=1;

a=[1 -0.9];

otrzymamy

po wykonaniu polecenia:

h=filter(b,a,imp);

Funkcja

impz

w przyborniku upraszcza powyższą operację wybierając liczbę generowanych

punktów oraz tworząc wykres słupkowy odpowiedzi filtru (używając wewnętrznie funkcji

stem

):

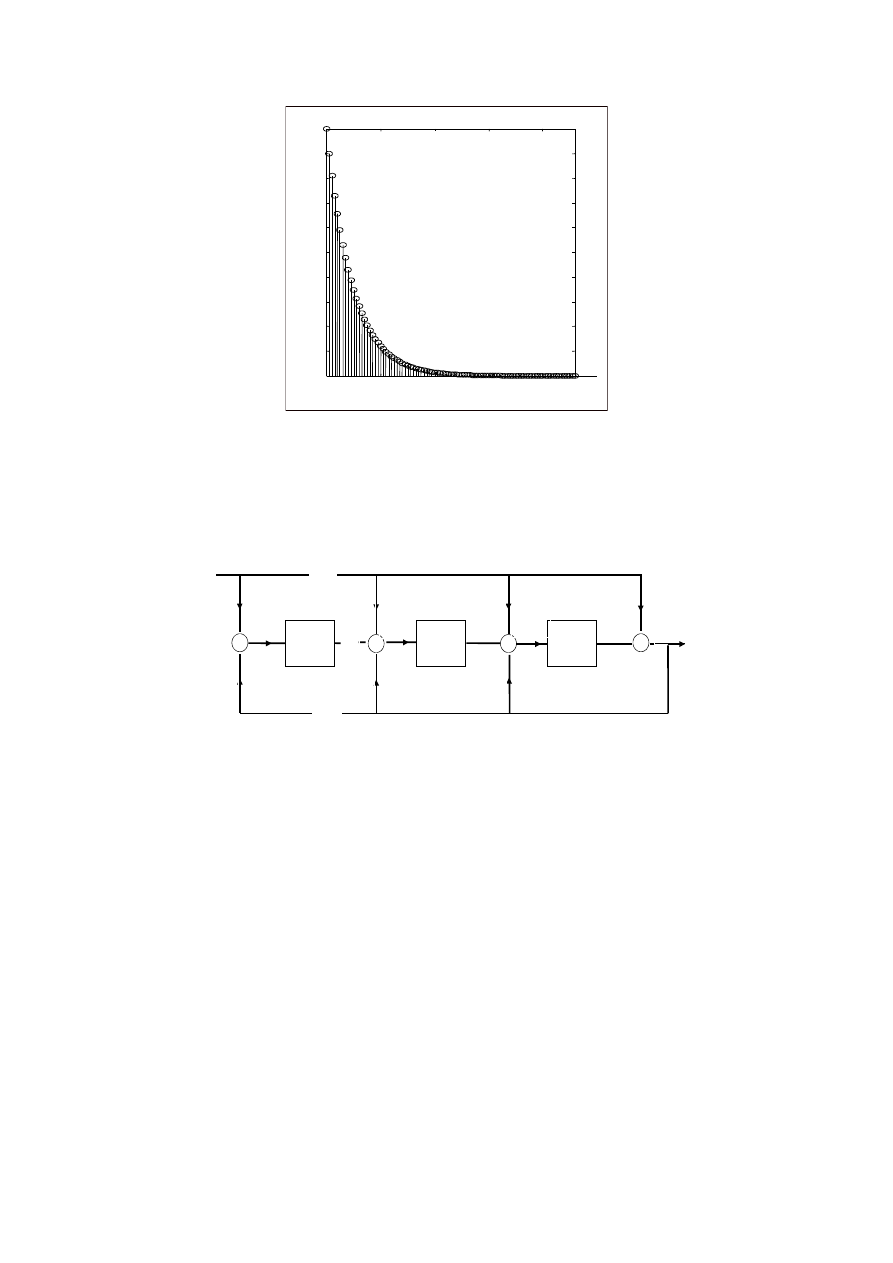
impz(b,a)

0

20

40

60

80

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Rys. 2 Odpowiedź impulsowa przykładowego filtru uzyskana za pomocą funkcji impz

Wykres pokazuje eksponencjalny rozkład 0.9

n

układu z pojedynczym biegunem.

Funkcja filter
Funkcja

filter

jest wprowadzana jako transpozycja struktury przedstawionej na rys. 3,

gdzie n-1 jest rzędem filtru.

Σ

Σ

Σ

Σ

z

n-1

(m)

z

-1

z

-1

z

-1

z

2

(m)

z

1

(m)

...

...

...

b(n)

b(1)

b(2)

b(3)

-a(n)

y(m)

-a(2)

-a(3)

x(m)

Rys. 3 Struktura blokowa filtru wprowadzanego w SPT

Jest to podstawowa forma filtru cyfrowego, posiadająca minimalną ilość elementów
opóźniających.
Przy m - tej próbce sygnału, funkcja

filter

rozwiązuje następujący układ równań

różnicowych:

)

m

(

y

)

n

(

a

)

m

(

x

)

n

(

b

)

m

(

z

)

m

(

y

)

1

n

(

a

)

1

m

(

z

)

m

(

x

)

1

n

(

b

)

m

(

z

)

m

(

y

)

2

(

a

)

1

m

(

z

)

m

(

x

)

2

(

b

)

m

(

z

)

1

m

(

z

)

m

(

x

)

1

(

b

)

m

(

y

1

n

1

n

2

n

2

1

1

−

=

−

−

−

+

−

=

=

−

−

+

=

−

+

=

−

−

−

⋮

⋮

( 6 )

W najbardziej podstawowej formie, funkcja

filter

wprowadza opóźnienia z

i

(1), i=1,...,n-1,

równe zero. Opóźnienia te można jednak nastawiać wprowadzając czwarty parametr
wejściowy w funkcji. Można także uzyskać dostęp do opóźnienia wprowadzanego przez
funkcję poprzez wykorzystanie drugiego parametru wyjściowego:

[y,zf]=filter(b,a,x,zi);

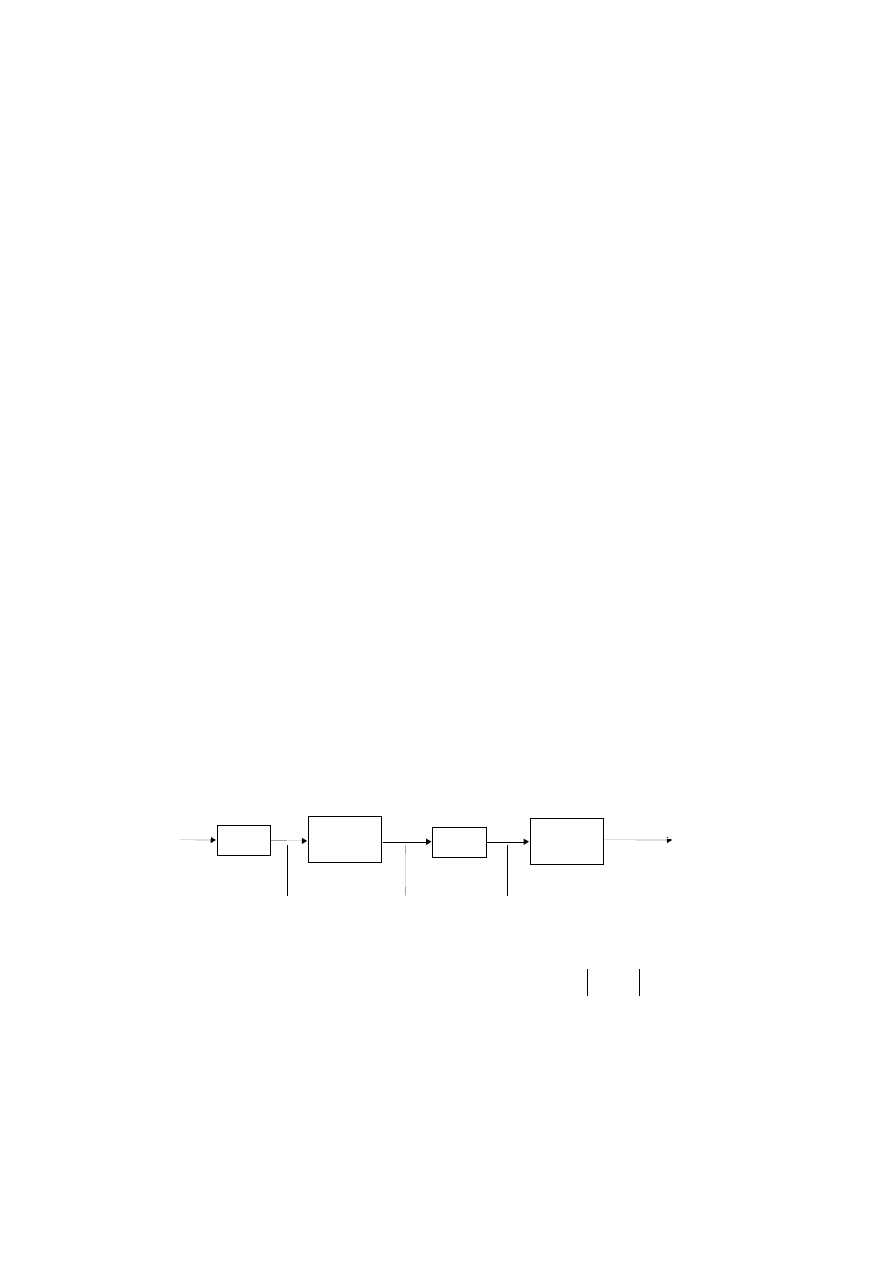
Dostęp do wyżej wymienionych parametrów jest użyteczny podczas filtrowania danych w
sekcjach, zwłaszcza gdy należy się liczyć z ograniczeniami pamięci. Przykładowe dane
zgromadzone zostały w dwóch segmentach po 5000 punktów każdy:

x1=randn(5000,1);
x2=randn(5000,1);

Załóżmy, że pierwsza sekwencja x1 odpowiada pierwszym 10 minutom danych, druga zaś x2
kolejnym 10 minutom. Cała sekwencja ma długość x = [x1;x2]. Jeśli nie posiadamy
wystarczającej ilości pamięci do przetworzenia całej sekwencji od razu, przefiltrujmy
podsekwencje jedna po drugiej. Do zapewnienia ciągłości filtrowanych danych, użyjmy
warunków końcowych z filtracji x1 jako warunków początkowych w wywołaniu filtracji x2:

[y1,zf]=filter(b,a,x1);
y2=filter(b,a,x2,zf);

W przyborniku dostępna jest również dodatkowa funkcja

filtic

, generująca zewnętrznie

warunki początkowe dla funkcji

filter

. Utwórzmy taką samą wartość opóźnienia jak w

przykładzie powyżej używając do tego celu funkcji

filtic

:

zf=filtic(b,a,flipud(y1),flipud(x1));

Ta funkcja jest użyteczna podczas filtracji krótkich sekwencji danych, ponieważ odpowiednie
warunki początkowe eliminują startowe stany nieustalone.

Podstawowe funkcje stosowane do filtracji
Oprócz funkcji

filter

w SPT znajdują się jeszcze dwie inne instrukcje, które dokonują

podstawowych operacji filtrowania. Są to

filtfilt

eliminująca zniekształcenia fazowe w

procesie filtrowania, oraz

fftfilt

, która dokonuje filtracji FIR (Finite Impulse Response) w

dziedzinie częstotliwościowej.

Ogólne zasady filtracji cyfrowej w Matlabie
Implementacja filtru FIR o liniowej fazie może być zrealizowane dla funkcji

filter

lub

conv

poprzez dodanie do sekwencji danych opóźnienia wyjścia o stałą liczbę próbek. Dla

filtrów IIR (Infinite Impulse Response) natomiast zniekształcenia fazowe są stosunkowo
duże. Funkcja

filtfilt

eliminuje te zniekształcenia, także w przypadku filtrów typu FIR.

Prześledźmy sposób działania funkcji

filtfilt

. Oznaczmy transformatę Z sekwencji x(n)

jako X(z) oraz transformatę Z sekwencji x(n) odwróconej w czasie jako X(1/z). Opisana
funkcja realizuje obliczenia według schematu przedstawionego na rys. 4.

Odwrotność

czasu

Odwrotność

czasu

H(z)

H(z)

X(z)

X(z)H(z)

X(1/z)H(1/z)

X(1/z)H(1/z)H(z)

Y(z)=X(z)H(z)H(1/z)

Rys. 4 Schemat działania funkcji filtfilt

Gdy



z



=1, co znaczy że z=e

j

ω

, wyjście redukuje się do:

2

j

j

)

e

(

H

)

e

(

X

ω

ω

⋅

. Wszystkie próbki

ciągu wyjściowego y(n) stanowią podwójnie przefiltrowany ciąg danych wejściowych x(n).
Dla przykładu przefiltrowano próbkę sygnału o długości 1 sekundy, próbkowanego z
częstotliwością 100 Hz, składającego się z dwóch sinusoidalnych składników, jednego o
częstotliwości 3 i drugiego o częstotliwości 40 Hz.

Fs=100;
t=0:1/Fs:1;

x=sin(2*pi*t*3)+0.25*sin(2*pi*t*40);

Utworzono również prosty uśredniający filtr FIR dziesiątego rzędu, a następnie
przefiltrowano sygnał

x

używając w tym celu obu funkcji

filtfilt

i

filter

.

b=ones(1,10)/10;
y=filtfilt(b,1,x);

yy=filter(b,1,x);
subplot(1,1,1);

plot(t,x,'black',t,y,'--black',t,yy,':black')

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

0 . 9

1

- 1 . 5

- 1

- 0 . 5

0

0 . 5

1

1 . 5

P r z e b i e g w e j c i o w y

ś

F i l t r a c j a f u n k c j f i l t f i l t

ą

F i l t r a c j a f u n k c j f i l t e r

ą

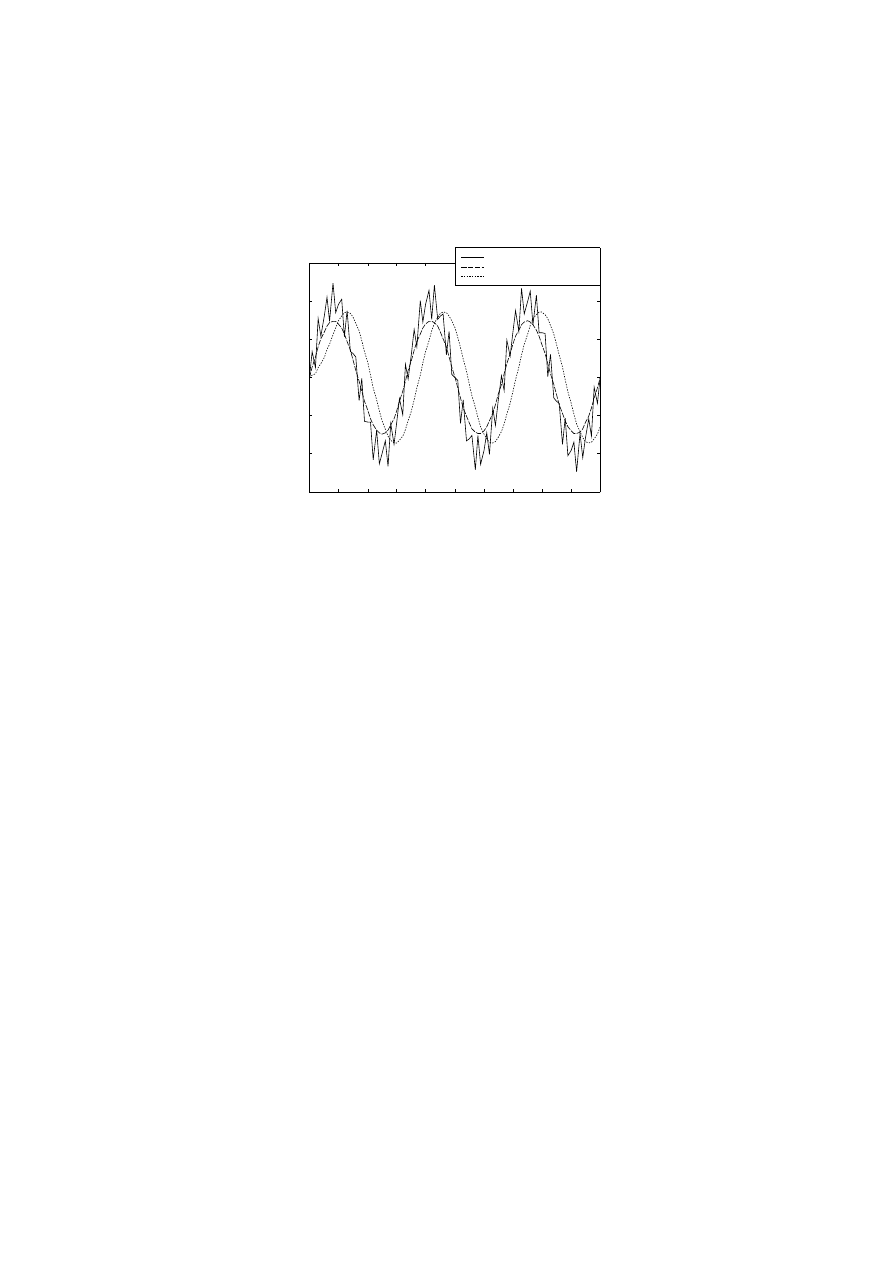
Rys. 5 Porównanie wyników filtracji sygnału dokonanej przez funkcje filtfilt i filter

Powyższy wykres pokazuje różnice pomiędzy zastosowaniem funkcji

filter

i

filtfilt

.

Obydwa filtry usunęły sinusoidę o częstotliwości 40 Hz z oryginalnego sygnału. Różnice
pomiędzy wykresami dotyczą zarówno ich amplitudy jak i fazy. Wynik działania funkcji

filtfilt

jest dokładnie w fazie z oryginalnym sygnałem o częstotliwości 3 Hz, podczas

gdy wynik funkcji

filter

jest przesunięty o około pięć próbek. W przypadku funkcji

filtfilt

także amplituda sygnału wyjściowego jest mniejsza, a to ze względu na kwadrat

modułu funkcji przenoszenia.
Funkcja

filtfilt

zmniejsza również wpływ stanów nieustalonych. Dla uzyskania

poprawnych wyników należy się upewnić, czy sekwencja przeznaczona do filtrowania,
posiada co najmniej trzykrotną długość rzędu filtru oraz czy kończy się zerami przy obydwu
brzegach.

Specyfikacja filtrów
Celem projektowania filtrów jest dokonanie zmian w zawartości składników
częstotliwościowych ciągu danych. Typowym wymaganiem może być np. usunięcie z
sygnału szumów o częstotliwościach powyżej 30 Hz z sekwencji danych próbkowanych z
częstotliwością 100 Hz. Ponadto w specyfikacji filtrów muszą być podane wymagania co do
szerokości pasma przepuszczania, tłumienia w paśmie zaporowym, dopuszczalnych
zniekształceń amplitudy lub fazy.
Dla wymagań, jak w przypadku podanym wyżej, wystarczający jest filtr typu Butterwortha
(IIR). Dla przykładu zaprojektowano filtr dolnoprzepustowy piątego rzędu, o częstotliwości
granicznej 30 Hz, dla danych wejściowych znajdujących się w wektorze

x

. Zaprojektowania

filtru i filtracji sygnału dokonano używając następujących poleceń:

[b,a]=butter(5,30/50);

y=filter(b,a,x);

Drugi argument wejściowy w funkcji

butter

wskazuje częstotliwość odcięcia filtru, która

jest normalizowana do połowy częstotliwości próbkowania (częstotliwość Nyquista).

Uwaga: Wszystkie funkcje Matlaba wykorzystujące filtry działają z normalizowaną
częstotliwością, więc nie jest wymagane podawanie częstotliwości próbkowania jako
dodatkowego argumentu. W przyborniku założono częstotliwości Nyquista jako jednostkową.
Normalizowana częstotliwość jest więc zawsze zawarta w przedziale 0

≤

f

≤

1. Dla układu z

częstotliwością próbkowania 1000 Hz, częstotliwość 300 Hz wynosi 300/500=0.6. W celu
przeliczenia znormalizowanej częstotliwości na częstość kątową (rad/s) mnożymy ją przez

π

.

By przeliczyć częstotliwość znormalizowaną na częstotliwość w [Hz], mnożymy ją przez
połowę częstotliwości próbkowania.

Najbardziej rygorystyczne wymagania stawiane filtrom zawierają takie parametry jak
dopuszczalne oscylacje w paśmie przepuszczania (Rp, w decybelach), tłumienie w paśmie
zaporowym (Rs, w decybelach), oraz stromość zbocza (Ws - Wp, w Hz)

0

Wp

Ws

10

10

-Rs/20

-Rp/20

A

m

pl

it

ud

a

fi

lt

ru

Częstotliwość

Rys. 6 Typowa charakterystyka filtru

Można zaprojektować filtry: Butterwortha, Chebyshewa typu I i typu II oraz filtr eliptyczny
spełniające te typy wymagań. Istnieją także funkcje w przyborniku estymujące minimalną
klasę filtru spełniającego żądane warunki.
Do wymagań zawierających bardziej rygorystyczne ograniczenia, jak np. liniowość fazy lub
stromość zbocza filtru, powinno stosować się filtry typu FIR lub typu IIR projektowane
bezpośrednio.

Projektowanie filtrów typu IIR
Zaletą filtrów IIR w stosunku do filtrów FIR jest to, że zapewniają większą stromość zbocza
przy mniejszym rzędzie filtru. Filtry IIR posiadają jednak nieliniową fazę, co jest zjawiskiem
negatywnym, jednak przetwarzanie danych w Matlabie jest realizowane głównie off line (tzn.
cała sekwencja dostępna jest przed rozpoczęciem operacji filtrowania). Sytuacja taka pozwala
na zastosowanie specjalnego rodzaju filtracji (funkcja

filtfilt

), w celu wyeliminowania

nieliniowych zniekształceń fazowych filtru IIR.

Klasyczne filtry IIR, a więc Butterwortha, Chebyshewa typu I i typu II, eliptyczny oraz filtr
Bessela, aproksymują w różny sposób idealny filtr „prostokątny”. Przybornik SPT zawiera
funkcje do tworzenia wszystkich tych typów klasycznych filtrów IIR w dziedzinach:
analogowej (ciągłej) i cyfrowej (dyskretnej) (z wyjątkiem filtru Bessela, który można
zrealizować jedynie w dziedzinie ciągłej). Przybornik umożliwia także skonfigurowanie filtru
jako dolnoprzepustowego, górnoprzepustowego, środkowoprzepustowego, lub

środkowozaporowego. Dla głównych typów filtrów można także znaleźć ich najmniejszy
rząd, spełniający zadane wymagania w części związanej z przepuszczaniem lub tłumieniem
oraz stromością zboczy.
Za pomocą funkcji

yulewalk

projektuje się filtry, których odpowiedź amplitudowa jest

aproksymacją zadanej funkcji. Pozwala ona więc na tworzenie filtrów pasmowych
niekoniecznie „prostokątnych”.

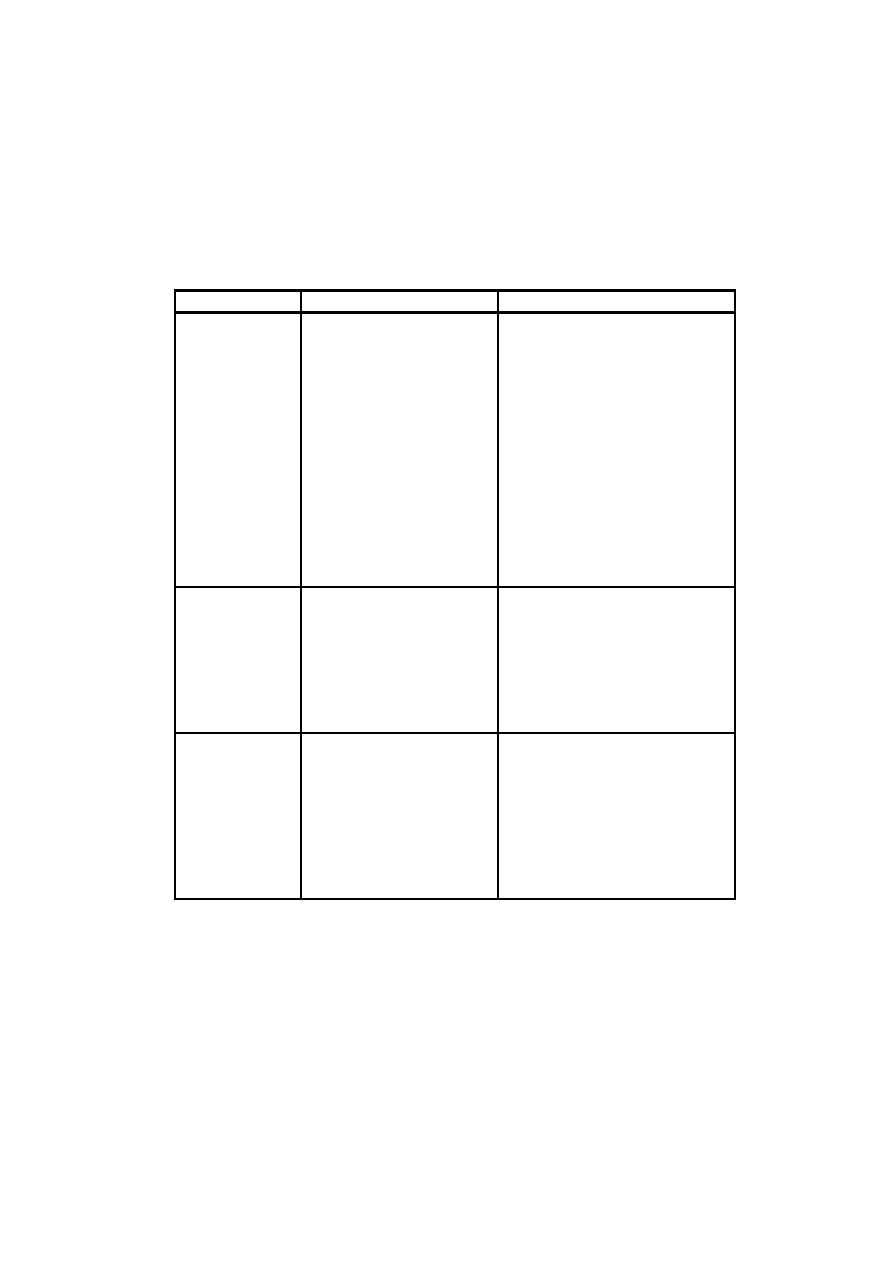
Tabela 1 Opisy konstrukcji filtrów IIR dostępnych w przyborniku.

Technika

Opis

Funkcja

Prototypo-
wanie
analogowe

Uzyskanie filtru
cyfrowego na podstawie
jego analogowego
dolnoprzepustowego
prototypu
unormowanego,
podanego w formie
transmitancji iloczynowej
modelu ciągłego
(Laplace’a), poprzez
transformację
częstotliwości i
dyskretyzację filtru.

Kompletne funkcje
projektujące:

bessel

,

butter

,

cheby1

,

cheby2

,

ellip

Klasa estymacji funkcji:

buttord

,

cheb1ord

,

cheb2ord

,

ellipord

Dolnoprzepustowe,
unormowane, analogowe
prototypy funkcji:

lp2lp

,

lp2hp

,

lp2bp

,

lp2bs

Funkcje dyskretyzujące filtry:

bilinear

,

impinvar

Projektowanie
bezpośrednie

Projektowanie filtrów
cyfrowych bezpośrednio
w dziedzinie dyskretnej
poprzez przybliżanie
charakterystyki
amplitudowej odcinkami
liniowymi.

youlewalk

Modelowanie
parametryczne

Projektowanie filtrów
cyfrowych, których
charakterystyka w
dziedzinie czasu lub
częstotliwości jest
przybliżeniem
charakterystyki
założonej.

Funkcje modelujące w
dziedzinie czasu:

lpc

,

prony

,

stmcb

Funkcje modelujące w
dziedzinie częstotliwości:

invfreqz

,

invfreqs

Do projektowania filtrów IIR można także zastosować metody modelowania
parametrycznego lub metody identyfikacji.

Filtry IIR projektowane poprzez prototypy analogowe
Podstawowa technika projektowania cyfrowych filtrów IIR wprowadzana w przyborniku
bazuje na przekształceniu klasycznego unormowanego analogowego filtru
dolnoprzepustowego na jego cyfrowy odpowiednik. Ten rozdział przedstawia metodę
projektowania oraz główne charakterystyki podstawowych typów filtrów.

Filtr dowolnego rzędu w konfiguracji dolnoprzepustowej, górnoprzepustowej,
środkowoprzepustowej lub środkowozaporowej, można łatwo utworzyć za pomocą funkcji
zestawionych w tabelce 2.
Standardowo każda z tych funkcji oblicza parametry filtru dolnoprzepustowego, należy
jedynie podać wymaganą częstotliwość odcięcia Wn w znormalizowanej częstotliwości
(częstotliwość Nyquista = 1 Hz). Dla filtru górnoprzepustowego należy dołączyć parametr
‘high’. Dla filtrów środkowozaporowych i środkowoprzepustowych należy zadać Wn jako
dwuelementowy wektor, zawierający częstotliwości krawędzi pasma przepuszczania. Dla
konfiguracji środkowozaporowej dodatkowo należy dołączyć parametr ‘stop’.

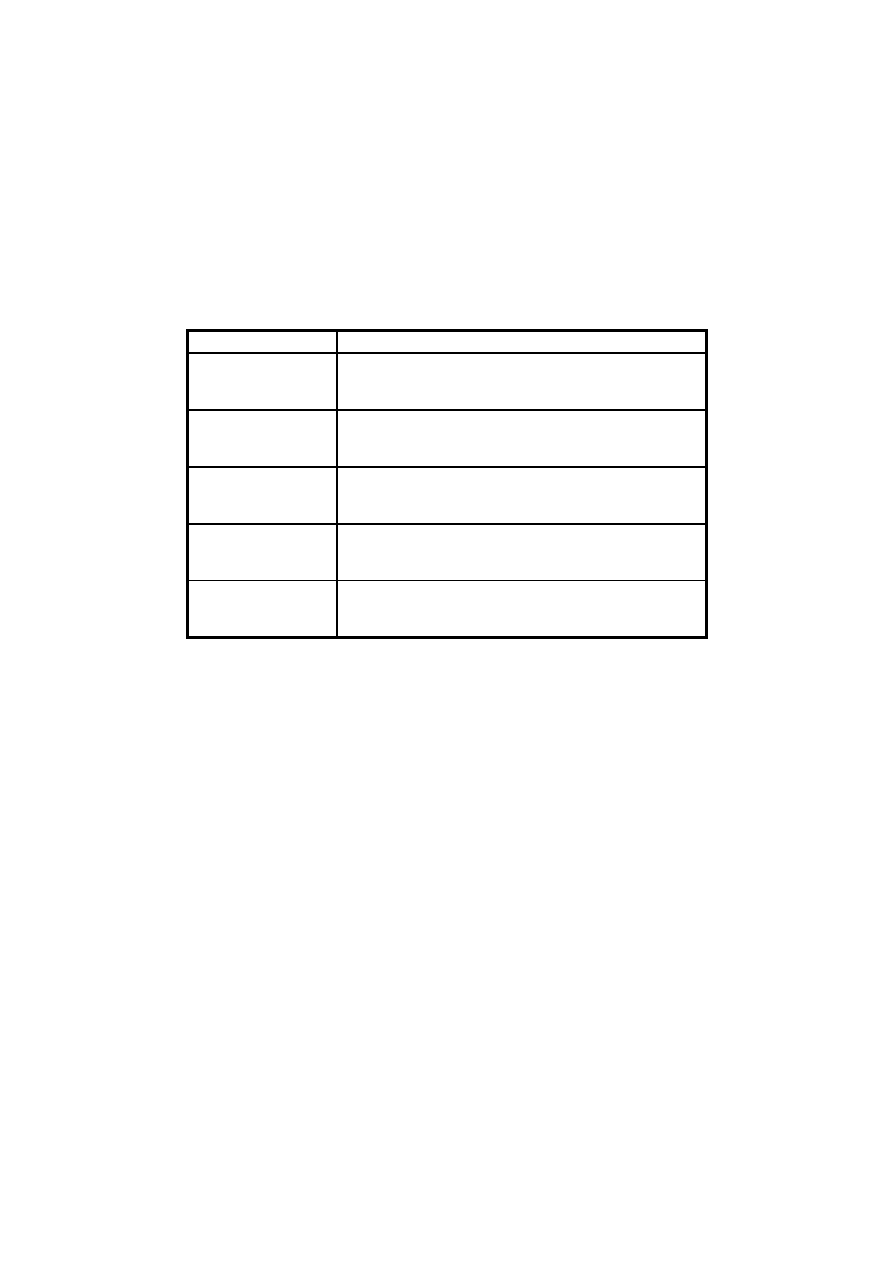
Tabela 2 Zestawienie funkcji do projektowania filtru IIR

Filtr

Funkcje projektujące

Butterwortha

[b,a]=butter(n,Wn,opcje)

[z,p,k]= butter(n,Wn,opcje)
[A,B,C,D]= butter(n,Wn,opcje)

Chebyshewa typ I

[b,a]=cheby1(n,Rp,Wn,opcje)
[z,p,k]= cheby1(n,Rp,Wn,opcje)

[A,B,C,D]= cheby1(n,Rp,Wn,opcje)

Chebyshewa typ II

[b,a]=cheby2(n,Rs,Wn,opcje)

[z,p,k]= cheby2(n,Rs,Wn,opcje)
[A,B,C,D]= cheby2(n,Rs,Wn,opcje)

Eliptyczny

[b,a]=ellip(n,Rp,Rs,Wn,opcje)
[z,p,k]= ellip (n,Rp,Rs,Wn,opcje)

[A,B,C,D]= ellip (n,Rp,Rs,Wn,opcje)

Bessela (jedynie
analogowy)

[b,a]=besself(n,Wn,opcje)

[z,p,k]= besself(n,Wn,opcje)
[A,B,C,D]= besself(n,Wn,opcje)

Przykłady tworzenia niektórych filtrów cyfrowych:

[b,a]=butter(5,0.4); - dolnoprzepustowy filtr Butterwortha

[b,a]=cheby1(4,1,[0.4 0.7]); - środkowoprzepustowy filtr Chebyshewa typu

I

[b,a]=cheby2(6,60,0.8,’high’); - górnoprzepustowy filtr Chebyshewa typu

II

[b,a]=ellip(4,1,60,[0.4,0.7],'stop');

- środkowozaporowy filtr eliptyczny

Do skonstruowania filtru analogowego (np. w celu jego symulacji) należy jako ostatni
dołączyć parametr ‘

s

’ i podać częstotliwość odcięcia w radianach na sekundę

[b,a]=butter(5,0.4,’s’); - analogowy filtr Butterwortha
Wszystkie przedstawione tu funkcje umożliwiają wyznaczenie parametrów równania filtru w
postaci funkcji przejścia, transmitancji iloczynowej lub przestrzeni stanu, zależnie od ilości
zadawanych argumentów wyjściowych.

Przybornik zawiera również funkcje obliczające minimalny rząd filtru, przy którym jeszcze
spełnia on zadane wymagania. Funkcje te zebrane zostały w tabelce 3. Są one bardzo
przydatne i często stosowane w połączeniu z funkcjami do konstrukcji filtrów.
Załóżmy, że poszukuje się filtru środkowoprzepustowego z pasmem przepuszczania od 1000
do 2000 Hz, pasmem zaporowym zaczynającym się przy 500 i 2500 Hz, o częstotliwość
próbkowania 10 000 Hz, z maksymalnie 1 dB błędem w paśmie przepuszczania i z co
najmniej 60 dB tłumieniem w paśmie zaporowym. Do konstrukcji użyto funkcji

buttord

.

Tabela 3 Zestawienie funkcji wyznaczających minimalny rząd filtrów.

Typ filtru

Klasa estymacji funkcji

Butterworth

[n,Wn]=buttord(Wp,Ws,Rp,Rs)

Chebyshew typ
I

[n,Wn]=cheb1ord(Wp,Ws,Rp,Rs)

Chebyshew typ
II

[n,Wn]=cheb2ord(Wp,Ws,Rp,Rs)

Elliptic

[n,Wn]=ellipord(Wp,Ws,Rp,Rs)

[n,Wn]=buttord([1000 2000]/5000,[500 2500]/5000,1,60)

•

n =

•

12

•

Wn =

•

0.1951 0.4080

[b a]=butter(n,Wn);

Filtr eliptyczny, spełniający te same wymagania, jest dany przez funkcję

ellip

.

[n,Wn]=ellipord([1000 2000]/5000,[500 2500]/5000,1,60)

•

n =

•

5

•

Wn =

•

0.2000 0.4000

[b a]=ellip(n,1,60,Wn);

Przybornik dostarcza pięć typów klasycznych filtrów IIR, z których każdy jest w sensie
pewnego kryterium optymalny. W rozdziale tym pokazano podstawowe postacie
analogowych prototypów dla tych filtrów oraz podano ogólną charakterystykę każdego z
nich.

Bezpośrednie projektowanie filtrów IIR
W przyborniku użyto terminu metody bezpośrednie do opisu metody projektowania filtrów
IIR, która znajduje filtr bazując na stawianych mu wymaganiach w dziedzinie dyskretnej.
Metoda bezpośrednia, odmiennie niż metoda analogowego prototypowania, nie jest
ograniczona standardowymi konfiguracjami filtrów (dolno-, środkowo- czy górno-
przepustową). Służy ona raczej do projektowania dowolnych filtrów o zadanej odpowiedzi
częstotliwościowej.

Funkcja

yulewalk

zrealizowana w SPT umożliwia projektowanie rekursywnego cyfrowego

filtru IIR poprzez dopasowanie odpowiedzi częstotliwościowej filtru do zadanego kształtu.
Nazwa funkcji

yulewalk

pochodzi od metody znajdowania przez nią współczynników filtru.

Funkcja ta znajduje odwrotną transformatę FFT dla idealnego zadanego widma mocy i
rozwiązuje zmodyfikowane równania Yule-Walkera na podstawie znajomości funkcji
autokorelacji. Składnia funkcji ma postać:

[b,a]= yulewalk(n,f,m);

Oblicza ona rzędowe wektory b i a składające się z n+1 współczynników licznika i
mianownika filtru IIR n-tego rzędu, którego charakterystyki amplitudowo-częstotliwościowe
aproksymują dane zawarte w wektorach f i m.
Wektor f jest wektorem punktów częstotliwościowych zawartych w granicach od 0 do 1,
gdzie 1 reprezentuje częstotliwość Nyquista. Wektor m jest wektorem zawierającym zadaną
amplitudę odpowiedzi dla punktów o częstotliwościach zawartych w f. Wektory f i m mogą

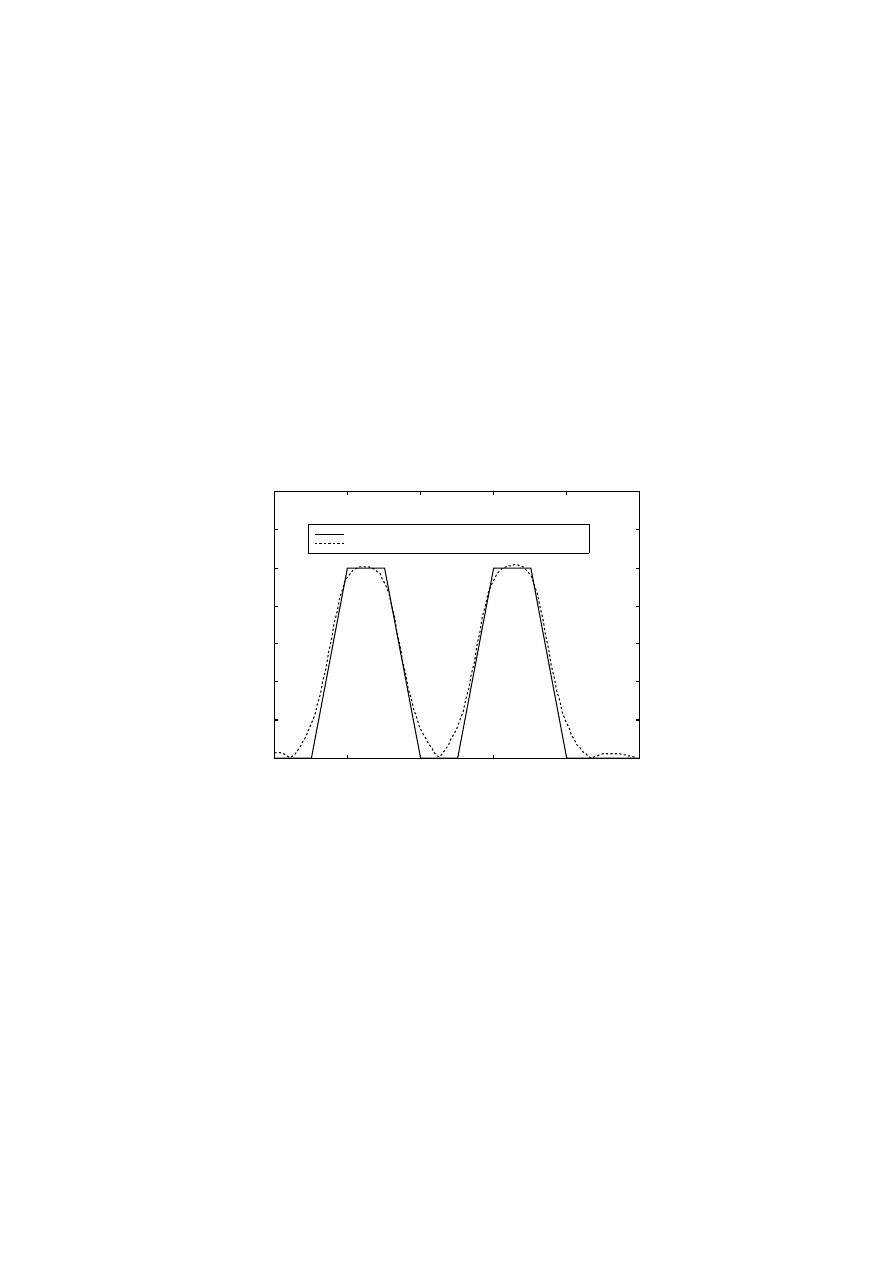
opisywać każdy składający się z liniowych odcinków kształt odpowiedzi częstotliwościowej,
włączając w to także odpowiedzi wielopasmowe (rys 7). Odpowiednik filtrów FIR tej funkcji
to

fir2

, która także projektuje filtr o odpowiedzi amplitudowej bazującej na dowolnym

kształcie składającym się z liniowych odcinków.
Należy zauważyć, iż funkcja

yulewalk

nie zawiera informacji o fazie, oraz brak jest

instrukcji pozwalającej na optymalizację rezultatów filtracji.

Dla przykładu przedstawiono projekt filtru pasmowego wykonanego za pomocą funkcji

yulewalk

. Wynikowa i przybliżana odpowiedź częstotliwościowa zostały przedstawione na

wykresie.

m=[0 0 1 1 0 0 1 1 0 0];
f=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 1];

[b,a]=yulewalk(10,f,m);
[h,w]=freqz(b,a,128);

plot(f,m,'black-',w/pi,abs(h),'black:')
legend('Zadana funkcja dla filtru',...

'Uzyskana charakterystryka amplitudowa filtru')

0

0 . 2

0 . 4

0 . 6

0 . 8

1

0

0 . 2

0 . 4

0 . 6

0 . 8

1

1 . 2

1 . 4

Z a d a n a f u n k c j a d l a f i l t r u

U z y s k a n a c h a r a k t e r y s t r y k a a m p l i t u d o w a f i l t r u

Rys. 7 Porównanie kształtu charakterystyki zadanej i uzyskanej przy pomocy funkcji youlewalk

Projektowanie filtrów typu FIR
Cyfrowe filtry ze skończonym czasem trwania odpowiedzi impulsowej (filtry FIR) mają w
porównaniu z filtrami dającymi nieskończoną odpowiedź impulsową (IIR) zarówno zalety jak
i wady.
Podstawowe zalety filtrów FIR to:

•

liniowa faza,

•

duża stabilność,

•

startowe warunki początkowe filtru posiadają skończony czas trwania.

Główną wadą filtrów FIR jest to, że często wymagają dużo wyższego rzędu niż filtry IIR do
osiągnięcia podobnych własności. Opóźnienie wprowadzane przez te filtry jest często dużo
większe niż dla podobnych filtrów typu IIR.

Liniowość fazy
Funkcje projektujące filtry FIR, konstruują filtry z liniową fazą. Współczynniki takiego filtru
posiadają parzystą lub nieparzystą symetrię. Zależnie od rodzaju tej symetrii oraz od tego, czy
rząd n filtru jest parzysty czy nieparzysty, liniowa faza filtru (zawarta w wektorze b o
długości n+1) posiada pewne ograniczenia co do jego charakterystyki amplitudowo-
częstotliwościowej.
Opóźnienia fazowe oraz opóźnienia grupowe filtrów FIR z liniową fazą są sobie równe i stałe
w całym paśmie przepuszczania. Dla n-tego rzędu takiego filtru całkowite opóźnienie
grupowe jest 2/n, a filtrowany sygnał jest opóźniony o 2/n (moduł jego transformaty Fouriera
jest skalowany przez odpowiedź amplitudową filtru). Te właściwości zabezpieczają kształt
przebiegu w paśmie przepuszczania, to znaczy nie wprowadzają dodatkowych zniekształceń
fazowych.
Funkcje

fir1

,

fir2

,

firls

, oraz

remez

umożliwiają projektowanie dolno-, górno-,

środkowoprzepustowych oraz środkowozaporowych filtrów FIR. Wszystkie one umożliwiają
dobór standardowych filtrów z liniową fazą typu I oraz II.
Uwaga: Ponieważ charakterystyka amplitudowo-częstotliwościowa filtrów typu II jest równa
zero przy częstotliwości Nyquista, za pomocą funkcji

fir1

nie może projektować filtrów

typu II w wypadku filtru górnoprzepustowego i środkowozaporowego. Dla parzystej wartości
n w tym przypadku,

fir1

dodaje jeden do rzędu filtru i tym samym tworzy filtr typu I.

Funkcje

firls

i

remez

umożliwiają projektowanie filtrów FIR z liniową fazą typu III i IV

pod warunkiem, że zostanie w ich wywołaniach zadany parametr 'hilbert' lub 'differentiator'.

Metoda okien
Rozważmy idealny, dolnoprzepustowy filtr cyfrowy z częstotliwością odcięcia

ω

0

[rad/s].

Moduł tego filtru wynosi jeden dla wszystkich częstotliwości z amplitudą mniejszą niż

ω

0

oraz zero dla częstotliwości z amplitudą pomiędzy

ω

0

i

π

. Jego odpowiedź impulsowa h(n)

wynosi:

)

n

(

c

sin

d

e

2

1

d

e

)

(

H

2

1

)

n

(

h

0

0

n

j

n

j

⋅

π

ω

⋅

π

ω

=

ω

⋅

π

⋅

=

ω

ω

⋅

π

⋅

=

∫

∫

ω

ω

−

ω

π

π

−

ω

( 7 )

gdzie n zmienia się od -

∞

do +

∞

.

Filtr ten nie jest realizowalny, ponieważ jego odpowiedź impulsowa jest nieskończona. W
celu utworzenia odpowiedzi impulsowej o skończonym czasie trwania należy zastosować
okno czasowe, ograniczające czas trwania h(n).
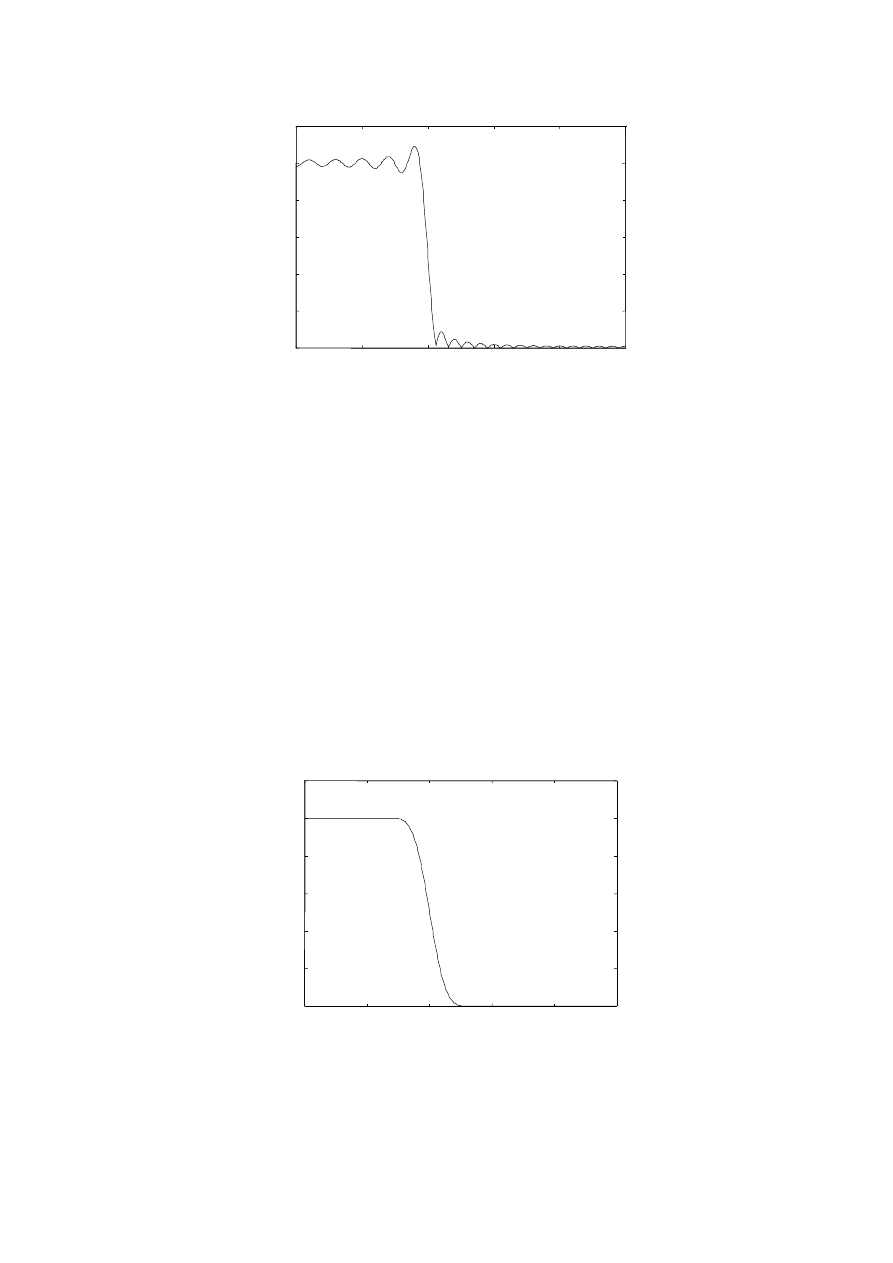
Przykładowy, filtr dolnoprzepustowy o długości 51 i częstotliwości odcięcia

ω

0.4

π

rad/sek

utworzony został za pomocą poniższej instrukcji:

b=0.4*sinc(0.4*(-25:25));

W tym przypadku do wyznaczenia odpowiedzi filtru zastosowano zwykłe okno prostokątne.
Według twierdzenia Parsevala spośród wszystkich filtrów o długości 51 ten z oknem
prostokątnym najlepiej przybliża idealny filtr dolnoprzepustowy.
Na wykresie (rys. 8) przedstawiono odpowiedź częstotliwościową tego filtru.

clf;

[H,w]=freqz(b,1,512,2);
plot(w,abs(H),'black'),

xlabel('Częstotliwość normalizowana do częst.
Nyquista'),

ylabel('Odpowiedź amplitudowa')

0

0.2

0.4

0.6

0.8

1

0

0.2

0.4

0.6

0.8

1

1.2

Częstotliwość znormalizowana do częstotliwości Nyquista

|H(j

ω

)|

Rys. 8 Charakterystyka częstotliwościowa przykładowego filtru dolnoprzepustowego

Na charakterystyce filtru, szczególnie w pobliżu krawędzi pasma, można zobaczyć oscylacje.
To zjawisko, nazywane efektem Gibbsa, nie znika dla wzrastającej długość filtru, ale
odpowiednie okno redukuje jego amplitudę. Mnożenie przez okno w dziedzinie czasu jest
równoważne splotowi lub wygładzaniu w dziedzinie częstotliwości.
Przykładowo dla filtru zaprojektowanego w poprzednim punkcie zastosowano okno
Hamminga o długości 51.

b=b.*hamming(51)';
[H,w]=freqz(b,1,512,2);

clf;
plot(w,abs(H),'black')

xlabel('Częstotliwość normalizowana do częst.
Nyquista'),

ylabel('Odpowiedź amplitudowa')

Jak można zaobserwować (rys. 9), oscylacje w znacznym stopniu zostały zredukowane.
Zostało to jednak okupione zmniejszeniem się nachylenia charakterystyki filtru oraz
wzrostem błędu kwadratowego.

0

0.2

0.4

0.6

0.8

1

0

0.2

0.4

0.6

0.8

1

1.2

Częstotliwość znormalizowana do częstotliwości Nyquista

|H(j

ω

)|

Rys. 9 Charakterystyka częstotliwościowa filtru wygładzona widmem okna Hamminga

Funkcje

fir1

i

fir2

w procesie projektowania filtrów FIR bazują na stosowaniu okien

czasowych. Mając zadany rząd oraz opis wymaganego filtru, funkcje te obliczają odwrotną
transformację Fouriera odpowiedzi zadanego filtru i poddają ją działaniu wybranego okna

czasowego. Obie standardowo używają okna Hamminga, można jednak stosować w nich okna
czasowe innego typu.

Projektowanie filtrów FIR dla pojedynczego pasma; funkcja

fir1

Funkcja

fir1

stosuje klasyczną metodę związaną z zastosowaniem okien do projektowania

cyfrowych filtrów FIR z liniową fazą. Przypomina ona projektowanie filtrów IIR w tym
sensie, że sformułowana jest do tworzenia filtrów w standardowych: dolno-, środkowo-,
górnoprzepustowych oraz środkowozaporowych konfiguracjach.
Sekwencja instrukcji:

n=50;
Wn=0.4;

b=fir1(n,Wn);

tworzy wektor

b

, zawierający współczynniki filtru n-tego rzędu, zaprojektowanego z

zastosowaniem okna Hamminga. Jest to dolnoprzepustowy filtr FIR z liniową fazą, o
częstotliwości odcięcia

Wn

.

Wn

jest liczbą z zakresu 0

÷

1, przy czym 1 odpowiada

częstotliwości Nyquista czyli połowie częstotliwości próbkowania. Występuje tu różnica w
stosunku do innych metod, gdzie

Wn

odpowiada punktowi o 6 dB spadku amplitudy.

Dla uzyskania górnoprzepustowego filtru należy dołączyć do listy parametrów ciąg znaków

‘high’

. Podczas tworzenia filtrów środkowo-przepustowych lub środkowo-zaporowych,

należy zadać

Wn

jako dwuelementowy wektor składający się z częstotliwości krawędzi pasma

przepuszczania, dodając parametr

‘stop’

dla konfiguracji zaporowej.

Instrukcja

fir1(n,Wn,okno)

stosowana do projektowania filtru zawiera okno podane w

wektorze kolumnowym

okno

. Wektor ten musi mieć długość n+1. Jeśli parametr nie zostanie

zadany, funkcja

fir1

standardowo zastosuje okno Hamminga.

Projektowanie filtrów FIR pasmowych; funkcja

fir2

Funkcja

fir2

umożliwia projektowanie filtrów FIR korzystając z metody okien, pozwalając

uzyskać dowolnie ukształtowaną charakterystykę częstotliwościową, przybliżaną za pomocą
odcinków liniowych. Tym różni się funkcja

fir2

w stosunku do funkcji

fir1

, która

umożliwia projektowanie filtrów jedynie w standardowych konfiguracjach.

n=50;
f=[0 0.4 0.5 1];

m=[1 1 0 0];
b=fir2(n,f,m);

Funkcja

fir2

daje w wyniku wektor wierszowy

b

, składający się z

n

+1 współczynników

filtru FIR

n

-tego rzedu, którego charakterystyka amplitudowo-fazowa jest dana poprzez

wektor

f

i

m

, gdzie

f

jest wektorem punktów częstotliwościowych w zakresie od 0 do 1 (1

reprezentuje częstotliwość Nyquista), zaś

m

jest wektorem składającym się z zadanych

odpowiedzi amplitudowych w punktach podanych w wektorze

f

. Odpowiednikiem tej funkcji

dla filtrów IIR jest funkcja

yulewalk

, tworząca filtry o odpowiedzi amplitudowej, bazującej

na dowolnym kształcie aproksymowanym odcinkami.

Projektowanie pasmowych filtrów FIR z zadanym pasmem przepuszczania
Funkcje

firls

i

remez

wykorzystują bardziej ogólne metody umożliwiające zadawanie

idealnego filtru, który ma być aproksymowany przez filtr cyfrowy.

Firls

i

remez

tworzą

transformatory Hilberta, układy różniczkujące oraz inne filtry posiadające nieparzystą
symetrię współczynników (typy III i IV filtrów z liniową fazą). Pozwalają one także na
zadawanie obszarów przejść, w których błędy nie są minimalizowane, podczas gdy w
pozostałej części charakterystyki filtru minimalizacja taka jest dokonywana.

Funkcja

firls

jest rozszerzeniem funkcji

fir1

i

fir2

o minimalizację całkowego błędu

kwadratowgo pomiędzy zadaną a rzeczywistą odpowiedzią częstotliwościową.
Funkcja

remez

wykorzystuje algorytm Pearks-McClellana, który przy wykorzystaniu

algorytmu wymiany Remeza oraz teorii aproksymacji Chebyshewa umożliwia projektowanie
filtrów, których rzeczywista odpowiedź częstotliwościowa jest w sposób optymalny
dopasowana do zadanej. Filtry te są optymalne w tym sensie, że minimalizują maksymalny
błąd pomiędzy zadaną i rzeczywistą odpowiedzią częstotliwościową (nazywane często
filtrami minimaksowymi). Filtry projektowane tą drogą wykazują zachowanie stałych
oscylacji w ich odpowiedziach częstotliwościowych. Algorytm Parks-McClellana
projektujący filtry FIR jest jednym z najbardziej znanych i szeroko stosowanych w praktyce
projektowania filtrów FIR.
Składnia dla funkcji

firls

i

remez

jest taka sama, jedyne różnice występują w

zastosowanych algorytmach minimalizacji. W kolejnym przykładzie pokazano, jak można
projektować filtry przy pomocy funkcji

firls

i

remez

z uwzględnieniem tych różnic.

Standardowy sposób działania funkcji

firls

i

remez

w projektowaniu filtrów typu I i II z

liniową fazą zależy od tego, czy zadany rząd filtru jest parzysty czy nieparzysty. Przykładowy
filtr dolnoprzepustowy z amplitudą 1 dla zakresu częstotliwości od 0 do 0.4 Hz oraz
amplitudą 0 dla przedziału od 0.5 do 1 Hz, zadano za pomocą następujących przedziałów.

n=20;
f=[0 0.4 0.5 1];

m=[1 1 0 0];
b=remez(n,f,m);

W zakresie częstotliwości od 0.4 do 0.5 Hz, funkcja

remez

nie dokonuje minimalizacji

błędów, ponieważ jest to obszar nachylenia zbocza filtru. Minimalizacja błędu w tym paśmie
jest również możliwa, ale należy liczyć się z dłuższym procesem przejściowym.
Dla porównania metody najmniejszych kwadratów projektowania filtrów z minimaksowym
projektowaniem filtrów, użyto funkcji

firls

do zbudowania podobnego filtru, jak w

przykładzie poprzednim:

bb=firls(n,f,m);

a następnie porównano ich charakterystyki częstotliwościowe.

[H,w]=freqz(b);

[HH,w]=freqz(bb);
plot(w/pi,abs(H),'black',w/pi,abs(HH),'black:')

grid
xlabel('Częstotliwość normalizowana do częst.

Nyquista'),
ylabel('Odpowiedź amplitudowa')

legend('Funkcja remez','Funkcja firls')

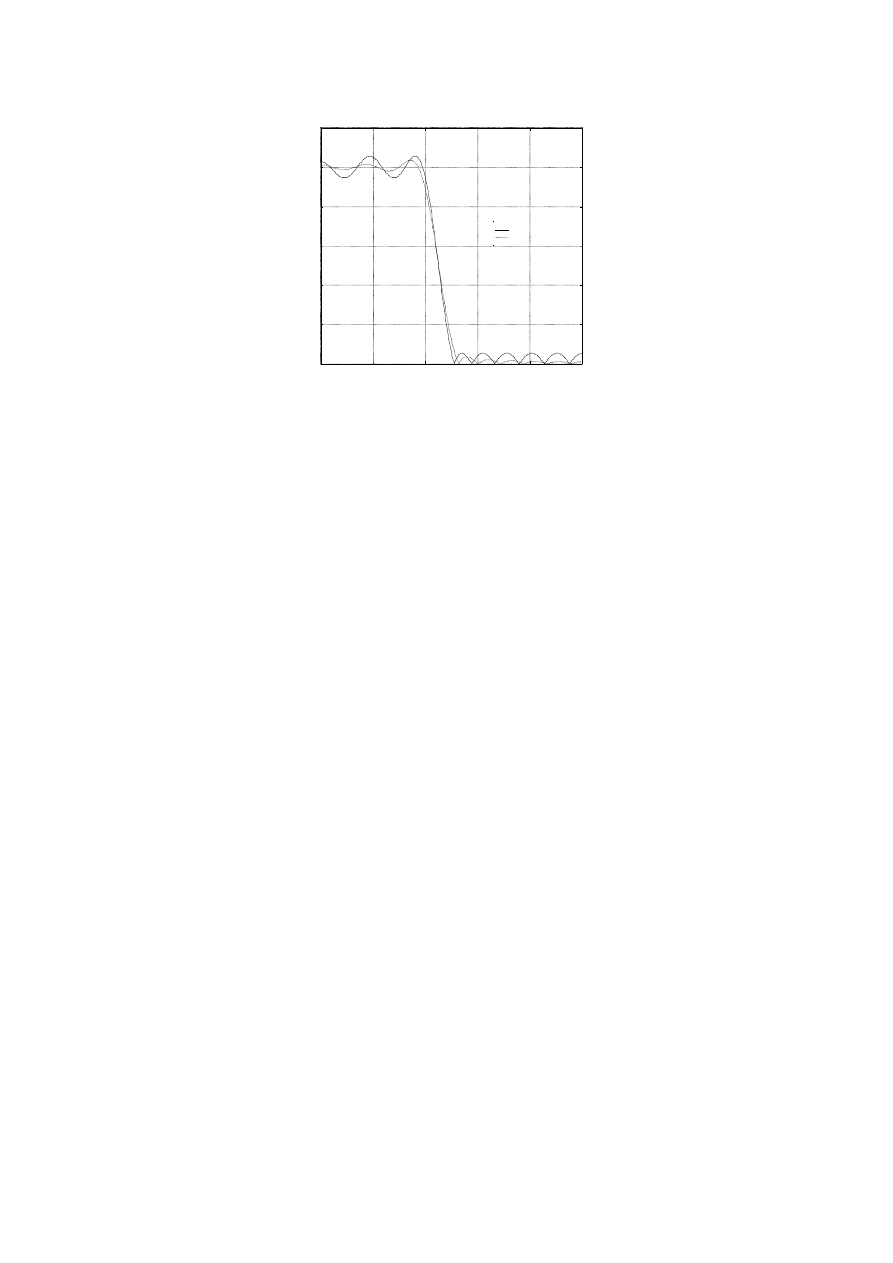
Na rysunku 10 można łatwo zauważyć, że filtr zaprojektowany za pomocą funkcji

remez

wykazuje stałe oscylacje tak w paśmie przepuszczania, jak i zaporowym. Filtr projektowany
funkcją

firls

posiada lepszy przebieg charakterystyki dla większej części obu pasm, ale

przy krawędziach (f=0.4 i f=0.5) jego charakterystyka ma przebieg dużo gorszy od
poprzedniego. Świadczy to o tym, że maksymalny błąd filtru

remez

ponad pasmem

przepuszczania i zaporowym jest mniejszy i w rzeczywistości ma on dla tej konfiguracji
krawędzi pasma i długości filtru wartość najmniejszą.

Funkcja remez

Funkcja firls

0

0.2

0.4

0.6

0.8

1

0

0.2

0.4

0.6

0.8

1

1.2

Częstotliwość znormalizowana do częstotliwości Nyquista

O

d

po

w

ie

d

ź

a

m

pl

itu

do

w

a

Rys. 10 Porównanie wyników działania funkcji remez i firls

W funkcjach

firls

i

remez

poszczególne pasma filtru traktowane są jako odcinki liniowe

reprezentujące przedziały częstotliwości. Bazując na funkcji o dowolnym kształcie,
składającym się z liniowych odcinków, można przedstawić filtr w dowolnej konfiguracji.
Funkcje

firls

i

remez

umożliwiają projektowanie filtrów dolno-, górno-,

środkowoprzepustowych oraz środkowozaporowych.
Przykłady parametrów dla wybranych filtrów zestawiono poniżej.

•

filtr środkowoprzepustowy:

f=[0 0.3 0.4 0.7 0.8 1];
m=[0 0 1 1 0 0];

(Wektory

f

i

m

definiuje się jako pięć pasm:

•

dwa zaporowe od 0.0 do 0.3 oraz od 0.8 do 1.0

•

pasmo przepuszczania od 0.4 do 0.7

•

dwa zbocza, od 0.3 do 0.4 i od 0.7 do 0.8 )

•

filtr górno- i środkowozaporowy:

f=[0 0.7 0.8 1];
m=[0 0 1 1];

f=[0 0.3 0.4 0.5 0.8 1];

m=[1 1 0 0 1 1];

•

filtr pasmowo-przepustowy:

f=[0 0.1 0.15 0.25 0.3 0.4 0.45 0.55 0.6 0.7 0.75 0.85 0.9 1];

m=[1 1 0 0 1 1 0 0 1 1 0 0 1 1];

Jeszcze innym przykładem zastosowania opisywanych funkcji jest projektowanie filtru,
posiadającego zbocze w formie liniowego połączenia pasma przewodzenia z zaporowym.
Zastosowanie takiego zabiegu może być pomocne w sterowaniu przeciekami odpowiedzi
amplitudowej przy słabo nachylonych zboczach.

f=[0 0.4 0.42 0.48 0.5 1];

m=[1 1 0.8 0.2 0 0];

Wektor wagi
Obie funkcje

firls

i

remez

pozwalają z różną wagą minimalizować błędy w pewnych

pasmach częstotliwości. Przykładowo, jeśli jako czwarty parametr w funkcji

remez

zostanie

podany wektor wagi

w=[1 10]

, zostanie zaprojektowany dolnoprzepustowy filtr z 10-krotnie

mniejszymi oscylacjami w paśmie zaporowym niż w paśmie przepuszczania.

n=20;

f=[0 0.4 0.5 1];
m=[1 1 0 0];

w=[1 10];
b=remez(n,f,m,w);

Wektor wagi jest zawsze połową długości wektorów

f

i

m

(musi być dokładnie jedna waga na

pasmo).

Projektowanie filtrów cyfrowych z wykorzystaniem narzędzi graficznych

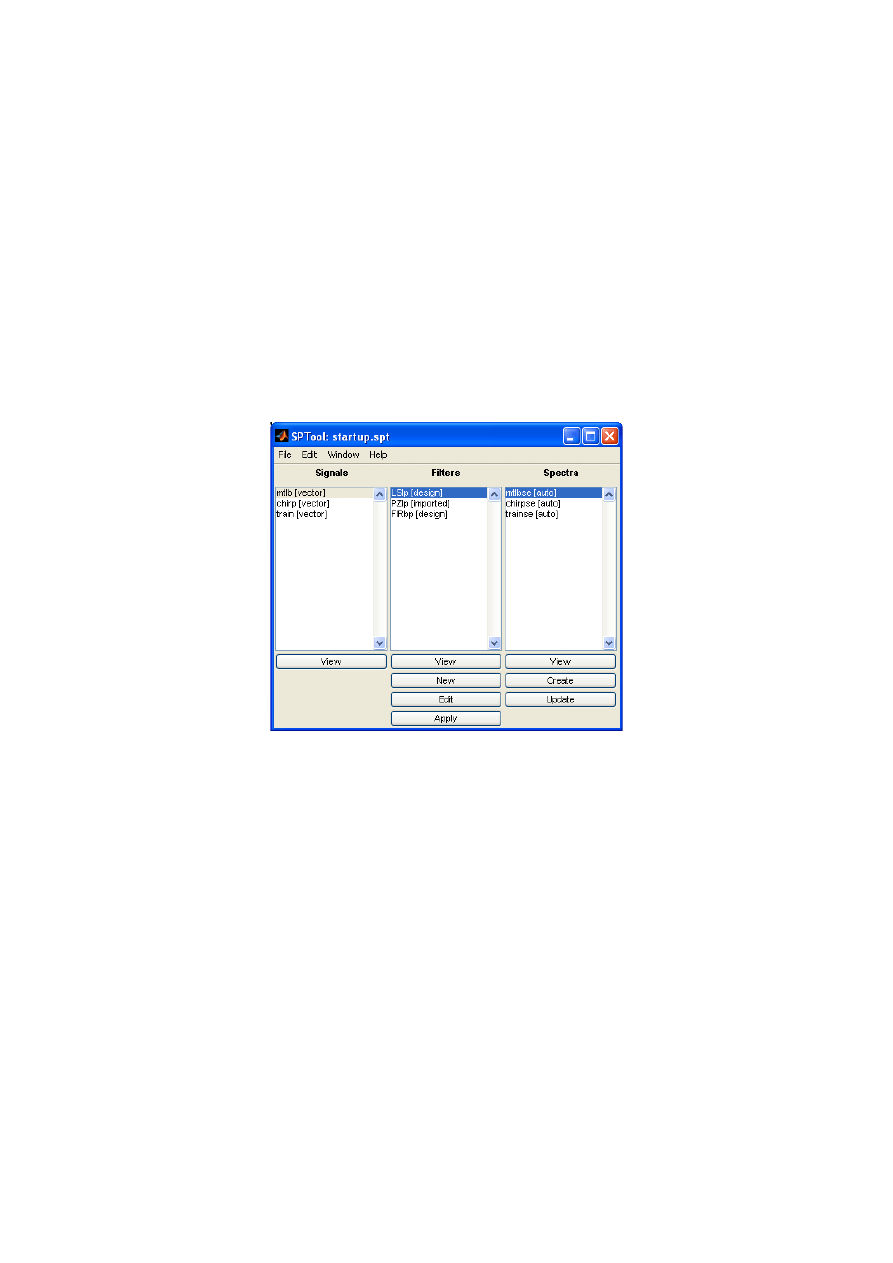
W przyborniku SPT dostępne jest narzędzie udostępniające graficzny interfejs użytkownika
dla czynności opisywanych w poprzednich podpunktach konspektu. Narzędzie uruchamiane
jest poprzez wpisanie polecenia:

sptool;

w oknie poleceń Matlaba. Widok okna po uruchomieniu pokazany jest na rysunku 11.

Rys. 11 Widok okna narzędzia SPTool

Idea użycia narzędzia w celu wykonania filtracji sygnału jest następująca:

1. Sygnał obrabiany należy zaimportować do interfejsu (File ->Import...)
2. Utworzyć za pomocą narzędzi graficznych nowy projekt filtru (Przycisk New w

kolumnie Filters).

3. Zaprojektować filtr zgodnie z wymaganiami.
4. Zapisać utworzony projekt filtru.
5. Wykonać filtrację poprzez zaznaczenie w kolumnie Signals zaimportowanego sygnału

oraz w kolumnie Filters zaprojektowanego filtru. Operacja filtracji wykonywana jest
po naciśnięciu przycisku Apply.

Zadania do wykonania

1. Skomentować przykłady zaprezentowane w części konspektu dotyczącego doboru

częstotliwości próbkowania sygnału. Wyjaśnić krótko mechanizmy powstawania
niejednoznaczności w prezentowanych przypadkach.

2. Wygenerować kilkusekundowy sygnał będący złożeniem trzech przebiegów

sinusoidalnych o częstotliwościach: 10, 80 i 120 Hz. Amplitudy sygnałów powinny

znajdować się w proporcjach 1:3:1 oraz fazy powinny być przesunięte o ok. 20

o

.

Należy zwrócić szczególną uwagę na dobór próbkowania sygnału.

3. Zaprojektować filtry pozwalające na odfiltrowania kolejnych składowych ze sygnału.

Filtry powinny być wykonane każdorazowo w wersji IIR oraz FIR.

4. Wykonać porównanie parametrów zaprojektowanych filtrów zestawiając ze sobą filtry

FIR i IIR odpowiednio w konfiguracjach dolnoprzepustowych, pasmowych oraz
górnoprzepustowych.

5. Dla jednej wybranej konfiguracji filtru wykonać porównanie filtracji za pomocą

polecenia filter oraz filtfilt. Porównanie przedstawić w postaci graficznej poprzez
nałożenie na siebie:
•

sygnału oryginalnego – nieprzefiltrowanego,

•

sygnału odfiltrowanego poleceniem filter,

•

sygnału odfiltrowanego poleceniem filtfilt.

6. Na wygenerowany sygnał testowy uzyskany w punkcie 2 nałożyć sygnał szumu

losowego na poziomie 10% wartości amplitudy sygnału oraz skomentować wyniki
filtracji zaprojektowanymi wcześniej filtrami.