ĆWICZENIE 45

WYZNACZANIE PRĘDKOŚCI LOTU CIAŁA

PRZY POMOCY WAHADŁA BALISTYCZNEGO

45.1 Opis teoretyczny

Bezpośredni pomiar prędkości lecącego ciała jest niełatwym zadaniem, jeżeli prędkość ta osiąga
stosunkowo duże wartości. Dlatego do tego rodzaju pomiarów stosuje się metody pośrednie. Jedna
z takich metod wykorzystuje zjawisko zderzenia niesprężystego ciał. Niech lecące ciało zderzy się
idealnie niesprężyście z innym ciałem o znacznie większej masie. Obie połączone masy zaczną się
poruszać z prędkością tyle razy mniejszą od prędkości badanego ciała, ile razy jego masa jest
mniejsza od masy ciała większego (co wynika z prawa zachowania pędu). Tą już znacznie mniejszą
prędkość jest już łatwo określić i na podstawie jej znajomości obliczyć szukaną prędkość badanego
ciała. Przedstawiona pokrótce idea ma zastosowanie w metodzie wahadła balistycznego.

..

45.2 Opis układu pomiarowego

Wahadło balistyczne jest to stosunkowo ciężkie ciało (o masie M), najczęściej w postaci

cylindra wypełnionego plasteliną i zawieszone na czterech nierozciągliwych niciach. W naszym
przypadku jest to stosunkowo ciężkie metalowe ramię umocowane obrotowo na jednym końcu.
Drugi koniec jest ponadto obciążony czterema dodatkowymi ciężarkami. Całość wyposażona jest w
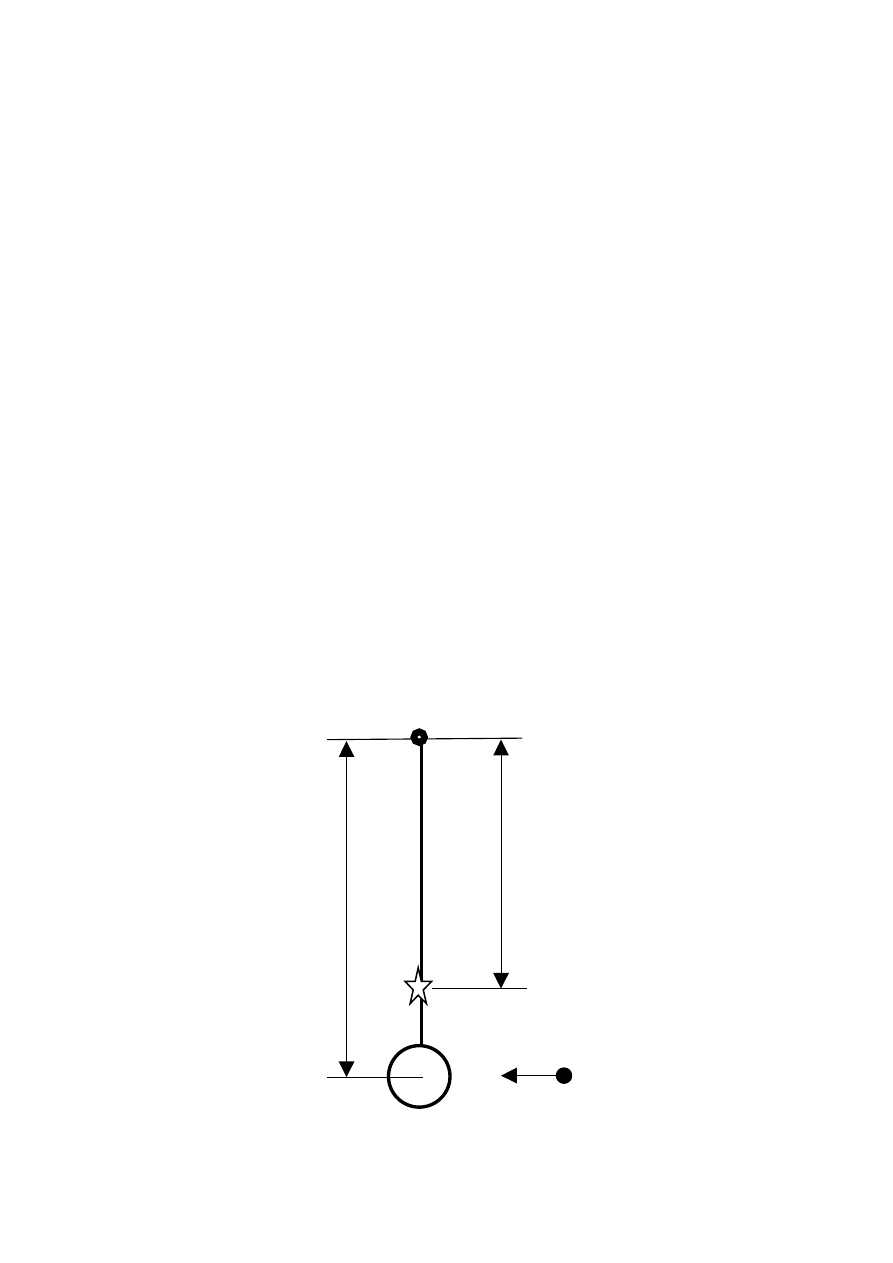
specjalny koszyk posiadający zaczep do wyłapywania kuli (patrz schematyczny rysunek 45.1)
Znane są:

R – odległość środka ciężkości C od osi obrotu = 178 mm

±

2mm

L – odległość od punktu wychwytu kuli do osi obrotu = 240mm

±

2mm

M – masa ramienia = 121,0 g

±

0,1 g

m – masa kuli = 32,5g

±

0,1 g

L

R

C

v

m

Rys.45.1 Schematyczny rysunek wahadła balistycznego

Stanowisko laboratoryjne wyposażone jest w sprężynową wyrzutnię kul o trzech zastawach.

Lecąca poziomo kula o masie m uderza w koszyk wahadła i grzęźnie w nim. Jest to zderzenie
idealnie niesprężyste. Dla określenia prędkości v kuli można więc zastosować prawo zachowania
momentu pędu w postaci:

V

m)

(M

R

mv

L

+

=

stąd szukana prędkość

m

L

V

m)

(M

R

v

+

=

(45.1)

Prędkość V jaką uzyskuje środek ciężkości ramienia w chwili tuż po uderzeniu kuli można
wyznaczyć z prawa zachowania energii napisanego dla środka ciężkości. Nabyta po zderzeniu
energia kinetyczna w miarę odchylania się wahadła od pionu przekształca się w postać potencjalną,
aż przy maksymalnym wychyleniu o kąt

ϕ

proces ten dobiegnie końca i wahadło znieruchomieje.

W wyniku środek ciężkości wahadła został uniesiony na wysokość h . To znaczy, że słuszna jest
zależność:

h

g

2

V

2

=

(45.2)

Między wysokością h , a kątem

ϕ

istnieje prosty związek, a mianowicie:

2

sin

R

2

)

cos

1

(

R

h

2

ϕ

ϕ

=

−

=

(45.3)

Zastosowane w eksperymencie laboratoryjnym urządzenie zaopatrzona jest w specjalną
wskazówkę, która zapamiętuje maksymalne wychylenie wahadła i pozwala z dużą dokładnością
odczytać kąt

ϕ

.

Uwzględniając dwa powyższe związki wzór (45.1) na szukaną prędkość uzyskuje ostateczną
postać:

2

sin

R

g

m

L

m)

(M

R

2

v

ϕ

+

=

(45.4)

która jest wykorzystywana w omawianym ćwiczeniu.

Zdjęcie stanowiska eksperymentalnego jest zaprezentowane na rys 45.2.

Rys.45.2 Zdjęcie stanowiska eksperymentalnego wahadła balistycznego

45.3. Przebieg pomiarów

1. Zaznajomić się z układem pomiarowym.
2. Umieścić okrągłą kulę w wyrzutni. Koniec iglicy wyrzutni jest namagnesowany. Do niego

należy przyczepić kulę zwracając pilną uwagę na to aby była umieszczona współosiowo z
iglicą!

3. Naciągnąć wyrzutnię do pierwszego stopnia i zabezpieczyć zastawką.
4. Ustawić wskaźnik końcowego wychylenia wahadła w pozycji pionowej.
5. Pociągając za sznurek zwolnić zastawkę. Po strzale kula grzęźnie w koszu wahadła.
6. Odczytać kąt

ϕ

końcowego wychylenia wahadła.

7. Powtórzyć 10 razy procedurę od punktu 2 do punktu 6
8. Powtórzyć czynności od punktu 2 do 7 stosując naciągi drugiego i trzeciego stopnia

45.4. Opracowanie wyników pomiarów.

1. Z każdej serii pomiarowej obliczyć średnią arytmetyczną

ϕ

, oraz jej średni błąd

kwadratowy.

2. Korzystając ze wzoru (45.4) wyznaczyć 3 zastosowane prędkości kuli oraz ich średnie błędy

kwadratowe.

3. Wykonać wykres zależności

)

F(

v

ϕ

=

nanosząc uzyskane punkty pomiarowe wraz z błędami.

4. Wyciągnąć wnioski.

45.5. Pytania kontrolne

1. Na czym polega metoda wahadła balistycznego?
2. W których miejscach w ćwiczeniu stosujemy zasady zachowania momentu pędu oraz energii?
3. W jaki sposób w ćwiczeniu można by praktycznie zwiększyć uzyskiwane prędkości kuli?

L i t e r a t u r a

[1] Piekara A.: Mechanika ogólna. PWN, Warszawa 1970.
[2] Kittel.C. , Knight W.D. , Ruderman M.A.:Mechanika. PWN W-wa 1973r
[3] Massalski J.M.: Fizyka dla inżynierów, cz.2, WNT, Warszawa 1975.
[4] Leyko J. . Mechanika ogólna, PWN, Warszawa 2002.