
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
1
Projekt budynku o konstrukcji mieszanej
Materiały pomocnicze do zajęć projektowych z „Konstrukcji betonowych 2” i „Konstrukcji żelbetowych 1b”
dla studentów studiów dziennych i zaocznych
Drogi Czytelniku,
Przekazujemy w Twoje ręce materiały pomocnicze obejmujące swoim zakresem podstawowe wiadomości na temat:
- doboru wymiarów przekrojów elementów żelbetowych,
- wymiarowania płyt jednokierunkowo zbrojonych,
- wymiarowania belek ciągłych,
- wymiarowania słupów i stóp fundamentowych,
- doboru i konstruowania zbrojenia dla wyżej wymienionych elementów.
W materiałach oprócz podstawowych wiadomości teoretycznych zostały także zamieszczone przykłady obliczeniowe,
które mamy nadzieję będą pomocne przy wdrażaniu się w trudną sztukę projektowania bezpiecznych konstrukcji
żelbetowych. Materiały dostosowane są do postanowień aktualnie obowiązującej normy
2002
:
03264
−
− B
PN
.
Pomimo naszych starań na pewno znajdziesz Czytelniku w nich niejasności, pomyłki, czy też braki potrzebnego
materiału, koniecznego do zrozumienia pracy przekroju żelbetowego. Pragniemy z góry Cię za te usterki przeprosić
i będziemy wdzięczne za wszystkie uwagi na ten temat przesłane na adres
mariaw@tu.kielce.pl
. Pozwoli nam to
w przyszłości uczynić materiały bardziej przyjaznymi dla studenta. Z wdzięcznością przyjmiemy także wszelkie sugestie
co Twoim zdaniem byłoby pomocne w nauczaniu projektowania konstrukcji żelbetowych.
Maria Włodarczyk
Barbara Goszczyńska
Budynek o konstrukcji mieszanej
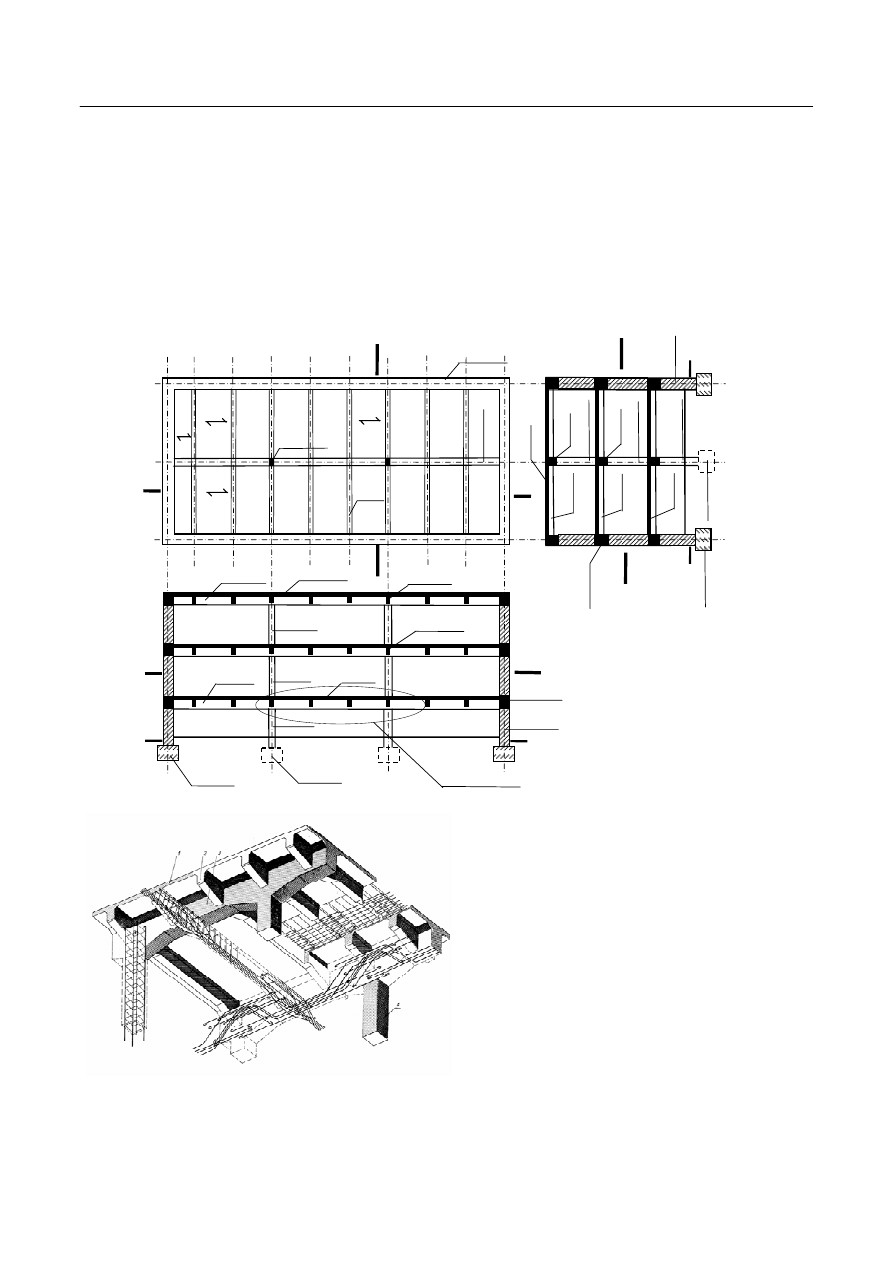
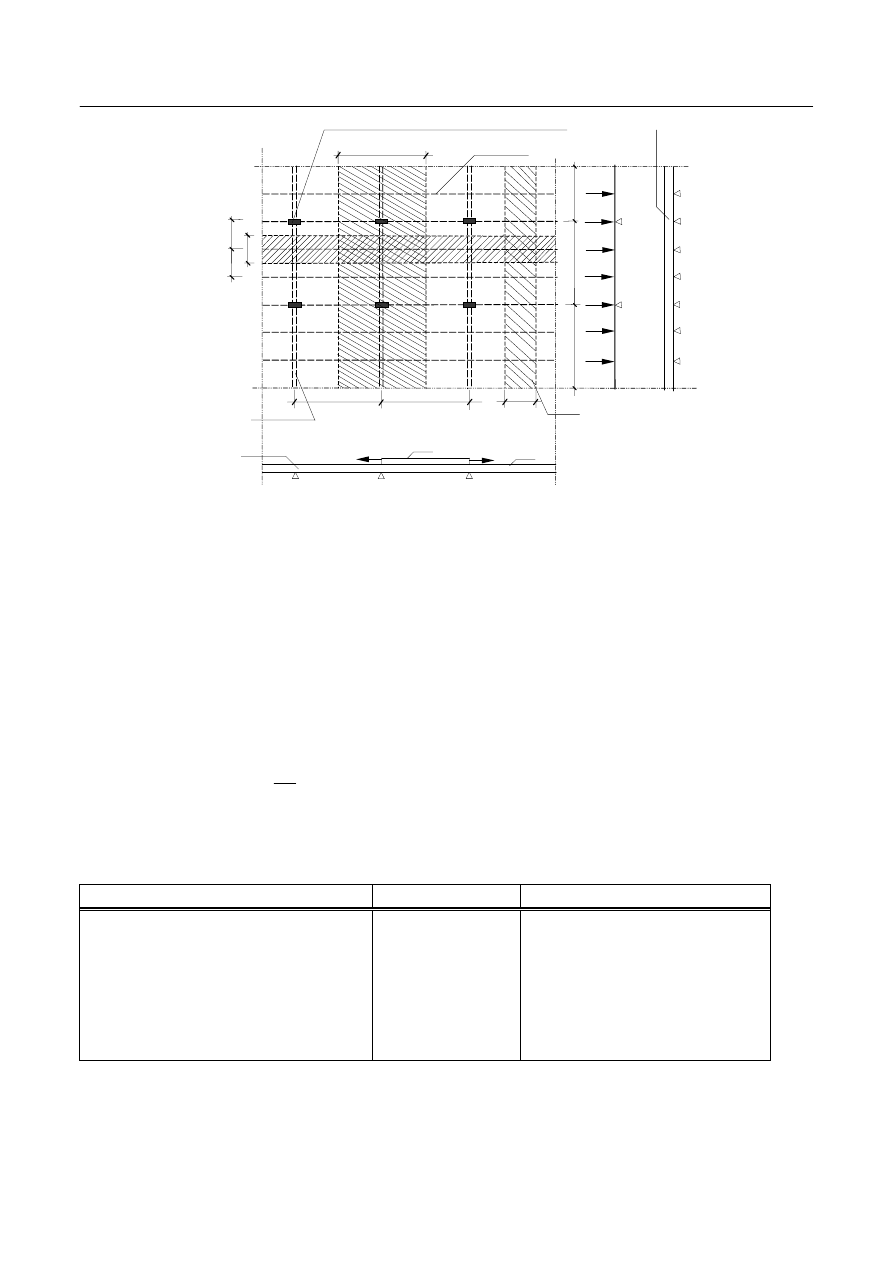
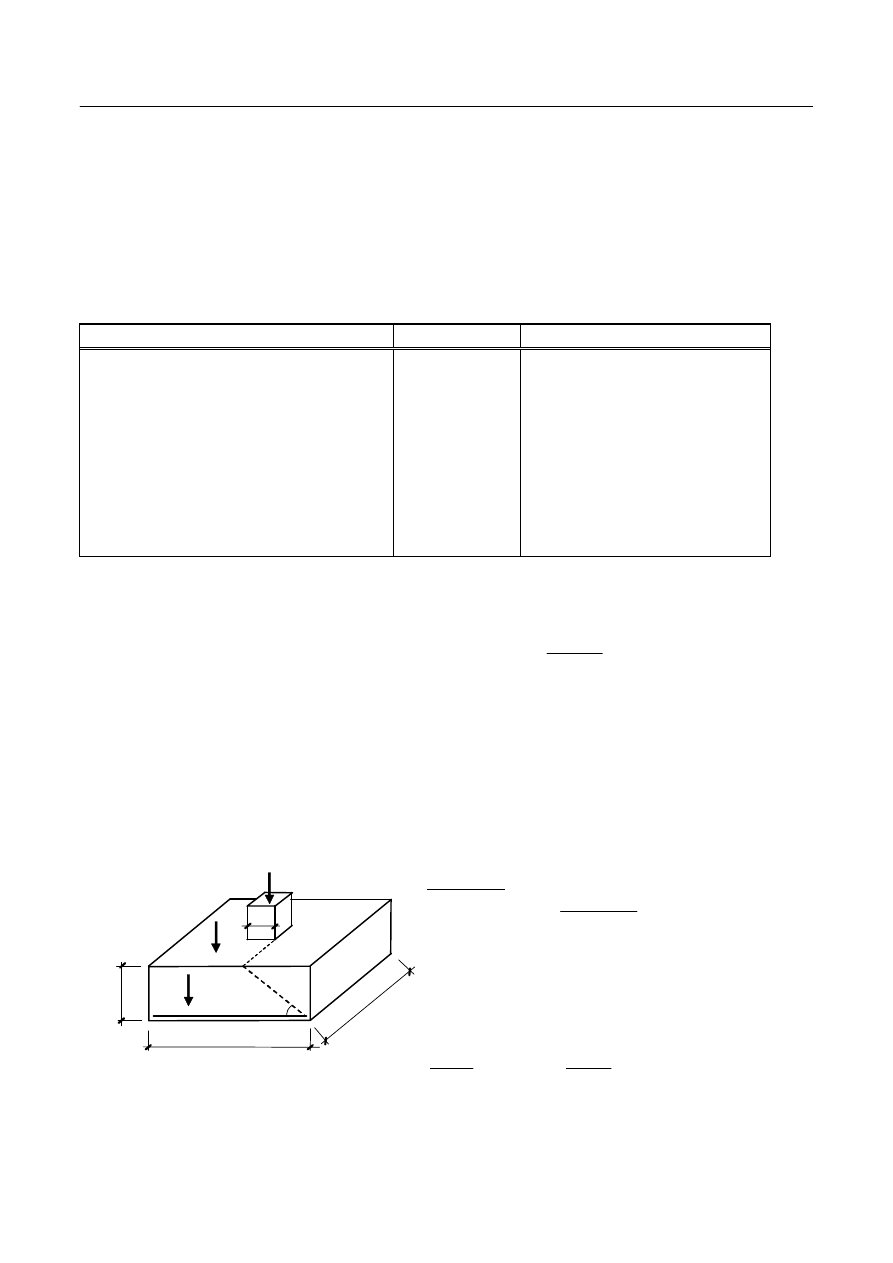
Budynek o konstrukcji mieszanej to taki (Rys. 1a), w którym konstrukcja wsporcza jest niejednolita – np.
złożona ze ścian i słupów. W projektowanym budynku konstrukcje wsporczą dla stropu stanowią zewnętrzne
ściany nośne – murowane natomiast wewnątrz słupy żelbetowe. Obciążenia od płyty stropowej zarówno na
ściany jak i na słupy przekazywane są poprzez belki (żebra i podciągi) stanowiące bezpośrednie podparcie
płyty stropowej, której wymiary (długość i szerokość) są zbyt duże żeby podparcie mogły stanowić jedynie
ściany zewnętrzne. Na grunt obciążenia przekazywane są odpowiednio poprzez ławy i stopy fundamentowe.
Strop płytowo – belkowy (Rys. 1b) to taki strop, w którym obciążenia pionowe przekazywane są z płyt
stropowych na belki (żebra i podciągi), stanowiące podparcie ciągłe płyty w dwóch kierunkach. „Praca”
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
2
płyty, a więc i jej grubość uzależniona jest od odległości między belkami. Jeżeli odległości między belkami
w jednym i drugim kierunku będą zbliżone, to i praca płyty w obu kierunkach będzie zbliżona. W przypadku
usytuowania w jednym kierunku belek (żeber) w małych odległościach, a drugim kierunku (podciągów)
w odległościach ok. trzykrotnie większych, można w przybliżeniu przyjąć, że płyty pracują w jednym
kierunku, w kierunku krótszego boku. Mamy zatem do obliczeń układ konstrukcyjny płyt opartych na
żebrach; żeber opartych na podciągach i ścianach zewnętrznych oraz podciągów podpartych na słupach
i ścianach zewnętrznych w drugim kierunku. Na podłoże obciążenia przekazywane są odpowiednio przez
stopy fundamentowe i ławy fundamentowe.
a)
Po
z.
2
.1
Po
z.
6
Poz.4.2
Poz.2.2
Po
z.
2
.3
Szczegół A
Poz. 2.2
Poz. 2.1
Poz. 5
Poz. 1.2
Poz. 1.3
Poz. 2.3
Poz. 4.1
Poz. 4.2
Poz. 4.3
C
Poz. 1.1
Poz. 7
Po
z.
2
.3
Poz. 6
Poz. 6
Po
z.
2.2
Po
z.
1.3
Po
z.
1
.2
Po
z.
1
.1
Rzut budynku C - C
Przekrój A-A
Pr
ze
krój B
-B
Poz. 2.1
Po
z.
5
Po
z.
7
Po
z.
4
.3
Po
z.
4
.2
Po
z.
4
.1
Po
z.
6.1
B
B
C
A
A
A
A
B
B
Poz. 6.1
b)
1. Płyta stropu.
2. Żebro stropu.
3. Podciąg stropu.
4. Słup.
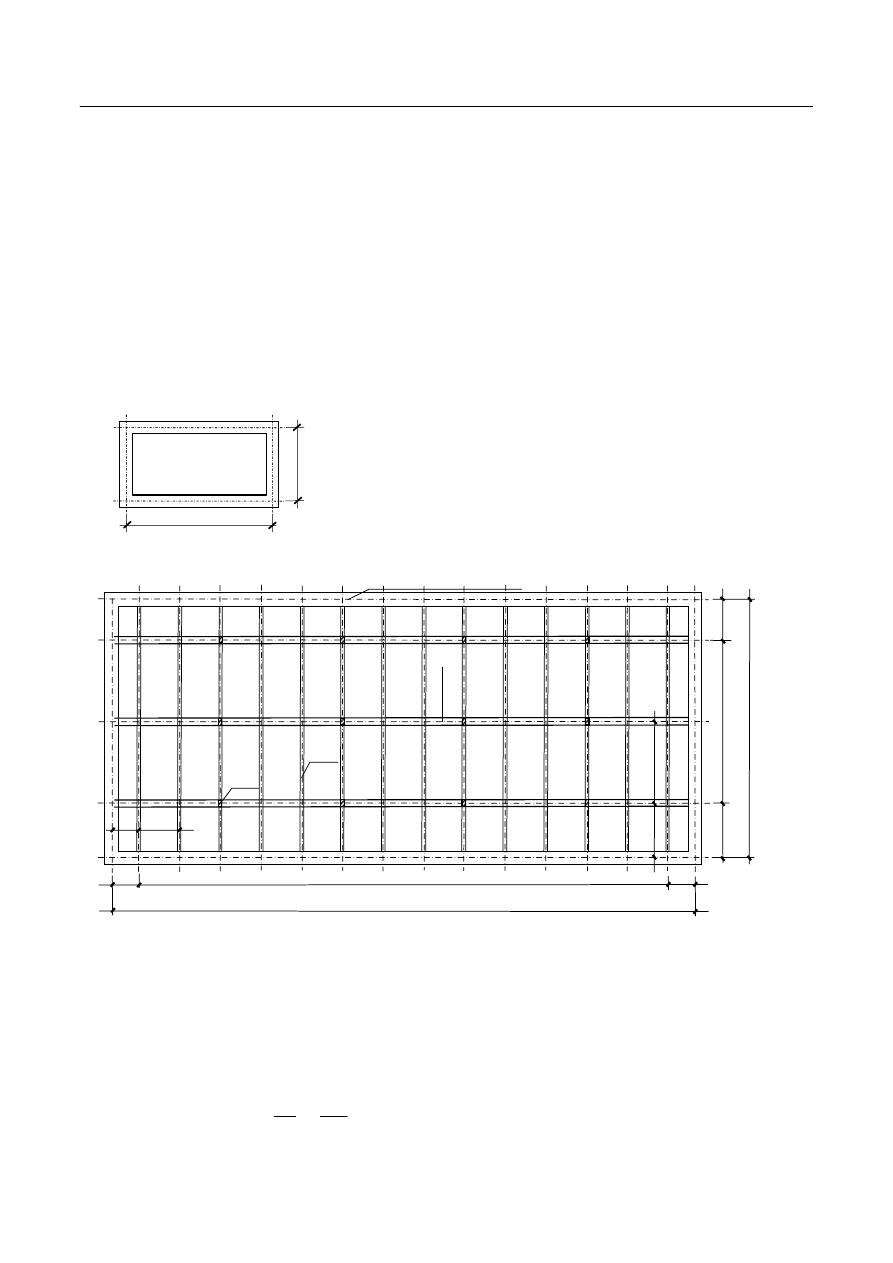
Rys. 1. Widok stropu płytowo – belkowego: a) schematyczne przedstawienie rzutu i przekroi budynku, b) szczegół A

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
3
Podstawowe wymagania do projektu
W celu poprawienia czytelności projektu w obliczeniach należy prowadzić numerację pozycji
obliczeniowych uszeregowaną w logiczny ciąg. Poniżej podano przykładową numerację pozycji
obliczeniowych dla projektowanego budynku:
Poz. 1. Stropodach.
Poz. 1.1. Płyta stropodachu.
Poz. 1.2. Żebro stropodachu.
Poz. 1.3. Podciąg stropodachu.
Poz. 2. Strop międzykondygnacyjny.
Poz. 2.1. Płyta stropu.
Poz. 2.2. Żebro stropu.
Poz. 2.3. Podciąg stropu.
Poz. 3. Klatka schodowa.
Poz. 3.1. Spocznik.
Poz. 3.2. Bieg.
Dalsze pozycje zależne od przyjętej konstrukcji schodów
Poz. 4. Słupy.
Poz. 4.1. Słup 3 kondygnacji.
Poz. 4.2. Słup 2 kondygnacji.
Poz. 4.3. Słup 1 kondygnacji.
Poz. 5. Stopa fundamentowa.
Poz. 6. Ściany zewnętrzne.
Poz. 6.1 Ściana podłużna
Poz. 6.2 Ściana poprzeczna
Poz. 7. Ławy fundamentowe.
Uwaga: Ten sam numer pozycji powinien się pojawić na rysunkach załączonych do projektu.
W celu jednoznacznego określenia zamierzeń autora projektu obliczenia należy ilustrować szkicami
i odpowiednimi słownymi komentarzami.
Wszystkie wartości w obliczeniach powinny wynikać z poprzednich obliczeń lub zamieszczonych tablic. Nie
zaleca się stosowania skrótów utrudniających sprawdzanie projektu.
Po obliczeniu i zwymiarowaniu elementu zalecane jest sporządzenie szkicu przyjętego zbrojenia. Może on
być wykonany w skali skażonej i powinien zawierać:
- numer pozycji i gabarytowe wymiary elementu,
- liczbę i średnicę zbrojenia w miejscach, w których zostało ono obliczone,
- liczbę zbrojenia odgiętego i obszar, na którym zostało obliczone,
- liczbę i rozstaw strzemion.
Zawartość projektu
1. Strona tytułowa (nazwa i adres jednostki wykonującej projekt, tytuł projektu, nazwisko autora
projektu i osoby sprawdzającej, liczbę ponumerowanych stron, rok i miejsce wykonania projektu).
2. Spis treści.
3. Wykaz rysunków dołączonych do projektu.
4. Temat projektu.
5. Opis techniczny.
6. Obliczenia statyczne i wymiarowanie.
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
4
W celach dydaktycznych zawartość projektu podano na przykładzie wykonywanego zadania projektowego.
Na rysunku 2 przedstawiono przykładową stronę tytułową do projektu wykonywanego na zajęciach
projektowych z „Konstrukcji betonowych 2”, lub „Konstrukcji żelbetowych 1b”.
POLITECHNIKA ŚWIĘTOKTRZYSKA W KIELCACH
WYDZIAŁ BUDOWNICTWA I INŻYNIERII ŚRODOWISKA
KATEDRA WYTRZYMAŁOŚCI MATERIAŁÓW I KONSTRUKCJI BETONOWYCH
ZAKŁAD KONSTRUKCJI ŻELBETOWYCH I BUDOWNICTWA PRZEMYSŁOWEGO
PROJEKT BUDYNKU O KONSTRUKCJI MIESZANEJ
Projekt zawiera ……… stron ponumerowanych
Wykonał: Sprawdził:
Nazwisko i imię Nazwisko i imię
autora projektu nauczyciela prowadzącego zajęcia
Grupa ….. rok akad. 2007/08
rodzaj studiów (zaoczne lub dzienne)
Kielce, styczeń 2008 rok
Rys. 2. Strona tytułowa do projektu.
1. WSTĘPNE PRZYJĘCIE WYMIARÓW
1.1. Płyty
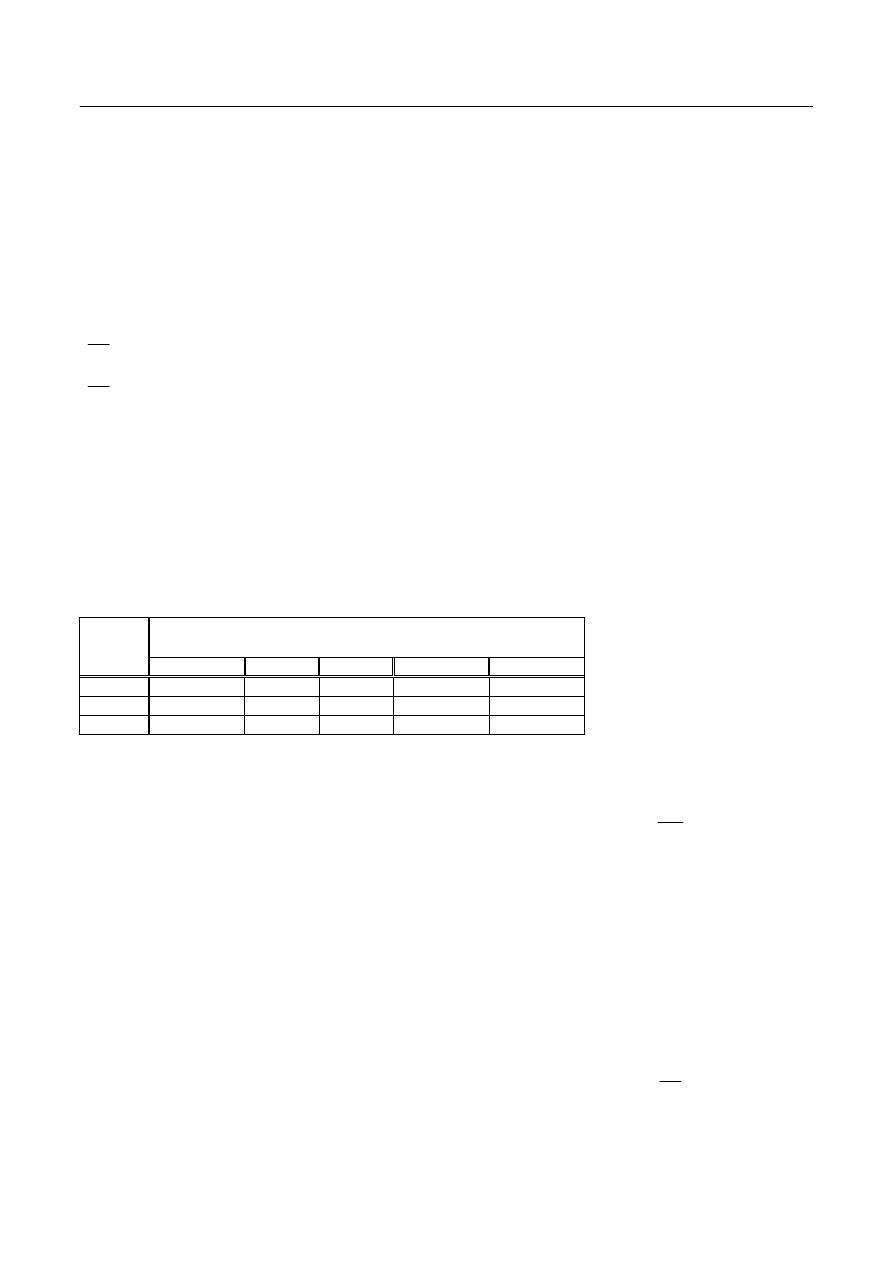
W tablicy 1 podano minimalne grubości płyt w zależności od przeznaczania obiektu i technologii
wykonania.
Tablica 1. Minimalne grubości płyt.
Przeznaczenie płyty
Płyty prefabrykowane [mm] Płyty monolityczne [mm]
Płyty stropowe w obiektach
budownictwa powszechnego
40 60
Płyty pod przejazdami
100 120
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
5
Grubość płyty musi być jednak tak dobrana, żeby zapewnione były:
- warunek stanu granicznego nośności (z uwagi na moment zginający),
- prawidłowe otulenie wkładek zbrojeniowych,
- warunek odpowiedniej ochrony przeciwpożarowej,
- warunkiem przekroczenia granicznych wartości ugięć.
Rozpiętość płyty stropowej należy tak dobrać by mieściła się w granicach 1.5
÷ 3.5 m.
Stosunek rozpiętości obliczeniowej płyty l
eff
do wysokości użytecznej przekroju d nie powinien przekraczać:
40
≤
d
l
eff
– dla płyt wolnopodpartych jednokierunkowo zbrojonych,
50
≤
d
l
eff
– dla płyt zamocowanych i ciągłych jednokierunkowo zbrojonych, oraz krzyżowo zbrojonych.
Przy szacowaniu grubości płyty należy również kierować się stanem granicznym ugięcia, co w uproszczeniu
można zrobić wykorzystując podane w Tablicy 13 zamieszczonej na str. 68 normy PN – B – 03264: 2002
maksymalne wartości stosunku rozpiętości l
eff
do wysokości użytecznej d, przy której można nie sprawdzać
ugięć.
W celu ekonomicznego przyjęcia grubości płyty (uniknięcie małego wykorzystania nośności strefy ściskanej
betonu, co występuje przy nadmiernej grubości płyty lub zbyt małej rozpiętości) w tablicy 2 podano zalecane
rozstawy żeber (rozpiętości płyt) i grubości płyt w zależności od obciążenia całkowitego. Wartości te nie są
obligatoryjne, wynikają jedynie z praktyki projektowej.
Tablica 2. Zalecane rozpiętości i grubości płyt.
Rozpiętość płyty w [m]
dla całkowitego obciążenia charakterystycznego q [kN/m
2
]
Grubość
płyty
[mm]
3.0 5.0
7.5 10.0 15.0
80 2.4
2.0
÷ 2.2 1.6 ÷ 1.8 nie stosować nie
stosować
90 2.8
2.4
÷ 2.6 2.0 ÷ 2.2
1.7
÷ 1.9
nie stosować
100 nie
stosować 2.9
÷ 3.1 2.2 ÷ 2.4
1.9
÷ 2.1
1.6
÷ 1.8
Grubość płyt dla
mm
120
≤
f
h
można stopniować co 10 mm, natomiast dla
mm
120
>
f
h
zalecane jest
stopniowanie co 20 mm.
Ekonomiczny procent zbrojenia dla płyt powinien mieścić się w granicach:
(
)
yd
f
190
2
.
1
7
.
0
÷
[%], gdzie f
yd
jest
to obliczeniowa granica plastyczności stali zbrojeniowej wyrażona w MPa.
1.2. Żebra i podciągi
Racjonalne rozpiętości żeber wynoszą
m
7
4
÷
, natomiast podciągów
m
8
5
÷
. Podane granice rozpiętości
mogą ulec zmianie, ponieważ mają związek z wielkością obciążeń i tak dla obciążeń
2
kN/m
10
≥
p
– ulegają
zmniejszeniu, a przy obciążeniu
2
kN/m
3
≤
p
– zwiększeniu. Wzrost rozpiętości elementów zwiększa udział
ciężaru własnego w obciążeniu całkowitym, natomiast zbyt małe rozpiętości powodują zwiększenie liczby
słupów i fundamentów, ograniczając funkcjonalność budynku.
Wysokość belek można przyjąć z warunku zapewnienia dostatecznej sztywności –
h
l
eff
. Wynikające stąd
szacunkowe relacje przyjmuje się zazwyczaj w zależności od rodzaju belek i wielkości obciążenia i tak dla:

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
6
- belek drugorzędnych i słabo obciążonych –
20
18
÷
=
h
l
eff
,
- żeber silnie i średnio obciążonych –
18
12
÷
=
h
l
eff
,
- podciągów słabo obciążonych w budownictwie powszechnym (
2
kN/m
5
<
p
) –
18
15
÷
=
h
l
eff
,
- podciągów silnie obciążonych: magazyny, zakłady przemysłowe (
2
kN/m
10
>
p
) –
12
9
÷
=
h
l
eff
.
Wymiary belek
b
h
l
eff
×
×
powinny być tak dobrane, żeby stopień zbrojenia podłużnego mieścił się
w granicach ekonomicznego procentu zbrojenia wynoszącego dla tych elementów
(
)
yd
f
190
0
.
2
0
.
1
÷
[%].
Związek pomiędzy szerokością i wysokością belek:
- belki prostokątne –
3.0
2.0
÷
=
b
h
,
- belki teowe –
4.0
2.5
÷
=
w
b
h
,
gdzie
w
b – szerokość środnika belki teowej.
Wymiary poprzeczne belek
W celu ujednolicenia wymiarów przekrojów zaleca się przestrzegać następującego stopniowania wymiarów
belek prostokątnych i teowych:
- szerokość: 150, 180, 200, 250 mm i dalej co 50 mm,
- wysokość: 250, 300 mm i dalej co 50 mm do 800 mm, a powyżej 800 mm co 100 mm.
1.3. Słupy
W celu łatwiejszego wykonania deskowań zaleca się przyjmować szerokość słupa równą szerokości
podciągu.
Przyjęcie wymiarów przekroju poprzecznego słupa:
Wymiary przekroju poprzecznego słupa żelbetowego w dużej mierze uzależnione są od wielkości
mimośrodu działania siły.
- Jeżeli mimośród jest na tyle mały, że cały przekrój jest ściskany lub
lim
eff
eff
ξ
ξ
>
to o wymiarach
przekroju poprzecznego decyduje głównie wartość siły działającej na słup. W tym wypadku przyjmuje
się przekrój kwadraty lub zbliżony do kwadratowego.
- Jeżeli natomiast mimośród jest na tyle duży, że w przekroju strefa rozciągana ma stosunkowo duży zasięg
(
lim
eff
eff
ξ
ξ
≤
), to o wymiarach przekroju poprzecznego słupa decyduje głównie wartość momentu
zginającego. W tym przypadku przyjmuje się przekrój prostokątny, wydłużony w kierunku działania
momentu o przekrojach zbliżonych do belki zginanej.
W literaturze możemy znaleźć szereg praktycznych zaleceń dotyczących przyjmowania wymiarów
poprzecznych słupów.
A. W przypadku dużego mimośrodu, gdy spodziewamy się, że siła działa poza przekrojem słupa, decydujące
znaczenie ma zbrojenie w strefie rozciąganej, a charakter pracy słupa przypomina zachowanie się belki
zginanej podwójnie zbrojonej. Algorytm postępowania w tym przypadku może być następujący:
a) zakłada się stopień zbrojenia
ρ
1
(ok.
%
0
.
2
%
0
.
1
1
≤
≤
ρ
), proporcje boków b/h, klasę betonu i stali,

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
7
b) z sumy sił na oś prostopadłą do przekroju i z sumy momentów względem wypadkowej bryły
naprężeń strefy ściskanej przekroju wyznaczamy:
=
cd
cc
yd
yd
e
Sd
f
α
f
ρ
b
f
ρ
e
N
h
2
-
1
1
1
c) stopień zbrojenia ściskanego można oszacować z warunku:
yd
cd
e
Sd
f
f
bd
d
e
N
ρ
/
0.33
-
2
1
2
+
=
gdzie: N
Sd
– siła w [MPa],
b
×d – pole powierzchni przekroju poprzecznego słupa [m
2
],
e
e
– mimośród statyczny,
f
cd
– wytrzymałość obliczeniowa betonu na ściskanie w konstrukcjach żelbetowych,
f
yd
– obliczeniowa granica plastyczności stali.
B. W przypadku, gdy liczymy się z występowaniem strefy rozciąganej, ale mimośród siły usytuowany jest
pomiędzy osiami zbrojenia, można postępować w następujący sposób:
a) zakłada się sumaryczny stopień zbrojenia
2
1
ρ
ρ
ρ
+
=
(ok.
%
3
2
÷
),
b) z zależności
ρ
yd
Sd
f
M
bd
2
2
=
przy założeniu proporcji boków i przyjęciu klasy stali obliczamy wymiary
przekroju,
c) przy zaokrąglaniu wymiarów dokonujemy ich zmniejszenia.
C. Jeżeli mimośród działania siły jest na tyle mały, że cały przekrój słupa będzie ściskany, – np.
w przypadku gdy mimośród działania siły wynika jedynie z mimośrodu niezamierzonego
a
e
e
=
0
, to
o wymiarach przekroju decyduje wartość siły ściskającej
N
Sd
. Słupy te przeważnie przyjmuje się
o przekroju kwadratowym.
Przekrój słupa można oszacować z zależności:
cd
cc
Sd
f
α
.
N
hb
9
0
≥
gdzie:
h – wymiar boku przekroju słupa – wysokość przekroju,
b – wymiar boku przekroju słupa – szerokość przekroju równa szerokości przekroju podciągu
N
Sd
– siła ściskającą działająca na słup,
α
cc
– współczynnik uwzględniający wpływ obciążenia długotrwałego, niekorzystny efekt sposobu
przyłożenia obciążenia, a w przypadku słupów również wpływ małych przekrojów, na
wytrzymałość obliczeniową betonu na ściskanie,
α
cc
= 1.0,
z wyjątkiem
- elementów konstrukcyjnych o wyjątkowym znaczeniu, których zniszczenie pociągałoby za sobą
katastrofalne skutki społeczne i materialne, dla których zaleca się przyjmować:
85
.
0
=
cc
α
,
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
8
- elementów ściskanych o małym przekroju poprzecznym
2
m
09
.
0
≤
c
A
, gdy jeden z boków lub
średnica przekroju są mniejsze niż 250 mm, dla których
α
cc
oblicza się ze wzoru:
85
.
0
=
cc
α
dla
2
2
m
09
.
0
m
04
.
0
≤
≤
c
A
,
04
.
0
/
85
.
0
c
cc
A
=
α
dla
2
m
04
.
0
<
c
A
,
Wymiary słupa należy zaokrąglać:
- przy
mm
600
≤
h
do pełnych 50 mm,
- przy mm
600
>
h
do pełnych 100 mm.
Najmniejsze wymiary przekroju nie mogą być mniejsze niż 250 mm.
Jeżeli słup jest bardzo smukły
15
>
h
l
o
, wymiary przekroju słupa należy zwiększyć.
W każdym z opisanych wyżej przypadków należy także sprawdzić warunek smukłości słupa.
2. PROJEKT WSTĘPNY
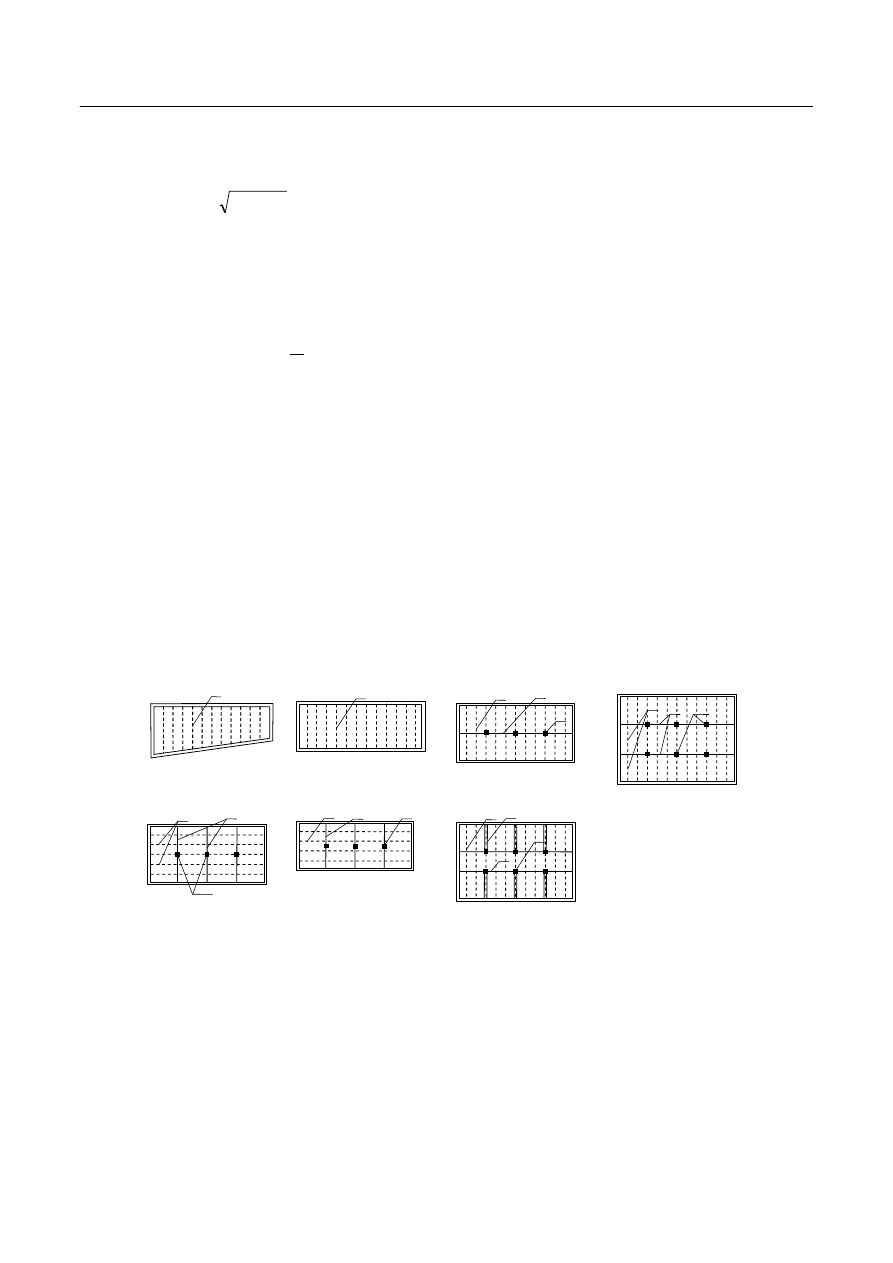
Zakres projektu wstępnego:
- przyjęcie siatki słupów oraz rozstawu i rozpiętości elementów,
- przyjęcie grubości płyty oraz wymiarów przekroju poprzecznego żeber, podciągów i słupów.
Przykładowe rozplanowanie żeber, podciągów i słupów w zależności od wymiarów rzutu budynku
przedstawiono na rysunku 3.
a)
b)
1
c)
1
2
3
d)
1
2
3
e)
1
2
3
f)
1
2
3
g)
1
4
2
3
Rys. 3. Przykładowe schematy rozplanowania żeber i podciągów monolitycznych.
1 – żebra, 2 – podciągi, 3 – słupy, 4 – żebra wzmocnione (pod ściankami działowymi.
Na rysunku 4 przedstawiono schemat rozdziału obciążeń na poszczególne elementy stropu.
1
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
9
l
1
l
1
l
1
l
2
słup (rozdział obciążenia z powierzchni l
2
× l
3
)
żebro
l
2
l
2
podciąg
1 m
płyta
l
3
l
3
l
3
podc
ią
g
P
+
G
pł
yta (
g+
p)
p
g
żebro
Rys. 4. Schemat rozdziału obciążeń na poszczególne elementy stropu.
Należy przyjąć jednakową klasę betonu dla płyt stropodachu i stropów międzypiętrowych oraz żeber,
podciągów i słupów. Inną klasę betonu można przyjąć dla ław i stóp fundamentowych oraz klatki schodowej
jeżeli stanowi konstrukcję samonośną.
Poz. 1. Stropodach
Poz. 1.1. Płyta stropodachu
A. Przyjęcie grubości płyty
mm
h
f
60
≥
,
50
eff
l
d
≥
Na etapie projektu wstępnego rozpiętość l
eff
można przyjmować równą rozpiętości osiowej elementu.
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN/m
2
]
Współczynnik
γ
f
Obciążenia obliczeniowe [kN/m
2
]
Obciążenia stałe
–
warstwy wykończeniowe
–
ciężar własny płyty h
f
×
γ
żb
= ___________
g
kpł
=
Σ
Obciążenie zmienne
–
obciążenie śniegiem p
kpł
= S
n
=
Obciążenie całkowite
q
kpł
= g
kpł
+ p
kpł
1.1
___________
g
Sdpł
=
Σ
p
Sdpł
= S
sdn
=
q
Sdpł
= g
Sdpł
+ p
Sdpł
Uwaga:
Ze względu na mały kąt pochylenia stropodachu pomijamy wpływ obciążenia wiatrem. Przy małych
kątach pochylenia dachu wiatr działa korzystnie – występuje ssanie, które odciąża konstrukcję.
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
10
C. Sprawdzenie przyjętej grubości płyty h
f
- statyka
l
pł
q
Sdpł
8
l
q
M
2
pł
Sdpł
Sd
=
(
)
Sd
Sd
M
M
9
.
0
8
.
0
1
÷
=
– zmniejszenie wielkości momentu zginającego
z uwagi na to, że płyta w rzeczywistości pracuje jako belka ciągła
wieloprzęsłowa.
- ze względu na zginanie
a
1
= c + 0.5
φ
,
gdzie:
φ
– średnica zbrojenia płyty (4.5
÷12 mm),
c – otulina zbrojenia.
d = h
f
– a
1
,
yd
Sd
S
f
z
M
A
1
1
=
,
gdzie
d
z
9
.
0
≈
d
A
S1
=
ρ
.
Procent zbrojenia płyty
ρ
powinien się zawierać w granicach procentu ekonomicznego dla płyty.
- stan graniczny ugięcia płyty
50
<
d
l
eff
, warunek konieczny dla płyt zbrojonych jednokierunkowo.
Stanu granicznego ugięć można nie sprawdzać jeżeli:
max
eff
eff
d
l
d
l
≤
, przy czym
max
eff
d
l
jest wielkością
odczytaną z tab. 13, str. 68,
2002
:
03264
B
PN
−
−
w zależności od procentu zbrojenia –
ρ
, naprężeń w stali
σ
s
i klasy betonu. Dla wartości pośrednich graniczne wartości z tabeli należy interpolować liniowo.
Wartość naprężeń w zbrojeniu rozciąganym
σ
s
wyznaczamy ze wzoru:
1
S
k
s
z A
M
σ
=
,
gdzie: M
k
– moment od obciążeń charakterystycznych,
d
z
9
.
0
=
.
Poz. 1.2. Żebro stropodachu
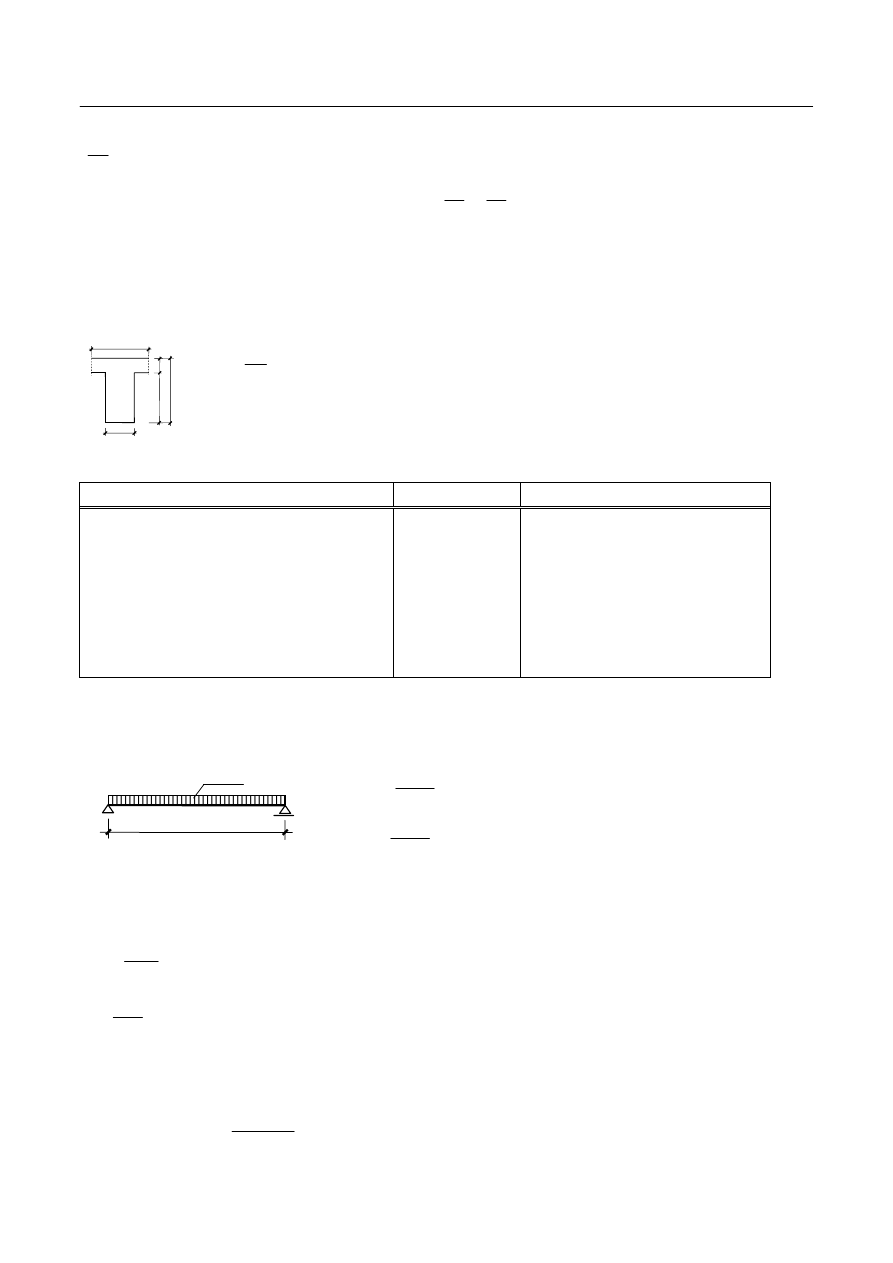
A. Przyjęcie wymiarów żebra
20
9
÷
=
h
l
eff
w zależności od rodzaju elementu i wielkości obciążenia (punkt 1.2).
l
eff
– rozpiętość żebra przyjąć w osiach.
b
w
b
eff
h
f
h
ż
h
ż
-h
f
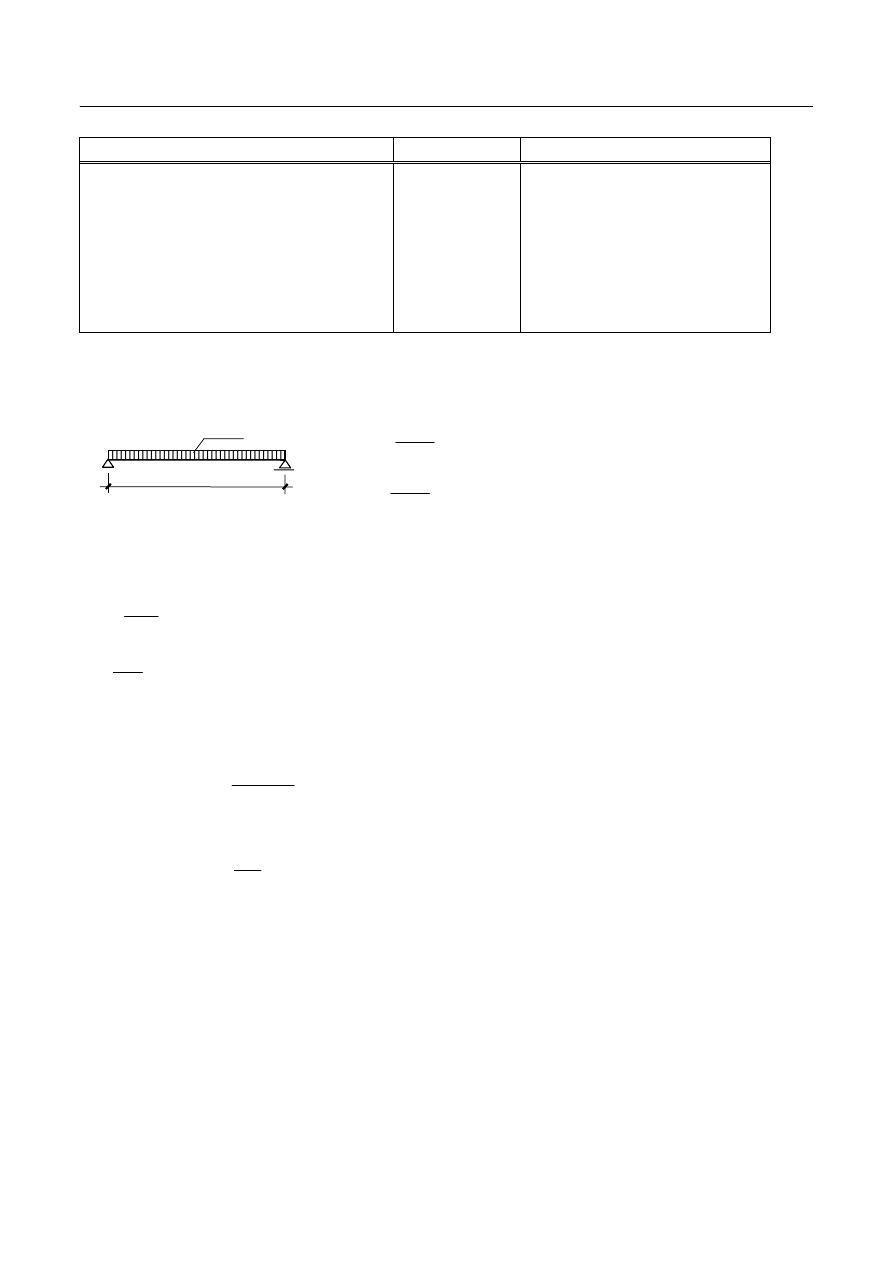
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
11
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN/m]
Współczynnik
γ
f
Obciążenia obliczeniowe [kN/m]
Obciążenie stałe
–
z poz. 1.1. g
kpł
× l
pł
=
–
ciężar własny żebra:
b
w
×(h
ż
- h
f
)
×
γ
żb
= ____________
g
kż
=
Σ
Obciążenie zmienne
–
z poz.1.1. p
kż
= p
kpł
× l
pł
=
Obciążenie całkowite
q
kż
= g
kż
+ p
kż
–
1.1
–
–
z poz. 1.1. g
Sdpł
× l
pł
=
___________
g
Sdż
=
Σ
–
z poz.1.1. p
Sdż
= p
Sdpł
× l
pł
=
q
Sdż
= g
Sdż
+ p
Sdż
C. Sprawdzenie przyjętych wymiarów żebra
- statyka
l
ż
q
Sdż
8
2
ż
Sdż
Sd
l
q
M
=
,
(
)
Sd
Sd
M
M
9
.
0
8
.
0
1
÷
=
,
2
ż
Sdż
Sd
l
q
V
=
- ze względu na zginanie
ż
h
a
1
.
0
1
=
1
a
h
d
ż
−
=
yd
Sd
S
f
z
M
A
1
1
=
, gdzie
d
z
9
.
0
≈
,
d
b
A
w
S
1
=
ρ
.
Procent zbrojenia żebra
ρ
powinien się zawierać w granicach procentu ekonomicznego dla belek.
- ze względu na ścinanie
θ
θ
ν
2
2
cot
1
cot
+
=
≤
z
b
f
V
V
w
cd
Rd
Sd
– graniczna siła poprzeczna ze względu na ukośne ściskanie powstająca
przy ścinaniu w elementach zginanych,
w którym:
−
=
250
1
6
.
0
ck
f
ν
(f
ck
w MPa)
gdzie: V
Rd2
– graniczna siła poprzeczna ze względu na ukośne ściskanie powstająca przy ścinaniu
w elementach zginanych,
f
ck
– wytrzymałość charakterystyczna betonu na rozciąganie,
z – ramię sił wewnętrznych (
d
z
9
.
0
=
),
0
.
2
cot
0
.
1
≤
≤
θ
.
Jeżeli:
2
Rd
Sd
V
V
>
– należy zwiększyć wymiary poprzeczne żebra.
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
12
- stan graniczny ugięcia żebra
Stanu granicznego ugięć można nie sprawdzać jeżeli:
max
eff
eff
d
l
d
l
≤
, przy czym
max
eff
d
l
jest wielkością
odczytaną z tab. 13, str. 68,
2002
:
03264
B
PN
−
−
.
Poz. 1.3. Podciąg stropodachu
A. Przyjęcie wymiarów przekroju poprzecznego
b
w
b
eff
h
f
h
p
h
p
-h
f
20
9
÷
=
h
l
eff
w zależności od rodzaju elementu i wielkości obciążenia (punkt 1.2).
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
Współczynnik
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
–
z poz. 1.2. g
kż
× l
ż
=
–
ciężar własny podciągu:
b
w
×(h
p
–
h
f
)
×
γ
żb
×l
pł
= ____________
G
kp
=
Σ
Obciążenie zmienne
–
obc. śniegiem: z poz.1.2. P
kp
= p
kż
× l
ż
=
Obciążenie całkowite
Q
kp
= G
kp
+ P
kp
–
1.1
–
–
z poz. 1.2. g
Sdż
× l
ż
=
___________
G
Sdp
=
Σ
–
z poz.1.2. P
Sdp
= p
Sdż
× l
ż
=
Q
Sdp
= G
Sdp
+ P
Sdp
C. Sprawdzenie przyjętych wymiarów podciągu
- statyka
l
p
Q
Sdp
Q
Sdp
l
p
/3
l
p
/3
l
p
/3
3
p
Sdp
Sd
l
Q
M
=
,
(
)
Sd
Sd
M
M
9
.
0
8
.
0
1
÷
=
,
Sdp
Sd
Q
V
=
- ze względu na zginanie
p
h
a
1
.
0
1
=
1
a
h
d
p
−
=
yd
Sd
S
f
z
M
A
1
1
=
, gdzie
d
z
9
.
0
≈
,
d
b
A
w
S
1
=
ρ
.
Procent zbrojenia podciągu
ρ
powinien się zawierać w granicach procentu ekonomicznego dla belek.
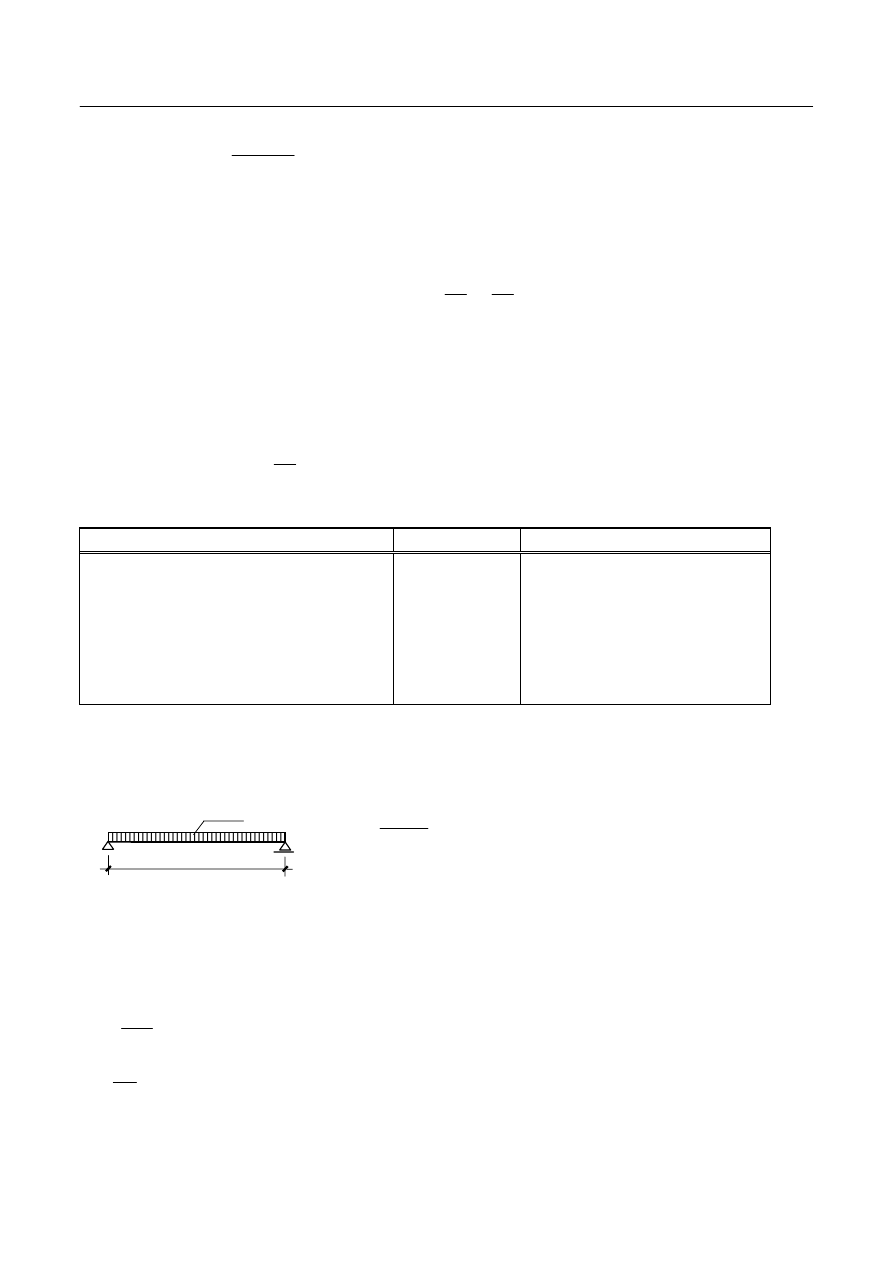
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
13
- ze względu na ścinanie
θ
θ
ν
2
2
cot
1
cot
+
=
≤
z
b
f
V
V
w
cd
Rd
Sd
Jeżeli:
2
Rd
Sd
V
V
>
– należy zwiększyć wymiary poprzeczne podciągu.
- stan graniczny ugięcia podciągu stropodachu
Stanu granicznego ugięć można nie sprawdzać jeżeli:
max
eff
eff
d
l
d
l
≤
.
Poz.2. Strop międzykondygnacyjny
Poz. 2.1. Płyta stropu
A. Przyjęcie grubości płyty
mm
h
f
60
≥
,
50
eff
l
d
≥
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN/m
2
]
Współczynnik
γ
f
Obciążenia obliczeniowe [kN/m
2
]
Obciążenia stałe
–
warstwy wykończeniowe
–
ciężar własny płyty h
f
×
γ
żb
= ____________
g
kpł
=
Σ
Obciążenie zmienne
–
obc. użytkowe p
kpł
=
Obciążenie całkowite
q
kpł
= g
pł
+ p
pł
1.1
___________
g
Sdpł
=
Σ
p
Sdpł
=
q
Sdpł
= g
Sdpł
+ p
Sdpł
C. Sprawdzenie przyjętej grubości płyty h
f
- statyka
l
pł
q
Sdpł
8
l
q
M
2
pł
Sdpł
Sd
=
,
(
)
Sd
Sd
M
M
9
.
0
8
.
0
1
÷
=
.
- ze względu na zginanie
a
1
= c + 0.5
φ
,
gdzie:
φ
– średnica zbrojenia płyty (4.5
÷12 mm),
c – otulina zbrojenia.
d = h
f
– a
1
,
yd
Sd
S
f
z
M
A
1
1
=
,
gdzie
d
z
9
.
0
≈
d
A
S1
=
ρ
. Procent zbrojenia płyty
ρ
powinien się zawierać w granicach procentu ekonomicznego dla płyty.
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
14
- stan graniczny ugięcia płyty
50
<
d
l
eff
, warunek konieczny dla płyt zbrojonych jednokierunkowo.
Stanu granicznego ugięć można nie sprawdzać jeżeli:
max
eff
eff
d
l
d
l
≤
.
Poz.2.2. Żebro stropu
A. Przyjęcie wymiarów żebra
b
w
b
eff
h
f
h
ż
h
ż
-h
f
20
9
÷
=
h
l
eff
w zależności od rodzaju elementu i wielkości obciążenia (punkt 1.2).
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN/m]
Współczynnik
γ
f
Obciążenia obliczeniowe [kN/m]
Obciążenia stałe
–
z poz. 2.1. g
kpł
× l
pł
=
–
ciężar własny żebra:
b
w
×(h
ż
–
h
f
)
×
γ
żb
= ____________
g
kż
=
Σ
Obciążenie zmienne
–
obc. użytkowe: z poz.2.1. p
kż
= p
kpł
×l
pł
=
Obciążenie całkowite
q
kż
= g
kż
+ p
kż
–
1.1
–
–
z poz. 2.1. g
Sdpł
× l
pł
=
___________
g
Sdż
=
Σ
–
z poz.2.1. p
Sdż
= p
Sdpł
× l
pł
=
q
Sdż
= g
Sdż
+ p
Sdż
C. Sprawdzenie przyjętych wymiarów żebra
- statyka
l
ż
q
Sdż
8
2
ż
Sdż
Sd
l
q
M
=
,
(
)
Sd
Sd
M
M
9
.
0
8
.
0
1
÷
=
,
2
ż
Sdż
Sd
l
q
V
=
- ze względu na zginanie
ż
h
a
1
.
0
1
=
1
a
h
d
ż
−
=
yd
Sd
S
f
z
M
A
1
1
=
, gdzie
d
z
9
.
0
≈
,
d
b
A
w
S
1
=
ρ
.
Procent zbrojenia żebra
ρ
powinien się zawierać w granicach procentu ekonomicznego dla belek.
- ze względu na ścinanie
θ
θ
ν
2
2
cot
1
cot
+
=
≤
z
b
f
V
V
w
cd
Rd
Sd
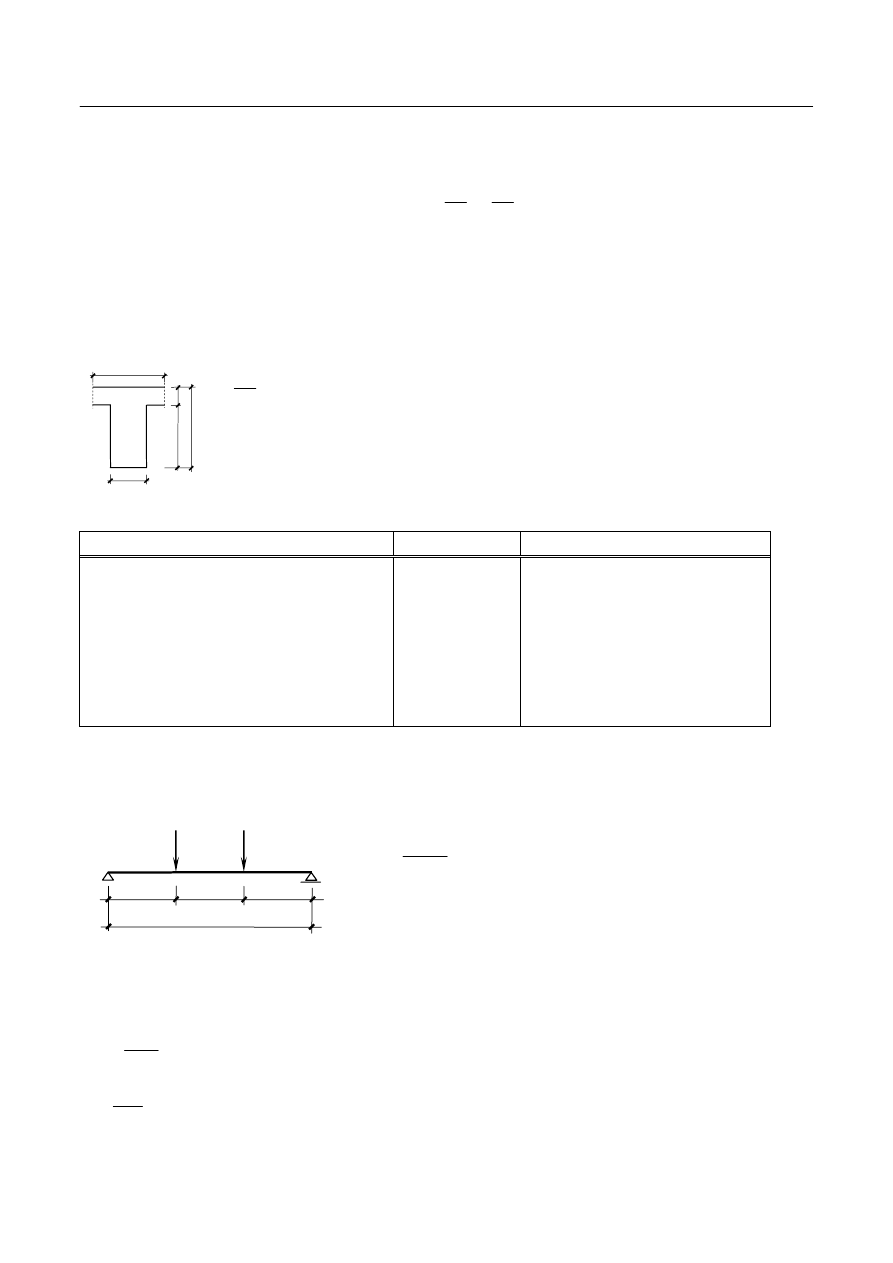
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
15
Jeżeli:
2
Rd
Sd
V
V
>
– należy zwiększyć wymiary poprzeczne żebra.
- stan graniczny ugięcia żebra
Stanu granicznego ugięć można nie sprawdzać jeżeli:
max
eff
eff
d
l
d
l
≤
.
Poz.2.3. Podciąg stropu
A. Przyjęcie wymiarów przekroju poprzecznego
b
w
b
eff
h
f
h
p
h
p
-h
f
20
9
÷
=
h
l
eff
w zależności od rodzaju elementu i wielkości obciążenia (punkt 1.2).
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
Współczynnik
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
–
z poz. 2.2. g
kż
× l
ż
=
–
ciężar własny podciągu:
b
w
×(h
p
- h
f
)
×
γ
żb
×l
pł
= ____________
G
kp
=
Σ
Obciążenie zmienne
–
obc. użytkowe: z poz.2.2. P
kp
= p
kż
× l
ż
=
Obciążenie całkowite
Q
kp
= G
kp
+ P
kp
–
1.1
–
–
z poz. 2.1. g
Sdż
× l
ż
=
___________
G
Sdp
=
Σ
–
z poz.2.2. P
Sdp
= p
Sdż
× l
ż
=
Q
Sdp
= G
Sdp
+ P
Sdp
C. Sprawdzenie przyjętych wymiarów podciągu
- statyka
l
p
Q
Sdp
Q
Sdp
l
p
/3
l
p
/3
l
p
/3
3
p
Sdp
Sd
l
Q
M
=
,
(
)
Sd
Sd
M
M
9
.
0
8
.
0
1
÷
=
,
Sdp
Sd
Q
V
=
- ze względu na zginanie
p
h
a
1
.
0
1
=
1
a
h
d
p
−
=
yd
Sd
S
f
z
M
A
1
1
=
, gdzie
d
z
9
.
0
≈
,
d
b
A
w
S
1
=
ρ
. Procent zbrojenia podciągu
ρ
powinien się zawierać w granicach procentu ekonomicznego dla
belek.
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
16
- ze względu na ścinanie
θ
θ
ν
2
2
cot
1
cot
+
=
≤
z
b
f
V
V
w
cd
Rd
Sd
. Jeżeli:
2
Rd
Sd
V
V
>
– należy zwiększyć wymiary poprzeczne podciągu.
- stan graniczny ugięcia podciągu stropodachu
Stanu granicznego ugięć można nie sprawdzać jeżeli:
max
eff
eff
d
l
d
l
≤
.
Poz. 4. Słupy
Poz. 4.1
Poz. 4.2
Poz. 4.3
Poz. 4.1. Słup najwyższej kondygnacji
A. Przyjęcie wymiarów słupa
W celu łatwiejszego wykonania deskowań zaleca się przyjmować szerokość słupa równą szerokości
podciągu.
p
sł
h
H
l
−
=
gdzie: H – wysokość kondygnacji,
h
p
– wysokość podciągu.
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
Współczynnik
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
–
z poz. 1.3. 3
×G
kp
=
–
ciężar własny słupa: b
×h×
γ
żb
×l
sł
= ______
N
kg
=
Σ
Obciążenie zmienne
–
obc. śniegiem: z poz.1.3 N
kp
= 3
×P
p
=
Obciążenie całkowite
N
k4.1
= N
kg
+ N
kp
–
1.1
–
–
z poz. 1.3: 3
× G
Sdp
=
___________
N
Sdg
=
Σ
–
z poz.1.3. N
Sdp
= 3
× P
Sdp
=
N
Sd4.1
= N
Sdg
+ N
Sdp
C. Sprawdzenie przyjętych wymiarów słupa
- ze względu na nośność słupa
Wstępnie nośność przekroju można sprawdzić z warunku jak dla słupów betonowych, przyjmując słup
kwadratowy przy czym szerokość słupa b powinna być równa szerokości podciągu b
p
(b = b
p
):
bh
f
N
N
cd
cc
Sd
sd
ϕα
=
≤
41
,
stąd wymiar przekroju słupa
b
f
α
N
h
cd
cc
.
Sd
ϕ
1
4
=
,
gdzie:
α
cc
– patrz punkt 1.3 (słupy betonowe),
f
cd
–wytrzymałość obliczeniowa betonu na ściskanie.
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
17
Na etapie projektu wstępnego można przyjąć
ϕ
= 0.9.
Jeżeli N
Sd
< N
Sd4.1
to należy przeprowadzić korektę przyjętego wymiaru słupa.
Poz. 4.2. Słup środkowej kondygnacji
A. Przyjęcie wymiarów słupa
Jak wyżej.
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
Współczynnik
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
–
z poz. 4.1 N
kg
=
–
z poz.2.3. 3
×G
kp
=
–
ciężar własny słupa:
b
×h
×γ
żb
×l
sł
= ____________
N
kg
=
Σ
Obciążenie zmienne
–
obc. użytkowe: z poz. 4.1. N
kp
–
z poz.2.3 N
kp
= 3
×P
kp
=
Obciążenie całkowite
N
k4.2
= N
kg
+ N
kp
–
1.1
–
–
z poz. 4.1 N
Sdg
–
z poz. 2.3: 3
×G
Sdp
=
___________
N
Sdg
=
Σ
–
z poz. 4.1. N
Sdp
–
z poz.2.3. N
Sdp
= 3
×P
Sdp
=
N
Sd4.2
= N
Sdg
+ N
Sdp
C. Sprawdzenie przyjętych wymiarów słupa
- ze względu na nośność słupa
bh
f
N
N
cd
cc
Sd
sd
ϕα
=
≤
42
,
stąd wymiar przekroju słupa
b
f
α
N
h
cd
cc
.
Sd
ϕ
2
4
=
Uwaga:
Należy zebrać obciążenia na słupy wszystkich kondygnacji.
Poz.5. Stopa fundamentowa
A. Zebranie obciążeń na stopę fundamentową
Obciążenie od słupa najniższej kondygnacji w postaci siły N
Sd
.
I SPOSÓB
fN
st
Sd
q
A
+Q
+Q
N
≤
2
1
gdzie: N
Sd
– siła od słupa,
Q
1
– ciężar gruntu zalegającego nad stopą,
Q
2
– ciężar stopy,
N
Sd
+ Q
1
+ Q
2
= 1.2N
Sd
fN
Sd
st
fN
st
Sd
q
N
A
q
A
N
.
2
.
1
2
1
=
→
≤
Wysokość stopy fundamentowej:
h
= (0.3
÷ 0.4) (B – a
s
)
gdzie: a
s
- wymiar słupa
B
L
h
Q
2
Q
1
N
Sd
α
a
s

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
18
II SPOSÓB
fN
st
st
Sd
q
A
h
A
.
+
N
≤
02
0
N
Sd
≤ A
st
(q
fN
– 0.02h)
h
q
N
A
fN
Sd
st
02
.
0
−
≥
[q
fN
w MPa]
Poz. 6. Ściana zewnętrzna nośna
Poz. 6.1. Ściana warstwowa
A. Ciężar ściany
B. Współczynnik przenikania ciepła k
Poz. 6.2. Wieniec
A. Ciężar wieńca
Poz. 7. Ława fundamentowa
A. Zebranie obciążeń
B. Przyjęcie wymiarów ławy fundamentowej
fN
ł
Sdśd
q
b
q
≤
2
.
1
→ b
ł
≥
fN
Sdśd
q
q
2
.
1
gdzie: q
Sdśc
– ciężar ściany (wielkość obliczeniowa),
b
ł
– szerokość ławy fundamentowej.
MATERIAŁY POMOCNICZE:
1. Kobiak J., Stachurski W.: Konstrukcje żelbetowe. Arkady, Warszawa 1984, tom I.
2. Kobiak J., Stachurski W.: Konstrukcje żelbetowe. Arkady, Warszawa 1987, tom II.
3. Starosolski W.: Konstrukcje żelbetowe według PN – B – 03264:2002 i Eurocodu 2. PWN, Warszawa 2006,
Tom I.
4. Starosolski W.: Konstrukcje żelbetowe według PN – B – 03264:2002 i Eurocodu 2. PWN, Warszawa 2007,
Tom II.
5. Łapko A.: Projektowanie konstrukcji żelbetowych. Arkady, Warszawa 2001.
6. Private communication: Goszczyński S.
7. Dąbrowski K., Stachurski W., Zieliński J.L.: Konstrukcje betonowe. Arkady, Warszawa 1982.
8. Private communication: Szwed A.
9. Łapko A., Jansen B.J.: Podstawy projektowania i algorytmy obliczeń konstrukcji żelbetowych. Arkady, Warszawa
2005.
10. Private communication: Jemioło S.
11. PN–B–03264:2002. Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i projektowanie.
12. PN–EN 1991–1–3. Eurocode 1. Oddziaływania na konstrukcje. Część 1–3: Oddziaływania ogólne – Obciążenia
śniegiem. Październik 2005.
13. PN–77/B–02011. Obciążenia w obliczeniach statycznych. Obciążenie wiatrem.
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
19
14. PN–82/B–02001. Obciążenia budowli. Obciążenie stałe.
15. PN–82/B–02000. Obciążenia budowli. Zasady ustalania wartości.
16. PN–82/B–02003. Obciążenia budowli. Obciążenia zmienne technologiczne. Podstawowe obciążenia
technologiczne i montażowe.
17. PN–EN ISO 6946. Komponenty budowlane i elementy budynku. Opór cieplny i współczynnik przenikania ciepła.
Metoda obliczania.
18. PN–81/B–03020. Grunty budowlane. Posadowienia bezpośrednie budowli. Obliczenia statyczne i projektowanie.
19. PN–74/B–02009. Obciążenia w obliczeniach statycznych. Obciążenie stałe i zmienne.
20. PN–EN ISO 3766:2002. Rysunek konstrukcyjny budowlany. Uproszczony sposób przedstawiania zbrojenia
betonu.
21. PN–B01025:2004. Rysunek budowlany. Oznaczenia graficzne na rysunkach architektoniczno – budowlanych.
22. PN–B01025:2000. Rysunek budowlany. Zasady wymiarowania na rysunkach architektoniczno – budowlanych.
PRZYKŁAD
B = 21.60 m
L = 34.10 m
H = 3.40 m
n = 3
p = 3.60 kN/m
2
q
fN
= 0.22 [MPa]
Lokalizacja Kielce
1. Podział stropu na układ płyt i belek
34100
2100
13
×2300
2100
2100 2300
530
0
550
0
530
0
2×
55
00
216
00
530
0
słup
żebro
podc
ią
g
ściana zewnętrzna - nośna
Poz.1. Stropodach
Poz. 1.1. Płyta stropodachu
A. Przyjęcie grubości płyty
Grubość płyty h
f
wyznaczono z następujących zależności:
cm
0
.
6
≥
f
h
,
50
eff
l
d
≥
=
cm
6
.
4
50
230 =
.
L
B

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
20
Wstępnie grubość płyty przyjęto cm
0
.
7
=
f
h
.
B. Zebranie obciążeń działających na płytę
Obciążenia
charakterystyczne [kN/m
2
]
γ
f
Obciążenia obliczeniowe [kN/m
2
]
Obciążenia stałe
g
kpł
= 2.80
g
Sdpł
= 3.28
Obciążenia zmienne
p
kpł
= 0.77
p
Sdpł
= 1.08
Obciążenie całkowite
q
kpł
= g
pł
+ p
pł
= 3.57
q
Sdpł
= g
Sdpł
+ p
Sdpł
= 4.36
C. Sprawdzenie przyjętej grubości płyty h
f
- statyka
2.30 m
4.36 kN/m
2
kNm/m
88
.
2
8
3
.
2
36
.
4
8
2
2
=
×
=
=
pł
Sdpł
Sd
l
q
M
kNm/m
2.45
88
.
2
85
.
0
85
.
0
1
=
×
=
=
Sd
Sd
M
M
- ze względu na zginanie
c = 1.5 cm
– otulina zbrojenia przyjęta zgodnie z tab. 21,
2002
:
03264
B
PN
−
−
φ
= 6 mm
– wstępnie przyjęta średnica zbrojenia płyty
cm
1.8
6
.
0
5
.
0
5
.
1
5
.
0
1
=
×
+
=
+
=
φ
c
a
cm
5.2
8
.
1
7
1
=
−
=
−
=
a
h
d
f
m
0.0468
cm
68
.
4
2
.
5
9
.
0
9
.
0
=
=
×
=
=
d
z
Na zbrojenie płyty zastosowano stal A-I (St3S):
MPa
210
=
yd
f
m
/
cm
49
.
2
m
/
m
10
49
.
2
10
210
0468
.
0
45
.
2
2
2
4
3
1
1
=
×
=
×
×
=
=
−
yd
Sd
S
f
z
M
A
%
48
.
0
20
.
5
49
.
2
1
=
=
=
d
A
S
ρ
∉
(
)
(
)
(
)
%
08
.
1
63
.
0
210
190
2
.
1
7
.
0
190
2
.
1
7
.
0
÷
=
÷
=
÷
=
yd
ek
f
ρ
.
- stan graniczny ugięcia płyty
50
23
.
44
0.052
2.30
<
=
=
d
l
eff
,
Grubość płyty dobrana prawidłowo.
Poz.1.2. Żebro stropodachu
A. Przyjęcie wymiarów żebra
b
w
b
eff
h
f
h
ż
h
ż
-h
f
18
12
÷
=
ż
eff
h
l
→
(
)
cm
55
.
30
83
.
45
550
18
1
12
1
18
1
12
1
÷
=
×
÷
=
÷
=
eff
ż
l
h
Wysokość żebra przyjęto: cm
35
=
ż
h

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
21
3.0
2.0
÷
=
w
ż
b
h
→
(
)
cm
67
.
11
50
.
17
35
0
.
3
1
0
.
2
1
0
.
3
1
0
.
2
1
÷
=
×
÷
=
÷
=
ż
w
h
b
Przyjęto szerokość żebra b
w
= 18 cm
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN/m]
γ
f
Obciążenia obliczeniowe [kN/m]
Obciążenia stałe
g
kż
= 7.86
g
Sdż
= 9.14
Obciążenia zmienne
p
kż
= 1.77
p
Sdż
= 2.48
Obciążenie całkowite
q
kż
= g
kż
+ p
kż
= 9.63
q
Sdż
= g
Sdż
+ p
Sdż
= 11.62
C. Sprawdzenie przyjętych wymiarów żebra
- statyka
5.50 m
11.62 kN/m
kNm
93
.
43
8
5
.
5
62
.
11
8
2
2
=
×
=
=
ż
Sdż
Sd
l
q
M
kNm
34
.
37
93
.
43
85
.
0
85
.
0
1
=
×
=
=
Sd
Sd
M
M
kN
96
.
31
2
5
.
5
62
.
11
2
=
×
=
=
ż
Sdż
Sd
l
q
V
- ze względu na zginanie
ż
h
a
1
.
0
1
=
=
m
0.035
cm
5
.
3
35
1
.
0
=
=
×
m
0.3150
cm
50
.
31
5
.
3
35
1
=
=
−
=
−
=
a
h
d
ż
m
0.2835
cm
35
.
28
50
.
31
9
.
0
9
.
0
=
=
×
=
=
d
z
Na zbrojenie żebra zastosowano stal A-II (18G2):
MPa
310
=
yd
f
2
2
4
3
1
cm
4.25
m
10
25
.
4
10
310
2835
.
0
34
.
37
1
=
×
=
×
×
=
=
−
yd
Sd
S
f
z
M
A
%
75
.
0
0075
.
0
50
.
31
18
25
.
4
1
=
=
×
=
=
d
b
A
w
S
ρ
∈
(
)
(
)
(
)
%
23
.
1
61
.
0
310
190
0
.
2
0
.
1
190
0
.
2
0
.
1
÷
=
×
÷
=
÷
yd
f
Ze względu na zginanie wymiary żebra dobrano prawidłowo.
- ze względu na ścinanie
Przyjęto beton klasy C20/25:
MPa
3
.
13
=
cd
f
,
MPa
20
=
ck
f
.
55
.
0
250
20
1
6
.
0
250
1
6
.
0
=
−
×
=
−
=
ck
f
ν
Przyjęto: cot
θ
= 1.0

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
22
kN
64
.
186
1
1
1
2835
.
0
18
.
0
10
3
.
13
55
.
0
cot
1
cot
kN
96
.
31
2
3
2
2
=
+
×
×
×
×
×
=
+
=
≤
=
θ
θ
ν
z
b
f
V
V
w
cd
Rd
Sd
Ze względu na ścinanie wymiary żebra dobrano prawidłowo.
- stan graniczny ugięcia żebra
kNm
41
.
36
8
5
.
5
63
.
9
8
2
2
1
=
×
=
=
pż
kż
k
l
q
M
kNm
30.95
41
.
36
85
.
0
85
.
0
1
=
×
=
=
k
k
M
M
MPa
256.87
kPa
12
.
256873
10
25
.
4
2835
.
0
95
.
30
4
1
=
=
×
×
=
=
−
S
k
s
z A
M
σ
max
d
l
eff
– wartość odczytujemy z tab. 13, 68,
2002
:
03264
B
PN
−
−
w zależności od procentu zbrojenia
ρ
,
naprężeń w stali
σ
s
i klasy betonu (wewnętrzne przęsło belki ciągłej).
(
)
00
.
30
35
50
.
0
75
.
0
50
.
0
75
.
0
35
30
max
=
+
−
−
−
=
d
l
eff
19
.
29
87
.
256
250
00
.
30
250
46
.
17
315
.
0
5
.
5
max
=
×
=
×
<
=
=
s
eff
eff
d
l
d
l
σ
.
Ze względu na stan graniczny ugięcia wymiary żebra dobrano prawidłowo.
Poz.1.3. Podciąg stropodachu
A. Przyjęcie wymiarów przekroju poprzecznego
b
w
b
eff
h
f
h
p
h
p
-h
f
18
15
÷
=
p
eff
h
l
→
(
)
cm
38
46
690
18
1
15
1
18
1
15
1
÷
=
×
÷
=
÷
=
eff
p
l
h
Wysokość podciągu przyjęto: cm
45
=
p
h
3.0
2.0
÷
=
w
p
b
h
→
(
)
cm
00
.
15
50
.
22
45
0
.
3
1
0
.
2
1
0
.
3
1
0
.
2
1
÷
=
×
÷
=
÷
=
p
w
h
b
Przyjęto szerokość podciągu: b
w
= 20 cm
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
G
kp
= 48.10
G
Sdp
= 55.73
Obciążenia zmienne
P
kp
= 9.74
P
Sdp
= 13.64
Obciążenie całkowite
Q
kp
= G
kp
+ P
kp
= 57.84
Q
Sdp
= G
Sdp
+ P
Sdp
= 69.37
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
23
C. Sprawdzenie przyjętych wymiarów podciągu
- statyka
6.90 m
69.37 kN
69.37 kN
2.30 m
2.30 m
2.30 m
kNm
55
.
159
3
90
.
6
37
.
69
3
=
×
=
=
p
Sdp
Sd
l
Q
M
kNm
62
.
135
55
.
159
85
.
0
85
.
0
1
=
×
=
×
=
Sd
Sd
M
M
kN
37
.
69
=
=
Sdp
Sd
Q
V
- ze względu na zginanie
50
.
4
00
.
45
1
.
0
1
.
0
1
=
×
=
=
p
h
a
cm
m
0.405
cm
5
.
40
50
.
4
00
.
45
1
=
=
−
=
−
=
a
h
d
p
m
0.3645
cm
45
.
36
5
.
40
9
.
0
9
.
0
=
=
×
=
=
d
z
Na zbrojenie podciągu zastosowano stal A-III (34GS):
MPa
350
=
yd
f
2
2
3
3
1
cm
10.63
m
10
063
.
1
10
350
3645
.
0
62
.
135
1
=
×
=
×
×
=
=
−
yd
Sd
S
f
z
M
A
%
31
.
1
0131
.
0
5
.
40
20
63
.
10
1
=
=
×
=
=
d
b
A
w
S
ρ
∉
(
)
(
)
(
)
%
08
.
1
54
.
0
350
190
0
.
2
0
.
1
190
0
.
2
0
.
1
÷
=
×
÷
=
÷
yd
f
Należy zwiększyć wymiary przekroju poprzecznego podciągu ze względu na zbyt duży procent zbrojenia.
Zwiększamy wymiary przekroju poprzecznego podciągu: h
p
= 50 cm, b
w
= 25 cm
i przeprowadzamy korektę
obliczeń.
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
G
kp
= 49.97
G
Sdp
= 57.80
Obciążenia zmienne
P
kp
= 9.74
P
Sdp
= 13.64
Obciążenie całkowite
Q
kp
= G
kp
+ P
kp
= 59.71
Q
Sdp
= G
Sdp
+ P
Sdp
= 71.44
C. Sprawdzenie przyjętych wymiarów podciągu
- statyka
6.90 m
71.44 kN
71.44 kN
2.30 m
2.30 m
2.30 m
kNm
31
.
164
3
90
.
6
44
.
71
3
=
×
=
=
p
Sdp
Sd
l
Q
M
kNm
66
.
139
31
.
164
85
.
0
85
.
0
1
=
×
=
×
=
Sd
Sd
M
M
kN
44
.
71
=
=
Sdp
Sd
Q
V

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
24
- ze względu na zginanie
p
h
a
1
.
0
1
=
= 0.1
×50 = 5.0 cm
m
0.45
cm
0
.
45
0
.
5
0
.
50
1
=
=
−
=
−
=
a
h
d
p
m
0.4050
cm
50
.
40
0
.
45
9
.
0
9
.
0
=
=
×
=
=
d
z
Na zbrojenie podciągu zastosowano stal A-III (34GS):
MPa
350
=
yd
f
2
2
4
3
1
cm
9.85
m
10
85
.
9
10
350
405
.
0
66
.
139
1
=
×
=
×
×
=
=
−
yd
Sd
S
f
z
M
A
%
88
.
0
0088
.
0
45
25
85
.
9
1
=
=
×
=
=
d
b
A
w
S
ρ
∈
(
)
(
)
(
)
%
08
.
1
54
.
0
350
190
0
.
2
0
.
1
190
0
.
2
0
.
1
÷
=
×
÷
=
÷
yd
f
Ze względu na zginanie wymiary podciągu dobrano prawidłowo.
- ze względu na ścinanie
Przyjęto beton klasy C20/25:
MPa
3
.
13
=
cd
f
,
MPa
20
=
ck
f
.
55
.
0
250
20
1
6
.
0
250
1
6
.
0
=
−
×
=
−
=
ck
f
ν
Przyjęto: cot
θ
= 1.0
kN
32
.
370
1
1
1
405
.
0
25
.
0
10
3
.
13
55
.
0
cot
1
cot
kN
71.44
2
3
2
2
=
+
×
×
×
×
×
=
+
=
≤
=
θ
θ
ν
z
b
f
V
V
w
cd
Rd
Sd
Ze względu na ścinanie wymiary podciągu dobrano prawidłowo.
- stan graniczny ugięcia podciągu
kNm
33
.
137
3
9
.
6
71
.
59
3
1
=
×
=
=
p
kp
k
l
Q
M
kNm
116.73
33
.
137
85
.
0
85
.
0
1
=
×
=
=
k
k
M
M
MPa
292.61
kPa
39
.
292611
10
85
.
9
405
.
0
73
.
116
4
1
=
=
×
×
=
=
−
S
k
s
z A
M
σ
max
d
l
eff
– wartość odczytujemy z tab. 13, 68,
2002
:
03264
B
PN
−
−
w zależności od procentu zbrojenia
ρ
,
naprężeń w stali
σ
s
i klasy betonu (wewnętrzne przęsło belki ciągłej).
(
)
96
.
28
30
75
.
0
88
.
0
75
.
0
00
.
1
30
28
max
=
+
−
−
−
=
d
l
eff
52
.
21
9
.
6
03
.
0
200
61
.
292
250
96
.
28
200
250
33
.
15
45
.
0
9
.
6
lim
max
=
×
×
×
=
<
=
=
eff
s
eff
eff
l
a
d
l
d
l
σ
.
Ze względu na stan graniczny ugięcia wymiary podciągu dobrano prawidłowo.

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
25
Poz.2. Strop międzykondygnacyjny
Poz. 2.1. Płyta stropu
A. Przyjęcie grubości płyty
Grubość płyty h
f
wyznaczono z następujących zależności:
cm
0
.
6
≥
f
h
,
50
eff
l
d
≥
=
cm
6
.
4
50
230 =
.
Wstępnie grubość płyty przyjęto cm
0
.
7
=
f
h
.
B. Zebranie obciążeń działających na płytę
Obciążenia
charakterystyczne [kN/m
2
]
γ
f
Obciążenia obliczeniowe [kN/m
2
]
Obciążenia stałe
g
kpł
= 2.62
g
Sdpł
= 3.06
Obciążenia zmienne
p
kpł
= 3.60
p
Sdpł
= 4.68
Obciążenie całkowite
q
kpł
= g
pł
+ p
pł
= 6.22
q
Sdpł
= g
Sdpł
+ p
Sdpł
= 7.74
C. Sprawdzenie przyjętej grubości płyty h
f
- statyka
2.30 m
7.74 kN/m
2
kNm/m
12
.
5
8
3
.
2
74
.
7
8
2
2
=
×
=
=
pł
Sdpł
Sd
l
q
M
kNm/m
4.35
12
.
5
85
.
0
85
.
0
1
=
×
=
=
Sd
Sd
M
M
- ze względu na zginanie
c
= 1.5 cm
– otulina zbrojenia przyjęta zgodnie z tab. 21,
2002
:
03264
B
PN
−
−
φ
= 6 mm
– wstępnie przyjęta średnica zbrojenia płyty;
cm
1.8
6
.
0
5
.
0
5
.
1
5
.
0
1
=
×
+
=
+
=
φ
c
a
cm
5.2
8
.
1
7
1
=
−
=
−
=
a
h
d
f
m
0.0468
cm
68
.
4
2
.
5
9
.
0
9
.
0
=
=
×
=
=
d
z
Na zbrojenie płyty zastosowano stal A-II (18G2):
MPa
310
=
yd
f
m
/
cm
00
.
3
m
/
m
10
00
.
3
10
310
0468
.
0
35
.
4
2
2
4
3
1
1
=
×
=
×
×
=
=
−
yd
Sd
S
f
z
M
A
%
58
.
0
20
.
5
00
.
3
1
=
=
=
d
A
S
ρ
∈
(
)
(
)
(
)
%
74
.
0
42
.
0
310
190
2
.
1
7
.
0
190
2
.
1
7
.
0
÷
=
÷
=
÷
=
yd
ek
f
ρ
.
Ze względu na zginanie grubość płyty dobrana prawidłowo.
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
26
- stan graniczny ugięcia płyty
50
23
.
44
0.052
2.30
<
=
=
d
l
eff
,
Wartość naprężeń w zbrojeniu rozciąganym
σ
s
:
kNm/m
11
.
4
8
3
.
2
22
.
6
8
2
2
1
=
×
=
=
pł
kpł
k
l
q
M
kNm/m
3.49
11
.
4
85
.
0
85
.
0
1
=
×
=
=
k
k
M
M
MPa
248.58
kPa
50
.
248575
10
00
.
3
0468
.
0
49
.
3
4
1
=
=
×
×
=
=
−
S
k
s
z A
M
σ
max
d
l
eff
– wartość odczytujemy z tab. 13, 68,
2002
:
03264
B
PN
−
−
w zależności od procentu zbrojenia
ρ
,
naprężeń w stali
σ
s
i klasy betonu (wewnętrzne przęsło belki ciągłej).
Przyjęto beton klasy C20/25.
(
)
40
.
33
35
5
.
0
58
.
0
50
.
0
75
.
0
35
30
max
=
+
−
−
−
=
d
l
eff
59
.
33
58
.
248
250
40
.
33
250
23
.
44
052
.
0
30
.
2
max
=
×
=
×
>
=
=
s
eff
eff
d
l
d
l
σ
, warunek nie został spełniony należy
zwiększyć grubość płyty.
Zwiększamy grubość płyty do 8 cm i przeprowadzamy korektę obliczeń:
B. Zebranie obciążeń działających na płytę
Obciążenia
charakterystyczne [kN/m
2
]
γ
f
Obciążenia obliczeniowe [kN/m
2
]
Obciążenia stałe
g
kpł
= 2.87
g
Sdpł
= 3.33
Obciążenia zmienne
p
kpł
= 3.60
p
Sdpł
= 4.68
Obciążenie całkowite
q
kpł
= g
pł
+ p
pł
= 6.47
q
Sdpł
= g
Sdpł
+ p
Sdpł
= 8.01
C. Sprawdzenie przyjętej grubości płyty h
f
- statyka
2.30 m
8.01 kN/m
2
kNm/m
29
.
5
8
3
.
2
01
.
8
8
2
2
=
×
=
=
pł
Sdpł
Sd
l
q
M
kNm/m
4.50
29
.
5
85
.
0
85
.
0
1
=
×
=
=
Sd
Sd
M
M
- ze względu na zginanie
c
= 1.5 cm
– otulina zbrojenia przyjęta zgodnie z tab. 21,
2002
:
03264
B
PN
−
−

Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
27
φ
= 6 mm
– wstępnie przyjęta średnica zbrojenia płyty
cm
1.8
6
.
0
5
.
0
5
.
1
5
.
0
1
=
×
+
=
+
=
φ
c
a
cm
6.2
8
.
1
8
1
=
−
=
−
=
a
h
d
f
m
0.0558
cm
58
.
5
2
.
6
9
.
0
9
.
0
=
=
×
=
=
d
z
Na zbrojenie płyty zastosowano stal A-II (18G2):
MPa
310
=
yd
f
m
/
cm
60
.
2
m
/
m
10
60
.
2
10
310
0558
.
0
50
.
4
2
2
4
3
1
1
=
×
=
×
×
=
=
−
yd
Sd
S
f
z
M
A
%
42
.
0
20
.
6
60
.
2
1
=
=
=
d
A
S
ρ
∈
(
)
(
)
(
)
%
74
.
0
42
.
0
310
190
2
.
1
7
.
0
190
2
.
1
7
.
0
÷
=
÷
=
÷
=
yd
ek
f
ρ
.
- stan graniczny ugięcia płyty
50
09
.
37
0.062
2.30
<
=
=
d
l
eff
, stan graniczny ugięć uznano za ograniczony.
Poz.2.2. Żebro stropu
A. Przyjęcie wymiarów żebra
b
w
b
eff
h
f
h
ż
h
ż
-h
f
18
12
÷
=
ż
eff
h
l
→
(
)
cm
55
.
30
83
.
45
550
18
1
12
1
18
1
12
1
÷
=
×
÷
=
÷
=
eff
ż
l
h
Wysokość żebra przyjęto: cm
40
=
ż
h
3.0
2.0
÷
=
w
ż
b
h
→
(
)
cm
30
.
13
00
.
20
40
0
.
3
1
0
.
2
1
0
.
3
1
0
.
2
1
÷
=
×
÷
=
÷
=
ż
w
h
b
Przyjęto szerokość żebra b
w
= 20 cm
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN/m]
γ
f
Obciążenia obliczeniowe [kN/m]
Obciążenia stałe
g
kż
= 8.33
g
Sdż
= 9.60
Obciążenia zmienne
p
kż
= 8.28
p
Sdż
= 10.76
Obciążenie całkowite
q
kż
= g
kż
+ p
kż
= 16.61
q
Sdż
= g
Sdż
+ p
Sdż
= 20.36
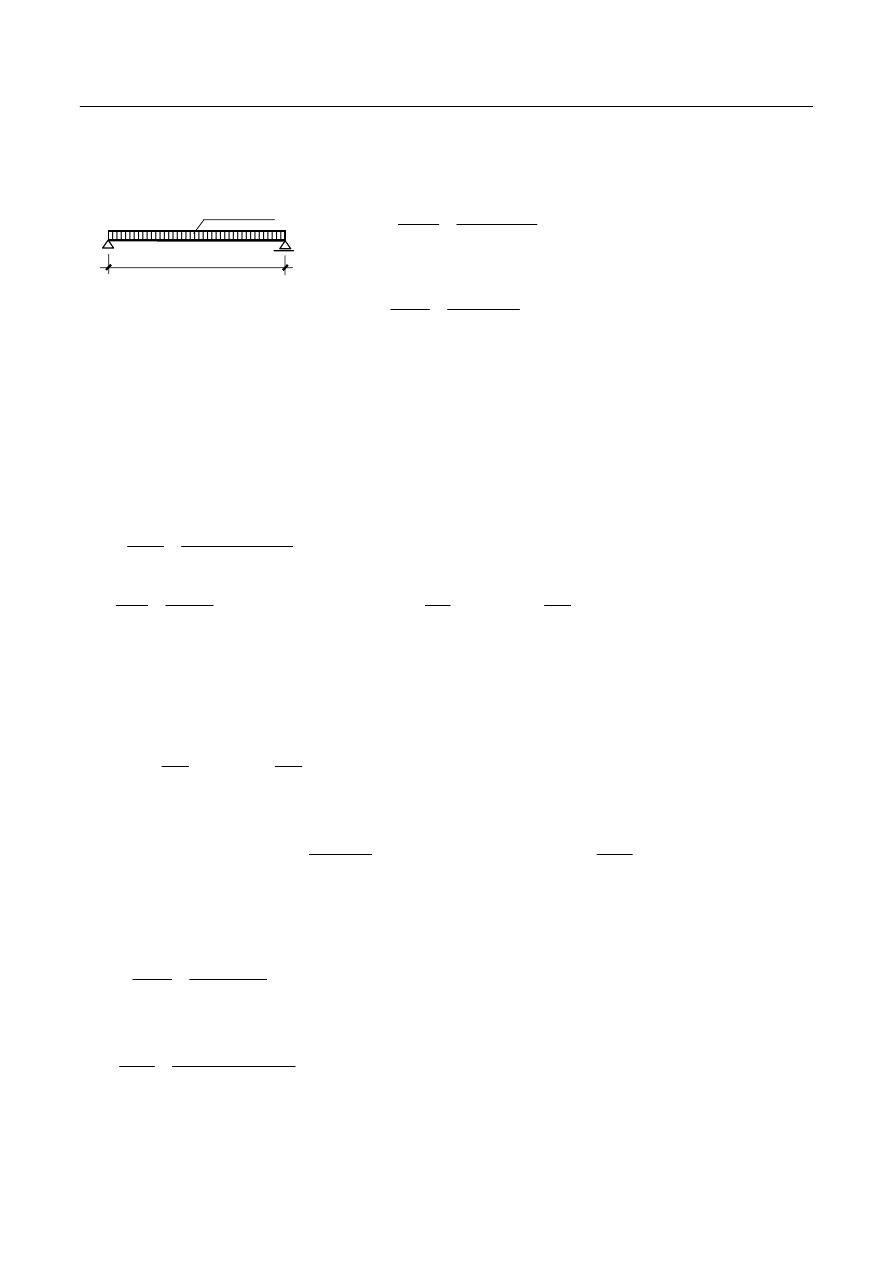
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
28
C. Sprawdzenie przyjętych wymiarów żebra
- statyka
5.50 m
20.36 kN/m
kNm
99
.
76
8
5
.
5
36
.
20
8
2
2
=
×
=
=
ż
Sdż
Sd
l
q
M
kNm
44
.
65
99
.
76
85
.
0
85
.
0
1
=
×
=
=
Sd
Sd
M
M
kN
99
.
55
2
5
.
5
36
.
20
2
=
×
=
=
ż
Sdż
Sd
l
q
V
- ze względu na zginanie
ż
h
a
1
.
0
1
=
= m
0.04
cm
0
.
4
40
1
.
0
=
=
×
m
0.36
cm
0
.
36
0
.
4
40
1
=
=
−
=
−
=
a
h
d
ż
m
0.324
cm
40
.
32
0
.
36
9
.
0
9
.
0
=
=
×
=
=
d
z
Na zbrojenie żebra zastosowano stal A-II (18G2):
MPa
310
=
yd
f
2
2
4
3
1
cm
6.52
m
10
52
.
6
10
310
324
.
0
44
.
65
1
=
×
=
×
×
=
=
−
yd
Sd
S
f
z
M
A
%
91
.
0
0091
.
0
36
20
52
.
6
1
=
=
×
=
=
d
b
A
w
S
ρ
∈
(
)
(
)
(
)
%
23
.
1
61
.
0
310
190
0
.
2
0
.
1
190
0
.
2
0
.
1
÷
=
×
÷
=
÷
yd
f
Ze względu na zginanie wymiary żebra dobrano prawidłowo.
- ze względu na ścinanie
Przyjęto beton klasy C20/25:
MPa
3
.
13
=
cd
f
,
MPa
20
=
ck
f
.
55
.
0
250
20
1
6
.
0
250
1
6
.
0
=
−
×
=
−
=
ck
f
ν
Przyjęto: cot
θ
= 1.0
kN
01
.
237
1
1
1
324
.
0
20
.
0
10
3
.
13
55
.
0
cot
1
cot
kN
99
.
55
2
3
2
2
=
+
×
×
×
×
×
=
+
=
≤
=
θ
θ
ν
z
b
f
V
V
w
cd
Rd
Sd
Ze względu na ścinanie wymiary żebra dobrano prawidłowo.
- stan graniczny ugięcia żebra
kNm
81
.
62
8
5
.
5
61
.
16
8
2
2
1
=
×
=
=
pż
kż
k
l
q
M
kNm
53.39
81
.
62
85
.
0
85
.
0
1
=
×
=
=
k
k
M
M
MPa
252.74
kPa
12
.
252736
10
52
.
6
324
.
0
39
.
53
4
1
=
=
×
×
=
=
−
S
k
s
z A
M
σ
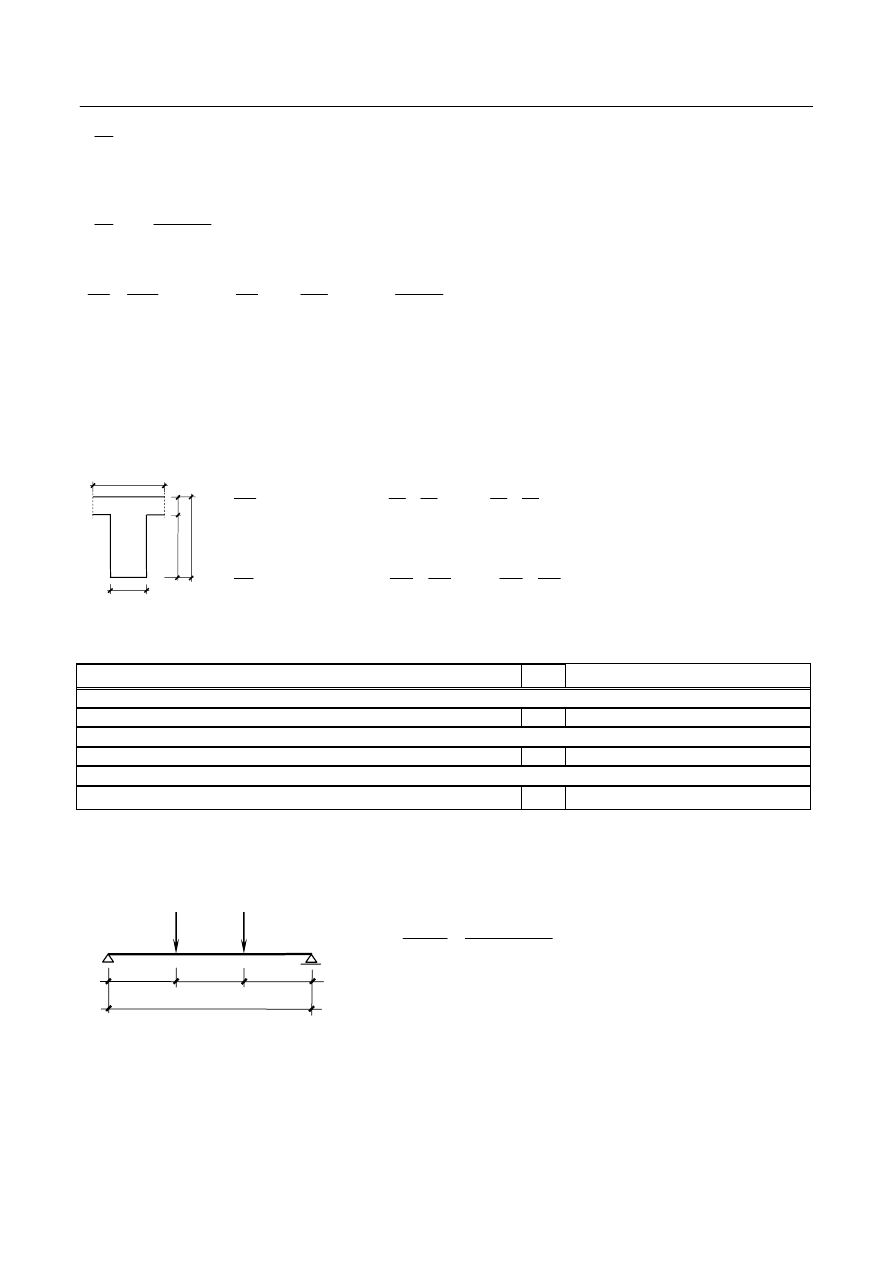
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
29
max
d
l
eff
– wartość odczytujemy z tab. 13, 68,
2002
:
03264
B
PN
−
−
w zależności od procentu zbrojenia
ρ
,
naprężeń w stali
σ
s
i klasy betonu (wewnętrzne przęsło belki ciągłej).
(
)
72
.
28
30
75
.
0
91
.
0
75
.
0
0
.
1
30
28
max
=
+
−
−
−
=
d
l
eff
41
.
28
74
.
252
250
72
.
28
250
27
.
15
36
.
0
5
.
5
max
=
×
=
×
<
=
=
s
eff
eff
d
l
d
l
σ
.
Ze względu na ugięcia wymiary żebra dobrano prawidłowo.
Poz.2.3. Podciąg stropu
A. Przyjęcie wymiarów przekroju poprzecznego
b
w
b
eff
h
f
h
p
h
p
-h
f
18
15
÷
=
p
eff
h
l
→
(
)
cm
33
.
38
46
690
18
1
15
1
18
1
15
1
÷
=
×
÷
=
÷
=
eff
p
l
h
Wysokość podciągu przyjęto: cm
50
=
p
h
3.0
2.0
÷
=
w
p
b
h
→
(
)
cm
67
.
16
00
.
25
50
0
.
3
1
0
.
2
1
0
.
3
1
0
.
2
1
÷
=
×
÷
=
÷
=
p
w
h
b
Przyjęto szerokość podciągu: b
w
= 25 cm
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
G
kp
= 52.25
G
Sdp
= 59.98
Obciążenia zmienne
P
kp
= 45.54
P
Sdp
= 59.18
Obciążenie całkowite
Q
kp
= G
kp
+ P
kp
= 97.79
Q
Sdp
= G
Sdp
+ P
Sdp
= 119.16
C. Sprawdzenie przyjętych wymiarów podciągu
- statyka
6.90 m
119.16 kN
119.16 kN
2.30 m
2.30 m
2.30 m
kNm
07
.
274
3
90
.
6
16
.
119
3
=
×
=
=
p
Sdp
Sd
l
Q
M
kNm
96
.
232
07
.
274
85
.
0
85
.
0
1
=
×
=
×
=
Sd
Sd
M
M
kN
16
.
119
=
=
Sdp
Sd
Q
V
- ze względu na zginanie
p
h
a
1
.
0
1
=
= 0.1
×50 = 5.0 cm
m
0.45
cm
0
.
45
0
.
5
0
.
50
1
=
=
−
=
−
=
a
h
d
p
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
30
m
0.405
cm
50
.
40
0
.
45
9
.
0
9
.
0
=
=
×
=
=
d
z
Na zbrojenie podciągu zastosowano stal A-III (34GS):
MPa
350
=
yd
f
2
2
3
3
1
cm
16.43
m
10
643
.
1
10
350
405
.
0
96
.
232
1
=
×
=
×
×
=
=
−
yd
Sd
S
f
z
M
A
%
46
.
1
0146
.
0
45
25
43
.
16
1
=
=
×
=
=
d
b
A
w
S
ρ
∉
(
)
(
)
(
)
%
08
.
1
54
.
0
350
190
0
.
2
0
.
1
190
0
.
2
0
.
1
÷
=
×
÷
=
÷
yd
f
Należy zwiększyć wymiary przekroju poprzecznego podciągu ze względu na zbyt duży procent zbrojenia.
Zwiększamy wymiary przekroju poprzecznego podciągu: h
p
= 60 cm, b
w
= 25 cm
i przeprowadzamy korektę
obliczeń.
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
G
kp
= 53.82
G
Sdp
= 61.73
Obciążenia zmienne
P
kp
= 45.54
P
Sdp
= 59.18
Obciążenie całkowite
Q
kp
= G
kp
+ P
kp
= 99.36
Q
Sdp
= G
Sdp
+ P
Sdp
= 120.91
C. Sprawdzenie przyjętych wymiarów podciągu
- statyka
6.90 m
120.91 kN
120.91 kN
2.30 m
2.30 m
2.30 m
kNm
86
.
277
3
90
.
6
91
.
120
3
=
×
=
=
p
Sdp
Sd
l
Q
M
kNm
18
.
236
86
.
277
85
.
0
85
.
0
1
=
×
=
×
=
Sd
Sd
M
M
kN
91
.
120
=
=
Sdp
Sd
Q
V
- ze względu na zginanie
p
h
a
1
.
0
1
=
= 0.1
×60 = 6.0 cm
m
0.54
cm
0
.
54
0
.
6
0
.
60
1
=
=
−
=
−
=
a
h
d
p
m
0.486
cm
60
.
48
0
.
54
9
.
0
9
.
0
=
=
×
=
=
d
z
Na zbrojenie podciągu zastosowano stal A-III (34GS):
MPa
350
=
yd
f
2
2
3
3
1
cm
13.88
m
10
388
.
1
10
350
486
.
0
18
.
236
1
=
×
=
×
×
=
=
−
yd
Sd
S
f
z
M
A
%
03
.
1
0103
.
0
54
25
88
.
13
1
=
=
×
=
=
d
b
A
w
S
ρ
∈
(
)
(
)
(
)
%
08
.
1
54
.
0
350
190
0
.
2
0
.
1
190
0
.
2
0
.
1
÷
=
×
÷
=
÷
yd
f
Ze względu na zginanie wymiary podciągu dobrano prawidłowo.
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
31
- ze względu na ścinanie
Przyjęto beton klasy C20/25:
MPa
3
.
13
=
cd
f
,
MPa
20
=
ck
f
.
55
.
0
250
20
1
6
.
0
250
1
6
.
0
=
−
×
=
−
=
ck
f
ν
Przyjęto: cot
θ
= 1.0
kN
39
.
444
1
1
1
486
.
0
25
.
0
10
3
.
13
55
.
0
cot
1
cot
kN
91
.
120
2
3
2
2
=
+
×
×
×
×
×
=
+
=
≤
=
θ
θ
ν
z
b
f
V
V
w
cd
Rd
Sd
Ze względu na ścinanie wymiary podciągu dobrano prawidłowo.
- stan graniczny ugięcia podciągu
kNm
53
.
228
3
9
.
6
36
.
99
3
1
=
×
=
=
p
kp
k
l
Q
M
kNm
194.25
53
.
228
85
.
0
85
.
0
1
=
×
=
=
k
k
M
M
MPa
279.62
kPa
07
.
287962
10
88
.
13
486
.
0
25
.
194
4
1
=
=
×
×
=
=
−
S
k
s
z A
M
σ
max
d
l
eff
– wartość odczytujemy z tab. 13, 68,
2002
:
03264
B
PN
−
−
w zależności od procentu zbrojenia
ρ
,
naprężeń w stali
σ
s
i klasy betonu (wewnętrzne przęsło belki ciągłej).
(
)
64
.
27
28
00
.
1
03
.
1
00
.
1
25
.
1
28
25
max
=
+
−
−
−
=
d
l
eff
48
.
21
9
.
6
03
.
0
200
62
.
279
250
64
.
27
200
250
78
.
12
54
.
0
9
.
6
lim
max
=
×
×
×
=
<
=
=
eff
s
eff
eff
l
a
d
l
d
l
σ
.
Ze względu na stan graniczny ugięcia wymiary podciągu dobrano prawidłowo.
Poz. 4. Słupy
Poz. 4.1
Poz. 4.2
Poz. 4.3
Poz. 4.1. Słup najwyższej kondygnacji
A. Przyjęcie wymiarów słupa
Przyjęto: b
sł
= 25 cm, h
sł
= 25 cm
m
90
.
2
50
.
0
40
.
3
=
−
=
−
=
p
sł
h
H
l
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
32
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
N
kg
= 155.32
N
Sdg
= 179.52
Obciążenia zmienne
N
kp
= 29.22
N
Sdp
= 40.92
Obciążenie całkowite
N
k41
= N
kg
+ N
kp
= 184.54
N
Sd41
= N
Sdg
+ N
Sdp
= 220.44
C. Sprawdzenie przyjętych wymiarów słupa
- ze względu na nośność słupa
Przyjęto beton C20/25:
MPa
3
.
13
=
cd
f
Na etapie projektu wstępnego można przyjąć
ϕ
= 0.9.
kN
13
.
748
25
.
0
25
.
0
10
3
.
13
0
.
1
9
.
0
kN
44
.
220
3
41
=
×
×
×
×
×
=
=
≤
=
bh
f
N
N
cd
cc
Sd
sd
ϕα
Poz.4.2. Słup środkowej kondygnacji
A. Przyjęcie wymiarów słupa
Przyjęto: b
sł
= 25 cm, h
sł
= 25 cm
m
80
.
2
60
.
0
40
.
3
=
−
=
−
=
p
sł
h
H
l
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
N
kg
= 322.01
N
Sdg
= 370.12
Obciążenia zmienne
N
kp
= 165.84
N
Sdp
= 218.57
Obciążenie całkowite
N
k42
= N
kg
+ N
kp
= 487.85
N
Sd42
= N
Sdg
+ N
Sdp
= 588.58
C. Sprawdzenie przyjętych wymiarów słupa
- ze względu na nośność słupa
kN
13
.
748
25
.
0
25
.
0
10
3
.
13
0
.
1
9
.
0
kN
58
.
588
3
42
=
×
×
×
×
×
=
=
≤
=
bh
f
N
N
cd
cc
Sd
sd
ϕα
Poz. 4.3. Słup najniższej kondygnacji
A. Przyjęcie wymiarów słupa
Przyjęto: b
sł
= 25 cm, h
sł
= 25 cm
m
80
.
2
60
.
0
40
.
3
=
−
=
−
=
p
sł
h
H
l
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
33
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
N
kg
= 498.70
N
Sdg
= 561.24
Obciążenia zmienne
N
kp
= 302.46
N
Sdp
= 396.11
Obciążenie całkowite
N
k43
= N
kg
+ N
kp
= 801.16
N
Sd43
= N
Sdg
+ N
Sdp
= 957.35
C. Sprawdzenie przyjętych wymiarów słupa
- ze względu na nośność słupa
kN
13
.
748
25
.
0
25
.
0
10
3
.
13
0
.
1
9
.
0
957.35
3
43
=
×
×
×
×
×
=
=
>
=
bh
f
N
N
cd
cc
Sd
sd
ϕα
Należy zwiększyć wysokość słupa
Wysokość słupa można wyznaczyć z przekształcenia wzoru na nośność słupa:
m
3190
.
0
25
.
0
10
3
.
13
0
.
1
9
.
0
60
.
954
3
3
.
4
=
×
×
×
×
=
≥
b
f
N
h
cd
cc
Sd
ϕα
Zwiększamy wymiary przekroju poprzecznego psłupa: h
sł
= 35 cm, b
sł
= 25 cm
i przeprowadzamy korektę
obliczeń.
B. Zebranie obciążeń
Obciążenia
charakterystyczne [kN]
γ
f
Obciążenia obliczeniowe [kN]
Obciążenia stałe
N
kg
= 500.61
N
Sdg
= 563.36
Obciążenia zmienne
N
kp
= 302.84
N
Sdp
= 396.11
Obciążenie całkowite
N
k43
= N
kg
+ N
kp
= 803.07
N
Sd43
= N
Sdg
+ N
Sdp
= 959.47
C. Sprawdzenie przyjętych wymiarów słupa
- ze względu na nośność słupa
kN
38
.
1047
35
.
0
25
.
0
10
3
.
13
0
.
1
9
.
0
959.47
3
43
=
×
×
×
×
×
=
=
<
=
bh
f
N
N
cd
cc
Sd
sd
ϕα
Poz.5. Stopa fundamentowa
A. Zebranie obciążeń na stopę fundamentową
Obciążenie od słupa najniższej kondygnacji w postaci siły kN
47
.
959
43
=
=
Sd
Sd
N
N
.
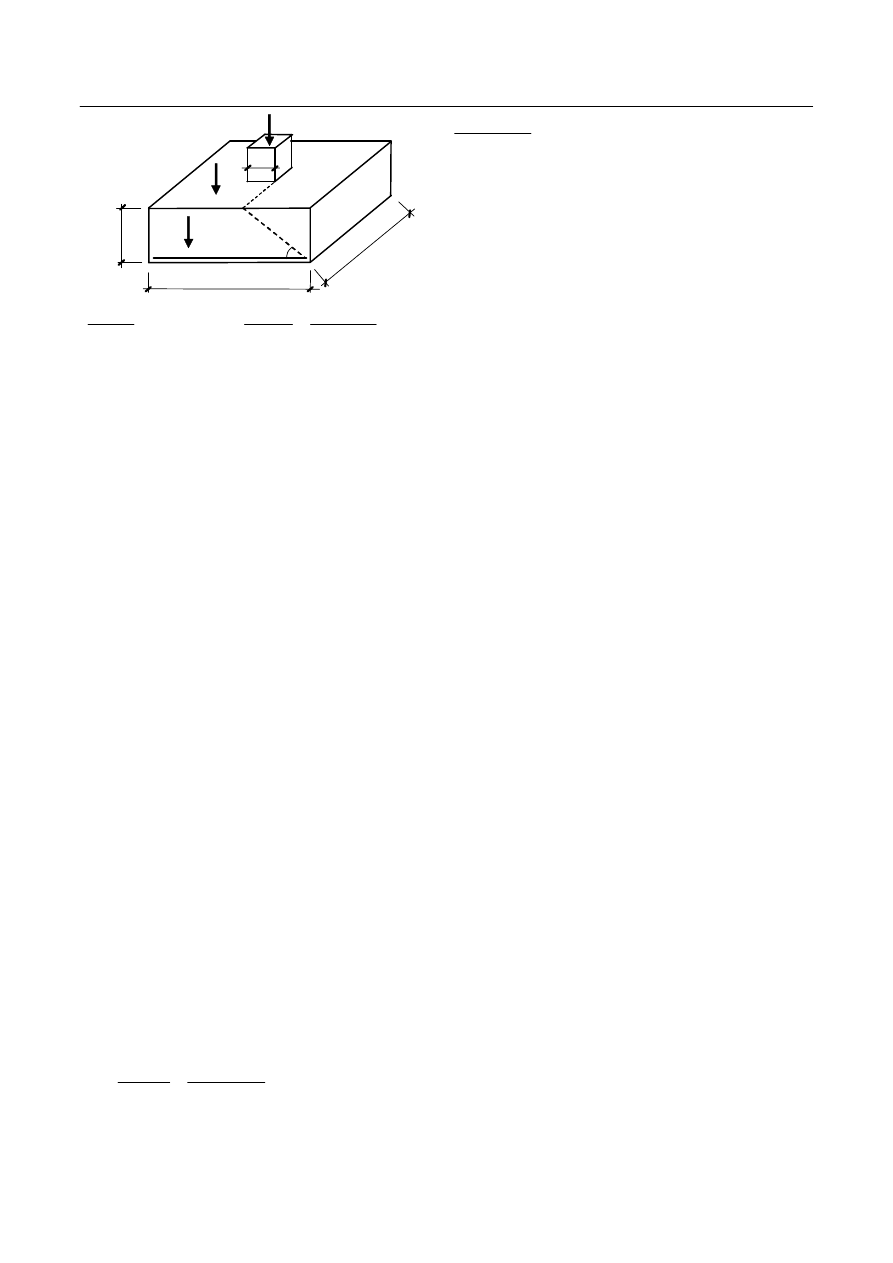
Budynek o konstrukcji mieszanej – wersja 2007
Dr inż. Maria WŁODARCZYK
Projekt wstępny STUDENT
Dr inż. Barbara GOSZCZYŃSKA
Do użytku wewnętrznego. Na prawach rękopisu.
34
fN
st
Sd
q
A
+Q
+Q
N
≤
2
1
gdzie: N
Sd
– siła od słupa,
Q
1
– ciężar gruntu zalegającego nad stopą,
Q
2
– ciężar stopy,
kN
36
.
1151
47
.
959
2
.
1
2
.
1
2
1
=
×
=
=
+
+
Sd
Sd
N
Q
Q
N
m
25
.
0
=
s
a
2
3
m
23
.
5
10
22
.
0
36
.
1151
2
.
1
2
1
=
×
=
=
→
=≤
fN
Sd
st
fN
st
Sd
q
N
A
q
A
N
.
Przyjęto stopę kwadratową:
m
30
.
2
=
= L
B
,
2
m
29
.
5
=
st
A
Wysokość stopy fundamentowej:
(
)(
) (
) (
) (
)
m
82
.
0
61
.
0
25
.
0
30
.
2
4
.
0
3
.
0
4
.
0
3
.
0
÷
=
−
×
÷
=
−
÷
=
s
a
B
h
Przyjęto wysokość stopy:
m
0.70
=
h
.
Poz. 6. Ściana zewnętrzna nośna
Poz. 6.1. Ściana warstwowa
A. Ciężar ściany
Ciężar ściany warstwowej: 6.26
kN/m
2
Ciężar ściany fundamentowej: 9.61 kN/m
2
B. Współczynnik przenikania ciepła U
Należy sprawdzić współczynnik przenikania ciepła zgodnie z obowiązującymi przepisami.
Poz. 6.2. Wieniec
A. Ciężar wieńca
Poz. 6.2.1. Wieniec najwyższej kondygnacji
Obciążenia od wieńca najwyższej kondygnacji: 5.27 kN/m
Poz. 6.2.1. Wieniec środkowej kondygnacji
Obciążenia od wieńca środkowej kondygnacji: 6.30kN/m
Poz. 7. Ława fundamentowa
A. Zebranie obciążeń
q
Sdsc
= 137.64 kN/m
B. Przyjęcie wymiarów ławy fundamentowej
cm
75
m
75
.
0
10
22
.
0
64
.
137
2
.
1
2
.
1
3
=
=
×
×
=
≥
fN
Sdsc
ł
q
q
b
Przyjęto szerokość ławy: cm
75
=
ł
b
B
L
h
Q
2
Q
1
N
Sd
α
a
s
Wyszukiwarka
Podobne podstrony:
Floor beam ver 1 Student id 178 Nieznany
met5zn regresja student id 2936 Nieznany
cit 2007 w interneciejw id 1173 Nieznany
Cw1 student id 122803 Nieznany
PAiRAII Instr 2007 lab2 id 3455 Nieznany
PROJEKT nr 1 STUDENT id 399181 Nieznany
met1zn student id 293607 Nieznany
matematyka 2007 maj id 284061 Nieznany
G1 PW D Czesc opisowa 1 id 1853 Nieznany
adhd student id 51541 Nieznany
PKD 2007 schemat id 359613 Nieznany
PK zaoczne STUDENCI 1 id 359548 Nieznany
2007 (klucz)id 25638 Nieznany (2)
Cw2 student id 123177 Nieznany
Miazdzyca dla Studentow id 2982 Nieznany
Info dla studentow id 213290 Nieznany
Pompa wentylator studenci id 28 Nieznany
GG 2007 2 41 id 190133 Nieznany
2 PKD 2007 schemat 2 id 156705 Nieznany
więcej podobnych podstron