Z. Kąkol-Notatki do Wykładu z Fizyki
11-1
Wykład 11
11. Elementy szczególnej teorii względności
11.1
Wstęp
Mechanika klasyczna oparta na zasadach dynamiki Newtona poprawnie opisuje zja-
wiska, w których prędkości ciał są małe w porównaniu z prędkością światła. Jednak
w zjawiskach atomowych, jądrowych i w astrofizyce spotykamy się z prędkościami
zbliżonymi do prędkości światła i wtedy zamiast mechaniki klasycznej musimy stoso-
wać mechanikę relatywistyczną opartą na szczególnej teorii względności opracowanej
przez Einsteina. Mechanika klasyczna nie jest sprzeczna z mechaniką relatywistyczną,
a stanowi jej szczególny przypadek (dla małych prędkości).
11.1.1 Zasada względności
Wiemy już, że gdy układ porusza się ze stałą prędkością po linii prostej to każde do-
świadczenie przebiega tak samo jakbyśmy się nie poruszali. Jednocześnie jakakolwiek
zmiana prędkości natychmiast jest przez nas zauważana.
Narzuca się wniosek, poparty przez niezliczone obserwacje, że żadne doświadczenie nie
pozwala nam stwierdzić, że się poruszamy (v = const). Inaczej mówiąc:
Prawa przyrody (w szczególności fizyki) są takie same bez względu na to, czy obserwu-
jemy je z układu nie poruszającego się, czy z ruchomego, ale poruszającego się bez
przyśpieszenia (czyli układu inercjalnego)
Ten wniosek, nazywany obecnie
zasadą względności
: sformułowano jeszcze za czasów
Galileusza.
11.1.2 Transformacja Galileusza
Omawiając zasady dynamiki Newtona stwierdziliśmy, że prawa przyrody (w
szczególności fizyki) są takie same bez względu na to, czy obserwujemy je z układu nie
poruszającego się, czy z ruchomego, ale poruszającego się bez przyśpieszenia (układy
inercjalne).
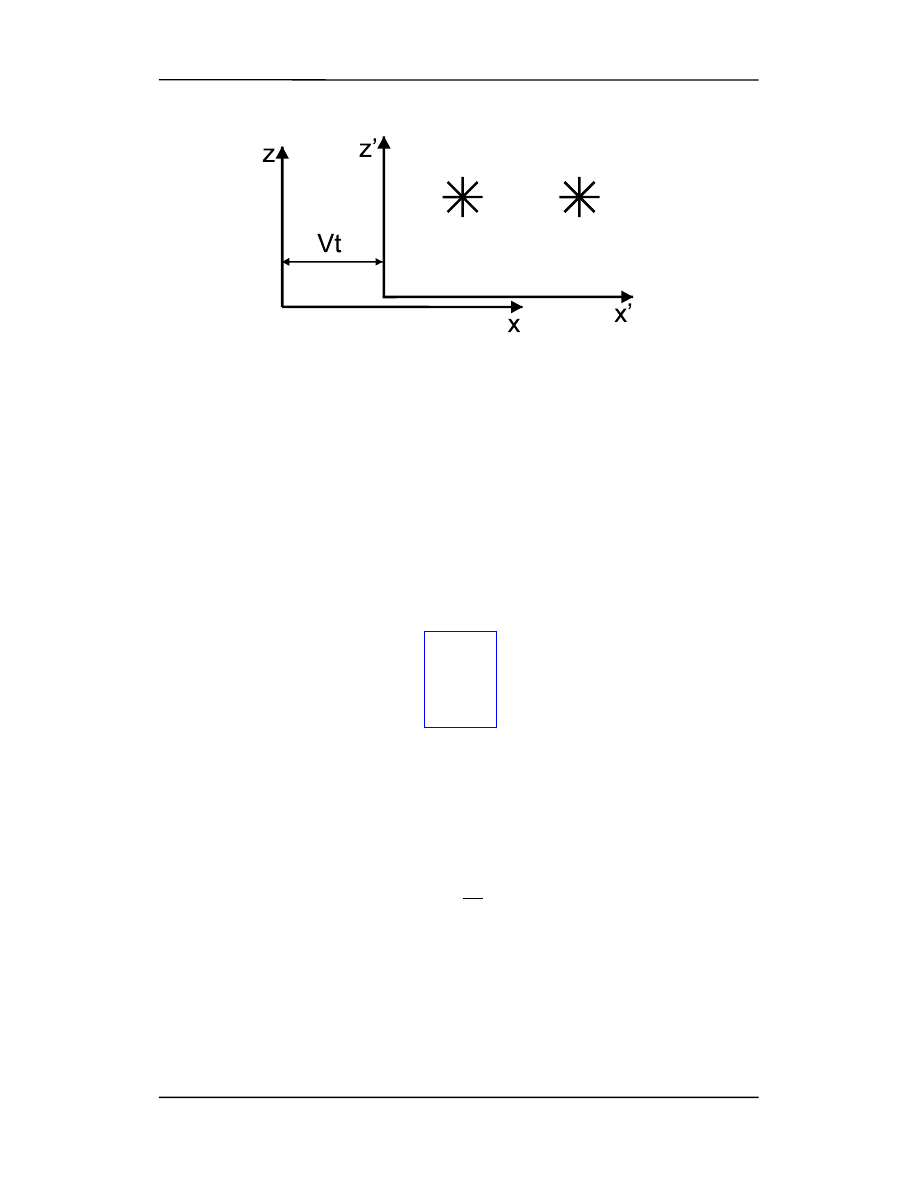
Spróbujemy teraz opisać zjawiska widziane z dwóch różnych inercjalnych układów
odniesienia, poruszających się względem siebie (rysunek). W tym celu wyobraźmy so-
bie, obserwatora na ziemi, który rejestruje dwa wybuchy na pewnej, jednakowej wyso-
kości. Odległość między miejscami wybuchów wynosi, (według ziemskiego obserwato-
ra)
∆
x, natomiast czas między wybuchami
∆
t. Te same dwa zdarzenia obserwowane są
przez pasażera samolotu lecącego z prędkością V po linii prostej łączącej miejsca wybu-
chów. Względem lokalnego układu odniesienia związanego z lecącym samolotem róż-
nica położeń wybuchów wynosi
∆
x’, a różnica czasu
∆
t’.
Porównajmy teraz spostrzeżenia obserwatorów na ziemi i w samolocie. Zróbmy to
np. z pozycji obserwatora na ziemi, który próbuje opisać to co widzą pasażerowie samo-
lotu.
Z. Kąkol-Notatki do Wykładu z Fizyki
11-2
Jeżeli, pierwszy wybuch nastąpił w punkcie x
1
’ (względem samolotu), a drugi po
czasie
∆
t, to w tym czasie samolot przeleciał drogę V
∆
t (względem obserwatora na
Ziemi) i drugi wybuch został zaobserwowany w punkcie
Vt
x
x
x
−
∆
+
=
'
'
1
2
czyli
Vt
x
x
x
x
−
∆
=
−
=
∆
'
'
'
1
2
Jednocześnie, ponieważ samolot leci wzdłuż linii łączącej wybuchy, to
∆
y’ =
∆
z’ = 0.
Oczywistym wydaje się też, że
∆
t’ =
∆
t.
Otrzymaliśmy więc
wzory przekładające wyniki obserwacji jednego obserwatora na
spostrzeżenia drugiego
.
t
t
z
z
y
y
Vt
x
x
=
=
=
−
=
'
'
'
'
(11.1)
Te równania noszą nazwę
transformacji Galileusza
Sprawdźmy, czy stosując powyższe wzory do opisu doświadczeń, otrzymamy takie sa-
me wyniki, niezależnie od układu w którym to doświadczenie opisujemy. Jako przykład
wybierzmy ciało poruszające wzdłuż osi x ruchem jednostajnie przyspieszonym z przy-
spieszeniem a. W układzie nieruchomym prędkość chwilowa ciała wynosi
t
x
u
∆
∆
=
Jego przyspieszenie jest stałe i równe a. Natomiast obserwator w pojeździe poruszają-
cym się wzdłuż osi x ze stałą prędkością V rejestruje, że w czasie
∆
t’ ciało przebywa
odległość
∆
x’. Zatem prędkość chwilowa ciała zmierzonego przez tego obserwatora
wynosi
Z. Kąkol-Notatki do Wykładu z Fizyki
11-3
'
'
'
t
x
u
∆
∆
=
Zgodnie z transformacją Galileusza
∆
x' =
∆
x - V
∆
t, oraz
∆
t' =
∆
t, więc
V
u
t
t
V
x
t
x
u
−
=
∆
∆
−
∆
=
∆
∆
=
'
'
'
Otrzymaliśmy prędkość względną jednego obiektu względem drugiego co jest wynikiem
intuicyjnie oczywistym. Natomiast przyśpieszenie w układzie poruszającym się wynosi
a
t
u
t
V
u
t
u
a
=
∆
∆
=
∆
−
∆
=
∆
∆
=
)
(
'
'
'
Widać, że w tym przypadku zastosowanie wzorów transformacji Galileusza daje wynik
zgodny z doświadczeniem. Jednak nie jest to prawdą w każdym przypadku. Miedzy in-
nymi stwierdzono, że ta transformacja zastosowana do równań Maxwella nie daje tych
samych wyników dla omawianych układów inercjalnych. W szczególności z praw
Maxwella wynika, że
prędkość światła jest podstawową stałą przyrody i powinna być
taka sama w każdym układzie odniesienia
.
Oznacza to na przykład, że gdy impuls światła rozchodzący się w próżni w kierunku x
jest obserwowany przez dwóch obserwatorów (patrz na tekst i rysunek powyżej) to za-
równo obserwator nieruchomy jak poruszający się z prędkością V (względem pierwsze-
go) zmierzą identyczną prędkość impulsu c = 2.998
⋅
10
8
m/s. Tymczasem zgodnie
z transformacją Galileusza i ze zdrowym rozsądkiem powinniśmy otrzymać wartość
c – V. Wykonano szereg doświadczeń, w których próbowano podważyć równania
Maxwella, a w szczególności próbowano pokazać, że prędkość światła, tak jak prędkość
dźwięku zależy od układu odniesienia (stosuje się do transformacji Galileusza). Naj-
sławniejsze z nich, to doświadczenie Michelsona-Morleya mające na celu wykrycie
wpływu ruchu orbitalnego Ziemi na prędkość światła poprzez pomiar prędkości światła
w kierunku prostopadłym i równoległym do ruchu Ziemi. Wszystkie te doświadczenia
dały wynik negatywny i musimy uznać, że prędkość światła w próżni jest jednakowa we
wszystkich inercjalnych układach odniesienia.
Prędkość światła c = 2.988
⋅
10
8
m/s we wszystkich układach odniesienia
.
Rozpatrzmy teraz niektóre wnioski wynikające ze stałości prędkości światła.
11.1.3 Dylatacja czasu
Załóżmy, że w rakiecie znajduje się przyrząd wysyłający impuls światła z punktu A,
który następnie odbity przez lustro Z, odległe od A o d powraca do punktu A, gdzie jest
rejestrowany (rysunek).
Czas
∆
t' jaki upływa między wysłaniem światła, a jego zarejestrowaniem przez obser-
watora będącego w rakiecie jest oczywiście równy
∆
t' = 2d/c (rysunek po lewej stronie).
Teraz to samo zjawisko opisujemy z układu nieruchomego, względem którego rakieta
porusza się w prawo z prędkością V. Chcemy, w tym układzie, znaleźć czas
∆
t przelotu
światła z punktu A do zwierciadła i z powrotem do A. Jak widać na rysunku (po prawej
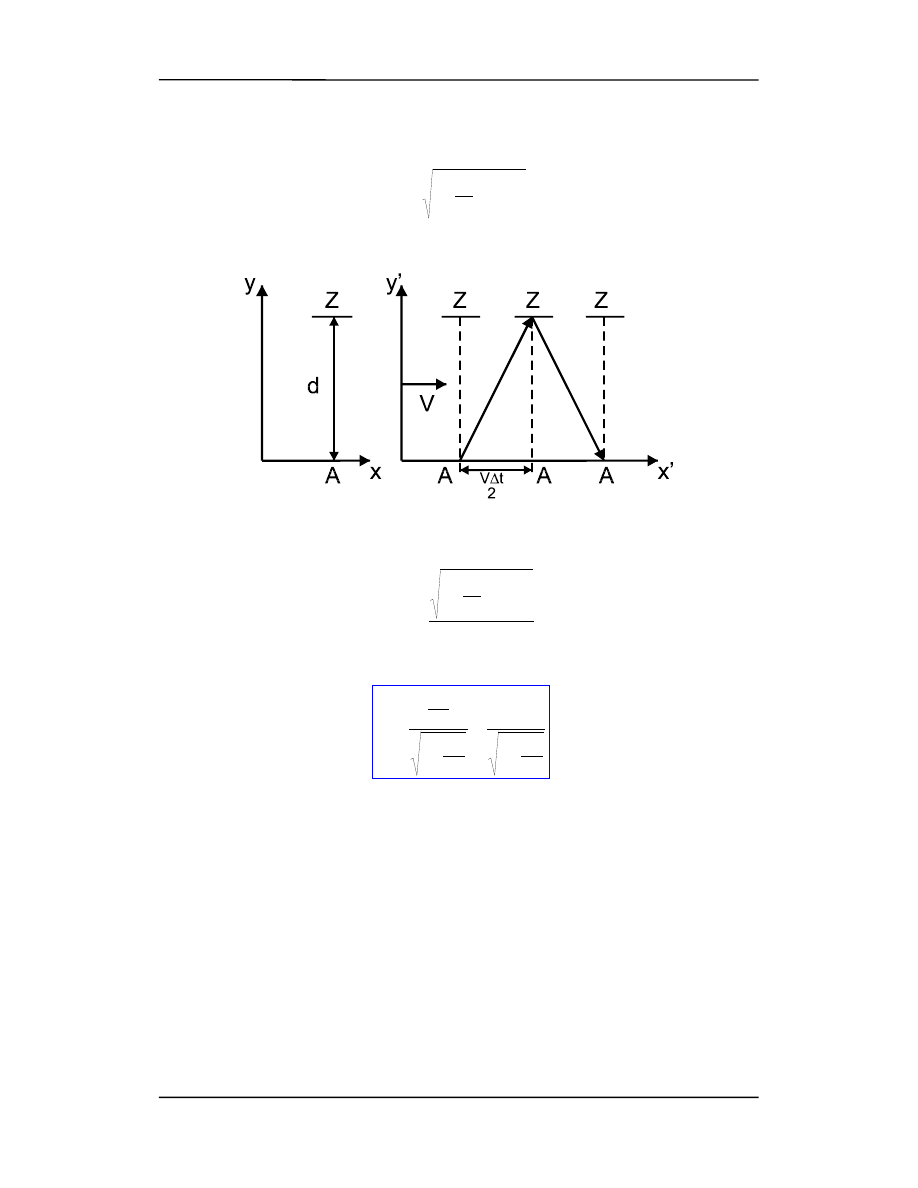
Z. Kąkol-Notatki do Wykładu z Fizyki
11-4
stronie) światło przechodząc od punktu A do zwierciadła Z porusza się po linii
o długości S
2
2
2
d
t
V
S
+
∆
=
Zatem czas potrzebny na przebycie drogi AZA (tj. dwóch odcinków S) wynosi
c
d
t
V
t
2
2
2
2
+
∆
=
∆
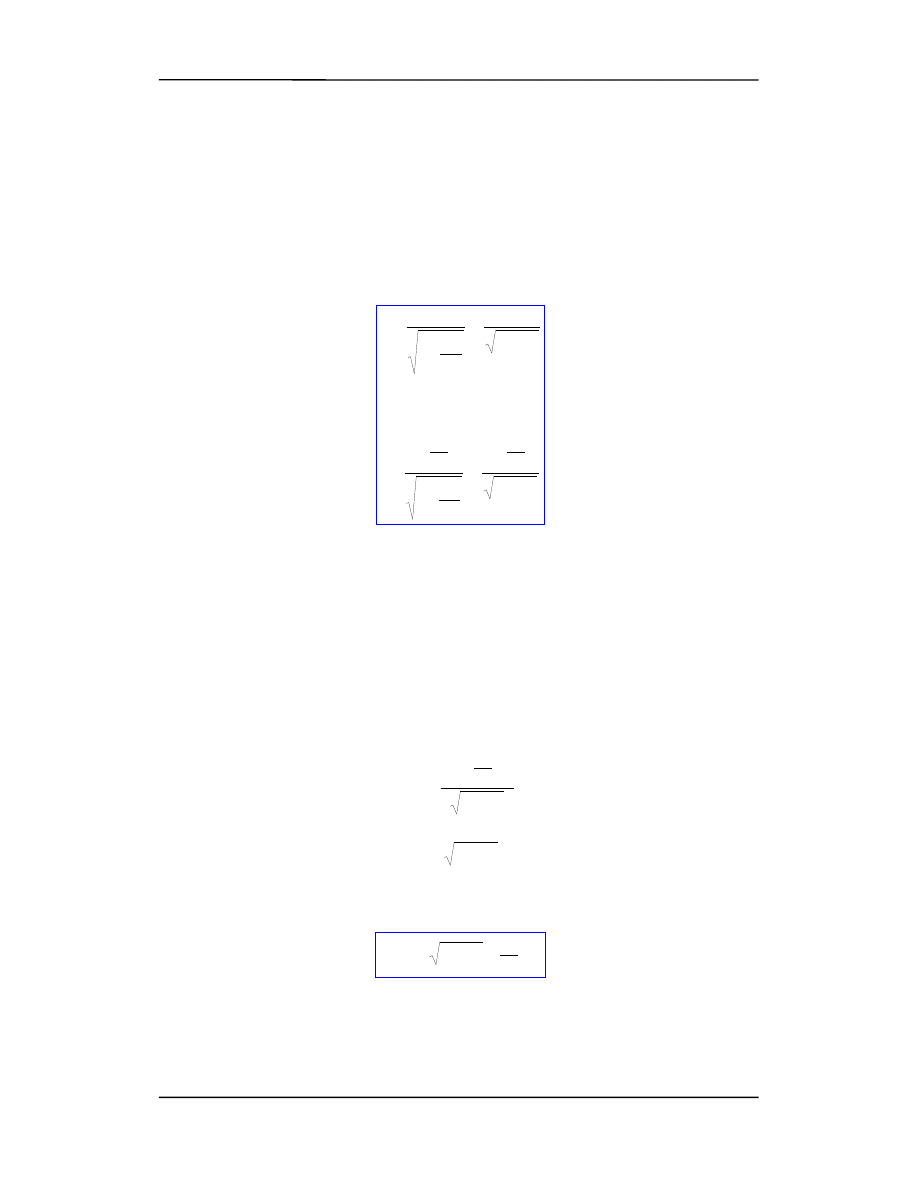
lub po przekształceniu
2
2
2
2
1
'
1
2
c
V
t
c
V
c
d
t
−
∆
=
−
=
∆
(11.2)
Widzimy, że warunek stałości prędkości światła w różnych układach odniesienia może
być spełniony tylko wtedy gdy, czas pomiędzy dwoma zdarzeniami obserwowanymi
i mierzonymi z różnych układów odniesienia jest różny.
W konsekwencji,
każdy obserwator stwierdzi, że poruszający się zegar idzie wolniej niż
identyczny zegar w spoczynku
.
To zjawisko
dylatacji czasu
jest własnością samego czasu i dlatego spowolnieniu ulega-
ją wszystkie procesy fizyczne gdy są w ruchu. Dotyczy to również reakcji chemicznych,
więc i np. biologicznego starzenia się.
Dylatację czasu zaobserwowano doświadczalnie min. za pomocą nietrwałych cząstek.
Cząstki takie przyspieszano do prędkości bliskiej prędkości światła i mierzono zmianę
ich czasu połowicznego zaniku.
Z. Kąkol-Notatki do Wykładu z Fizyki
11-5
11.2
Transformacja Lorentza
Szukamy ponownie (jak w przypadku transformacji Galileusza) wzorów przekłada-
jących spostrzeżenia jednego obserwatora na obserwacje drugiego. Chcemy znaleźć
transformację współrzędnych ale taką, w której obiekt poruszający się z prędkością rów-
ną c w układzie nieruchomym (x, y, z, t), również w układzie (x', y', z', t') poruszającym
się z prędkością V wzdłuż osi x będzie poruszać się z prędkością c.
Transformacja współrzędnych, która uwzględnia niezależność prędkości światła od
układu odniesienia ma postać
2
2
2
2
2
2
2
2
1
1
'
'
'
1
1
'
β
β
−
−
=
−
−
=
=
=
−
−
=
−
−
=
x
c
V
t
c
V
x
c
V
t
t
z
z
y
y
Vt
x
c
V
Vt
x
x
(11.3)
gdzie
β = V/c. Te równania noszą nazwę
transformacji Lorentza
.
Omówimy teraz niektóre wnioski wynikające z transformacji Lorentza.
11.2.1 Jednoczesność
Przyjmijmy, że według obserwatora w rakiecie poruszającej się wzdłuż osi x' (czyli
także wzdłuż osi x, bo zakładamy, że te osie są równoległe) pewne dwa zdarzenia za-
chodzą równocześnie
∆
t' = t
2
' - t
1
' = 0, ale w rożnych miejscach x
2
' - x
1
' =
∆
x'
≠
0.
Sprawdźmy, czy te same zdarzanie są również jednoczesne dla obserwatora w spoczyn-
ku. Z transformacji Lorentza wynika, że
2
2
1
'
β
−
∆
−
∆
=
∆
x
c
V
t
t
t
V
x
x
∆
+
−
∆
=
∆
2
1
'
β
Łącząc oba powyższe równania otrzymujemy związek
'
1
'
2
2
x
c
V
t
t
∆
−
−
∆
=
∆
β
(11.4)
Jeżeli teraz uwzględnimy fakt, że zdarzenia w układzie związanym z rakietą są jedno-
czesne
∆
t' = 0 to otrzymamy ostatecznie
Z. Kąkol-Notatki do Wykładu z Fizyki
11-6
'
1
2
2
x
c
V
t
∆
−
=
∆
β
(11.5)
Widzimy, że równoczesność zdarzeń nie jest bezwzględna, w układzie nieruchomym te
dwa zdarzenia nie są jednoczesne.
11.2.2 Skrócenie długości
Teraz rozpatrzmy inny przykład. W rakiecie poruszającej się z prędkością V, wzdłuż
osi x' leży pręt o długości L'. Sprawdźmy jaką długość tego pręta zaobserwuje obserwa-
tor w układzie nieruchomym.
Pomiar długości pręta polega na zarejestrowaniu dwóch zjawisk zachodzących rów-
nocześnie na końcach pręta (np. zapalenie się żarówek). Ponieważ żarówki zapalają się
na końcach pręta to
∆
x' = L'. Ponadto żarówki zapalają się w tym samym czasie (dla ob-
serwatora w układzie spoczywającym ) to dodatkowo
∆
t = 0. Uwzględniając te warunki
otrzymujemy na podstawie transformacji Lorentza
x
L
∆
−
=
2
1
1
'
β
∆
x jest długością pręta L w układzie nieruchomym więc
2
1
'
β
−
=
=
∆
L
L
x
(11.6)
Okazuje się, że pręt ma mniejszą długość, jest krótszy.
11.2.3 Stałość przedziału czasoprzestrzennego
Pomimo, że powyższy opis kłóci się ze zdrowym rozsądkiem i doświadczeniem
życia codziennego to jednak po bliższej analizie transformacja Lorentza może już nie
wydawać się aż tak dziwna. Wyobraźmy sobie pręt o dł. np. .20m. umieszczony w ukła-
dzie współrzędnych w taki sposób, że rzut tego odcinka na oś x wynosi
∆
x, a na oś y
∆
y.
Jeśli teraz ktoś znajdzie się w drugim układzie współrzędnych, obróconym względem
pierwszego o kąt
α, to spoglądając na ten odcinek
z tego układu mierzy jego współrzędne jako
∆
x
’
i
∆
y
’
. Czy jest to dla nas dziwne? Oczywiście nie.
Możemy także przetłumaczyć opis w jednym ukła-
dzie na opis w drugim (znaleźć transformację)
∆
x
’
=
∆
x cos
α +
∆
y sin
α
∆
y
’
=-
∆
x sin
α +
∆
y cos
α
Poszczególne wyniki obserwacji
∆
x i
∆
y dla jednego człowieka, oraz, odpowiednio,
∆
x'
i
∆
y' dla drugiego są różne, lecz suma ich kwadratów tj.
długość pręta jest taka sama
.
y'
y
x'
x
α
Z. Kąkol-Notatki do Wykładu z Fizyki
11-7
Związek między
∆
x i
∆
y, a
∆
x' i
∆
y' jest dany przez liniową kombinację podobnie jak
w transformacji Lorentza. Tylko, że tutaj wiemy, że
∆
x i
∆
y to odległości, a tam
∆
x i
∆
t
to wielkości innego rodzaju.
Szczególna teoria względności dowodzi, że
czas jest ściśle powiązany z odległością
i naprawdę żyjemy w 4-wymiarowej przestrzeni; czasoprzestrzeni
. Co więcej, podobna
wielkość jak odległość w naszym przykładzie też istnieje: jest nią
przedział czasoprze-
strzenny
(
∆
x)
2
-(c
∆
t)
2
, który jest niezmiennikiem transformacji Lorenzta, czyli jest taki
sam w dwóch układach
(
∆
x)
2
-(c
∆
t)
2
=(
∆
x’)
2
-(c
∆
t’)
2
(11.7)
11.2.4 Dodawanie prędkości
Uprzednio rozważaliśmy obiekt spoczywający w rakiecie. Teraz zajmiemy się przy-
padkiem gdy obiekt ma już pewną prędkość U
x
' w ruchomym układzie odniesienia (tj.
względem rakiety). Sprawdzimy jaką prędkość U
x
zarejestruje nieruchomy obserwator,
w układzie którego rakieta porusza się z prędkością V wzdłuż osi x. Z transformacji Lo-
rentza wynika, że
2
1
'
β
−
∆
−
∆
=
∆
t
V
x
x
2
2
1
'
β
−
∆
−
∆
=
∆
x
c
V
t
t
Dzieląc te równania przez siebie otrzymujemy
t
x
c
V
V
t
x
x
c
V
t
t
V
x
t
x
∆
∆
−
−
∆
∆
=
∆
−
∆
∆
−
∆
=
∆
∆
2
2
1
'
'
a po podstawieniu
'
'
'
t
x
U
x
∆
∆
=
i
t
x
U
x
∆
∆
=
2
1
'
c
VU
V
U
U
x
x
x
−
−
=
(11.8a)
Równanie (11.8a) można rozwiązać ze względu na U
x
Z. Kąkol-Notatki do Wykładu z Fizyki
11-8
2
'
1
'
c
VU
V
U
U
x
x
x
+
+
=
(11.8b)
W ogólności, jeśli obiekt przesuwa się z prędkością
'
'
'
y
x
V
V
V
j
i
+
=
, względem ob-
serwatora w rakiecie (poruszającej się z prędkością U wzdłuż osi x) to prędkość
y
x
V
V
V
j
i
+
=
tego przedmiotu zarejestrowana w nieruchomym układzie wyniesie
2
'
1
'
c
UV
V
U
V
x
x
x
+
+
=
(11.9a)
V
y
= V
y
'
(11.9b)
Przykład 1
Dwa naddźwiękowe samoloty odrzutowe lecą ku sobie na kursie kolizyjnym. Ich
prędkości względem Ziemi wynoszą odpowiednio: samolot 1 V
x
= 1500km/h, samolot 2
U = 3000km/h. Jaką wartość prędkości pierwszego samolotu zmierzy obserwator w sa-
molocie drugim?
Samolot 2 jest układem, względem którego prędkość obiektu (czyli samolotu 1) chcemy
obliczyć, przy znanej prędkości w układzie związanym z Ziemią. Ponieważ V
x
= 1500
km/h, U = - 3000 km/h (bo przeciwny kierunek). stąd na podstawie równania (11.9a)
V
x
' = 4497.77 km/h.
11.2.5 Zależność masy od prędkości
Dotychczas zajmowaliśmy się kinematyką ruchu ciała obserwowanego z dwóch
układów odniesienia poruszających się względem siebie ze stałą prędkością. Teraz
chcemy odpowiedzieć na pytanie jak można opisać zachowanie ciała pod wpływem sił
w sytuacji, gdy transformacja Lorentza, (a nie Galileusza) jest prawdziwa. Chodzi o to,
czy druga zasada dynamiki Newtona F = dp/dt może być stosowana i czy zasada za-
chowania pędu ma taką samą postać we wszystkich układach inercjalnych.
Okazuje się, że warunkiem zachowania pędu przy transformacji z jednego układu
odniesienia do innego jest uwzględnienie zależność masy ciała m od jego prędkości V,
danej następującym wyrażeniem
2
2
0
1
)
(
c
V
m
V
m
−
=
(11.10)
w którym m
0
oznacza
masę spoczynkową
, czyli masę nieruchomego ciała. Zauważmy
ponadto, że masa cząstki rośnie wraz z prędkością i zmierza do nieskończoności gdy
V
à c.
Rozpatrzmy teraz ruch ciała pod wpływem stałej siły F działającej równolegle do
kierunku ruchu. Zależność prędkości ciała od czasu obliczamy na podstawie drugiej za-
Z. Kąkol-Notatki do Wykładu z Fizyki
11-9
sad dynamiki Newtona. Uwzględniając zależność masy od prędkości (11.10) otrzymu-
jemy
2
0
0
1
)
(
+
=
c
m
Ft
m
Ft
t
V
Porównanie zależność prędkości ciała od czasu działania siły w mechanice klasycznej
i relatywistycznej jest pokazane na rysunku poniżej. W przeciwieństwie do opisu kla-
sycznego, z powyższej zależności wynika, że cząstki nie da się przyspieszać w nieskoń-
czoność działając stałą siłą.
Zmiana masy z prędkością została potwierdzona wieloma doświadczeniami
przeprowadzonymi dla cząstek elementarnych.
11.2.6 Równoważność masy i energii
Einstein pokazał, że zasada zachowania energii jest spełniona w mechanice relatywi-
stycznej pod warunkiem, że pomiędzy masą i całkowitą energią ciała zachodzi związek
2
mc
E
=
(11.11)
gdzie m zależy od prędkości ciała V zgodnie zrównaniem (11.10). To znane powszech-
nie równanie Einsteina opisuje równoważność masy i energii. Wynika z niego, że ciało
w spoczynku ma zawsze pewną energię związaną z jego masa spoczynkową
2
0
0
c
m
E
=
Energię kinetyczną ciała poruszającego się z prędkością V obliczamy odejmując od
energii całkowitej energię spoczynkową (nie związaną z ruchem)
0
1
Pr
ędkość relatywistyczna
Pr
ędkość klasyczna
Przedzia
ł mechaniki klasycznej
V
/c
t
Z. Kąkol-Notatki do Wykładu z Fizyki
11-10
2
0
2
0
2
0
)
(
c
m
m
c
m
mc
E
E
E
k
−
=
−
=
−
=
Widzimy, że mechanika relatywistyczna wiąże energię kinetyczną z przyrostem masy
ciała. Na zakończenie zobaczmy jaką wartość przyjmuje energia całkowita, jeśli pręd-
kość V jest mała. Dla małego V równanie (11.10) można przybliżyć (rozwijając w sze-
reg) do postaci
+
≈
−
=
2
2
0
2
2
0
2
1
1
)
(
c
V
m
c
V
m
V
m
Podstawiając tę wartość do wyrażenia na energię całkowitą otrzymujemy
2
)
(
2
0
2
0
2
V
m
c
m
c
V
m
E
+
≈
=
Pierwszy wyraz jest energią związaną z istnieniem samej masy (energia spoczynkowa)
natomiast drugi jest klasyczną energią kinetyczną związaną z ruchem ciała. Otrzymali-
śmy rozwiązanie klasyczne jako graniczny przypadek (dla małych prędkości) rozwiąza-
nia relatywistycznego.
Stąd o krok już było do stwierdzenia, że jeżeli masa spoczynkowa cząstki zostanie
zmniejszona o
∆
m, to nastąpi wyzwolenie energii
∆
E =
∆
mc
2
. Te wnioski zostały po-
twierdzone doświadczalnie i omówimy je na dalszych wykładach.