RW – 1.2 – dr inż. Jan Ruchel

1/4

Macierze

PODSTAWY ALGEBRY MACIERZY

Macierz A

m,n

,

gdzie

„ m „ to ilość wierszy, „ n „ ilość kolumn

a

i,j

element macierzy z

”i-tego„ wiersza, „j-tej„ kolumny

Operacje na macierzach

Równość macierzy

A

m,n

= B

m,n

.

def

a

i,j

= b

i,j

8

6

4

2

4

3

2

1

8

6

4

2

4

3

2

1

Dodawanie (odejmowanie) macierzy

A

m,n

± B

m,n

= C

m,n

.

def

c

i,j

= a

i,j

± b

i,j

9

2

13

5

2

3

5

2

1

2

0

2

4

0

12

3

2

1

Mnożenie macierzy przez skalar

A

m,n

* c = B

m,n

.

def

b

i,j

= a

i,j

* c

2

0

3

3

1

3

1

2

1

4

2

1

3

1

0

1

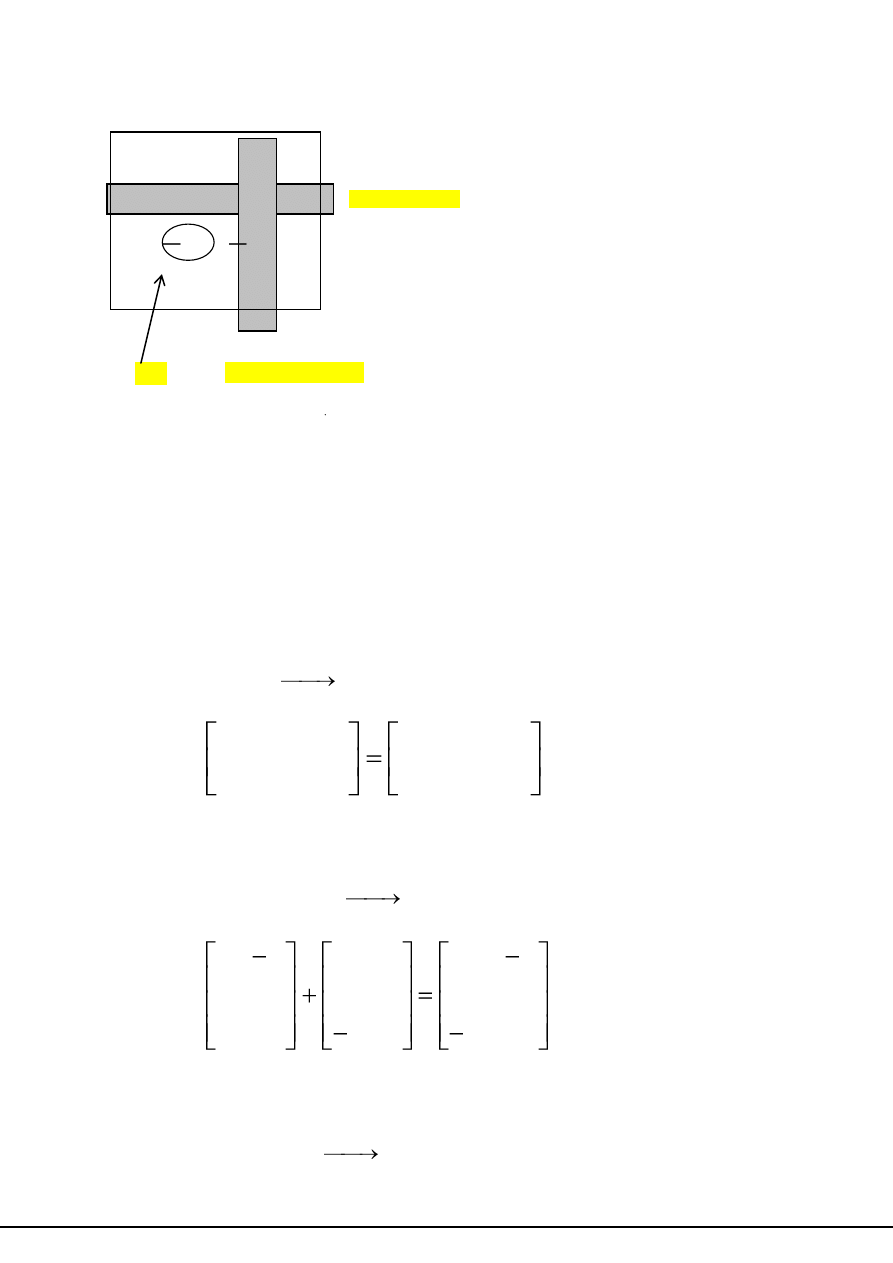
WIERSZ A

i

KOLUMNA A

(j)

A

3,2

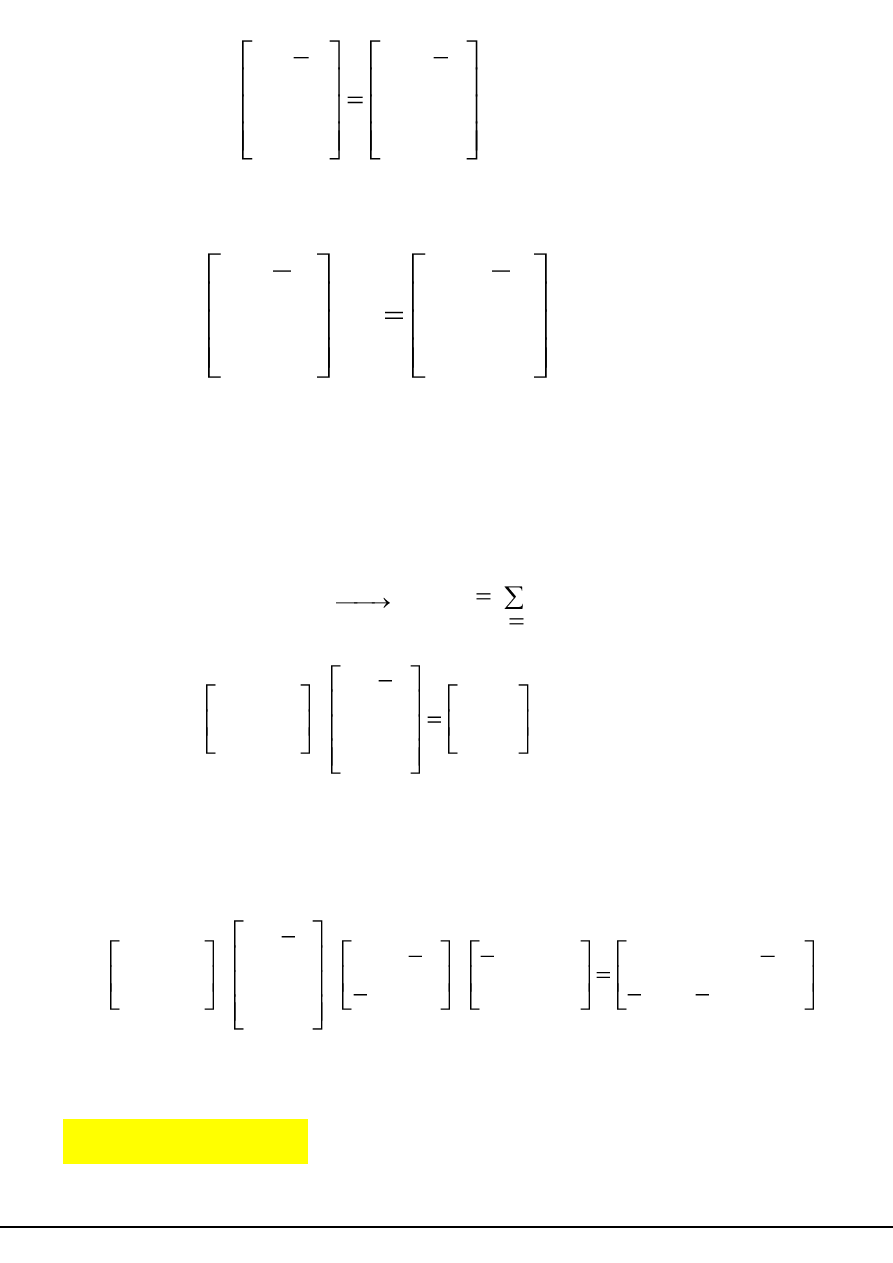
RW – 1.2 – dr inż. Jan Ruchel

2/4

Macierze

16

0

48

12

8

4

4

0

12

3

2

1

*

4

Mnożenie macierzy przez skalar jest przemienne

16

0

48

12

8

4

4

*

4

0

12

3

2

1

A

m,n

* c = c * A

m,n

Iloczyn dwóch macierzy

Iloczyn wierszy(sumo-mnożenie) pierwszej macierzy i
odpowiadających elementów kolumn drugiej macierzy

A

m,n

* B

n,s

= C

m,s

.

def

j

k

b

n

k

k

i

a

j

i

c

,

1

*

,

,

2

9

14

7

4

0

2

3

2

1

*

1

2

3

3

2

1

Iloczyn wielu macierzy

A

m,n

* B

n,s

* C

s,t

* D

t,v

= E

m,v

15

16

37

63

0

21

0

1

2

3

0

1

*

1

2

2

1

*

4

0

2

3

2

1

*

1

2

3

3

2

1

Iloczyn wielu macierzy

A

1

2

3

3

2

1

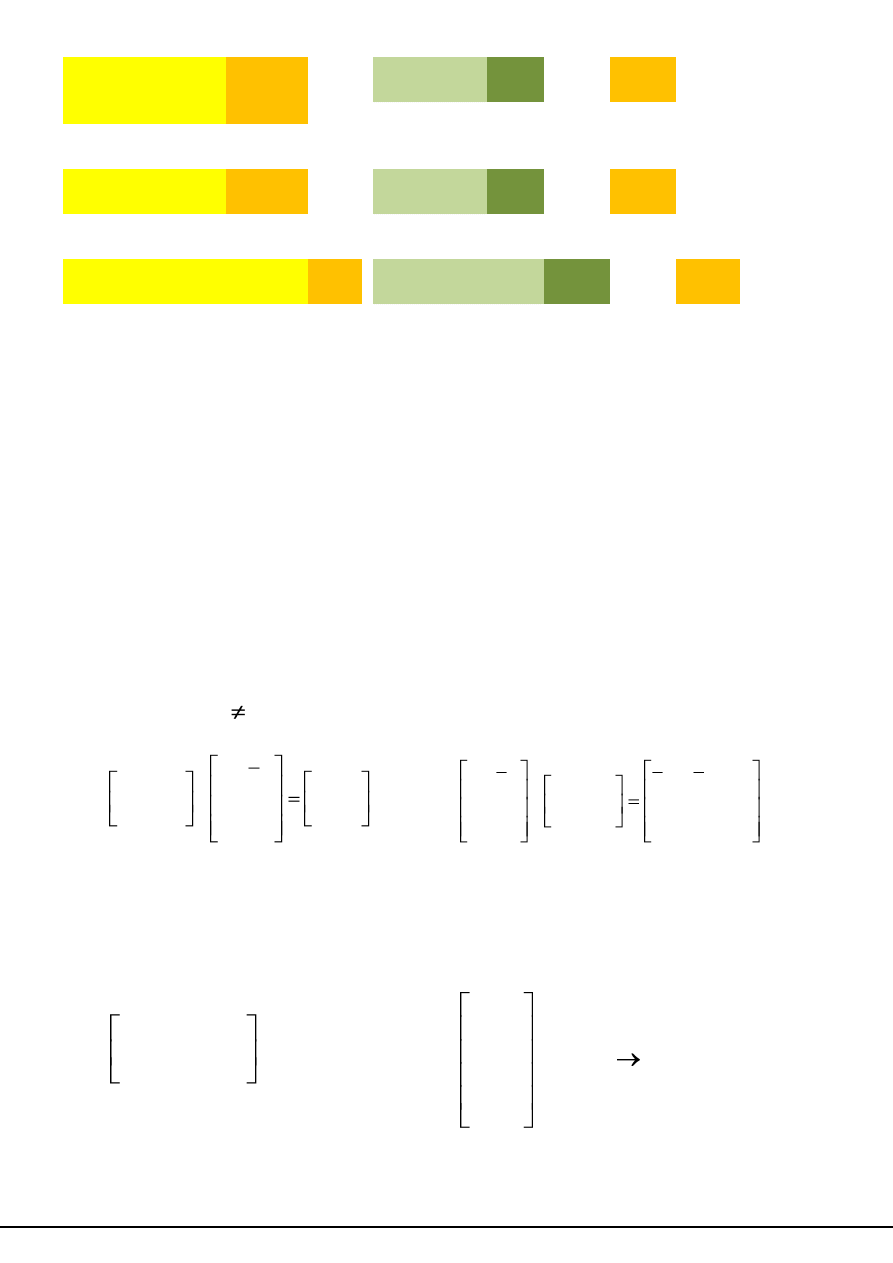
RW – 1.2 – dr inż. Jan Ruchel

3/4

Macierze

B

A*B

SUMA

1

-2

-1

7

14

21

21

3

2

5

9

2

11

11

0

4

4

C

A*B*C

SUMA

1

-2

-1

-21

0

-21

-21

-2

1

-1

5

-16

-11

-11

D

A*B*C*D

SUMA

-1

0

3

2

21

0

-63

-42

-42

2

1

0

3

-37

-16

15

-38

-38

Mnożenie macierzy jest łączne

A

m,n

* B

n,s

* C

s,t

= A

m,n

* (B

n,s

* C

s,t

)

Mnożenie macierzy jest rozdzielne względem dodawania

( A

m,n

+ B

m,n

) * C

n,s

= A

m,n

* C

n,s

+ B

m,n

* C

n,s

Mnożenie macierzy nie jest przemienne

A

m,n

* B

n,s

B

n,s

* A

m,n

2

9

14

7

4

0

2

3

2

1

*

1

2

3

3

2

1

≠

4

8

12

11

10

9

1

2

5

1

2

3

3

2

1

*

4

0

2

3

2

1

Transpoza macierzy

Macierz transponowaną względem macierzy A

m,n

nazywa się taką

macierz

T

m

n

A

,

w której wiersze odpowiadają kolumnom macierzy A

m,n

8

6

4

2

4

3

2

1

T

8

4

6

3

4

2

2

1

a

T

i,j

a

j,i

Transpoza macierzy posiada następujące własności:

RW – 1.2 – dr inż. Jan Ruchel

4/4

Macierze

(A

T

)

T

= A

Transpoza macierzy transponowanej przywraca pierwotną macierz

8

4

6

3

4

2

2

1

T

8

6

4

2

4

3

2

1

(A

T

+ B + C)

T

= (A

T

)

T

+ B

T

+ C

T

= A + B

T

+ C

T

Transpoza sumy macierzy jest sumą macierzy transponowanych

(ABCD)

T

= D

T

C

T

B

T

A

T

Transpoza iloczynu macierzy jest iloczynem macierzy
transponowanych w odwrotnej kolejności.