
Podstawowe elementy stosowane
w mikroelektronice
Wstęp
1. Podstawy elektrotechniki
1.1. Podstawowe pojęcia
1.2. Podstawowe prawa elektrotechniki
2. Bierne elementy elektroniczne
2.1. Rezystor
2.2. Kondensator
2.3. Cewka
2.4. Proste układy z elementami biernymi
3. Czynne elementy elektroniczne
3.1. Dioda
3.2. Tranzystor
3.3. Proste układy z elementami aktywnymi
Podsumowanie
Bibliografia
„Sądzę, że na światowym rynku jest miejsce dla jakichś
5 komputerów.”
Thomas Watson, prezes IBM, 1943

2
Wstęp
Wiesz już co to jest mikroelektronika i czemu jest tak ważna. Zanim jednak przej-
dziemy do szczegółów z nią związanych, przypomnimy sobie najważniejsze pojęcia
z zakresu elektryczności oraz najważniejsze wielkości elektryczne. Jest to niezwy-
kle ważne, gdyż elektronika to właśnie umiejętność sterowania tymi wielkościa-
mi! Aby móc nimi sterować, potrzebujemy do tego narzędzi, którymi są elementy
elektroniczne, a które zostaną omówione w dalszej części kursu. W kolejnym te-
macie wykorzystamy te elementy do budowy najważniejsze układów cyfrowych
— takich, które występują niemal w każdym układzie scalonym. Zapowiada się
naprawdę interesująco, a więc do roboty!

3
1. Podstawy elektrotechniki
Zgodnie z zapowiedzią, chciałbym najpierw przypomnieć najważniejsze pojęcia
związane z elektrycznością. Zapewne większość z nich jest ci znana ze szkoły śred-
niej czy nawet podstawowej. Doskonale zdaję sobie sprawę, że w temacie tym mo-
żesz nie znaleźć niczego nowego i może nawet momentami będzie on dla ciebie
nudny, lecz chcę pewne ważne rzeczy usystematyzować oraz przypomnieć. Proszę,
nie lekceważ tego tematu, ponieważ wiele osób, które nawet zawodowo zajmują się
elektroniką ma problemy z podstawami, o czym się już za chwilę przekonasz.
1.1. Podstawowe pojęcia
Współczesna fizyka wyróżnia cztery podstawowe oddziaływania:
— grawitacyjne, czyli przyciąganie dwóch mas,
— elektromagnetyczne, czyli oddziaływanie związane z ładunkami elektrycznymi,
— słabe, czyli trudne do uchwycenia oddziaływanie odpowiedzialne np. za roz-
pad β,
— silne, czyli oddziaływanie między najmniejszymi składnikami materii, odpowia-
dające m.in. za istnienie jądra atomów.
Na tych czterech oddziaływaniach zasadza się cała fizyka. Dwa ostatnie oddzia-
ływania, czyli słabe i silne, występują między najmniejszymi składnikami materii
i być może słyszysz o nich po raz pierwszy, jednak nie będziemy się nimi zajmowali
podczas tego kursu. Nas oczywiście najbardziej interesuje oddziaływanie elektro-
magnetyczne.
Ładunek elektryczny
Zadam ci teraz pytanie — spróbuj najpierw sam na nie odpowiedzieć, a dopiero
później przeczytaj podaną poniżej definicję. Pytanie brzmi: co to jest ładunek elek-
tryczny? Pewnie ciśnie ci się na myśl wiele odpowiedzi — może jest to coś związa-
nego z elektronem, a może z prądem elektrycznym. No cóż, muszę cię zmartwić,
ale nie o to chodzi. Nie przyjmuj się — mało która osoba, nawet zawodowo zajmu-
jąca się zagadnieniami związanymi z elektrycznością, zna odpowiedź na to pyta-
nie i dlatego zachęcam cię do uważnej lektury tego podtematu, ponieważ właśnie
najprostsze rzeczy sprawiają najwięcej problemów. A odpowiedź jest bardzo prosta
i brzmi:
Ładunek elektryczny
jest to własność materii, która powoduje, że oddziałuje ona
z polem elektromagnetycznym.
Przeanalizujmy tę definicję dokładniej. Ładunek elektryczny to własność materii
— oznacza to, że ładunek jest pewną własnością (cechą), którą może posiadać ma-
teria. Jest to tak samo dobra cecha jak np. kolor czy masa. Ładunek elektryczny jest
związany z materią — nie możemy wziąć do ręki „trochę” ładunku, możemy nato-
miast wziąć trochę materii, która ma ładunek. Coś, co nie jest materią, nie może
posiadać ładunku (np. przestrzeń). Brzmi to może trochę abstrakcyjnie, ale infor-
macje te są bardzo ważne i mam nadzieje, że już mniej więcej zaczynasz rozumieć
co to jest ładunek. Dalsza część definicji mówi nam, jak stwierdzić czy jakaś mate-

4
ria ma ładunek, czy nie. Jeśli oddziałuje z polem elektromagnetycznym, to posia-
da ładunek, w przeciwnym razie nie ma go. Czyli na przykład — jeśli wezmę tro-
chę materii i umieszczę ją w pobliżu innej materii, o której wiem już, iż ma ładu-
nek i będą one na siebie oddziaływały (np. odpychały się lub przyciągały), to mogę
z czystym sumienie stwierdzić: ta pierwsza materia posiada ładunek! Jeśli nie do
końca rozumiesz tę definicję, spróbuj raz jeszcze spokojnie ją przeczytać i zrozu-
mieć, gdyż więcej nie będziemy do tego wracać.
Wiemy już co to jest ładunek, wiemy jak zbadać czy jest, czy go nie ma — pozosta-
je jeszcze zmierzyć jego ilość. Jednostką ładunku elektrycznego jest Coulomb [C].
1 C to spora ilość ładunku i w mikroelektronice nie operuje się tak dużymi wiel-
kościami. Kolejną ważną cechą jest znak ładunku. Zaobserwowano, iż występują
dwa rodzaje ładunków — jedne oznaczono jako ładunki ujemne, drugie jako do-
datnie. Ponadto zaobserwowano, iż ładunki przeciwnych znaków przyciągają się,
a tych samych odpychają.
Ostatnią ważną cechą ładunku jest to, iż występuje on w pewnych porcjach zwa-
nych kwantami ładunku bądź ładunkiem elementarnym. Oznacza to, że nie można
„wziąć” pół ładunku elementarnego
1
, a jedynie jego wielokrotność, czyli np. jeden,
dwa, siedemnaście czy milion. Wartość ładunku elementarnego wynosi w przybli-
żeniu 1,602 · 10
–19
C, a oznacza się go jako 1 e.
Zapewne, gdy spytałem cię o ładunek elektryczny pomyślałeś o elektronie. No
właśnie, co to jest elektron? Otóż elektron jest to trwała cząstka, której ładunek
jest ujemny i co do wartości równy ładunkowi elementarnemu (1 e). Myślę, że
w definicji tej wszystko jest jasne z wyjątkiem jednego — co to jest cząstka. Jest to
faktycznie bardzo nieprecyzyjne pojęcie, które oznacza coś bardzo małego, a zara-
zem będącego najbardziej podstawowym budulcem materii. Z cząstek zbudowany
jest nasz świat, a elektron jest jedną z nich. Cząstka, która posiada ładunek dodat-
ni o wartości 1 e to proton. Elektrony oraz protony mogą występować samodziel-
nie, a więc możesz „wziąć do ręki” np. jeden elektron — jest teoretycznie możliwe,
choć w praktyce bardzo trudne.
Prąd
Wiemy już co to jest ładunek elektryczny, zróbmy więc kolejny ważny krok — każ-
my mu poruszać się. Oczywiście po moim stwierdzeniu powinieneś zaprotestowa-
łeś — jak ładunek ma się poruszać, przecież on nie istnieje, istnieje tylko materia,
która może mieć własność ładunku i ona może się poruszać. Jeśli o tym pomyśla-
łeś, oznacza to, że dobrze rozumiesz pojęcie ładunku, a jeśli nie, to wróć może
jeszcze na chwilę do początku tego podtematu. Powyższe stwierdzenie o ruchu ła-
dunku jest pewnym skrótem myślowym, którego będę bardzo często używał. Mam
oczywiście na myśli ruch materii, która posiada ładunek elektryczny. Skoro już
wszystko jasne — każmy poruszać się ładunkowi dzięki temu zdefiniujemy kolejne
ważne pojęcie:
Prąd
jest to uporządkowany ruch ładunków elektrycznych. Kierunek prądu to kie-
runek ruchu ładunków dodatnich.
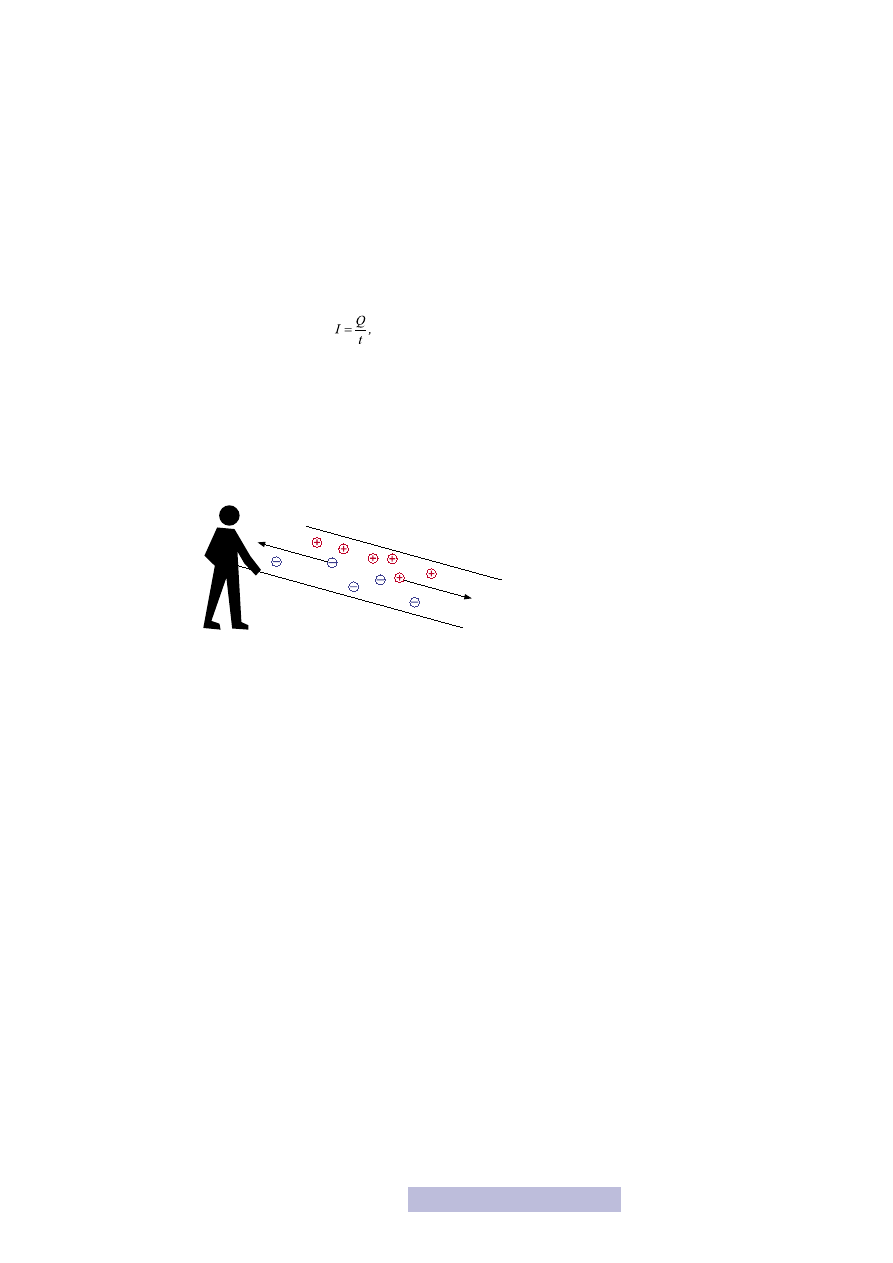
Zagadnienie to, mam nadzieję, jest jasne, należy jedynie wyjaśnić, jak to jest z tym
kierunkiem (rys. 1). Ważne jest określenie kierunku, w którym ładunek się porusza
— umownie (w hołdzie Franklinowi) przyjęto, że pokazujemy kierunek ruchu ła-
dunków dodatnich. Jeśli porusza się ładunek ujemny, to tak, jakby w drugą stronę
poruszał się ładunek dodatni. Prąd elektryczny jest to ruch elektronów, a elektron
ma ładunek ujemny. Dlatego tak naprawdę ładunki poruszają się w drugą stronę
niż to oznaczamy. Gdyby — dla odmiany — poruszającymi się cząstkami nie były
elektrony, a protony, które mają ładunek dodatni, to ich kierunek ruchu oznaczyli-
byśmy jako kierunek przepływu prądu.
1
Nie jest to do końca
prawdą, gdyż np. kwarki
(najmniejsze obecnie
znane składniki materii)
posiadają ułamkowy
ładunek, jednak nigdy nie
występują pojedynczo,
a dobierają się tak, aby ich
sumaryczny ładunek był
elementarny.
5
Przepływ prądu można przedstawić jako przepływ strumienia wody. Przyjmijmy,
że woda składa się z tak małych kropli, że nie można ich już podzielić na mniejsze.
Taka kropla to ładunek elementarny, a uporządkowany ruch kropli to przepływ
wody, czyli prądu. Za pomocą wody trudno pokazać ruch ładunków dodatnich
i ujemnych — mnie przynajmniej takiej analogii nie udało się odnaleźć.
Kiedy patrzysz na rzekę, możesz bez problemu określić, czy płynie nią dużo, czy
mało wody. Teoretycznie możliwe jest nawet policzenie liczby kropli przepływają-
cych w określonym czasie. Tak samo można mierzyć wielkość prądu, zwaną także
natężeniem prądu. Jest to liczba elementarnych ładunków, które przypłynęły w cią-
gu jednej sekundy. Zapisując to wzorem, otrzymamy:
gdzie: I — prąd, Q — ładunek, t — czas.
Jednostką natężenia jest amper [A]. Jeśli przez przewód płynie prąd o natężeniu
1 ampera, oznacza to, że w ciągu jednej sekundy przypływa jeden Coulomb ładun-
ków, czyli 1 C = 1 A ⋅ 1 s. Amper to duża jednostka i w mikroelektronice używamy
raczej jej części, np. miliamperów, czyli tysięcznych części ampera.
Napięcie
Kolejnym ważnym pojęciem, o jakim chciałbym powiedzieć jest napięcie. O ile
prąd można łatwo wyobrazić sobie, o tyle przy napięciu posłużę się pewną analo-
gią. Wyobraź sobie, że stoisz nad rwącym strumieniem w pięknych górach i obmy-
wasz właśnie twarz w spienionej, orzeźwiającej wodzie; robisz sobie chwilę prze-
rwy, rozglądając się po okolicy. Jednak huk strumienia zagłusza wszystkie twoje
myśli z wyjątkiem jednej — czemu ta woda płynie? Chwilka zastanowienia i odpo-
wiedź oczywista — ponieważ spływa z góry. No właśnie, aby woda mogła płynąć,
musi spadać z jakiejś wysokości. W górach łatwo to zaobserwować, na nizinach
trudniej, ale tak jest. Jeśli nie przekonuje cię to, to inny przykład: wylewamy wodę
z wiadra — zawsze będzie ona płynąć w kierunku ziemi. A więc aby woda popły-
nęła, musi istnieć różnica wysokości między miejscem, z którego woda wypływa
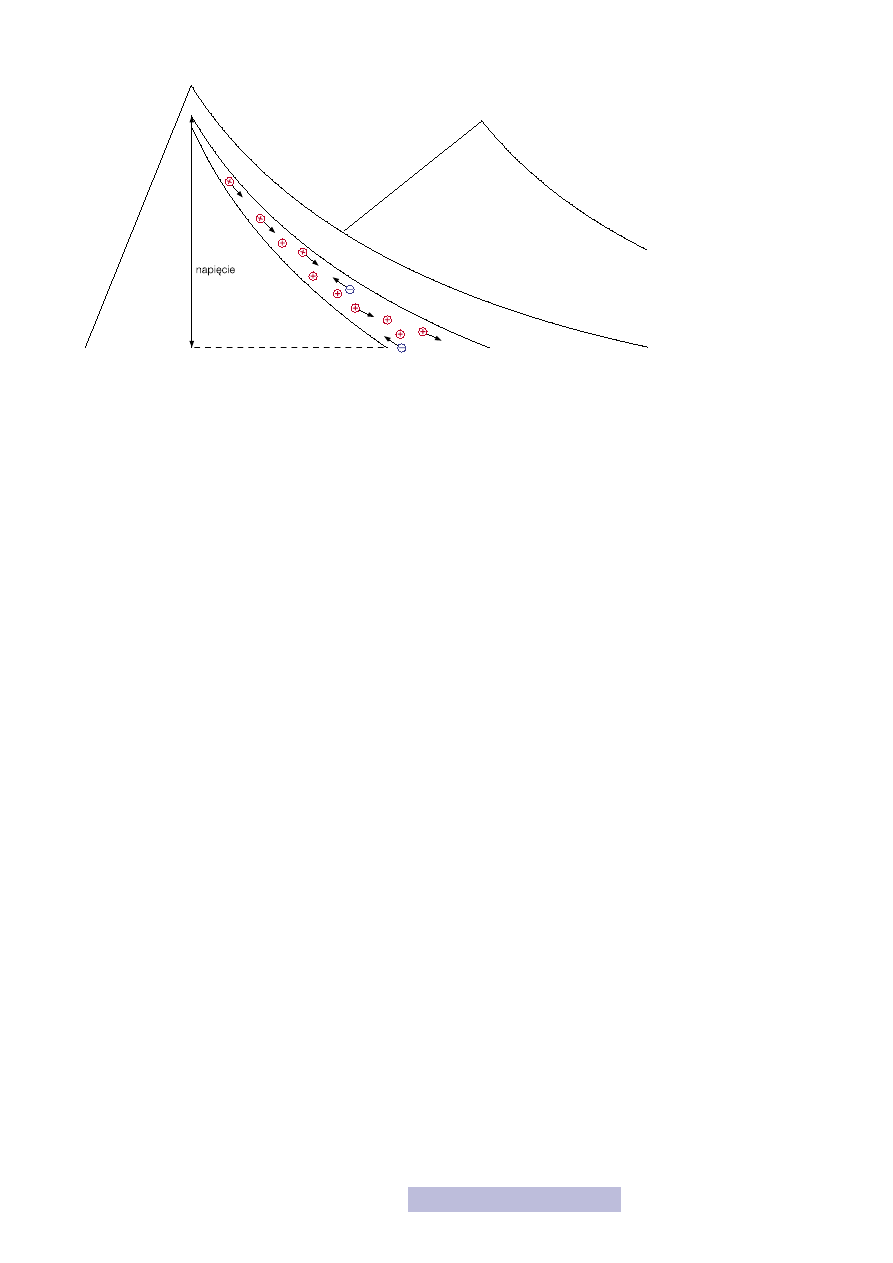
i gdzie uchodzi. Ta właśnie różnica wysokości jest analogią napięcia, czyli im wyż-
sze napięcie, tym nasze ładunki elementarne pokonują większą wysokość (rys. 2).
Od razu dostrzegamy, że napięcie i prąd muszą być ze sobą jakoś powiązane, po-
nieważ im większa wysokość, z której spuszczamy wodę, tym szybciej ona płynie.
Dlatego strumyk w górach jest rwący, a rzeka na nizinie płynie leniwie. Taki zwią-
zek oczywiście istnieje i mówi o nim słynne prawo Ohma. Oczywiście od razu wi-
dzimy, że bez napięcia, bez różnicy poziomów nie może popłynąć prąd, natomiast
może istnieć napięcie bez prądu.
Rysunek 1
Przepływ prądu elektrycznego
6
Napięcie, podobnie jak prąd, możemy mierzyć — jego jednostką jest volt.
Zanim przejdziemy do ostatniego ważnego pojęcia, wróćmy jeszcze na chwilę do
obrazu górskiego strumyka. Leżysz sobie wygodnie i odpoczywasz, piękne słoń-
ce, lekki wiatr, aż nie chce się iść dalej. Jednak ty łatwo się nie poddajesz i z za-
interesowaniem patrzysz na górę, na którą chcesz wejść. Jednocześnie widzisz, że
to z jej szczytu wypływa ten piękny strumyk. Na oko możesz ocenić ile metrów
zostało ci do szczytu, a więc wiesz, jaką różnicę wysokości pokonała woda, czy-
li znasz wartość napięcia. W duchu pewnie myślisz — fajnie, tylko, że strumyk tę
wysokość pokonuje w dół, a ja będę musiał do góry. Mając to na uwadze, na pew-
no jeszcze chwilę odsapniesz i w tym momencie zauważysz, że strumyk nie zatrzy-
muje się w tym miejscu, w którym stoisz, ale płynie dalej w dół. I gdybyś stanął
niżej, np. u podnóża góry, różnica wysokości byłaby większa. Ba, pewnie ta struż-
ka za kilka dni, może tygodni wpadnie do morza i gdybyś stanął nad jego brze-
giem, to dopiero odczułbyś różnicę wysokości. Już chyba widzisz, że napięcie jest
pojęciem względnym, mierzy względną różnicę wysokości, czyli różnicę między
jakimiś dwoma punktami, np. między szczytem góry, z której wypływa strumyk
a miejscem, w którym stoisz. Ale przecież nawet na mapach wysokość podawa-
na jest najczęściej w wartościach bezwzględnych, czyli od poziomu morza. I wła-
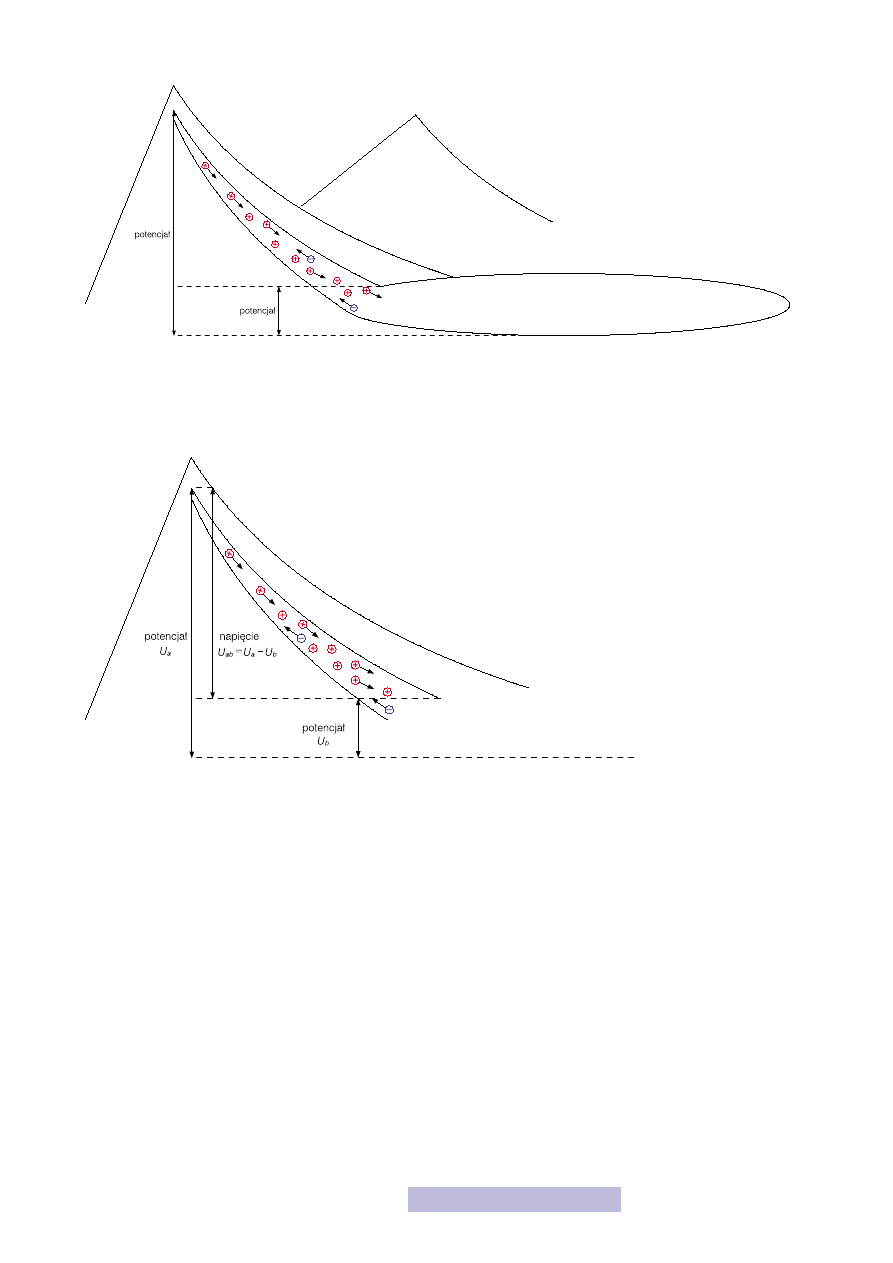
śnie taka bezwzględna wysokość nazywana jest potencjałem (rys. 3). Zatem każdy
punkt w układzie znajduje się na pewnej wysokości, a więc ma swój potencjał. Róż-
nica potencjałów między dwoma punktami, czyli różnica wysokości, to właśnie na-
pięcie. Pozostaje tylko kwestia, jak liczyć tę bezwzględną wysokość, który punkt
będzie tym elektronicznym poziomem morza. W każdym układzie elektronicznym
wyróżniamy tzw. masę. Jest to właśnie taka umowna zerowa wysokość, względem
której mierzymy wszystkie pozostałe potencjały. Oczywiście potencjały mogą być
ujemne (podobnie strumyk, który wpłynie na obszar depresji znajduje się poniżej
poziomu morza).
Rysunek 2
Napięcie
7
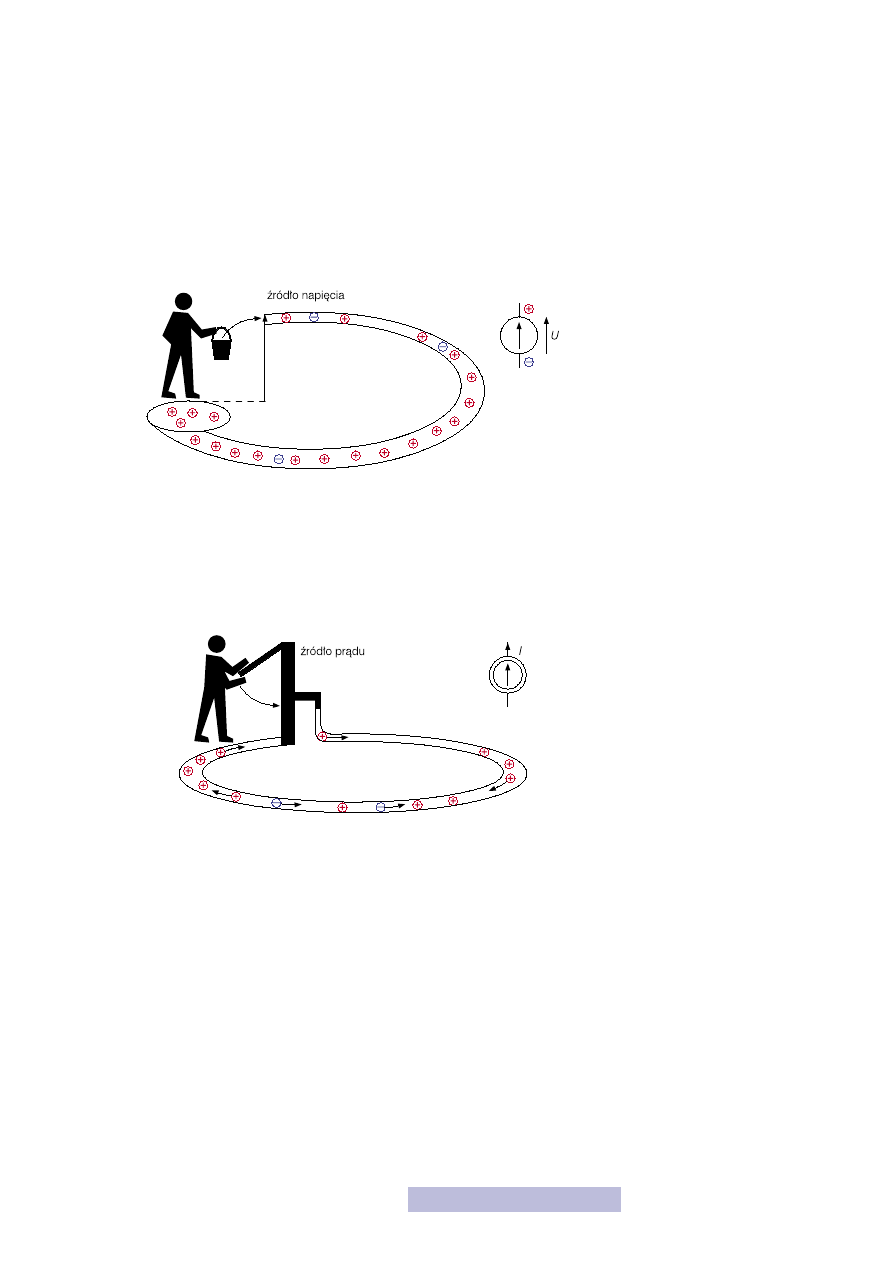
Potencjał jest niezwykle ważny pojęciem i od tej chwili będziemy go często używać.
Bardzo ważny jest również związek napięcia i potencjału. Napięcie między dwoma
punktami to po prostu potencjał jednego punktu minus potencjał drugiego punk-
tu. Związek między tymi wielkościami pokazuje rysunek 4.
Moc
Ostatnim ważnym pojęciem jest moc. Oczywiście moc nie jest związana wyłącz-
nie z elektrycznością, lecz będziemy potrzebowali tego pojęcia, dlatego chciałbym
je przypomnieć. Moc jest to ilość wykonanej pracy w jednostce czasu. Jeśli np. sil-
nik posiada dużą moc, to w tym samym czasie wykonuje on większą pracę niż sil-
nik o mniejszej mocy.
Wyobraź sobie teraz, że stoisz obok wodospadu i na jego dole znajduje się młyn
wodny. Im wyższy jest ten wodospad, z tym większą energią woda uderza w koło
młyńskie, a więc może wykonać większą pracę. Równocześnie im więcej wody pada
na koło, tym więcej pracy może ono wykonać. Przekładając to na język elektryczno-
ści, moc jest to praca, którą wykonuje płynący prąd w jednostce czasu. Moc jest tym
większa, im większe jest napięcie oraz natężenie prądu. Zachodzi zależność:
P = U · I,
gdzie: U — napięcie, I — natężenie prądu.
Rysunek 3
Pojęcie potencjału
Rysunek 4
Napięcie a potencjał
8
Źródło prądu i napięcia
Na pewno zapytasz mnie skąd wziąć napięcie czy prąd. Odpowiedź jest oczywista
— ze źródła. Rozróżniamy dwa rodzaje źródeł:
— napięciowe, czyli takie, które daje nam określone napięcie,
— prądowe, czyli takie, które daje nam określony prąd.
Gdybyśmy mieli użyć analogii do strumienia wody, to źródło napięcia jest takim
elementem, który bierze wodę i podnosi ją na pewną określoną wysokość (rys.
5). Idealne źródło napięcia powinno podnieść każdą ilość wody, lecz w praktyce
wszystkie źródła napięciowe mają ograniczoną wydolność prądową.
Natomiast źródło prądowe można przyrównać do pompy, która pompuje określo-
ną ilość wody w danym czasie (rys. 6). Idealne źródło prądowe powinno zawsze
pompować tę samą ilość prądu, bez względu na opory, które napotyka w czasie
pracy, lecz w praktyce wszystkie źródła prądowe mają ograniczony zakres pracy,
w którym prąd ma ustalone natężenie.
O ile ze źródłami napięciowymi spotykasz się na co dzień i są one dla ciebie czymś
normalnym (np. bateryjka czy gniazdko w pokoju), o tyle źródła prądowe są zdecy-
dowanie rzadziej spotykane, a być może słyszysz o nich pierwszy raz.
Źródła — czy to napięciowe, czy prądowe — mogą być stałe bądź zmienne. Jaka
jest różnica? Skupmy się na źródle napięciowym. Otóż źródło napięcia stałego to
takie źródło, które daje nam cały czas to samo napięcie, nic nie zmienia się w trak-
cie jego działania. Natomiast źródło zmiennego napięcia na wyjściu daje nam prze-
bieg, który zmienia się w czasie. Oczywiście ten przebieg może wyglądać chaotycz-
nie (rys. 7a) i na niewiele nam się przyda. Bardziej interesujące są przebiegi zmien-
ne okresowe, a więc takie, które co pewien czas powtarzają się. Przykłady takich
najważniejszych przebiegów pokazane zostały na rysunku 7. Zwróć szczególną
uwagę na tzw. przebieg prostokątny (rys. 7d), gdyż często będziemy z niego korzy-
stać i jak sam niedługo zobaczysz, to najważniejszy przebieg z punktu widzenie mi-
kroelektroniki.
Rysunek 5
Źródło napięcia
Rysunek 6
Źródło prądu

9
Pozostaje wyjaśnić jeszcze jedną kwestię. Kiedy spojrzysz na źródło napięcia stałe-
go, np. na bateryjkę, zobaczysz oznaczenia + i –. Plus oznacza potencjał jest wyż-
szy, a minus niższy. W przypadku źródeł zmiennych nie ma takich oznaczeń, po-
nieważ raz jedna elektroda może mieć wyższy potencjał, a raz druga. Dlatego np.
w gniazdku sieciowym dziurki nie są oznaczane.
1.2. Podstawowe prawa elektrotechniki
Poznałeś już trzy najważniejsze pojęcia elektrotechniki — ładunek, prąd i napięcie.
Teraz zajmijmy się najważniejszymi prawami, które rządzą tymi wielkościami.
Zasada zachowania ładunku
Zasada zachowania ładunku została zaobserwowana przez B. Franklina i brzmi
ona następująco:
Ładunek elektryczny w układzie odosobnionym jest wielkością stałą.
Oznacza to, że jeśli tylko nie dostarczamy bądź nie zabieramy z układu ładunków, to
ich ilość jest stała. Możemy je przenosić między poszczególnymi elementami ukła-
du, tak jak przy pocieraniu jedwabiu o szkło przenosimy ładunki z jednego materia-
łu na drugi, ale co byśmy nie robili — ich ilość zawsze będzie stała (rys. 8).
Rysunek 7
Przykładowe przebiegi napięcia
zamiennego
Rysunek 8
Zasada zachowania ładunku
10
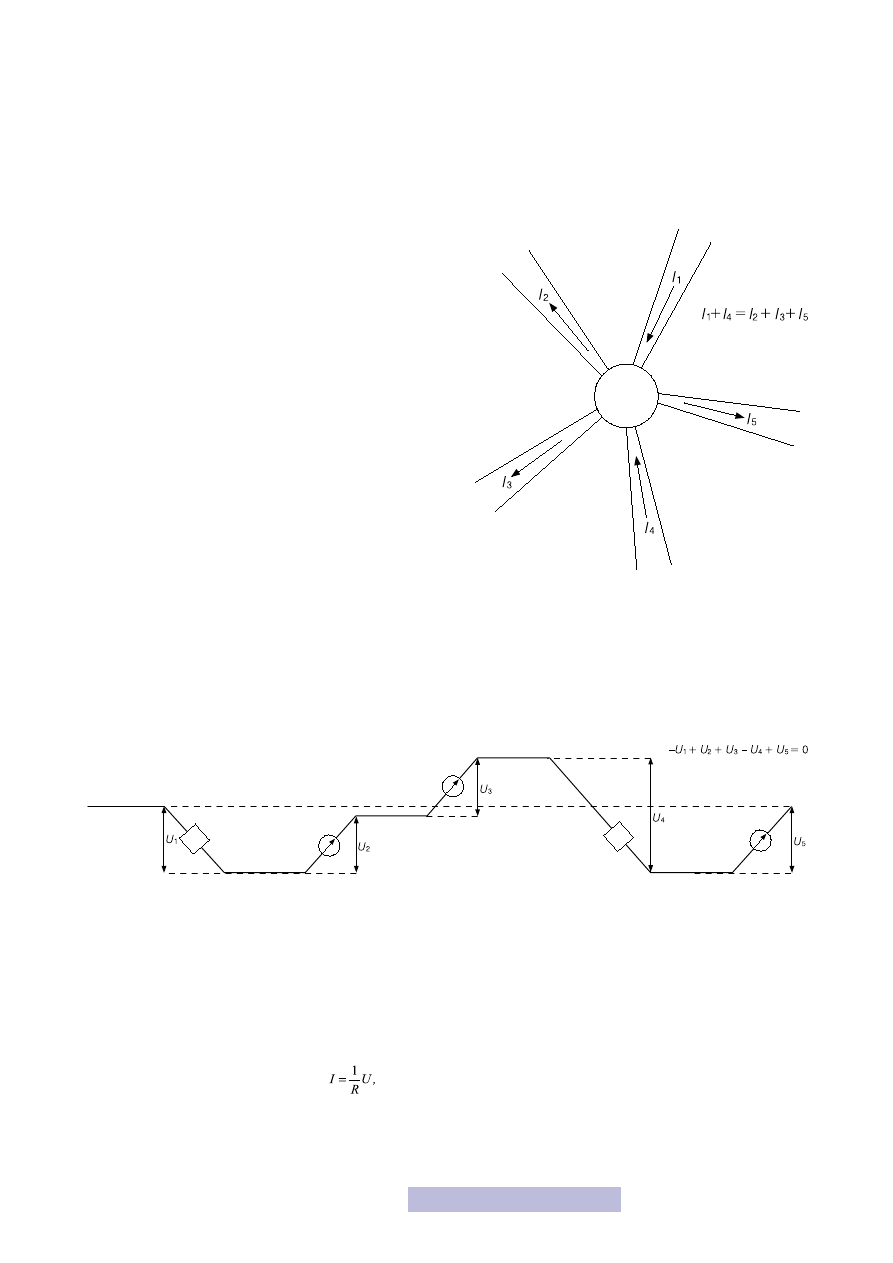
Prawa Kirchhoffa
Wprost z zasady zachowania ładunku wynika I prawo Kirchhoffa, które brzmi:
Suma natężeń prądów wpływających do węzła
jest równa
sumie natężeń prądów
z niego wypływających.
Węzeł jest to dowolny punkt w obwodzie, do którego dopływa i z którego wypły-
wa prąd (rys. 9). Prawo to wydaje się oczywiste, tym bardziej, że znamy już zasa-
dę zachowania ładunku. Jeśli do jakiegoś punktu dopłynie
określona liczba ładunków, to w tym samym czasie taka
sama liczba musi z niego odpłynąć. Gdyby więcej ich do-
pływało niż odpływało, to ich liczba w tym punkcie zwięk-
szałaby się, a nie ma możliwości ich magazynowania. Na-
tomiast gdyby więcej ich odpływało niż dopływało, wów-
czas należałoby te dodatkowe ładunki skądś wziąć, a na to
nie pozwala nam zasada zachowania ładunku. A więc osta-
tecznie musi ich dokładnie tyle samo przypływać co od-
pływać.
Analogicznie jak dla prądów, istnieje także prawo Kirch-
hoffa dla napięć i brzmi ono:
Suma spadków napięć wzdłuż dowolnego oczka w obwo-
dzie wynosi zero.
Wyjaśnijmy najpierw, co to jest oczko. Jest to dowolna za-
mknięta droga w obwodzie, czyli taka, że idąc nią, wró-
cimy do tego samego punktu, od którego zaczęliśmy wy-
prawę. Przypomnijmy sobie naszą interpretację napięcia jako „wysokości”, z której
spływa prąd. Prąd w obwodzie może przepłynąć na niższy poziom, ewentualnie
może zostać „wpompowany” na wyższy poziom. Gdy jednak prześledzimy „wzlo-
ty” i „upadki” naszego prądu wzdłuż pewnej zamkniętej drogi, to zawsze wrócimy
na ten poziom, a więc w sumie nic się nie stało, suma musi być równa zero. Myślę,
że kiedy przeanalizujesz to na przykładzie dowolnego obwodu, szybko zrozumiesz,
jak to prawo działa (rys. 10).
Prawo Ohma
Ostatnim ważnym prawem elektrotechniki, o jakim powiemy, jest znane chyba
każdemu prawo Ohma. Wiąże ono ze sobą prąd oraz napięcie i brzmi:
Natężenie prądu jest wprost proporcjonalne do przyłożonego napięcia. Współczyn-
nikiem proporcjonalności jest odwrotność wielkości zwanej rezystancją.
Prawo to zapisujemy wzorem:
gdzie: U — napięcie, I — prąd, R — rezystancja.
Rysunek 9
I prawo Kirchhoffa
Rysunek 10
II prawo Kirchhoffa

11
Już wcześniej zauważyliśmy, że musi istnieć związek między prądem a na-
pięciem, ponieważ jeśli nasze ładunki płyną z większej wysokości, to
w tym samym czasie przepłynie ich więcej. Z drugiej strony, jeśli chcemy,
aby przepłynęło ich więcej, to musimy zwiększyć wysokość. I o tym mówi
właśnie prawo Ohma — im większe napięcie (czyli nasza wysokość), tym
większy prąd (liczba ładunków w czasie) i ta zależność jest wprost pro-
porcjonalna. Współczynnikiem proporcjonalności jest odwrotność rezy-
stancji. Co to jest rezystancja? Najprościej można by powiedzieć, że jest
to kurek dla naszego prądu (rys. 11). Jeśli go przykręcimy, czyli rezystan-
cja będzie duża, to przy tym samym napięciu (tej samej wysokości) popły-
nie mały prąd. Jeśli natomiast go odkręcimy (mała rezystancja), strumień
naszych ładunków napotka mniejsze ograniczenia i ładunki będą mogły popłynąć
w większej liczbie. Z drugiej strony, jeśli „przykręcimy kurek”, a jednak chcemy
uzyskać odpowiednio duży prąd, musimy zwiększyć wysokość, czyli napięcie.
„Pokonanie” takiego zaworu wymaga wykonania przez prąd pewnej pracy, co
oznacza spadek napięcia na rezystorze. Wartość potencjału przed rezystorem jest
większa niż za nim (rys. 12). Wróćmy na chwilkę do II prawa Kirchhoffa. Na ry-
sunku 10 przedstawione były właśnie takie spadki napięć. Gdyby obwód był zło-
żony tylko ze źródeł napięcia oraz rezystorów, to rysunek wyglądałby następują-
co: źródło napięcia przenosi prąd na odpowiednią wysokość, a każdy z rezystorów
przenosi prąd na niższy poziom.
Rezystancję można zmierzyć, a jej jednostką jest oczywiście Ohm [Ω]. Dane ciało
ma rezystancje jednego Ohma, gdy po przyłożeniu napięcia 1 V popłynie przez nie
prąd o wartości 1 A.
Mam nadzieje, że prawo Ohma nie ma już dla ciebie żadnych tajemnic, gdyż dość
często będziemy z niego korzystali. Jest ono bardzo proste, ale ma bardzo poważne
konsekwencje. Spróbuj samemu przeanalizować różne przypadki dotyczące tego,
w jaki sposób napięcie, prąd i rezystancja zależą od siebie.
Kiedy do wyrażenia opisującego moc (P = U · I) podstawimy prawo Ohma lub jego
przekształcenie (U = R · I), uzyskamy dwa ważne wyrażenia opisujące ilość mocy,
jaka wydziela się na rezystorze:
Interpretacja wzorów jest bardzo ważną umiejętnością, dlatego spójrz na powyższe
wzory i postaraj się samodzielnie zrozumieć, co one mówią. Przedyskutuj to z pro-
wadzącym zajęcia.
Wygodnie jest oznaczać prąd i napięcie strzałkami (rys. 12) — strzałka prądu po-
kazuje oczywiście kierunek przepływu prądu, natomiast strzałka napięcia poka-
zuje, gdzie jest wyższy potencjał. Podobnie jak w baterii, wyższy i niższy potencjał
możemy oznaczać przez + i –. Wówczas strzałka zawsze wskazuje +. Przez rezy-
stor prąd płynie od wyższego potencjału do niższego, zatem strzałka napięcie bę-
dzie miała odwrotny kierunek niż prądu (rys. 11). I tak będzie dla wszystkich ele-
mentów biernych.
Rysunek 11
Prawo Ohma
Rysunek 12
Prawo Ohma — oznaczenia

12
2. Bierne elementy elektroniczne
Zakończyliśmy już najnudniejszą, choć bardzo ważną część tego modułu. Przy-
pomnieliśmy sobie najważniejsze wielkości elektryczne oraz prawa nimi rządzące.
Czas wreszcie przejść od abstrakcji do konkretów. A więc spróbujmy wykorzystać
to, co już wiemy.
Elektronika to sterowanie wielkościami elektrycznymi. Aby sterować, potrzebuje-
my narzędzi, a najprostszymi narzędziami są właśnie elementy elektroniczne. I ni-
mi zajmiemy się teraz — oczywiście najpierw grupą najprostszych elementów, czyli
elementami biernymi. Pewnie zastanawiasz się, skąd wzięła się ta nazwa i co ona
oznacza? Spróbuję to wyjaśnić na przykładzie, którym — mam nadzieję — prze-
mówi do każdego. Wyobraź sobie, że idziesz do jakiegoś państwowego urzędu, za-
łatwić jakąś formalność. Wchodzisz do pokoju 107, a tam za biurkiem siedzi pani,
która od 20 lat udziela każdej wchodzącej osobie takiej samej odpowiedzi. I choć-
by stanął przed nią Albert Einstein, ze sprawą, o jakiej ona w życiu nie słyszała, to
i tak powie mu: „Formularze są na biurku przed pokojem, proszę wypełnić druko-
wanymi literami, zanieść do pokoju 211 i za dwa tygodnie przyjść do mnie po de-
cyzję”. Ta osoba jest bierna. Inny przykład — już przyjemniejszy. Wchodzisz do po-
rządnego banku, wita cię uśmiechnięta pani, która od razu pyta w czym może po-
móc. Mówisz, że chcesz założyć konto. Ona przygląda się tobie, widzi eleganckiego
człowieka sukcesu, obowiązkowo w garniturze z najnowszej kolekcji i z dobranym
pod kolor laptopem. I od razu wie, że za tego klienta dostanie niezłą premię, dlate-
go z miejsca proponuje ci konto dla VIP-ów, z wszystkimi udogodnieniami, jakich
tylko sobie życzysz. Oczywiście wie, że nie masz czasu, dlatego od razu przecho-
dzi do konkretów oferty, jednocześnie wypełniając za ciebie wszystkie formularze,
a ty tylko składasz podpis. Zaraz za tobą wchodzi starszy pan, emeryt, który chce
załatwić tę samą sprawę — założyć konto. Ona prosi, żeby usiadł, proponuje mu
kawę, opowiada o banku, o jego długoletniej historii, po czym proponuje konto dla
seniorów. Ta osoba jest aktywna.
Podobnie jest z elementami elektronicznymi. Elementy bierne to takie, które za-
wsze reagują tak samo na sytuację. Zawsze robią swoje i nic więcej. Oczywiście to
nic złego — takie elementy są bardzo potrzebne, pełnią ważne role w układach,
o czym za chwilę sam się przekonasz.
2.1. Rezystor
Najprostszym i chyba najczęściej stosowanym elementem biernym w elektronice
jest rezystor. Jest to po prostu element, który posiada określoną wartość rezystan-
cji. Przed chwilą poznaliśmy prawo Ohma, więc już wiesz, co to jest rezystancja.
Jednak przypomnę — jest to taki zawór na płynący prąd. Im większa rezystancja,
tym mniejszy prąd przy tym samym napięciu. Z prawa Ohma możesz wywniosko-
wać więcej — rezystor jest elementem biernym. Dlaczego? Ponieważ przykładasz
do niego określone napięcie, a on odpowiada określonym prądem i nic więcej.
Proponuję, żebyś przy najbliższej okazji poszedł do sklepu z elementami elektronicz-
nymi i poprosił o dowolny rezystor. Kosztuje on 5, maksymalnie 10 groszy. Zobacz
Rysunek 13
Rezystory
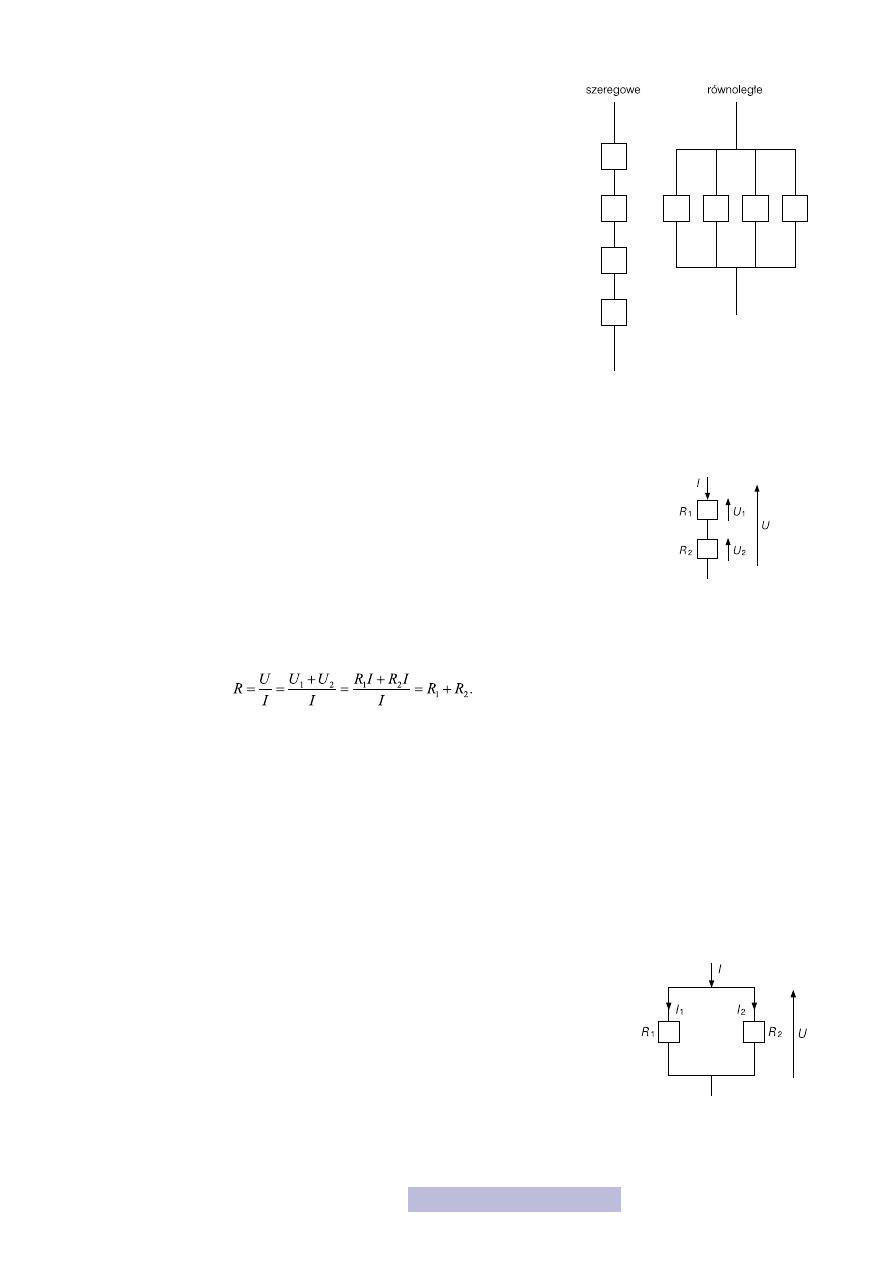
13
dokładnie jak wygląda. Ma dwa wyprowadzenia, do których przykładamy
napięcie i między którymi płynie prąd. Następnie przełam go — zobacz co
jest w środku. Istnieją różne typy rezystorów, ale najprawdopodobniej ten,
który kupiłeś to taka węglowa masa i nic więcej w nim ciekawego nie zoba-
czysz. To naprawdę prosty element. Jego symbol na schematach elektrycz-
nych to prostokąt z dwoma wyprowadzeniami.
Najważniejsze, co musisz wiedzieć o rezystorze, to to, że jeśli ma on rezy-
stancję R, a do końcówek przyłożysz napięcie U, to popłynie prąd I = U/R,
albo jeśli przez rezystor przepuścisz prąd I, to odłoży się na nim napięcie
R · I i to wszystko.
Rezystory możemy ze sobą łączyć i to na dwa sposoby (rys. 14):
— szeregowo, a więc jeden za drugim,
— równolegle, a więc jeden obok drugiego.
Czujesz chyba intuicyjnie, że połączenie szeregowe dwóch rezystorów musi
dać większą rezystancję, ponieważ wstawienie dwóch zaworów bardziej ograniczy
płynący prąd. Teraz zapewne zapytasz o ile.
Policzmy to! Załóżmy, że bierzemy dwa rezystory o rezystancji R
1
i R
2
i łączymy je
szeregowo (rys. 15).
Przypuśćmy, że przez ten układ płynie prąd o wartości I. Ponieważ nigdzie nie ma
żadnych rozgałęzień, więc z I prawa Kirchhoffa wynika, że taki sam prąd wpły-
wa do pierwszego rezystora, taki sam z niego wypływa i wpływa do drugiego, aż
w końcu taki sam wypływa na koniec z drugiego rezystora. Skoro tak, to — na
podstawie prawa Ohma — napięcie na pierwszym rezystorze wynosi: U
1
= R
1
· I, na
drugim U
2
=R
2
· I. Zatem — na podstawie II prawa Kirchhoffa — napięcie w całym
układzie wynosi U = U
1
+ U
2
. Z definicji rezystancja układu to napięcie podzielone
przez prąd, ostatecznie otrzymujemy zatem:
Powyższym wzór oznacza, że jeśli weźmiesz dwa rezystory o rezystancji R
1
i R
2
i połączysz je szeregowo, to efekt będzie taki sam, jakbyś w to miejsce włożył jeden
rezystor o rezystancji R = R
1
+ R
2
. Zobaczmy jak to wygląda w przykładach:
R
1
= 4 Ω, R
2
= 5 Ω, to R = R
1
+ R
2
= 4 Ω + 5 Ω = 9 Ω.
R
1
= 1000 Ω, R
2
= 2 Ω, to R = R
1
+ R
2
= 1000 Ω + 2 Ω = 1002 Ω ≈ 1000 Ω = R
1
.
Zwróć uwagę szczególnie na drugi przykład, gdyż przyda się on nam w dalszej czę-
ści kursu. Jeśli jeden z rezystorów jest dużo większy od drugiego, to rezystancja
szeregowego połączenia takich rezystorów jest praktycznie równa rezystancji tego
większego.
Analogicznie postąpimy przy połączeniu równoległym. Weźmy dwa rezystory R
1
i R
2
i połączmy je równolegle (rys. 16).
Przypuśćmy, że przykładamy napięcie U. Zgodnie z prawem Ohma, przez pierwszy
rezystor popłynie prąd I
1
= U/R
1
, a przez drugi I
2
= U/R
2
. Prądy te łączą się w jed-
nym węźle, więc — zgodnie z I prawem Kirchhoffa — prąd płynący przez cały
układ jest równy I = I
1
+ I
2
. Zbierając powyższe wzory oraz korzystając z definicji
rezystancji układu, ostatecznie otrzymujemy:
Rysunek 14
Połączenia rezystorów
Rysunek 15
Połączenie szeregowe
rezystorów
Rysunek 16
Połączenia równoległe
rezystorów

14
Zapiszmy to w bardziej czytelnej formie:
Jeśli przyjrzysz się dokładnie powyższemu wzorowi, zapewne dojdziesz do ważne-
go wniosku, a mianowicie: połączenie równoległe ma zawsze mniejszą rezystancję
niż każdy ze składowych rezystorów. Zresztą zobaczmy to na dwóch przykładach:
R
1
= 4 Ω, R
2
= 5 Ω, to
R
1
= 1000 Ω, R
2
= 2 Ω, to
Zwróć, podobnie jak poprzednio, uwagę na drugi z przykładów. Jeśli masz dwa re-
zystory — jeden o dużej, drugi o małej rezystancji, to rezystancja takiego połącze-
nia jest w przybliżeniu równa rezystancji mniejszego z nich. A więc odwrotnie niż
przy połączeniu szeregowym. Zapamiętaj te przykłady, gdyż niedługo będziemy ich
potrzebowali.
2.2. Kondensator
Drugim, niezwykle ważnym elementem biernym, stosowanym w elektronice jest
kondensator.
Mówiąc najprościej, kondensator to taki pojemnik na ładunki elektryczne. Dostar-
cza się mu ładunków, on gromadzi je w sobie i następnie, kiedy będzie potrzeba,
„odda” je. Jest to prosty element, choć już bardziej skomplikowany niż rezystor.
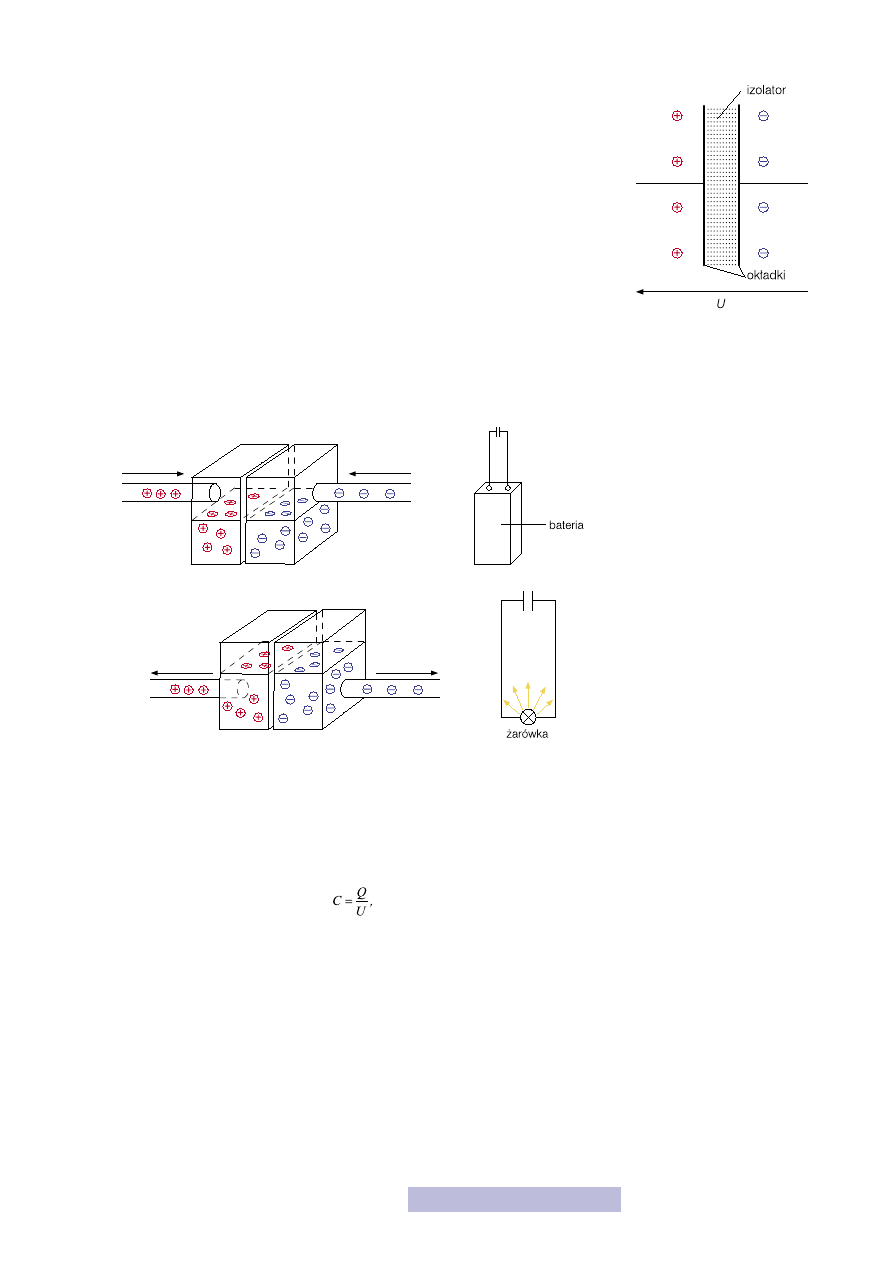
Na zewnątrz ma dwie elektrody, którymi dostarczamy i odbieramy ładunki (rys.
17). Wewnątrz zbudowany jest z dwóch okładek, oddzielonych materiałem izo-
lującym (rys. 18). Na jednej okładce magazynowane są ładunki dodatnie, na dru-
giej ujemne. Mówiąc precyzyjniej, w trakcie ładowania na jedną okładkę elektrony
są dostarczane, a z drugiej są usuwane. Natomiast w trakcie rozładowywania nad-
miar elektronów usuwany jest z jednej okładki, a na drugą dostarczane są braku-
jące elektrony.
Podobnie jak w przypadku rezystorów, proponuję ci w sklepie elektronicznym ku-
pić kilka kondensatorów, przyjrzeć im się z bliska, zobaczyć co jest w środku. Koszt
na pewno będzie większy niż w przypadku rezystorów, ale nie powinien przekro-
czyć kilku złoty. Tym razem nie powiem ci, co powinieneś zobaczyć, ponieważ jest
wiele różnych typów kondensatorów (rys. 17), a nie wiem, jakie kupisz. Najlepiej
poszukaj w Internecie informacji na jego temat. Niemniej jednak przedstawiona
powyżej zasada działania występuje w każdym, tylko w różny sposób są przecho-
wywane ładunki.
Rysunek 17
Kondensatory
15
Wyobraź sobie teraz, że do okładek przykładasz napięcie. Elektrony są umiesz-
czane na jednej okładce, z drugiej wyciągane. Umieszczanie kolejnych elektronów
jest coraz trudniejsze, ponieważ te, które już znajdują się na okładce, odpychają te,
które chcą na nią wpłynąć. Natomiast z drugiej okładki coraz trudniej wyciągnąć
elektrony, gdyż pozostające ładunki dodatnie je przyciągają. W pewnym momencie
ustala się pewien stan równowagi, co znaczy, że kolejnych ładunków nie można już
umieścić na okładkach. To jest właśnie stan naładowania kondensatora. Jeśli teraz
podniesiemy przyłożone napięcie, to do kondensatora „dopompowanych” zostanie
trochę ładunków, aż znowu uzyskamy stan naładowania. Natomiast, gdy napięcie
spadnie, rozpocznie się oddawanie ładunków do układu — rozładowywanie.
Proponuję proste doświadczenie. Kup kondensator o jak największej pojemności,
baterię 9 V oraz jak najmniejszą żarówkę. Następnie zewrzyj jedną elektrodę kon-
densatora z jedną elektrodą baterii, druga z drugą, potrzymaj chwilę (rys. 19). Tym
samym sprawisz, że kondensator naładuje się. Następnie do kondensatora podłącz
żarówkę (rys. 20). Jeśli wszystko jest w porządku, to zobaczysz krótkie mrugnięcie,
kondensator rozładuje się, a płynący prąd spowoduje na krótko świecenie żarówki.
Ważną własnością kondensatora jest pojemność. Pewnie myślisz, że pojemność to
po prostu maksymalna liczba ładunków, jaka mieści się w kondensatorze. Jednak
przed chwilą doszliśmy do wniosku, że liczba ładunków zależy od przyłożonego
napięcia. Skoro tak, to pojemność można zdefiniować jako stosunek liczby ładun-
ków do napięcia:
gdzie: C — pojemność, Q — ładunek, U — napięcie.
To bardzo ważny wzór i wynika z niego, że jeśli do kondensatora o pojemności C
przyłożymy napięcie U, to zgromadzi się w nim ładunek Q = C · U. Natomiast, gdy
w tym kondensatorze umieścimy ładunek Q, to napięcie między jego elektrodami
będzie wynosiło U = Q/C. Zapamiętaj te zależności.
Zapewne zastanawiasz się teraz: „Kondensator, to dwie okładki przedzielone izo-
latorem. Od czego zależy wiec jego pojemność?”. Odpowiedzią jest wzór, który
podam poniżej.
Rysunek 18
Budowa i działanie
kondensatora
Rysunek 19
Ładowanie kondensatora
Rysunek 20
Rozładowanie kondensatora

16
gdzie: ε — stała dielektryczna izolatora, S — powierzchnia okładek, d — odległość
między okładkami.
Ten zagadkowy ε, to po prostu pewna stała związana z materiałem, jaki został uży-
ty do wykonania dielektryka. Natomiast ze wzoru wynika, że pojemność jest tym
większa, im większa jest powierzchnia okładek i im bliżej siebie one leżą.
2.3. Cewka
Ostatnim elementem biernym jest cewka. Nie będę tutaj omawiał tego elementu ze
względu na znikome znaczenie dla mikroelektroniki. Chciałbym tylko, abyś wie-
dział, że coś takiego istnieje. Cewka, podobnie jak kondensator magazynuje ener-
gię, którą później może oddać do układu. Cewką najczęściej jest skręcony w sprę-
żynkę drut.
2.4. Proste układy z elementami biernymi
Poznałeś już najprostsze elementy stosowane w elektronice. Najwyższy czas zbudo-
wać za ich pomocą jakieś układy. Będą to dwa proste układy składające się tylko
z rezystorów i kondensatorów.
Dzielnik napięciowy
W pierwszym temacie powiedzieliśmy sobie, że układ elektroniczny służy do prze-
twarzania wielkości elektrycznych, a więc podajemy wielkość (wielkości) na wej-
ście i uzyskujemy wielkość (wielkości) na wyjściu. I w taki sposób należy rozpocząć
analizę każdego układu.
Pierwszym układem, który zbudujemy będzie dzielnik napięciowy.
Jak sama nazwa wskazuje, jego zadaniem będzie podzielenie na-
pięcia wejściowego. A więc na wejście podajesz napięcie, a na wyj-
ściu uzyskujesz jakąś część tego napięcia (rys. 21). Zanim przejdzie-
my dalej, spróbuj samodzielnie pomyśleć, jak wykonać taki układ.
Podpowiem, że wystarczy wziąć dwa rezystory i wykorzystać pra-
wo Ohma. Pomyśl nad tym trochę.
Mam nadzieję, że udało ci się! Poniżej znajduje się moja propozycja takiego układu
(rys. 22). Myślę, że twoja jest bardzo podobna, ponieważ chyba niczego więcej nie
można stworzyć z dwóch rezystorów. Przeanalizujmy ten układ.
Rysunek 21
Dzielnik napięciowy
— zasada działania
Rysunek 22
Dzielnik napięciowy — schemat
17
Napięcie wejściowe (U
we
) podajemy na dwa szeregowo połączone rezystory, oznaczo-
ne na rysunku jako R
1
i R
2
. Rezystancja takiego układu rezystorów wynosi R
1
+ R
2
.
Zatem zgodnie z prawem Ohma w układzie popłynie prąd I = U
we
/(R
1
+ R
2
). Jeśli
masz wątpliwości dotyczące tego, czemu tak jest, przypomnij sobie prawo Ohma.
Napięciem wyjściowym (U
wyj
) jest napięcie na rezystorze R
2
. Przez ten rezystor pły-
nie policzony przed chwilą prąd I, a więc to napięcie jest równe: U
wyj
= R
2
· I. Po
podstawieniu otrzymujemy:
Powyższy wzór nie pozostawia już żadnych wątpliwości, napięcie wyjściowe U
wyj
stanowi część napięcia wejściowego U
we
. Jaką część? R
2
/(R
1
+ R
2
) napięcia wejścio-
wego.
Policzmy, jak zachowuje się nasz układ w konkretnych przykładach.
Na początek niech R
1
= 1 Ω, a R
2
= 3 Ω. Wówczas: U
wyj
= 0,75 · U
we
— czyli, jeśli
podasz np. 4 V, to na wyjściu uzyskasz 3 V.
Teraz dwa przykłady, które proponuję zapamiętać, ponieważ będą nam później po-
trzebne:
R
1
= 1000 Ω, R
2
= 1 Ω. Wówczas: U
wyj
≈ 0,001 · U
we
. Oznacza to, że dla napięć wej-
ściowych rzędu kilku woltów napięcie wyjściowe jest praktycznie równe 0 V.
R
1
= 1 Ω, R
2
= 1000 Ω. Wówczas: U
wyj
= 0,999 · U
we
. Oznacza to, że napięcie wyj-
ściowe jest praktycznie równe napięciu wejściowemu.
Z powyższych przykładów chciałbym, abyś zapamiętał, że jeśli w dzielniku napię-
ciowym rezystory bardzo różnią się od siebie wartością, to na wyjściu albo mamy
0 V albo napięcie wejściowe.
Układy RC
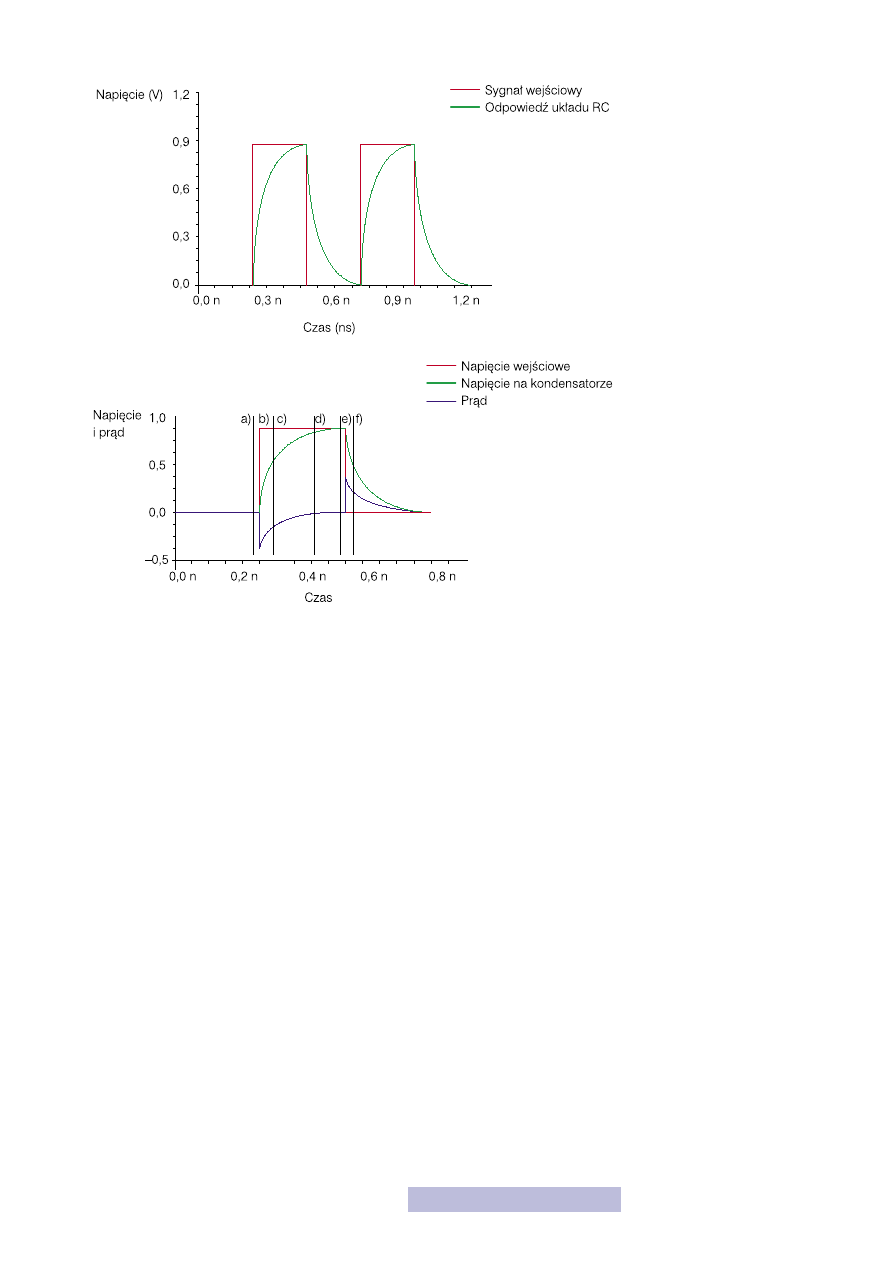
Drugim układem, a właściwie dwoma układami, które przeanalizujemy, będą tzn.
układy RC. Tym razem niczego nie będziesz musiał projektować. Przeanalizujemy
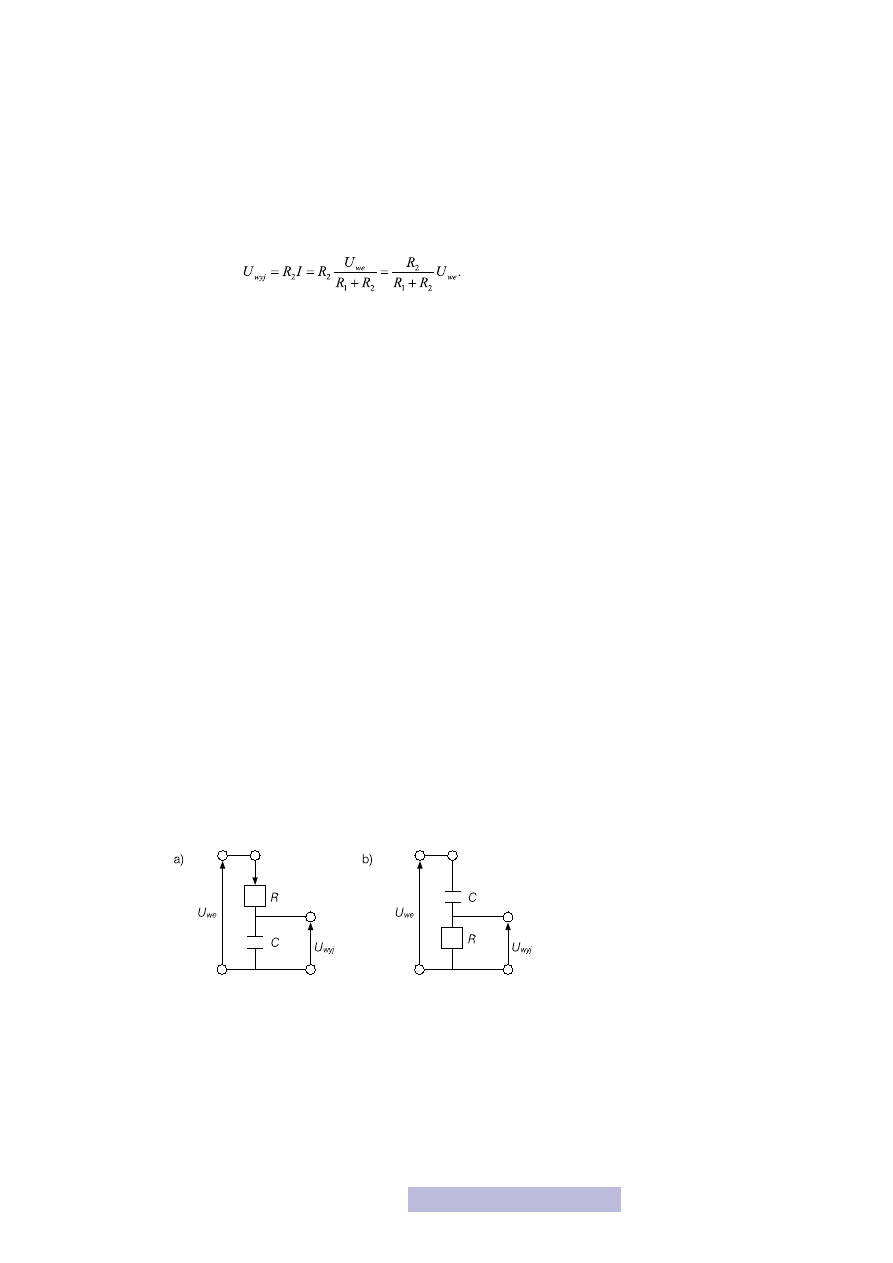
tylko zachowanie tych układów i zastanowimy się, do czego można ich użyć. Układ
RC to szeregowe połączenie rezystora i kondensatora (rys. 23). W obu przypad-
kach napięcie wejściowe podajemy na oba elementy. Natomiast wyjściem w przy-
padku a) jest napięcie na kondensatorze, a w b) na rezystorze.
Skupmy się najpierw na układzie pierwszym. Wyobraź sobie, że do układu na wej-
ście podłączasz zmienny przebieg prostokątny (rys. 7d). W dzielniku napięciowym
po podaniu napięcia na wejście błyskawicznie otrzymywaliśmy odpowiedź na wyj-
ściu. A co będzie działo się w tym przypadku? Porównuj każdy opisany poniżej
krok z rysunkiem 25.
Rysunek 23
Układy RC
18
W kondensatorze nie ma ładunków, a — jak pamiętasz — napięcie na kondensa-
torze jest proporcjonalne do liczby ładunków: U = Q/C. I dopóki to napięcie na
wejściu wynosi 0 V, to nic się nie dzieje (a). Jednak po chwili to napięcie skacze do
ustalonej wartości (b). Prąd w obwodzie zaczyna płynąć, ładunki są dostarczane do
kondensatora. Jednak na drodze prądu pojawia się zawór — rezystor, który ogra-
nicza prąd. Mimo to ładunki docierają do kondensatora i napięcie na nim zaczy-
na rosnąć. Z upływem czasu coraz więcej ładunków jest w kondensatorze i coraz
trudniej dopłynąć nowym (c). Dlatego prąd maleje i napięcie coraz wolniej rośnie.
W końcu kondensator jest naładowany, prąd przestaje płynąć i na kondensatorze
napięcie jest takie samo jak na wejściu (d). Taki stan trwa dopóki napięcie nie spad-
nie znowu do zera (e). Kondensator zaczyna się rozładowywać. Najpierw prąd jest
duży, ponieważ dużo ładunków znajduje się w kondensatorze (f). Ponieważ dużo
ładunków wypływa, to napięcie szybko spada. W pewnym momencie ładunki wy-
czerpią się i wracamy do stanu takiego jak na początku (a) i wszystko zaczyna się
od nowa. Cały omówiony przebieg możesz zobaczyć na wykresie (rys. 24).
Do czego może służyć taki układ? Choćby do wprowadzenia dodatkowego opóź-
nienia. Wyobraź sobie, że masz dwa urządzenia i jedno ma się włączyć jako pierw-
sze. Wówczas taki prosty układ jest bardzo przydatny. Do jednego urządzenia
doprowadzasz napięcie bezpośrednio, a do drugiego przez ten układ. Włączasz
i pierwsze urządzenie zaczyna działać. Drugie włącza się dopiero wtedy, gdy nała-
duje się kondensator i napięcie na nim będzie zbliżone do wyjściowego. Ta właśnie
cecha układu RC, czyli opóźnianie sygnału, będzie potrzebna w dalszej części kur-
su. Opóźnienie jest tym większe, im większy jest rezystor — co chyba oczywiste
— wówczas ładunki wolniej dopływają do kondensatora. Również opóźnienie jest
tym większe, im większy jest kondensator, gdyż uzyskanie napięcia wymaga więk-
szej liczby ładunków.
Rysunek 24
Odpowiedzi układów RC
na skok napięcia
Rysunek 25
Analiza układu RC

19
Na koniec omówmy jeszcze krótko układ drugi. Otóż w tym przypadku wszystko
przebiega dokładnie tak samo jak poprzednio, z tą różnicą, że napięciem wyjścio-
wym jest napięcie na rezystorze. Z prawa Ohma wiadomo, że napięcie na rezysto-
rze jest wprost proporcjonalne do prądu. A więc już wszystko powinno być jasne
(rys. 25). Najpierw prąd jest duży, zatem napięcie wyjściowe w momencie włącze-
nia ma najwyższą wartość, a następnie spada do zera. I to wszystko. Prawda, że
proste?
20
3. Czynne elementy elektroniczne
Poznałeś już najważniejsze bierne elementy elektroniczne — dzięki nim udało ci się
nawet skonstruować działające układy elektroniczne. Fakt, że proste, ale przecież
nikt nie mówił, że będzie trudno. Te dwa układy wykorzystamy już w następnym
module i to do konstrukcji „czegoś”, co jest w każdym procesorze! Skoro już znasz
elementy bierne, potrafisz się nimi posługiwać, czas poznać elementy czynne.
Elementy czynne to elementy elektroniczne, które potrafią zmieniać swoje działa-
nie w zależności od warunków, w jakich pracują. Dla porównania, nasz rezystor
ograniczał prąd i niewiele go obchodziło, w którą stronę ten prąd płynie, ani jak
jest duży. Miał ograniczać, to ograniczał — i to zawsze. Ważny, lecz mało ciekawy
przypadek. Elementy czynne już takie bezkrytyczne nie będą — będą zaintereso-
wane tym, co dzieje się w układzie i w zależności od tego różnie mogą działać.
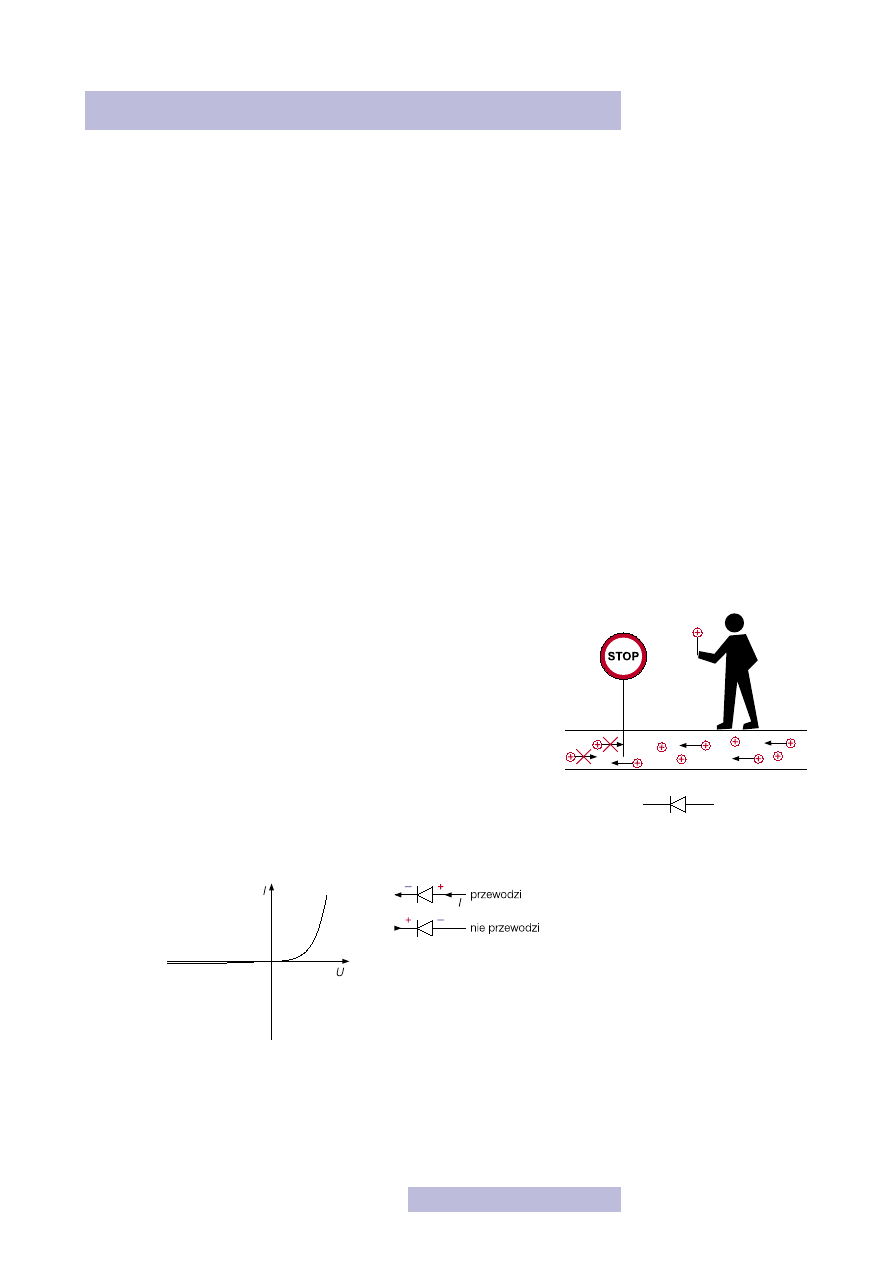
3.1. Dioda
Najprostszym elementem czynnym jest dioda. Potrafi ona niewiele, ale jakże ważne
jest jej zadanie. Otóż przepuszcza ona prąd tylko w jedną stronę! A więc dioda za-
pewnia nam jeden kierunek przepływu prądu. Dioda wygląda bardzo
podobnie jak rezystor (rys. 26), też ma dwie elektrody — anodę i kato-
dę. W rezystorze było jednak obojętne, do której elektrody przyłożymy
wyższy czy niższy potencjał — przewodził on w obu kierunkach. W dio-
dzie już tak nie jest. Jeśli do anody przyłożysz większy potencjał (+) niż
do katody (–), to dioda przewodzi prąd, jeśli odwrotnie — nie przewo-
dzi. I to jest właściwie cała tajemnica tego elementu. Na schemacie dio-
da oznaczana jest jako trójkącik skierowany „w mur” (rys. 27). Jeśli prąd
płynie tak jak pokazuje trójkącik, to wszystko w porządku, „mur” zosta-
je przebity. Natomiast, gdy chce płynąć odwrotnie, trafia na przeszkodę
i płynąć nie może. Kiedy przyjrzysz się dokładniej symbolowi diody, zo-
baczysz po stronie tego „muru” K, które symbolizuje umiejscowienie katody. Wiel-
kiego wyboru nie ma — druga elektroda musi być anodą.
Bardzo ważnym narzędziem w elektronice są charakterystyki — czy to elementów,
czy całych układów. Dość często będziemy je wykorzystywać i za ich pomocą bę-
dziemy przeprowadzali analizy. Dlatego ważne jest, abyś oswoił się z charaktery-
stykami i nauczył się je czytać.
Rysunek 26
Dioda i jej działanie
Rysunek 27
Charakterystyka
prądowo-napięciowa
diody prostowniczej
21
Na rysunku 27 została przedstawiona przykładowa charakterystyka prądowo-na-
pięciowa diody. Na poziomej osi mamy napięcie U
AK
, a na osi pionowej mamy prąd
I, płynący przez diodę. Napięcie U
AK
to oczywiście napięcie między anodą i katodą.
Spójrzmy najpierw na lewą część wykresu — tam napięcie U
AK
jest ujemne, a więc
na anodzie jest niższy potencjał niż na katodzie. Mówiąc prościej, na katodzie jest
plus, a na anodzie minus, wówczas — jak wiemy z opisu działania diody — jest ona
w stanie zaporowym i nie przewodzi prądu. I to widać na charakterystyce — prąd
I jest równy zero. Odwróćmy sytuację, napięcie U
AK
staje się dodatnie, a więc na
anodzie jest wyższy potencjał (+) niż na katodzie (–) — dioda jest w przewodzeniu.
Jednak spójrz, jak wygląda to na charakterystyce. Najpierw, mimo że napięcie jest
dodatnie, dioda nie przewodzi prądu. Napięcie dalej rośnie i w pewnym momencie
dioda zaczyna przewodzić. Napięcie, przy którym dioda zaczyna przewodzić nazy-
wamy napięciem progowym (dla diod krzemowych wynosi ono ok. 0,7 V). Potem
napięcie zmienia się już niewiele, a prąd gwałtownie rośnie, dioda już „pełną parą”
przewodzi prąd.
Zapewne zastanawiasz się, do czego służy dioda? No cóż, gdybym miał omówić
choćby część zastosowań diod, to na pewno do końca całego kursu nie przeczy-
tałbyś o niczym innym. Wspomnę jedynie o dwóch najważniejszych. Pierwszym,
chyba najbardziej naturalnym zastosowaniem, jest prostowanie przebiegów zmien-
nych. Drugim zastosowaniem, niezwykle ważnym z punktu widzenia mikroelek-
troniki, jest stabilizacja napięcia. Za pomocą diod można skonstruować układ, któ-
ry ustabilizuje napięcie, a więc zabezpiecza przed jego nagłymi i dużymi zmianami.
Buduje się go w oparciu o diody Zenera.
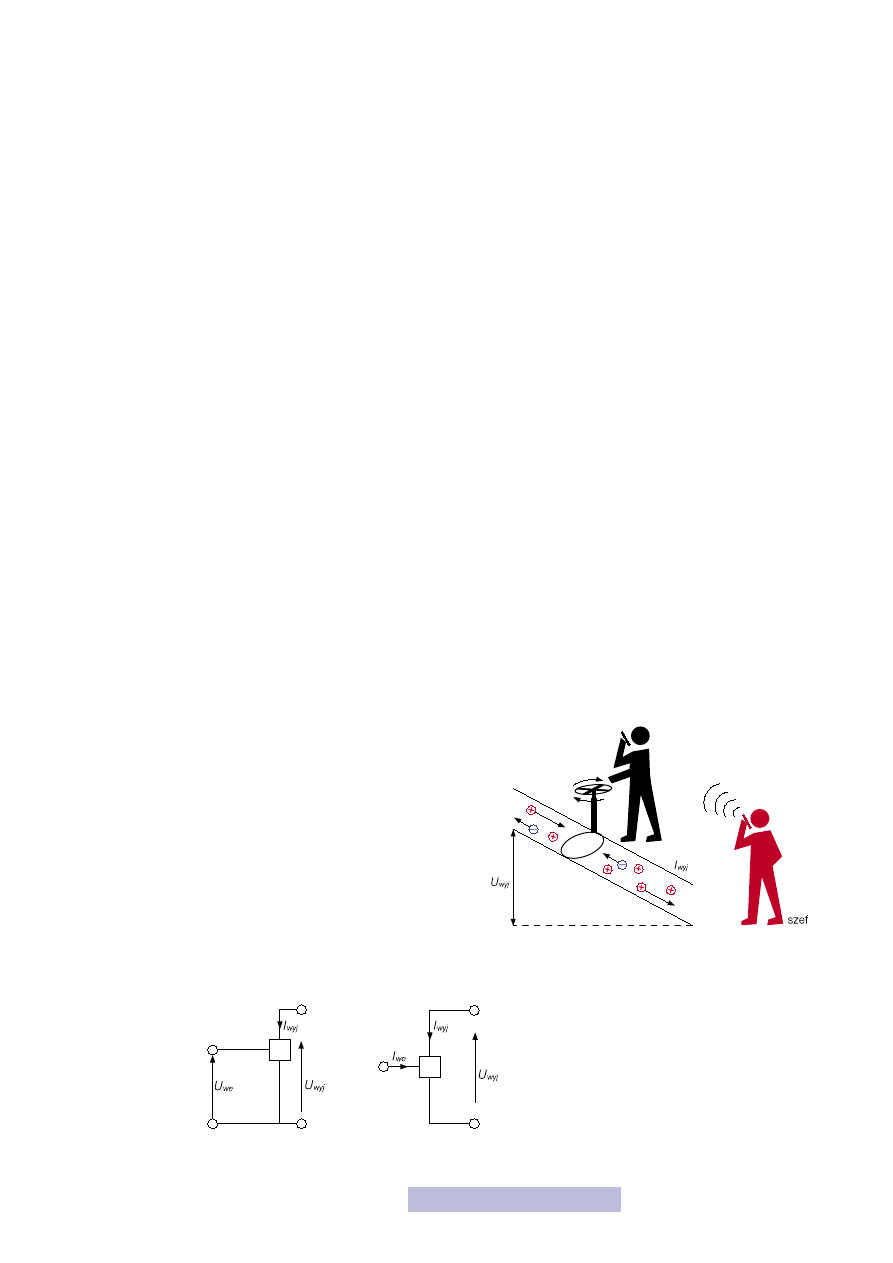
3.2. Tranzystor
Wiesz już jak działa i do czego może służyć dioda. Przypomnę, że jej zadaniem
jest przepuszczanie prądu w jedną stronę, a w drugą blokowanie. Jednak przepusz-
czanie prądu w pewnych warunkach, a w innych nie, to dla
nas za mało. Chcielibyśmy jeszcze mieć kontrolę nad tym, ile
tego prądu przepuszczamy. A więc chcemy mieć taki „kurek”
na prąd (rys. 28), który można w razie potrzeby mocniej od-
kręcić, ewentualnie przykręcić, albo nawet w ogóle zakręcić.
Takim właśnie „kurkiem” jest rezystor, a regulowanym „kur-
kiem” jest najważniejszy element w elektronice — tranzystor.
Nazwa tranzystor pochodzi od złożenia dwóch słów:
trans-
fer re
sistor
, a więc sterowana rezystancja. To fantastyczne
urządzenie, które odpowiada za obserwowany postęp, to naj-
ważniejszy składnik każdego układu mikroelektronicznego.
W każdym komputerze znajdują się obecnie setki milionów
tranzystorów. Zanim jednak zaczniemy budować układy złożone z milionów tych
elementów, przyjrzyjmy się najpierw, jaka jest zasada ich działania (rys. 29).
Rysunek 28
Idea działania tranzystora
Rysunek 29
Zasada działania tranzystora
22
W tej chwili chciałbym, abyś traktował tranzystor jako taką „czarną skrzynkę”. Co
znajduje się w środku, dowiesz się już w czwartym module. Ba poznasz nawet jak
się taką „czarną skrzyneczkę” wykonuje!
Tranzystory dzielimy na dwie grupy:
— tranzystory bipolarne,
— tranzystory unipolarne.
Z punktu widzenia współczesnej mikroelektroniki oraz niniejszego kursu intereso-
wać nas będą wyłącznie tranzystory unipolarne i to też nie wszystkie, lecz tylko ich
wybrana grupa — tranzystory MOS. Niemniej jednak przyjrzymy się teraz krótko
obu grupom.
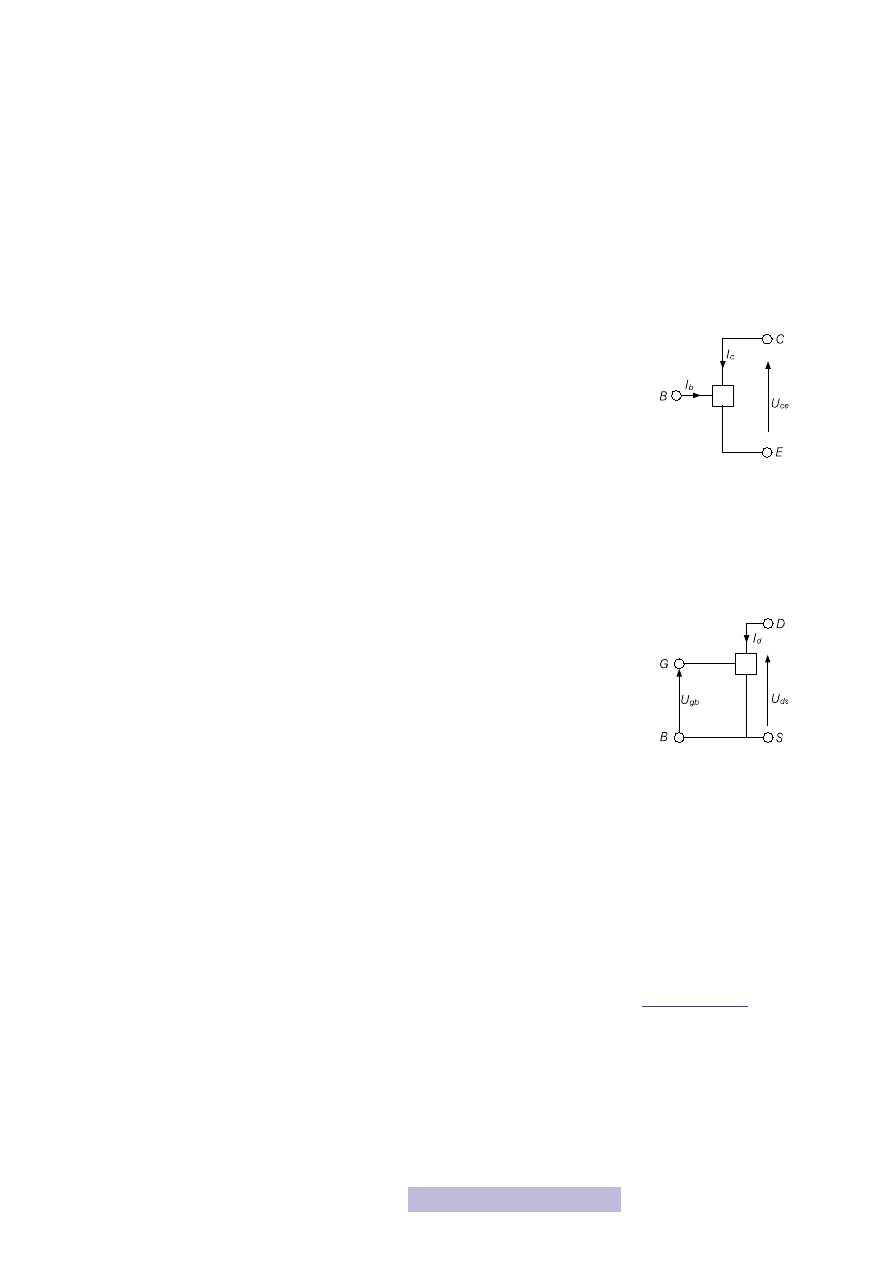
Tranzystory bipolarne
Tranzystory bipolarne mają najczęściej trzy elektrody, nazwane: baza (B), kolektor
(C) i emiter (E). Wejściem w tych tranzystorach jest prąd płynący przez elektrodę
bazy. Natomiast wyjściowa rezystancja znajduje się między elektrodami kolektora
i emitera (rys. 30). Zatem jeśli przez elektrodę bazy nie przepływa żaden prąd, to
tranzystor jest wyłączony, między elektrodami kolektora i emitera występuje bar-
dzo duża rezystancja, a więc praktycznie nie płynie prąd miedzy emiterem a kolek-
torem. Natomiast, gdy prąd zaczyna płynąć przez bazę, to rezystancja zmniejsza
się i prąd między emiterem a kolektorem również zaczyna płynąć. Im więcej prą-
du płynie przez bazę, tym mniejsza jest rezystancja, czyli tranzystor jest bardziej
„otwarty” — to cała tajemnica jego działania. Jako że ten typ tranzystorów ma ra-
czej niszowe zastosowanie w mikroelektronice, nie będziemy się nim więcej zajmo-
wać. Najważniejsze, żebyś wiedział, że takie tranzystory istnieją i że są sterowane
prądem bazy.
Tranzystory unipolarne
Drugą, o wiele ważniejszą z punktu widzenia mikroelektroniki, grupę tranzysto-
rów stanowią tranzystory unipolarne (rys. 31). Mają one najczęściej trzy elektrody
2
nazwane: bramka (G od ang. gate), źródło (S od ang. source) oraz dren (D od ang.
drain). A więc już same nazwy elektrod są zupełnie inne niż w tranzystorze bipolar-
nym. Jednak dużo ważniejsza różnica tkwi w sterowaniu tymi tranzystorami. Otóż
tranzystory unipolarne są sterowane za pomocą potencjału na elektrodzie bramki!
Zmieniając ten potencjał, zmienia się rezystancja między źródłem a drenem. I to
jest jedna z najważniejszych różnic i jednocześnie bardzo ważna przyczyna ich sto-
sowania w mikroelektronice. Sterowanie napięciem jest zdecydowanie łatwiejsze
niż prądem.
W przypadku tranzystorów bipolarnych sytuacja była prosta — jeśli prąd płynął
przez bazę, to tranzystor przewodził, jeśli nie płynął — nie przewodził. W tranzy-
storach unipolarnych nie jest to takie proste. Wszystko zależy od typu tranzystora
— np. możesz podać zerowe napięcie sterujące i jeden typ tranzystora będzie prze-
wodził, a drugi nie.
Tranzystory unipolarne to ogromna i bardzo zróżnicowana grupa przyrządów. Na
szczęście my będziemy zajmować się tylko jednym — najważniejszym z punktu wi-
dzenia mikroelektroniki — tranzystorem MOS.
Rysunek 30
Tranzystor bipolarny
Rysunek 31
Tranzystor unipolarny
2
Za chwilę przekonasz się,
że najważniejszy dla
mikroelektroniki tranzy-
stor MOS ma cztery elek-
trody. Czwarta elektroda
jest najczęściej zwarta do
źródła lub drenu, dlatego
stwierdzenie to nadal
pozostaje w mocy.
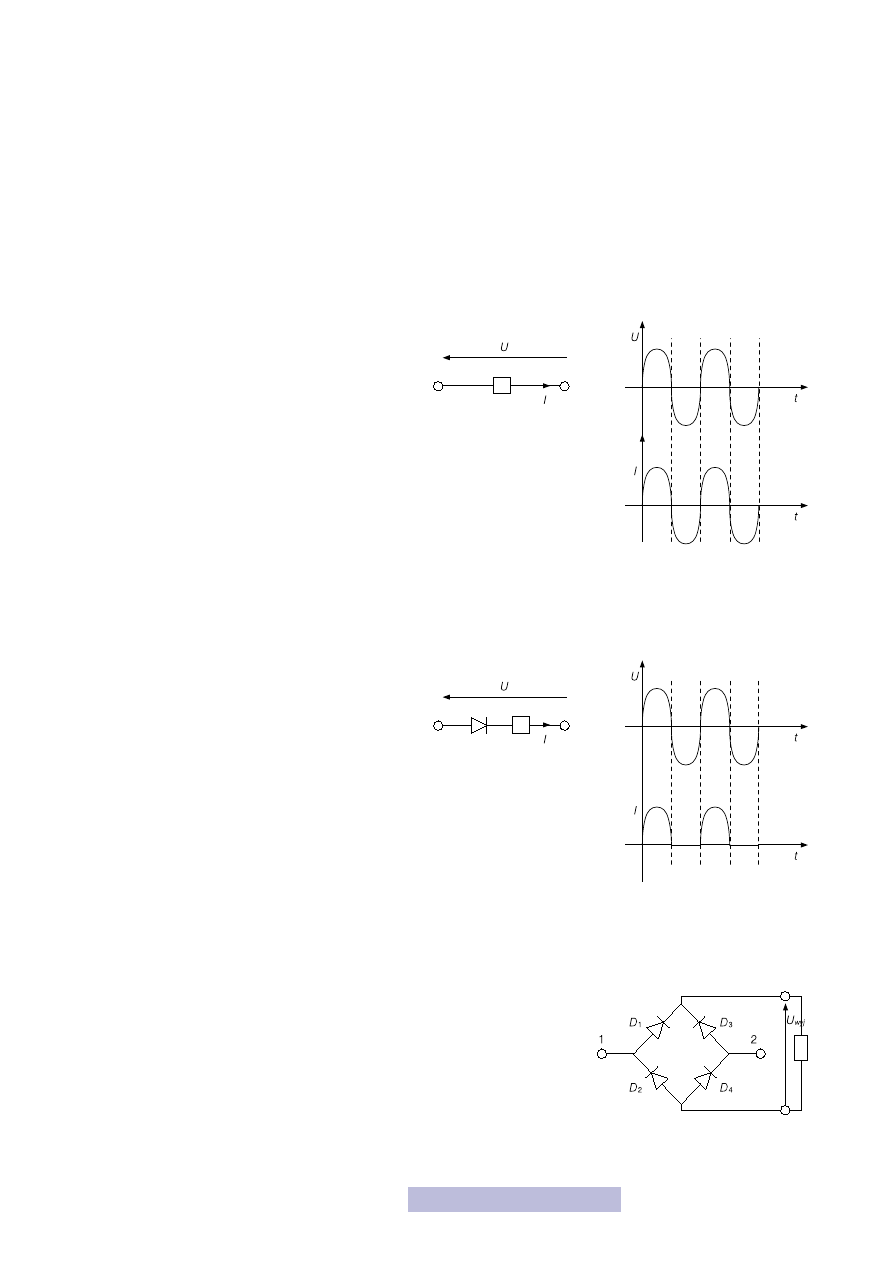
23
3.3. Proste układy z elementami aktywnymi
Na koniec chciałbym pokazać dwa proste układy elektroniczne wykorzystujące ele-
menty aktywne. Pierwszym będzie układ prostownika i jego modyfikacja, a drugim
przełącznik tranzystorowy. Chciałbym, abyś dokładnie przeanalizował te układy.
Prostownik
Naszym zadaniem jest zbudowanie układu prostującego płynący prąd. Załóżmy, że
mamy źródło napięcia przemiennego — niech to będzie zwykłe gniazdko w ścia-
nie. Napięcie w gniazdku jest przemiennym przebiegiem, zmieniającym swoją war-
tość po sinusoidzie od –311 V do +311 V. Jeśli napięcie między punktem A i B jest
dodatnie, oznacza to, że punkt A ma wyższy poten-
cjał niż B. Natomiast gdy napięcie jest ujemne, ozna-
cza to, że wyższy potencjał ma punkt B, a niższy A.
I tak należy rozumieć znak przy napięciu.
Podłączymy teraz rezystor do gniazdka. Przebieg na-
pięcia i prądu na rezystorze pokazany został na ry-
sunku 32. Zgodnie z prawem Ohma prąd jest wprost
proporcjonalny do napięcia, a więc gdy napięcie jest
dodatnie płynie w jedną stronę, gdy ujemne w dru-
gą. Oznaczmy przepływ prądu w jedną stronę jako
prąd dodatni, a w drugą jako ujemny. Naszym zada-
niem jest wykonanie takiego układu, w którym prąd
płynął będzie tylko w jedną stronę.
Naturalnym rozwiązaniem jest wstawienie do układu diody. Wiadomo, że prze-
puszcza ona prąd tylko w jedną stronę. Wstawmy ją szeregowo do układu (rys. 33).
W zależności od tego, w którą stronę ją wstawimy, będzie blokowała albo ujemny,
albo dodatni prąd. W naszym układzie wstawiliśmy
ją tak, aby blokowała ujemny prąd. Wynik działa-
nia takiego układu został pokazany na rysunku 33.
Przeanalizujmy dokładnie jego działanie i odpowie-
my na pytanie skąd biorą się przedstawione przebie-
gi. Kiedy na układ podawane jest napięcie dodatnie,
to po lewej stronie (punkt 1) jest wyższy potencjał
niż po prawej (punkt 2), zatem na anodzie diody wy-
stępuje wyższy potencjał niż na katodzie. Dioda jest
więc w stanie przewodzenia i przepuszcza prąd. Prąd
przez nią przepływa, jest ograniczany tylko przez re-
zystor. Natomiast gdy napięcie na układzie jest ujem-
ne, to po prawej stronie jest wyższy potencjał niż po
lewej, zatem na anodzie jest niższy potencjał niż na katodzie, dioda jest w stanie
blokowania prądu. Spróbuj teraz samodzielnie przeanalizować układ, w którym
dioda została wstawiona odwrotnie.
Oczywiście możesz od razu powiedzieć, że to marny prostownik, ponieważ
— owszem — prąd płynie w jedną stronę, ale są momenty, kiedy w ogóle nie pły-
nie. To fakt i dlatego w praktyce do prostowania wykorzystuje się tzw. mostek
Gretza. Jest to układ czterech diod, połączonych jak na rysunku 34. Przeana-
lizujmy działanie tego układu. Kiedy podawane jest napięcie dodatnie (wyż-
szy potencjał w punkcie 1 niż 2), to po lewej stronie jest wyższy potencjał niż
po prawej. Zatem prąd może przepłynąć przez diodę D
1
, rezystor i diodę D
4
.
W przypadku, gdy napięcie jest ujemne, po lewej stronie jest niższy potencjał
niż po prawej. Zatem prąd może przepłynąć przez diodę D
3
, rezystor i diodę
D
2
. Tym razem otrzymaliśmy zdecydowanie lepszy prostownik.
Rysunek 32
Przebieg napięcia i prądu
na rezystorze
Rysunek 33
Układ prostownika
i jego przebiegi
Rysunek 34
Mostek Gretza
24
Przełącznik tranzystorowy
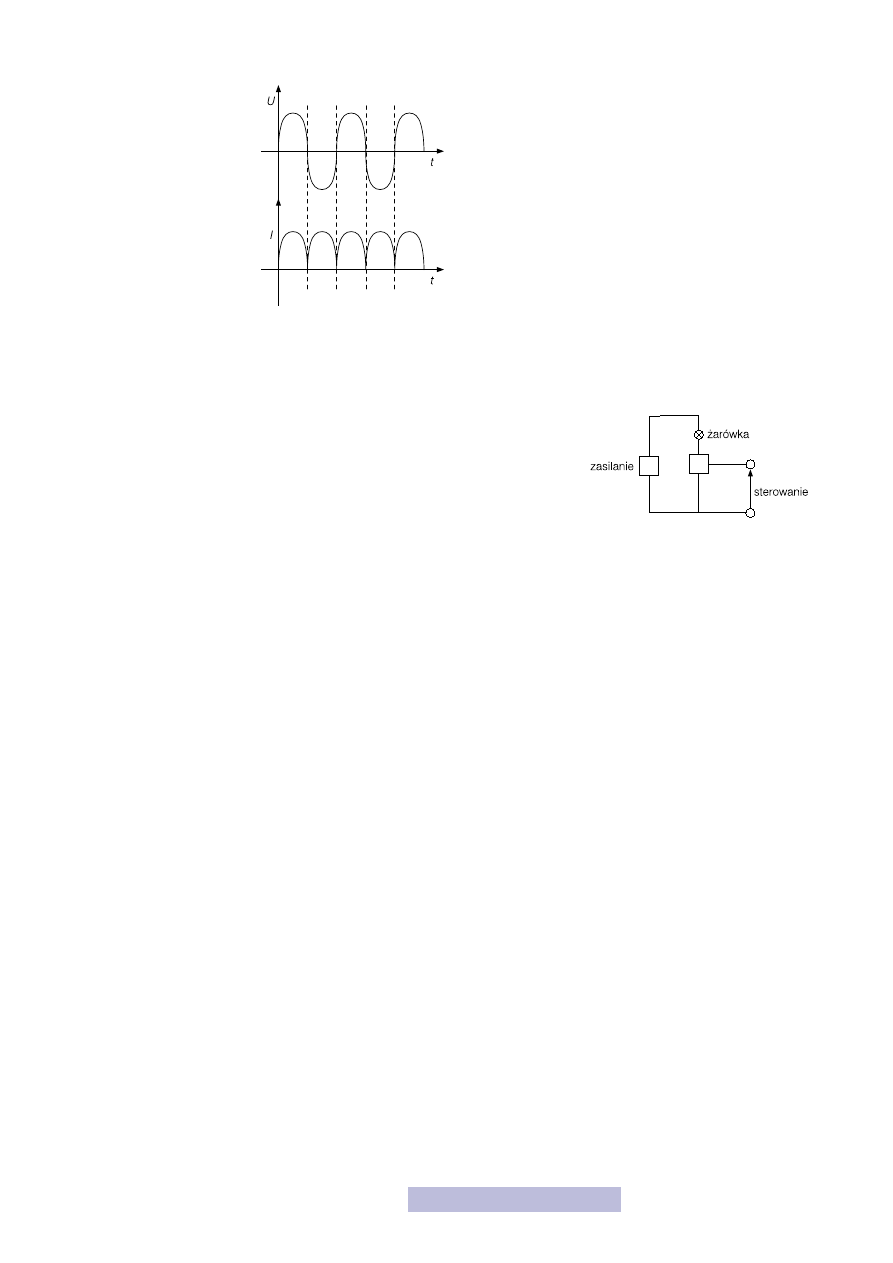
Na koniec chciałbym pokazać niezwykle ważny układ, a mianowicie klucz tranzy-
storowy. Zadanie tego układu jest bardzo proste — jest to taki elektroniczny włącz-
nik. Dokładnie taki sam, jaki na ścianie, służący do włączania światła. Różnica po-
lega na tym, że aby go włączyć lub wyłączyć podamy odpowiednie napięcie.
Kiedy podłączysz żarówkę do napięcia zasilania, będzie świeciła cały czas,
a nie o to nam chodzi.
Na pewno łatwo poradziłbyś sobie z tym problemem — znasz już bowiem
taki element jak tranzystor. Jako że chcemy sterować napięciem, bierzemy
odpowiedni tranzystor unipolarny i wstawiamy go w szereg z żarówką. Po-
dajesz pewne napięcie sterujące na tranzystor, tak aby jego rezystancja była bar-
dzo mała. Wówczas tranzystor bez przeszkód przewodzi prąd, a żarówka świeci.
Następnie podajesz takie napięcie, aby rezystancja tranzystora była bardzo duża.
Wówczas prąd w obwodzie praktycznie nie płynie, a żarówka przestaje świecić.
Proste, ale niezwykle ważne!
Rysunek 35
Przebieg prądu i napięcia
w układzie z mostkiem Gretza
Rysunek 36
Klucz tranzystorowy

25
Podsumowanie
W niniejszym module przebyłeś długą drogę. Zaczynałeś od absolutnych podstaw,
a więc od pojęcia ładunku, prądu i napięcia. Choć są to pojęcia powszechnie znane,
jednak ich dokładne i precyzyjne zrozumienie stanowi podstawę. Czemu? Ponie-
waż elektronika to nauka o przetwarzaniu tych wielkości i pojęciami tymi będzie-
my ciągle operowali. Następnie poznałeś podstawowe prawa mówiące jak te wiel-
kości zależą od siebie i jak można je przetwarzać. W dalszej części poznałeś naj-
prostsze bierne elementy pozwalające przetwarzać wielkości elektryczne, a miano-
wicie rezystor oraz kondensator. To bardzo proste, ale zarazem bardzo ważne ele-
menty, z których będziemy często korzystać. Za ich pomocą zbudowałeś proste, ale
niezwykle ważne układy dzielnika napięciowego oraz RC. Z tych układów skorzy-
stamy już w następnym module. Chciałem, abyś zobaczył jak konstruuje się układy,
z czego się składają i na czym polega przetwarzanie w nich wielkości elektrycznych
oraz to, co jest wejściem, a co wyjściem i jak analizować takie układy.
Na koniec poznałeś dwa najważniejsze elementy aktywne — diodę i tranzystor.
Od tego momentu zaczyna się ta właściwa elektronika. Oczywiście stwierdzenie,
że poznałeś te elementy jest mocno przesadzone, gdyż jedynie opisałem jakościową
zasadę ich działania. Niemniej jednak wiesz już to, co najważniejsze — że tranzy-
stor to sterowany rezystor o bardzo dużym zakresie zmian rezystancji. Co więcej,
za pomocą tych elementów zbudowaliśmy proste, ale działające układy.

26
Bibliografia
1. Beck R., 1991: Technologia krzemowa, PWN, Warszawa.
2. Europractice. Witryna internetowa.
, stan z 26 wrze-
śnia 2006 r.
3. IBM. Witryna internetowa.
, stan z 26 września 2006 r.
4. Intel. Witryna internetowa.
, stan z 26 września 2006 r.
5. International Technology Roadmap for Semiconductors. Witryna internetowa.
, stan z 26 września 2006 r.
6. Kalisz J., 1998: Podstawy elektroniki cyfrowej, Wydawnictwa Komunikacji
i Łączności, Warszawa.
7. Marciniak W., 1984: Przyrządy półprzewodnikowe i układy scalone, Wydaw-
nictwa Naukowo-Techniczne, Warszawa.
8. Marciniak W., 1991: Przyrządy półprzewodnikowe MOS, Wydawnictwa Na-
ukowo-Techniczne, Warszawa.
9. Massucci J., 2001: Projekt Milenium, Wydawnictwo Amber sp. z o. o., Warszawa.
10. Napieralska M., Jabłoński G., 2002: Podstawy mikroelektroniki, Wydawnic-
twa PŁ, Łódź.
11. University of California, Berkeley. Witryna internetowa.
, stan z 26 września 2006 r.
Document Outline
- Podstawowe elementy stosowane w mikroelektronice
Wyszukiwarka
Podobne podstrony:
podstawy prawoznawstwa stosowanie prawa
Modul 3 Podstawy elektroniki cyfrowej
Modul 5 Podstawowe zagadnienia wspolczesnej gospodarki pienieznej i rynku dobr
Podstawowe elementy planowania i podejmowania decyzji
(8) Podstawowe elementy organizowaniaid 1180
Metodyka nauczania podstawowych elementów technicznych w mini piłce nożnej
008 Podstawowe materiały stosowane do produkcji rękojeści
PODSTAWOWE TECHNIKI STOSOWANE W SOCJOTERAPII
A-03 Komparator, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (moduł C), Pod
M5 Charakterystyki podstawowych elementów elektronicznych, AGH, MiBM - I rok, Elektrotechnika, Spraw
Zadania Podstawowe Elementy Automatyki
Laboratorium Instalacji I Oświetlenia, Pomiary natężenia oświetlenia i luminancji v2, Celem ćwiczeni
Wykład 7 PODSTAWOWE ELEMENTY ORGANIZOWANIA
charektyrystyki czestotliwosciowe podstawowych elementow
Stopy żelaza są podstawowym tworzywem stosowanym we współczesnej technice
Obróbka skrawaniem PODSTAWOWE ELEMENTY SKŁADOWE PROCESU TECHNOLOGICZNEGO
Psychologia Zarzadzania, CZYM JEST OSOBOWOŚĆ W UJĘCIU SOCJOLOGICZNYM ORAZ JAKIE SĄ JEJ PODSTAWOWE EL
Lekka atletyka, LA Podstawowe elementy pchnięcia kulą, Konspekt nr
więcej podobnych podstron