R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

401

WYKŁADY 5-6

Optymalny wybór c.d. Funkcja popytu

konsumpcyjnego.

Optymalny wybór konsumenta to taki koszyk konsumpcyjny

x

,

którego użyteczność jest nie mniejsza niż użyteczność każdego innego

koszyka ze zbioru budżetowego (tzn. u(

x

)



u(x)).

Zapis matematyczny

Optymalny wybór

x

jest rozwiązaniem następującego problemu

optymalizacyjnego (PO)

(P O) : u(x)



max

przy

warunkach ograniczających

(*)

d

x

p

x

p

x

p

m

m

2

2

1

1









...

,

x

1

,

0



x

2

,

0



. ...

, x

m

,

0



gdzie p

1

, p

2

, ...,p

m

– ceny, d – dochód.

Uwagi.



W przypadku rosnącej funkcji użyteczności nierówność (*)

można zastąpić równością.



Można wykazać (dowód pomijamy), że jeżeli funkcja

użyteczności

R

R

u

n





:

jest ciągła i silnie wklęsła to dla

każdego d > 0 i wektora cen p = (p

1

p

2

...p

m

) > 0 istnieje

dokładnie jeden optymalny wybór.



Zauważmy, że przy ustalonej funkcji użyteczności optymalny

wybór zależy od dochodu d i cen p = (p

1

p

2

...p

m

). Przy

zmianie cen lub dochodu zmienia się koszyk optymalnego

wyboru.

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

402

Funkcja popytu konsumenta

Przyporządkowanie cenom i dochodom optymalnych

wyb

orów nazywa się funkcją popytu konsumpcyjnego.

x

1

(p

1

,p

2

,...,p

m

, d)

x

2

(p

1

,p

2

,...,p

m

, d)

.



funkcja popytu

x

m

(p

1

,p

2

,...,p

m

, d)

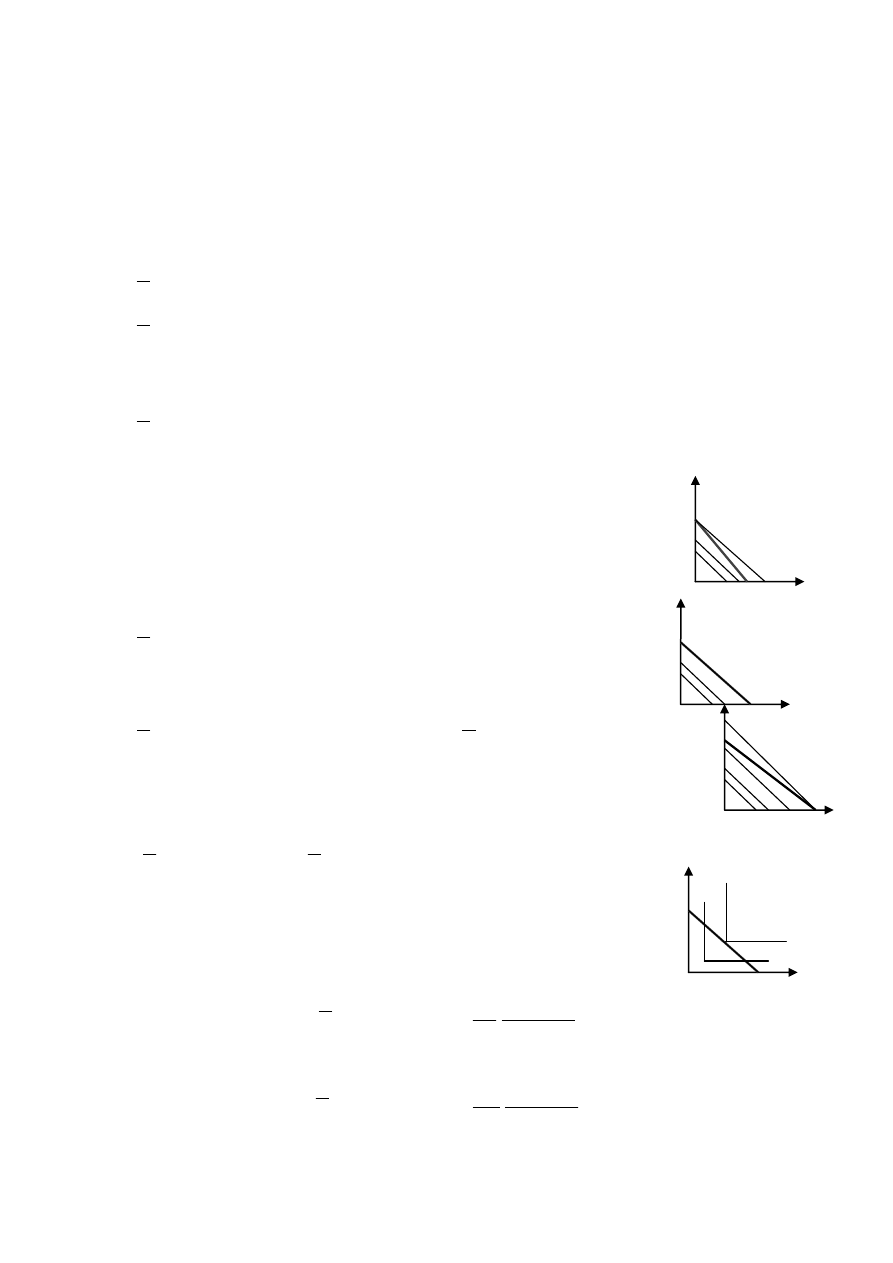
Przykłady m=2 a

1. u(x

1

,x

2

)= x

1

+x

2.

Substytuty doskonałe (Rys.a,b,c)



)

,

,

(

d

p

p

x

2

1

1

















2

1

1

2

1

1

2

1

p

p

dla

p

d

p

p

dla

p

d

0

z

licz

dow

p

p

dla

0

/

]

/

,

[

.

.

b



)

,

,

(

d

p

p

x

2

1

2

)

,

,

(

)

/

(

/

d

p

p

x

p

p

p

d

2

1

1

2

1

2



. c

2. u(x

1

,x

2

) = min {x

1

,x

2

}. Dobra doskonale komplementarne.

x

1

(p

1

,p

2

, d)=

x

1

(p

1

,p

2

, d)=d/(p

1

+

p

2

) (Rys. d )

d

3. u(x

1

,x

2

) = x

a

1

b

2

x

; a > 0, b > 0. C-D.

)

(

)

,

,

(

b

a

a

p

d

d

p

p

x

1

2

1

1





)

(

)

,

,

(

b

a

b

p

d

d

p

p

x

2

2

1

2





R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

403

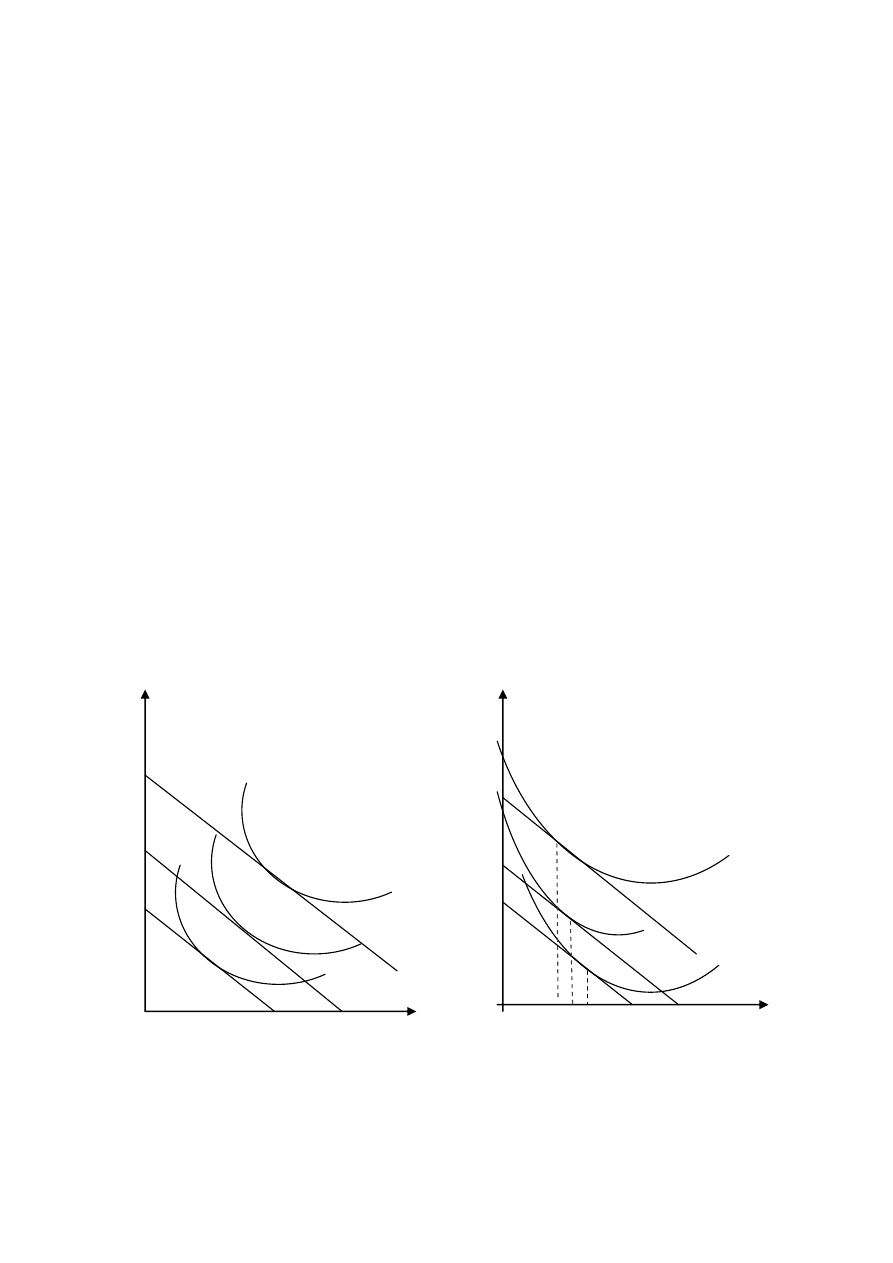
Pytanie : Jak zmienia się popyt gdy zmienia się dochód

a ceny są stałe?

Def.

Towarem wyższego rzędu (normalnym)

nazywamy towar, na który konsument zwiększa popyt,

gdy wzrasta jego dochód.

Def.

Towarem niższego rzędu (poślednim)

nazywamy towar, na który konsument zmniejsza

popyt, gdy wzrasta dochód.

x

2

x

2

x

1

x

1

Ref.2. Rys.6.1. Oba dobra są normalne. Ref.2. Rys.6.2. Towar 1 jest pośledni

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

404

Zakładamy,że ceny p=(p

1

,p

2

) są ustalone.

Def. Granicę:

d

d

p

p

x

d

d

p

p

x

2

1

i

2

1

i

0

d













)

,

,

(

)

,

,

(

lim

nazywamy popytem krańcowym na i-ty towar

względem dochodu konsumenta w punkcie (p

1

,p

2

,d ) i

oznaczamy

d

d

p

p

x

2

1

i





)

,

,

(

.

Jeżeli

d

d

p

p

x

2

1

i





)

,

,

(

> 0 dla wszystkich d > 0 to dobro „i” jest

normalne.

Przykład. W przypadku preferencji C-D

)

(

)

,

,

(

b

a

a

p

d

d

p

p

x

1

2

1

1





)

(

)

,

,

(

b

a

b

p

d

d

p

p

x

2

2

1

2





Zatem

d

d

p

p

x

2

1

1





)

,

,

(

=

)

(

b

a

a

p

1

1



> 0,

d

d

p

p

x

2

1

2





)

,

,

(

=

)

(

b

a

b

p

1

2



>0

Oba dobra są normalne.

Popyt krańcowy względem dochodu informuje

-

w przybliżeniu - o ile zmieni się popyt na i-ty towar jeśli

dochód wzrośnie o jednostkę pieniężną (a ceny

pozostają stałe).

Dla m=2 wpływ dochodu na popyt wyrażany

jest za pomocą ścieżki ekspansji dochodowej i krzywej Engla.

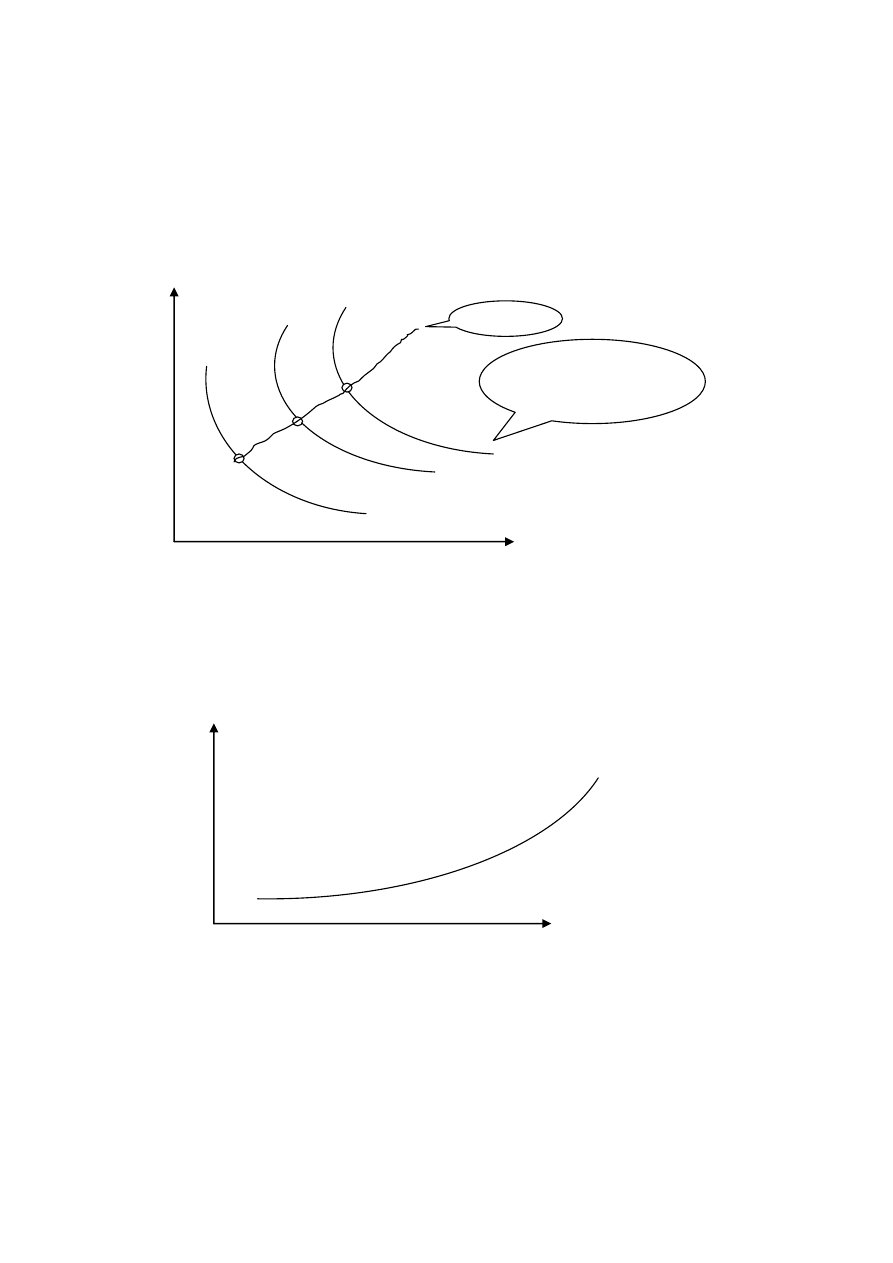
R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

405

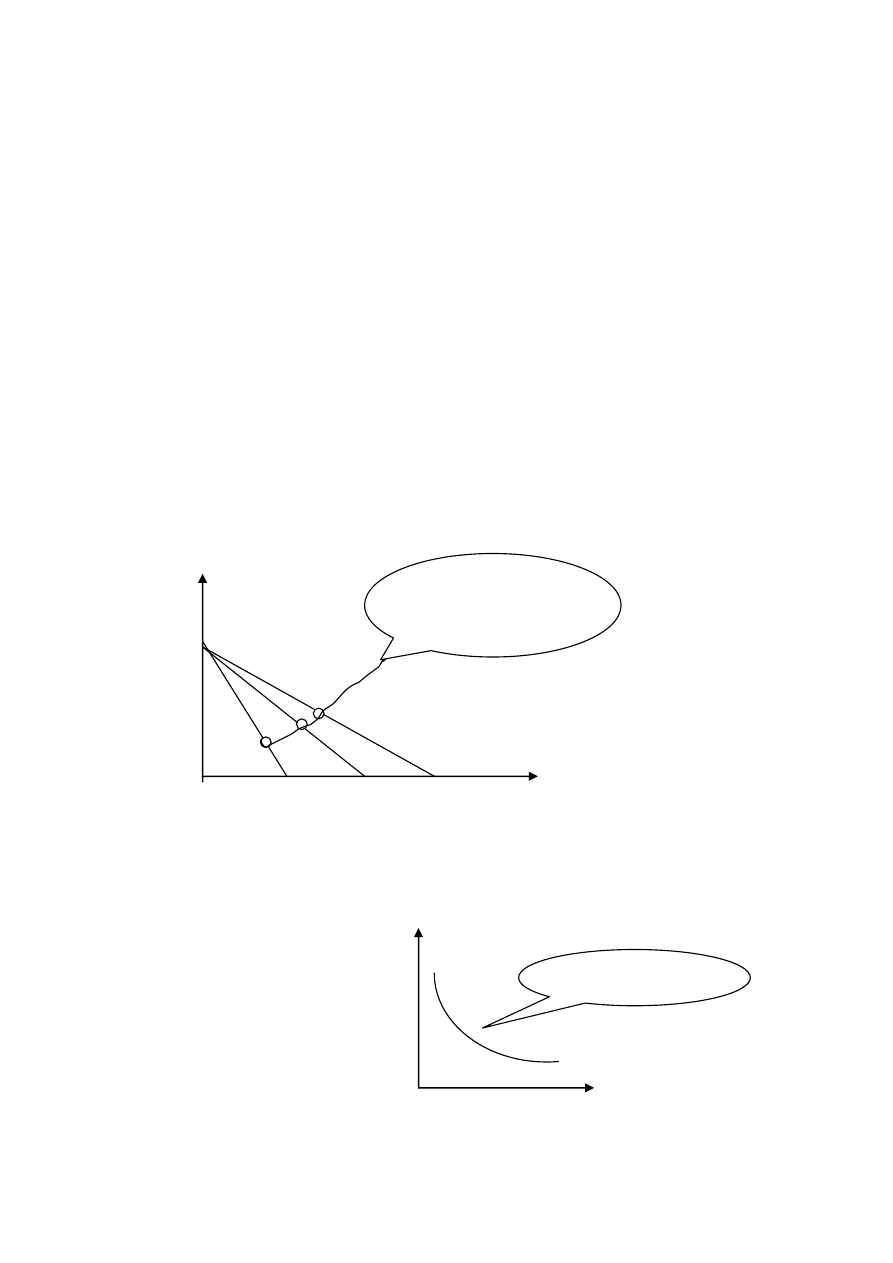
Ścieżka ekspansji dochodowej (krzywa oferty

dochodowej, krzywa zapotrzebowania.) = krzywa

łącząca optymalne koszyki przy różnych poziomach

dochodów (przypominamy – ceny są ustalone).

x

2

x

1

Krzywa wyrażająca zależność popytu od dochodu

nazywa się krzywą Engla (Ref.2. Rys. 6.3 B).

d

x

1

Przykłady. Por. Ref.2. Rys.6.4, Rys.6.5 i Rys 6.6

ścieżka

krzywe

indyferencji

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

406

W przypadku dóbr doskonale substytucyjnych ,

doskonale komplementarnych i preferencji Cobba-

Douglasa ścieżki ekspansji dochodowej i krzywe

Engla są półprostymi wychodzącymi z początku

układu.

Okazuje się, że własność tę mają tzw. preferencje

jednokładne.

Def.

Preferencje nazywają się jednokładne jeśli

spełniają warunek

(x

1

,x

2

)



(y

1

,y

2

)



(t x

1

,t x

2

)



(t y

1

,t y

2

), t > 0.

Analiza popytu przy ustalonym dochodzie.

Def. Towar nazywamy

towarem zwykłym jeżeli popyt

na towar maleje kiedy cena wzrasta (dochód i ceny

pozostałych towarów są stałe) (por. Ref. 2. Rys 6.9.).

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

407

Def. Towar nazywamy towarem Giffena

, jeżeli popyt

na ten towar spada wraz ze spadkiem ceny (por.Ref.2.

Rys.6.10)

Dla m=2 wpływ cen na zmianę popytu wyrażany jest za

pomocą ścieżki ekspansji cenowej i krzywej popytu ( lub

odwróconej krzywej popytu)

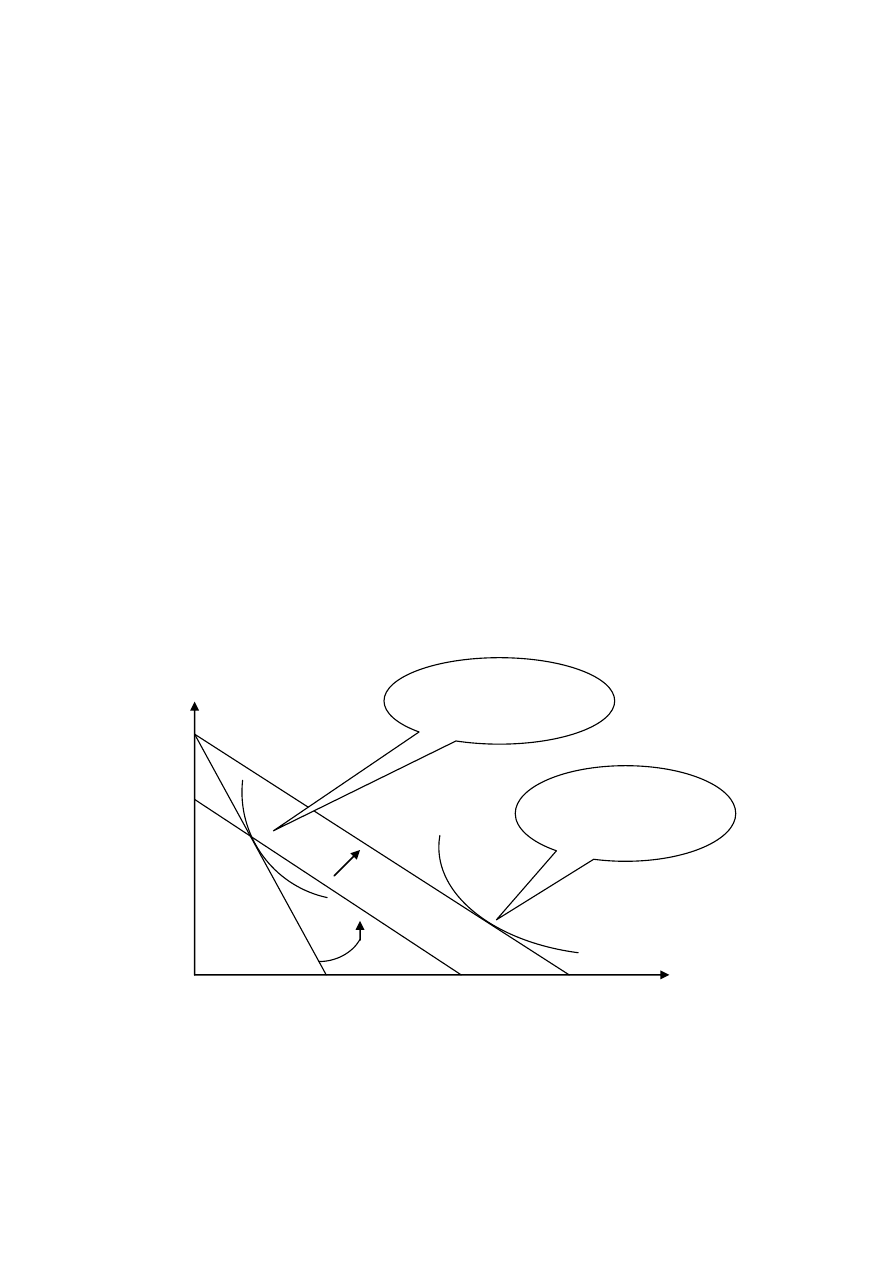
Ścieżka ekspansji cenowej (krzywa oferty cenowej) =

krzywa łącząca optymalne koszyki otrzymane dla różnych

wartości cen towaru 1 (2) przy ustalonym dochodzie i

ustalonej cenie towaru 2 (1).

x

2

x

1

Ref.2. Rys.6.11. A.

Krzywa popytu towaru 1 (2) przedstawia optymalne

wybory towaru 1 (2) jako funkcję ceny towaru 1 (2).

p

1

Ref. 2. Rys.6.11. B

. x

1

krzywa oferty

cenowej

krzywa popytu

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

408

Przykłady. Krzywe oferty cenowej i krzywe popytu w przypadku

substytutów doskonałych, dóbr doskonale komplementarnych podane

są w podręczniku Variana (por Ref.2) Rozdz. 6.6.

Przykład. Preferencje opisane są za pomocą funkcji

użyteczności: u(x

1

,x

2

)= ln x

1

+ x

2

1.

Znaleźć ogólną funkcję popytu.

2.

Znaleźć krzywą popytu dla dobra 1.

3.

Znaleźć odwróconą krzywą popytu dla dobra 1

ln x

1

+ x

2



max

p

1

x

1

+ p

2

x

2

= d,

x

1



0, x

2



0

Z warunku p

1

x

1

+ p

2

x

2

= d wynika, że x

2

= (d - p

1

x

1

)/p

2

. Zatem

x

2

= (d - p

1

x

1

)/p

2



0



d



p

1

x

1



x

1



d/p

1

max

/ 1

p

d

1

x



{ln x

1

+ (d - p

1

x

1

)/p

2

}.

Mamy jednowymiarowe zadanie optymalizacyjne. Punkty, w

których może być realizowane maksimum to: punkt brzegowy

x

1 =

d/p

1

oraz

punkty z przedziału (0,d/p

1

), w których zeruje

sie pochodna.

(ln x

1

+ (d - p

1

x

1

)/p

2

)



= 1/x

1

– p

1

/p

2

= 0; x

1

=p

2

/p

1

Ad 1. Rozważmy dwa przypadki :

a) d/p

1

> p

2

/p

1.

. Zatem

x

1

(p

1

,p

2

,d ) = p

2

/p

1

,

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

409

x

2

(p

1

,p

2

,d) =

2

1

2

1

p

p

p

p

d



=

2

2

p

p

d



b) d/p

1

<p

2

/p

1

. Zatem

x

1

(p

1

,p

2

,d) = d/p

1

,

x

2

(p

1

,p

2

,d) =0.

Ad 2. x

1

(p

1

) = min {

2

p

,d}/p

1

,

Ad 3. p

1

(x

1

) = min {

2

p

,d}/x

1

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

410

WYKŁAD 6

Analiza popytu przy zmianie cen. Tożsamość Słuckiego.

m=2.

Założenia. Preferencje są monotoniczne i ściśle wypukłe.

Optymalne wybory są optimami wewnętrznymi.

x

1

(p

1

,p

2

,d )

– popyt na dobro 1.

Niech:

2

p

= const., d = const.

Pytanie. Jak działa zmiana p

1

n

a popyt?

Problem. Wydobyć efekt substytucyjny i dochodowy.

x

2

A

x

1

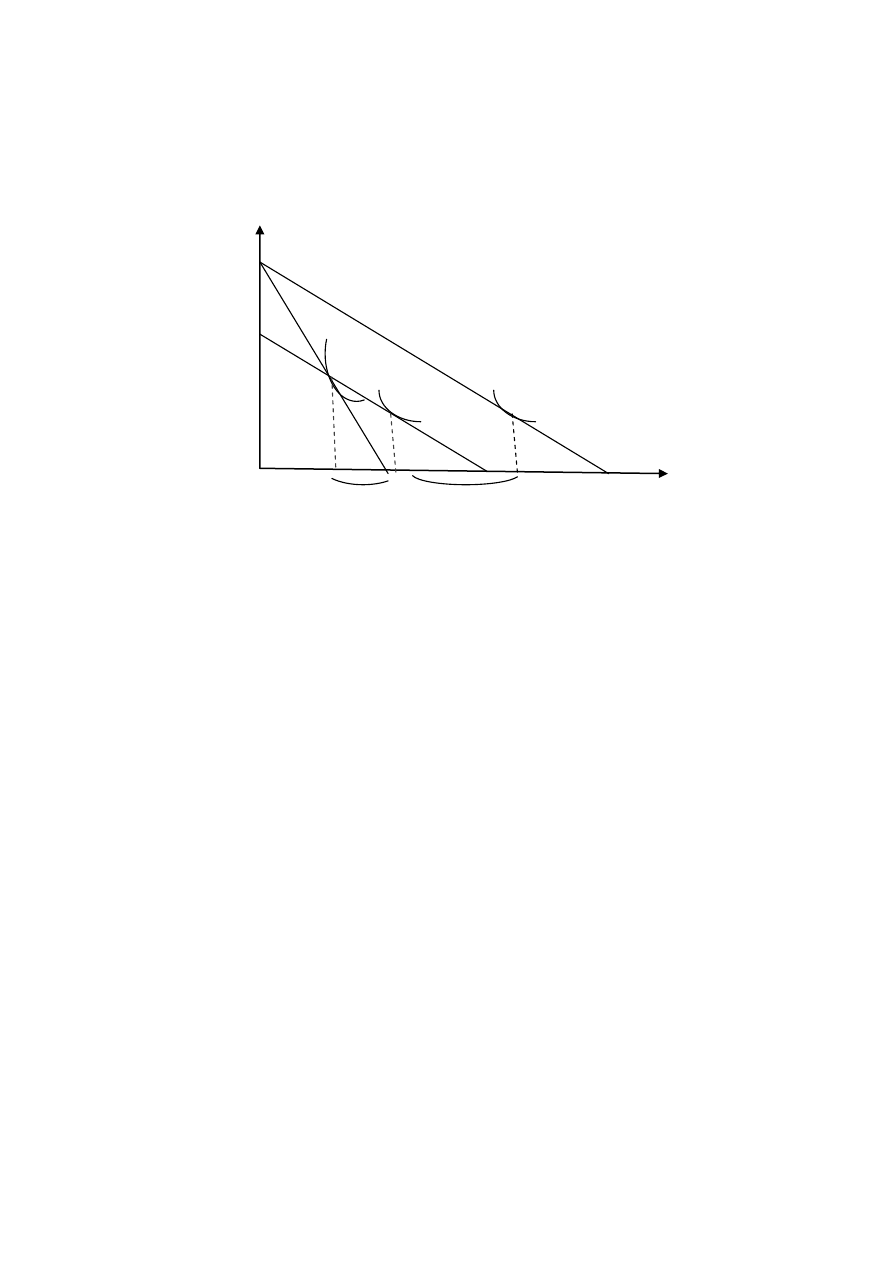
Ref.2 . Rys. 8.1. Komentarz

: obrót i przesuniecie

Kiedy cena p

1

np.

zmaleje przy d=const.,p

2

=const., to linia budżetu obraca się

wokół punktu A i robi się mniej stroma. Ten

ruch rozbijamy na obrót wokół

początkowego wyboru i przesunięcie równoległe do punktu A.

wybór początkowy

wybór końcowy

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

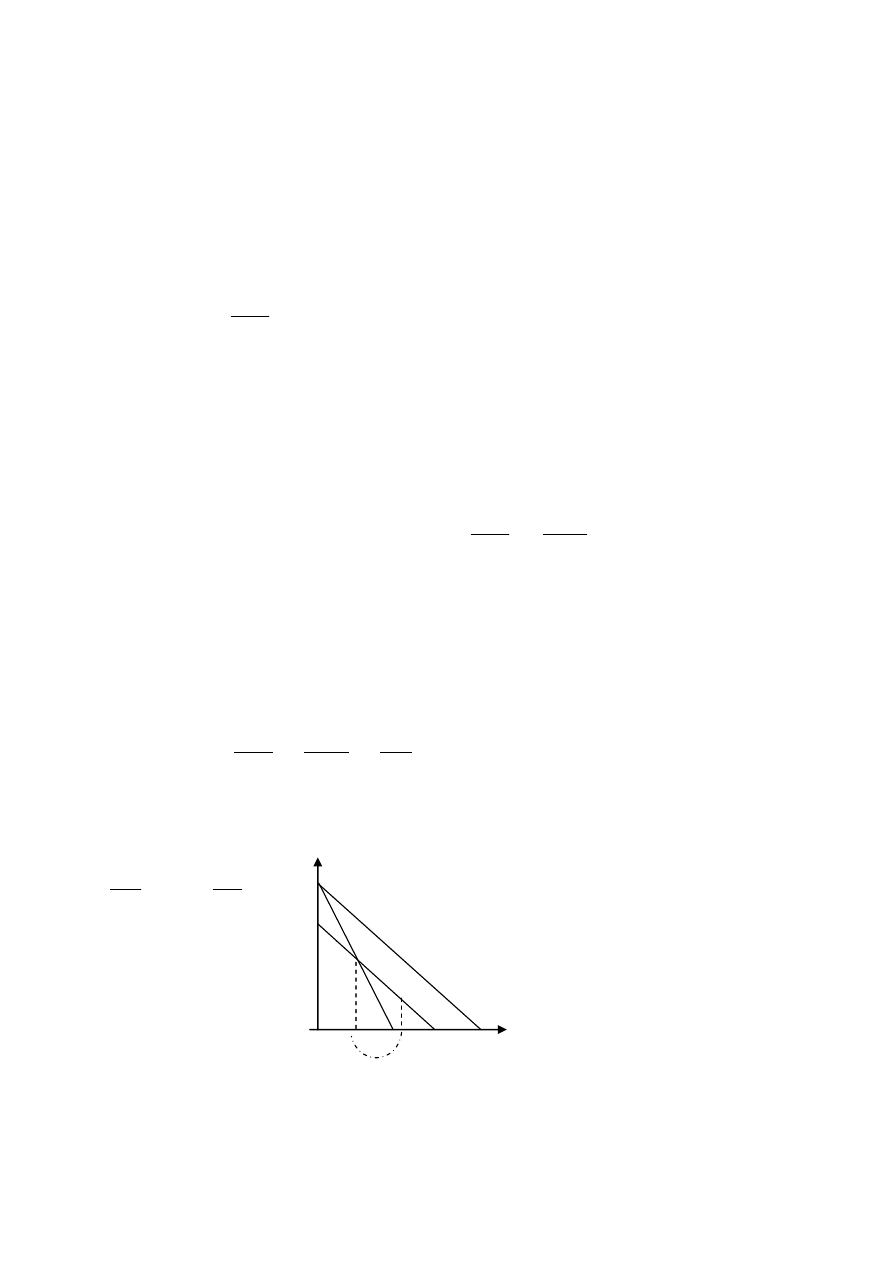
411

drugie dobro

d/p

2

A x

1

=x

1

(p

1

,d), y

1

=x

1

(

,

), z

1

=x

1

(

,d)

/p

2

( Por. Ref.2 . Rys. 8.2.)

x y z

efekt substytucyjny

efekt dochodowy

d/

pierwsze dobro

Efekt substytucyjny:

1

1

s

1

p

x

x







(

,

d



) -

)

,

(

d

p

x

1

1

Efekt dochodowy:

1

1

d

1

p

x

x







(

,

d

) -

1

1

p

x



(

,

d



)

Efekt całkowity:

1

1

1

p

x

x







(

,d) -

)

,

(

d

p

x

1

1

Tożsamość Słuckiego:

1

1

p

x



(

,d)-

)

,

(

d

p

x

1

1

=[

1

1

p

x



(

,

d



)-

)

,

(

d

p

x

1

1

]+[

1

1

p

x



(

,d)-

1

1

p

x



(

,

d



)]

1

x



=

s

1

x



+

d

1

x



Efekt całkowity = Efekt substytucyjny + Efekt dochodowy

Zauważmy, że

d = p

1

x

1

(p

1

,d) +

2

p x

2

(p

1

,d)

d



=

1

p



x

1

(p

1

,d) +

2

p x

2

(p

1

,d)



d



-

d

=

1

p



x

1

(p

1

,d) - p

1

x

1

(p

1

,d)

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

412

(*)

d



=

d

+ (

1

p



-

p

1

)

x

1

(p

1

,d)

Wyznaczania efektów. Przykład numeryczny.

Popyt na dobro 1 dany jest wzorem:

)

,

(

d

p

x

1

1

=

1

p

3

d

.

Początkowy dochód: d = 150; początkowa cena p

1

= 10; nowa

cena

1

p



= 5. Wyznacz efekt substytucyjny i dochodowy.

Rozwiązanie.

a) Początkowy wybór:

)

,

(

d

p

x

1

1

=

1

p

3

d

=

30

150

= 5.

b) Wyznaczanie

d



-

pomocnicza wielkość dochodu przy

obróconej linii budżetowej. Ze wzoru (*) mamy

d



=

d

+ (

1

p



-p

1

) x

1

(p

1

,d) = 150

– 5 5=125.

1

1

p

x



(

,

d



) =

3

25

5

3

125

p

3

d

1











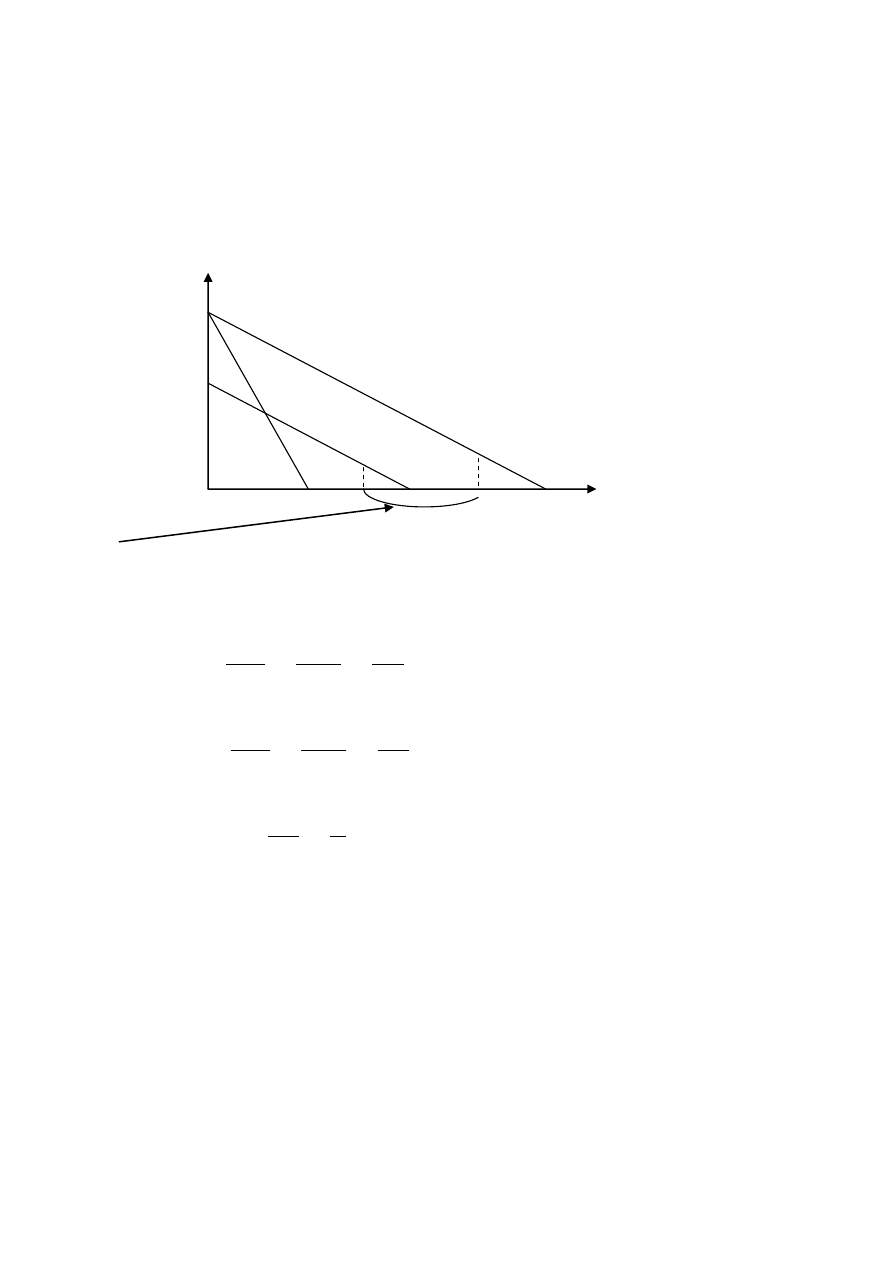
c) Efekt substytucyjny:

s

1

x



=

1

1

p

x



(

,

d



) - x

1

(p

1

,d) =

3

10

5

3

25





x

y

Obserwacja

: Znak

s

1

x



= - Znak (

1

1

p

p





)

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

413

Ogólnie. Efekt substytucyjny jest ujemny w następującym sensie:

zmiana popytu wywołana efektem substytucyjnym zachodzi w

kierunku przeciwnym do ruchu cen.

c) Przykład c.d. Wyznaczanie efektu dochodowego

x

2

x

y z

x

1

1

1

d

1

p

x

x







(

,

d

) ---

1

1

p

x



(

,

d



)





)

,

(

d

p

x

1

1

10

3

30

5

3

150

p

3

d

1

















)

,

(

d

p

x

1

1

3

25

5

3

125

p

3

d

1











3

5

3

25

10

x

d

1









.

Obserwacja

.

W

przeciwieństwie

do

efektu

substytucyjnego, znaku efektu dochodowego nie można

ustalić na podstawie ruchu cen.

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

414

1

x



-----

całkowita zmiana popytu.

Pytanie: czy można ustalić znak efektu całkowitego?

Rozważmy dobro normalne

( takie

dobro ,że jeśli dochód

rośnie, to popyt na nie rośnie, dochód maleje, to popyt maleje)

Niech

1

p



>p

1

.

Zatem

0

p

p

p

1

1

1











,

a więc

d



>

d bo

d



=

d

+ (

1

p



-p

1

) x

1

(p

1

,d)

.

Mamy więc

1

1

p

x



( ,d)-

)

,

(

d

p

x

1

1

=[

1

1

p

x



( ,

d



)-

)

,

(

d

p

x

1

1

]+[

1

1

p

x



( ,d)-

1

1

p

x



( ,

d



)]

1

x



=

s

1

x



+

d

1

x



(----)



(---) (---)





bo efekt subst.



bo dobro normalne.

dobro zwykłe

Wniosek.

Prawo popytu: Jeśli popyt na

dobro wzrasta, kiedy dochód rośnie ( tzn.

dobro jest normalne) to popyt na to dobro

musi spadać kiedy cena dobra rośnie

(dobro zwykłe).

R.Rempała. Ekonomii matematycznej. 2015. Wykłady 5-6

415

Ćwiczenia. Zestaw 3.

1.

Relacja preferencji opisana jest za pomocą funkcji użyteczności

)

,

(

2

1

x

x

u

2

1

x

x





. Podaj nazwę dóbr, których dotyczy ta relacja.

2.

Relacja preferencji opisana jest za pomocą funkcji użyteczności

)

,

(

2

1

x

x

u

)

,

min(

2

1

x

x



. Podaj nazwę dóbr, których dotyczy ta relacja.

3.

Obliczono, że krańcowa użyteczność pierwszego i drugiego dobra w ustalonym

koszyku wynoszą odpowiednio:

3

2

x

u

4

1

x

u

2

1

/

/

,

/

/













. Czy

prawdą jest, że krańcowa stopa substytucji pierwszego dobra przez drugie w

przypadku wspomnianego koszyka wynosi

–3/8?

4.

Relacja preferencji jest opisana funkcją użyteczności

)

,

(

2

1

x

x

u

2

1

x

2

x





.

Czy prawdą jest, że

a) (2,3)



(3,3)

..........

b) (1,2)



(1,1)

..........

5.

Zauważono, że relacja preferencji jest monotoniczna a optymalnym wyborem

jest optimum wewnętrzne. Podaj wartość krańcowej stopy substytucji

pierwszego dobra przez drugie w punkcie optymalnego wyboru przy linii

budżetowej.

15

x

3

x

2

2

1





.

6.

Funkcja popytu wyrażona jest wzorem:

1

1

p

d

5

2

x





,

2

2

p

d

5

3

x





; (p

1

,p

2

)-

ceny, d-

dochód. Czy prawdą jest, że

a)

dobra 1i 2 są normalne,?

b)

dobra 1i 2 są zwyczajne

c)

krzywa Engla dla każdego dobra jest opisana funkcją liniową.

d)

krzywa popytu, dla dobra 1 jest opisana równaniem:

1

1

1

p

d

5

2

p

x





)

(

.