
Jacek Kabziński
Automatyka i sterowanie
————————————————————————————————————————
2
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
Silnik serwo
0
d
dt
d
J
( t ) B ( t ) M ( t )
dt
θ ω
ω τ
ω
=
=
−
−
( t ) K i( t ) K i( t )
τ
τ
ϕ
=
=
1
m
m
m
di
u( t ) L
Ri( t ) e ( t )
dt
e ( t ) K
( t ) K
( t )
ϕω
ω
=
+
+
=
=
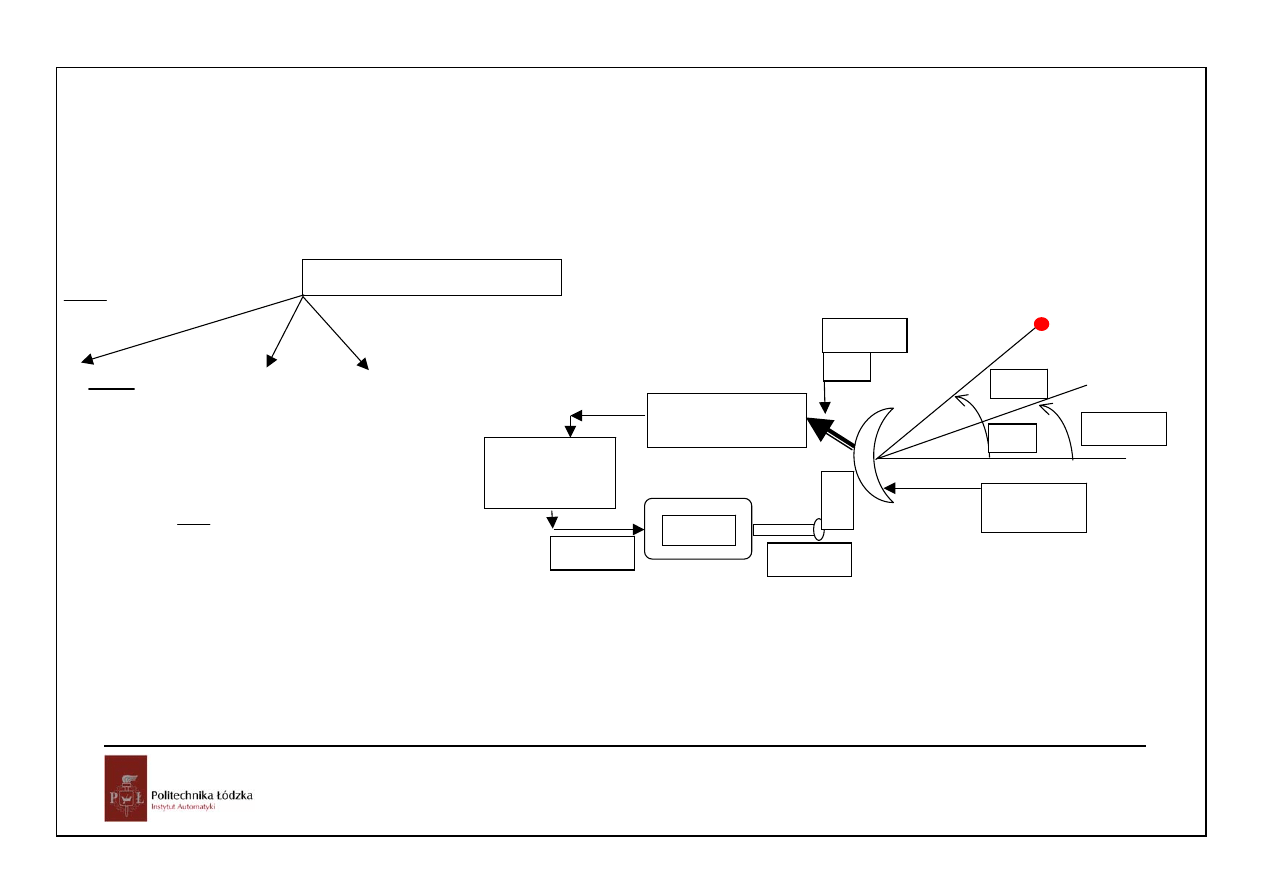
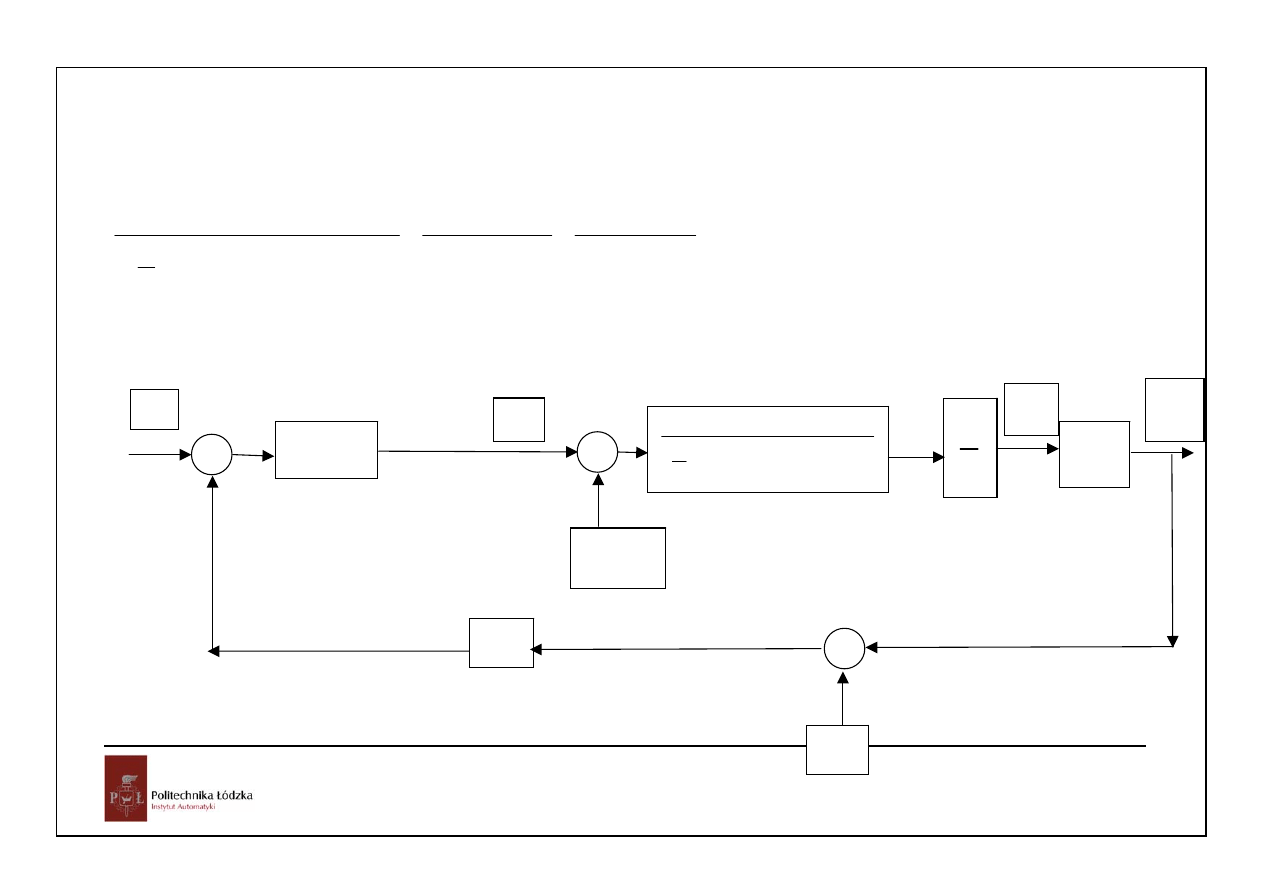
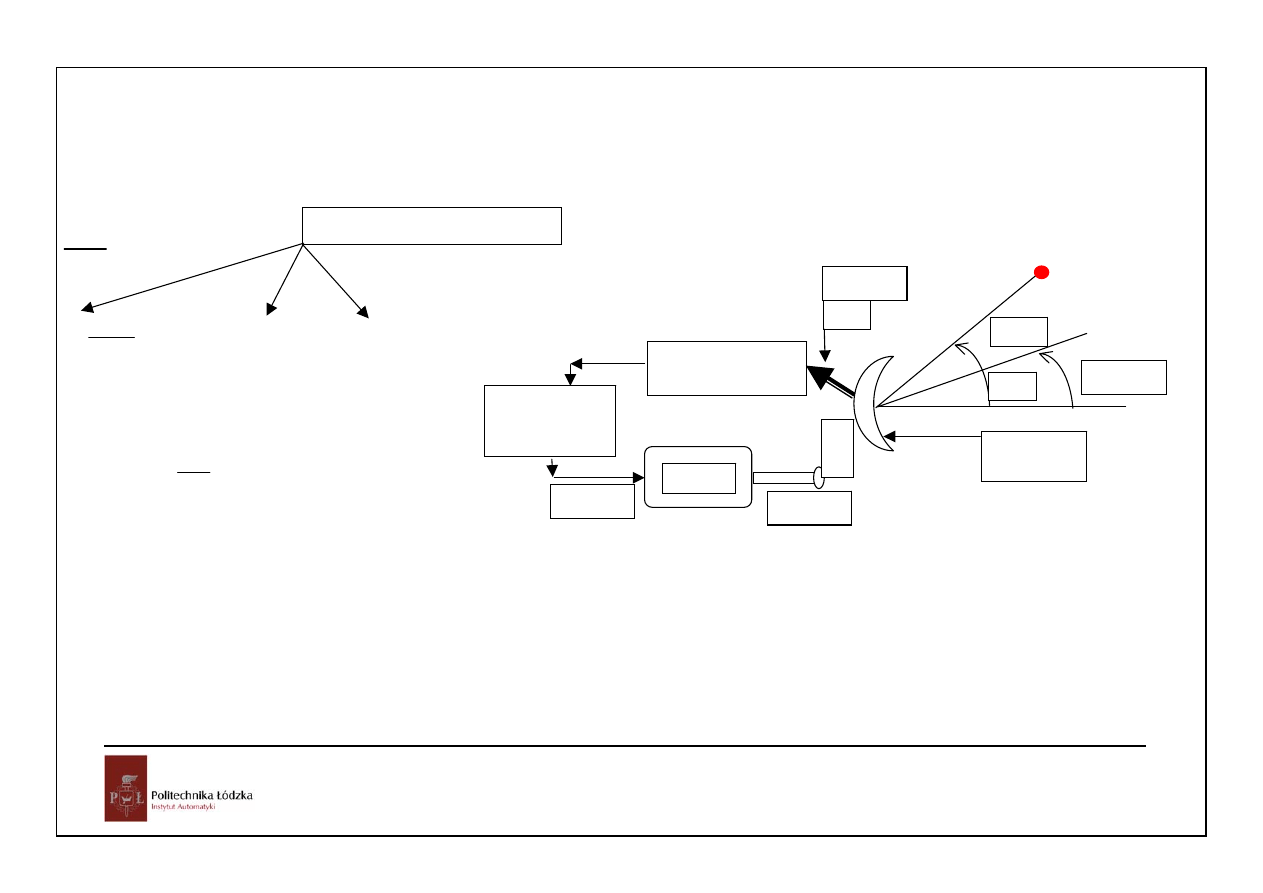
silnik
Układ pomiaru i
sterowania
Wzmacniacz
mocy
θ
a
(t)
r(t)
e(t)
θ (t)
u(t)
r(t)
θ
a
(t)
zakłócenie
Uwzględnia maszynę roboczą

3
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
0
1
( s )
( s )
s
Js ( s ) K i( s ) B ( s ) M ( s )
τ
θ
ω
ω
ω
=
=
−
−
m
u( s ) Lsi( s ) Ri( s ) K
( s )
ω
=
+
+
(
)
(
)
1
1
1
m
m
R
i( s )
u( s ) K
( s )
u( s ) K
( s )
L
Ls R
s
R
ω
ω
=
−
=
−
+
+
(
)
(
)
0
0
1
1
1
B
( s )
K i( s ) M ( s )
K i( s ) M ( s )
J
Js B
s
B
τ
τ
ω
=
−
=
−
+
+
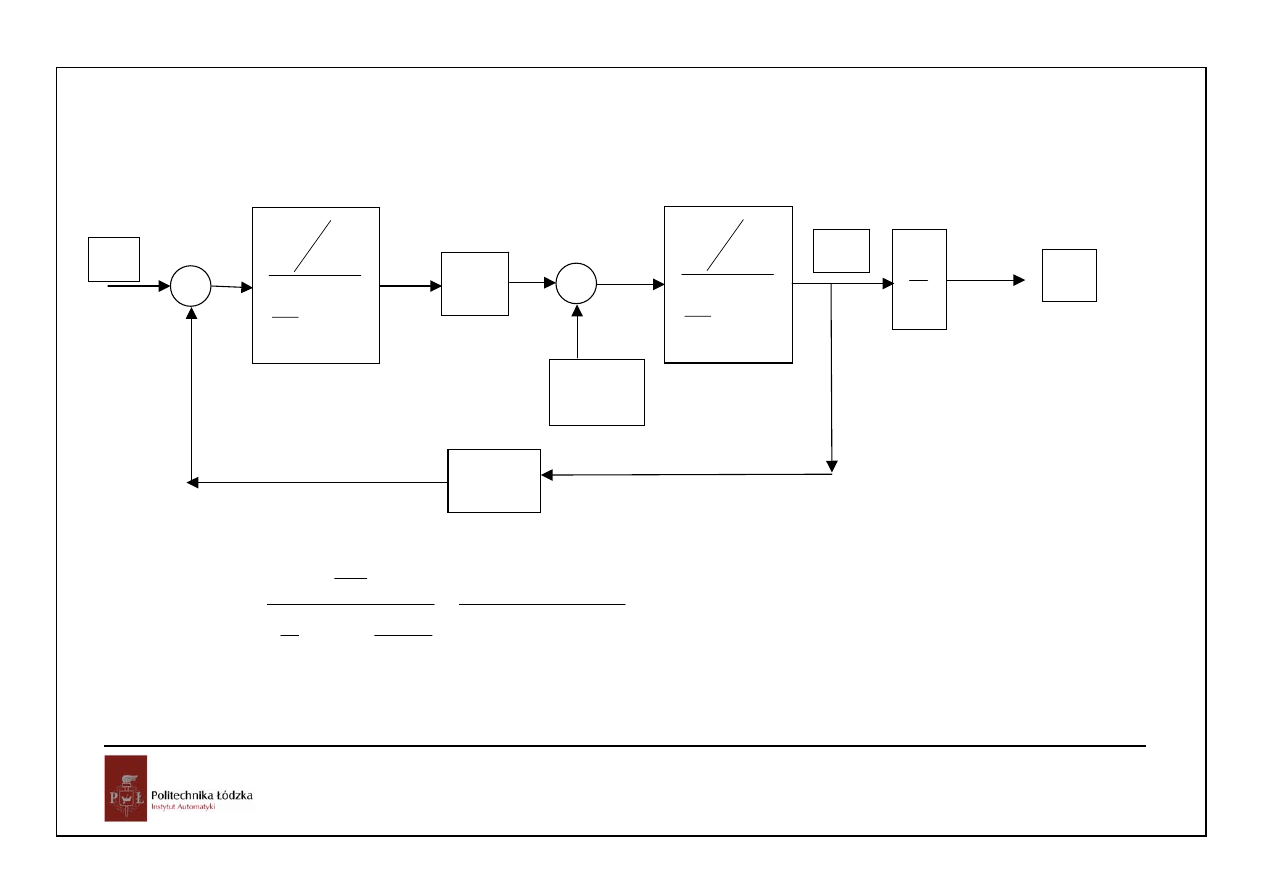
4
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
0
1
u
m
m
K
K
RB
L
T
J
K K
JRs RB K K
s
B
RB
τ
τ
ω
τ
τ
≈ ⇒
=
=
+
+
⎛
⎞
+ +
⎜
⎟
⎝
⎠
1
1
R
L
s
R
+
K
τ
1
1
B
J
s
B
+
0
M
−
m
K
−
1
s
θ
u
ω
5
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
(
)
1
1
1
1
1
1
1
1
1
1
1
1
u
m
m
m
R
B
K
L
J
K
s
s
K
R
B
RB
T
L
J
K K
L
s
s
s
JRs RB
K K
R
B
K
K
R
B
RB
R
L
J
s
s
R
B
τ
τ
τ
ω
τ
τ
τ
+
+
=
=
=
⎛
⎞⎛
⎞
⎛
⎞
+
+ +
+
+
+
⎜
⎟⎜
⎟
⎜
⎟
+
⎝
⎠⎝
⎠
⎝
⎠
+
+
(
)
0
u
m
K
L ~
T
JRs RB
K K
τ
ω
τ
≈
⇒
=
+
+
C( s )
m
K
JRs RB K K
τ
τ
+
+
0
M
K M
−
1
−
1
s
θ
u
p
K
a
θ
r
N
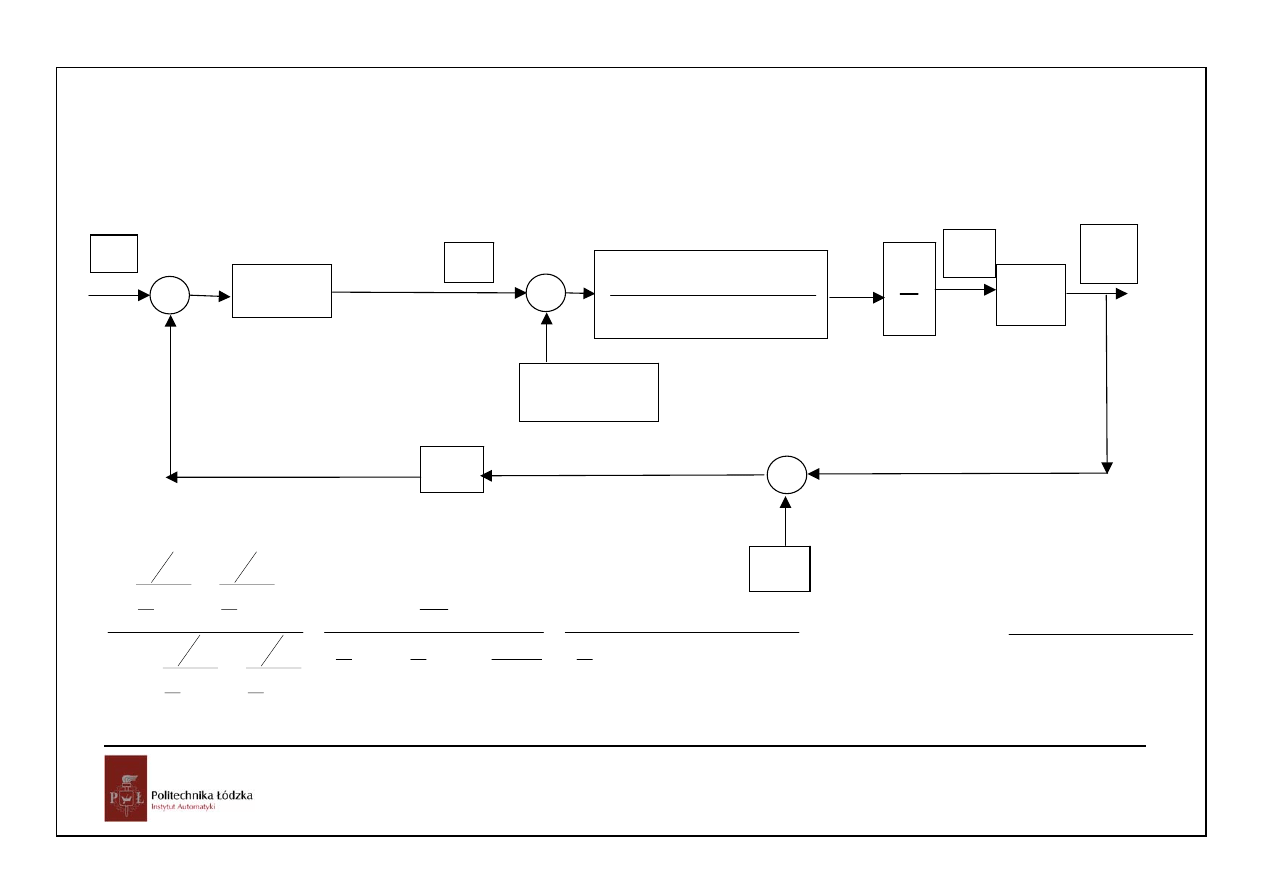
6
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
(
)
0
0
a
u
m
K
L
T
JRs RB K K s
θ
τ
≈ ⇒
=
+
+
C( s )
m
K
JRs RB K K
τ
τ
+
+
0
M
K M
−
1
−
1
s
θ
u
p
K
a
θ
r
N
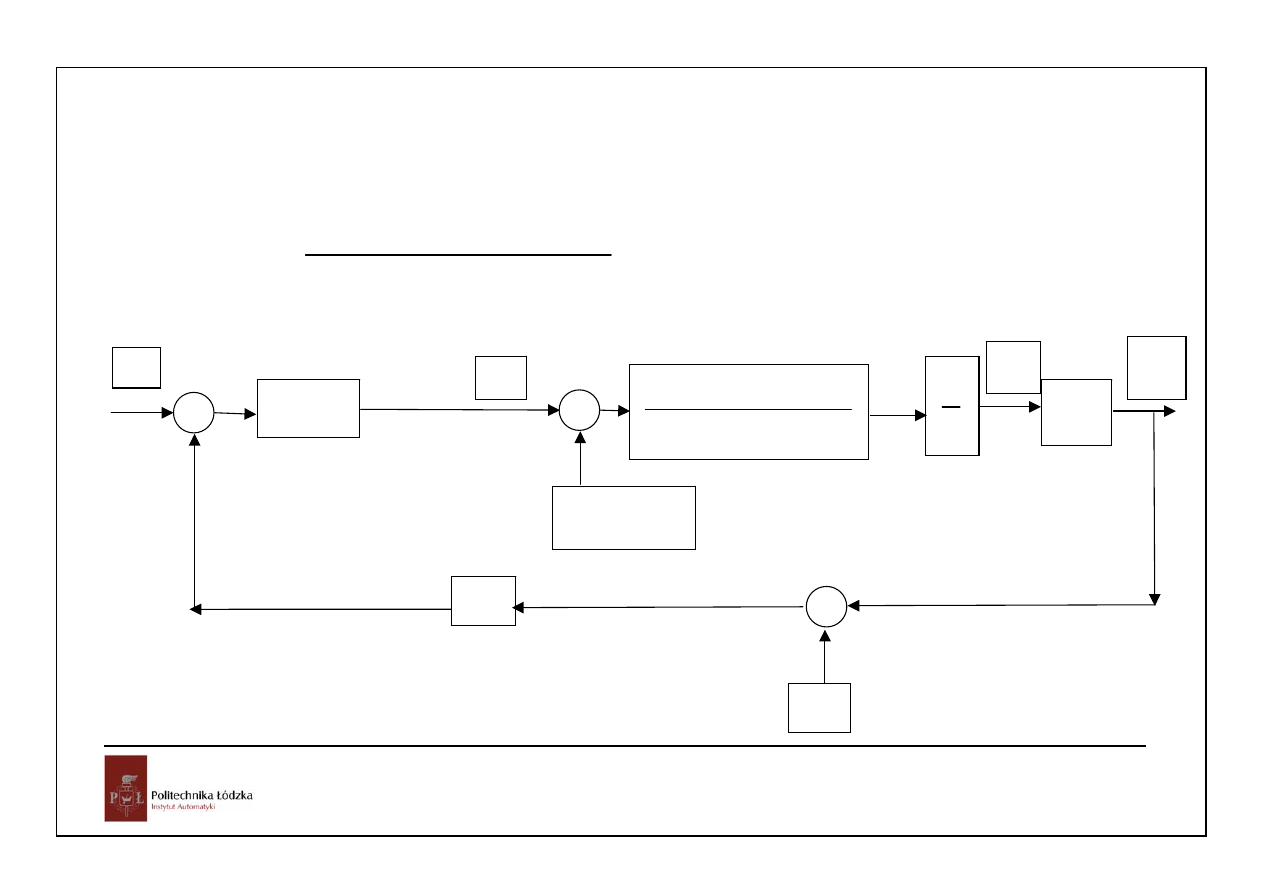
7
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
(
)
0
2
4
4
1
2
3
2
1
a
u
m
K
T
s( s
)( s
)
s( s
s
)
L
s
JRs RB
K K
s
R
θ
τ
=
=
=
+
+
+ +
⎛
⎞
⎛
⎞
+
+
+
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
C( s )
(
)
1
m
K
L
s
JRs RB
K K
R
τ
τ
⎛
⎞
+
+
+
⎜
⎟
⎝
⎠
z
M
−
1
−
1
s
θ
u
p
K
a
θ
r
N
8
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
0
d
dt
d
J
( t ) B ( t ) M ( t )
dt
θ ω
ω τ
ω
=
=
−
−
( t ) K i( t ) K i( t )
τ
τ
ϕ
=
=
1
m
m
m
di
u( t ) L
Ri( t ) e ( t )
dt
e ( t ) K
( t ) K
( t )
ϕω
ω
=
+
+
=
=
silnik
Układ pomiaru i
sterowania
Wzmacniacz
mocy
θ
a
(t)
r(t)
e(t)
θ (t)
u(t)
r(t)
θ
a
(t)
zakłócenie
Uwzględnia maszynę roboczą

9
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
0
d
dt
d
J
K i( t ) B ( t ) M ( t )
dt
τ
θ ω
ω
ω
=
=
−
−
0
d
dt
d
K
B
M ( t )
i( t )
( t )
dt
J
J
J
τ
θ ω
ω
ω
=
=
−
−
m
di
L
K
( t ) Ri( t ) u( t )
dt
ω
= −
−
+
1
m
di
K
R
( t )
i( t )
u( t )
dt
L
L
L
ω
= −
−
+
a
p
K
θ
θ
=

10
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
1
2
2
3
2
3
2
3
1
m
dx
x
dt
dx
K
B
x
x
d
dt
J
J
dx
K
R
x
x
u( t )
dt
L
L
L
τ
=
=
−
−
= −
−
+
1
1
2
2
3
3
0
1
0
0
0
0
0
1
1
0
0
m
x
x
d
B
K
x
x
u
d
dt
J
J
x
x
K
R
L
L
L
τ
⎡
⎤
⎡ ⎤
⎢
⎥
⎢ ⎥
⎡ ⎤
⎡ ⎤
⎡ ⎤
⎢
⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢
⎥
=
−
+
+
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢
⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢
⎥
⎣ ⎦
⎣ ⎦
⎣ ⎦ ⎢ ⎥
−
−
⎢
⎥
⎣ ⎦
⎣
⎦
1
p
y K x
=
0 0
p
y
K
x
⎡
⎤
= ⎣
⎦
Ustalamy dane:
L=0.1
J=1
b=(3-sqrt(5/2))/2
R=(3-b/J)*L
Ktau=sqrt(2*L*J-R*b)
Km=Ktau
Kp=4*L*J/Ktau
L = 0.1000
J =1
b =0.7094
R =0.2291
Ktau =0.1936
Km =0.1936
Kp =2.0656
I obliczamy macierze

11
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
A =
0 1.0000 0
0 -0.7094 0.1936
0 -1.9365 -2.2906
B =
0
0
10
C =
2.0656 0 0
D=0
sprawdzamy transmitancję wyznaczonego układu
>>
[np, dp]=SS2TF(A,B,C,D)
plants=tf(np, dp)
np =
0 0.0000 -0.0000 4.0000
dp =
1.0000 3.0000 2.0000 0
Transfer function:
2.22e-015 s^2 - 4.441e-016 s + 4
--------------------------------
s^3 + 3 s^2 + 2 s
Nie jest to oczywiście jedyna możliwość wyboru
zmiennych stanu. Np.:
[A1,B1,C1,D1]=tf2ss(np,dp)
A1 =
-3.0000 -2.0000 0
1.0000 0 0
0 1.0000 0
B1 =
1
0
0
C1 = 0.0000 -0.0000 4.0000
D1 = 0
12
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
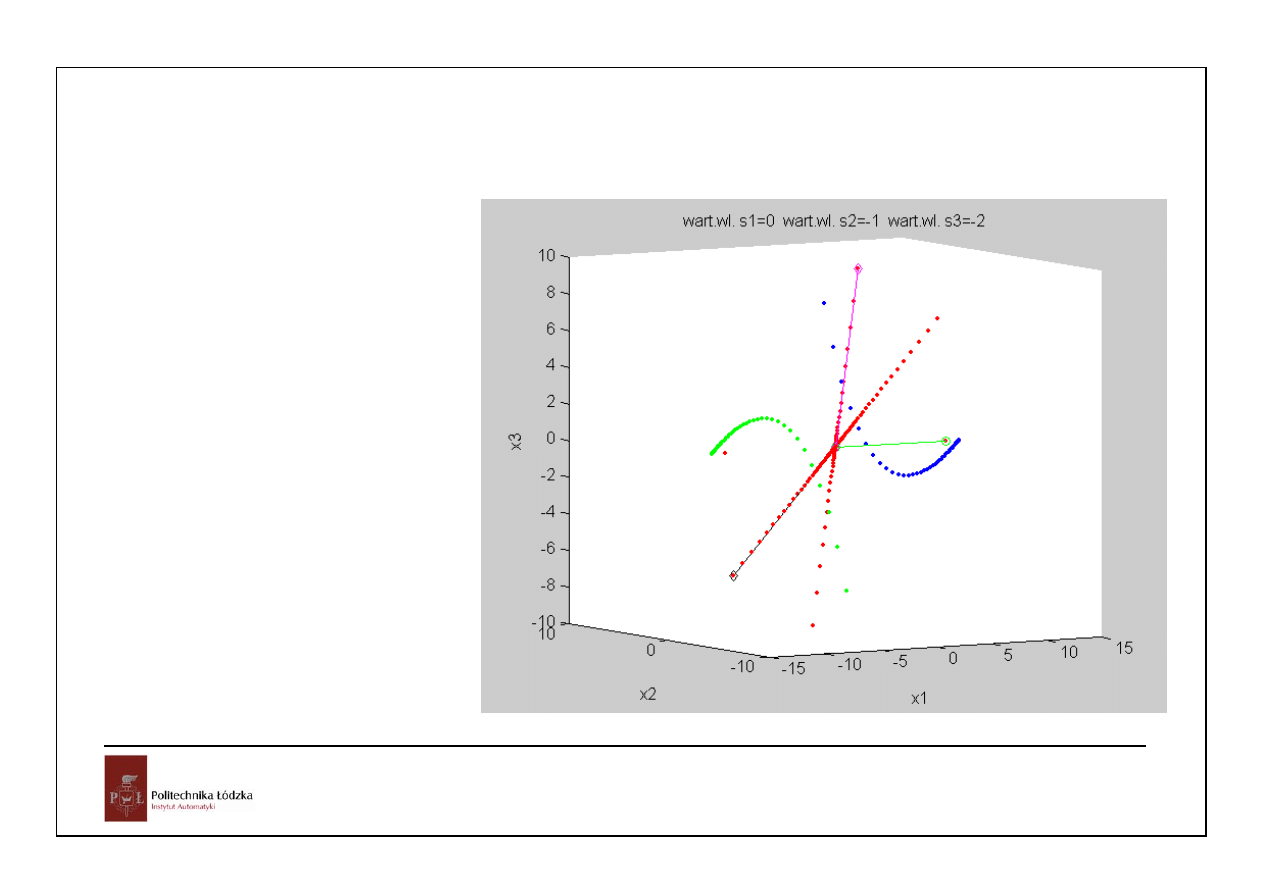
Zbadajmy strukturę własną obiektu:
[V,S]=eig(A)
V =
1.0000 -0.4850 0.0740
0 0.4850 -0.1480
0 -0.7277 0.9862
S =
0 0 0
0 -1.0000 0
0 0 -2.0000
Sprawdzimy sterowalność układu
>> Qs=[B A*B A*A*B]
Qs =
0 0 1.9365
0 1.9365 -5.8095
10.0000 -22.9057 48.7171
13
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
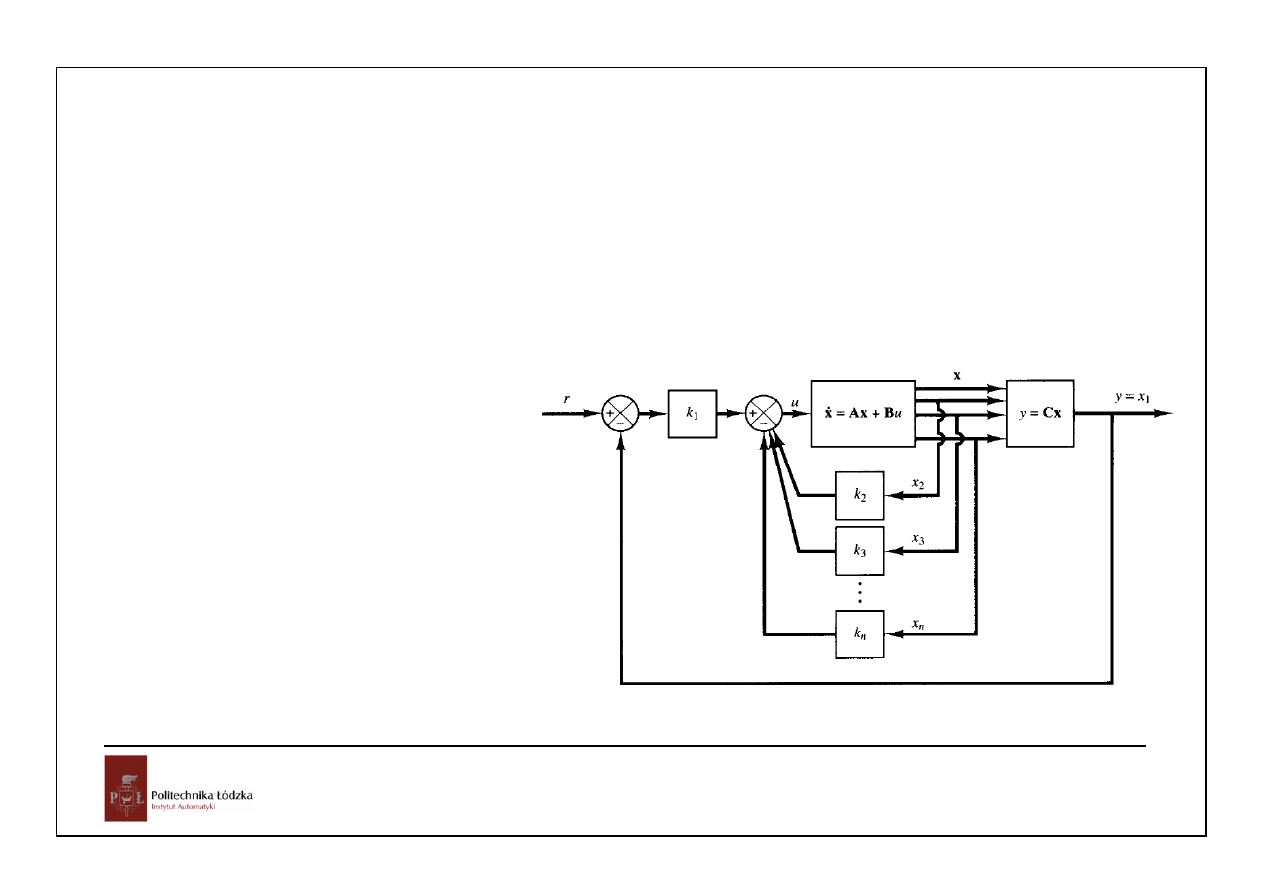
Załóżmy dostępność wszystkich zmiennych stanu
wyznaczmy sprzężenie zwrotne od wektora stanu
przesuwające bieguny układu zamkniętego do
położeń podanych w wektorze p:
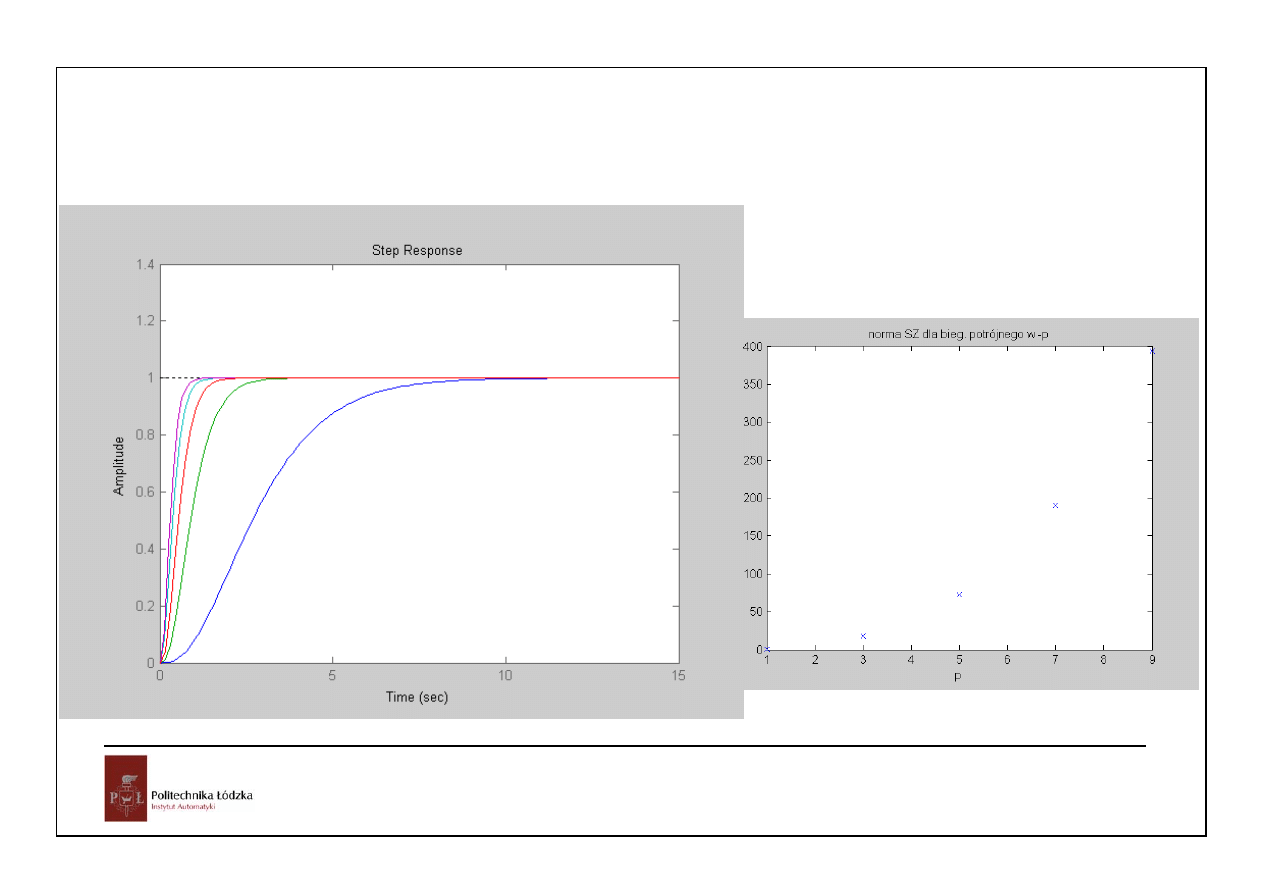
figure
hold on
nsz=[]
for i=1:2:10
p=-i*[1 1 1];
K=acker(A,B,p);
Az=A-B*K;
plantz=SS(Az,B*K(1)/C(1),C,D);
step(plantz)
nsz=[nsz,norm(K)]
end
figure
plot([1:2:10],nsz,'x')
title('norma SZ dla bieg. potrójnego w -
p');xlabel('p')
14
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
nsz =
0.7303 17.5927 72.6433 189.8392
393.8280
15
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
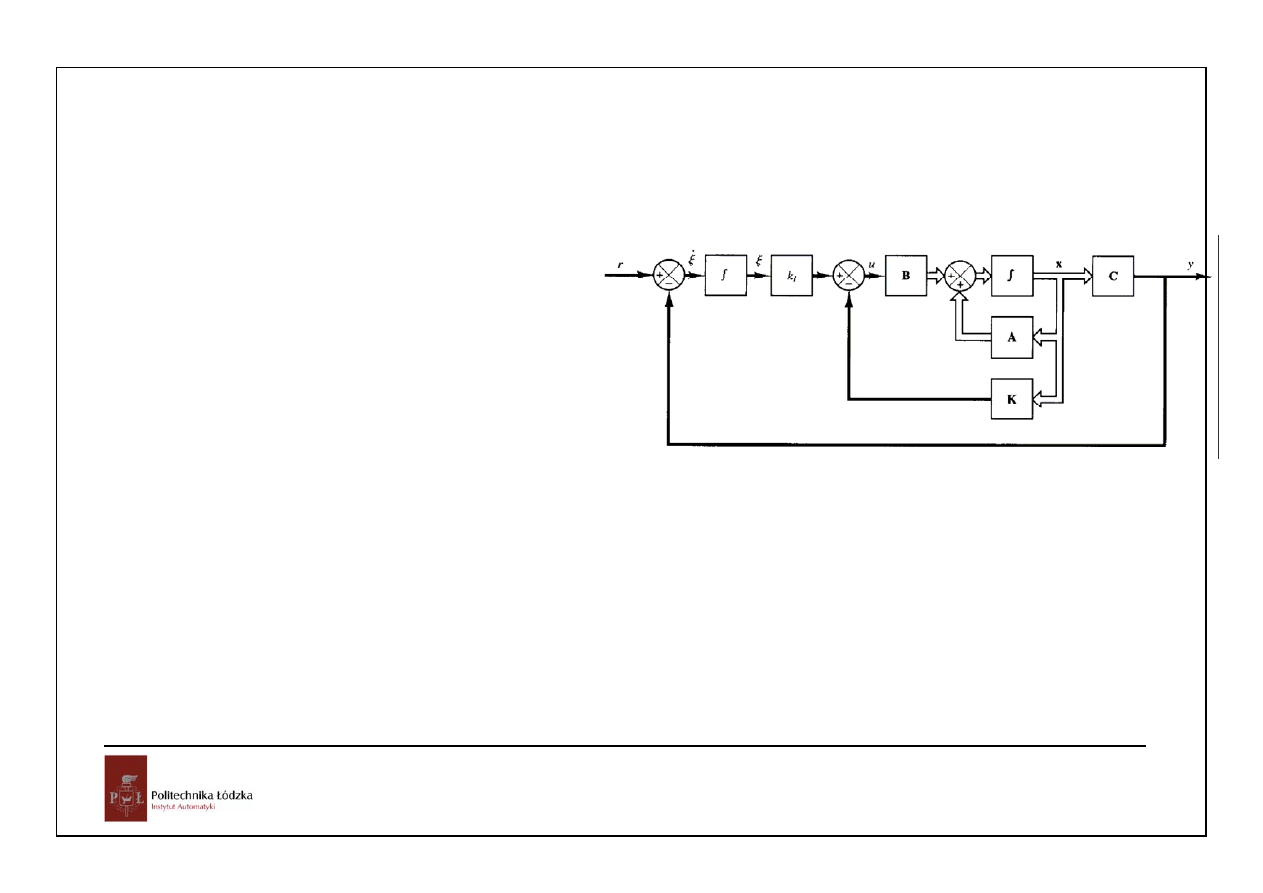
Spróbujmy dołożyć jeszcze jedno całkowanie:
% z całkowaniem
Atyl=[A [0;0;0];-C 0]
Btyl=[B;0]
Qstyl=[Btyl Atyl*Btyl Atyl*Atyl*Btyl
Atyl*Atyl*Atyl*Btyl]
rank(Qstyl)
p=-5*[1 1 1 1];
Ktyl=acker(Atyl,Btyl,p);
Aztyl=Atyl-Btyl*Ktyl;
plantzc=SS(Aztyl,[0;0;0;1],[C 0],D);
figure
step(plantzc)
Ktyl =
258.1989 70.1989 1.7000 -156.2500
16
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego

17
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
Zbudujmy obserwator:
Qo=[C;C*A;C*A*A]
rank(Qo)
p=-5*[1 1 1];
K=acker(A,B,p)
Ke=acker(A',C',2*p)'
Qo =
2.0656 0 0
0 2.0656 0
0 -1.4654 0.4000
ans =
3
K =
64.5497 33.3009 1.2000
Ke =
1.0e+003 *
0.0131
0.1051
1.1224
18
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
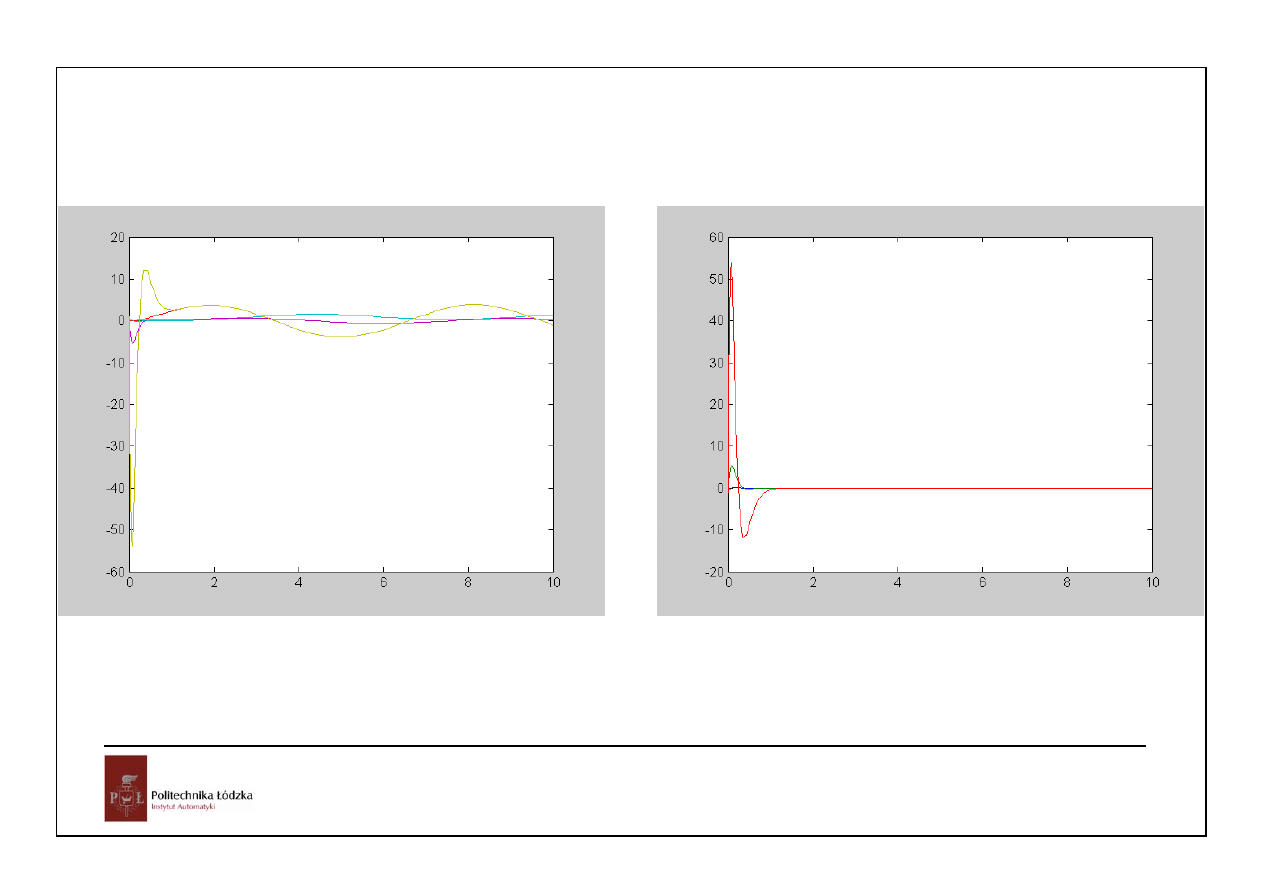
19
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
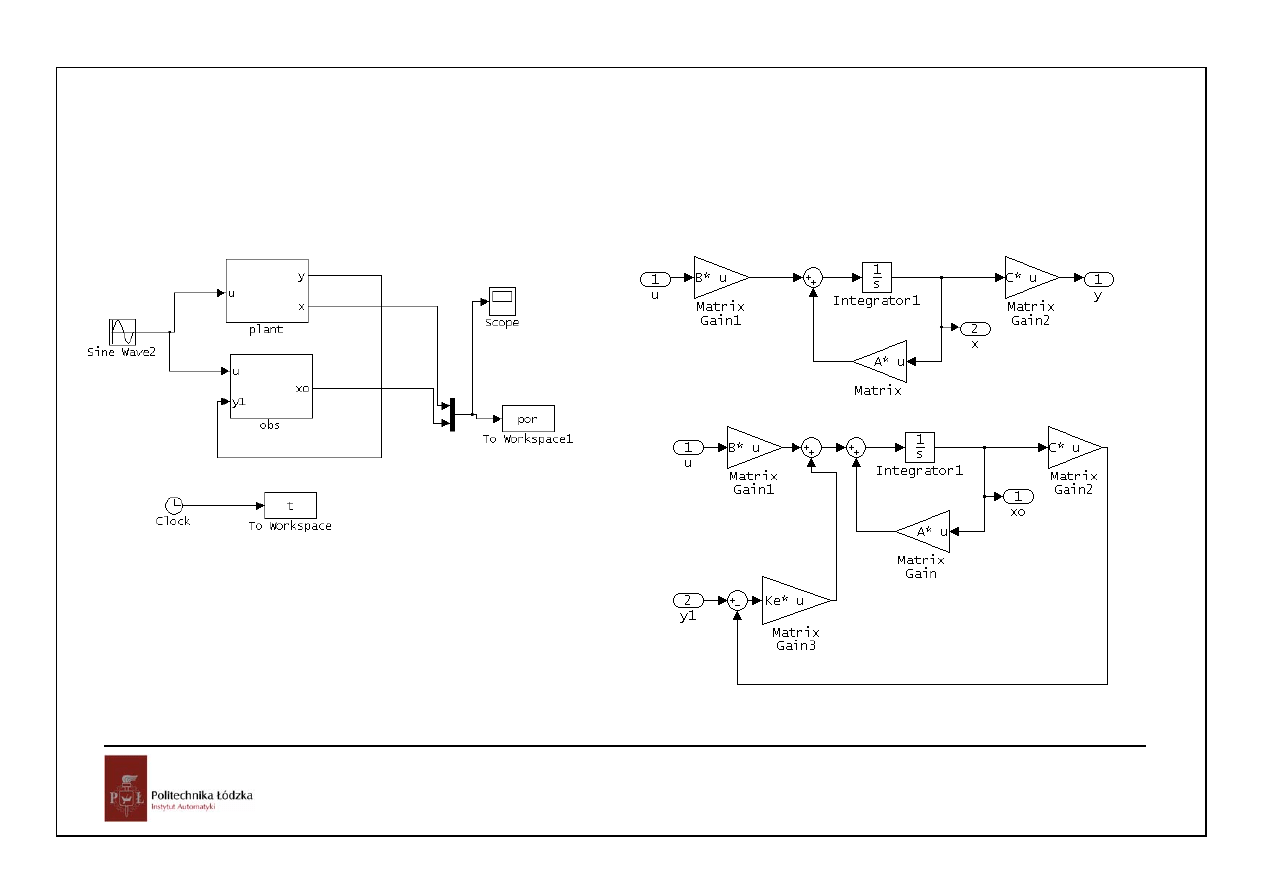
Zmienne stanu układu i obserwatora
błędy odtwarzania zmiennych stanu
wymuszenie sinusoidalne, warunki początkowe układu i obserwartora różniły się o 1 w każdej zmiennej
20
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
Praca obserwatora w układzie zamkniętym:
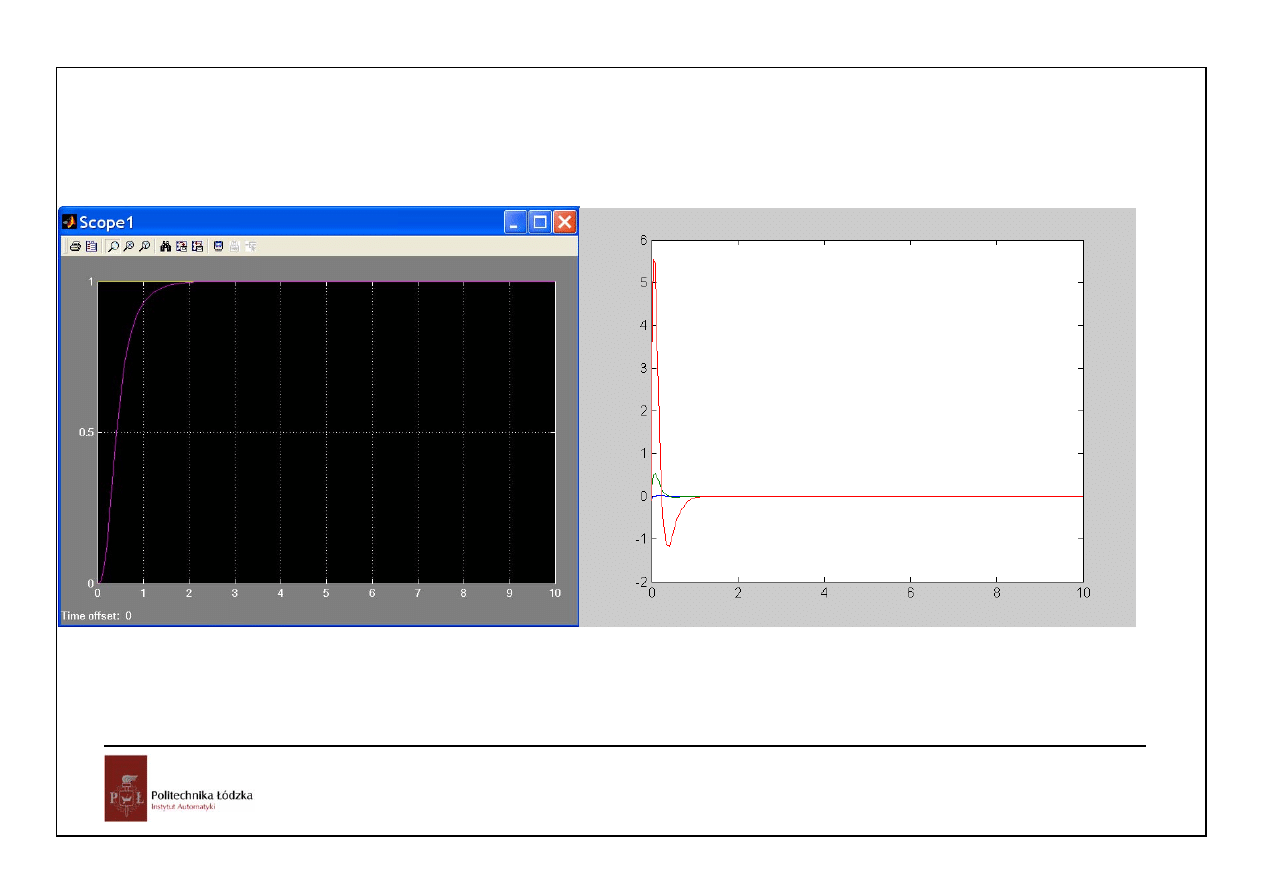
21
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
odpowiedź
jednostkowa
u.z.
błędy odtwarzania zmiennych stanu
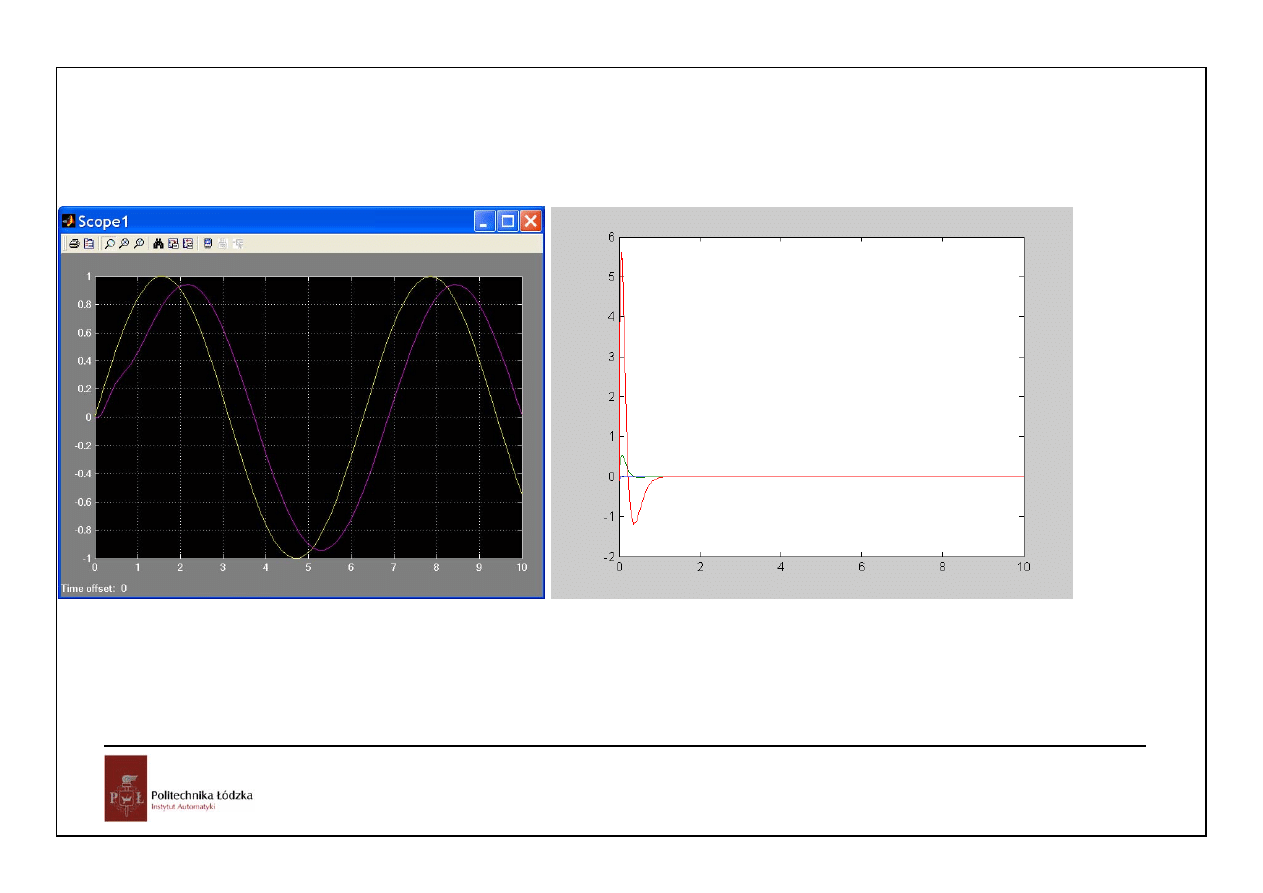
22
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
odpowiedź na wymuszenie sinusoidalne
błędy odtwarzania zmiennych stanu
23
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
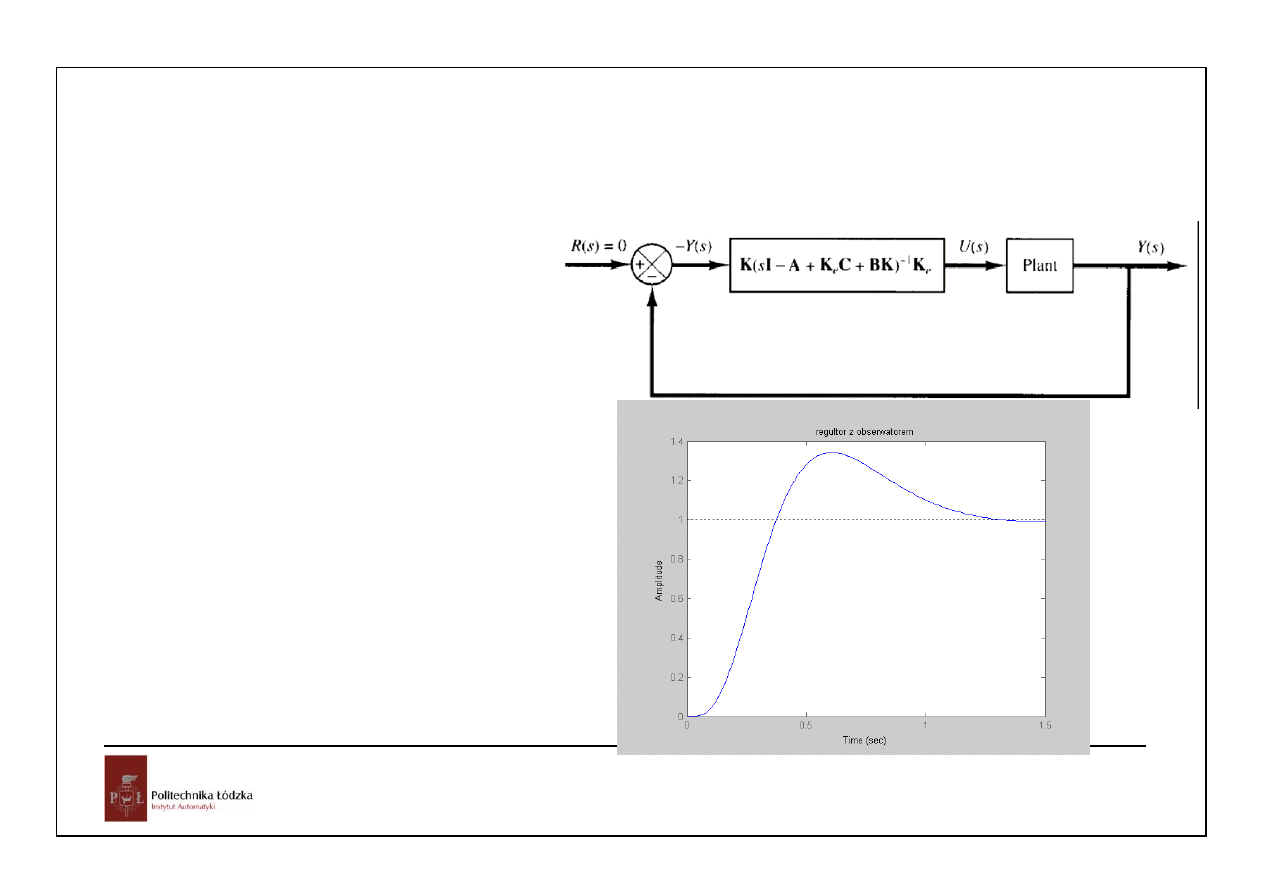
Regulator z obserwatorem można
przedstawić w postaci transmitancji:
Aro=A-Ke*C-B*K
RO=SS(Aro,Ke,K,0)
[nro dro]=ss2tf(Aro,Ke,K,0)
Tro=tf(nro,dro)
figure
step(feedback(series(RO,plant),1))
title ('regultor z obserwatorem')
Transfer function:
5689 s^2 + 2.528e004 s + 3.125e004
----------------------------------
s^3 + 42 s^2 + 697 s + 5700
24
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
(
)
0
2
4
4
1
2
3
2
1
a
u
m
K
T
s( s
)( s
)
s( s
s
)
L
s
JRs RB
K K
s
R
θ
τ
=
=
=
+
+
+ +
⎛
⎞
⎛
⎞
+
+
+
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
,
T=0.5!
C( z )
(
)
1
m
K
L
s
JRs RB
K K
R
τ
τ
⎛
⎞
+
+
+
⎜
⎟
⎝
⎠
1
sT
e
s
−
−
1
−
1
s
θ
u
p
K
a
θ
r
G(z)

25
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
(
)
1
1
2
2
2
4
2
3
4
1
2
3 4
1
1
1
2
1
2
t
t
L
L
t
e
e
( t )
s ( s
)( s
)
s
s
( s
) ( s
)
−
−
−
−
⎧
⎫
⎧
⎫
−
−
=
+
+
+
=
− +
−
⎨
⎬
⎨
⎬
+
+
+
+
⎩
⎭
⎩
⎭
{
} {
}
(
)
(
)
2
0 5
2
0 5
1
2
2
3 4
1
3 4
1
3
4
1
1
3
4
1
0 6065
0 3679
1
kT
kT
. k
k
.
z
z
z
z
Z kT
e
e
Z k
e
e
z
z e
z e
z
z
z
z
z
z
z
.
z
.
z
−
−
−
−
−
−
− +
−
=
− +
−
=
−
+
−
=
−
−
−
−
=
−
+
−
−
−
−
−
(
)
(
)(
)(
)
2
2
2
3
2
1
1
3
4
1
0 6065
0 3679
1
0 05824
0 1629
0 02753
0 05824
0 1629
0 02753
1 9744
1 1975
0 2231
1
0 6065
0 3679
z
z
z
z
G( z )
z
z
z
.
z
.
z
.
z
.
z
.
.
z
.
z
.
z
.
z
.
z
.
z
z
.
z
.
⎛
⎞
⎛
⎞
= −
−
+
−
=
⎜
⎟
⎜
⎟⎜
⎟
−
−
−
⎝
⎠
−
⎝
⎠
+
+
+
+
=
=
−
+
−
−
−
−
Stosując pierwszy wariant metody bezpośredniej znajdujemy reprezentację w przestrzeni stanu:
26
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
[
]
0
1
0
0
0
0
1
0
0 02753 0 1629 0 05824
0 2231
1 1975 1 9744
1
d
d
d
A
B
C
.
.
.
.
.
.
⎡
⎤
⎡ ⎤
⎢
⎥
⎢ ⎥
=
=
=
⎢
⎥
⎢ ⎥
⎢
⎥
⎢ ⎥
−
⎣
⎦
⎣ ⎦
Oczywiście ten układ jest całkowicie sterowalny i obserwowalny. Układ dyskretny jest niedoskonałym
modelem układu ciągłego:
27
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
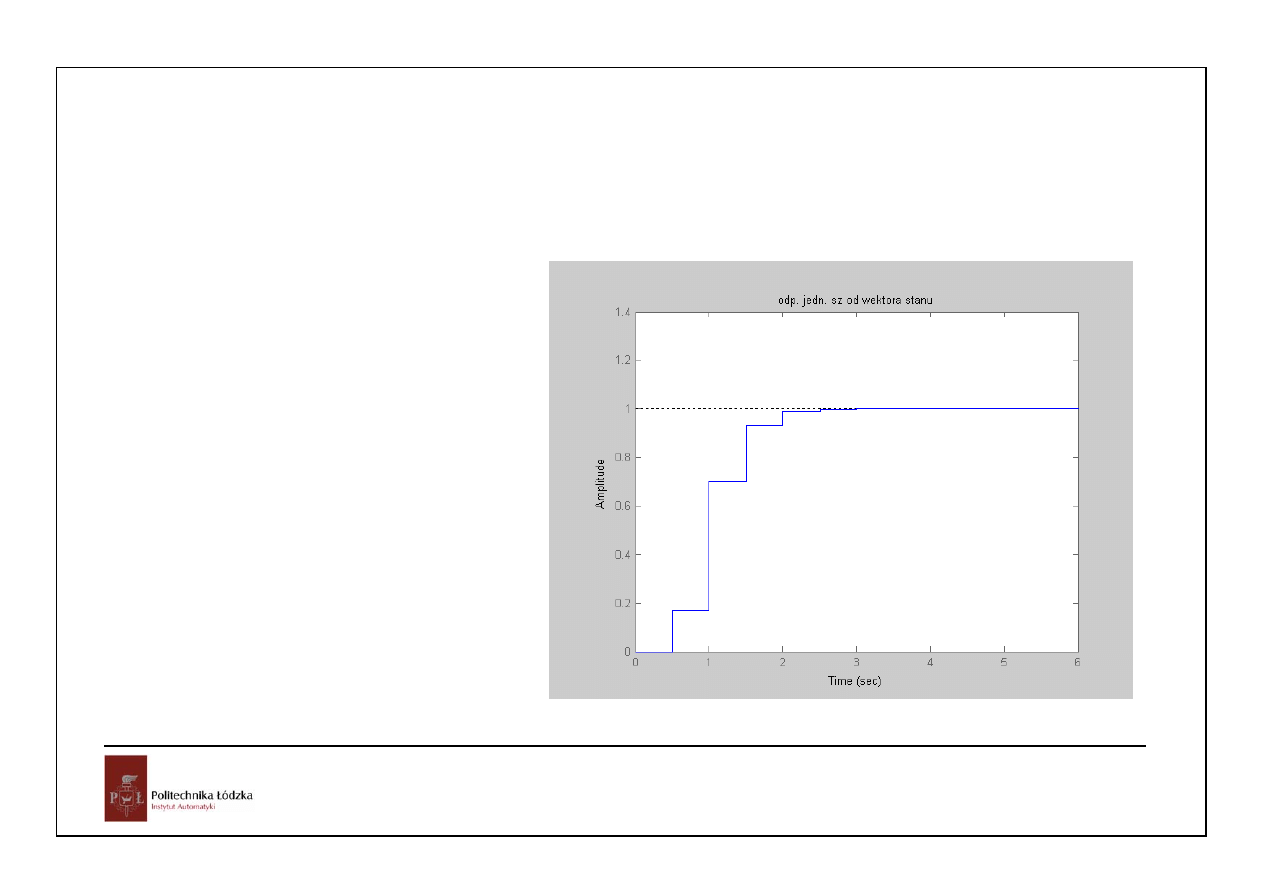
Przypuśćmy że dysponujemy zmiennymi stanu układu dyskretnego – zaprojektujmy sprzężenie zwrotne
ustalające bieguny w położeniu p
% sprzężenie od wektora stanu
p=0.1*[1 1 1];
Kd=acker(Ad,Bd,p);
Azd=Ad-Bd*Kd;
plantzd=SS(Azd,Bd/0.3411,Cd,0,Ti);
figure
step(plantzd)
title ('odp. jedn. sz od wektora stanu')
Kd =
0.2221 -1.1675 1.6744
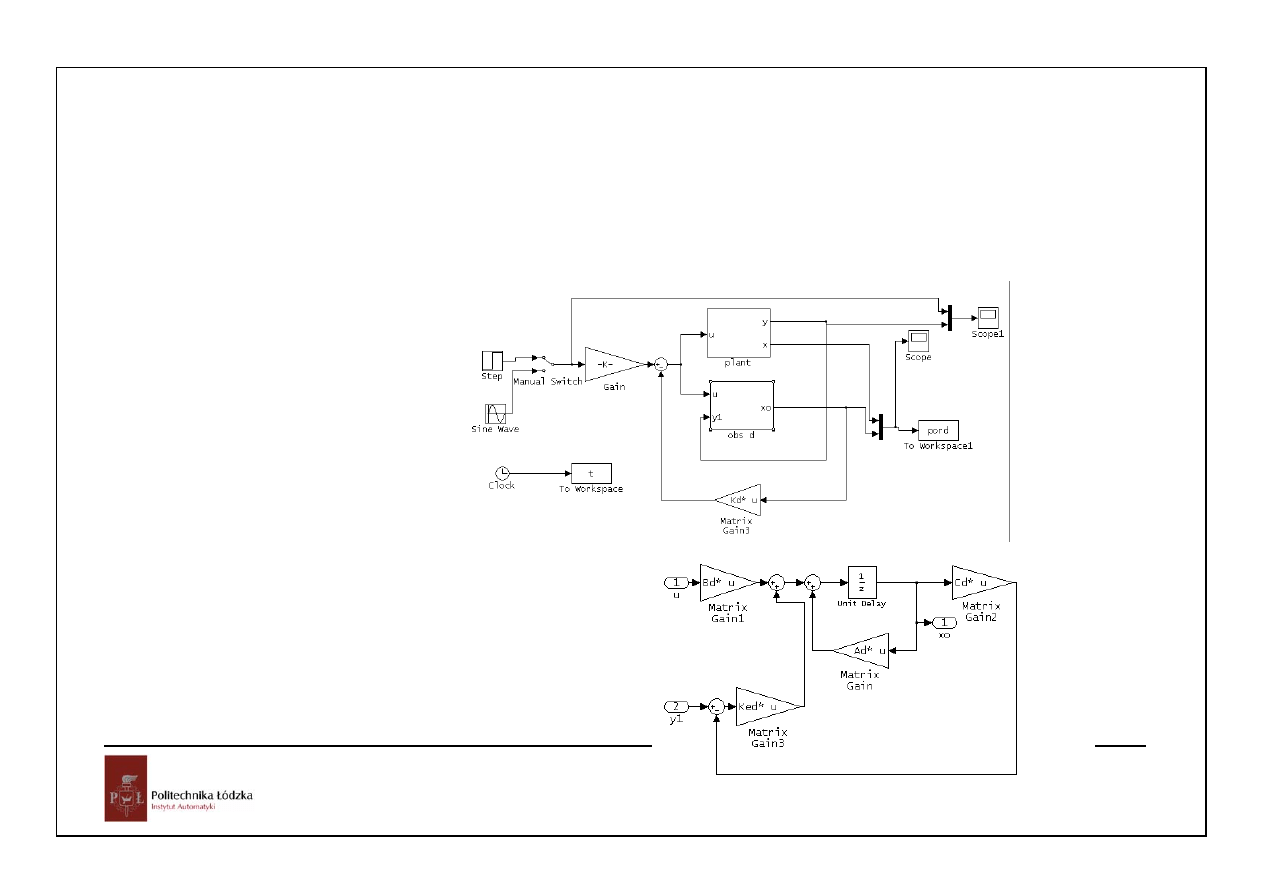
28
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
Oczywiście tymi zmiennymi stanu nie dysponujemy (można wytworzyć z pomiarów analogiczne
zmienne stanu układu ciągłego). Zaprojektujmy układ z obserwatorem:
%obserwator
pd=0.1*[1 1 1];
Kd=acker(Ad,Bd,pd)
Ked=acker(Ad',Cd',0.5*pd)'
Kd =
0.2221 -1.1675 1.6744
Ked =
3.6723
7.1487
9.5943
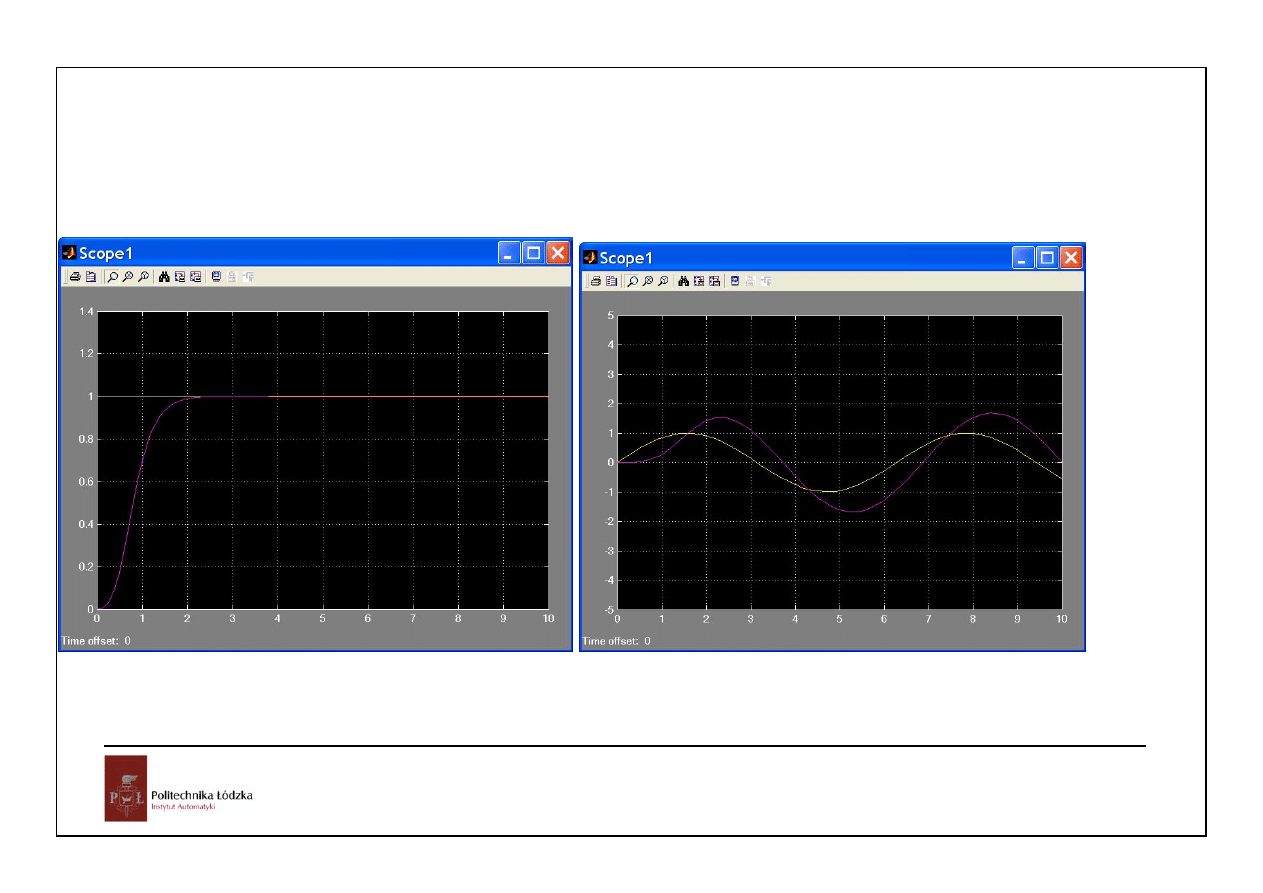
29
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
wymuszenie:
skokowe
sinusoidalne
odpowiedź układu ciągłego z dyskretnym obserwatorem
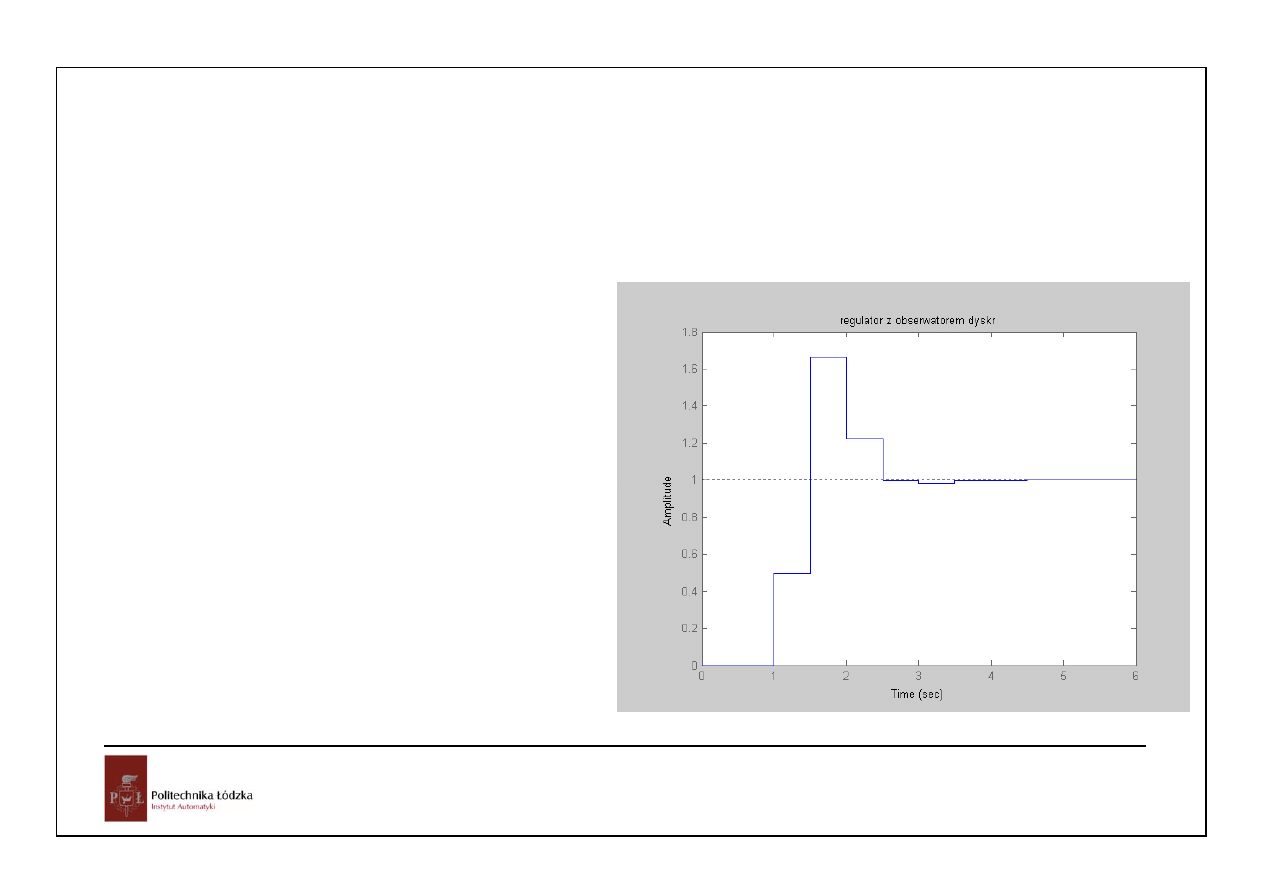
30
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
Realizacja regulatora i obserwatora w jednej transmitancji:
Arod=Ad-Ked*Cd-Bd*Kd
ROd=SS(Arod,Ked,Kd,0,Ti)
figure
step(feedback(series(ROd,plantd),1))
title ('regulator z obserwatorem dyskr')
[nrod drod]=ss2tf(Arod,Ked,Kd,0)
Tror=tf(nro,dro,Ti)
nrod =
0 8.5341 -7.7074 1.6867
drod =
1.0000 1.5244 1.3977 0.2081
Transfer function:
5689 z^2 + 2.528e004 z + 3.125e004
----------------------------------
z^3 + 42 z^2 + 697 z + 5700 Sampling time: 0.5
31
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego

32
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
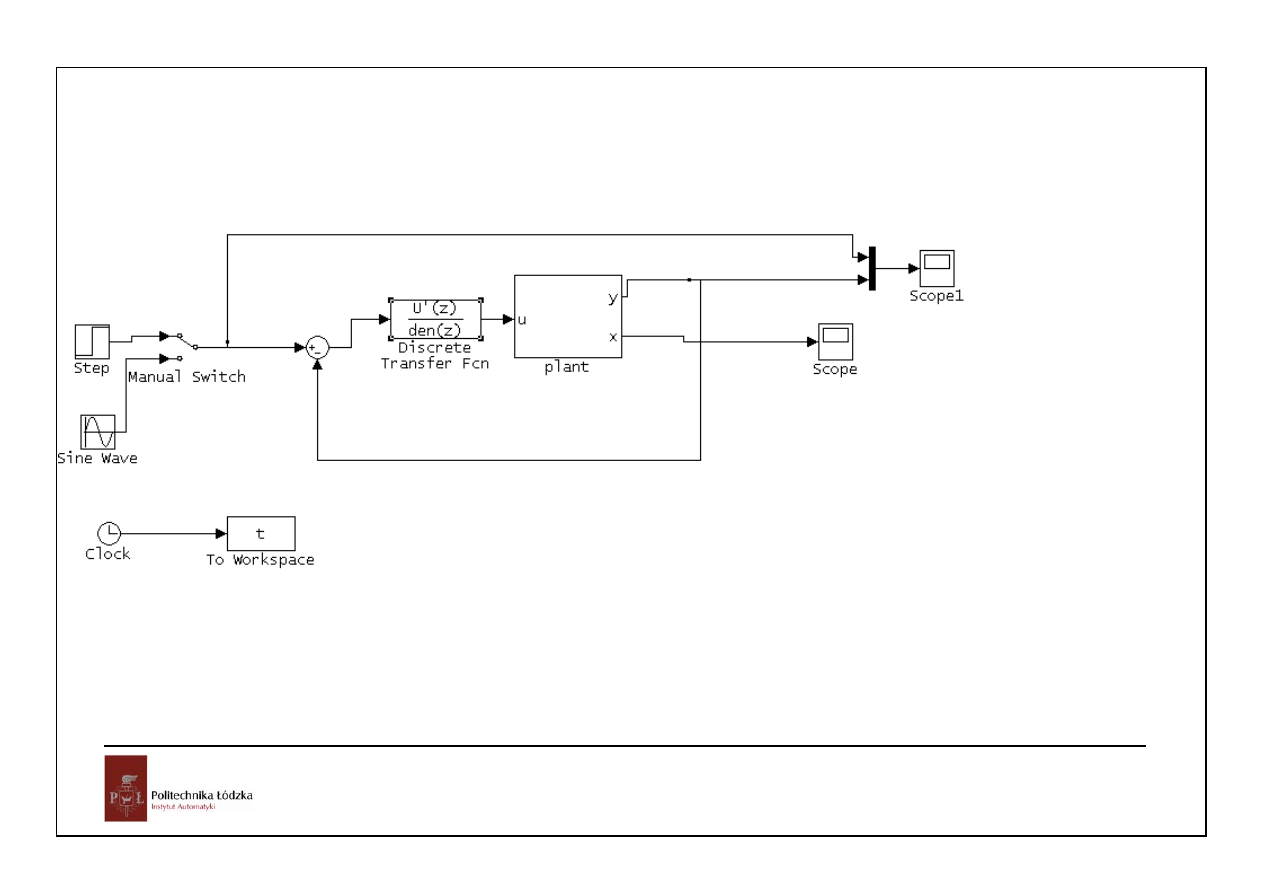
Obliczanie sterowania dead-beat
Układ
)
(
)
(
)
(
)
(
)
)
1
((
kT
cx
kT
y
kT
bu
kT
Ax
T
k
x
=
+
=
+
należy wyposażyć w regulator zapewniający zanikanie przebiegów przejściowych w N okresach impulsowania i zerowy uchyb
ustalony przy wymuszeniu jednostkowym.
[
]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
−
−
)
0
(
)
(
)
)
1
((
)
(
1
0
u
T
u
T
N
u
b
A
Ab
b
x
A
NT
x
N
N
#
"
1
)
(
)
(
=
=
NT
cx
NT
y
N
k
dla
NT
u
kT
u
kT
x
T
k
x
≥
=
=
+
)
(
)
(
),
(
)
)
1
((

33
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
)
(
)
(
)
(
NT
bu
NT
Ax
NT
x
+
=
Jeśli A nie ma wart wł. równych 1, to macierz I-A jest odwracalna i
)
(
)
(
)
(
1
NT
bu
A
I
NT
x
−
−
=
1
)
(
)
(
)
(
1
=
−
=
−
NT
bu
A
I
c
NT
y
)
1
(
1
)
(
1
)
(
1
o
G
b
A
I
c
NT
u
=
−
=
−
Potem wyznacza się x(NT), potem ciąg sterujący.
Jeśli A ma wart wł. równą 1, to u(NT)=0 i
(
)
0
)
(
=
−
NT
x
A
I
Równanie to ma wiersze liniowo zależne – jeden z nich należy zastąpić przez
1
)
(
=
NT
cx
Stąd wyznacza się x(NT), potem ciąg sterujący.
Przyjmiemy x
0
=0 i N=3

34
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
Zadanie
Kod Matlaba
Rezultat
Jeśli A ma wart wł. równą 1, to u(NT)=0 i
(
)
0
)
(
=
−
NT
x
A
I
Równanie to ma wiersze liniowo zależne – jeden
z nich należy zastąpić przez
1
)
(
=
NT
cx
%DEADBEAT
IAd=eye(size(Ad))-Ad;
XNT=inv([Cd;IAd(1:2,:)])*[1;0;0]
N=3
XNT =
4.0214
4.0214
4.0214
N =
3
Obliczenie ciągu sterującego:
[
]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
−
−
)
0
(
)
(
)
)
1
((
)
(
1
0
u
T
u
T
N
u
b
A
Ab
b
x
A
NT
x
N
N
#
"
U=inv([Ad*Ad*Bd,Ad*Bd,Bd])*XNT
U =
4.0214
-3.9184
0.8972
Obliczenie kolejnych wartości
wektora stanu i wyjścia:
X1=Bd*U(1);
X2=Ad*X1+Bd*U(2);
X3=Ad*X2+Bd*U(3);
Y=[0;Cd*X1;Cd*X2;Cd*X3]
Y =
0
0.2342
0.8893
1.0000
Dla sprawdzenia
35
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
Obliczenie kolejnych wartości uchybu
E0=1-Y(1)
E1=1-Y(2)
E2=1-Y(3)
E0 =
1
E1 =
0.7658
E2 =
0.1107
Obliczenie transmitancji regulatora i
odpowiedź jednostkowa
TrReg=tf(U',[E0,E1,E2],Ti)
figure
step(feedback(series(TrReg,plantd),1))
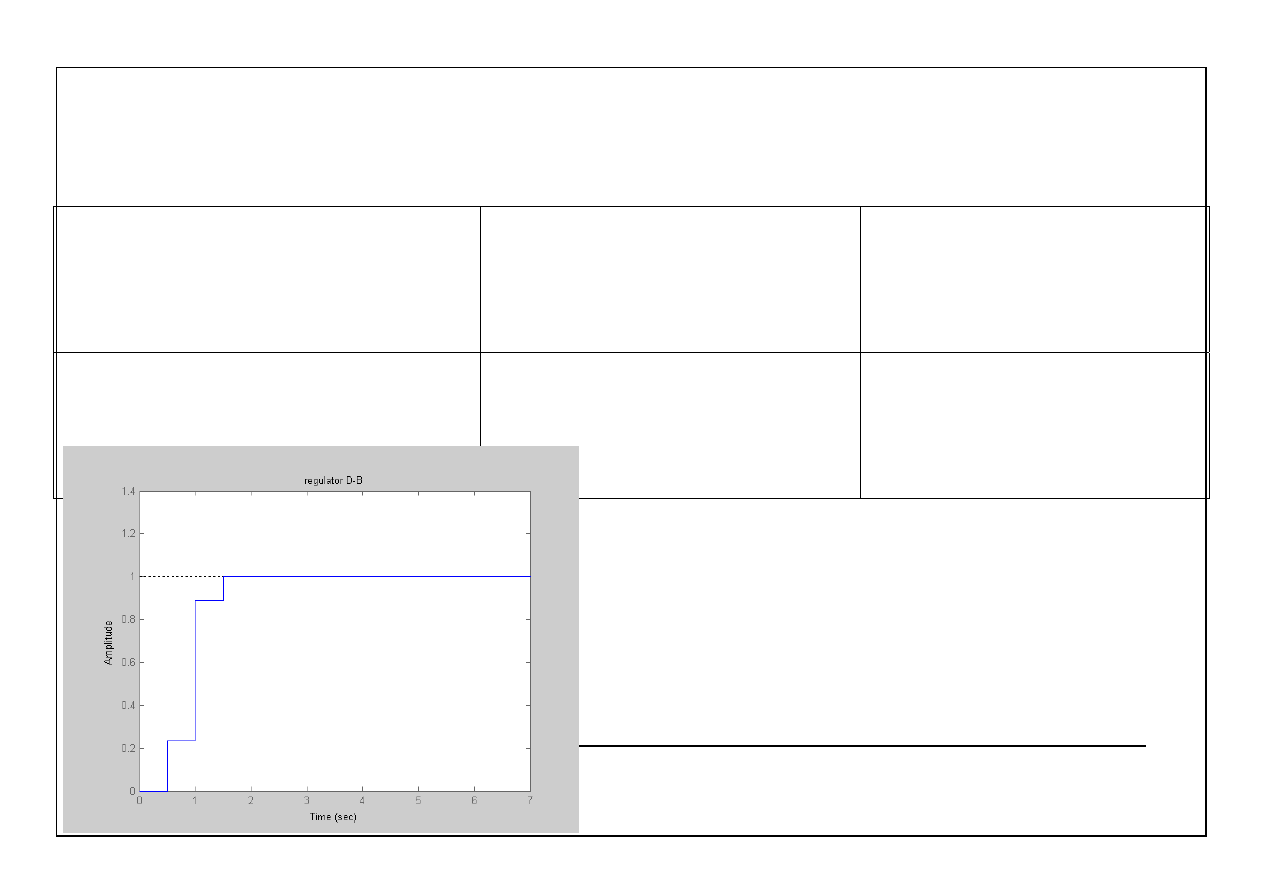
title ('regulator D-B')
Transfer function:
4.021 z^2 - 3.918 z + 0.8972
----------------------------
z^2 + 0.7658 z + 0.1107
Sampling time: 0.5
36
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
37
Automatyka i sterowanie 10 Przykłady - zmienne stanu
Układy czasu ciągłego
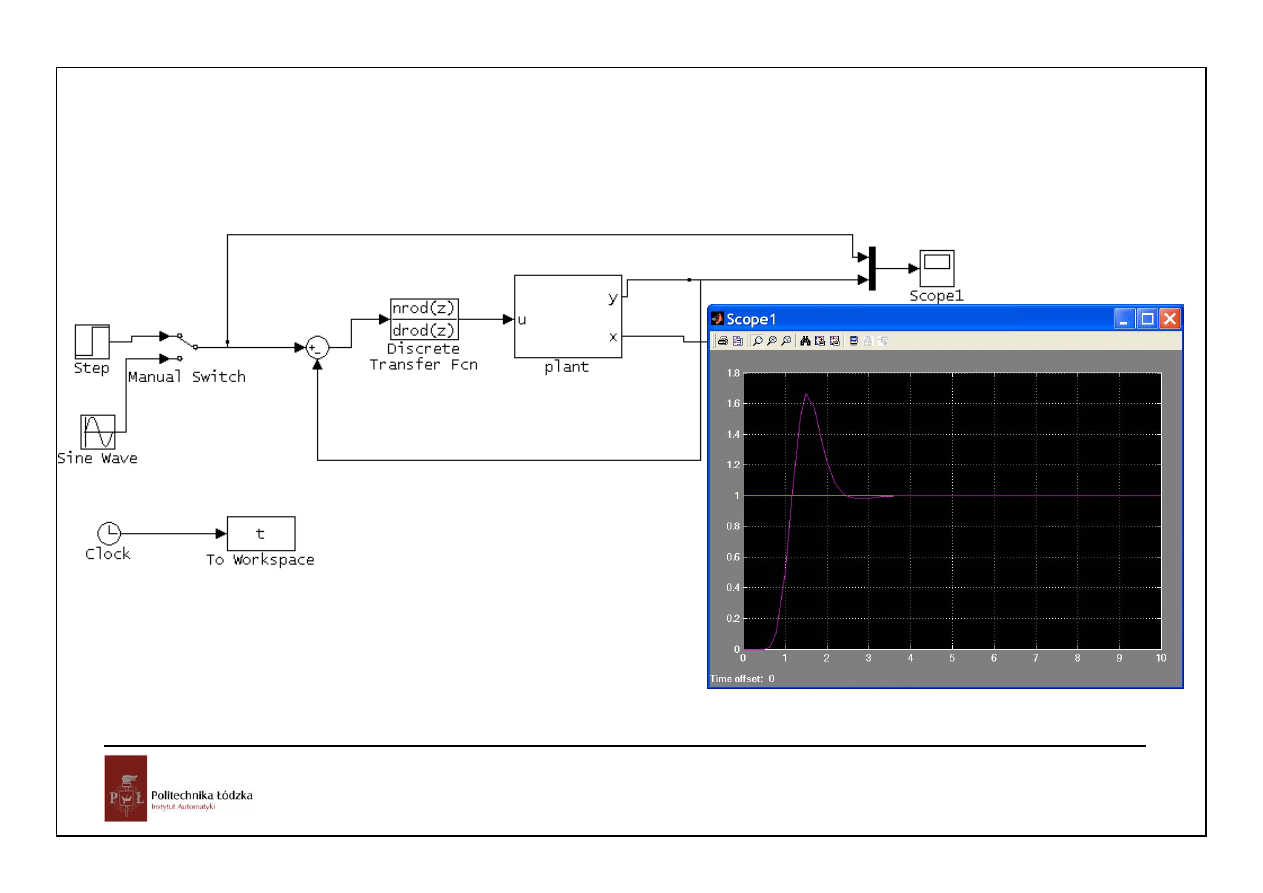
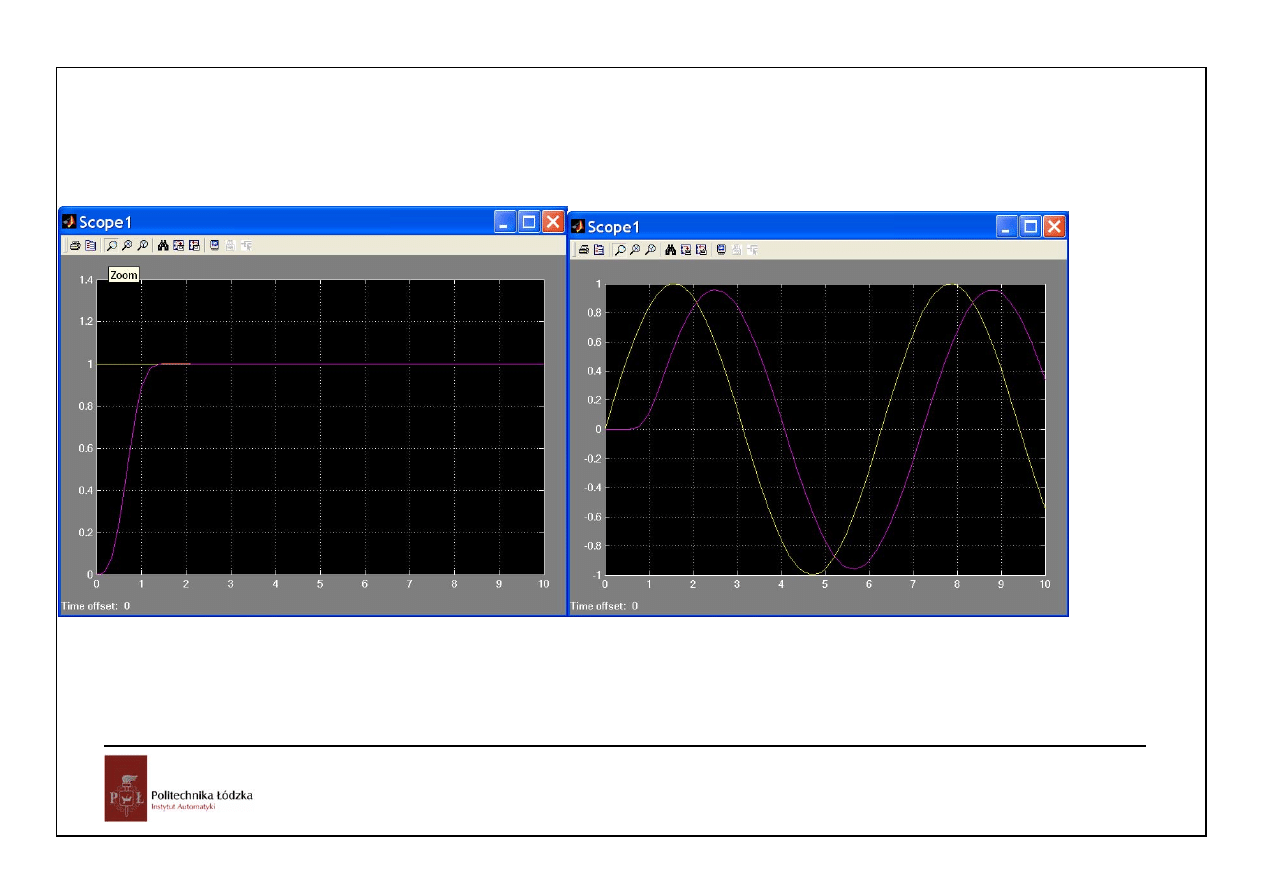
wymuszenie:
skokowe
sinusoidalne
odpowiedź układu ciągłego z dyskretnym regulatorem dead-beat
Wyszukiwarka
Podobne podstrony:
automatyka i sterowanie wyklad 16
automatyka i sterowanie wyklad Nieznany (16)
automatyka i sterowanie wyklad 15
automatyka i sterowanie wyklad Nieznany (8)
automatyka i sterowanie wyklad Nieznany (2)
automatyka i sterowanie wyklad 3
automatyka i sterowanie wyklad Nieznany (7)
automatyka i sterowanie wyklad Nieznany (14)
automatyka i sterowanie wyklad Nieznany (12)
automatyka i sterowanie wyklad Nieznany (5)
automatyka i sterowanie wyklad 9
automatyka i sterowanie wyklad 11
automatyka i sterowanie wyklad 4
automatyka i sterowanie wyklad 5
automatyka i sterowanie wyklad Nieznany (10)
automatyka i sterowanie wyklad Nieznany (3)
automatyka i sterowanie wyklad 8
automatyka i sterowanie wyklad 2
automatyka i sterowanie wyklad 15
więcej podobnych podstron