
Jacek Kabziński
Automatyka i sterowanie
————————————————————————————————————————

2
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Układy z czasem ciągłym, jedno wejście – jedno wyjście (continous time single
input- single output –SISO)
Liniowe, stacjonarne równanie różniczkowe, transmitancja operatorowa, odpowiedź układu
warunek realizowalności, n – rząd układu
stałe współczynniki, zależne od struktury i parametrów fizycznych układu.
Do rozwiązania takiego równania potrzebne są warunki początkowe: y(0), y’(0), …,y
(n-1)
(0) i oczywiście
pełna znajomość sygnału wejściowego i jego pochodnych.
Możemy wyznaczyć rozwiązanie korzystając z transformaty Laplace’a
( )
(
)
( )
(
)
1
1
1
1
0
1
1
0
...
( )
...
( )
n
n
m
m
n
n
m
m
a y
a y
a y a y t
b u
b u
b u b u t
−
−
−
−
+
+ +
+
=
+
+ +
+
m
n
≥
[
]
0
st
L f ( t )
f ( t )e dt
F( s )
∞
−
=
=
∫

3
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Pamiętamy, że
0
df ( t )
L
sF( s ) f ( )
dt
⎡
⎤ =
−
⎢
⎥
⎣
⎦
[
]
2
2
2
0
0
0
0
0
d f ( t )
d df ( t )
df ( t )
L
L
sL
f '( ) s sF( s ) f ( )
f '( )
dt
dt
dt
dt
s F( s ) sf ( ) sf '( )
⎡
⎤
⎡
⎤
⎛
⎞
⎡
⎤
=
=
−
=
−
−
=
⎜
⎟
⎢
⎥
⎢
⎥
⎢
⎥
⎝
⎠
⎣
⎦
⎣
⎦
⎣
⎦
=
−
−
.....
(
)
(
)
2
1
1
2
0
0
0
0
k
k
k
k
k
k
k
d f ( t )
L
s F( s ) s
f ( ) s
f '( )
sf
( ) f
( )
dt
−
−
−
−
⎡
⎤
=
−
−
− −
−
⎢
⎥
⎣
⎦
…
Przy zerowych warunkach początkowych wykonujemy transformatę Laplace’a obu stron równania:
( )
(
)
( )
(
)
0
1
1
1
0
1
1
1
...
...
b
s
b
s
b
s
b
s
U
a
s
a
s
a
s
a
s
Y
m
m
m
m
n
n
n
n
+
+
+
+
=
+
+
+
+
−
−
−
−

4
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
i otrzymujemy transmitancję układu:
1
0
1
0
...
( )
( )
( )
=
( )
...
( )
m
m
n
n
b s
b s b
Y s
L s
G s
U s
a s
a s a
M s
+ +
+
=
=
+ +
+
Znając transmitancję można wyznaczyć odpowiedź układu na dowolny sygnał wejściowy.
Transformata sygnału wyjściowego: Y(s)=G(s)·U(s) , czyli
( )
( )
1
1
( )
( )
y t
L Y s
L
G s U s
−
−
=
=
⎡
⎤
⎡
⎤
⎣
⎦
⎣
⎦
Jeżeli wymuszenie jest impulsem Diraca:
u( t )
( t )
δ
=
, czyli U(s)=1, to otrzymujemy odpowiedź
impulsową układu:
czyli odpowiedź impulsowa jest oryginałem transmitancji, a interpretując wzór
( )
( )
1
1
( )
( )
y t
L Y s
L
G s U s
−
−
=
=
⎡
⎤
⎡
⎤
⎣
⎦
⎣
⎦
( )
1
( )
( )
y t
g t
L G s
−
=
=
⎡
⎤
⎣
⎦

5
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
można powiedzieć, że odpowiedź na dowolne wymuszenie przy zerowych warunkach początkowych jest
splotem odpowiedzi impulsowej i tego wymuszenia.
Jeżeli wykorzystamy np. metodę residuów do wyznaczenia oryginału odpowiedzi, to musimy rozważyć
bieguny transmitancji G(s) (czyli miejsca zerowe jej mianownika M(s)) i ewentualne bieguny U(s), która
też może być funkcją wymierną. Jeżeli te dwa zbiory biegunów są rozłączne to:
(
)
(
)
(
)
(
)
j
j
j
j
j
j
j
j
st
st
s s
s s
j:s jest bieg .Y ( s )
j:s jest bie
st
s s
j:s jest bie
st
s s
j
g .U
:s jest bie
( s )
g
g .G(
.Y ( s )
s )
y( t )
Re s Y ( s )e
Re s G( s )U( s )e
Re s G(
Re s G( s )U( s )
s )
e
e
U( s )
=
=
=
=
=
=
=
=
+
∑
∑
∑
∑
składowa przejściowa odpowiedzi
składowa ustalona odpowiedzi

6
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Jeżeli warunki początkowe nie są zerowe, to po wykonaniu transformaty Laplace’a zamiast
Y ( s )M ( s ) L( s )U( s )
=
otrzymamy
Y ( s )M ( s ) W ( s ) L( s )U( s )
−
=
gdzie W(s) jest wielomianem stopnia nie wyższego niż n-1, którego współczynniki zależą tylko od
warunków początkowych (a nie od wymuszenia). Wtedy
W ( s )
M ( s )
L( s )
U( s )
M
Y (
( s )
s )
=
+
składowa swobodna
składowa wymuszona
Na właściwości składowej swobodnej odpowiedzi mają wpływ bieguny transmitancji (czyli miejsca
zerowe jej wielomianu M(s)) i oczywiście warunki początkowe.
Na właściwości składowej przejściowej odpowiedzi mają wpływ bieguny i zera transmitancji (czyli
miejsca zerowe jej wielomianu M(s) i L(s)).
Na właściwości składowej ustalonej odpowiedzi mają wpływ bieguny wymuszenia.

7
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Jeżeli wymuszeniem jest funkcja jednostkowa, a warunki początkowe są zerowe to
( )
( )
1
1
1
( )
y t
L Y s
L G s
s
−
−
⎡
⎤
=
=
⎡
⎤
⎣
⎦
⎢
⎥
⎣
⎦
i jeśli biegunem G(s) nie jest 0 to:
0
1
0
1
1
j
j
j
j
st
s s
j:s jest bieg .G( s )
st
s s
j:s jest bieg
st
s
.G( s )
Re s G( s ) e
s
Re s G
y( t )
( s ) e
s
Re s G( s ) e
s
G( )
=
=
=
⎛
⎞
⎜
⎟
⎝
⎠
⎛
⎞
⎜
⎛
⎞
⎟
⎝
⎠
=
+
+
=
⎜
⎟
⎝
⎠
=
∑
∑

8
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Transmitancję G(s) można przedstawić w rozwinięciu na ułamki proste. Jeśli przyjmiemy, że bieguny
transmitancji są pojedyncze – rzeczywiste lub zespolone parami sprzężone, to takie rozwinięcie
transmitancji jest równoznaczne z przedstawieniem jej w postaci połączenia równoległego kilku
transmitancji: rzędu 1 (odpowiadają biegunom rzeczywistym) i rzędu 2, które odpowiadają biegunom
zespolonym sprzężonym, czyli są transmitancjami elementów oscylacyjnych. Odpowiedź układu o
transmitancji G(s) można więc postrzegać jak sumę odpowiedzi transmitancji rzędu 1 i 2 wynikających z
rozkładu na ułamki proste.
Układ nazywamy stabilnym, jeśli składowa przejściowa jego odpowiedzi zanika. Koniecznym i
dostatecznym warunkiem stabilności będzie więc zanikanie składowych przejściowych odpowiedzi
wszystkich układów wynikających z rozkładu na ułamki proste, czyli ujemne bieguny rzeczywiste i
ujemne części rzeczywiste biegunów zespolonych (wszystkie bieguny położone w lewej
półpłaszczyźnie płaszczyzny zespolonej).
9
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Układ pierwszego rzędu, związki miedzy biegunem a przebiegami czasowymi:
1
1
1
at
f
n
a
Y ( s ) G( s )R( s )
s( s a )
s s a
y( t ) c ( t ) c ( t )
e
−
=
=
= −
+
+
=
+
= −

10
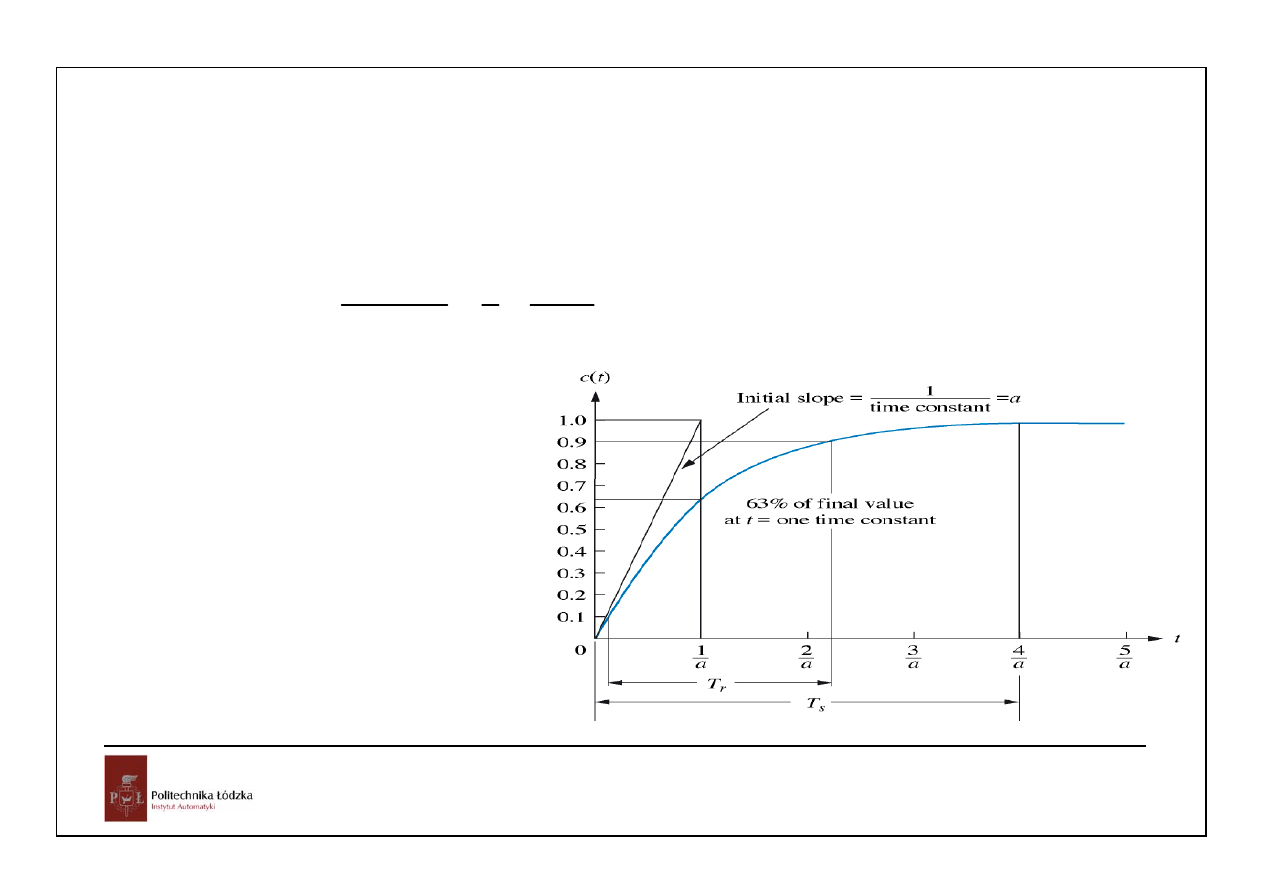
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
T
c
stała czasowa
T
R
czas narastania – od wartości 0.1do osiągnięcia 0.9 wartości ustalonej
T
S
czas regulacji do osiągnięcia i utrzymania wartości +- 2% od wartości ustalonej
1
2 31 0 11 2 2
4
C
R
S
T
/ a
.
.
.
T
a
a
a
T
a
=
=
−
=
=

11
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Układ drugiego rzędu, związki miedzy parametrami (wsp. tłumienia i pulsacja drgań własnych),
biegunami a przebiegami czasowymi:
2
2
2
2
2
2
2
2
0
0
0
0
0
0
1
2
n
n
d y( t )
dy( t )
M
f ( t ) B
Ky( t )
dt
dt
M ( s Y ( s ) sy( ) y'( )) F( s ) B( sY ( s ) y( )) KY ( s )
y'( ) y( )
Ms Y ( s ) BsY ( s ) KY ( s ) F( s )
G( s )
Ms
Bs K
s
( B / M )s K / M
s
s
ςω
ω
=
−
−
−
−
=
−
−
−
=
=
+
+
=
=
+
+
+
+
=
+
+
KM
B
M
K
n
2
;
=
=
ς
ω
12
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
http://www.wiley.com/college/nise/0471794759/swf/SOcalculator.swf
2
2
2
2
1
2
2
1
1
1
1
1
n
n
n
n
n
n
1
2
1
2
s
s
=0
s
s
gdy
s ,s rzeczywiste
gdy
zespolone
gdy
s =s rzeczywiste
ςω
ω
ςω ω ς
ςω ω ς
ς
ς
ς
+
+
⇒
= −
+
−
= −
−
−
> ⇒
< ⇒
= ⇒
2
2
2
2
2
2
2
1
2
2
1
1
1
n
n
n
n
n
n
n
t
n
G(s)
s
s
odp. jednostkowa Y(s)
s( s
s
)
y( t )
e
cos(
t
)
,
tan (
)
ςω
ω
ςω
ω
ω
ςω
ω
βω
ϕ
β
ς
β
ς
ϕ
β
−
−
=
+
+
=
+
+
= −
−
=
−
=
13
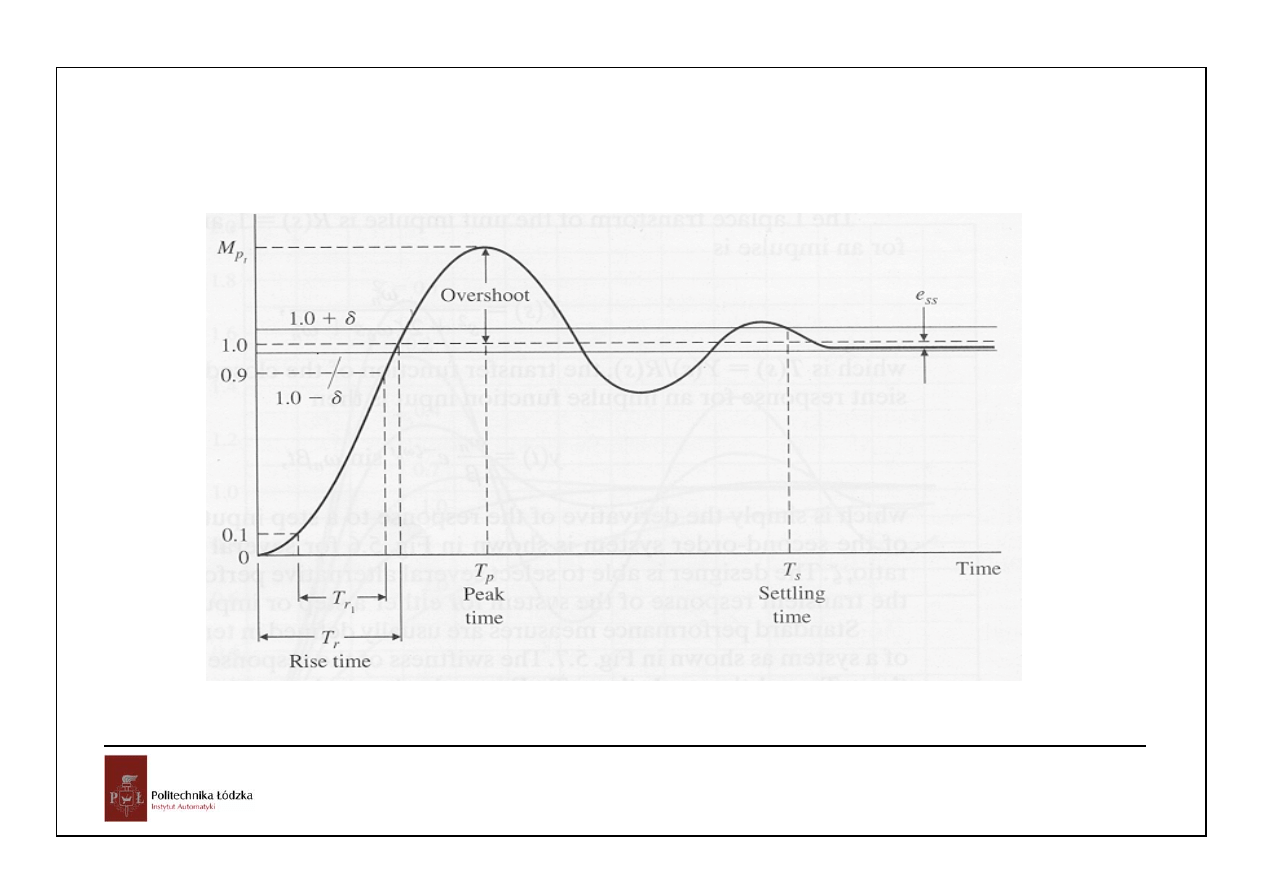
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych

14
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
2
2
2
2
2
2
1
1
2
0
1
1
100
n
t
n
n
n
t
n
n
n
p
n
n
/
p
/
L[ y'( t )] sY ( s )
( s
s
)
y'( t )
e
sin(
t )
t
T
M
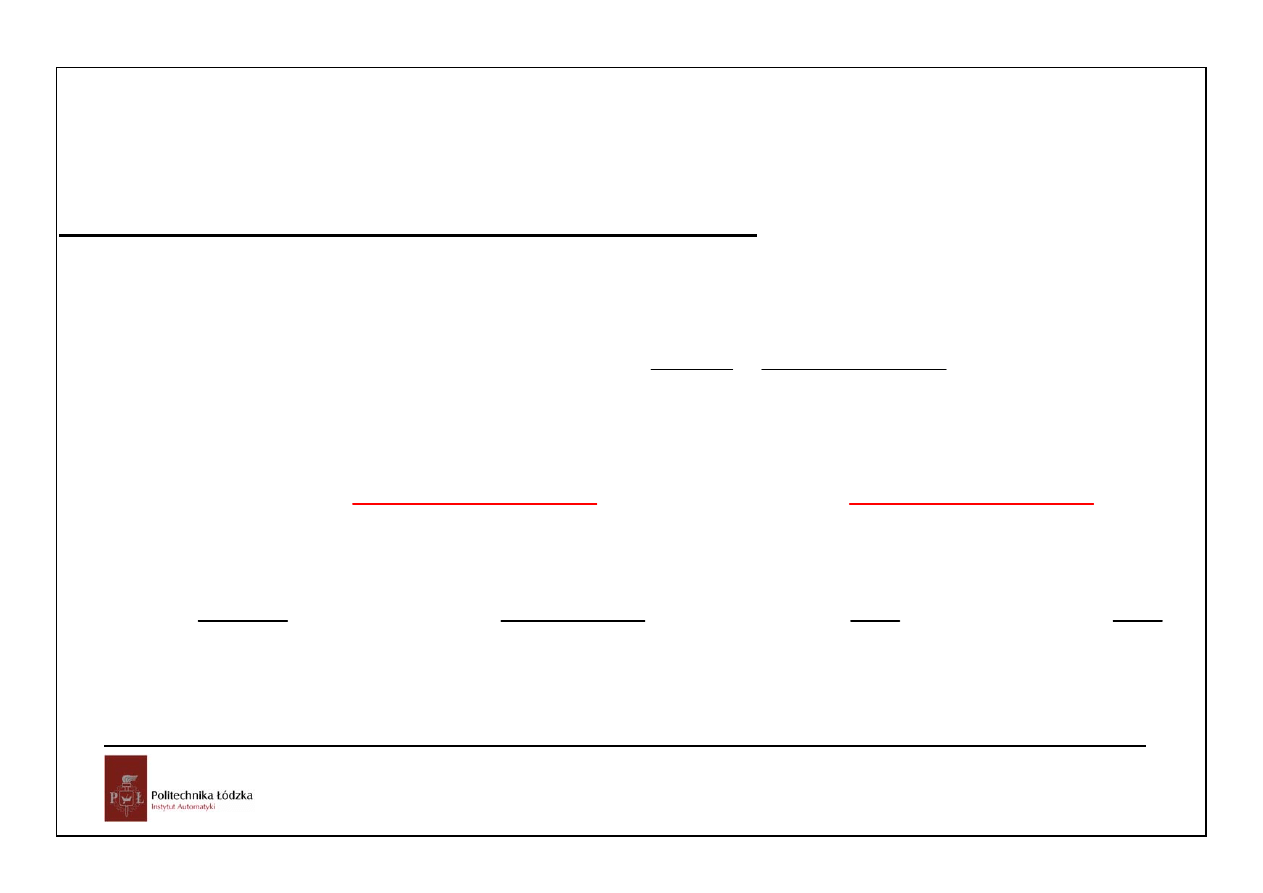
e
Przeregulowanie
P.O.
e
ζω
ζπ
ς
ζπ
ς
ω
ζω
ω
ω
ω β
β
ω β
π
π
π
ω β ω
ς
−
−
−
−
−
=
=
+
+
=
=
⇓
=
⇓
=
=
−
= +
=
0 02
4
4
4
n s
T
n s
s
n
e
.
T
T
ζω
ζω
τ
ζω
−
<
≅
⇓
≅
=
15
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Transmitancja widmowa. Charakterystyki częstotliwościowe
Rozważmy ustaloną składową odpowiedzi stabilnego układu o transmitancji G(s) na wymuszenie
m
u( t ) U cos( t )
ω
=
Transformatą Laplace’a tego wymuszenia jest
(
)(
)
2
2
m
m
U s
U s
U( s )
s
s
j
s
j
ω
ω
ω
=
=
+
−
+
mamy więc dwa
bieguny związane z wymuszeniem.
(
)(
)
(
)(
)
(
)
2
2
2
2
j t
j t
j t
j
st
t
st
ust
m
m
s j
s
j
m
m
m
m
U s
U s
Re s G( s )
e
Re s G( s )
e
s
j
s
j
s
j
y ( t )
U
j
U j
U
U
G( j )
e
G( j )
e
G( j )
e
G( j )
e
j
s
j
j
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−
−
=
=−
⎛
⎞
⎛
⎞
+
⎜
⎟
⎜
⎟
−
+
−
+
⎝
⎠
⎝
=
−
=
+
−
=
+
⎠
−
−

16
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
j ( )
j ( )
G( j ) G( j ) e
G( j ) G( j ) e
ϕ ω
ϕ ω
ω
ω
ω
ω
−
=
−
=
(
)
(
)
(
)
(
)
(
)
(
)
2
2
1
2
j
t
(
)
j
t
(
)
j
t
(
)
j
t
(
)
m
m
ust
m
m
U
U
y ( t ) G( j )
e
G( j )
e
G( j ) U
e
e
G( j ) U cos
t
( )
ω ϕ ω
ω ϕ ω
ω ϕ ω
ω ϕ ω
ω
ω
ω
ω
ω ϕ ω
+
−
+
+
−
+
=
+
=
=
+
=
+
jx
jx
e
cos x
j sin x
e
cos x
j sin x
−
=
+
=
−
(
)
1
2
jx
jx
cos x
e
e
−
=
+
17
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Transmitancja widmowa:
j ( )
G( j ) G( j ) e
P( ) jQ( )
ϕ ω
ω
ω
ω
ω
=
=
+
2
2
Q( )
A( )
P ( ) Q ( ),
( ) arctg
P( )
ω
ω
ω
ω
φ ω
ω
=
+
=
m
m
Y ( )
A( )
X ( )
ω
ω
ω
=
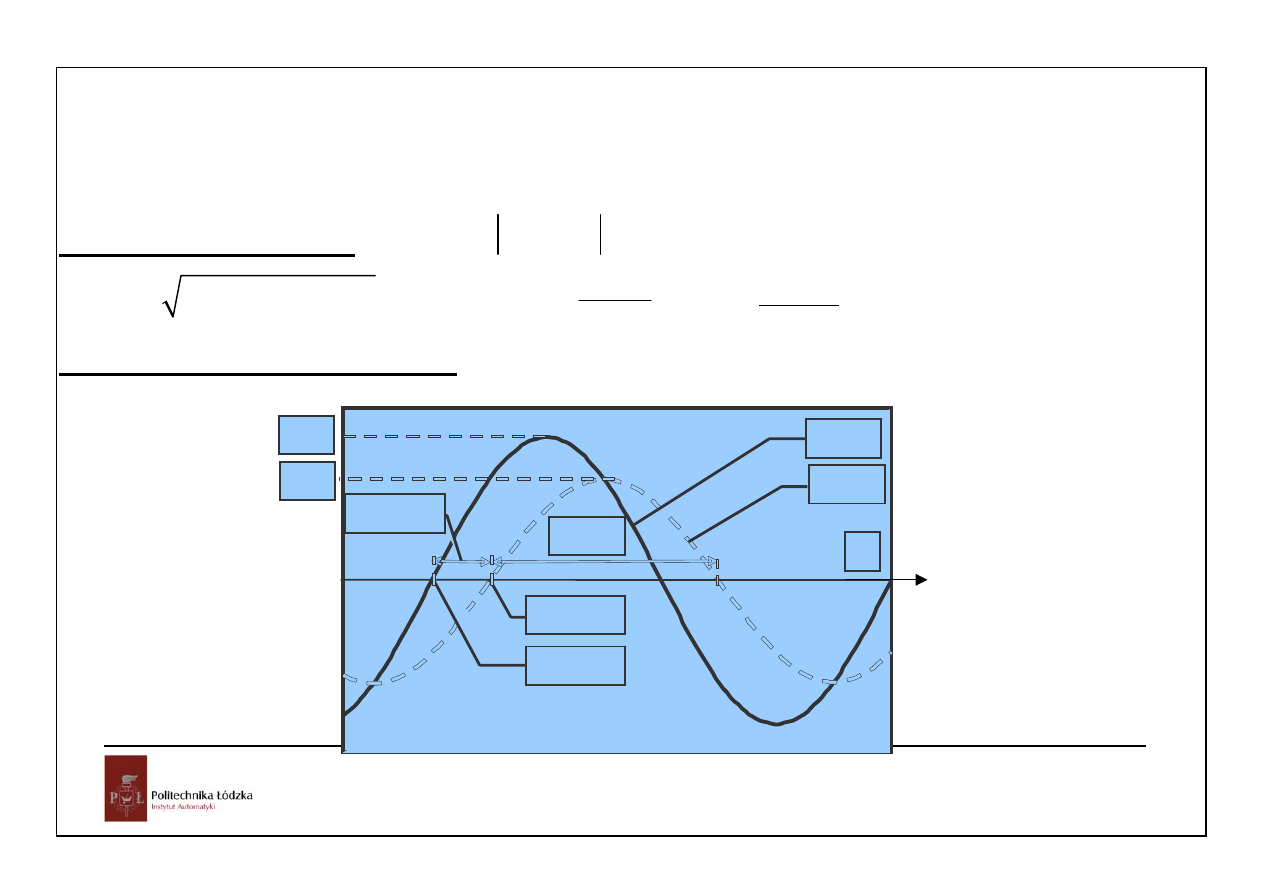
Charakterystyki częstotliwościowe mogą być mierzone:
U
m
Y
m
u(t)
y(t)
t
T/2
t
ϕ
=
ϕ/ω
t
y
=
φ
u
/
ω
t
x
=
φ
x
/
ω

18
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Charakterystyka amplitudowo-fazowa
Charakterystyki logarytmiczne:
10
10
20
20
Lm( )
log A( )
log |G( j )|
ω
ω
ω
=
=
i
( )
ϕ ω
w funkcji częstotliwości przedstawionej w
skali logarytmicznej.
Pasmo przenoszenia – zakres pulsacji, w którym charakterystyka modułu nie opada bardziej niż 3dB
poniżej wzmocnienia w stanie ustalonym (dla małej pulsacji). Oznaczmy prawy kraniec pasma
przenoszenia przez
3dB
ω
. Im większa
3dB
ω
, tym szybszy układ. W przybliżeniu:
czas narastania
3
0 35
2
R
dB
.
T
πω
≈
19
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
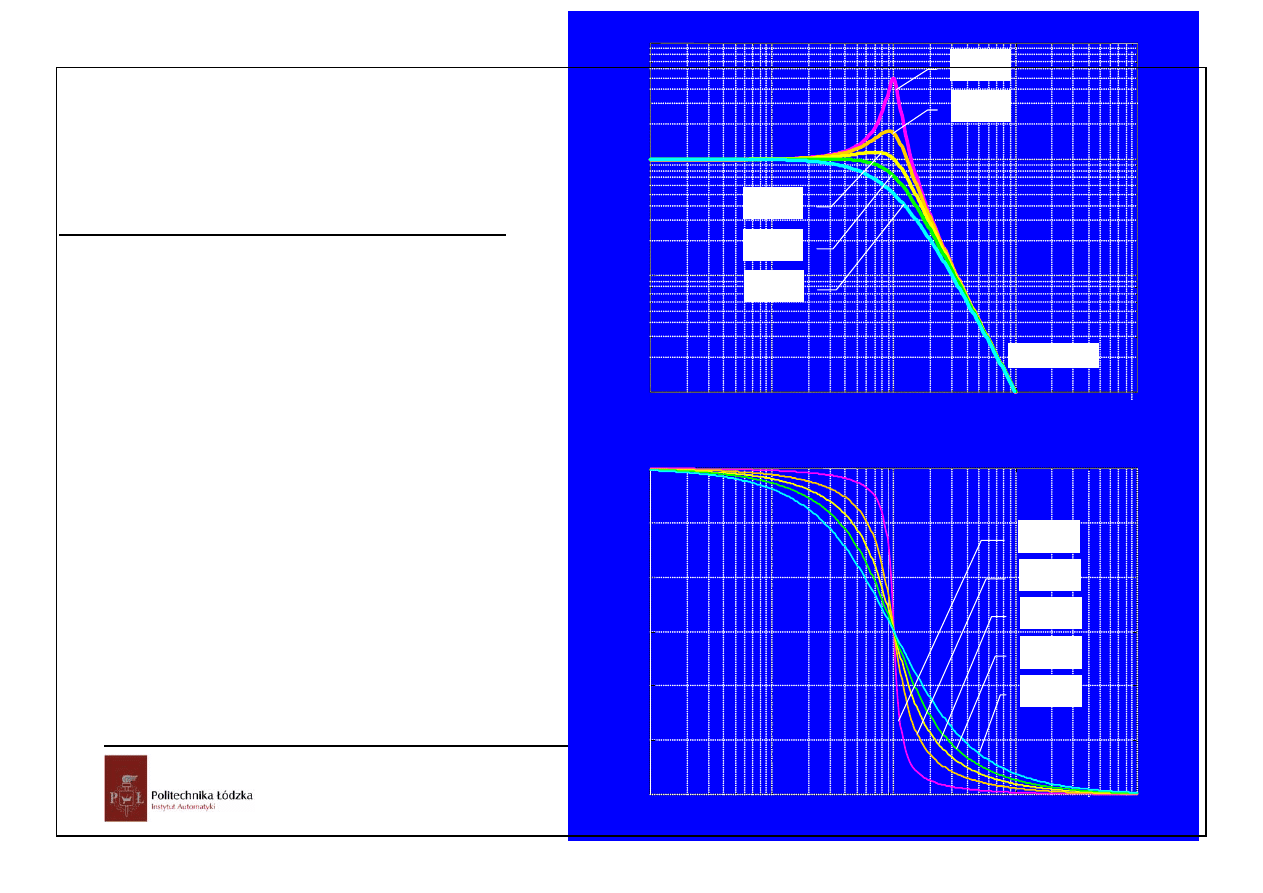
Charakterystyki elementu drugiego rzędu.
0.01
0.1
1
100
10
1
10
0.1
0.01
A(
ω)
ω/ω
n
ζ=0.1
ζ=0.3
ζ=0.5
ζ=0.7
ζ=1
-40dB/dek
0.01
-180
°
-150
°
-120
°
-90
°
-60
°
-30
°
0
°
0.1
1
10
100
ω/ω
n
ϕ(ω)
ζ=0.1
ζ=0.3
ζ=0.5
ζ=0.7
ζ=1
20
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
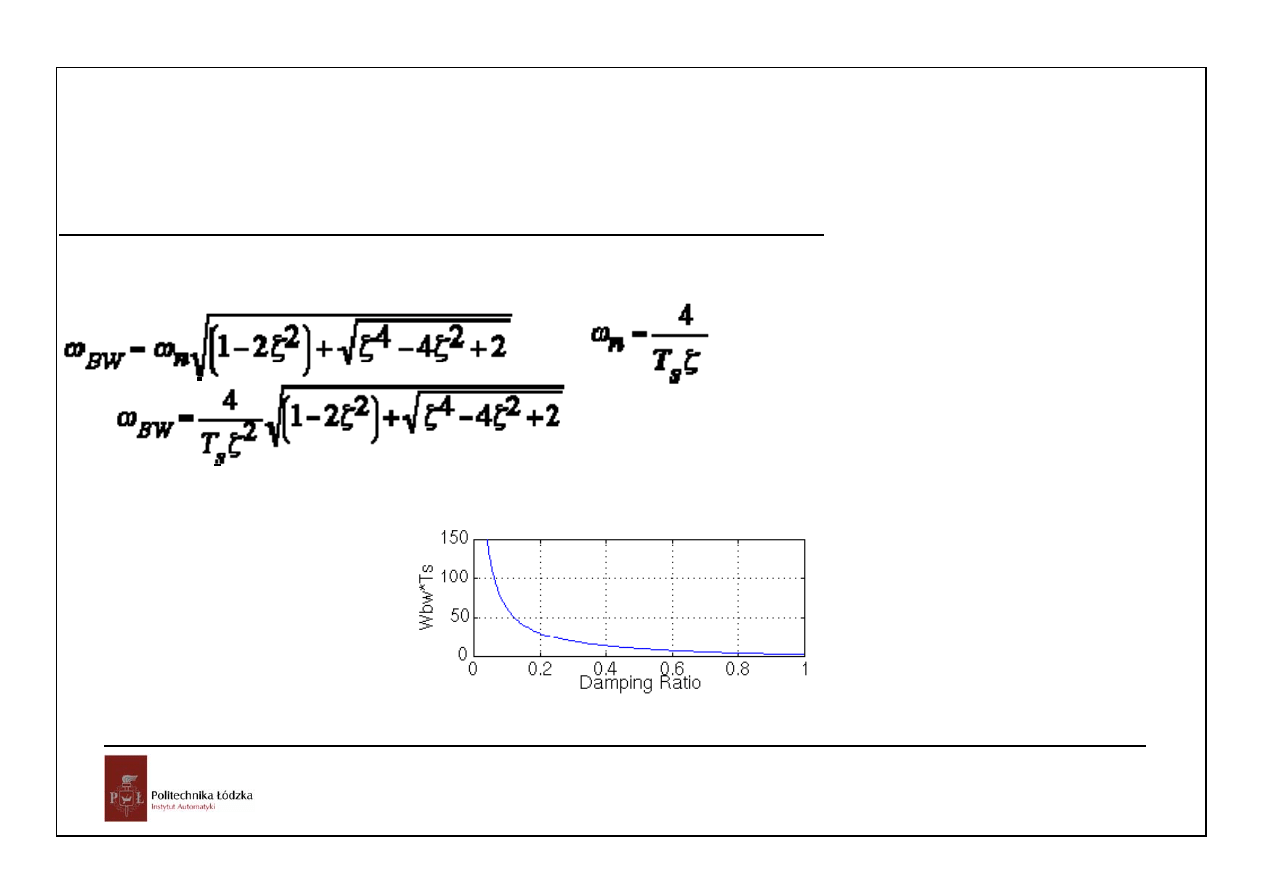
Związki przebiegów czasowych i charakterystyk częstotliwościowych:
Czas regulacji T
S
a pasmo przenoszenia
BW
ω
21
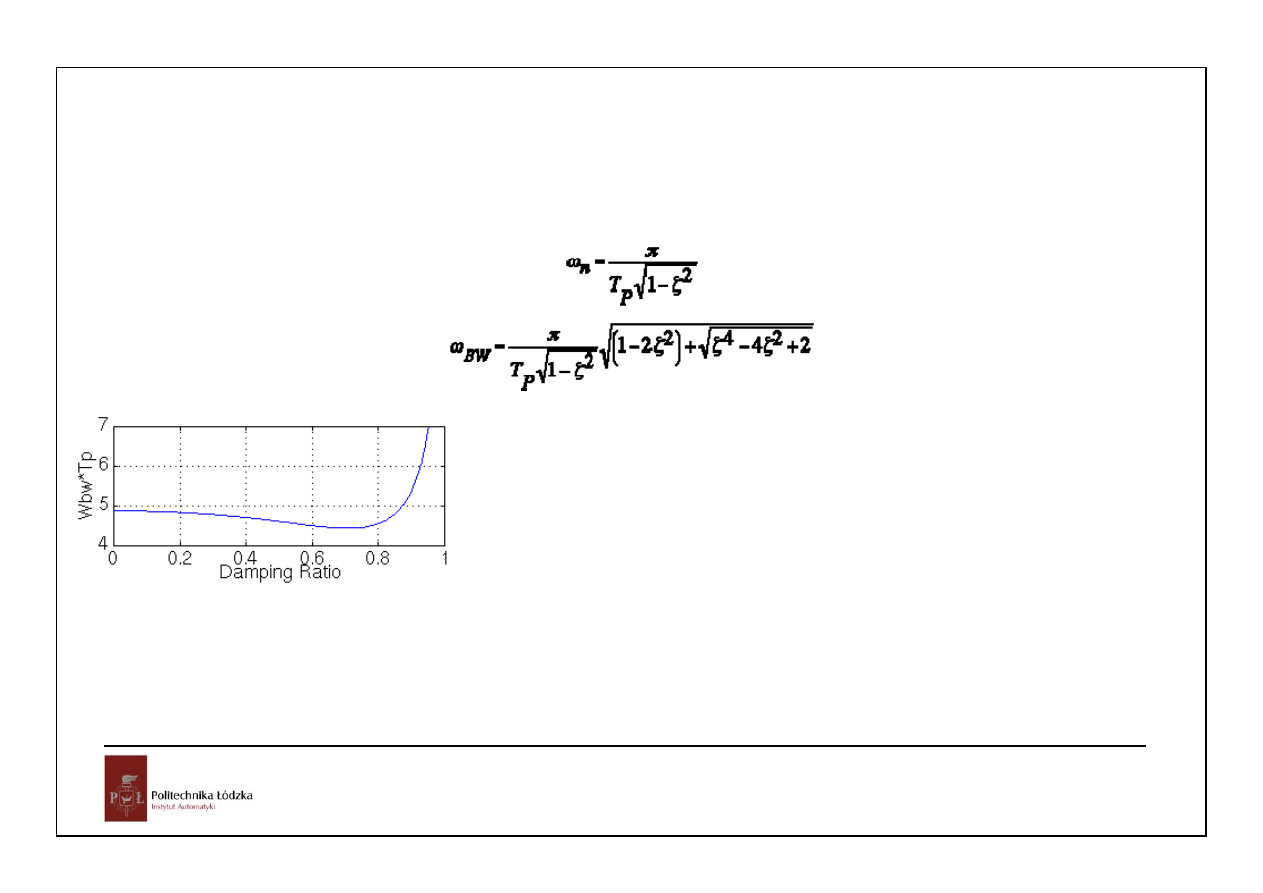
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Czas narastania T
P
a pasmo przenoszenia

22
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Układy z czasem ciągłym, jedno wejście – jedno wyjście (continous time multi input-
multi output –MIMO)
Macierz transmitancji i opis w przestrzeni stanu
Jeśli układ ma wiele wejść i wyjść, to można opisać go macierzą transmitancji:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
)
(
)
(
)
(
)
(
)
(
1
1
11
s
G
s
G
s
G
s
G
s
lp
l
p
G
( )
( )
( )
i
ij
j
Y s
G s
U s
=
1
11
1
1
1
p
l
l
lp
p
Y ( s )
G ( s )
G ( s ) U ( s )
Y ( s )
G ( s )
G ( s ) U ( s )
⎡
⎤ ⎡
⎤
⎡
⎤
⎢
⎥ ⎢
⎥
⎢
⎥ =
⎢
⎥ ⎢
⎥
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
⎣
⎦ ⎣
⎦ ⎣
⎦
Y ( s ) G( s )U( s )
=
Wiadomo, że równanie różniczkowe
można zastąpić układem n równań różniczkowych stopnia pierwszego. Także z transmitancji można
( )
(
)
( )
(
)
1
1
1
1
0
1
1
0
...
( )
...
( )
n
n
m
m
n
n
m
m
a y
a y
a y a y t
b u
b u
b u b u t
−
−
−
−
+
+ +
+
=
+
+ +
+

23
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
otrzymać taki układ równań różniczkowych, na przykład tak:
(I wariant metody bezpośredniej)
1
0
1
1
1
n
n
n
n
n
n
Y ( s )
b s
b s
b
G( s )
U( s )
s
a s
a
−
−
+
+ +
=
=
+
+ +
=
1
2
1
2
0
1
1
n
n
n
n
n
n
b s
b s
b
b
s
a s
a
−
−
−
+
+ +
+
+
+ +
0
0
1
2
2
0
1
1
1
~
~
,
,
~
~
,
~
~
b
a
b
b
b
a
b
b
b
a
b
b
n
n
n
−
=
−
=
−
=
1
2
1
2
0
1
1
1
n
n
n
n
b s
b z
b s
G( s ) b
a s
a s
−
−
−
−
−
+
+ +
=
+
+
+ +
(
)
1
2
0
1
2
1
1
1
n
n
n
n
U( s )
Y ( s ) b U( s )
b s
b s
b s
a s
a s
−
−
−
−
−
=
+
+
+ +
+
+ +
1
1
1
n
n
U( s )
E( s )
a s
a s
−
−
=
+
+
+

24
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
(
)
1
2
1
2
n
n
E( s ) U( s )
a s
a s
a s
E( s )
−
−
−
=
−
+
+ +
1
n
X ( s ) s E( s )
−
=
1
1
2
1
1
n
n
n
X ( s ) sX ( s ) s
E( s ), ,X ( s ) sX ( s ) s E( s )
− +
−
−
=
=
=
=
wtedy:
1
1
1
1
1
1
0
1
0
0
0
0
1
0
1
n
n
n
n
n
n
x ( t )
x ( t )
u( t )
x ( t )
x ( t )
x ( t )
a
a
a
x ( t )
−
−
−
⎡
⎤ ⎡
⎤ ⎡
⎤ ⎡ ⎤
⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎥
⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎥
=
+
⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎥
⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎥
−
−
−
⎣ ⎦
⎣
⎦ ⎣
⎦ ⎣
⎦

25
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
[
]
1
1
1
0
1
n
n
n
n
x ( t )
y( t )
b
b
b
b u( t )
x ( t )
x ( t )
−
−
⎡
⎤
⎢
⎥
⎢
⎥
=
+
⎢
⎥
⎢
⎥
⎣
⎦
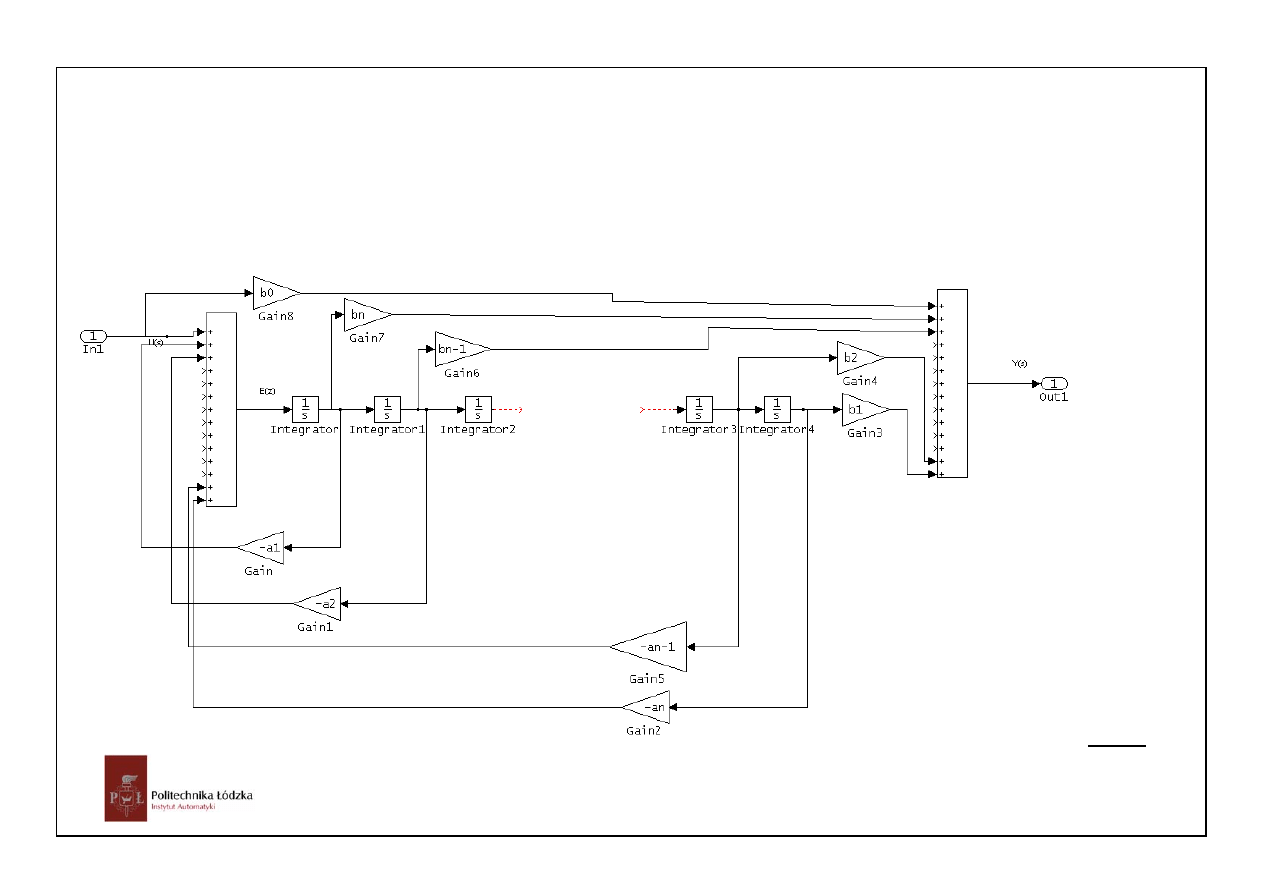
26
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych

27
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Uzyskaliśmy opis układu w postaci:
d
x( t ) Ax( t ) Bu( t )
dt
y( t ) Cx( t ) Du( t )
=
+
=
+
x(t) – wektor zmiennych stanu o wymiarze nx1,
u(t) – wektor wejść/sterowań o wymiarze 1x1
y(t) – wektor wyjść o wymiarze 1x1
do rozwiązania takiego układu równań różniczkowych konieczny jest warunek początkowy np.
x(t
0
)=x
0
Uzyskana macierz stanu A jest macierzą w postaci Frobeniusa. Współczynniki jej wielomianu
charakterystycznego są widoczne w ostatnim wierszu (w kolejności od najmniejszej potęgi z
przeciwnymi znakami) – czyli wielomian charakterystyczny macierzy stanu jest identyczny z
mianownikiem transmitancji, a wartości własne macierzy stanu identyczne z biegunami transmitancji.

28
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Uzyskany opis w postaci równań stanu nie jest jedyny – tej samej transmitancji mogą odpowiadać różne
równania stanu, w zależności od wybory zmiennych stanu.
Także układu o wielu wejściach i wielu wyjściach można opisywać przy pomocy równań stanu.
Dalej rozważać będziemy opis układu w postaci:
równanie stanu
d
x( t ) Ax( t ) Bu( t )
dt
y( t ) Cx
równ
(
a
t )
ni
Du(
e wy ś
t )
j cia
=
+
=
+
x(t) – wektor zmiennych stanu o wymiarze nx1,
u(t) – wektor wejść/sterowań o wymiarze rx1
y(t) – wektor wyjść o wymiarze mx1
z warunkiem początkowym x(0)=x
0
lub bardziej ogólnie x(t
0
)=x
0
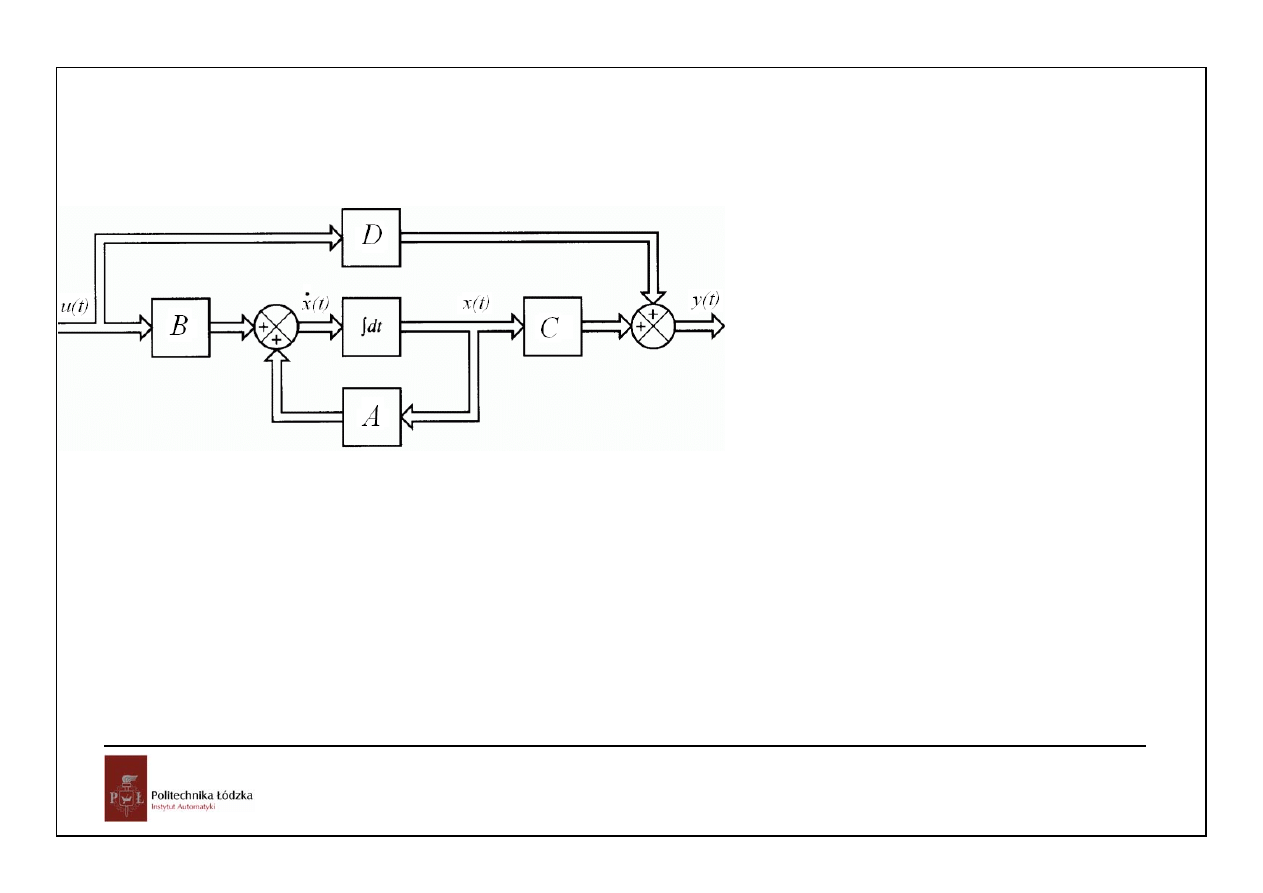
29
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Do rozwiązania równania stanu użyjemy transformaty Laplace’a:
(
)
(
)
(
)
0
0
1
1
0
sX ( s ) x
AX ( s ) BU( s )
sI
A X ( s ) x
BU( s )
X ( s )
sI
A
x
sI
A
BU( s )
−
−
−
=
+
−
=
+
=
−
+
−
Macierz (sI-A)
-1
jest nazywana rezolwentą macierzy A, a jej oryginał

30
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
(
)
{
}
(
)
(
)
1
1
1
adj sI
A
( t ) L
sI
A
L
det sI
A
−
−
−
⎧
⎫
−
⎪
⎪
Φ
=
−
=
⎨
⎬
−
⎪
⎪
⎩
⎭
macierzą fundamentalną albo tranzycyjną równania
d
x( t ) Ax( t )
dt
=
. Rozwiązaniem tego równania
z warunkiem początkowym x(0)=x
0
będzie
(
)
1
0
X ( s )
sI A
x
−
=
−
czyli
0
x( t )
( t )x
= Φ
a rozwiązaniem równania
d
x( t ) Ax( t ) Bu( t )
dt
=
+
z warunkiem początkowym x(0)=x
0
będzie
(
)
(
)
1
1
0
X ( s )
sI
A
x
sI
A
BU( s )
−
−
=
−
+
−
, czyli
0
0
t
x( t )
( t )x
( t
)Bu( )d
τ
τ τ
= Φ
+ Φ −
∫
splot

31
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Poszukamy innego przedstawienia macierzy tranzycyjnej – w postaci szeregu potęgowego względem t:
2
3
0
1
2
3
0
i
i
i
( t ) K
K t K t
K t
K t
∞
=
Φ
=
+
+
+
+
=
∑
(
)
2
3
0
0
1
2
3
0
0
0
i
i
i
x( t )
( t )x
K
K t K t
K t
x
K t x
∞
=
= Φ
=
+
+
+
+
=
∑
0
t
=
:
0
K
I
=
(
)
2
3
1
2
3
4
0
2
3
4
x( t )
K
K t
K t
K t
x
=
+
+
+
+
(
)
(
)
2
3
2
3
1
2
3
4
0
0
1
2
3
0
2
3
4
K
K t
K t
K t
x
A K
K t K t
K t
x
+
+
+
+
=
+
+
+
+
0
t
=
:
1
0
K
AK
=
1
K
A
=
(
)
(
)
2
3
2
3
1
2
3
4
0
0
1
2
3
0
2
3
4
d
d
K
K t
K t
K t
x
A
K
K t K t
K t
x
dt
dt
+
+
+
+
=
+
+
+
+
(
)
(
)
2
2
2
3
4
0
1
2
3
0
2
2 3
3 4
2
3
K
K t
K t
x
A K
K t
K t
x
+ ⋅
+ ⋅
+
=
+
+
+

32
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
0
t
=
:
2
1
2
K
AK
=
2
2
2
A
K
!
=
3
2
3
K
AK
=
3
3
3
A
K
!
=
4
3
4K
AK
=
4
4
4
A
K
!
=
czyli
2 2
3 3
0
2
3
i i
i
A t
A t
A t
( t ) I
At
!
!
i!
∞
=
Φ
= +
+
+
+
=
∑
przez podobieństwo z
2 2
3 3
0
1
2
3
at
i i
i
a t
a t
a t
e
at
!
!
i!
∞
=
= +
+
+
+
=
∑
oznaczamy
At
( t ) e
Φ
=

33
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Jeżeli warunek początkowy jest dany w x(t
0
)=x
0
to dla t>t
0
0
0
0
t
t
x( t )
( t t )x
( t
)Bu( )d
τ
τ τ
= Φ −
+ Φ −
∫
Związek rozwiązania z wartościami własnymi macierzy stanu – mody układu.
Przypomnienie:
0
i
i
i i
v
, Av
s v
≠
=
definicja wartości wektorów własnych
(
)
0
i
i
s I
A v
−
=
(
)
0
i
det s I
A
−
=

34
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
(
)
det sI
A
−
wielomian charakterystyczny A
(
)
0
det sI
A
−
=
równanie charakterystyczne
czyli jest n wartości własnych A rzeczywistych lub zespolonych parami sprzężonych, jedno lub
wielokrotnych. Dalej zakładamy, że wartości własne są jednokrotne.
Równania definiujące wektory i wartości własne można zapisać łącznie:
[
] [
]
1
2
2
1
1
1
2
1
0
0
0
0
0
0
n
n
n
s
s
s
S
S
A
v
v
v
v
v
v
V V
V
V
V
,
V
A
S
A
A
−
−
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎦
=
=
=
⎥
⎣
=

35
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Rozpatrzmy równanie
d
x( t ) Ax( t )
dt
=
i zastosujmy przekształcenie zmiennych stanu:
Vz( t ) x( t )
=
1
1
0
0
0
0
d
V
z( t ) AVz( t ), z( ) V x( ) V x
z
dt
−
−
=
=
=
=
1
1
1
0
0
0
0
d
z( t ) V AVz( t ), z( ) V x( ) V x
z
dt
−
−
−
=
=
=
=
1
2
1
1
0
0
0
0
0
0
0
0
0
0
n
s
s
d
z( z )
z( t ), z( ) V x( ) V x
z
dt
s
−
−
⎡
⎤
⎢
⎥
⎢
⎥
=
=
=
=
⎢
⎥
⎢
⎥
⎣
⎦

36
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
0
0
1 2
i
i i
i
i
d
z ( t ) s z ( t ), z ( ) z
i
, ,...,n
dt
=
=
=
0
1 2
i
s t
i
i
z ( t ) e z
i
, ,...,n
=
=
1
2
0
0
0
0
0
0
0
n
s t
s t
s t
e
e
z( t )
z( ),
e
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦

37
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
1
2
0
0
0
0
0
0
0
n
s t
s t
s t
e
e
Vz( t ) V
z( ),
e
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
1
2
1
0
0
0
0
0
0
0
n
s t
s t
s t
e
e
x( t ) V
V x( ),
e
−
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
1
1
2
T
T
T
n
w
w
V :
w
−
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦

38
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
1
0
i
n
s t
T
i
i
i
x( t )
e v w x( ),
=
=
∑
0
x( t )
( t )x
= Φ
czyli
1
2
1
0
0
0
0
0
0
n
s t
s t
s t
e
e
( t ) V
V
e
−
⎡
⎤
⎢
⎥
⎢
⎥
Φ
=
⎢
⎥
⎢
⎥
⎣
⎦
1
i
n
s t
T
i
i
i
( t )
e v w
=
Φ
=
∑
0
0
t
x( t )
( t )x
( t
)Bu( )d
τ
τ τ
= Φ
+ Φ −
∫

39
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
( )
0
1
1
0
0
1
0
i
i
i
i
t
n
n
s t
s t
T
T
i
i
i
i
i
i
t
n
s t
s
T
i
i
i
x( t )
e v w x
e
v w Bu( )d
e v w x
e
Bu( )d
τ
τ
τ τ
τ τ
−
=
=
−
=
=
+
=
⎡
⎤
=
+
⎢
⎥
⎣
⎦
∑
∑
∫
∑
∫
Właściwości macierzy tranzycyjnej:
1.
0
( ) I
Φ
=
2.
(
)
{ }
1
2
1
2
0
n
n
s s
s t
tr A t
s t
s t s t
det ( t ) e e
e
e
e
+ +
Φ
=
=
=
≠
3. wartościami własnymi
( t )
Φ
są liczby
1
2
n
s t
s t
s t
e ,e , ,e
, wektorami własnymi wektory własne A
4.
1
1
( t )A A ( t ),
( t )A
A
( t )
−
−
Φ
= Φ
Φ
=
Φ

40
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
5.
2 2
3 3
2
3 2
2 2
3 3
2
3
2
3
2
3
2
3
d
d
A t
A t
A t
A t
( t )
I
At
A
dt
dt
!
!
!
!
A t
A t
A I
At
A ( t )
!
!
⎛
⎞
Φ
=
+
+
+
+
= +
+
+
=
⎜
⎟
⎝
⎠
⎛
⎞
=
+
+
+
+
= Φ
⎜
⎟
⎝
⎠
6.
( t )
Φ
jest rozwiązaniem równania (macierzowego, różniczkowego)
d
( t ) A ( t )
dt
Φ
= Φ
z
warunkiem początkowym
0
( ) I
Φ
=
7.
2 2
3 3
2
2 3
0
0
2
3
2
3
t
t
A
A
At
A t
( )d
I
A
d
It
!
!
!
!
τ
τ
τ τ
τ
τ
⎛
⎞
Φ
=
+
+
+
+
= +
+
+
⎜
⎟
⎝
⎠
∫
∫
jeśli
0
det( A )
≠
, to

41
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
8.
(
) (
)
2 2
3 3
2
2 3
0
0
2
2 3
2 2
3 3
1
1
1
1
2
3
2
3
2
3
2
3
t
t
A
A
At
A t
( )d
I
A
d
It
!
!
!
!
At
A t
A t
A t
A A It
A
At
!
!
!
!
A
( t ) I
( t ) I A
τ
τ
τ τ
τ
τ
−
−
−
−
⎛
⎞
Φ
=
+
+
+
+
= +
+
+
=
⎜
⎟
⎝
⎠
⎛
⎞
⎛
⎞
=
+
+
+
=
+
+
+
=
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
=
Φ
−
= Φ
−
∫
∫
9.
1
1
2
2
1
1
0
0
0
0
0
0
0
0
0
0
0
0
n
n
s t
s t
s t
s t
s t
s t
e
e
e
e
( t ) ( t ) V
V V
V
I
e
e
−
−
−
−
−
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
Φ
Φ − =
=
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦

42
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Opis w przestrzeni stanu a transmitancja
Opis układu w postaci:
równanie stanu
d
x( t ) Ax( t ) Bu( t )
dt
y( t ) Cx
równ
(
a
t )
ni
Du(
e wy ś
t )
j cia
=
+
=
+
x(t) – wektor zmiennych stanu o wymiarze nx1,
u(t) – wektor wejść/sterowań o wymiarze rx1
y(t) – wektor wyjść o wymiarze mx1
Wyznaczymy macierz transmitancji:
(
)
(
)
(
)
0
0
1
1
0
sX ( s ) x
AX ( s ) BU( s )
sI
A X ( s ) x
BU( s )
X ( s )
sI
A
x
sI
A
BU( s )
−
−
−
=
+
−
=
+
=
−
+
−
ale przy zerowych warunkach początkowych:

43
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
(
)
1
X ( s )
sI
A
BU( s )
−
=
−
(
)
1
Y ( s )
C sI
A
B D U( s ) G( s )U( s )
−
⎡
⎤
=
−
+
=
⎣
⎦
(
)
(
)
(
)
1
adj sI
A
G( s ) C sI
A
B D C
B D
det sI
A
−
−
=
−
+ =
+
−
mogą wystąpić skrócenia – transmitancja może być niższego rzędu niż wymiar wektora stanu!!

44
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
Liniowe przekształcenie zmiennych stanu:
Opis układu w postaci:
równanie stanu
d
x( t ) Ax( t ) Bu( t )
dt
y( t ) Cx
równ
(
a
t )
ni
Du(
e wy ś
t )
j cia
=
+
=
+
x(t) – wektor zmiennych stanu o wymiarze nx1,
u(t) – wektor wejść/sterowań o wymiarze rx1
y(t) – wektor wyjść o wymiarze mx1
wprowadzamy nowe zmienne stanu:
0
Pq( t ) x( t ), det P
=
≠
równanie stanu
d
Pq( t ) APq( t ) Bu( t )
nowe
dt
y( t ) CPq( t ) Du( t )
now
równanie wyjś a
e
ci
=
+
=
+

45
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
1
1
równanie st
d
q( t ) P APq( t ) P Bu( t )
nowe
dt
y( t ) CPq( t ) Du( t )
anu
równanie wyjścia
nowe
−
−
=
+
=
+
1
1
d
q( t ) Aq( t ) Bu( t )
A P AP, B P B
dt
y( t ) Cq( t ) Du( t )
C CP
−
−
=
+
=
=
=
+
=
wartości własne nowej macierzy stanu są takie same jak starej!!
Jaka będzie transmitancja:
46
Automatyka i sterowanie 2 Modele ciągłych, liniowych, stacjonarnych układów dynamicznych
(
)
(
)
(
)
(
)
(
)
1
1
1
1
1
1
1
1
1
1
1
G( s ) C sI
A
B D CP sI P AP
P B D
CP P
sI
A P
P B D CPP
sI
A
PP B D
C sI
A
B D G( s )
−
−
−
−
−
−
−
−
−
−
−
=
−
+ =
−
+ =
⎡
⎤
=
−
+ =
−
+ =
⎣
⎦
=
−
+ =
liniowe przekształcenie zmiennych stanu nie zmienia transmitancji!!
bo
(
)
1
1
1
MN
N M
−
−
−
=
Wyszukiwarka
Podobne podstrony:
automatyka i sterowanie wyklad 15
automatyka i sterowanie wyklad Nieznany (8)
automatyka i sterowanie wyklad Nieznany (2)
automatyka i sterowanie wyklad 3
automatyka i sterowanie wyklad Nieznany (7)
automatyka i sterowanie wyklad Nieznany (14)
automatyka i sterowanie wyklad 16
automatyka i sterowanie wyklad Nieznany (12)
automatyka i sterowanie wyklad Nieznany (16)
automatyka i sterowanie wyklad Nieznany (5)
automatyka i sterowanie wyklad 9
automatyka i sterowanie wyklad 11
automatyka i sterowanie wyklad 4
automatyka i sterowanie wyklad 5
automatyka i sterowanie wyklad Nieznany (10)
automatyka i sterowanie wyklad Nieznany (3)
automatyka i sterowanie wyklad 8
automatyka i sterowanie wyklad 15
automatyka i sterowanie wyklad Nieznany (8)
więcej podobnych podstron