J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
1
Związki między składowymi stanu naprężeń
Ćwiczenie 6
w układzie prostokątnym i biegunowym – c.d.
Zagadnienie:
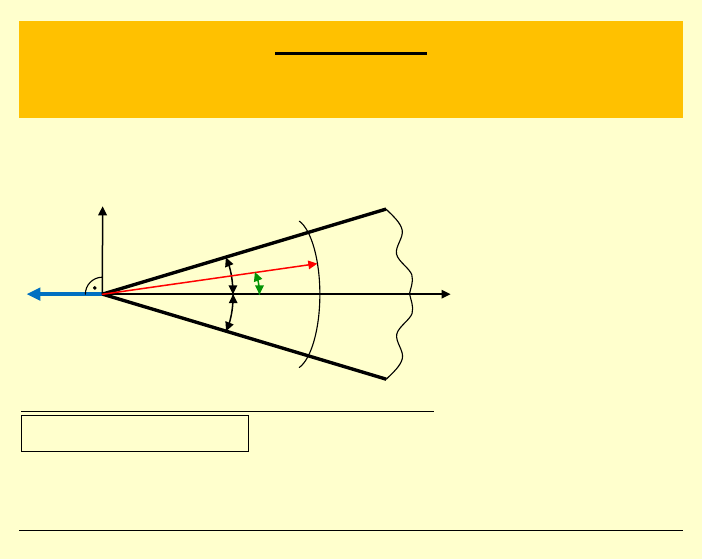
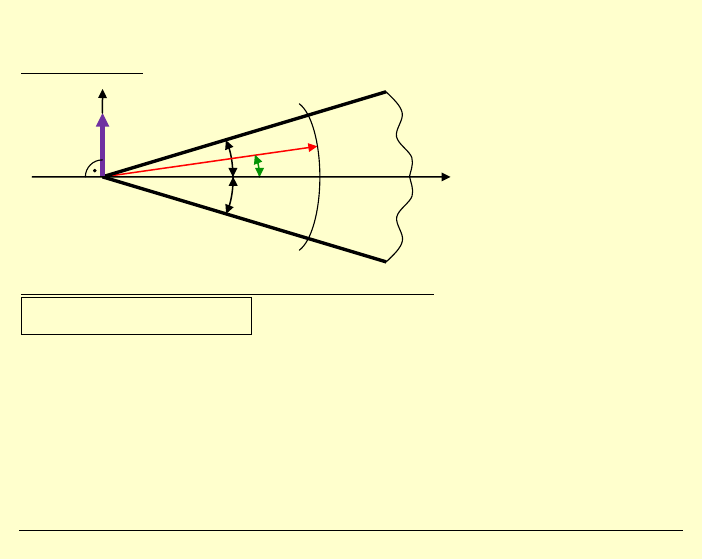
Tarcza sprężysta w postaci klina nieograniczonego
Obliczyć składowe stanu naprężenia w układzie biegunowym.
( )
,
sin
F r
C r
ϕ
ϕ
ϕ
= ⋅ ⋅ ⋅
Przewidujemy funkcję naprężeń w postaci:
, gdzie:
C
const
=
(prosta postać funkcji, podobnie jak wielomiany niższych stopni w
przypadku układu ortokartezjańskiego)
2
x
1
P
1
x
g
×
r
ϕ
α
α
,
r
ϕ
–
współrzędne
biegunowe
2
α
–
kąt wierzchołkowy
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
2
Sprawdzamy równanie biharmoniczne:
( )
,
sin
F
F r
C r
ϕ
ϕ
ϕ
=
= ⋅ ⋅ ⋅
– funkcja nap
rężeń
( )
( )
4
2
2
,
,
0
F r
F r
ϕ
ϕ
∇
= ∇ ∇
=
( )
( )
( )
( )
( )
( )
2
2
2
2
2
2
2
2
2
2
,
,
,
1
1
1
1
0
F r
F r
F r
r
r
r
r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
∂
∂
+ ⋅
+ ⋅
+ ⋅
+ ⋅
=
∂
∂
∂
∂
∂
∂
Obliczamy:
(
)
2
2
2
2
( , )
sin
0
F r
C r
r
r
ϕ
ϕ
ϕ
∂
∂
→
=
⋅ ⋅ ⋅
=
∂
∂
(
)
1
( , )
1
1
sin
sin
F r
C r
C
r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
→ ⋅
= ⋅
⋅ ⋅ ⋅
= ⋅ ⋅ ⋅
∂
∂
(
)
(
)
2
2
2
2
2
2
2
1
( , )
1
1
sin
sin
cos
F r
C r
C r
C r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
→ ⋅
= ⋅
⋅ ⋅ ⋅
= ⋅
⋅ ⋅
+ ⋅ ⋅ ⋅
∂
∂
∂
(
)
(
)
2
1
cos
cos
sin
2 cos
sin
C
C r
C r
C r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ ϕ
ϕ
=
⋅
⋅ ⋅
+ ⋅ ⋅
− ⋅ ⋅ ⋅
= ⋅ ⋅
− ⋅
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
3
Operator Laplace’a we współrzędnych biegunowych:
( )
( )
( )
( )
2
2
2
2
2
2
,
,
,
1
1
,
F r
F r
F r
F r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∇
=
+ ⋅
+
⋅
∂
∂
∂
(
)
1
0
sin
2 cos
sin
C
C
r
r
ϕ
ϕ
ϕ ϕ
ϕ
= + ⋅ ⋅ ⋅
+ ⋅ ⋅
− ⋅
=
2
cos
C
r
ϕ
⋅
( )
( )
( )
( )
( )
( )
2
2
2
2
2
2
2
2
2
2
,
,
,
1
1
1
1
F r
F r
F r
r
r
r
r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
∂
∂
+ ⋅
+ ⋅
+ ⋅
+ ⋅
=
∂
∂
∂
∂
∂
∂
Równanie biharmoniczne:
( )
( )
( )
2
2
2
2
2
1
1
2
cos
C
r
r
r
r
r
ϕ
ϕ
∂
∂
∂
+ ⋅
+
⋅
⋅
=
∂
∂
∂
2
2
2
2
2
2
1
2
1
2
cos
cos
cos
C
C
C
r
r
r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
=
⋅
+ ⋅
⋅
+
⋅
⋅
=
∂
∂
∂
3
3
3
4
2
2
cos
cos
cos
0
C
C
C
r
r
r
ϕ
ϕ
ϕ
=
⋅
−
⋅
−
⋅
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
4
2
2
2
1
1
rr
F
F
r
r
r
σ
ϕ
∂
∂
= ⋅
+
⋅
∂
∂
Składowe stanu naprężeń:
(
)
1
sin
2 cos
sin
C
C
r
r
ϕ
ϕ
ϕ ϕ
ϕ
= ⋅ ⋅ ⋅
+ ⋅ ⋅
− ⋅
=
2
cos
C
r
ϕ
⋅
2
2
F
r
ϕϕ
σ
∂
=
=
∂
0
1
r
F
r r
ϕ
σ
ϕ
∂
∂
= −
⋅
∂
∂
(
)
1
sin
C r
r r
ϕ
ϕ
ϕ
∂
∂
= −
⋅
⋅ ⋅ ⋅
∂
∂
(
)
(
)
1
sin
cos
sin
cos
C r
C r
C
r r
r
ϕ
ϕ
ϕ
ϕ ϕ
ϕ
∂
∂
= −
⋅
⋅ ⋅
+ ⋅ ⋅ ⋅
= − ⋅
+ ⋅
=
∂
∂
0
Zatem:
d
ϕ
ϕ
α
α
2
x
1
P
1
x
g
×
rr
σ
r d
ϕ
⋅
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
5
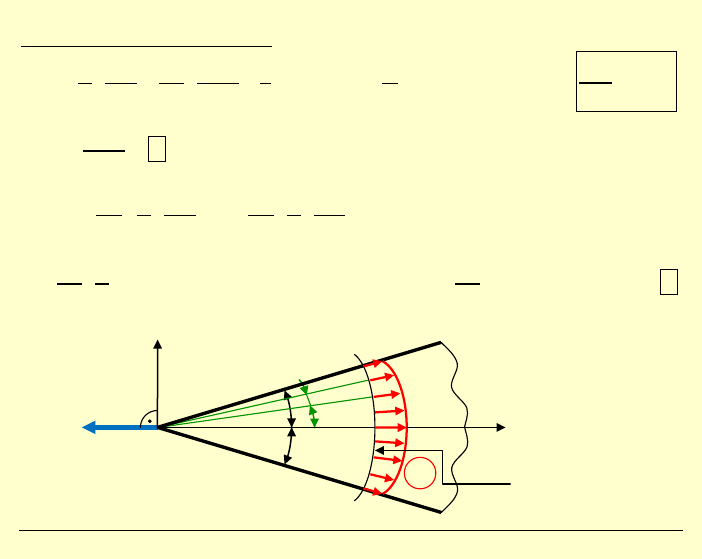
Stałą
C
wyznaczamy z warunku równowagi względem osi
1
x
„wyciętego” fragmentu klina:
1
0
x
P
=
∑
1
0
2
cos
rr
g r d
P
α
σ
ϕ
ϕ
⋅
⋅
⋅ ⋅ ⋅
=
∫
, gdzie: g r d
element powierzchni
ϕ
⋅ ⋅
→
zatem:
1
0
2
2
cos
cos
C
g r d
P
r
α
ϕ
ϕ
ϕ
⋅
⋅
⋅
⋅ ⋅ ⋅
=
∫
(
)
2
1
0
4
cos
C g
d
P
α
ϕ
ϕ
→
⋅ ⋅
=
∫
Pomocnicze obliczenie całki:
(
)
2
2
cos
sin
d
ϕ
ϕ
ϕ ϕ
+
⋅
=
∫
(
)
2
2
1
cos
sin
sin 2
2
d
ϕ
ϕ
ϕ
ϕ
−
⋅
=
∫
dodając stronami:
2
1
1
1
cos
sin 2
2
4
d
C
ϕ ϕ
ϕ
ϕ
⋅
=
+
+
∫
odejmując stronami:
2
1
1
1
sin
sin 2
2
4
d
C
ϕ ϕ
ϕ
ϕ
⋅
=
−
+
∫
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
6
Podstawiając wynik obliczeń pomocniczych:
(
)
2
1
0
4
cos
C g
d
P
α
ϕ
ϕ
⋅ ⋅
=
∫
1
0
1
1
4
sin 2
2
4
C g
P
α
ϕ
ϕ
⋅ ⋅
+
=
1
1
1
4
sin 2
2
4
C g
P
α
α
⋅ ⋅
+
=
(
)
1
2
sin 2
C g
P
α
α
⋅ ⋅
+
=
(
)
1
2
sin 2
P
C
g
α
α
→ =
⋅
+
2
2
2
1
1
rr
F
F
r
r
r
σ
ϕ
∂
∂
= ⋅
+
⋅
∂
∂
S
tąd:
2
cos
C
r
ϕ
=
⋅
(
)
1
2
cos
2
sin 2
P
r
g
ϕ
α
α
= ⋅
⋅
⋅
+
(
)
1
2
cos
2
sin 2
rr
P
g
r
ϕ
σ
α
α
⋅
=
⋅
⋅
+
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
7
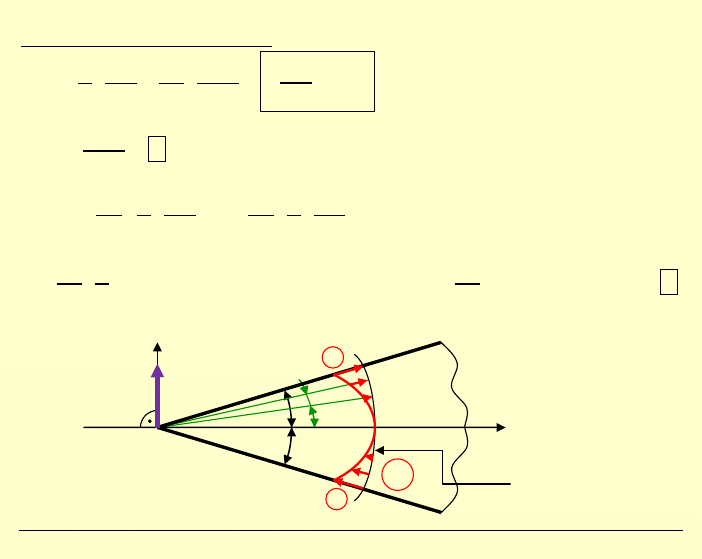
Analogia:
Podobnie postępujemy dla obciążenia tarcza sprężystej
siłą pionową
:
( )
,
cos
F r
C r
ϕ
ϕ
ϕ
= ⋅ ⋅ ⋅
Przewidujemy funkcję naprężeń w postaci:
, gdzie:
C
const
=
(prosta postać funkcji, podobnie jak wielomiany niższych stopni w
przypadku układu ortokartezjańskiego)
Równanie biharmoniczne:
dla
( )
,
cos
F
F r
C r
ϕ
ϕ
ϕ
=
= ⋅ ⋅ ⋅
–
funkcja naprężeń
( )
( )
4
2
2
,
,
0
F r
F r
ϕ
ϕ
∇
= ∇ ∇
=
→ równanie jest spełnione!
,
r
ϕ
–
współrzędne
biegunowe
2
α
–
kąt wierzchołkowy
r
ϕ
α
α
g
×
1
x
2
P
2
x
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
8
2
2
2
1
1
rr
F
F
r
r
r
σ
ϕ
∂
∂
= ⋅
+
⋅
=
∂
∂
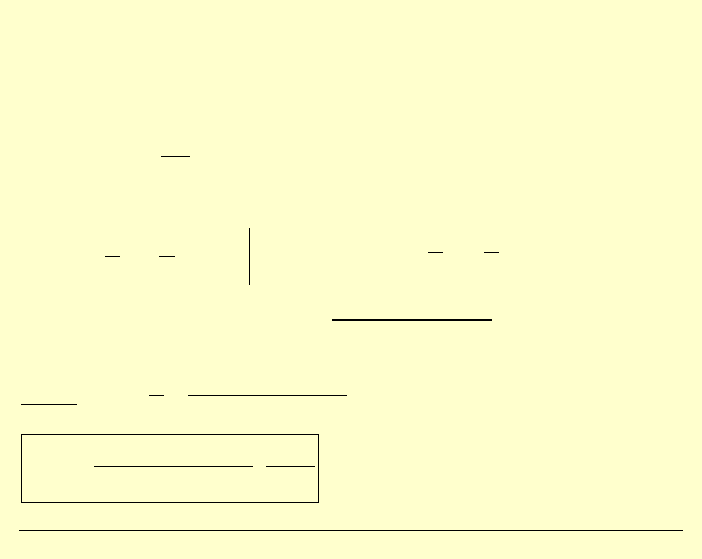
Składowe stanu naprężeń:
2
sin
C
r
ϕ
−
⋅
2
2
F
r
ϕϕ
σ
∂
=
=
∂
0
1
r
F
r r
ϕ
σ
ϕ
∂
∂
= −
⋅
∂
∂
(
)
1
cos
C r
r r
ϕ
ϕ
ϕ
∂
∂
= −
⋅
⋅ ⋅ ⋅
∂
∂
(
)
(
)
1
cos
sin
cos
sin
C r
C r
C
r r
r
ϕ
ϕ
ϕ
ϕ ϕ
ϕ
∂
∂
= −
⋅
⋅ ⋅
+ ⋅ ⋅ ⋅
= − ⋅
+ ⋅
=
∂
∂
0
Zatem:
d
ϕ
ϕ
α
α
g
×
rr
σ
r d
ϕ
⋅
1
x
2
x
2
P
+
−
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
9
Stałą
C
wyznaczamy z warunku równowagi:
2
0
2
sin
rr
g r d
P
α
σ
ϕ
ϕ
− ⋅
⋅
⋅ ⋅ ⋅
=
∫
, gdzie: g r d
element powierzchni
ϕ
⋅ ⋅
→
zatem:
2
0
2
2
sin
sin
C
g r d
P
r
α
ϕ
ϕ
ϕ
− ⋅ −
⋅
⋅
⋅ ⋅ ⋅
=
∫
(
)
2
2
0
2
sin
C g
d
P
α
ϕ
ϕ
→
⋅ ⋅
=
∫
Podstawiając wynik obliczeń pomocniczych:
2
0
1
1
4
sin 2
2
4
C g
P
α
ϕ
ϕ
⋅ ⋅
−
=
2
1
1
4
sin 2
2
4
C g
P
α
α
→
⋅ ⋅
−
=
(
)
2
2
sin 2
C g
P
α
α
⋅ ⋅
−
=
(
)
2
2
sin 2
P
C
g
α
α
→ =
⋅
−
S
tąd:
rr
σ
=
(
)
2
2
sin
2
sin 2
P
r
g
ϕ
α
α
− ⋅
⋅
⋅
−
(
)
2
2
sin
2
sin 2
rr
P
g
r
ϕ
σ
α
α
⋅
= −
⋅
⋅
−
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
10
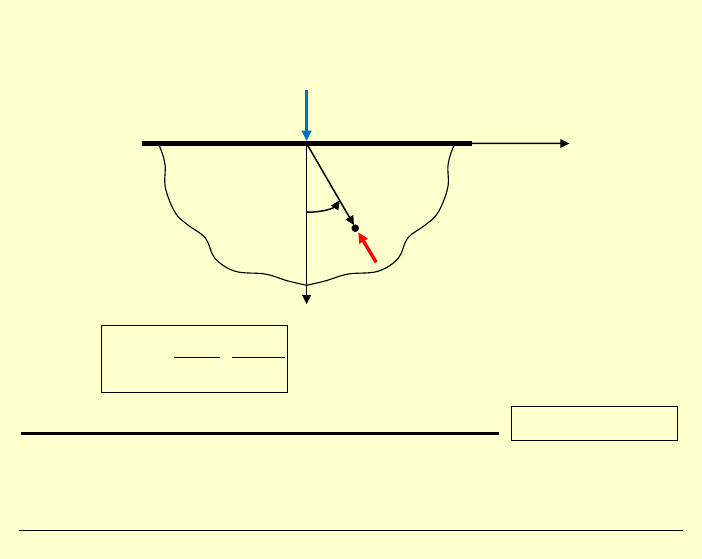
Przypadek szczególny:
tarcza półnieskończona, obciążona siłą
skupioną na brzegu (tzw. zagadnienie Flamanta):
2
cos
rr
P
g
r
ϕ
σ
π
⋅
= −
⋅
⋅
0
r
ϕ
σ
=
0
ϕϕ
σ
=
Punkt osobliwy rozwiązania teorii sprężystości
0
rr
r
σ
→ ⇒
→ ∞
:
Uwaga:
Przez zmianę modelu ciała na model sprężysto–plastyczny
unikamy tej
osobliwości!
r
ϕ
rr
σ
1
x
P
2
x
g
×
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
11
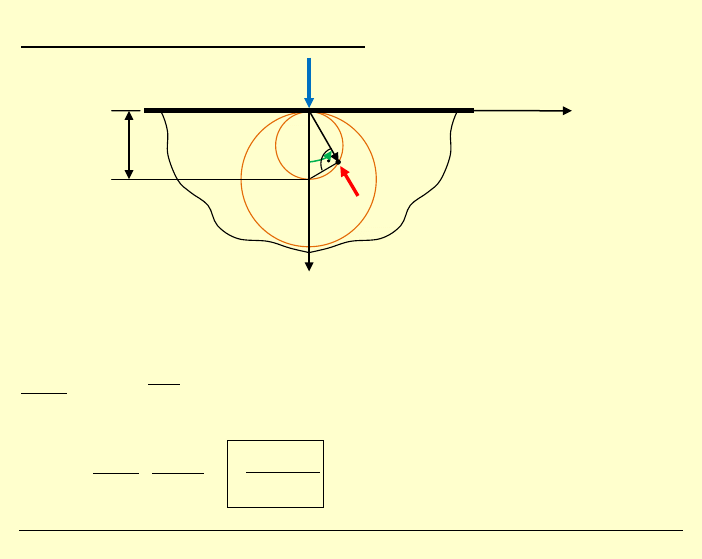
Interpretacja rozkładu naprężeń:
Kon
struujemy rodzinę okręgów stycznych do krawędzi tarczy,
wszystkie o promieniach
R
.
stąd:
cos
2
r
R
ϕ
=
Wzór na naprężenia normalne:
2
cos
rr
P
g
r
ϕ
σ
π
⋅
= −
⋅
=
⋅
P
g R
π
−
⋅ ⋅
ϕ
rr
σ
r
1
x
P
2
x
g
×
2R
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
12
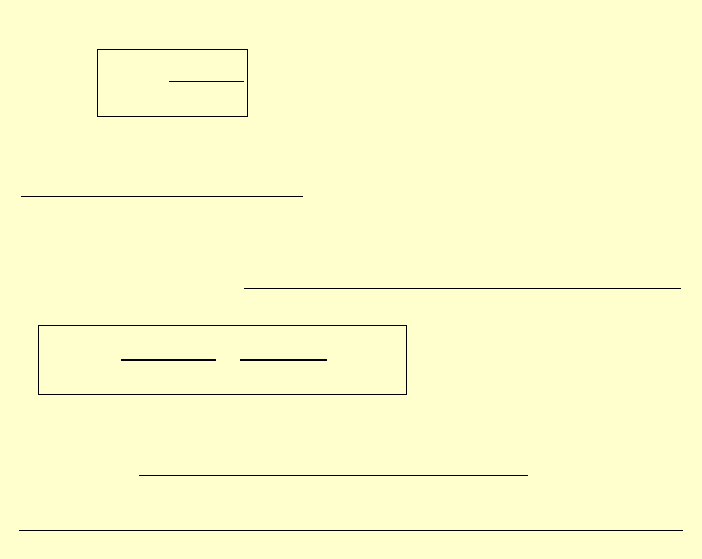
Mamy:
rr
P
g R
σ
π
= −
⋅ ⋅
Wniosek:
N
aprężenie radialne jest stałe
R
na każdym okręgu o promieniu !
Ponieważ
(1)
0
ϕϕ
σ
σ
=
=
oraz
(2)
rr
σ
σ
=
są naprężeniami głównymi
(gdyż:
0
r
ϕ
σ
= ), to
największą wartość naprężenia stycznego
(1)
(2)
max
2
2
P
const
g R
σ
σ
τ
π
−
=
=
=
⋅ ⋅
w punkcie otrzymamy ze wzoru:
na okręgu o promieniu
R
(do porównania z Wytrzymałością Materiałów)
Linie te
można wyznaczyć eksperymentalnie, za pomocą
elastooptyki (fotosprężystości)!
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
13
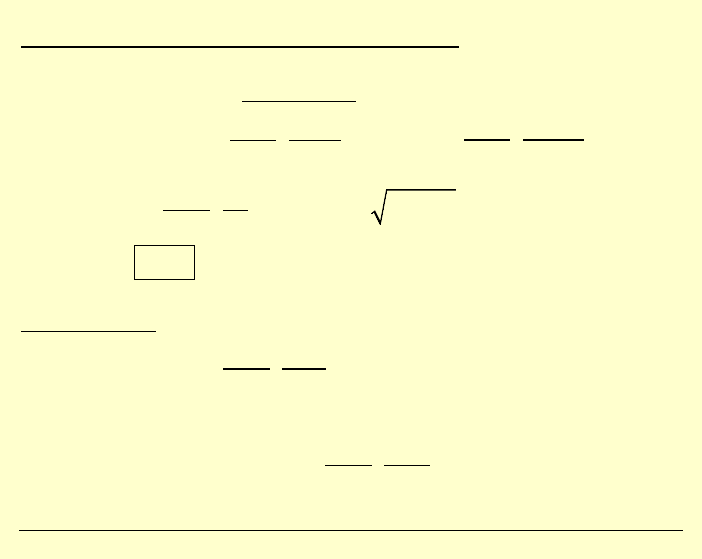
Naprężenia w układzie ortokartezjańskim:
Na podstawie wzorów odwrotnych
2
11
cos
rr
σ
σ
ϕ
=
⋅
otrzymamy:
2
2
cos
cos
P
g
r
ϕ
ϕ
π
⋅
= −
⋅
⋅
⋅
3
2
cos
P
g
r
ϕ
π
⋅
= −
⋅
⋅
zatem:
3
1
11
4
2
x
P
g
r
σ
π
⋅
= −
⋅
⋅
, gdzie:
(
)
2
2
2
4
2
2
1
2
1
2
r
x
x
r
x
x
=
+
⇒
=
+
przy czym:
1
0
x
≥
!
2
2
1 2
22
4
2
sin
x x
P
g
r
ϕϕ
σ
σ
ϕ
π
⋅
=
⋅
= −
⋅
⋅
Analogicznie:
oraz:
2
1
2
12
21
4
2
sin
cos
r
x x
P
g
r
ϕ
σ
σ
σ
ϕ
ϕ
π
⋅
=
=
⋅
⋅
= −
⋅
⋅
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
14
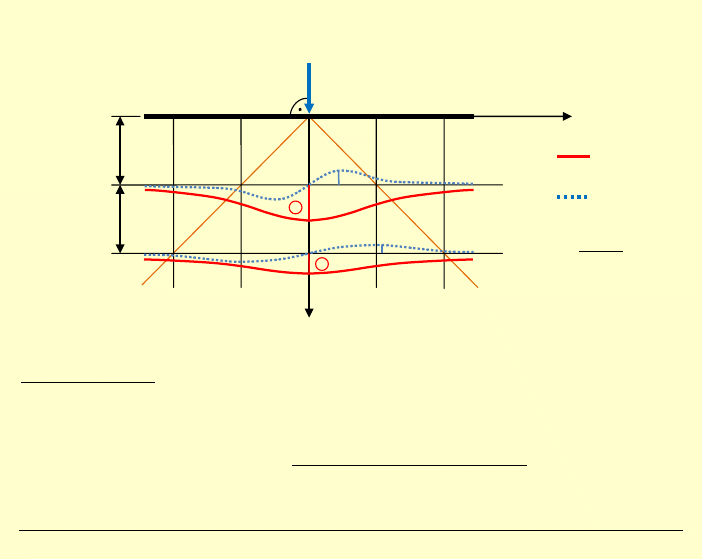
Wykresy
11
σ
oraz
12
σ
dla
1
x
const
=
:
Praktycznie: wykresy te opisuj
ą zagadnienie „rozchodzenia się”
siły skupionej w ośrodku izotropowym, jednorodnym.
Poza trójkątem równoramiennym, zakreślanym przez proste
nachylone pod kątem 45°, dla celów inżynierskich
0, 208
można przyjąć
naprężenia jako równe zeru!
1
x
R
P
2
x
R
R
−
2R
−
2R
+
R
+
0, 637
0, 318
0,159
0, 080
11
σ
12
σ
P
g R
×
⋅
−
−
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
15
Dyskusja!
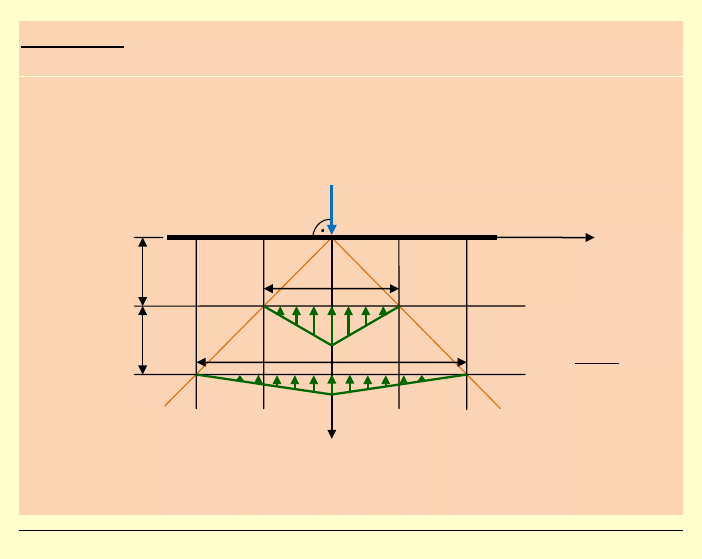
1) Przybliżenia rozkładów naprężeń
a)
rozkład trójkątny:
(
przybliżenie po stronie bezpiecznej)
1
x
R
P
2
x
R
R
−
2R
−
2R
+
R
+
1, 0
0, 5
P
g R
×
⋅
2R
4R
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
16
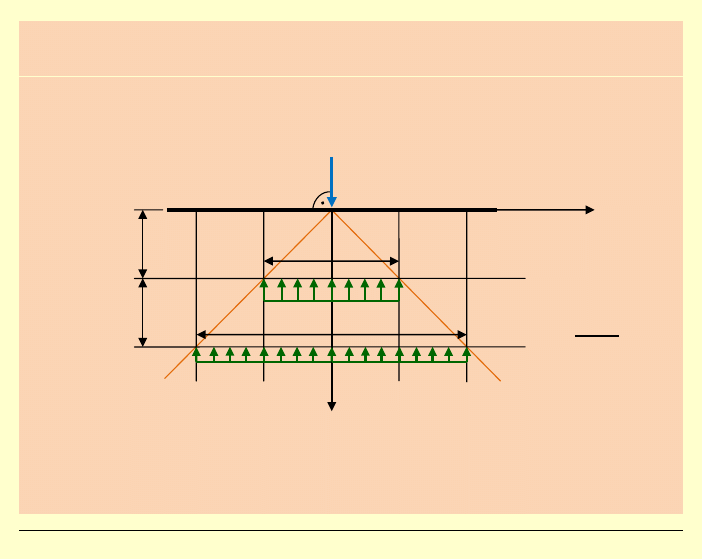
b)
rozkład równomierny:
(
przybliżenie po stronie niebezpiecznej, ale z użytecznym wynikiem)
1
x
R
P
2
x
R
R
−
2R
−
2R
+
R
+
0, 5
0, 25
P
g R
×
⋅
2R
4R
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 6 • KMBiM WILiŚ PG
17
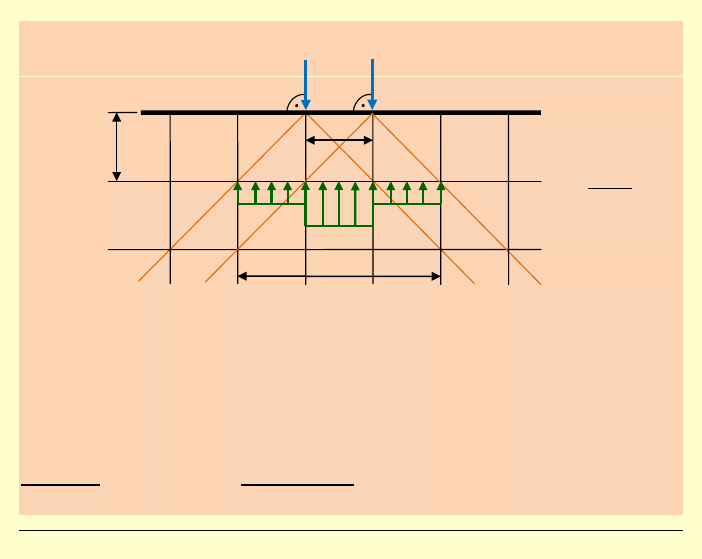
2) Superpozycja stanów
naprężenia, przykładowo:
3) Zastosowania praktyczne:
→ otwory montażowe w ścianie (poza strefą naprężeń)
→ można obliczyć wysokość, od której w ścianie obciążonej siłami
skupionymi użyty materiał może być słabszy
Uwaga: Wzory na
naprężenia dla tarcz obciążonych siłami
skupionymi (PSN) są słuszne również dla PSO!
R
R
P
P
3R
0, 5
0, 5
1, 0
P
g R
×
⋅
Document Outline