Fizyka 14 PP

Termodynamika

– poziom podstawowy

Zadanie 1. (1 pkt)

Źródło: CKE 2005 (PP), zad. 8.

Zadanie 2. (2 pkt)

Źródło: CKE 2005 (PP), zad. 17.



     

 

   

  





 







      

       



 

 







 

 







 

 







 

 





   

           

          

 

   

      

           

   





 









































 





     

 

   

         

          

          

    


 




    


 




   

         

  

             

           

     







 

 

 

     



 





















  

   

         

    



   

   

       

          

           

             



Zadanie 3. (3 pkt)

Źródło: CKE 2005 (PP), zad. 19.

     



 





















  

   

    

   

   

       





     

 

             



          

           

  

        

 



     

 



  

        

Zadanie 4. (2 pkt)

Źródło: CKE 2005 (PP), zad. 21.

     



 

   

        

 

 

 

   

           

           

          

          

    

     



 

   

        

   

    

Zadanie 5. (2 pkt)

Źródło: CKE 2005 (PP), zad. 26.



     

 

   

           

       

             

          

          

  



   

     

           

 

     

Zadanie 6. (1 pkt)

Źródło: CKE 01.2006 (PP), zad. 5.

Egzamin maturalny z fizyki i astronomii

Arkusz I

W zadaniach od 1. do 8. wybierz i zaznacz jedną poprawną odpowiedĨ.

Zadanie 1. (1 pkt)

Dwaj kolarze zbliĪali siĊ do mety, jadąc jeden obok drugiego ruchem jednostajnym

z prĊdkoĞcią 15 m/s. W odlegáoĞci 100 m od mety jeden z nich przyspieszyá i jadąc ruchem

jednostajnie przyspieszonym po szeĞciu sekundach minąá metĊ. W jakiej odlegáoĞci od mety

znajdowaá siĊ wówczas drugi kolarz jadący do koĔca z niezmienną prĊdkoĞcią?

A. 2,5 m

B. 5 m

C. 10 m

D. 15 m

Zadanie 2. (1 pkt)

Cechy charakterystyczne róĪnych typów gwiazd przedstawia siĊ za pomocą diagramu

Hertzspunga-Russella (H – R). Na osiach wspóárzĊdnych tego diagramu odáoĪona jest

A. temperatura powierzchni (typ widmowy) i jasnoĞü absolutna (absolutna wielkoĞü

gwiazdowa).

B. jasnoĞü absolutna (absolutna wielkoĞü gwiazdowa) i odlegáoĞci od Ziemi.

C. Ğrednica gwiazdy i temperatura jej powierzchni.

D. temperatura powierzchni i odlegáoĞci od Ziemi.

Zadanie 3. (1 pkt)

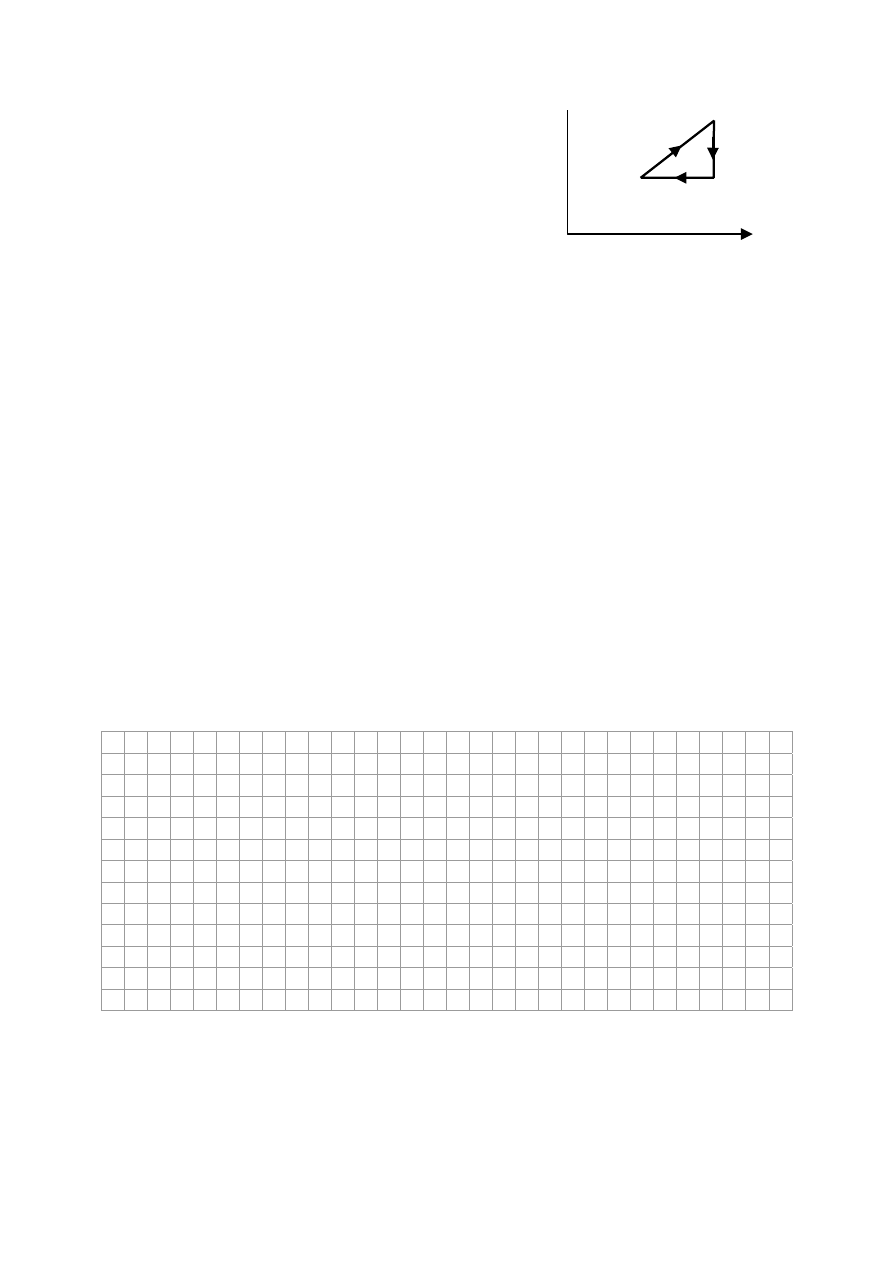
PomiĊdzy nieruchomy stóá i poruszającą siĊ jak na rysunku linijkĊ wáoĪono okrągáy oáówek.

Oáówek porusza siĊ (zakáadając, Īe nie wystĊpują poĞlizgi)

A. w lewo z prĊdkoĞcią o wartoĞci

B. w prawo z prĊdkoĞcią o wartoĞci

C. w prawo z prĊdkoĞcią o wartoĞci

D. w lewo z prĊdkoĞcią o wartoĞci

Zadanie 4. (1 pkt)

Planety w ruchu dookoáa SáoĔca poruszają siĊ po orbitach bĊdących

A. okrĊgami.

B. hiperbolami.

C. elipsami.

D. parabolami.

Zadanie 5. (1 pkt)

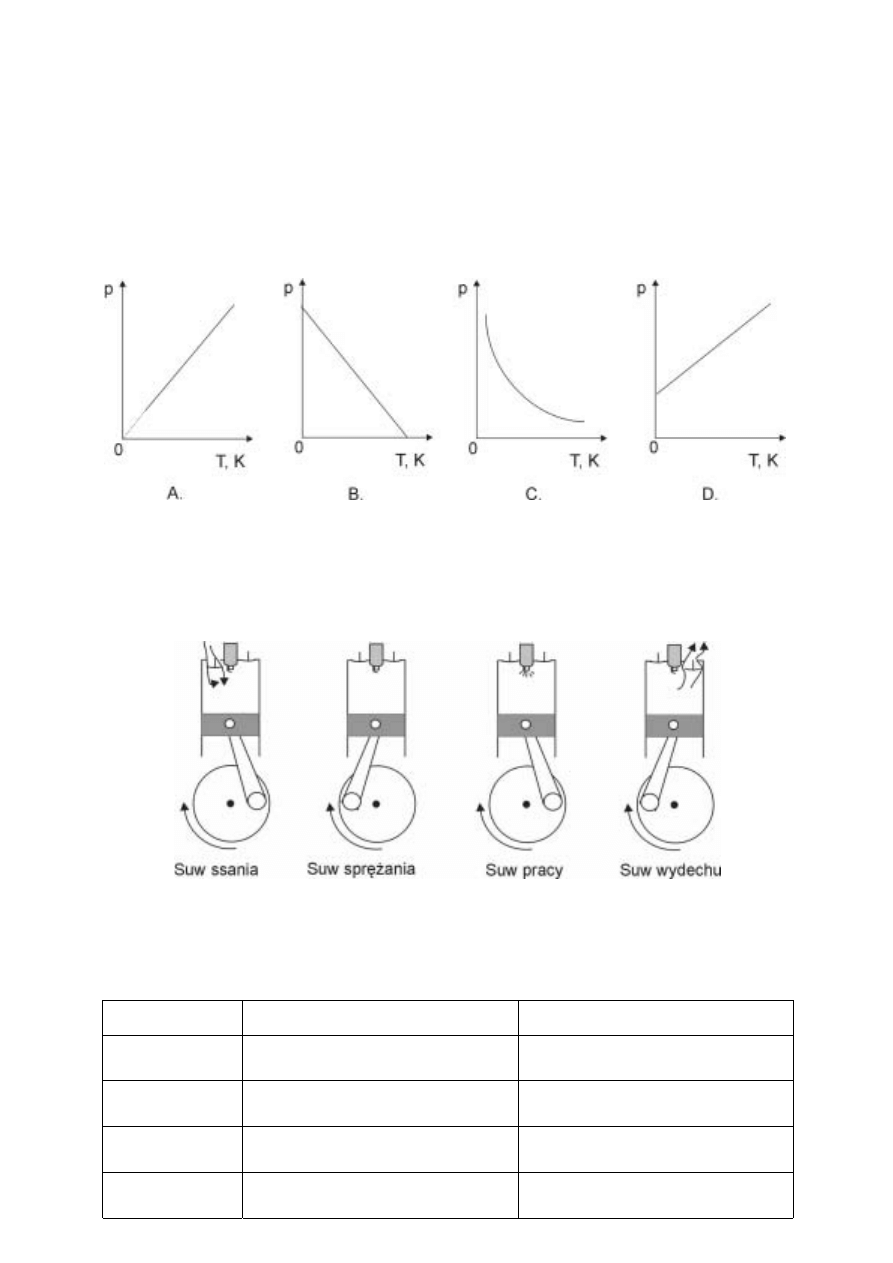
Wykres przedstawia przemianĊ gazu doskonaáego. Jest to przemiana

A. izotermiczna.
B. izochoryczna.
C. izobaryczna.
D. adiabatyczna.

p, Pa

T, K

Zadanie 7. (2 pkt)

Źródło: CKE 01.2006 (PP), zad. 15.

Zadanie 8. (3 pkt)

Źródło: CKE 01.2006 (PP), zad. 16.

Egzamin maturalny z fizyki i astronomii

Arkusz I

14.2

Zapisz, jak zmieni siĊ stosunek prĊdkoĞci wzglĊdnej obliczonej w sposób

relatywistyczny do wartoĞci prĊdkoĞci obliczonej w sposób klasyczny, jeĞli wartoĞci

prĊdkoĞci rakiet zostaną zwiĊkszone.

(1 pkt)

Zadanie 15. Gaz (2 pkt)

Wykres przedstawia zaleĪnoĞü

ciĞnienia od temperatury staáej masy

gazu doskonaáego. ObjĊtoĞü tego gazu

w stanie (1.) wynosi V

. Oblicz, ile

wynosi objĊtoĞü V

w stanie (3.).

Zadanie 16. Silnik (3 pkt)

Silnik cieplny, wykonując pracĊ 2,5 kJ, przekazaá do cháodnicy 7,5 kJ ciepáa. Oblicz

sprawnoĞü tego silnika.

Egzamin maturalny z fizyki i astronomii

Arkusz I

14.2

Zapisz, jak zmieni siĊ stosunek prĊdkoĞci wzglĊdnej obliczonej w sposób

relatywistyczny do wartoĞci prĊdkoĞci obliczonej w sposób klasyczny, jeĞli wartoĞci

prĊdkoĞci rakiet zostaną zwiĊkszone.

(1 pkt)

Zadanie 15. Gaz (2 pkt)

Wykres przedstawia zaleĪnoĞü

ciĞnienia od temperatury staáej masy

gazu doskonaáego. ObjĊtoĞü tego gazu

w stanie (1.) wynosi V

. Oblicz, ile

wynosi objĊtoĞü V

w stanie (3.).

Zadanie 16. Silnik (3 pkt)

Silnik cieplny, wykonując pracĊ 2,5 kJ, przekazaá do cháodnicy 7,5 kJ ciepáa. Oblicz

sprawnoĞü tego silnika.

Zadanie 9. (3 pkt)

Źródło: CKE 05.2006 (PP), zad. 20.

Zadanie 10. (1 pkt)

Źródło: CKE 11.2006 (PP), zad. 3.

Zadanie 11. (1 pkt)

Źródło: CKE 11.2006 (PP), zad. 4.

Zadanie 12. (1 pkt)

Źródło: CKE 11.2006 (PP), zad. 5.

Egzamin maturalny z fizyki i astronomii

Arkusz I

Zadanie 19. Echo (3 pkt)

JeĪeli dwa jednakowe dĨwiĊki docierają do ucha w odstĊpie czasu dáuĪszym niĪ 0,1 s są

sáyszane przez czáowieka oddzielnie (powstaje echo). JeĞli odstĊp czasu jest krótszy od 0,1 s

dwa dĨwiĊki odbieramy jako jeden o przedáuĪonym czasie trwania (powstaje pogáos). Oblicz,

w jakiej najmniejszej odlegáoĞci od sáuchacza powinna znajdowaü siĊ pionowa Ğciana

odbijająca dĨwiĊk, aby po klaĞniĊciu w dáonie sáuchacz usáyszaá echo. Przyjmij, Īe wartoĞü

prĊdkoĞci dĨwiĊku w powietrzu wynosi 340 m/s.

Zadanie 20. Zbiornik z azotem (3 pkt)

Stalowy zbiornik zawiera azot pod ciĞnieniem 1200 kPa. Temperatura gazu wynosi 27

Zbiornik zabezpieczony jest zaworem bezpieczeĔstwa, który otwiera siĊ gdy ciĞnienie gazu

przekroczy 1500 kPa. Zbiornik wystawiono na dziaáanie promieni sáonecznych, w wyniku

czego temperatura gazu wzrosáa do 77

C. Podaj, czy w opisanej sytuacji nastąpi otwarcie

zaworu. OdpowiedĨ uzasadnij, wykonując niezbĊdne obliczenia. Przyjmij, Īe objĊtoĞü

zbiornika mimo ogrzania nie ulega zmianie.

Nr zadania

18.1 18.2

Maks. liczba pkt

Wypeánia

egzaminator! Uzyskana liczba pkt

Próbny egzamin maturalny z fizyki i astronomii

Poziom podstawowy

ZADANIA ZAMKNIĉTE

W zadaniach od 1. do 10. wybierz i zaznacz jedną poprawną odpowiedĨ.

Zadanie 1. (1 pkt)

O tym, Īe siáy dziaáające na KsiĊĪyc siĊ nie równowaĪą, moĪemy wnioskowaü na podstawie

tego, Īe
A. KsiĊĪyc porusza siĊ po torze krzywoliniowym.

B. okres obiegu KsiĊĪyca dookoáa Ziemi jest wiĊkszy niĪ okres obrotu Ziemi wokóá osi.

C. KsiĊĪyc jest zwrócony do Ziemi zawsze tą samą stroną.

D. okres obiegu KsiĊĪyca wokóá Ziemi jest równy okresowi jego obrotu wokóá osi.

Zadanie 2. (1 pkt)

Na cząstkĊ poruszającą siĊ z prĊdkoĞcią

w obszarze pola magnetycznego o indukcji

dziaáa siáa

(rys.).Sytuacja przedstawiona na rysunku dotyczy

A. protonu.

B. elektronu.

C. neutronu.

D. cząstki

Zadanie 3. (1 pkt)

JeĪeli zaáoĪymy, Īe podczas powolnego zmniejszania objĊtoĞci gazu jego temperatura

pozostaje staáa, to na pewno
A. praca wykonana nad gazem jest równa zeru.

B. praca wykonana nad gazem jest równa ciepáu oddanemu przez gaz.

C. ciepáo pobrane przez gaz jest równe pracy wykonanej przez gaz.

D. ciepáo oddane przez gaz jest równe zeru.

Zadanie 4. (1 pkt)

Silnik cieplny oddaje do cháodnicy 4 razy wiĊcej ciepáa niĪ zamienia na pracĊ. SprawnoĞü

silnika jest równa
A. 1/5.

B. 1/4.

C. 1/3.

D. 1/2.

Zadanie 5. (1 pkt)

W zewnĊtrznej warstwie SáoĔca o gruboĞci okoáo 100 000 km materia o wyĪszej temperaturze

unosi siĊ ku powierzchni gdzie oddaje czĊĞü energii do otoczenia i po oziĊbieniu spáywa do

wnĊtrza SáoĔca. Zjawisko to nazywamy
A. promieniowaniem cieplnym.

B. przewodnictwem cieplnym.

C. konwekcją.

D. protuberancją.

Próbny egzamin maturalny z fizyki i astronomii

Poziom podstawowy

ZADANIA ZAMKNIĉTE

W zadaniach od 1. do 10. wybierz i zaznacz jedną poprawną odpowiedĨ.

Zadanie 1. (1 pkt)

O tym, Īe siáy dziaáające na KsiĊĪyc siĊ nie równowaĪą, moĪemy wnioskowaü na podstawie

tego, Īe
A. KsiĊĪyc porusza siĊ po torze krzywoliniowym.

B. okres obiegu KsiĊĪyca dookoáa Ziemi jest wiĊkszy niĪ okres obrotu Ziemi wokóá osi.

C. KsiĊĪyc jest zwrócony do Ziemi zawsze tą samą stroną.

D. okres obiegu KsiĊĪyca wokóá Ziemi jest równy okresowi jego obrotu wokóá osi.

Zadanie 2. (1 pkt)

Na cząstkĊ poruszającą siĊ z prĊdkoĞcią

w obszarze pola magnetycznego o indukcji

dziaáa siáa

(rys.).Sytuacja przedstawiona na rysunku dotyczy

A. protonu.

B. elektronu.

C. neutronu.

D. cząstki

Zadanie 3. (1 pkt)

JeĪeli zaáoĪymy, Īe podczas powolnego zmniejszania objĊtoĞci gazu jego temperatura

pozostaje staáa, to na pewno
A. praca wykonana nad gazem jest równa zeru.

B. praca wykonana nad gazem jest równa ciepáu oddanemu przez gaz.

C. ciepáo pobrane przez gaz jest równe pracy wykonanej przez gaz.

D. ciepáo oddane przez gaz jest równe zeru.

Zadanie 4. (1 pkt)

Silnik cieplny oddaje do cháodnicy 4 razy wiĊcej ciepáa niĪ zamienia na pracĊ. SprawnoĞü

silnika jest równa
A. 1/5.

B. 1/4.

C. 1/3.

D. 1/2.

Zadanie 5. (1 pkt)

W zewnĊtrznej warstwie SáoĔca o gruboĞci okoáo 100 000 km materia o wyĪszej temperaturze

unosi siĊ ku powierzchni gdzie oddaje czĊĞü energii do otoczenia i po oziĊbieniu spáywa do

wnĊtrza SáoĔca. Zjawisko to nazywamy
A. promieniowaniem cieplnym.

B. przewodnictwem cieplnym.

C. konwekcją.

D. protuberancją.

Próbny egzamin maturalny z fizyki i astronomii

Poziom podstawowy

ZADANIA ZAMKNIĉTE

W zadaniach od 1. do 10. wybierz i zaznacz jedną poprawną odpowiedĨ.

Zadanie 1. (1 pkt)

O tym, Īe siáy dziaáające na KsiĊĪyc siĊ nie równowaĪą, moĪemy wnioskowaü na podstawie

tego, Īe
A. KsiĊĪyc porusza siĊ po torze krzywoliniowym.

B. okres obiegu KsiĊĪyca dookoáa Ziemi jest wiĊkszy niĪ okres obrotu Ziemi wokóá osi.

C. KsiĊĪyc jest zwrócony do Ziemi zawsze tą samą stroną.

D. okres obiegu KsiĊĪyca wokóá Ziemi jest równy okresowi jego obrotu wokóá osi.

Zadanie 2. (1 pkt)

Na cząstkĊ poruszającą siĊ z prĊdkoĞcią

w obszarze pola magnetycznego o indukcji

dziaáa siáa

(rys.).Sytuacja przedstawiona na rysunku dotyczy

A. protonu.

B. elektronu.

C. neutronu.

D. cząstki

Zadanie 3. (1 pkt)

JeĪeli zaáoĪymy, Īe podczas powolnego zmniejszania objĊtoĞci gazu jego temperatura

pozostaje staáa, to na pewno
A. praca wykonana nad gazem jest równa zeru.

B. praca wykonana nad gazem jest równa ciepáu oddanemu przez gaz.

C. ciepáo pobrane przez gaz jest równe pracy wykonanej przez gaz.

D. ciepáo oddane przez gaz jest równe zeru.

Zadanie 4. (1 pkt)

Silnik cieplny oddaje do cháodnicy 4 razy wiĊcej ciepáa niĪ zamienia na pracĊ. SprawnoĞü

silnika jest równa
A. 1/5.

B. 1/4.

C. 1/3.

D. 1/2.

Zadanie 5. (1 pkt)

W zewnĊtrznej warstwie SáoĔca o gruboĞci okoáo 100 000 km materia o wyĪszej temperaturze

unosi siĊ ku powierzchni gdzie oddaje czĊĞü energii do otoczenia i po oziĊbieniu spáywa do

wnĊtrza SáoĔca. Zjawisko to nazywamy
A. promieniowaniem cieplnym.

B. przewodnictwem cieplnym.

C. konwekcją.

D. protuberancją.

Zadanie 13. (2 pkt)

Źródło: CKE 11.2006 (PP), zad. 16.

Zadanie 14. (1 pkt)

Źródło: CKE 2007 (PP), zad. 9.

Zadanie 15. (2 pkt)

Źródło: CKE 2007 (PP), zad. 19.

Próbny egzamin maturalny z fizyki i astronomii

Poziom podstawowy

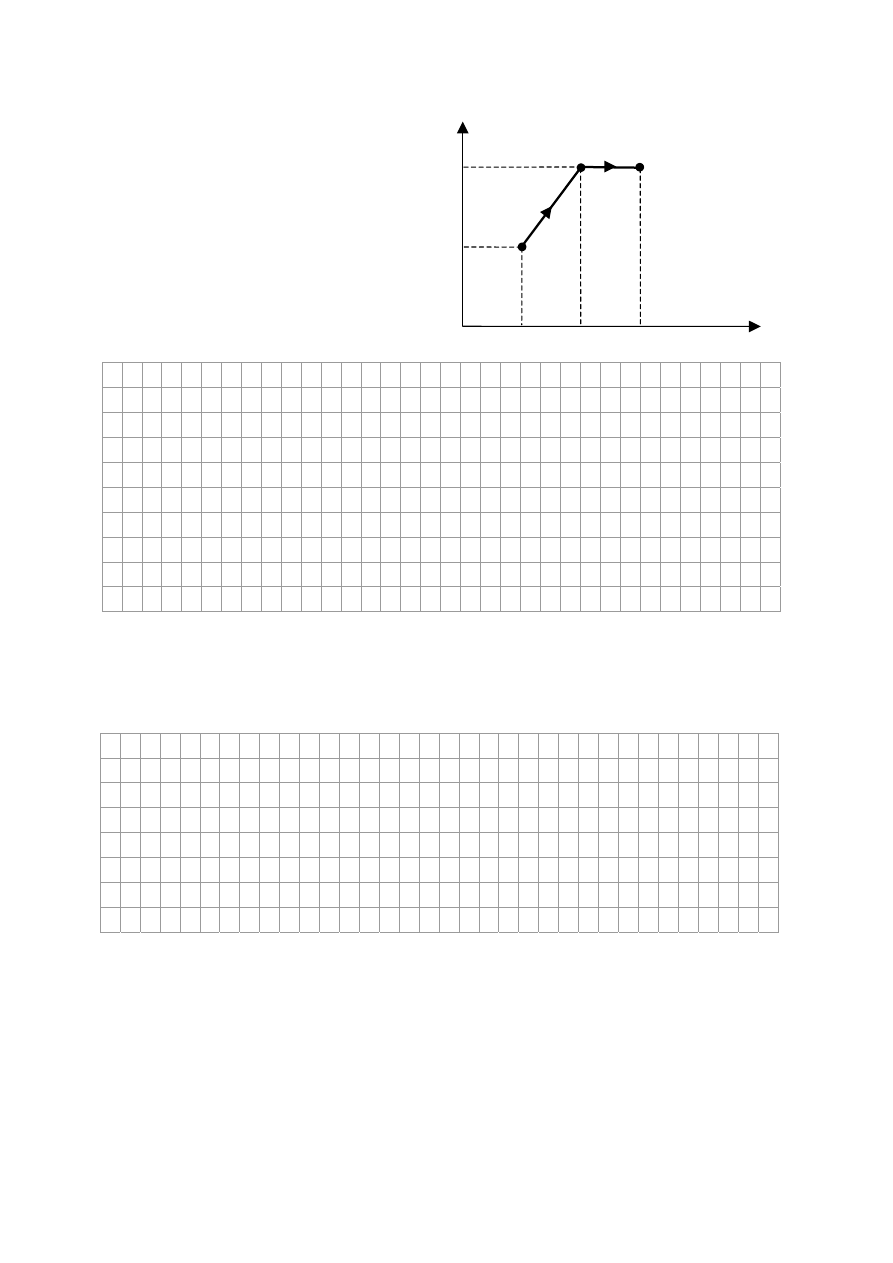
Zadanie 16. Przemiany gazu (2 pkt)

Gaz ulega przemianom (na wykresie zaznaczonym, jako

1 – 2, 2 – 3, 3 – 1), w których zmieniają siĊ ciĞnienie,

objĊtoĞü i temperatura gazu.

16.1.

(1 pkt)

Zapisz, w której z tych przemian jednoczesnej zmianie

ulegają: ciĞnienie, objĊtoĞü i temperatura gazu.

.......................................................................................................................................................

16.2.

(1 pkt)

Zapisz, w którym z punktów (na wykresie zaznaczonych, jako punkt 1, 2 lub 3) temperatura

gazu jest najwyĪsza.

.......................................................................................................................................................

Zadanie 17. GwóĨdĨ (5 pkt)

Máotek o masie 0,5 kg poruszający siĊ z prĊdkoĞcią o wartoĞci 10 m/s, podczas wbijania

gwoĨdzia w drewno, uderza prostopadle jego gáówkĊ i po upáywie 0,002 s zatrzymuje siĊ.

17.1.

(2 pkt)

Oblicz Ğrednią wartoĞü siáy z jaką máotek dziaáa na gwóĨdĨ w czasie uderzenia.

17.2.

(3 pkt)

Oblicz wysokoĞü z jakiej naleĪaáoby swobodnie upuĞciü ten máotek aby uderzenie wbiáo

gwóĨdĨ na tĊ samą gáĊbokoĞü.

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

Zadanie 6. (1 pkt)

Wiązka dodatnio naáadowanych cząstek pochodzenia kosmicznego dociera do Ziemi

prostopadle do jej powierzchni w okolicach równika (rys.). W wyniku dziaáania ziemskiego

pola magnetycznego zostanie ona odchylona w kierunku

A. póánocnym.

B. poáudniowym.

C. wschodnim.

D. zachodnim.

Zadanie 7. (1 pkt)

RozciągniĊcie sprĊĪyny o 1 cm z poáoĪenia równowagi wymaga wykonania pracy 2 J.

RozciągniĊcie tej samej sprĊĪyny o 3 cm, równieĪ z poáoĪenia równowagi, wymaga

wykonania pracy

A. 6 J.

B. 12 J.

C. 18 J.

D. 24 J.

Zadanie 8. (1 pkt)

Podczas przejĞcia wiązki Ğwiatáa z oĞrodka o wiĊkszym wspóáczynniku zaáamania do oĞrodka

o mniejszym wspóáczynniku zaáamania

dáugoĞü fali

prĊdkoĞü fali

roĞnie,

maleje,

roĞnie,

maleje,

Zadanie 9. (1 pkt)

SprawnoĞü silnika cieplnego wynosi 20%. W ciągu 1 godziny silnik oddaje do cháodnicy

20 kJ energii. W tym czasie pobiera on z grzejnika energiĊ cieplną o wartoĞci

A. 25 kJ.

B. 40 kJ.

C. 50 kJ.

D. 100 kJ.

Zadanie 10. (1 pkt)

Trzy czwarte początkowej liczby jąder pewnego izotopu promieniotwórczego ulega

rozpadowi w czasie 24 godzin. Okres poáowicznego rozpadu tego izotopu jest równy

A. 2 godziny.

B. 4 godziny.

C. 8 godzin.

D. 12 godzin.

oĞ obrotu Ziemi

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

18.2. (4 pkt)

Przedstaw na wykresie zaleĪnoĞü wychylenia tego wahadáa od czasu. Na wykresie zaznacz

wartoĞci liczbowe amplitudy oraz okresu drgaĔ.

obliczenia

wykres

19. Gaz (2 pkt)

W cylindrze o objĊtoĞci 15 dm

znajduje siĊ wodór. CiĞnienie wodoru jest równe 1013,82 hPa,

a jego temperatura wynosi 27

Oblicz liczbĊ moli wodoru znajdujących siĊ w cylindrze.

Zadanie 13.1 (1 pkt)

Zadanie 13.2 (1 pkt)

Zadanie 16. (1 pkt)

Źródło: CKE 2008 (PP), zad. 4.

Zadanie 17. (1 pkt)

Źródło: CKE 2008 (PP), zad. 5.

Zadanie 18. (5 pkt)

Źródło: CKE 2008 (PP), zad. 18.

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

ZADANIA ZAMKNIĉTE

W zadaniach od 1. do 10. wybierz i zaznacz na karcie odpowiedzi jedną

poprawną odpowiedĨ.

Zadanie 1. (1 pkt)

Ziemia pozostaje w spoczynku wzglĊdem

A. SáoĔca.

B. KsiĊĪyca.

C. Galaktyki.

D. satelity geostacjonarnego.

Zadanie 2. (1 pkt)

JeĪeli podczas ruchu samochodu, na prostoliniowym odcinku autostrady energia kinetyczna

samochodu wzrosáa 4 razy, to wartoĞü prĊdkoĞci samochodu wzrosáa

razy.

B. 2 razy.

C. 4 razy.

D. 16 razy.

Zadanie 3. (1 pkt)

ZaleĪnoĞü energii potencjalnej i kinetycznej od czasu podczas swobodnego spadania ciaáa

z pewnej wysokoĞci poprawnie przedstawiono na

A. wykresie 1.

B. wykresie 2.

C. wykresie 3.

D. wykresie 4.

Zadanie 4. (1 pkt)

Promienie sáoneczne ogrzaáy szczelnie zamkniĊtą metalową butlĊ z gazem. JeĪeli pominiemy

rozszerzalnoĞü termiczną butli, to gaz w butli ulegá przemianie

A. izobarycznej.

B. izochorycznej.

C. izotermicznej.

D. adiabatycznej.

, E

wykres 1

wykres 2

, E

wykres 4

wykres 3

, E

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

Zadanie 5. (1 pkt)

Unoszenie siĊ w górĊ iskier nad páonącym ogniskiem w bezwietrzny dzieĔ jest spowodowane

zjawiskiem

A. dyfuzji.

B. konwekcji.

C. przewodnictwa.

D. promieniowania.

Zadanie 6. (1 pkt)

Gdy w atomie wodoru elektron przejdzie z orbity pierwszej na drugą, to promieĔ orbity

wzrasta czterokrotnie. WartoĞü siáy przyciągania elektrostatycznego dziaáającej pomiĊdzy

jądrem i elektronem zmaleje w tej sytuacji

A. 2 razy.

B. 4 razy.

C. 8 razy.

D. 16 razy.

Zadanie 7. (1 pkt)

W cyklotronie do zakrzywiania torów naáadowanych cząstek wykorzystuje siĊ

A. staáe pole elektryczne.

B. staáe pole magnetyczne.

C. zmienne pole elektryczne.

D. zmienne pole magnetyczne.

Zadanie 8. (1 pkt)

Ziemia krąĪy wokóá SáoĔca w odlegáoĞci w przybliĪeniu 4 razy wiĊkszej niĪ Merkury.

Korzystając z trzeciego prawa Keplera moĪna ustaliü, Īe okres obiegu Ziemi wokóá SáoĔca

jest w porównaniu z okresem obiegu Merkurego dáuĪszy

okoáo

A. 2 razy.

B. 4 razy.

C. 8 razy.

D. 16 razy.

Zadanie 9. (1 pkt)

Jądro izotopu ulegáo rozpadowi promieniotwórczemu. Powstaáo nowe jądro zawierające

o jeden proton wiĊcej i o jeden neutron mniej niĪ jądro wyjĞciowe. Przedstawiony powyĪej

opis dotyczy rozpadu

A. alfa.

B. gamma.

C. beta plus.

D. beta minus.

Zadanie 10. (1 pkt)

Przyrząd sáuĪący do uzyskiwania i obserwacji widma promieniowania elektromagnetycznego

A. kineskop.

B. mikroskop.

C. oscyloskop.

D. spektroskop.

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

Zadanie 16. Metalowa puszka (2 pkt)

Do pustej metalowej puszki po napoju, poáoĪonej tak, Īe moĪe siĊ toczyü po poziomej uziemionej

metalowej páycie, zbliĪamy z boku na niewielką odlegáoĞü dodatnio naelektryzowaną paáeczkĊ.

WyjaĞnij, dlaczego puszka zaczyna siĊ toczyü. OkreĞl, w którą stronĊ bĊdzie toczyü siĊ

puszka.

Zadanie 17. Elektron (1 pkt)

Oblicz koĔcową, relatywistyczną wartoĞü pĊdu elektronu przyspieszanego w akceleratorze

do prĊdkoĞci 0,8 c. ZaáóĪ, Īe początkowa wartoĞü prĊdkoĞci przyspieszanego elektronu jest

znikomo maáa.

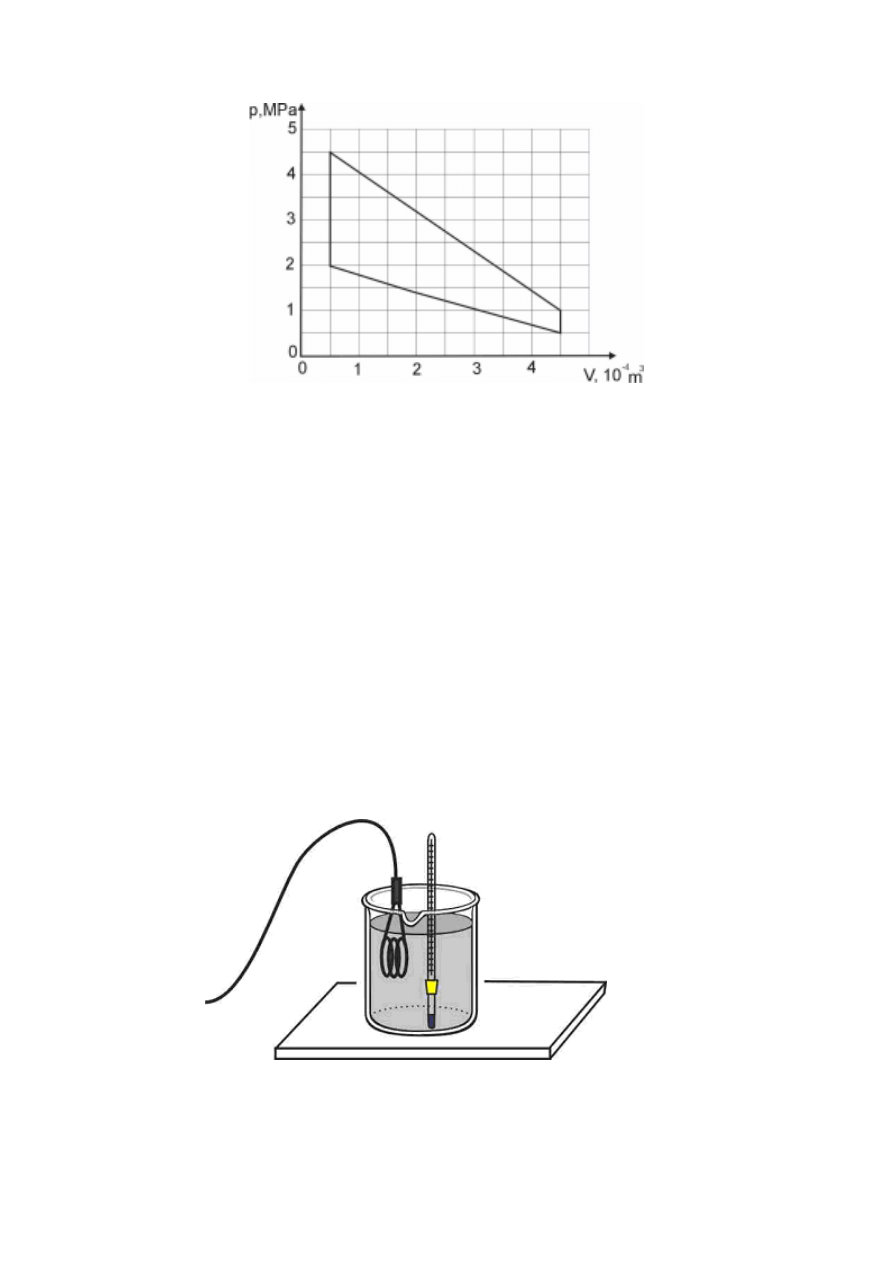
Zadanie 18. Przemiana izotermiczna (5 pkt)

Gaz o temperaturze

C poddano

przemianie izotermicznej. CiĞnienie

początkowe gazu wynosiáo 800 hPa.

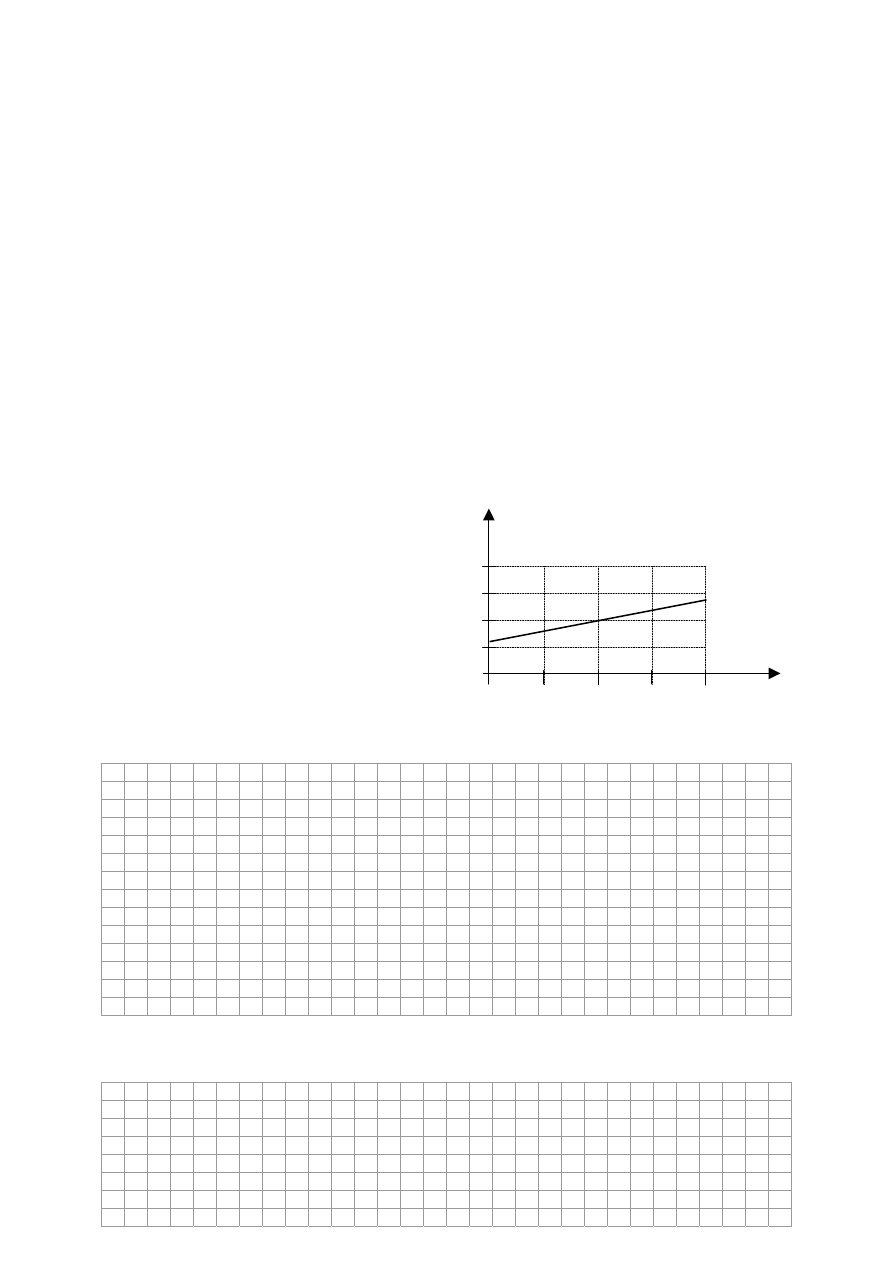
Wykres przedstawia zaleĪnoĞü gĊstoĞci

gazu od jego ciĞnienia dla tej przemiany.

Podczas przemiany masa gazu nie

ulegaáa zmianie.

p, hPa

d, kg/m

800

1000 1100 1200

0,04

0,06

0,08

0,12
0,10

900

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

Zadanie 18.1 (3 pkt)

Oblicz masĊ molową tego gazu.

Zadanie 18.2 (2 pkt)

Podaj, czy w tej przemianie objĊtoĞü gazu rosáa, czy malaáa. OdpowiedĨ uzasadnij.

Zadanie 19. Soczewka (4 pkt)

ZdolnoĞü skupiająca soczewki páasko-wypukáej wykonanej z materiaáu o wspóáczynniku

zaáamania równym 2 i umieszczonej w powietrzu wynosi 2 dioptrie.

Zadanie 19.1 (3 pkt)

Oblicz promieĔ krzywizny wypukáej czĊĞci soczewki.

Zadanie 19.2 (1 pkt)

Napisz, czy ta soczewka moĪe korygowaü wadĊ dalekowzrocznoĞci.

Nr zadania

16. 17. 18.1. 18.2. 19.1. 19.2.

Maks. liczba pkt

Wypeánia

egzaminator! Uzyskana liczba pkt

Zadanie 18.1 (3 pkt)

Zadanie 18.2 (2 pkt)

Zadanie 19. (1 pkt)

Źródło: CKE 2009 (PP), zad. 4.

Zadanie 20. (5 pkt)

Źródło: CKE 2009 (PP), zad. 14.

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

ZADANIA ZAMKNIĉTE

W zadaniach od 1. do 10. wybierz i zaznacz na karcie odpowiedzi jedną poprawną

odpowiedĨ.

Zadanie 1. (1 pkt)

Samochód porusza siĊ po prostoliniowym odcinku autostrady. DrogĊ przebytą przez

samochód opisuje równanie: s = 15 t + 1,5 t

(w ukáadzie SI z pominiĊciem jednostek).

WartoĞci prĊdkoĞci początkowej i przyspieszenia samochodu wynoszą odpowiednio

WartoĞü prĊdkoĞci początkowej, m/s

WartoĞü przyspieszenia, m/s

0,75

Zadanie 2. (1 pkt)

Maáą kulkĊ przymocowaną do nici wprawiono w ruch jednostajny po okrĊgu w páaszczyĨnie

poziomej. Przyspieszenie doĞrodkowe kulki jest związane ze zmianą

A. wartoĞci prĊdkoĞci liniowej.

B. kierunku prĊdkoĞci liniowej.

C. wartoĞci prĊdkoĞci kątowej.

D. kierunku prĊdkoĞci kątowej.

Zadanie 3. (1 pkt)

Piáka uderza o podáogĊ z prĊdkoĞcią o wartoĞci 2 m/s skierowaną prostopadle do podáogi

i odbija siĊ od niej z prĊdkoĞcią o wartoĞci 1,5 m/s. BezwzglĊdna wartoĞü zmiany prĊdkoĞci

piáki podczas odbicia wynosi

A. 0 m/s.

B. 0,5 m/s.

C. 2,5 m/s.

D. 3,5 m/s.

Zadanie 4. (1 pkt)

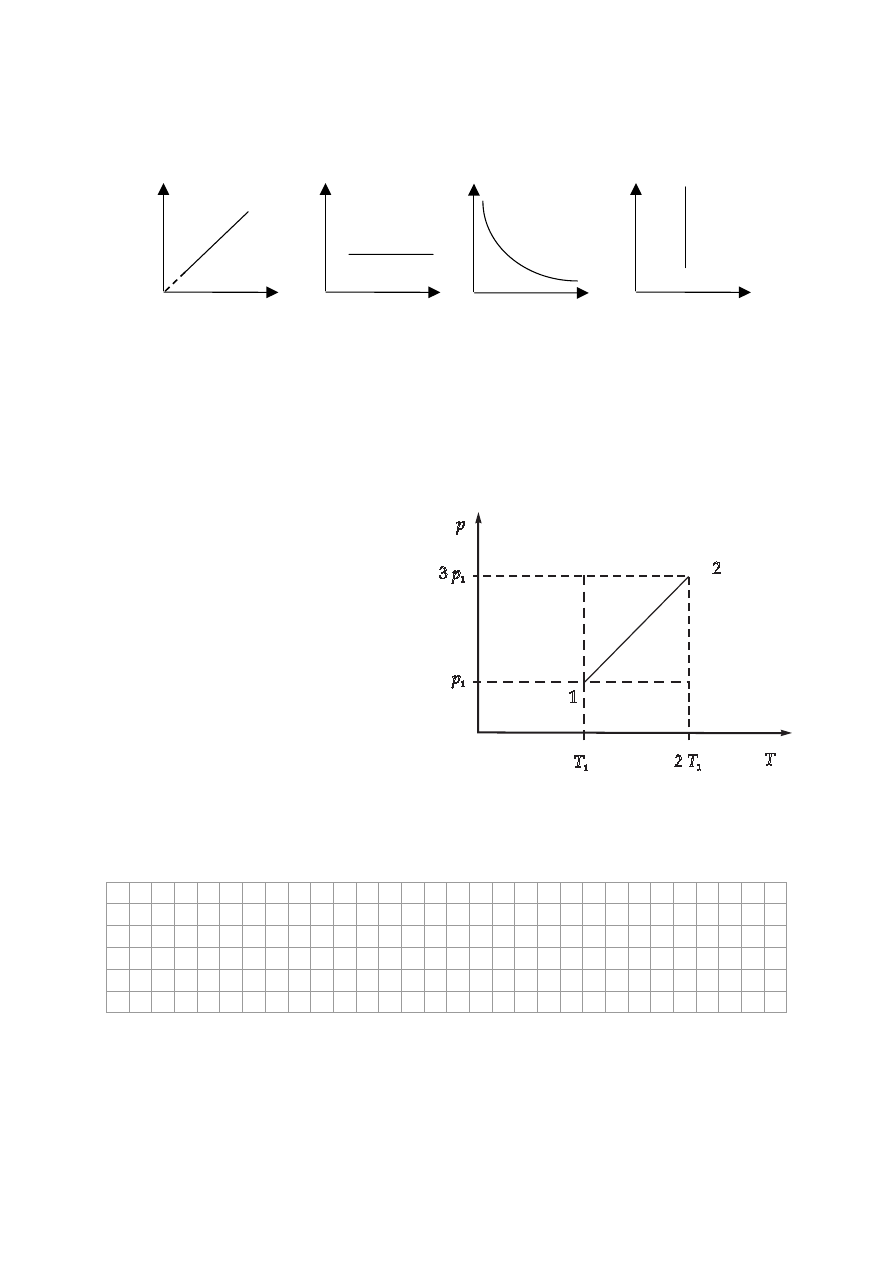
Staáą masĊ gazu poddano przemianie gazowej. Pierwszą zasadĊ termodynamiki dla tej

przemiany moĪna zapisaü: ǻU = Q. PrzemianĊ tĊ poprawnie przedstawiono na wykresie

oznaczonym numerem

A. 1.

B. 2.

C. 3.

D. 4.

1 2 3 4

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

Zadanie 13. Wózek (3 pkt)

Wózek o masie 0,5 kg, poáączony ze Ğcianą za pomocą sprĊĪyny, wprawiono w drgania (rys.).

Na wykresie przedstawiono zaleĪnoĞü siáy powodującej ruch wózka od jego przemieszczenia.

W obliczeniach pomiĔ opory ruchu.

F, N

– 2

x, m

0,025

– 0,025

Zadanie 13.1 (2 pkt)

Oblicz wspóáczynnik sprĊĪystoĞci sprĊĪyny.

Zadanie 13.2 (1 pkt)

WykaĪ, Īe maksymalna wartoĞü przyspieszenia wózka wynosi 4

m/s

Zadanie 14. Przemiana gazowa (5 pkt)

W cylindrze zamkniĊtym ruchomym

táokiem

znajduje

siĊ 48 g gazu.

Temperatura początkowa gazu wynosiáa

C, a ciĞnienie 800 hPa. ObjĊtoĞü gazu

byáa równa 0,047 m

. Gaz poddano

przemianie 1 – 2, gdzie cyframi 1 i 2

oznaczono odpowiednio stan początkowy

oraz koĔcowy gazu.

3 p

2 T

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

Zadanie 14.1 (2 pkt)

Ustal, jak zmieniáa siĊ (wzrosáa czy zmalaáa) gĊstoĞü gazu w tej przemianie. OdpowiedĨ

uzasadnij, zapisując odpowiednie zaleĪnoĞci.

Zadanie 14.2 (3 pkt)

Ustal, który z wymienionych w tabeli gazów poddano przedstawionej powyĪej przemianie.

OdpowiedĨ uzasadnij, wykonując konieczne obliczenia.

Rodzaj gazu

Masa 1 mola, g

azot

hel

tlen

dwutlenek wĊgla

Zadanie 15. Laser (3 pkt)

Laser helowo neonowy o mocy 0,02 W wysyáa w ciągu jednej sekundy 6,35·10

fotonów.

Oblicz dáugoĞü fali Ğwiatáa emitowanego przez ten laser.

Nr zadania

13.1 13.2 14.1 14.2 15.

Maks. liczba pkt

Wypeánia

egzaminator!

Uzyskana liczba pkt

Zadanie 20.1 (2 pkt)

Egzamin maturalny z fizyki i astronomii

Poziom podstawowy

Zadanie 14.1 (2 pkt)

Ustal, jak zmieniáa siĊ (wzrosáa czy zmalaáa) gĊstoĞü gazu w tej przemianie. OdpowiedĨ

uzasadnij, zapisując odpowiednie zaleĪnoĞci.

Zadanie 14.2 (3 pkt)

Ustal, który z wymienionych w tabeli gazów poddano przedstawionej powyĪej przemianie.

OdpowiedĨ uzasadnij, wykonując konieczne obliczenia.

Rodzaj gazu

Masa 1 mola, g

azot

hel

tlen

dwutlenek wĊgla

Zadanie 15. Laser (3 pkt)

Laser helowo neonowy o mocy 0,02 W wysyáa w ciągu jednej sekundy 6,35·10

fotonów.

Oblicz dáugoĞü fali Ğwiatáa emitowanego przez ten laser.

Nr zadania

13.1 13.2 14.1 14.2 15.

Maks. liczba pkt

Wypeánia

egzaminator!

Uzyskana liczba pkt

Zadanie 20.2 (3 pkt)

Zadanie 21. (3 pkt)

Źródło: CKE 2010 (PP), zad. 14.

Egzamin maturalny z fizyki i astronomii

poziom podstawowy

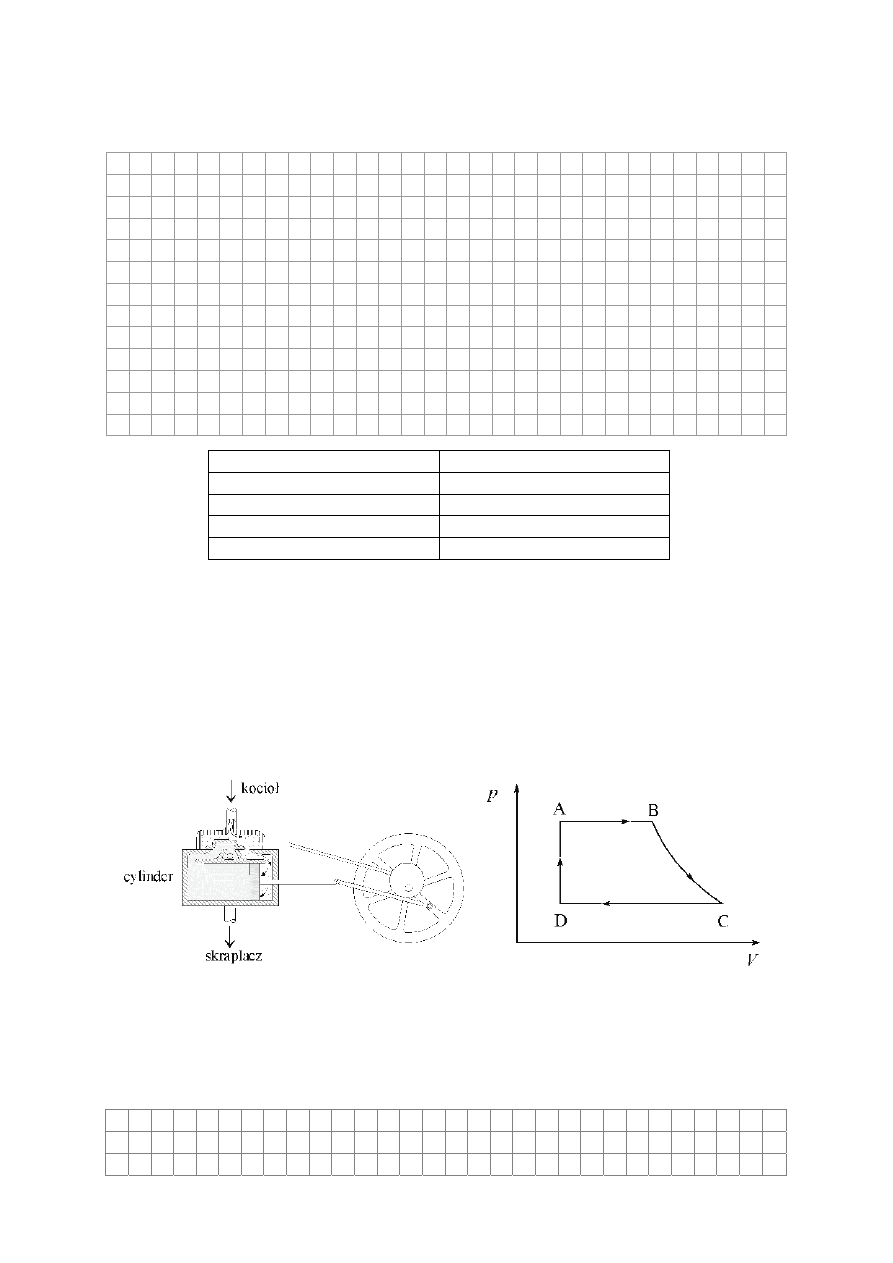
Zadanie 14. Silnik parowy (3 pkt)

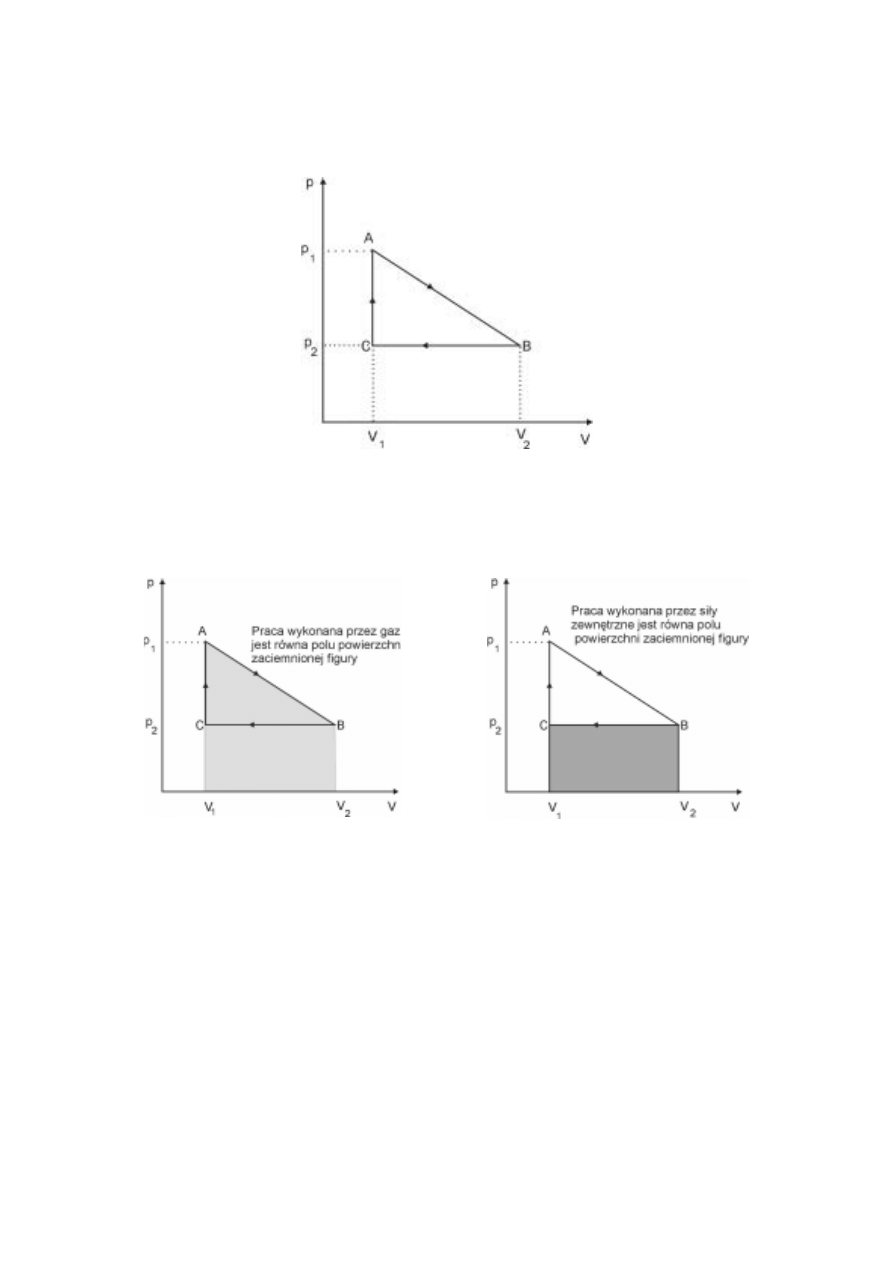
PoniĪej przedstawiono schemat táokowego silnika parowego oraz cykl przemian

termodynamicznych związanych z jego pracą. W silniku parowym gorąca para wodna pod

wysokim ciĞnieniem jest wprowadzana z kotáa do cylindra. Ulega tam rozprĊĪaniu najpierw

pod staáym ciĞnieniem, a nastĊpnie, gdy dopáyw pary jest juĪ zamkniĊty, rozprĊĪanie odbywa

siĊ bardzo szybko, bez wymiany ciepáa z otoczeniem – co powoduje czĊĞciowe skroplenie siĊ

pary. Wracający táok, przy otwartym kanale wylotowym, wypycha z cylindra do skraplacza

mieszaninĊ wody i pary. NastĊpnie cykl pracy silnika siĊ powtarza.

Zadanie 14.1 (1 pkt)

Zaznacz na wykresie pracĊ uĪyteczną (wykonaną przez silnik) w jednym cyklu.

Zadanie 14.2 (1 pkt)

Zapisz nazwĊ przemiany jakiej podlega gaz/para na odcinku A–B.

Zadanie 14.3 (1 pkt)

W silniku parowym temperatura dostarczanej pary wynosi 227 °C, temperatura w skraplaczu

jest równa 27 °C. Oblicz teoretyczną sprawnoĞü silnika Carnota pracującego przy tych

samych temperaturach, co opisany silnik parowy.

Nr zadania

13.1 13.2 14.1 14.2 14.3

Maks. liczba pkt

Wypeánia

egzaminator

Uzyskana liczba pkt

Zadanie 21.1 (1 pkt)

Zadanie 21.2 (1 pkt)

Egzamin maturalny z fizyki i astronomii

poziom podstawowy

Zadanie 14. Silnik parowy (3 pkt)

PoniĪej przedstawiono schemat táokowego silnika parowego oraz cykl przemian

termodynamicznych związanych z jego pracą. W silniku parowym gorąca para wodna pod

wysokim ciĞnieniem jest wprowadzana z kotáa do cylindra. Ulega tam rozprĊĪaniu najpierw

pod staáym ciĞnieniem, a nastĊpnie, gdy dopáyw pary jest juĪ zamkniĊty, rozprĊĪanie odbywa

siĊ bardzo szybko, bez wymiany ciepáa z otoczeniem – co powoduje czĊĞciowe skroplenie siĊ

pary. Wracający táok, przy otwartym kanale wylotowym, wypycha z cylindra do skraplacza

mieszaninĊ wody i pary. NastĊpnie cykl pracy silnika siĊ powtarza.

Zadanie 14.1 (1 pkt)

Zaznacz na wykresie pracĊ uĪyteczną (wykonaną przez silnik) w jednym cyklu.

Zadanie 14.2 (1 pkt)

Zapisz nazwĊ przemiany jakiej podlega gaz/para na odcinku A–B.

Zadanie 14.3 (1 pkt)

W silniku parowym temperatura dostarczanej pary wynosi 227 °C, temperatura w skraplaczu

jest równa 27 °C. Oblicz teoretyczną sprawnoĞü silnika Carnota pracującego przy tych

samych temperaturach, co opisany silnik parowy.

Nr zadania

13.1 13.2 14.1 14.2 14.3

Maks. liczba pkt

Wypeánia

egzaminator

Uzyskana liczba pkt

Zadanie 21.3 (1 pkt)

Wyszukiwarka

Podobne podstrony:
G W I A Z D Y, Fizyka, 14.Astronomia
FIZYKA (14)
Fizyka 14
fizyka współczesna pp
fizyka kwantowa pp
fizyka model pp
Fizyka 10 PP
K O S M O L O G I A, Fizyka, 14.Astronomia
arkusz fizyka poziom pp rok 2005 model
Fizyka 13 PP klucz(2)
fizyka współczesna pp klucz

więcej podobnych podstron