Mec hanika kw antowa 1

ELEMENTY MECHANIKI KWANTOWEJ

Mechanika kwantowa (albo mechanika falowa) zajmuje si“ ruchami
mikroczsteczek i ich oddzia»ywaniami (o ile nie prowadz do zmiany liczby
i rodzaju mikroczstek)

Zajmiemy si“ mechanik kwantow nierelatywistyczn.

Hipoteza de Broglie’a (1924 r.)

Jeóeli Ñwiat»o ma dwoist falowo-czstkow natur“,

fale o cz“stoÑci i d»ugoÑci

czstki o energii

i p“dzie

to takóe czstki o niezerowej masie powinny mieƒ tak natur“.
Czstki takie, o energii i p“dzie , zachowuj si“ jak

fale o cz“stoÑci

i d»ugoÑci

.

(E i p rozumiane s tu w sensie relatywistycznym:

,

)

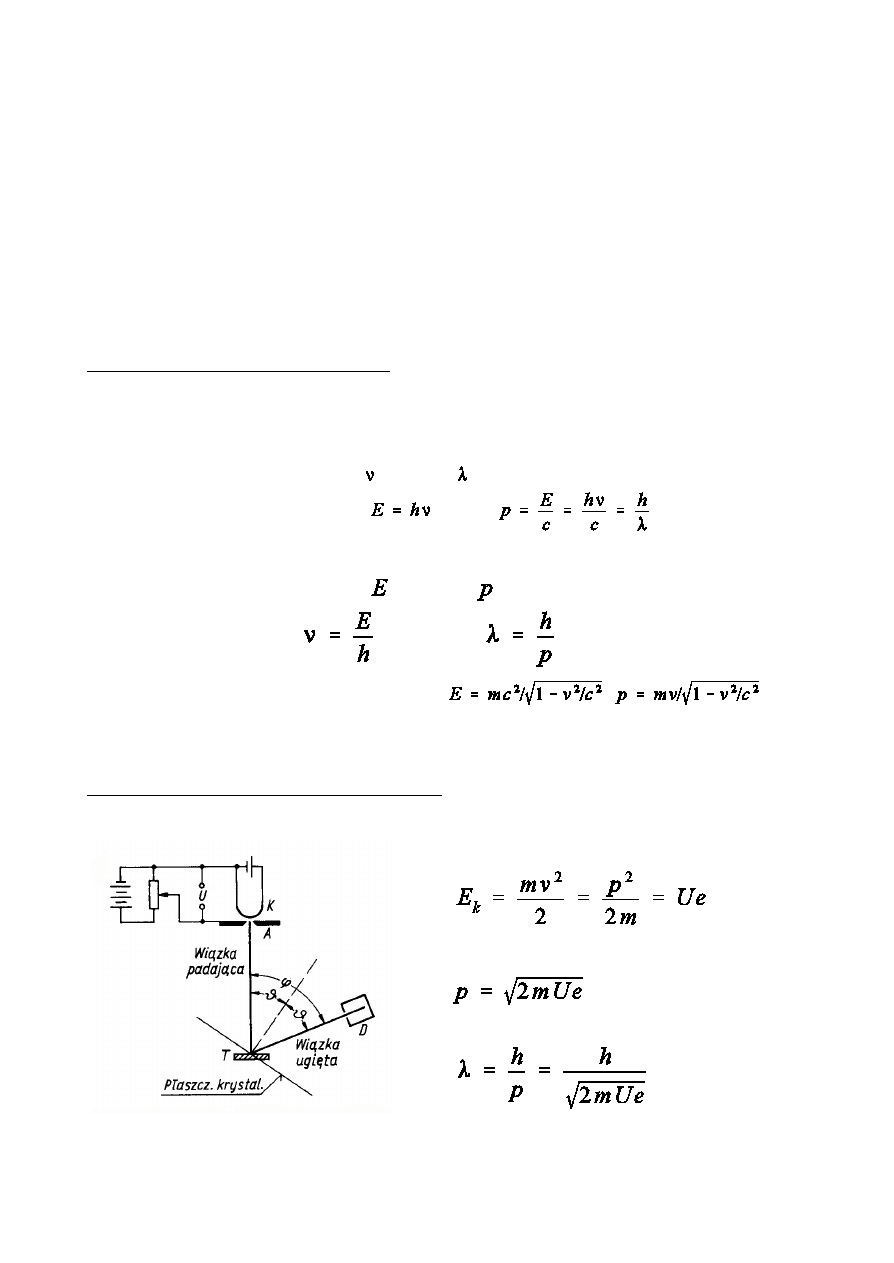
DoÑwiadczenie Davissona i Germera - pierwsze potwierdzenie hipotezy de

Broglie'a (1927 r.)

Mec hanika kw antowa 2

S

k

- p»aszczyzny sieciowe

CD - r ó ó n i c a d r ó g c i  g ó w

falowych P

1

B i P

2

B

Wzmocnienie, gdy

(warunek Braggów)

,

,

,

,

Wniosek:

Kaódej poruszajcej si“ czstce materialnej moóna przypisaƒ fal“ materii,

której d»ugoу jest okreÑlona wzorem de Broglie'a

.

Materia, podobnie jak promieniowanie, wykazuje dualizm falowo-czstkowy.

Mec hanika kw antowa 3

Funkcja falowa

W mechanice kwantowej czstkom przypisuje si“ funkcje falowe

w ogólnoÑci b“dce superpozycjami monochromatycznych fal de Broglie’a

Sens fizyczny funkcji falowej

Interpretacja Borna (1926 r.)

Sama funkcja falowa nie ma bezpoÑredniej interpretacji fizycznej.
Interpretacj“ fizyczn ma natomiast kwadrat modu»u funkcji falowej

tak, óe

gdzie

- prawdopodobie½stwo tego, óe czstka znajdzie si“ wewntrz

obszaru o obj“toÑci

.

Funkcja Q cz“sto jest rozumiana jako funkcja znormalizowana
(unormowana), czyli spe»niajca warunek

(wtedy

)

G“stoу prawdopodobie½stwa znalezienia czstki w danym elemencie
przestrzeni

Mec hanika kw antowa 4

Opis ruchu czstki swobodnej za pomoc monochromatycznej fali de
Broglie’a

w jednym wymiarze, dla czstki

poruszajcej si“ wzd»uó os x

w przestrzeni trójwymiarowej, dla czstki

poruszajcej si“ w kierunku

Czstki opisane tak fal maj ÑciÑle okreÑlon energi“ i p“d, ale ich
zaleónoу po»oóenia od czasu nie jest okreÑlona.

Pr“dkoу fazowa a pr“dkoу grupowa fal de Broglie'a

Wynik ten nie jest sprzeczny z teori wzgl“dnoÑci, gdyó aby mówiƒ o
pr“dkoÑci czstki, naleóy jej przyporzdkowaƒ nie fal“ monochromatyczn,
a grup“ fal. Pr“dkoу fazowa fal de Broglie’a zaleóy od ich d»ugoÑci fali, a
wi“c fale te podlegaj dyspersji, a w konsekwencji pr“dkoу grupowa jest
róóna od pr“dkoÑci fazowej

Pr“dkoу grupowa fal de Broglie'a jest równa pr“dkoÑci przemieszczania si“
czstki.

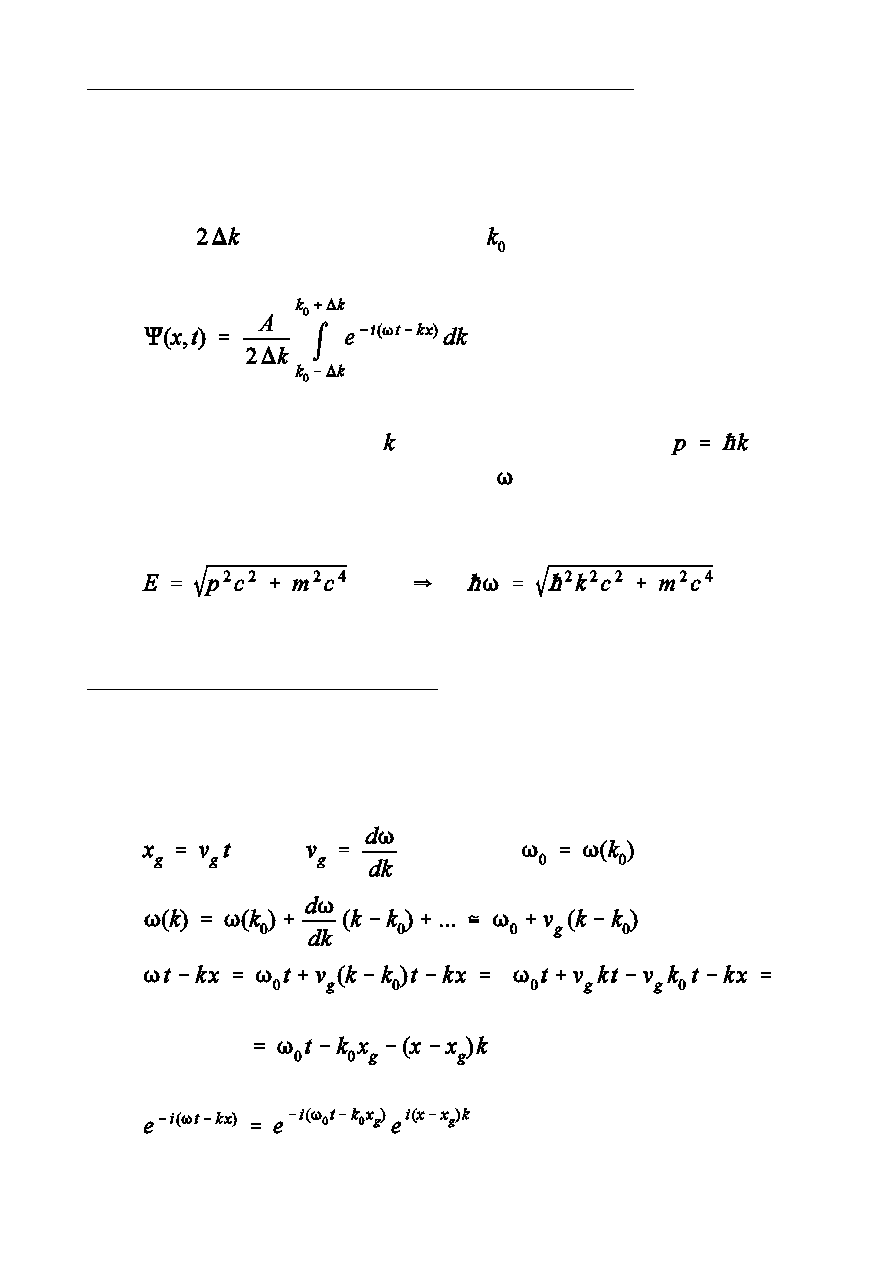
Mec hanika kw antowa 5

Opis ruchu czstki swobodnej za pomoc paczki falowej

Dla uproszczenia weïmy czstk“ poruszajc si“ równolegle do osi x, w jej
dodatnim kierunku. Takiej czstce moóna przypisaƒ grup“ fal p»askich o
wartoÑciach modu»u wektora falowego zawartych w pewnym przedziale (o
szerokoÑci

) wokó» pewnej wartoÑci

Zwróƒmy uwag“, óe rozmycie oznacza rozmycie p“du (bo

) oraz,

óe w takim przypadku wartoÑci cz“stoÑci s równieó rozmyte wewntrz

pewnego przedzia»u, co wynika relacji energii i p“du

Zasada nieokreÑlonoÑci Heisenberga

Aby dok»adniej przeanalizowaƒ konsekwencje rozmycia energii i p“du w
paczce falowej, wykonajmy ca»kowanie we wzorze opisujcym paczk“

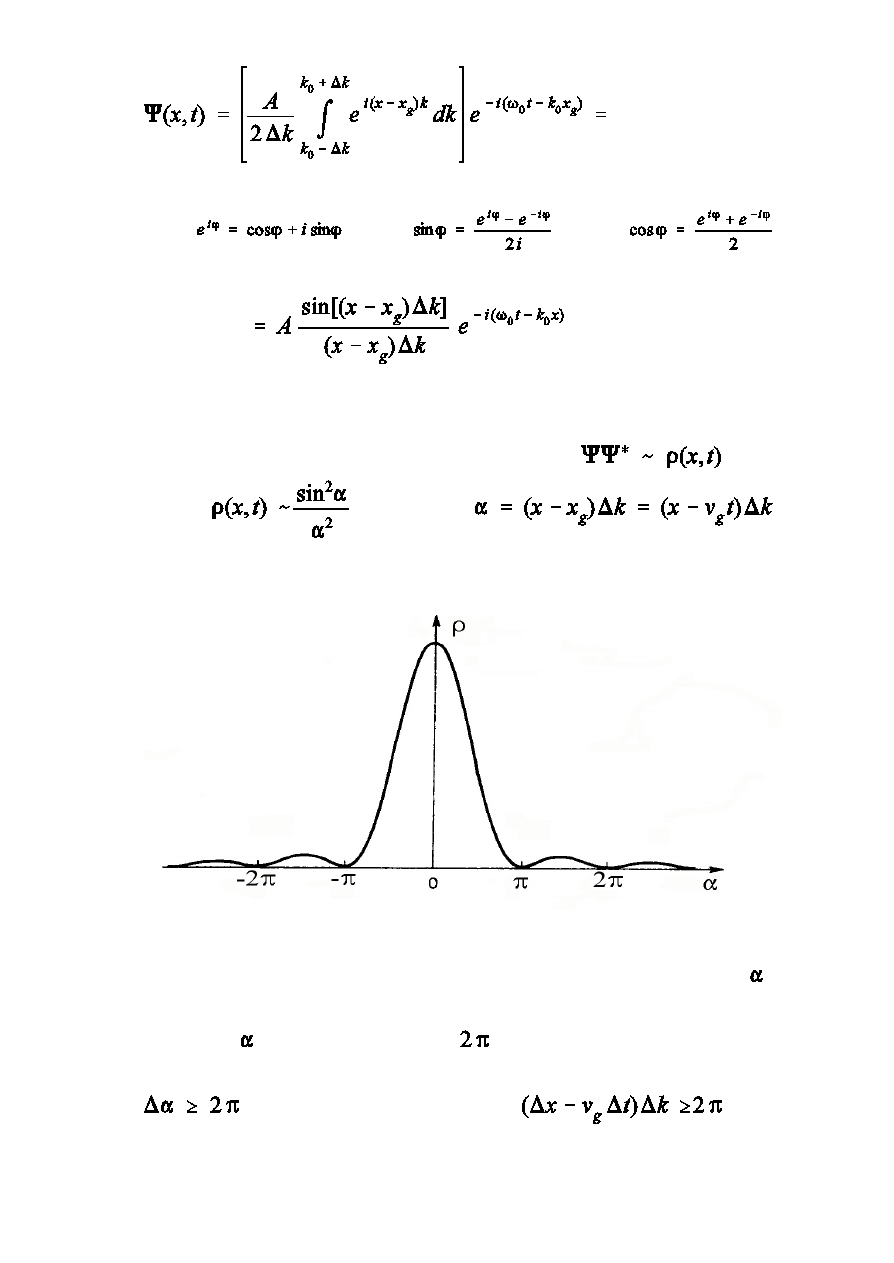
Mec hanika kw antowa 6

,

,

Sens fizyczny ma kwadrat modu»u funkcji falowej

Std mamy

, gdzie

Dla czstki opisanej paczk falow mamy pewien zakres wartoÑci (nie

pojedyncz wartoу). Moóna w pierwszym przyblióeniu przyjƒ, óe
nieokreÑlonoу wynosi co najmniej

czyli, óe

Mec hanika kw antowa 7

PokazaliÑmy, óe dla czstki swobodnej opisanej paczk falow

1. JeÑli ustalimy czas (

), to

6

6

6

W analogiczny sposób moóna otrzymaƒ

Niemoóliwe jest jednoczesne okreÑlenie p“du i po»oóenia czstki

2. JeÑli ustalimy po»oóenie (

), to

6

6

6

Energia czstki w danym stanie moóe byƒ okreÑlona z tym
wi“ksz dok»adnoÑci, im d»uóej czstka znajduje si“ w tym
stanie

Mec hanika kw antowa 8

Równanie Schrödingera (1926)

,

,

,

Funkcja

spe»nia warunek

, gdzie

. (gradient U ze znakiem minus jest

równy wypadkowej sile dzia»ajcej na czstk“). JeÑli U nie zaleóy od

czasu, to

jest energi potencjaln czstki.

Funkcja falowa musi spe»niaƒ tzw. warunki naturalne. Zgodnie z nimi
funkcja falowa musi byƒ:

!

cig»a,

!

g»adka - pochodne

,

,

powinny byƒ cig»e,

!

jednoznaczna,

!

ograniczona,

!

funkcja

powinna byƒ ca»kowalna, tzn. ca»ka

powinna mieƒ wartoу sko½czon.

Mec hanika kw antowa 9

Stan stacjonarny czstki stan, w któr ym

,

g“stoу

prawdopodobie½stwa znalezienia czstki w
danym obszarze przestrzeni nie zaleóy od czasu.

Stan stacjonarny jest charakterystyczny dla stacjonarnego pola si»

. Dla stanu stacjonarnego funkcja falowa moóe byƒ

zapisana jako iloczyn funkcji zaleónej tylko od wspó»rz“dnych i funkcji
zaleónej tylko od czasu

gdzie E jest energi ca»kowit czstki

Postaƒ równania Schrödingera dla stanu stacjonarnego

s t a c j o n a r n e r ó w n a n i e

Schr öd ing e ra , r ó wn a n i e
Schrödingera bez czasu.

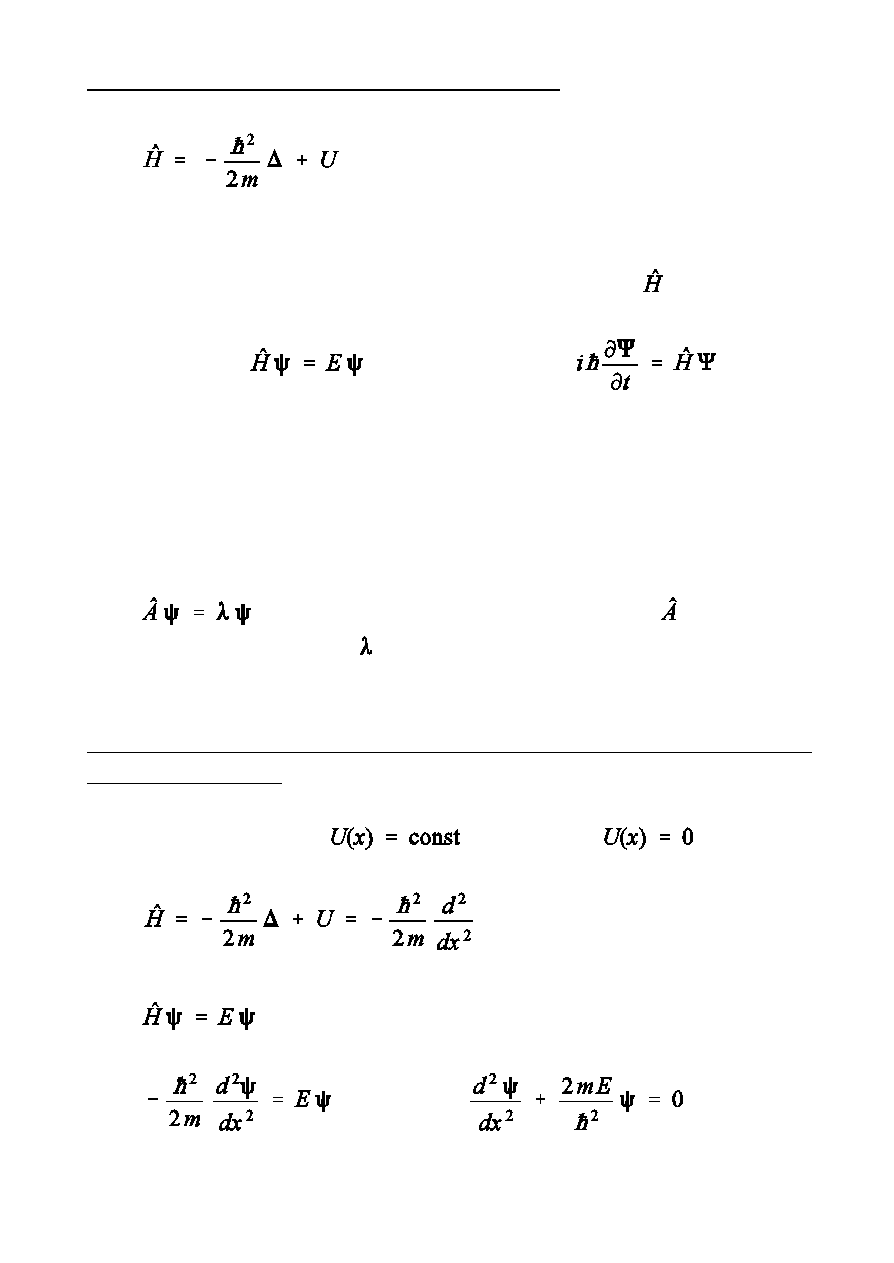
Mechanika kwantowa 10

Równanie Schrödingera w zapisie operatorowym

operator energii ca»kowitej, operator

Hamiltona, hamiltonian

Postaƒ równania Schrödingera z uóyciem operatora

bez czasu

z czasem

Zagadnienie w»asne

R

funkcja w»asna operatora

wartoу w»asna

Rozwizanie równania Schrödingera dla przypadku nieograniczonego ruchu
czstki wzd»uó osi x

W tym przypadku

. Przyjmijmy

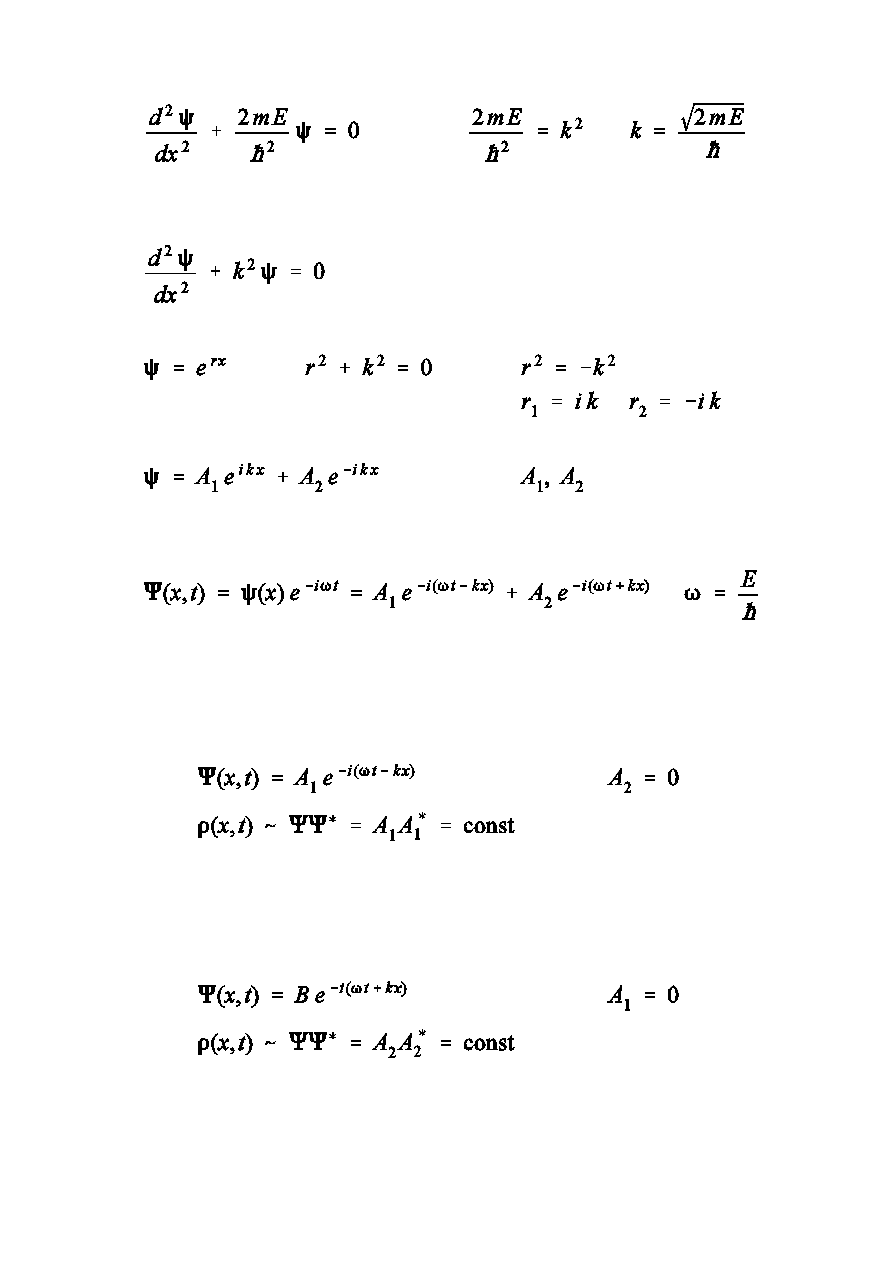
Mechanika kwantowa 11

- sta»e

Dla czstki poruszajcej si“ w dodatnim kierunku osi x

(przyjmujemy

)

Dla czstki poruszajcej si“ w ujemnym kierunku osi x

(przyjmujemy

)