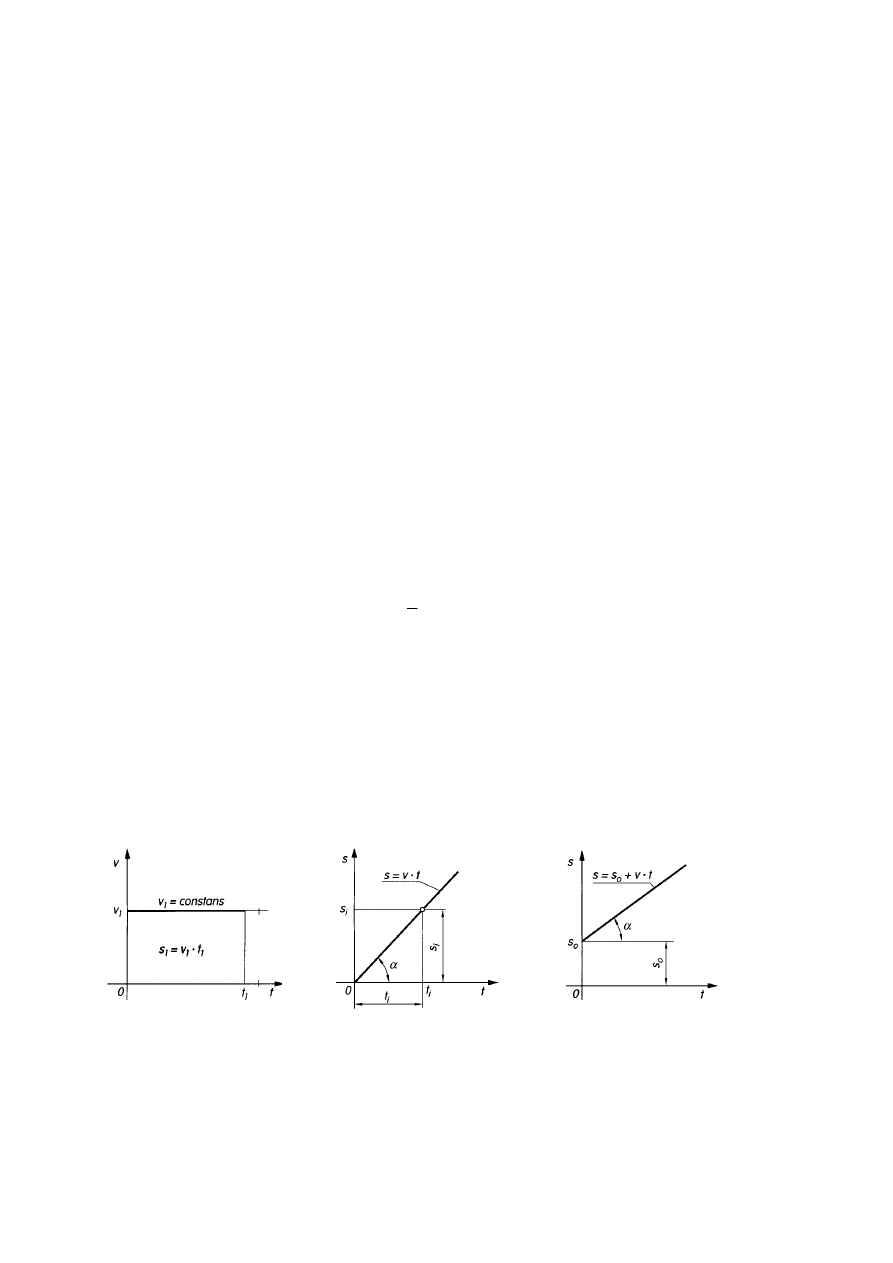
Kinematyka i dynamika punktu i ciała sztywnego

Materiał nauczania

Kinematyka jest działem mechaniki zajmującym się badaniem ruchu ciał bez

uwzględniania przyczyn, które ten ruch wywołują. Ruchem nazywamy zmianę położenia
ciała względem innego ciała, które traktowane jest jako układ odniesienia. Ze względu układ
odniesienia ruch dzielimy na:

−−−−

ruch bezwzględny; jest to ruch określony w ruchomym układzie odniesienia,

−−−−

ruch względny; jest to ruch określony względem ruchomego układu odniesienia.

Ruch punktu możemy określić równaniem prędkości:

v

=

( )

t

f

i równaniem ruchu:

s

=

( )

t

f

Ze względu kształt toru ruch można podzielić na:

−−−−

prostoliniowy

−

torem jest linia prosta,

−−−−

krzywoliniowy

−

torem jest dowolna linia na geometryczna na płaszczyźnie (ruch płaski)

lub w przestrzeni (ruch przestrzenny).

Ruch prostoliniowy jednostajny

W ruchu prostoliniowym jednostajnym stosunek drogi do czasu, w którym ta droga

została przebyta, nazywamy prędkością. Prędkość ma wartość stałą

v

=

t

s

= const [m/s]

Droga w ruchu jest proporcjonalna do czasu trwania ruchu.

s

=

t

v

⋅

równanie ruchu prostoliniowego jednostajnego

Wykresem prędkości w ruchu jednostajnym jest odcinek równoległy do osi czasu, a pole

zawarte pod wykresem prędkości przedstawia w odpowiedniej podziałce drogę. Graficznym
odwzorowaniem drogi jest linia prosta nachylona do osi t pod kątem

α

. Wartość kąta

α

przedstawia zależność

tg

α

=

v

=const

Jeżeli czas jest liczony od chwili, w której punkt przebył już drogę

o

s , to całkowita droga

wynosi

s

=

o

s +

t

v

⋅

a)

b)

Rys. 1. Wykresy: a) prędkości, b) drogi

Ruch prostoliniowy zmienny

Prędkość punktu zmienia się. Jeżeli prędkość rośnie, to mamy do czynienia z ruchem

przyspieszonym, a gdy maleje z ruchem opóźnionym.

Stosunek przyrostu drogi do przyrostu czasu nazywamy prędkością średnią punktu.

v

=

t

s

∆

∆

=

1

2

1

2

t

t

s

s

−

−

Prędkością chwilową nazywamy granicę wyrażenia

t

s

∆

∆

, jeżeli przyrost t

∆

dąży do zera.

v

=lim

t

s

∆

∆

, gdy t

∆

→

0

Dla określenia przyspieszenia wyznaczamy przyrosty prędkości.
Przyspieszeniem średnim nazywamy stosunek przyrostu prędkości do czasu, w którym ten
przyrost nastąpił.

a

=

t

v

∆

∆

=

1

2

1

2

t

t

v

v

−

−

[m/s

2

]

Przyspieszenie chwilowe określa zależność

a

=lim

t

v

∆

∆

, gdy t

∆

→

0

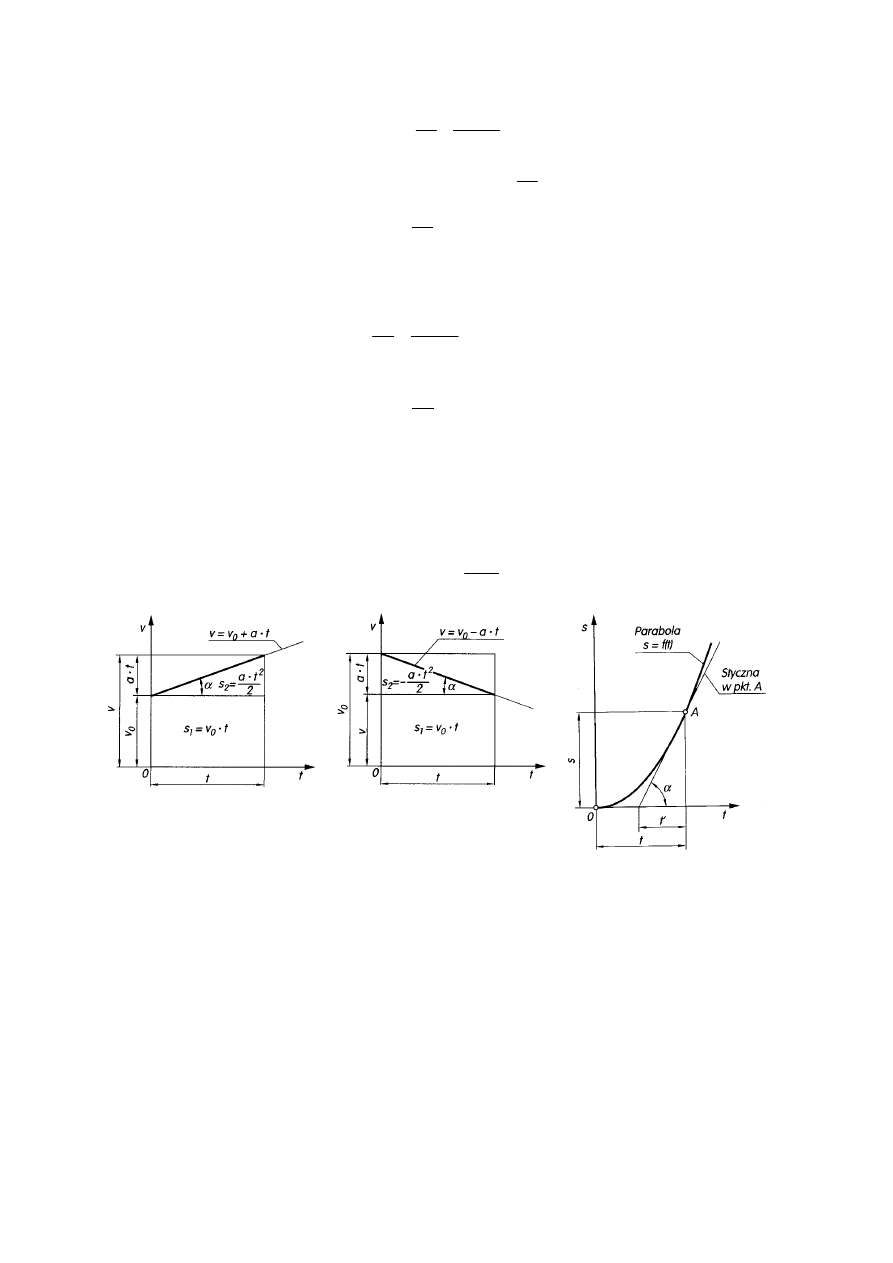
Równanie prędkości ruchu jednostajnie zmiennego przyspieszonego

t

a

v

v

o

⋅

+

=

Równanie prędkości ruchu jednostajnie zmiennego opóźnionego

t

a

v

v

o

⋅

−

=

Równanie drogi

2

2

t

a

t

v

s

o

⋅

±

⋅

=

a)

b)

Rys. 2. Wykresy: a) prędkości, b) drogi

Ruch krzywoliniowy jednostajny

Torem takiego ruchu jest linia krzywa, do której styczne są wektory prędkości o równych

wartościach.
Miejsce geometryczne wektorów prędkości wykreślonych ze wspólnego punktu nazywamy
hodografem prędkości. Hodograf w ruchu krzywoliniowym jednostajnym jest łukiem okręgu
o promieniu równym wartości prędkości poruszającego się punktu.

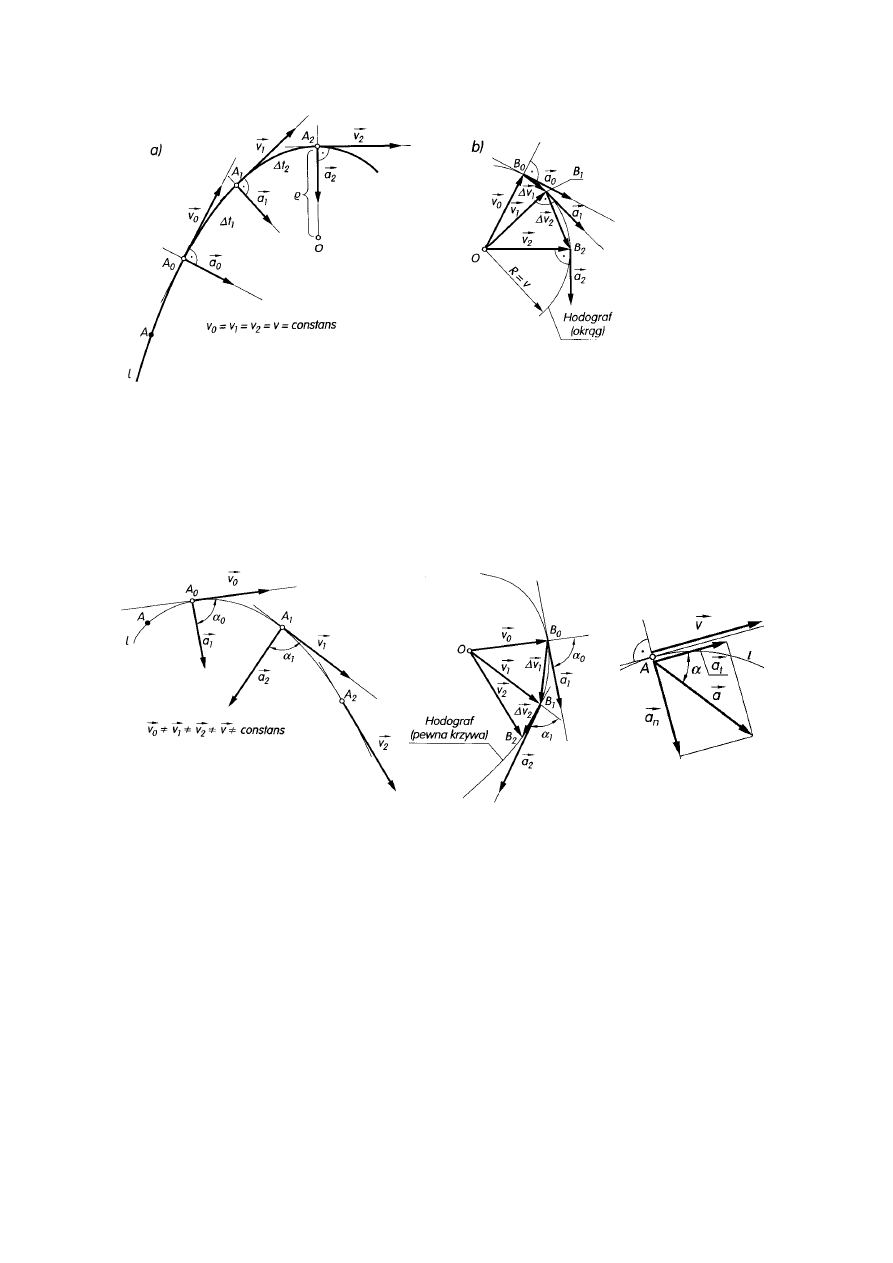
Rys. 3. Ruch krzywoliniowy jednostajny: a) wektory prędkości, b) hodograf prędkości

Przyspieszenie chwilowe ma kierunek prostopadły (normalny) do prędkości

poruszającego się punktu. Przyspieszenie związane ze zmianą kierunku wektora prędkości
nazywa się przyspieszeniem normalnym.

Ruch krzywoliniowy zmienny

Wektory prędkości w tym ruchu zmieniają kierunek i wartość.

a)

b)

c)

Rys. 4. Ruch krzywoliniowy zmienny: a) wektory prędkości, b) hodograf prędkości, c) przyspieszenie

Przyspieszenie w ruchu krzywoliniowym zmiennym tworzy z wektorem prędkości kąt

α

.

Po rozłożeniu przyspieszenia na dwa kierunki otrzymujemy przyspieszenie:

−−−−

normalne (dośrodkowe)

n

a

, o kierunku prostopadłym do toru i wartości

n

a

=

α

sin

⋅

a

,

−−−−

styczne

t

a , o kierunku prędkości i wartości

t

a =

α

cos

⋅

a

.

Na podstawie kierunków i wartości składowych przyspieszenia

n

a i

t

a można ustalić

klasyfikację ruchów:

n

a

≠

0

t

a

≠

0

−−−−

ruch krzywoliniowy zmienny

n

a =0

t

a

≠

0

−−−−

ruch prostoliniowy zmienny

n

a

≠

0

t

a =0

−−−−

ruch krzywoliniowy jednostajny

n

a =0

t

a =0

−−−−

ruch prostoliniowy jednostajny

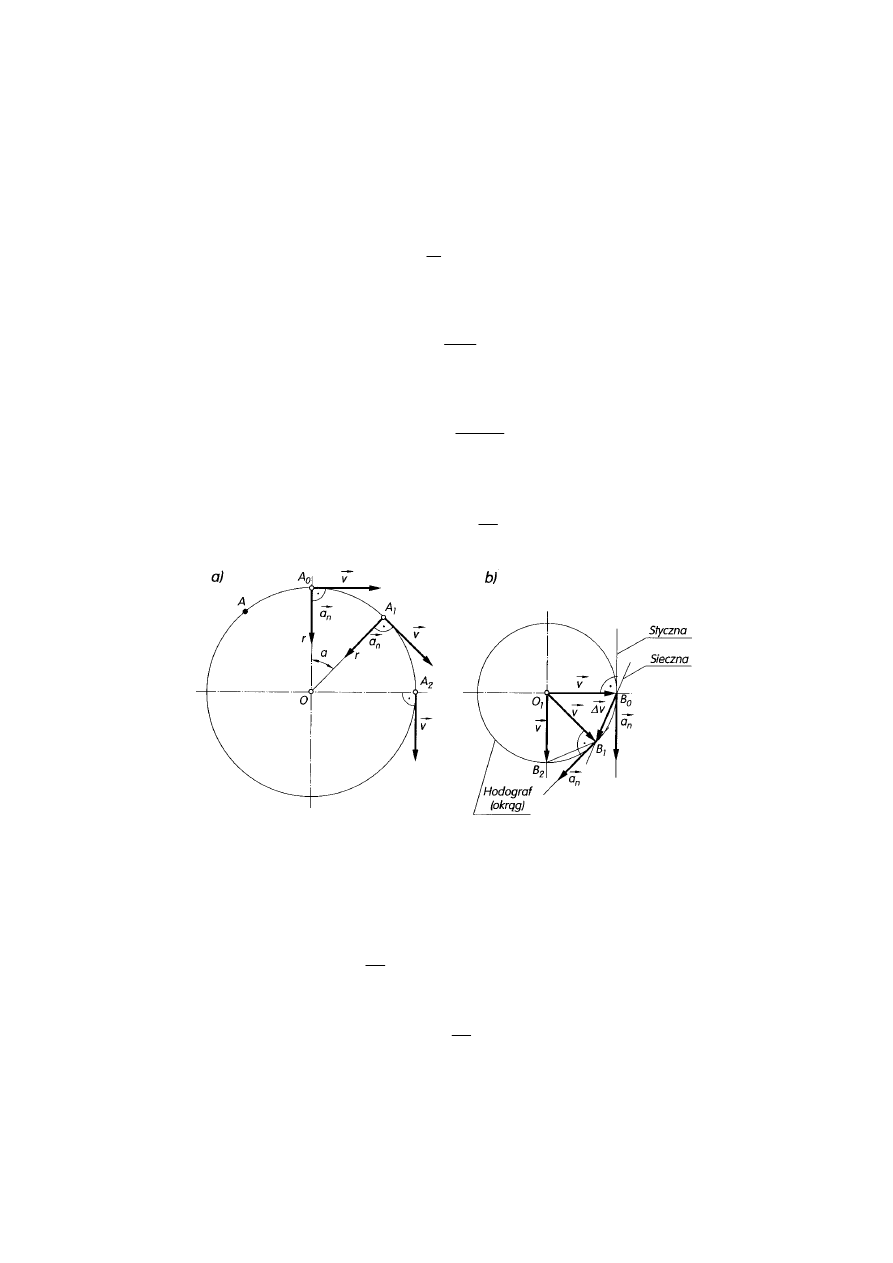
Ruch jednostajny po okręgu

W czasie ruchu po okręgu o promieniu

r punkt materialny przebywa w równych

odstępach czasu równe drogi oraz zatacza równe kąty

α

. Prędkość punktu poruszającego się

po okręgu nazywamy prędkością liniową lub obwodową.
Stosunek drogi kątowej

α

do czasu, w którym ta droga została przebyta, nazywamy

prędkością kątową

ω

.

ω

=

t

α

[rad/s]

Często prędkość kątową uzależniamy od ilości obrotów na minutę, wielkość tę nazywamy
prędkością obrotową.

ω

=

30

n

⋅

π

Prędkość liniowa

v

w ruchu jednostajnym po okręgu jest stała, równa iloczynowi prędkości

kątowej

ω

i promienia r .

v

=

r

⋅

ω

=

30

r

n

⋅

⋅

π

W ruchu jednostajnym po okręgu wartość przyspieszenia stycznego jest równa zeru,
a przyspieszenie normalne obliczamy ze wzorów

n

a

=

r

⋅

2

ω

=

r

v

2

Rys. 5. Ruch punktu po okręgu: a) prędkość i przyspieszenie, b) hodograf prędkości

Ruch zmienny po okręgu koła

W ruchu zmiennym po okręgu koła występuje przyspieszenie normalne i styczne do toru.

Wielkością charakteryzującą ten ruch jest przyspieszenie kątowe, które jest stosunkiem
przyrostu prędkości kątowej do przedziału czasu, gdy ten dąży do zera.

ε

=lim

t

∆

ω

, gdy

0

→

∆

t

[rad/s

2

]

Przyspieszenie normalne

n

a

=

r

v

2

Przyspieszenie styczne

t

a

=

ε

⋅

r

,

gdzie r

−

promień koła.

Ciała sztywne mogą poruszać się ruchem:

−−−−

postępowym,

−−−−

obrotowym,

−−−−

płaskim.

W ruchu postępowym punkty ciała sztywnego zakreślają jednakowe tory, na których

wszystkie punkty mają jednakową prędkość i przyspieszenie.

W ruchu obrotowym ciała sztywnego punkty wykonują ruch dookoła prostej, zwanej osią

obrotu. Jeżeli prędkość kątowa jest wielkością stałą ruch nazywa się ruchem obrotowym
jednostajnym, a jeżeli zmienną ruchem obrotowym zmiennym.

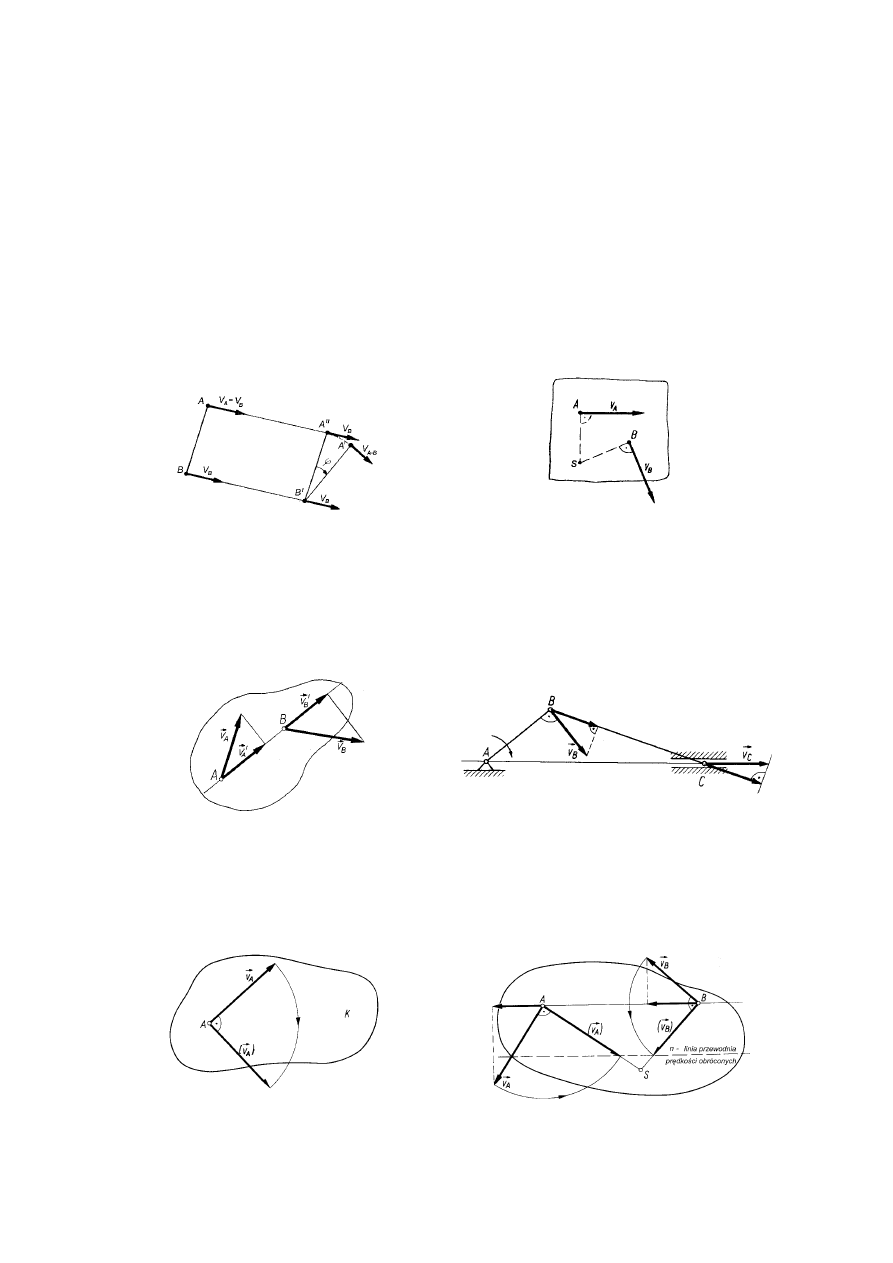
Ruch płaski ciała sztywnego może być rozpatrywany jako suma dwóch ruchów:

postępowego z prędkością dowolnego punktu ciała i obrotowego dookoła tego punktu
z prędkością kątową lub może być w każdej chwili ruchem obrotowym dookoła chwilowego
ś

rodka obrotu (S

−

środek chwilowego obrotu jest punktem przecięcia normalnych do

wektorów prędkości).

a)

b)

A

B

B

A

V

V

V

−

+

=

r

r

r

Rys. 6. Ruch płaski bryły: a) suma ruchu postępowego i obrotowego, b) ruch obrotowy względem środka

chwilowego obrotu

Prędkość punktów w ruchu płaskim możemy wyznaczyć kilkoma metodami:

−−−−

z wykorzystaniem twierdzenia o rzutach prędkości:

Rzuty prędkości dwu punktów ciała sztywnego, poruszającego się ruchem płaskim, na

prostą łączącą te punkty są sobie równe.

Rys. 7. Rzuty prędkości i zastosowanie twierdzenia o rzutach prędkości

−−−−

metodą prędkości obróconych:
Linie działania prędkości obróconych wszystkich punktów poruszającego się przekroju

przecinają się w chwilowym środku obrotu S. Końce wektorów prędkości obróconych leżą na
prostej równoległej do prostej łączącej te punkty zwaną linią przewodnią prędkości
obróconych.

Rys. 8. Prędkość obrócona i linia przewodnia prędkości obróconych

−−−−

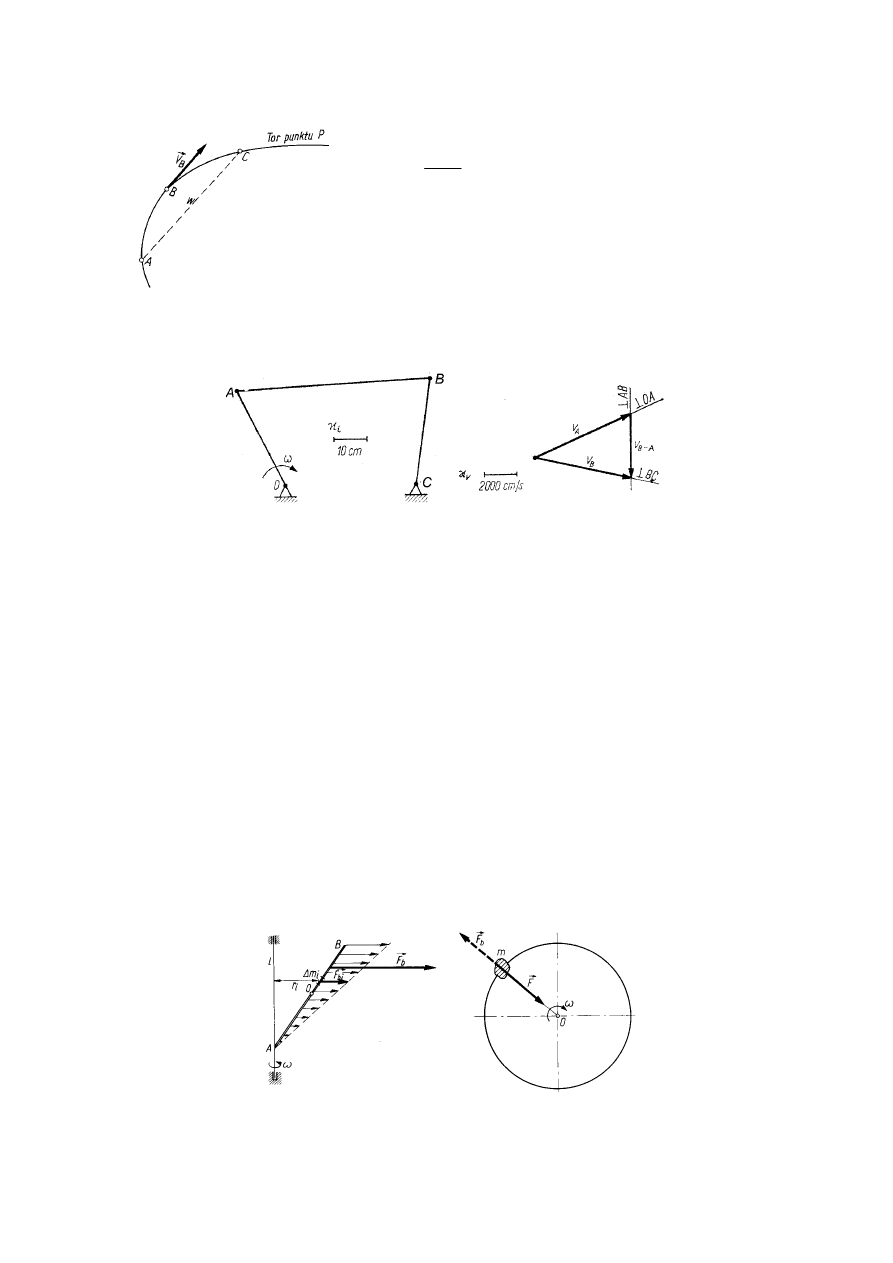
metodą toru ocechowanego:

Prędkość w punkcie B:

t

w

k

v

B

∆

⋅

⋅

=

2

gdzie:

B

v

−

Prędkość w punkcie B w cm/s

w

−

długość siecznej, w cm

t

∆

−

czas, w jakim punkt przebywa drogę między sąsiednimi

punktami, w s,

k

−

podziałka długości

Rys. 9. Wyznaczanie prędkości metodą toru ocechowanego

−−−−

metodą planu prędkości:

Rys. 10. Wyznaczanie prędkości w czworoboku przegubowym metodą planu

W metodzie tej na podstawie równania wektorowego

A

B

A

B

v

v

v

−

+

=

r

r

r

wyznacza się wykreślnie wartości i kierunki prędkości

B

v

i prędkości względnej

A

B

v

−

.

Dynamika bada związki między ruchem ciała i przyczynami, który ten ruch wywołują.

Oparta jest na trzech prawach Newtona.

Pierwsze prawo ( prawo bezwładności): Punkt materialny lub ciało sztywne, na który nie

działa żadna siła, lub działają siły równoważące się, pozostaje w spoczynku lub w ruchu
jednostajnym prostoliniowym.

Drugie prawo: Przyspieszenie punktu materialnego lub ciała sztywnego jest

proporcjonalne do wartości siły działającej na ten punkt i ma kierunek oraz zwrot zgodnie
z działającą siłą

F

=

a

m

⋅

(dynamiczne równanie ruchu punktu)

Trzecie prawo: Każdemu działaniu towarzyszy równe, lecz przeciwnie zwrócone

przeciwdziałanie.
Z drugim prawem związana jest siła bezładności, która jest zwrócona przeciwnie niż
przyspieszenie ruchu.

a)

b)

Rys. 11. Siły bezwładności w ruchu obrotowym: a) pręta, b) punktu

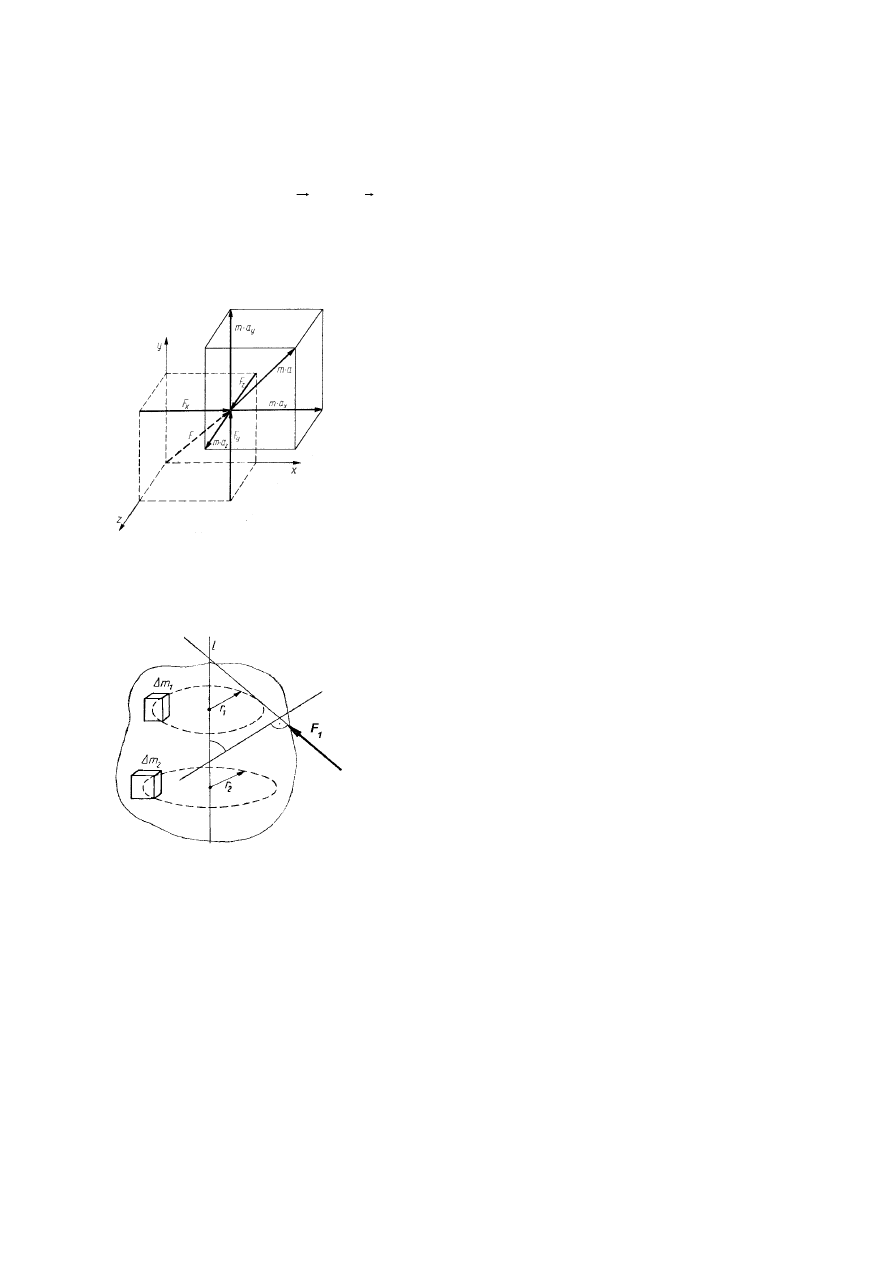
Siła bezwładności jest równa iloczynowi masy poruszającego się ciała i przyspieszenia tego
ruchu.
Suma wszystkich sił zewnętrznych działających na punkt materialny znajdujący się w ruchu
równoważy się w każdej chwili z siłą bezwładności tego punktu.

F

+

( )

a

m

⋅

−

=0

zasada D

′

Alemberta

W ruchu postępowym badanie ruchu sprowadza się do badania jednego punktu, przy czym
najczęściej punkt ten jest środkiem masy ciała. Siła F działająca na środek masy ciała
w przestrzennym prostokątnym układzie osi współrzędnych ,

x y

, z rozłożona może być na

trzy składowe, które wywołują ruch wzdłuż tych osi.

Dynamiczne równania ruchu postępowego

x

x

a

m

F

⋅

=

y

y

a

m

F

⋅

=

z

z

a

m

F

⋅

=

Rys. 12. Ruch postępowy i równanie dynamiczne ruchu

W uchu obrotowym ciała sztywnego dookoła nieruchomej osi wyznaczmy dynamiczne
równanie ruchu dla każdej elementarnej masy z uwzględnieniem elementarnego momentu
obrotowego.

Dynamiczne równania ruchu obrotowego dla
elementarnej masy

i

i

i

a

m

F

⋅

∆

=

Elementarny moment obrotowy

⋅

∆

=

⋅

i

i

i

m

r

F

2

i

r

ε

⋅

Dynamiczne równanie ruchu obrotowego ciała
sztywnego

ε

⋅

=

J

M

M

−

moment bezwładności ciała

J

−

masowy moment bezwładności ciała

ε

−

przyspieszenie kątowe

Rys. 13. Ruch obrotowy i równanie dynamiczne ruchu obrotowego

Masowe momenty bezwładności pól o prostych figurach i brył geometrycznych

wyznacza się najczęściej względem osi przechodzącej przez środek masy (osie główne lub
ś

rodkowe) korzystając ze wzorów z tabel.

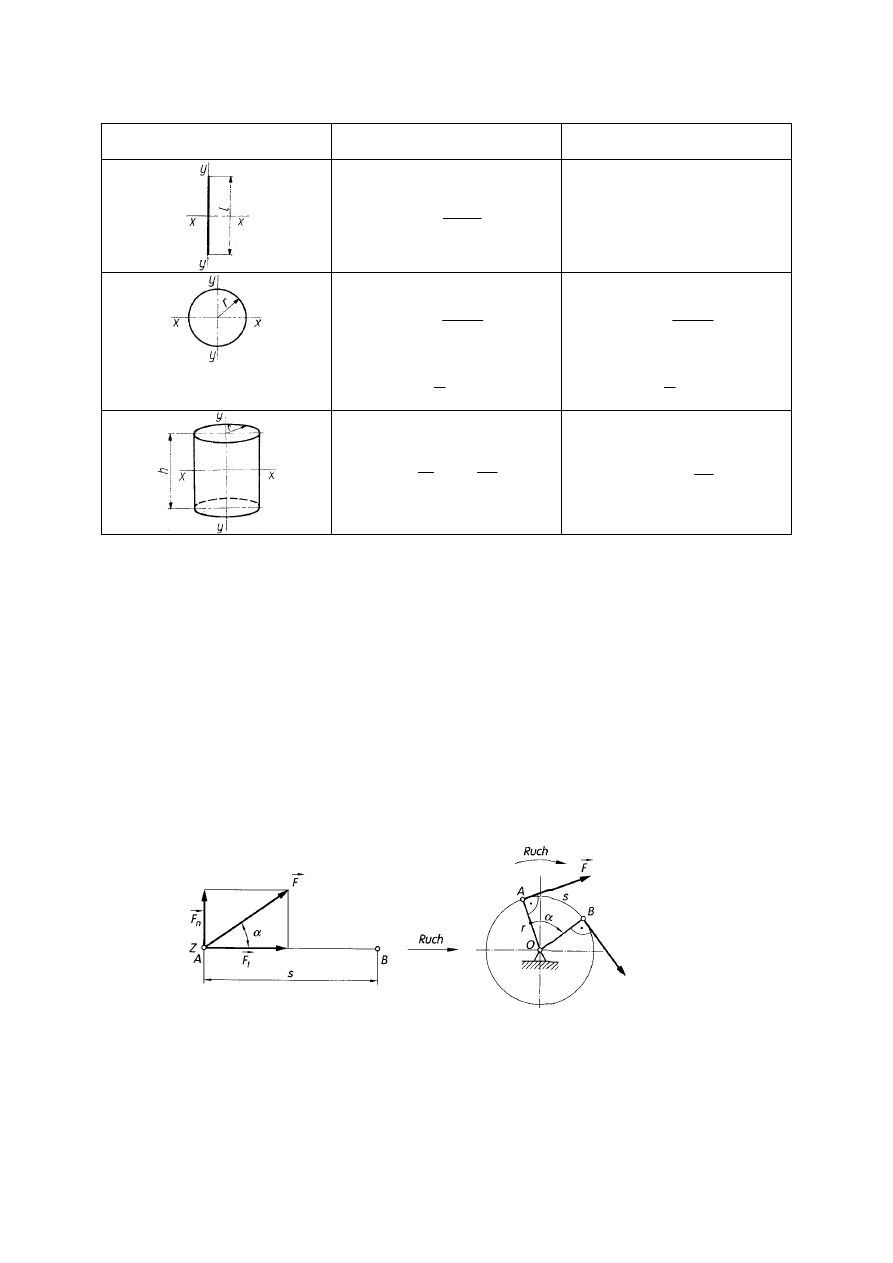
Tabela 1. Masowe momenty bezwładności prostych figur i brył geometrycznych

Rysunek figury

(bryły)

x

J

y

J

x

J =

12

2

l

m

⋅

y

J =0

koło

x

J =

4

2

r

m

⋅

kula

x

J =

2

5

2

r

m

⋅

⋅

y

J =

4

2

r

m

⋅

y

J =

2

5

2

r

m

⋅

⋅

x

J =













+

3

4

2

2

h

r

m

y

J =

2

2

r

m

⋅

Gdy oś obrotu jest przesunięta równolegle do osi głównej masowy moment bezwładności

oblicza się korzystając z twierdzenia Steinera.

2

z

m

J

J

o

l

⋅

+

=

Moment bezwładności ciała sztywnego względem dowolnej osi jest równy sumie

momentu bezwładności

o

J względem osi równoległej do prostej l i przechodzącej przez

ś

rodek masy oraz iloczynu masy i ciała i kwadratu odległości między nimi.

Z ruchomym punktem, który pod działaniem siły może się przesuwać wzdłuż

określonego toru, związana jest praca.

Praca mechaniczna w ruchu prostoliniowym jest równa iloczynowi siły działającej

wzdłuż kierunku ruchu i drogi, jaką przebył punkt zaczepienia tej siły.

Praca w ruchu obrotowym wyraża się iloczynem momentu obrotowego M oraz kąta

obrotu

α

wyrażonego w radianach.

a)

b)

s

F

W

⋅

=

α

cos

⋅

[1J = N

⋅

1m]

α

⋅

=

M

W

Rys. 14. Praca w ruchu: a) prostoliniowym, b) obrotowym

Jednostką pracy w układzie jednostek SI jest dżul (J). Jest to praca wykonana siłą jednego
niutona na drodze jednego metra.
Do oceny pracy zostało wprowadzone pojęcie mocy.

Moc P jest to iloraz pracy i czasu, w którym ta praca została wykonana.

t

W

P

=

[W], 1W=

s

J

1

v

F

P

⋅

=

w ruchu prostoliniowym

α

⋅

=

M

P

w ruchu obrotowym.

Jednostką mocy w układzie jednostek SI jest wat (W), czyli praca jednego dżula

wykonana w czasie jednej sekundy.
W urządzeniach mechanicznych moment obrotowy (skręcający) oblicza się ze wzoru:

=

M

95514, 14

n

P

⋅

[N

⋅

m]

P

−

moc w kW

n

−

prędkość obrotowa w obr/min.

Sprawnością maszyny

η

nazywamy stosunek pracy użytecznej

u

W do pracy włożonej W .

W

W

u

=

η

lub

W

W

u

=

η

⋅

100%

Sprawność można również określić stosunkiem mocy użytecznej

u

P do mocy włożonej P .

p

P

u

=

η

Jeżeli maszyna składa się z kilku mechanizmów, to sprawność ogólna jest iloczynem

sprawności poszczególnych mechanizmów.

n

η

η

η

η

η

⋅

⋅

⋅

⋅

=

K

3

2

1

Sprawność jest liczbą niemianowaną zawartą w przedziale

1

0

<

<

η

.